11.2015-2016第2学期初2年级数学期末考试题-石景山
2016年石景山初三数学二模试题及答案(word版)

石景山区2016年初三综合练习数 学 试 卷学校 姓名 准考证号下面各题均有四个选项,其中只有一个..是符合题意的. 1.据有关部门数据统计,2015年中国新能源汽车销量超过33万辆,创历史新高.数据“33万”用科学记数法表示为A .43310⨯B .43.310⨯C .53.310⨯D .60.3310⨯2.下列计算正确的是A .632a a a =⋅B .()222b a ab = C .()532a a =D .42232a a a =+3.如图,数轴上有四个点M ,P ,N ,Q ,若点M ,N 表示的数互为相反数,则 图中表示绝对值最大的数对应的点是 A .点M B .点N C .点P D .点Q 4.若312--x x 在实数范围内有意义,则x 的取值范围是 A .3≠x B .21>x 且3≠x C .2≥x D .21≥x 且3≠x 5.从长度分别是2,3,4的三条线段中随机抽出一条,与长为1,3的两条线段首尾顺次相接,能构成三角形的概率是 A .1 B .32 C .31D .0 6.将代数式2105x x -+配方后,发现它的最小值为A .30-B .20-C .5-D .07.《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x 人,物品价格为y 钱,可列方程组为A .⎩⎨⎧=+=-y x y x 4738B .⎩⎨⎧=-=+y x y x 4738 C .⎩⎨⎧=-=-4738x y x y D .⎩⎨⎧=-=-4738y x y x PMNQ8.如图,若AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =58°,则∠BCD 的度数为A .32°B .58°C .64°D .116° 9.如图,为了估计河的宽度,在河的对岸选定一个目标 点A ,在近岸取点B ,C ,D ,E ,使点A ,B ,D 在一 条直线上,且AD ⊥DE ,点A ,C ,E 也在一条直线上 且DE ∥BC .如果BC=24m ,BD=12m ,DE=40m ,则 河的宽度AB 约为 A .20mB .18mC .28mD .30m10.如图1,在等边△ABC 中,点D 是BC 边的中点,点P 为AB 边上的一个动点,设AP =x ,图1中线段DP 的长为y ,若表示y 与x 的函数关系的图象如图2所示,则等边△ABC 的面积为A .4B .C .12D .二、填空题(本题共18分,每小题3分)11.分解因式:2484x x -+= .12.某班学生分组做抛掷瓶盖实验,各组实验结果如下表:根据表中的信息,估计掷一枚这样的瓶盖,落地后盖面朝上的概率为 . (精确到0.01)13.写出一个函数,满足当x>0时,y 随x 的增大而减小且图象过(1,3),则这个函数的表达式为 .14.甲、乙两名队员在5次射击测试中,成绩如下表所示:若需要你根据两名队员的5次成绩,选择一名队员参加比赛,你会选择队员 ,选择的理由是 .ECDB A PCBA图1 图2第14题图 第15题图15.如图为44⨯的正方形网格,图中的线段均为格点线段(线段的端点为格点),则12345∠+∠+∠+∠+∠的度数为 .16.为预防“手足口病”,某学校对教室进行“药熏消毒”.消毒期间,室内每立方米空气中的含药量y (mg)与时间x (分钟)的函数关系如图所示.已知,药物燃 烧阶段,y 与x 成正比例,燃完后y 与x 成 反比例.现测得药物10分钟燃完,此时教 室内每立方米空气含药量为8mg .当每立方 米空气中含药量低于1.6mg 时,对人体才能 无毒害作用.那么从消毒开始,经过 分钟后教室内的空气才能达到安全要求.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分)解答应写出文字说明,演算步骤或证明过程.17113tan303-⎛⎫+-︒ ⎪⎝⎭.18.已知0142=++x x ,求代数式()()71212++--x x x 的值.19.解方程:221111x x x x --=--. 20.如图,在Rt △ABC 中,∠ABC=90°,点D 在边AB 上,且DB =BC ,过点D 作EF ⊥AC于E ,交CB 的延长线于点F .求证:AB=BF .21.在平面直角坐标系xOy 中,一次函数12y x b =+的图象与y 轴交于点A ,与反比例函数8y x=的图象交于点P (2,m ). (1)求m 与b 的值;成绩/环 五次射击测试成绩54321y(2)取OP 的中点B ,若△MPO 与△AOP 关于点B 中心对称,求点M 的坐标.22.为了促进旅游业的发展,某市新建一座景观桥.桥的拱肋ADB 可视为抛物线的一部分,桥面AB 可视为水平线段,桥面与拱肋用垂直于桥面的杆状景观灯连接,拱肋的跨度AB 为40米,桥拱的最大高度CD 为16米(不考虑灯杆和拱肋的粗细),求与CD 的距离为5米的景观灯杆MN 的高度.23.如图,CD 垂直平分AB 于点D ,连接CA ,CB ,将BC 沿BA 的方向平移,得到线段DE ,交AC 于点O ,连接EA ,EC . (1)求证:四边形ADCE 是矩形; (2)若CD =1,AD =2,求sin ∠COD 的值.24.阅读下面材料:当前,中国互联网产业发展迅速,互联网教育市场增长率位居全行业前列.以下是根据某媒体发布的2012 2015年互联网教育市场规模的相关数据,绘制的统计图表的一部分.(1)2015年互联网教育市场规模约是亿元(结果精确到1亿元),并补全条形 统计图;(2)截至2015年底,约有5亿网民使用互联网进行学习,互联网学习用户的年龄分布 如右图所示,请你补全扇形统计图,并估年份年增长率/%年份市场规模/亿元OECDBA学习用户分布图截至2015年底互联网36-55其他GHEFB CD A 计7-17岁年龄段有 亿网民通过互联 网进行学习;(3)根据以上材料,写出你的思考、感受或建议(一条即可).25.如图,在Rt △ACB 中,∠C =90°,D 是AB 上一点,以BD 为直径的⊙O 切AC 于点E ,交BC 于点F ,连接DF . (1)求证:DF=2CE ;(2)若BC =3,sin B =54,求线段BF 的长.26.阅读下面材料:小骏遇到这样一个问题:画一个和已知 矩形ABCD 面积相等的正方形.小骏发现:延长AD 到E ,使得DE =CD ,以AE 为直径作半圆,过点D 作AE 的垂线, 交半圆于点F ,以DF 为边作正方形DFGH , 则正方形DFGH 即为所求. 请回答:AD ,CD 和DF 的数量关系为 . 参考小骏思考问题的方法,解决问题:画一个和已知□ABCD 面积相等的正方形,并写出画图的简要步骤.27.已知关于x 的方程()021222=-+-+m m x m x .(1) 求证:无论m 取何值时,方程总有两个不相等的实数根;(2) 抛物线()m m x m x y 21222-+-+=与x 轴交于()0,1x A ,()0,2x B 两点,且210x x <<,抛物线的顶点为C ,求△ABC 的面积;(3) 在(2)的条件下,若m 是整数,记抛物线在点B ,C 之间的部分为图象G (包含B ,C 两点),点D 是图象G 上的一个动点,点P 是直线b x y +=2上的一个动点,若线段DP 的最小值是55,请直接写出b 的值.BB CDA28.如图,正方形ABCD ,G 为BC 延长线上一点,E 为射线BC 上一点,连接AE . (1)若E 为BC 的中点,将线段EA 绕着点E 顺时针旋转90°,得到线段EF ,连接CF .①请补全图形;②求证:∠DCF =∠FCG ;(2)若点E 在BC 的延长线上,过点E 作AE 的垂线交∠DCG 的平分线于点M ,判断AE 与EM 的数量关系并证明你的结论.29.在平面直角坐标系xOy 中,对图形W 给出如下定义:若图形W 上的所有点都在以原点为顶点的角的内部或边界上,在所有满足条件的角中,其度数的最小值称为图形的坐标角度,例如,下图中的矩形ABCD 的坐标角度是90°.(1)已知点)3,0(-A ,)1,1(--B ,在点)0,2(C ,)0,1(-D ,)2,2(-E 中,选一点,使得以该点及点A ,B 为顶点的三角形的坐标角度为90°,则满足条件的点为 ;(2)将函数2ax y =)31(≤≤a 的图象在直线1=y 下方的部分沿直线1=y 向上翻折,求所得图形坐标角度m 的取值范围;(3)记某个圆的半径为r ,圆心到原点的距离为l ,且)1(3-=r l ,若该圆的坐标角度︒≤≤︒9060m .直接写出满足条件的r 的取值范围.石景山区2016年初三综合练习E GD C BAMAB C DGE数学答案及评分参考阅卷须知:为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分,解答右端所注分数,表示考生正确做到这一步应得的累加分数.一、选择题(本题共30分,每小题3分)二、填空题(本题共18分,每小题3分) 11.()241x -;12.0.53;13.如3y x=,答案不唯一; 14.选择队员甲,理由:甲乙成绩的平均数相同,甲的成绩比乙的成绩稳定; 15.225︒;16.50.三、解答题(本题共72分,第17-26题,每小题5分,第27题7分,第28题7分,第29题8分) 17.解:原式=233-………………………………………………4分 =5-…………………………………………………………5分18.解:原式=2221227x x x x -+--+ ………………………………………2分 =248x x --+.……………………………………………………3分 2410x x ++=∴241x x +=- .……………………………………………………… 4分∴原式=()248x x -++189.=+= ………………………………………………………5分 19. 解:去分母得:2(1)(21)1x x x x +--=-…………………………………1分 解得:2x =………………………………………………………………4分经检验,2x =是原方程的解……………………………………………5分 ∴原方程的解为2x =20.证明:∵EF ⊥AC ,∴∠A +∠ADE =90°.∵∠ABC =90°,∴∠F +∠FDB =90°,∠DBF ∴∠A =∠F ………………………………1分在△ABC 和△FBD 中A FABC FBD BC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△FBD ………………………………4分∴AB =BF .………………………………………5分 21.解:(1)∵12y x b =+与8y x =交于点P (2,m ),∴4m =,3b =.………………………………………………………2分(2)法一:由中心对称可知,四边形OAPM 是平行四边形 ∴OM ∥AP 且OM =AP∵一次函数12y x b =+的图象与y 轴交于点A (0,3)(2,4),(0,0)A P O ∴∴由平移规律可得点A 关于点B 对称点M 的坐标为(2,1).………5分 法二:∵一次函数12y x b =+的图象与y 轴交于点A ∴(0,3)A . ∵B 为OP 的中点∴(1,2)B .∴点A 关于点B 对称点M 的坐标为(2,1).………………5分22.解:如图建立坐标系………………………………………………………………1分设抛物线表达式为216y ax =+分 由题意可知,B 的坐标为(20,0) ∴400160a +=∴125a =-∴211625y x =-+…………………………………………………………………4分 ∴当5x =时,15y =答:与CD 距离为5米的景观灯杆MN 的高度为15米.………………………5分23.(1)证明:由已知得BD //CE ,BD =CE . ∵CD 垂直平分AB ,∴AD =BD ,∠CDA =90°.∴AD //CE ,AD =CE .∴四边形ADCE 是平行四边形.…………………………………1分 ∴平行四边形ADCE 是矩形. …………………………………2分(2) 解:过D 作DF ⊥AC 于F ,OEC D BA在Rt △ADC 中,∠CDA =90°,∵CD =1,AD =2, 由勾股定理可得:AC∵O 为AC 中点,∴OD…………………………………3分 ∵AC DF AD DC ⋅=⋅,∴DF. ………………………4分 在Rt △ODF 中,∠OFD =90°,∴sin ∠COD =DF OD =45………5分 24.(1)1610,并补全图形; ……………………………………………………2分 (2)1.6; ………………………………………………………………………4分 (3)略.…………………………………………………………………………5分 25.(1)证明:连接OE 交DF 于G ,∵AC 切⊙O 于E ,∴∠CEO =90°. 又∵BD 为⊙O 的直径,∴∠DFC =∠∵∠C =90°,∴四边形CEGF ∴CE =GF ,∠EGF =90°∴DF =2CE .(2)解:在Rt △ABC 中,∠C =90°,∵BC =3,4sin 5B =,∴AB =5.…………………………………3分设OE =x ,∵OE //BC ,∴△AOE ∽△ABC . ∴OE AO BC AB =,∴535x x -=,∴158x =.………………………4分 ∴BD =154. 在Rt △BDF 中,∠DFB =90°,∴BF =94…………………………5分 26.解:2DF AD CD =⋅………………………………………………………………1分解决问题:法一:过点A 作AM ⊥BC 于点M ,延长AD 到E ,使得DE =AM ,以AE 为直径作半圆,过点 D 作AE 垂线,交半圆于点F ,以DF 为边 作正方形DFGH ,正方形DFGH 即为所求.……………………………………………………………………………………5分法二:如图,过点A 作AM ⊥BC 于点M ,过点D 作DN ⊥BC 交BC 延长线于点N ,将平行四边形 转化为等面积矩形,后同小骏的画法.……………………………………………………………………………………5分 说明:画图2分,步骤2分.27.解:(1)∵1=a ,()12-=m b ,m m c 22-=∴()()0424144222>=---=-=∆m m m ac b∴无论m 取任何实数时,方程总有两个不相等的实数根. ……2分 (2)令,则()021222=-+-+m m x m x ()()02=-++m x m x ∴m x -=或2+-=m x ∵210x x <<∴m x -=1,22+-=m x …………………………………………4分 ∴2=AB当1+-=m x 时,1-=y ∴1-=c y∴121=⨯=∆c ABC y AB S .………………………………………5分 (3) 0=b 或3-=b . …………………………………………………….. 7分28.(1)①补全图形,如图所示.…………………………………..1分②法一:证明:过F 作FH ⊥BG 于H ,连接EH ……..2分F EG DC B ADA/ 12 由已知得AE ⊥EF ,AE =EF .在正方形ABCD 中,∵∠B =∠AEF=∠EHF =90°,∴∠AEB +∠FEC =90°∠AEB +∠BAE =90°∴∠BAE =∠HEF∴△ABE ≌△EHF .…………………………………………………..3分∴BE =FH ,AB =EH ,∵E 为BC 中点,∴BE =CE =CH =FH .∴∠DCF =∠HCF=45°. …………………………………………..4分法二证明:取线段AB 的中点H ,连接EH . …………………………………..2分由已知得AE ⊥EF ,AE =EF .∴∠AEB +∠FEC =90°.在正方形ABCD 中,∵∠B =90°,∴∠AEB +∠BAE =90°.∴∠FEC =∠BAE . ∵AB =BC ,E ,H 分别为AB ,BC 中点,∴AH=EC ,∴△ECF ≌△AHE .…………………………………………………..3分∴∠ECF =∠AHE =135°,∴∠DCF =∠ECF -∠ECD =45°.∴∠DCF =∠HCF .…………………………………………………..4分(2)证明:在BA 延长线上取一点H ,使BH =BE ,连接EH . …………..5分在正方形ABCD 中,∵AB =BC ,∴HA =CE . ∵∠B =90°,∴∠H =45°. ∵CM 平分∠DCG ,∠DCG =∠BCD =90°,∴∠MCE =∠H=45°.∵AD //BG ,∴∠DAE =∠AEC .∵∠AEM =∠HAD =90°, ∴∠HAE =∠CEM .∴△HAE ≌△CEM .………………………………………………. 6分∴AE =EM . ………………………………………………………. 7分29. (1)满足条件的点为)0,1(-D ,)2,2(-E ……………………………… 3分 H F E G D CB A HMA B C D GE12 / 12(2)当1=a 时,角的两边分别过点)(1,1-,)(1,1,此时坐标角度︒=90m ; 当3a =时,角的两边分别过点)(1,33-,)(1,33,此时坐标角度︒=60m ,所以︒≤≤︒9060m ;……………………………………………………… 6分(3)3233≤≤-r .…………………………………………………….8分 O。
2015-2016学年北京市石景山区初一年级第二学期期末数学试卷(含答案)

石景山区2015—2016学年第二学期期末考试试卷初一数学考 生 须 知1.本试卷共5页,共八道大题,28道小题.满分100分,考试时间100分钟. 2.在试卷和答题卡上准确填写学校名称、班级、姓名.3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答. 4.考试结束,将本试卷和答题卡一并交回.一、选择题(本大题共30分,每小题3分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若a b >,则下列不等式正确的是 A .33a b < B .ma mb > C .11a b -->-- D .1122a b +>+2.下列运算正确的是A .236x x x ⋅=B .235a a a +=C .32y y y ÷=D .()32626m m -=-3.将321x y -=变形,用含x 的代数式表示y ,正确的是A .123yx +=B .312x y -=C .132xy -=D .123yx -=4.为了测算一块600亩试验田里新培育的杂交水稻的产量,随机对其中的10亩杂交水稻的产量进行了检测,在这个问题中,数字10是A .个体B .总体C .样本容量D .总体的样本5.如图,直线AB ,CD 被直线EF 所截,交点分别为点E ,F .若AB ∥CD ,下列结论正确的是A .23∠=∠B .24∠=∠C .51∠=∠D .3180AEF ∠+∠=︒6.下列命题的逆命题为真命题的是A .对顶角相等B .如果1x =,那么1x =C .直角都相等D .同位角相等,两直线平行7.某居民小区开展节约用电活动,对该小区30户家庭的节电量情况进行了统计,五月份与四月份相比,节电情况如下表:节电量(度)10 20 30 40 户数215103则五月份这30户家庭节电量的众数与中位数分别为A .20,20B .20,25C .30,25D .40,20第5题图FB CEDA 543218.如图,OB ⊥CD 于点O ,12∠=∠,则2∠与3∠的关系是A .23∠=∠B .2∠与3∠互补C .2∠与3∠互余D .不确定9.不等式组42103x x >⎧⎪⎨-+≥⎪⎩的整数解为A .0,1,2,3B .1,2,3C .2,3D .310.已知23m =,54=n ,则n m 232+的值为 A .45B .135C .225D .675二、填空题(本共18分,每小题3分)11.分解因式:442-+-m m = .12.一个角的补角比这个角大20︒,则这个角的度数为 °. 13.将462++x x 进行配方变形后,可得该多项式的最小值为 .14.如图,在长方形网格中,四边形ABCD 的面积为 .(用含字母a ,b 的代数式表示) 15.现定义运算“*”,对于任意有理数a ,b ,满足()()22a b a b a b a b a b -≥⎧⎪*=⎨-<⎪⎩. 如532537*=⨯-=,113121222*=-⨯=-,计算:()21*-=;若35x *=,则有理数x 的值为 ;16.观察等式1416224⨯=,2426624⨯=,34361224⨯=,44462024⨯=,…,根据你发现的规律直接写出8486⨯= ;用含字母的等式表示出你发现的规律为 .三、计算题(本题共8分,每小题4分) 17.)312(622ab b a ab --.18.已知错误!未找到引用源。
北京市石景山2010-2011学年度第二学期初二数学期末综合练习及答案

石景山2010-2011学年度第二学期期末考试初 二 数 学一、选择题(本题共24分,每小题3分)在每个小题给出的四个备选答案中,只有一个是正确的,请将所选答案前的字母填写在各小题后的括号内.1.在平面直角坐标系中,将点(3)P ,-1沿x 轴方向向左..平移2个单位得到点Q ,则点Q 的坐标是( )A .(5)P ,-1B .(1)P ,-1 C .(3)P ,1 D .(3)P ,-3 2.一次函数23y x =-+的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限3. 如图,在平行四边形ABCD 中,AB =5,BC =7,CE 平分∠BCD ,则AE 的长是( )A .4B .2C .2.5D .3.54.如图,四边形ABCD 的对角线互相平分,要使它成为矩形,那么需要添加的条件是( )A .AB CD =B .AD BC = C .AB BC =D .AC BD =5.关于x 的一元二次方程2320x x k -+=有两个不相等的实数根,则实数k 的取值范围是( )A .k ≤98B .k ≥98C . k <98D .k >98第3题图 第4题图6.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表:如果要选择一个成绩高且发挥比较稳定的人参赛,则这个人应是( ) A .甲 B .乙 C .丙 D .丁7. 一次函数b kx y +=(0≠k )的图象如图所示,当y >0时,x 的取值范围是( )A .x >1B .x <1C .x >-2D .x <-2第7题图 第8题图8.如图,边长为4的正方形ABCD 绕点A 逆时针旋转45°后,得到正方形'''D C AB ,边''C B 与DC 交于点O ,则四边形OD AB '的周长是( )A .28B .8C .28+D .244+二、填空题(本题共15分,每小题3分)9.函数y =x 的取值范围是 .10.一个正多边形的每个外角都是72°,这个正多边形的边数是__________.11.如图,四边形ABCD 是矩形,60ABD ∠=︒,延长BC 到E ,使BE =BD ,则∠CDE 的度数是 °.12.如图:在平面直角坐标系中,直线l 垂直于x 轴,垂足(2,0),已知点A (1,3),请你在直线l 找一点P ,使PO PA +的值最小,则点P 的坐标是 .第11题图13.已知:如图,在平面直角坐标系中,有两个全等菱形,其中(0,0),A G ,一只蚂蚁由A 点开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走12厘米后所处位置的点的坐标是 ,行走2010厘米后所处位置的点的坐标是 .'D EDC BA三、解答题(本题共25分,每小题5分) 14.解方程: 2420x x -+= 解:15.已知关于x 的一元二次方程240x kx +-=的一个根是1x =,求方程的另一个根. 解:16.在平面直角坐标系中,我们将一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x ,y 轴分别交于点A ,B ,则△OAB 为此函数的坐标三角形.(1)求函数y =-x +1的坐标三角形的面积;(2)若函数y =-x +b (b >0)的坐标三角形周长为224+,求b 的值. 解:17.已知关于x 的一元二次方程0222=++n mx x (0<mn )有两个相等的实数根,求nmm n +的值. 解:18.如图,矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE .且点G 在矩形ABCD 内部. 延长BG 交DC 于点F , 求证:GF=DF证明:四、解答题(本大题共2个小题,每小题6分,共12分)19.已知一次函数b kx y +=,当2=x 时,4=y ,当1=x 时,4-=y . (1)求一次函数的解析式;(2)将该函数的图象向上平移8个单位,求平移后的图象与x 轴交点的坐标. 解:20.已知:如图,直角梯形纸片ABCD 中,AD ∥BC ,∠A =90°,AB =AD =6,将DC 沿DF 翻折使点C 落在边AB 上的点E 处,若EB =2AE ,∠EDF =45°.求FC 的长.解:FED CBA五、操作题(本题6分)21.从边长为a 的大正方形纸板中间挖去一个边长为b 的小正方形后,可以将其截成四个相同的等腰梯形拼成一个平行四边形. (1)请你在图2中大致画出拼图示意图;(2)若拼成的平行四边形ABCD ,已知∠A =45°,AB =8,AD =边长a 的值. 解:六、解答题(本题6分)22.小明骑自行车去上学,途中有一部分路段是上坡路段1s ,另一部分是平坦路段2s ,小明上学所走的路程s (米)与时间t (分钟)之间的函数关系如图所示.根据图象,解答下列问题:(1)小明家到学校的路程是 米;他在上学途中上坡时所用时间是 分钟; (2)求小明上学时走路程1s (米)与时间t (分钟)之间的函数关系式;(3)若小明放学后按原路返回,在返回过程中,走路段1s 时是上学时速度的1.5倍,问:小明走段路1s 时所用的时间为多少分钟?解:图 1a A图2七、解答题(本题6分)23.北京市郊有许多优秀的旅游景点,某旅行社对5月份本社接待的一日游游客首选景点作了一次抽样调查,调查结果如下图表.(1)请在上述频数分布表中填写空缺的数据,并补全统计图;(2)该旅行社预计6月份接待一日游游客4000人,请你估计首选A 景点的人数. 解:八、解答题(本题6分)24.已知:直线4y kx k =++(0k ≠)过点B (1.0),与y 轴交于点C .(1)若点A (x ,y )是直线4y kx k =++上的一个动点,当点A 运动过程中,试写出△AOB 的面积S 与x 的函数关系式,并指明x 的取值范围;(2)在直线BC 上是否存在一点P ,使以P 、O 、C 为顶点的三角形是等腰三角形.若存在,请直接写出满足条件的所有P 点的坐标;若不存在,请说明理由.解:一日游游客首选景点频数分布表 一日游游客首选景点统计图 人数景点 O xy石景山区2010—2011学年度第二学期期末考试初二数学参考答案一、选择题(本题共8个小题,每小题3分,共24分)二、填空题(本题共5个小题,每小题3分,共15分)9. 1≥x 10. 5 11.30 12. (2,2)13.()……1分;(-)……3分三、解答题(本题共25分,每小题5分)14. 解:(其它解法酌情给分)2(2)2x -= ………………………………………………………………2分2x -= ………………………………………………………3分∴12x =22x =分15. 解:由题意140k +-=,得3k = ………………………………………………2分∴原方程为2340x x +-=解之11x =,24x =- ………………………………………………………………4分 ∴方程的另一个根是4x =.………………………………………………………5分 16.解:(1) ∵ 直线y =-x +1与x 轴的交点坐标为(1,0),与y 轴交点坐标为(0,1)∴21=∆OAB S ……………………………………………………………2分 (2) 直线y =-x +b 与x 轴的交点坐标为(b ,0),与y 轴交点坐标为(0,b ),b b b AB 222=+= ………………………………………4分∴2242+=++b b b ,得b =2…………………………………………5分17.解:04422=-=∆n m ………………………………………1分n m ±= ………………………………………2分∵0<mn ∴n m -= ………………………………………3分 ∴2-=+nmm n ………………………………………5分 18.证明:联结EF ………………………………………1分则∠EGF =∠D =90° ………………………………………2分 EG = AE = ED ………………………………………3分 EF = EF∴Rt △EGF ≌ Rt △EDF ………………………………………4分 ∴GF = DF ………………………………………5分四、计算与证明题(本题共12分,每小题6分) 19.解:(1)⎩⎨⎧-=+=+442b k b k …………………………………………1分∴⎩⎨⎧-==128b k …………………………………………2分∴一次函数的解析式为128-=x y(2)将128-=x y 的图象向上平移8个单位得48-=x y ……………………4分 当0=y 时,21=x ∴平移后的图象与x 轴交点的坐标为)0,21(……………………………………6分20. 解:过D 作DG ⊥BC 于G ,连结EF ……………………………………1分由已知可得四边形ABGD 为正方形,DE ⊥DC ∴∠ADE +∠EDG =90°=∠GDC +∠EDG ∴∠ADE =∠GDC又∵∠A =∠DGC 且AD =GD∴△ADE ≌△GDC ………………………………3分 ∴GC =AE =2设FC =x ,则BF =BC -CF =6+2-x ,BE =2AE =4由勾股定理x 2=28x (-)+42,解得:x =5∴FC =5. ……………………………………6分五、操作题(本题6分)21……………………………………2分⑵ 由题意84a b AB a b +==⎧⎪⎨-==⎪⎩……………………………………4分 解得:a =6 ……………………………………6分GFEDCBA六、解答题(本题6分)22.解:(1)2800;6(考察学生生活经验即上坡速度较慢)………………………2分 (2)设11k t s = ()06t ≤≤∵ 图象经过点()6,1200 ∴ 120016k =解方程,得 1200k = ∴1200t s = ()06t ≤≤ ………………………………………4分(3)小明返回时走段路1s 所用时间为1200(1.5200)4÷⨯=(分钟) ………………………………………6分答: 小明返回时走段路1s 所用时间为4分钟.七、解答题(本题6分)23.解:(1) 0.05, 450. ………………………………………2分图略. ………………………………………4分 (2) 解:4000×0.2=800(人) . ………………………………………6分八、解答题(本题6分)24.解:(1)由题意22y x =-+S =y OB ⨯⨯21①1<x 时,点A 在轴上方: S =()122121+-=+-⨯⨯x x ……………1分 ②1>x 时,点A 在轴下方: S =()122121-=+-⨯⨯-x x ……………2分(2)满足条件的所有P 点坐标为: P 1(1,21),P 2 (56,58-),P 3(552,2554+-),P 4(552-,2554+)…6分。
石景山区16年初二数学期末试题

北京市石景山区2015—2016学年度第二学期期末考试初二数学试题一、选择题(每小题3分,共24分,每小题只有一个答案符合题意) 1.若一个正多边形的一个外角是40°,则这个正多边形的边数是( ).A .10B .9C .8D .6 2.若532q =,则q 的值是( ). A .103B .215 C .310D .1523.下列四张扑克牌图案中,是中心对称图形的是( ).A B C D4.执行如图所示程序框图,y 与x 之间函数关系所对应图象为( )5.初二年级1x 甲,x 乙,得分的方差依次为2S 甲,2S 乙,则下列关系中完全正确的是( ).A .x x =乙甲,22S S >乙甲B . x x =乙甲,22S S <乙甲 C .x x >乙甲,22S S >乙甲 D . x x <乙甲,22S S <乙甲 A D CB 第4题6.综合实践课上,小超为了测量某棵树的高度,用长为2m 的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点(如图).此时竹竿与这一点相距6m,与树相距15m ,则树的高度为 ( ) .A . 4mB . 5mC . 7mD . 9m 7.王老师组织摄影比赛,小语上交的作品如下:七寸照片(长7英寸,宽5英寸);将照片贴在一张矩形衬纸的正中央,照片四周外露衬纸的宽度相同;矩形衬纸的面积为照片面积的3倍.设照片四周外露衬纸的宽度为x 英寸(如图),下面所列方程正确是( ) .A .(7)(5)375x x ++⨯=⨯B .(72)(52)375x x ++=⨯⨯C .(72)(52)375x x ++⨯=⨯D .(7)(5)375x x ++=⨯⨯8.如图:已知P 是线段AB 上的动点(P 不与A,B 重合),4AB =,分别以AP ,PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ,连结EF ,设EF 的中点为G ;连结PG ,当动点P 从点A 运动到点B 时,设 PG=m ,则m 的取值范围是( ).A2m ≤< B .2m << C .4m < D32m ≤< 二、填空题(本题共21分,每空3分) 9.方程22x x =的解为_________________.10.函数y =x 的取值范围是___________.11.在菱形ABCD 中, AC =6,BD =8,则菱形ABCD的周长为__________,面积为________. 12. 如图,在△ABC 中,∠ACB=58°,D ,E 分别是AB , AC 中点.点F 在线段DE 上,且AF ⊥CF ,则∠F AE = °.13.在平面直角坐标系xOy 中,O 是坐标原点,将直线y x =绕原点O 逆时针旋转15°,再向上平移3个单位得到直线l ,则直线l 的解析式为_______________________. 14.给出定义:若直线与一个图形有且只有两个公共点,则直线与该图形位置关系是相交.坐标系xOy 中, 以()1,1A --, B (3,0), ()1,1C , D (0,3)为顶点,顺次连结AB 、BC 、CD 、DA 构成图形M .若直线y x b =-+与M 相交,则b 的取值范围是____________.第6题 第7题 第8题第12题15.用配方法...解方程:23630x x --= 解:16.已知:关于x 的一元二次方程2230x x m --+=有实数根.(1)求m 的取值范围;(2)若m 为符合条件的最小整数,求此时方程的根. 解:(1)(2)17.如图,直线x y l 2:1=与直线3:2+=kx y l 在同一平面直角坐标系内交于点P . (1)直接..写出..不等式2x > kx +3的解集 (2)设直线2l 与x 轴交于点A ,求△OAP 的面积. 解:(1)______________________ (2)18.我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD 中,E ,F ,G ,H 分别是AB ,BC ,CD ,DA 的中点,依次连接各边中点得到中点四边形EFGH . (1)这个中点四边形EFGH 的形状是_________________(2)请证明你的结论.证明:19.如图,在矩形ABCD 中,AB =5,BC =4,将矩形ABCD 翻折,使得点B 落在CD 边上的点E 处,折痕AF 交BC 于点F ,求FC 的长.解:20.如图,在平面直角坐标系xOy 中,O 是坐标原点,一次函数y kx b =+的图象与x 轴交 于点A (3-,0),与y 轴交于点B ,且与正比例函数43y x =的图象的交点为C (m ,4) (1) 求一次函数y kx b =+的解析式;(2) D 是平面内一点,以O 、C 、D 、B 四点为顶点的四边形 是平行四边形,直接写出....点D 的坐标.(不必写出推理过程)(1)解:(2)点D 的坐标为_____________________________________________________B五、列方程解应用题(本题5分)21.小明对新发地水果批发市场某种水果销售情况调查发现:如果每千克盈利10元,每天可售出500千克.对市场进一步调查发现,在进价不变的情况下,若每千克这种水果在原售价的基础上每涨价1元,则日销售量将减少20千克.如果市场每天销售这种水果盈利了6 000元,同时顾客又得到了实惠..........,那么每千克这种水果涨了多少元? 解:六、解答题(本题10分,每题5分)22.小辰根据北京市统计局发布的有关数据制作的统计图表的一部分,请你结合下面图表中提供的信息解答下列问题.(注:能源消费量的单位是万吨标准煤,简称标煤).(1)2010年北京市新能源和可再生能源消费量是____________万吨;并补全条形统计图并在图中标明相应数据......; (2)2010年北京市能源消费总量约是____________万吨标煤(结果精确到百位)? (3)据 “十二五”规划,到2015年,本市能源消费总量比2010年增长31%,其中新能源和可再生能源利用量占全市能源消费总量的6%.小辰调查发现使用新能源每替代一万吨标煤,可减少二氧化碳排放量约为2万吨,到2015年,由于新能源和可再生能源的开发利用,北京市可减少二氧化碳排放量约为多少万吨? 解:“十一五”期间北京市新能源和可再生能源消费量统计图2010年北京市各类能源消费量占能源消费总量的百分比统计图23.已知关于x 的方程 03)13(2=+++x m mx . (1)求证: 不论m 为任何实数, 此方程总有实数根;(2)若方程()23130mx m x +++=有两个不同的整数根,且m 为正整数,求m 的值. 解:(1)证明:(2)解:图1CFE图324. 数学课外选修课上李老师拿来一道问题让同学们思考.原问题:如图1,已知△ABC ,在直线BC 两侧..,分别画出两个..等腰三角形△DBC ,△EBC 使其面积与△ABC 面积相等;(要求:所画的两个三角形一个以BC 为底.一个以BC 为腰);小伟是这样思考的:我们学习过如何构造三角形与已知三角形面积相等.如图2,过点A 作直线l ∥BC ,点D 、E 在直线l 上时,ABC DBC EBC S S S ∆∆∆==,如图3,直线l ∥BC ,直线l 到BC 的距离等于点A 到BC 的距离,点D 、E 、F 在直线l 上,则A B C D B C E B CF BS S S S ∆∆∆∆===.利用此方法也可以计算相关三角形面积,通过做平行线,将问题转化,从而解决问题.(1)请你在下图中,解决李老师提出的原问题;参考小伟同学的想法,解答问题:(2)如图4,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,若每个正六边形的边长为1, △ABC 的顶点都在格点上,则△ABC 的面积为________.(3)在平面直角坐标系xOy 中,O 是坐标原点,()()1,0,0,2,A B -D 是直线l :321+=x y 上一点,使△ABO 与△ABD 面积相等,则D 的坐标为_______________.图2B 备用图1 备用图2 B备用图325.已知:在正方形ABCD 中,E 、G 分别是射线CB 、DA 上的两个动点,点F 是CD 边上,满足EG ⊥BF , (1)如图1,当E 、G 在CB 、DA 边上运动时(不与正方形顶点重合),求证:GE =BF . (2)如图2,在(1)的情况下,连结GF,求证:FG BE +>.(3)如图3. 当E 、G 运动到BC 、AD 的反向延长线时,请你直接写出....FG 、BE 、BF 三者的数量关系(不必写出证明过程). (1)证明:(2)证明:(3)FG 、BE 、BF 三者的数量关系为______________________________________A 图1A 图2图3北京市石景山区2015—2016学年度第二学期期末考试初二数学答案及评分参考一、选择题(本题共8道小题,每小题3分,共24分)二、填空题(本题共21分,每空3分)9. 120,2x x ==(漏解扣1分,出现错解0分) 10.3x ≥; 11.20,24.12.61° 13.3y =+ 14.22b -<<或3b =(对一种得2分); 三、解答题(本题共3个小题,每小题5分,共15分)15.解:原方程化为:2210x x --= ………………………………………………1分 22111x x -+=+ ………………………………………………2分 ()212x -= ………………………………………………3分∴1211x x == ………………………………………………5分 16.解:(1)由题意:0∆≥ ………………………………………………1分 即:()4430m --≥解得 2m ≥ ………………………………………………3分 (2)当2m =时,原方程化为2210x x -+=解得121x x == ………………………………………………5分(阅卷说明:若考生答案为1x =,扣1分)17. 解:(1)x > 1;………………………………………………1分(2)把1=x 代入x y 2=,得2=y .∴点P (1,2). ……………………………………………………………2分 ∵点P 在直线3+=kx y 上, ∴32+=k . 解得 1-=k .∴3+-=x y . ………………………………………………………………3分 当0=y 时,由30+-=x 得3=x .∴点A (3,0). ……………………4分∴32321=⨯⨯=∆OAP S ………………………………………………5分 四、解答题(本题共15分,每小题5分)18. (1)平行四边形; ……………………………………… 1分(2)证明:连结AC ……………………………………… 2分∵E 是AB 的中点,F 是BC 中点,∴EF ∥AC ,EF =12AC .同理HG ∥AC ,HG =12AC . …………… 4分∴EF ∥HG ,EF =HG ,∴四边形EFGH 是平行四边形. ……………………………………… 5分 19.解法一:由题意,△ABF ≌△AEF得AE =AB =5,AD =BC =4,EF =BF . …………………………… 1分 在Rt △ADE 中,由勾股定理,得DE =3. …………………………………… 2分 在矩形ABCD 中,DC =AB =5. ∴CE =DC -DE =2. …………………………………………………………… 3分设FC =x ,则EF =4-x .在Rt △CEF 中,()22242x x -=+. .……… ……… 4分 解得23=x . ………………………………… …… 5分 即FC =23. 解法二:由题意,△ABF ≌△AEF得AE =AB =5,AD =BC =4,EF =BF . …………………………… 1分 在Rt △ADE 中,由勾股定理,得DE =3. …………………………………… 2分 在矩形ABCD 中,DC =AB =5. ∴CE =DC -DE =2. ………………………………… 3分 由题意∠AED +∠FEC =90° 在Rt △CEF 中,∠EFC +∠FEC =90° ∴∠EFC =∠AED . 又∵∠D =∠C =90°, ∴Rt △AED ∽Rt △EFC∴CF CEDE DA= .……… ………4分 ∴FC =23.………………………………… …… 5分20. 解:(1)∵点C (m ,4)在直线43y x =上, ∴443m =,解得3m =. ……………………………………………… 1分∵点A (3-,0)与C (3,4)在直线(0)y kx b k =+≠上,B∴03,43.k b k b =-+⎧⎨=+⎩ 解得2,32.k b ⎧=⎪⎨⎪=⎩ ……………………………………………… 2分 ∴一次函数的解析式为223y x =+. ………………………………………………3分 (2) 点D 的坐标为(3-,2-)或(3,6)(3,2)…………………………………………… 5分(阅卷说明:出现正确解得1分,三个点计算都正确得2分)五、列方程解应用题(本题5分)21.解:设市场某天销售这种水果盈利了6 000元,同时顾客又得到了实惠时,每千克这种水果涨了x 元 …………………………………………… 1分 由题意得 (10)(50020)6000x x +-=……………………………………………3分 整理,得 215500x x -+=.解得 15x =,210x =. ……………………………………………4分 因为顾客得到了实惠,应取 5x =答:销售这种水果盈利6 000元,同时顾客又得到了实惠时,每千克这种水果涨5元. .…………………………………………… 5分六、解答题(本题10分,每题5分)22.解:⑴ 补全统计图如右图,所补数据为98+36+78.5+8+2.8=223.3. ………2分⑵ 2010年北京市总能耗量约是223.3÷3.2%≈7000(万吨标煤).………3分⑶到2015年,由于新能源和可再生能源的开发利用北京市可减少二氧化碳排放量约为7000×(1+31%)×6%×2=1100.4(万吨).………………………5分23. 解:(1)当m =0时,原方程化为,03=+x此时方程有实数根 x =3-. ……………………………………… 1分当m ≠0时,原方程为一元二次方程.∵()()222311296131m m m m m ∆=+-=-+=-≥0.∴ 此时方程有两个实数根. …………………………………………3分综上, 不论m 为任何实数时, 方程 03)13(2=+++x m mx 总有实数根.(2)∵mx 2+(3m +1)x +3=0.解得 13x =-,21x m=- ………………………………………4分 ∵方程()23130mx m x +++=有两个不同的整数根,且m 为正整数,∴1m = …………………………………5分七、解答题(本题5分)24. (1)……………………………2分(2) △ABC 的面积为 ………………………3分(3) 则D 的坐标为 ()2,4 28,33⎛⎫- ⎪⎝⎭………………………5分八、几何探究(本题5分) 25.(既可以理解为平移也可以理解为旋转)(1)证明:延长DA 至M ,使AM =CF ,连结MB ∵四边形ABCD 是正方形∴BA =BC ,∠MAB =∠C =90°,∠ABC =90°∴△BAM ≌△BCF∴BM =BF ,∠MBA =∠FBC ……………1分 ∴∠MB F=90°,∴MB ∥GE∴四边形MBEG 是平行四边形 ∴MB =GE∴ GE =BF … …………………2分(2)连结MF ∵ BM =BF ,且∠MBF =90°∴△MBF 是等腰直角三角形∴MF = …………………3分 ∵ 四边形MBEG 是平行四边形∴MG =BE在△MGF 中,MG +FG >MF∴FG BE +> …………………4分 (3BE FG +> …………………5分选择第8题思路提示:8. 将AE ,BF 延长交于C ,连结GC ,△ABC 是等边三角形。
10.2015-2016第2学期初1期末数学考试题答案-石景山

石景山区2015—2016学年第二学期期末综合练习初一数学 答案及评分参考一、选择题(本题共30分,每小题3分)11.2)214(-m ; 12.80︒;13.1;14.10ab ;15.5;4.16.7224;24)1(100)610)(410(++=++n n n n (n 为正整数). 三、计算题(本题共8分,每小题4分)17.解:原式=)2123223b a b a +- ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分18.解:原式= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分当时,原式=2 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分四、分解因式(本题共6分,每小题3分)19.解:原式= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分=. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分20.解:原式= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分=. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分五、解方程(组)或不等式(组)(本题共10分,每小题5分)21.解:3204112+-<-x x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分1132042++-<-x x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分 62-<-x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分 ∴3>x ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分 这个不等式的解集在数轴上表示为:⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分22.解:得, ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分将1=x 代入得 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分∴⎩⎨⎧-==.y ,x 21⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分六、读句画图(本题共4分) 23.答案略.(只画出一种情况的扣1分)七、解答题(本题共10分,每小题5分)24.证明:∵PM ⊥EF (已知),∴∠APQ +2∠=90°(垂直定义).⋯⋯⋯⋯2分∵∠1+2∠=90°(已知)∴∠APQ=∠1(等角的余角相等).⋯⋯⋯⋯4分∴AB ∥CD (内错角相等两直线平行).⋯⋯⋯5分25.解:①是∠ 2 , ………………………………1分 ④是∠AMD . ………………………………2分理由②是两直线平行,内错角相等;………………………………3分 理由③是角平分线定义; ………………………………4分 ∠CMD 的度数是21°. ………………………………5分26.解:设能生产帽子x 件,生产T 恤y 件.………………………………1分根据题意,得……………………………………………………3分解得 ……………………………………………………4分答:能生产帽子1900件,生产T 恤4100件. ……………………5分27.解:(1)a =__775__; ………………………………2分 (2)4月30日至5月3日接待观众人数的日平均增长量;263697775=-=x ; ………………………………2分(3)估计该活动在5月4日接待观众约为__801___人.……………5分八、解答题(本题4分)28.解:由题意可得, ………………………………2分解之,⎪⎩⎪⎨⎧==.213,6b a ………………………………4分。
石景山区2015初三数学二模综合练习答案

1 1 OC y A OC yB 2 2 A 1 1 4 3 4 1 2 2 4 ………………………………………………5 分
初三数学试卷答案第 2 页(共 7 页)
22.解:设荧光笔和笔记本的单价分别是 x 元, y 元…………………………1 分
O D A C E B x y
EC 2 2 设 C t , t 2t 2 , E t , t 2 , 0 t 3
则 CD
2 ∴ EC yE yC t 3t
3 9 t ………………………6 分 2 4 3 ∵当 0 t , EC 随 t 的增大而增大, 2 3 当 t 3 , EC 随 t 的增大而减小; 2 3 9 ∴当 t 时, ECmax 2 4 ∵ CD 随 EC 增大而增大, 9 2 为所求.………………………7 分 ∴ CDmax 8
AD EB, ADC ∠BEC , DC CE ,
A
D O E B C M
△ ADC ≌△ BEC .……………………4 分 AC CB .……………………5 分 1 18.解:原式= 2 2 9 4 ………………………………4 分 2
=7………………………………5 分
D B E
P
O
∴ OC OD 6 ,∴ CP PD 6 ∴ P6,6 ……………………5 分
初三数学试卷答案第 4 页(共 7 页)
A
C
x
五、解答题(本题满分 7 分) 27.解: (1)当 m 0 时, x 2 当 m 0 时, 3m 1 4m 2m 2
∴ a 2a 1 3a a ………………………………………………1 分 ∵ m 0 ∴ a 1 ∴ m 3 , A 1, 3 、 B 3, 1 ∴所求反比例函数解析式为: y ∴ 3a 2b .………………………………4 分
2015-2016学年北京市石景山八年级下学期期末数学试题(含答案)
在直线 AB 上截取 B1B2= BB1,过点 B2 分别作 x、y 轴的垂线,垂足分别为点 A2 、C2,得到矩形 OA2B2C2;
在直线 AB 上截取 B2B3= B1B2,过点 B3 分别作 x、y 轴的垂线,垂足分别为点 A3、C3 ,得到矩形
OA3B3C3;……;则点 B1 的坐标是
;第 3 个矩形 OA3B3C3 的面积是
A. m 1
B. m 1
C. m 1且 m 0
D. m 1且 m 0
8.如图,将边长为 3cm 的等边△ ABC 沿着边 BC 向右平移 2cm,得到△ DEF,则四边形 ABFD 的周长为
()
A.15cm A
B.14cm D
C.13cm
D.12cm
S/平方米 160
B
EC
F
第 8 题图
E
D
C
B
23 .列方程解应用题: 某地区 2013 年的快递业务量为 2 亿件,受益于经济的快速增长及电子商务发展等多重因素,快递业务迅 猛发展,2015 年的快递业务量达到 3.9 2 亿件.求该地区这两年快递业务量的年平均增长率.
24.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是 当月用电量不超过 240 度时实行“基础电价”;第二档是当用电量超过 240 度时,其中的 2 40 度仍按照“基 础电价”计费,超过的部分按照 “提高电价”收费.设每个家庭月用电量为 x 度时,应交电费为 y 元.具体收 费情况如折线图所示,请根据图象回答下列问题: (1)“基础电价”是_________元/度; (2)求出当 x>240 时,y 与 x 的函数表达式; (3)小石家六月份缴纳电费 132 元,求小石家这个月用电量为多少度?
石景山区2015—2016学年初一数学第二学期期末考试试题答案

(2)4月30日至5月3日接待观众人数的日平均增长量:
;………………………………4分
(或 )
(3)估计该活动在5月4日接待观众约为__801___人.…………5分
八、解答题(本题4分)
28.解:由题意可得, …………………………2分
解之, ………………………………4分
理由 是角平分线定义;………………………………4分
∠CMD的度数是21°.………………………………5分
26.解:设生产帽子x件,生产T恤y件.………………………………1分
根据题意,得
……………………………………………………3分
解得 ……………………………………………………4分
答:生产帽子1900件,生产T恤4100件. ……………………5分
∵∠1+ =90°(已知)
∴∠APQ=∠1(同角的余角相等).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
∴AB∥CD(内错角相等,两直线平行).⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
25.解:①是∠2,………………………………1分
是∠AMD.………………………………2分
理由②是两直线平行,内错角相等;………………………………3分
= .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
20.解:原式= ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
= .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
五、解方程(组)或不等式(组)(本题共10分,每小题5分)
21.解: ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯3分
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
这个不等式的解集在数轴上表示为:
16.7224; (n为正整数).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
60
O 12 第 9 题图
4 t /小时
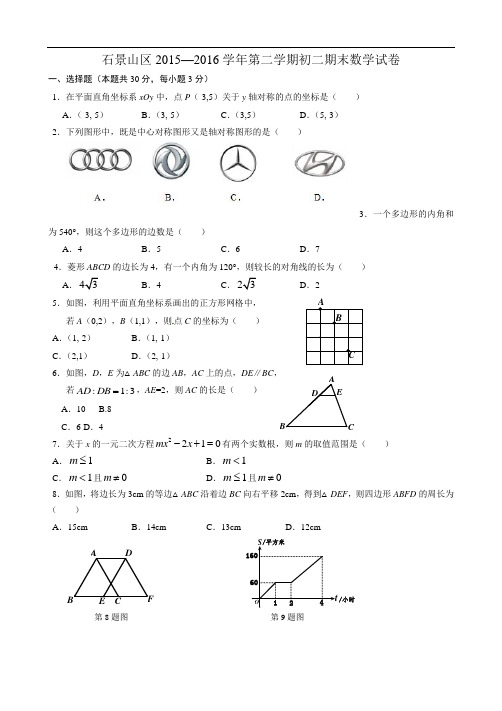
9.园林队在某公园进行绿化,中间休息了一段时间.绿化面积 S(单位:平方米)
与工作时间 t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小
时绿化面积为( )
A.40平方米
B.50平方米
C.80平方米
D.100平方米
10.如右图,矩形 ABCD 中,AB=2,BC=4,P 为矩形边
A
E
D
C
B
(2)若B 60,BC 2 ,求四边形 AECD 的面积.
23.列方程解应用题: 某地区 2013年的快递业务量为 2 亿件,受益于经济的快速增长及电子商务发展 等多重因素,快递业务迅猛发展,2015年的快递业务量达到 3.92亿件.求该地区 这两年快递业务量的年平均增长率.
4.考试结束,将本试卷和答题卡一并交回.
一、选择题(本题共 30分,每小题 3 分)
下面各题均有四个选项,其中只有一个是符合题意的.
1.在平面直角坐标系 xOy 中,点 P(-3,5)关于 y 轴对称的点的坐标是( )
A.(-3,-5)
B.(3,-5)
C.(3,5)
D.(5,-3)
2.下列图形中,既是中心对称图形又是轴对称图形的是( )
AN 平分∠MAD,交射线 DC 于点 N.
(1)如图 1,若点 M 在线段 CB 上
①依题意补全图 1; ②用等式表示线段 AM,BM,
DN 之间的数量关系,并证明;
(2)如图 2,若点 M 在线段 CB 的延
M
长线上,请直接写出线段 AM,
B
A
BM,DN 之间的数量关系.
初二数学试卷 第 5 页(共 6 页)
A
D
上的一个动点,运动路线是 A→B→C→D→A,设 P 点
经过的路程为 x,以 A,P,B 为顶点的三角形面积为 y, B P
C
则下列图象能大致反映 y 与 x 的函数关系的是( )
y
y
y
y
4
4
4
4
O
6 8 12 x O 2 6 8 12 x O
6 12 x O 2 6 12 x
A.
B.
C.
D.
二、填空题(本题共 18分,每小题 3 分) 11.如图,点 D,E 分别为△ABC 的边 AB,BC 的中点,
在直线 AB 上截取 B1B2= BB1 ,过点 B2 分别 作 x、y 轴的垂线,垂足分别为点 A2 、C2, 得到矩形 OA B C ;
22 2
在直线 AB 上截取 B2B3= B1 B2 ,过点 B3 分别 作 x、y 轴的垂线,垂足分别为点 A3、C3,
C3 C2 C1 B
AO
B3 B2 B1
A
A
E
D
D
B
C
第 13 题图
F
B
C
第 14 题图
14.如图,在□ABCD 中,BC=5,AB=3,BE 平分∠ABC 交 AD 于点 E,交对角
线 AC 于点 F,则 S△AEF
S△CBF =
.
A
D
15.如图,矩形 ABCD 中,AB=8,AD=10,点 E 为 DC 边
E
上的一点,将△ADE 沿直线 AE 折叠,点 D 刚好落在
(1)求证:方程总有两个实数根2 ; (2)若方程的两个实数根都是整数,求正整数 m 的值.
22.如图,Rt△ABC 中,ACB 90 ,CD 是斜边 AB 上的中线,分别过点 A,C 作 AE∥DC,CE∥AB, 两线交于点 E. (1)求证:四边形 AECD 是菱形;
初二数学试卷 第 4 页(共 6 页)
况如折线图所示,请根据图象回答下列问题:
y (元)
(1)“基础电价”是_________元/度;
(2)求出当 x>240 时,y 与 x 的函数表达
216
式;
120
B A
(3)小石家六月份缴纳电费 132元, 求小石家这个月用电量为多少度?
O
240 400
x(度)
25.已知正方形 ABCD 中,点 M 是边 CB(或 CB 的延长线)上任意一点,
C
D
A D
初二数学试卷 第 2 页(共 6 页)
B
E
C
若 DE=3cm,则 AC=
cm.
12.已知一次函数 y (m 2)x m ,若 y 随 x 的增
大而增大,则 m 的取值范围是
.
13.如图,在△ABC 中,D 是 AB 边上的一点,连接 CD,请添加一个适当的条
件
,使△ACD ∽△ABC(只填一个即可).
()
A. m 1
B. m 1
C. m 1 且 m 0
D. m 1且 m 0
8.如图,将边长为 3cm的等边△ABC 沿着边 BC 向右平移 2cm,得到△DEF,则
四边形 ABFD 的周长为( )
A.15cm
B.14cm
C.13cm
D.12cm
A
D
S/平方米 160
B
EC
F
第 8 题图
BC 边上的点 F 处,则 CE 的长是
.
B
FC
第 15 题图
16.如图,在平面直角坐标系 xOy 中,一次函数 y=x+1与 x、y 轴分别交于点 A、B,
在直线 AB 上截取 BB1=AB,过点 B1 分别
作 x、y 轴的垂线,垂足分别为点 A1、C1,
y
y=x+1
得到矩形 OA B C ;
11 1
石景山区 2015—2016学年第二学期初二期末试卷
数学
学校
姓名
准考证号
1.本试卷共 6 页,共三道大题,26道小题.满分 100分,考试时间 100分
考
钟.
生 2.在试卷和答题卡上准确填写学校名称、姓名和考号.
须 3.试卷答案一律填涂或书写在答题卡上,在试卷上作答无效.在答题卡上,
知 选择题、作图题用 2B铅笔作答,其他试题用黑色字迹签字笔作答.
A B
A.(1,-2)
B.(1,-1)
C.(2,1)
D.(2,-1)
C
6.如图,D,E 为△ABC 的边 AB,AC 上的点,DE∥BC,
若 AD : DB 1 : 3 ,AE=2,则 AC 的长是( )
A.10
B.8
B
初二数学试卷 第 1 页(共 6 页)
A DE
C
C.6
D.4
7.关于 x 的一元二次方程 mx2 2x 1 0 有两个实数根,则 m 的取值范围是
A1 A2 A3 x
得到矩形 OA B C ;……;
33 3
则点 B1 的坐标是
;第 3 个矩形 OA B C 的面积是
;
33 3
第 n 个矩形 OAnBnCn 的面积是
(用含 n 的式子表示,n 是正整
数).
初二数学试卷 第 3 页(共 6 页)
三、解答题(本题共 52分,第 17-24题,每小题 5 分;第 25-26题,每小题 6 分)
20.如图,在矩形 ABCD 中,E 为 AD 边上的一点,
A
过 C 点作 CF⊥CE 交 AB 的延长线于点 F.
(1)求证:△CDE ∽△CBF;
B
(2)若 B 为 AF 的中点,CB=3,DE=1,求 CD 的长.
F
ED C
21.已知关于 x 的一元二次方程 mx (3m 2)x 6 0 (m≠0) .
解答应写出文字说明,演算步骤或证明过程.
17.用适当的方法解方程: x 6x 1 0 .
2
18.如图,在□ABCD 中,E,F 是对角线 BD 上的两点且 BE=DF,联结 AE,CF. 求证:AE=CF.
A
E B
D F
C
19.一次函数 y kx b 的图象与正比例函数 y2 mx 交于点 A(-1,2), 1 与 y 轴交于点 B(0,3). (1)求这两个函数的表达式; (2)求这两个函数图象与 x 轴所围成的三角形的面积.
24.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分
两档收费:第一档是当月用电量不超过 240度时实行“基础电价”;第二档是当
用电量超过 240度时,其中的 240度仍按照“基础电价”计费,超过的部分按照
“提高电价”收费.设每个家庭月用电量为 x 度时,应交电费为 y 元.具体收费情
A.
B.
C.
D.
3.一个多边形的内角和为 540°,则这个多边形的边数是( )
A.4
B 的边长为 4,有一个内角为 120°,则较长的对角线的长为(
)
A. 4 3
B.4
C. 2 3
D.2
5.如图,利用平面直角坐标系画出的正方形网格中, 若 A(0,2),B(1,1),则点 C 的坐标为( )
