人教A版高中数学必修三试卷算法初步测试题(一)
人教A版高中数学必修三练习:第一章算法初步1.1算法与程序框图含答案

分层训练·进阶冲关A基(建用20分)1. 以下对于算法的法中正确的个数有( B )①求解某一的算法是独一的;②算法必在有限步操作以后停止;2③x-x>2 019 是一个算法 ;④算法行后必定生确立的果.A.1B.2C.3D.42.以下所中 , 不可以一个算法求解的是 ( D ) A. 用“二分法”求方程 x2-3=0 的近似解 ( 精准度 0.01)B.解方程C.求半径 2 的球的体D.求 S=1+2+3+⋯的3. 程序框符号“”可用于( B )A. 出 a=10B.a=10C.判断 a=10D.入 a=14.如所示的程序框 , 已知 a1=3, 出的果 7, a2的是( C )A.9B.10C.11D.125.以下图的流程图 , 当输入的值为 -5 时, 输出的结果是( D )A.-3B.-2C.-1D.26.依据以下图的程序框图 , 使适当作绩不低于 60 分时 , 输出“及格”, 当作绩低于 60 分时 , 输出“不及格” , 则 ( A )A. 框 1 中填“是” , 框 2 中填“否”B. 框 1 中填“否” , 框 2 中填“是”C.框 1 中填“是” , 框 2 中可填可不填D.框 2 中填“否” , 框 1 中可填可不填7.下边是某人出家门先打车去火车站 , 再坐火车去北京的一个算法 , 请增补完好 .第一步 , 出家门 .第二步 ,打车去火车站.第三步 , 坐火去北京 .8. 使用配方法解方程x2-4x+3=0 的算法的步是②①④③( 填序号).22①配方得 (x-2) =1; ②移得 x -4x=-3;9.行如所示的程序框 , 出的 S= 0.99 .10.行如所示的程序框 , 假如入的 x,t 均 2, 出的 S=7.11.求 1+3+5+7+⋯+31 的算法 , 并画出相的程序框 .【分析】第一步 :S=0;第二步 :i=1;第三步 :S=S+i;第四步 :i=i+2;第五步 :若 i 不大于 31, 返回履行第三步 ,不然履行第六步 ;第六步 :输出 S 值.程序框图如图 .12.设计一个算法求知足 10<x2<1 000 的全部正整数 , 并画出程序框图 . 【分析】算法步骤以下 :第一步 ,x=1.第二步 ,假如 x 2 >10, 那么履行第三步 ;不然履行第四步 .第三步 ,假如 x 2 <1 000, 那么输出 x; 不然结束程序 .第四步 ,x=x+1,转到第二步.程序框图如图 :B组提高练( 建议用时 20 分钟)13.履行以下图的程序框图 , 若输入 n=8, 则输出的 k= ( B )A.2B.3C.4D.514. 以下图的程序框图所表示的算法的功能是( C )A.算 1+ + +⋯+的B.算 1+ + +⋯+的C.算 1+ + +⋯+的D.算 1+ + +⋯+的15.行如所示的程序框 , 运转相的程序 , 最后出的果16.若框所示程序运转的出果 S=132,那么判断框中填入的对于 k 的判断条件是k≤10?或 k<11? .17. 已知直 l1:3x-y+12=0 和直 l 2:3x+2y-6=0, 一个算法 , 求 l 1和l2及 y 所成的三角形的面.【分析】算法以下 :第一步 ,解方程组得 l 1,l2的交点为 P(-2,6).第二步 ,在方程 3x-y+12=0中,令 x=0, 得 y=12, 进而获得 l1与 y 轴的交点为 A(0,12).第三步 ,在方程 3x+2y-6=0中,令 x=0, 得 y=3, 进而获得 l 2与 y 轴的交点为 B(0,3).第四步 ,求出△ABP 的边长 AB=12-3=9.第五步 ,求出△ABP 的边 AB 上的高 h=2.第六步 ,依据三角形的面积公式计算S=·AB·h=×9×2=9.第七步 ,输出 S.18.利用梯形的面积公式计算上底为 4, 下底为 6, 面积为 15 的梯形的高 . 请设计出该问题的算法及程序框图.【分析】依据梯形的面积公式S= (a+b)h,得h=,此中 a 是上底,b 是下底 ,h 是高 ,S 是面积 ,只需令 a=4,b=6,S=15,代入公式即可.算法以下 :第一步 ,输入梯形的两底a,b 与面积 S 的值 .第二步 ,计算 h=.第三步 ,输出 h.该算法的程序框图以下图:C组培优练 ( 建议用时 15 分钟 )19.履行以下图的程序框图所表达的算法 , 假如最后输出的 S值为, 那么判断框中实数 a 的取值范围是[2 015,2 016).20.运转以下图的程序框图 .(1) 若输入 x 的值为 2, 依据该程序的运转过程达成下边的表格, 并求输出的 i 与 x 的值 .第 i 次i=1i=2i=3i=4i=5ix=2×3(2)若输出 i 的值为 2, 求输入 x 的取值范围 .【分析】 (1)第 i 次i=1i=2i=3i=4i=5x=2 ×3 i61854162486由于 162<168,486>168,因此输出的 i 的值为 5,x 的值为 486.(2)由输出 i 的值为 2, 则程序履行了循环体 2 次,即解得<x ≤56.因此输入 x 的取值范围是.封闭 Word 文档返回原板块。
(压轴题)高中数学必修三第二章《算法初步》测试题(答案解析)(1)
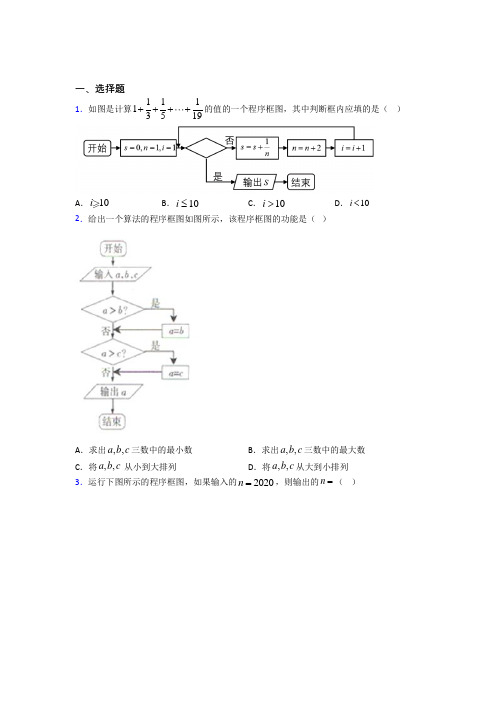
一、选择题1.如图是计算11113519++++的值的一个程序框图,其中判断框内应填的是( )A .10iB .10i ≤C .10i >D .10i < 2.给出一个算法的程序框图如图所示,该程序框图的功能是( )A .求出,,a b c 三数中的最小数B .求出,,a b c 三数中的最大数C .将,,a b c 从小到大排列D .将,,a b c 从大到小排列3.运行下图所示的程序框图,如果输入的2020n =,则输出的n =( )A.6 B.7 C.63 D.644.执行如图所示的程序框图,输出a的值为118,则ε的值可以是()A.0.06B.0.03C.0.2D.0.045.已知函数1()(1)g xx x=+,程序框图如图所示,若输出的结果1011S=,则判断框中可以填入的关于n的判断条件是()A . 10?n ≤B .10?n >C . 11?n ≤D . 11?n > 6.《张丘建算经》中如下问题:“今有马行转迟,次日减半,疾五日,行四百六十五里,问日行几何?”根据此问题写出如下程序框图,若输出465S =,则输入m 的值为( )A .240B .220C .280D .2607.在如图算法框图中,若6a =,程序运行的结果S 为二项式5(2)x +的展开式中3x 的系数的3倍,那么判断框中应填入的关于k 的判断条件是( )A .3k <B .3k >C .4k <D .4k > 8.某程序框图如图所示,则该程序运行后输出的值是( )A .3-B .3-C .3D .3 9.若正整数N 除以正整数m 后的余数为r ,则记为(,)Mod N m r =,例如(10,4)2Mod =.如图所示的程序框图的算法源于我国古代数学名著《孙子算经》中的“中国剩余定理”,则执行该程序框图输出的i =( )A .8B .18C .23D .3810.如图给出的是计算1111246102+++⋅⋅⋅+的值的一个程序框图,其中判断框中应填入的是( )A .102i >B .102i ≤C .100i >D .100i ≤ 11.定义语句“mod r m n =”表示把正整数m 除以n 所得的余数赋值给r ,如7mod31=表示7除以3的余数为1,若输入56m =,18n =,则执行框图后输出的结果为( )A .6B .4C .2D .112.执行如图所示的程序框图,若输入的6n =,则输出S =A.514B.13C.2756D.310二、填空题13.如图是一个算法流程图,则输出的S的值为______.14.执行如图所示的程序框图,输出的S值为__________.15.已知流程图如图,则输出的i=________.16.某程序流程框图如图所示,现执行该程序,输入下列函数()2sin 3f x x π=, ()2cos 3f x x π=,()4tan 3f x x π=,则可以输出的函数是()f x =__________.17.执行如图所示的程序框图,输出的T =______.18.如图所示的程序框图输出的值是 .19.阅读如图所示的程序框图,该程序输出的结果是__________.20.已知下列程序INPUTtIFt≤3TH ENC=0.2ELSEC=0.2+0.1*(t-3)ENDIFPRINTCEND当输入t=5时,输出结果是____.三、解答题21.已知函数1,00,03,0x xy xx x+>⎧⎪==⎨⎪--<⎩,设计一个算法,输入自变量x的值,输出对应的函数值.(1)请写出算法步骤;(2)画出算法框图.22.有关专家建议预测,在未来几年内,中国的通货膨胀率保持在3%左右,这将对我国经济的稳定有利无害.所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情况下,某种品牌的钢琴2015年的价格是10 000元,试分析其算法并用流程图描述这种钢琴今后四年的价格变化情况,并输出四年后的价格.23.已知函数f(x)=221(0)25(0)x xx x⎧-≥⎨-<⎩每输入一个x值,都得到相应的函数值,画出程序框图并写出程序.24.已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(x n,y n),…(1)若程序运行中输出的一个数组是(9,t),求t的值.(2)程序结束时,共输出(x ,y )的组数为多少?(3)写出程序框图的程序语句.25.已知函数y=21,0,1,0,x x x x ⎧>⎪⎪⎨⎪<⎪⎩设计一个算法的程序框图,计算输入x 的值,输出y 的值. 26.一队士兵来到一条有鳄鱼的深河的左岸,只有一条小船和两个小孩,这条船只能承载两个小孩或一个士兵.试设计一个算法,将这队士兵渡到对岸,并将这个算法用程序框图表示.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】 分析式子11113519++++的特征,可以得到程序框图的功能是求11113519S =++++的值,观察循环量i 的特征,得到结果.【详解】 由于程序框图的功能是求11113519S =++++的值, 分母n 的初值为1,终值为19,步长为2,故程序共执行10次,故循环变量i 的值不大于10时,应不满足条件,继续执行循环,大于10时,应满足条件,退出循环,故判断框内应填的是i >10,故选:C.【点睛】思路点睛:该题考查的是有关程序框图的问题,解题思路如下:(1)观察式子的特征,得到程序框图的功能; (2)由式子的项数,得到循环量i 的特征,得到结果.2.A解析:A 【分析】对a 、b 、c 赋三个不等的值,并根据程序框图写出输出的结果,可得知该程序的功能. 【详解】令2a =,3b =,1c =,则23>不成立,21>成立,则1a =,输出的a 的值为1, 因此,该程序的功能是求出a 、b 、c 三数中的最小数,故选A . 【点睛】本题考查程序框图的功能,解题的关键就是根据题意将每个步骤表示出来,考查分析问题的能力,属于中等题.3.A解析:A 【分析】根据题中所给的框图,模拟执行程序框图,求得结果. 【详解】输入2020100n =>,且不是奇数,赋值1010100n =>,且不是奇数, 赋值505100n =>,且是奇数,赋值252100n =>,且不是奇数, 赋值126100n =>,且不是奇数,赋值63100n =<, 赋值()2log 6316n =+=,输出6. 故选:A 【点睛】该题考查的是有关程序框图的问题,涉及到的知识点有计算程序框图的输出结果,属于简单题目.4.C解析:C 【分析】该程序是二分法求方程的近似解的方法,模拟执行程序框图,计算端点处的函数值,再由中点处的函数值,结合函数零点存在定理,即可得到所求值. 【详解】解:该程序是二分法求方程的近似根的方法, 由流程图可得()1120g =-<,()20f >,可得32m =,302f ⎛⎫< ⎪⎝⎭, 可得方程的根介于(1,2),进而介于31,2⎛⎫⎪⎝⎭,由52520416f ⎛⎫=-< ⎪⎝⎭,可得方程的根介于5(4,3)2,由118m =,1112120864f ⎛⎫=-< ⎪⎝⎭,可得方程的根介于11(8,3)2,由31110.2288-=<,可得输出的值为118, 故选:C . 【点睛】本题主要考查了程序框图和算法的应用,模拟执行程序框图,考查二分法求方程近似值的方法,属于基础题.5.A解析:A 【分析】按照程序框图执行几次,找出此框图的算法功能,再根据已知条件1011S =进一步判断框内条件即可. 【详解】按照程序框图依次执行:110,1,01122S n S ===+=-⨯ 1111112,11+12232233n S ==-+=--=-⨯以此类推,可得111S n =-+ . 若1011S =,可得10n =,若要输出1011S =,则判断框内应填10n ≤?. 故选:A. 【点睛】本题主要考查根据程序框图的输出结果判断程序框图中的选择条件,考查逻辑推理能力.6.A解析:A 【分析】根据程序框图,依次循环计算,可得输出的S 表达式.结合465S =,由等比数列求和公式,即可求得m 的值. 【详解】由程序框图可知,0,0S i ==,1S m i ==,22mS m i =+= ,324m mS m i =++=,4248m m mS m i =+++= ,524816m m m mS m i =++++= 此时输出S .所以46524816m m m mm ++++= 即1111146524816m ⎛⎫++++= ⎪⎝⎭由等比数列前n 项和公式可得5112465112m ⎛⎫- ⎪⎝⎭⨯=- 解得240m = 故选:A 【点睛】本题考查了循环结构程序框图的应用,等比数列求和的应用,属于中档题.7.C解析:C 【分析】根据二项式(2+x )5展开式的通项公式,求出x 3的系数,模拟程序的运行,可得判断框内的条件. 【详解】∵二项式5(2)x +展开式的通项公式是5152r r r r T C x -+=⋅⋅,令3r =,3233152T C x +∴=⋅⋅,332356(4)21408x x C x∴⨯⋅⋅=,∴程序运行的结果S 为120, 模拟程序的运行,由题意可得 k=6,S=1不满足判断框内的条件,执行循环体,S=6,k=5 不满足判断框内的条件,执行循环体,S=30,k=4 不满足判断框内的条件,执行循环体,S=120,k=3此时,应该满足判断框内的条件,退出循环,输出S 的值为120. 故判断框中应填入的关于k 的判断条件是k <4? 故选:C 【点睛】本题考查了二项式展开式的通项公式的应用问题,考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,属于中档题.8.D解析:D 【分析】 该框图的功能是计算:234562017sinsin sin sin sin sin sin3333333πππππππ+++++++,再根据正弦函数的周期性以及特殊角的三角函数值计算可得答案. 【详解】该框图的功能是计算:234562017sinsinsin sin sin sin sin3333333πππππππ+++++++.因为7132017sinsinsin sin 3333ππππ=====28142012sinsin sin sin3333ππππ=====, 39152013sinsin sin sin03333ππππ=====,410162014sin sin sin sin 3333ππππ=====,511172015sinsin sin sin33332ππππ=====-, 612182016sinsin sin sin 03333ππππ=====, 所以234562017sin sinsin sin sin sin sin3333333πππππππ+++++++3373363360336(336()336022222=⨯+⨯+⨯+⨯-+⨯-+⨯=. 故选:D 【点睛】本题考查了程序框图的循环结构,考查了三角函数的周期性以及特殊角的三角函数值,理解程序框图的功能是解题关键,属于基础题.9.C解析:C 【分析】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量i 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【详解】由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出同时满足条件: ①被3除余2, ②被5除余3, ③被7除余2, 故输出的i 为23, 故选C . 【点睛】本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.10.B解析:B 【解析】 【分析】根据题目所求表达式1111246102+++⋅⋅⋅+中最后一个数字1102,确定填写的语句.【详解】由于题目所求是1111246102+++⋅⋅⋅+,最后一个数字为1102,即当102i =时,判断是,继续循环,2104i i =+=,判断否,退出程序输出S 的值,由此可知应填102i ≤.故选B. 【点睛】本小题主要考查填写程序框图循环条件,属于基础题.11.C解析:C 【解析】 【分析】模拟执行程序框图,只要按照程序框图规定的运算方法逐次计算,直到达到输出条件即可得到输出的m 的值. 【详解】第一次进入循环,因为56除以18的余数为2,所以2r,18m =,2n =,判断r 不等于0,返回循环;第二次进入循环,因为18除以2的余数为0, 所以0r =,2m =,0n =,判断r 等于0, 跳出循环,输出m 的值为2.故选C. 【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要12.B解析:B 【解析】 【分析】首先确定流程图所实现的功能,然后利用裂项求和的方法即可确定输出的数值. 【详解】由流程图可知,程序输出的值为:1111023344556S =++++⨯⨯⨯⨯, 即1111111123344556S ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭111263=-=. 故选B . 【点睛】本题主要考查流程图功能的识别,裂项求和的方法等知识,意在考查学生的转化能力和计算求解能力.二、填空题13.【解析】【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S 的值模拟程序的运行过程分析循环中各变量值的变化情况可得答案【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循 解析:7【解析】 【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S 的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案. 【详解】模拟程序的运行,可得1S =,1i =满足条件4i <,执行循环体,2S =,2i = 满足条件4i <,执行循环体,4S =,3i = 满足条件4i <,执行循环体,7S =,4i =此时,不满足条件4i <,退出循环,输出S 的值为7. 故答案为7. 【点睛】本题主要考查程序框图的循环结构流程图,属于中档题. 解决程序框图问题时一定注意以下几点:(1) 不要混淆处理框和输入框;(2) 注意区分程序框图是条件分支结构还是循环结构;(3) 注意区分当型循环结构和直到型循环结构;(4) 处理循环结构的问题时一定要正确控制循环次数;(5) 要注意各个框的顺序,(6)在给出程序框图求解输出结果的试题中只要14.37【解析】根据图得到:n=18S=19n=12S=31n=6S=37n=0判断得到n>0不成立此时退出循环输出结果37故答案为:37解析:37 【解析】根据图得到:n=18,S=19,n=12 S=31,n=6,S=37,n=0,判断得到n>0不成立,此时退出循环,输出结果37. 故答案为:37.15.9【解析】根据流程图可得:否;否;否;否;是输出故答案为9解析:9 【解析】根据流程图可得:1,3S i ==,否,133S =⨯=,3i =;否339S =⨯=,5i =; 否9545S =⨯=,7i =;否457315S =⨯=,9i =;是输出9i =,故答案为9.16.【分析】根据得知函数的图象关于点对称由可得知函数的周期为于此可在题中三个函数中找出合乎条件的函数作出输出结果【详解】可知函数的图象关于点对称由得所以函数的周期为由三角函数的周期公式可知函数和的最小正解析:()2cos 3f x x π=. 【分析】 根据()302f x f x ⎛⎫+--= ⎪⎝⎭得知函数()y f x =的图象关于点3,04⎛⎫- ⎪⎝⎭对称,由()f x + 302f x ⎛⎫+= ⎪⎝⎭可得知函数()y f x =的周期为3,于此可在题中三个函数中找出合乎条件的函数作出输出结果. 【详解】()302f x f x ⎛⎫+--= ⎪⎝⎭,可知函数()y f x =的图象关于点3,04⎛⎫- ⎪⎝⎭对称,由()302f x f x ⎛⎫++=⎪⎝⎭,得()3322f x f x f x ⎛⎫⎛⎫+=-=- ⎪ ⎪⎝⎭⎝⎭,所以函数()y f x =的周期为3.由三角函数的周期公式可知,函数()2sin3f x x π=和()2cos 3f x x π=的最小正周期为3,函数()4tan3f x x π=的最小正周期为34,不合乎要求; 对于函数()2sin3f x x π=,323sin sin 04342f ππ⎡⎤⎛⎫⎛⎫-=⨯-=-≠ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦;对于函数()2cos3f x x π=,323cos cos 04342f ππ⎡⎤⎛⎫⎛⎫⎛⎫-=⨯-=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,合乎题意. 所以,函数()2cos3f x x π=的图象关于点3,04⎛⎫- ⎪⎝⎭对称, 故输出的函数为()2cos 3f x x π=,故答案为()2cos 3f x x π=. 【点睛】本题考查程序框图,考查三角函数的周期性和对称性,能根据抽象函数关系式得出函数的基本性质,是解本题的关键,属于中等题.17.16【解析】第一次运行:;第二次运行:;第三次运行:此时程序结束所以输出的解析:16 【解析】第一次运行:1,145,123,134T S S n T ===+==+==+=;第二次运行:45,549,325,459T S S n T =<==+==+==+=;第三次运行:9,9413,527,9716T S S n T ===+==+==+=.此时1613T S =>=,程序结束,所以输出的16T =18.144【分析】直接利用循环结构计算循环各个变量的数值当满足判断框的条件推出循环输出结果【详解】判断前第1次判断循环;第2次判断循环第3次判断循环;第4次判断循环;第5次判断循环;第6次判断循环;第7解析:144 【分析】直接利用循环结构,计算循环各个变量的数值,当10k =满足判断框的条件,推出循环,输出结果. 【详解】判断前,2c =,第1次判断循环,1,2,2,3a b k c ====; 第2次判断循环,2,3,3,5a b k c ==== 第3次判断循环,3,5,4,8a b k c ====; 第4次判断循环,5,8,5,13a b k c ====; 第5次判断循环,8,13,6,21a b k c ====; 第6次判断循环,13,21,7,34a b k c ====; 第7次判断循环,21,34,8,55a b k c ====; 第8次判断循环,34,55,9,89a b k c ====; 第9次判断循环,55,89,10,144a b k c ====; 第10次判断不满足判断框条件,退出循环,输出144c =, 故答案为144. 【点睛】本题考查循环结构的应用,注意每一步循环的变量的数值,计算准确是解题的关键.19.120【分析】由题意首先确定程序的功能然后计算其输出结果即可【详解】由题意可得题中流程图的功能为计算的值据此计算可得输出的结果为故答案为120【点睛】识别运行程序框图和完善程序框图的思路:(1)要明解析:120 【分析】由题意首先确定程序的功能,然后计算其输出结果即可. 【详解】由题意可得,题中流程图的功能为计算12345S =⨯⨯⨯⨯的值, 据此计算可得输出的结果为120S =. 故答案为120. 【点睛】识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)要识别、运行程序框图,理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证.20.4【分析】由已知中的程序语句可知该程序的功能是计算分段函数 的值将t=5代入即可得到答案【详解】由已知中程序语句可知该程序的功能是: 计算分段函数 的值 故答案为04【点睛】算法是新课标高考的一大解析:4 【分析】由已知中的程序语句可知该程序的功能是计算分段函数 0.2,30.20.1(3),3t C t t ≤⎧=⎨+->⎩的值,将t =5代入即可得到答案. 【详解】由已知中程序语句可知该程序的功能是: 计算分段函数 0.2,30.20.1(3),3t C t t ≤⎧=⎨+->⎩的值50.20.1(53)0.4t C =∴=+-=,故答案为0.4. 【点睛】算法是新课标高考的一大热点,其中算法的交汇性问题已成为高考的一大亮,这类问题常常与函数、数列、不等式等交汇自然,很好地考查考生的信息处理能力及综合运用知识解决问題的能力,解决算法的交汇性问题的方:(1)读懂程序框图、明确交汇知识,(2)根据给出问题与程序框图处理问题即可.三、解答题21.(1)详见解析;(2)详见解析 【分析】(1)根据分段函数求值时的运算步骤,先判断自变量所在的范围,然后带入对应的解析式中求解,即可写出算法; (2)根据算法即可画出算法框图. 【详解】解:(1)算法如下: 第一步,输入自变量x 的值.第二步,判断0x >是否成立,若成立,计算1y x =+,否则,执行下一步. 第三步,判断0x =是否成立,若成立,令0y =,否则,计算3y x =--. 第四步,输出y .(2)算法框图如下图所示.【点睛】本题主要考查利用条件结构设计算法求分段函数的值,以及绘制算法框图,属于中档题. 22.见解析 【解析】 【分析】用P(单位:元)表示钢琴的价格,根据指数函数的性质写出算法步骤,进而得到流程图. 【详解】用P(单位:元)表示钢琴的价格,算法步骤如下: 2016年 P =10 000×(1+3%)=10 300(元); 2017年 P =10 300×(1+3%)=10 609(元); 2018年 P =10 609×(1+3%)=10 927.27(元); 2019年 P =10 927.27×(1+3%)=11 255.088 1(元). 因此,价格的变化情况表为: 年份 2015 2016 2017 2018 2019 钢琴的10 00010 30010 60910 927.2711 255.088 1价格【点睛】本题考查苏菲的设计及流程图,属基础题.23.见解析【分析】由条件可得函数为分段函数,这样就要进行判断,然后进行求解【详解】用变量x y ,分别表示自变量和函数值,步骤如下:第一步,输入x 的值第二步,判断x 的范围,若0x ≥,则用解析式21y x =-求函数值;否则,用225y x =-求函数值第三步,输出y 的值程序框图和程序如下.【点睛】本题考查的知识点是设计程序解决问题,由已知条件不难发现函数为分段函数,故需要进行对输入值的判定,然后再代入求解.24.(1)-4;(2)1009;(3)答案见解析.【解析】试题分析:(1)利用所给的程序框图运行程序可得当x=9时,y=-4,则t 的值为-4.(2)结合程序的算法和循环结构的特点可知共输出(x ,y )的组数为1009;(3)将所给的程序框图翻译为算法语句,利用循环语句设计相应的程序即可,注意循环语句应设计为DO 语句的形式.试题(1)由程序框图知,当x=1时,y=0;当x=3时,y=-2;当x=9时,y=-4,所以t=-4.(2)当n=1时,输出一对,当n=3时,又输出一对,…,当n=2 017时,输出最后一对,共输出(x ,y )的组数为20182=1 009. (3)程序框图的程序语句如下:x =1y =0n =1DOPRINT (x ,y )n =n +2x =3*xy =y -2LOOP UNTIL n >2 017END点睛:程序框图的条件结构和循环结构分别对应算法语句的条件语句和循环语句,两种语句的阅读理解是复习重点.输入、输出和赋值语句是任何一个算法必不可少的语句,一个语句可以输出多个表达式.在赋值语句中,一定要注意其格式的要求,如“=”的右侧必须是表达式,左侧必须是变量;一个语句只能给一个变量赋值;变量的值始终等于最近一次赋给它的值,先前的值将被替换.25.答案见解析【解析】【试题分析】主要结构是有一个选择结构,当0x >时为1x,当0x <时为21x ,当0x =时直接退出程序.【试题解析】根据题意,其自然语言算法如下.第一步,输入x.第二步,判断x>0是否成立.若成立,则输出y=1x,结束算法; 若不成立,则判断x<0是否成立.若成立,则输出y=21x ,结束算法;若不成立,也结束算法. 程序框图如右:【点睛】画程序框图的规则如下:(1)一个完整的程序框图必须有起止框,用来表示程序的开始和结束.(2)使用标准的图形符号表示操作,带箭头的流程线表示算法步骤的先后顺序,框图一般按从上到下、从左到右的方向画(3)算法中间要处理数据或计算,可分别写在不同的处理框中.(4)如果一个流程由于纸面等原因需要分开画.要在断开处画上连结点,并标出连结的号码.如图一.实际 上它们是同一点,只是化不才分开画.用连结点可避免流程线的交叉或过长,使流程图清晰.(5)注释框不是流程图必需的部分,只是为了提示用户 一部分框图的作用以及对某些框图的操作结果进行说明.它帮助阅读流程图的用户更好的理解流程图的来龙去脉.(6)在图形符号内用于描述的语言要非常简练清楚26.答案见解析【解析】试题分析:利用已知条件写出算法,再写成程序框图.试题第1步,两个儿童将船划到右岸;第2步,他们中间一个上岸,另一个划回来;第3步,儿童上岸,一个士兵划过去;第4步,士兵上岸,让儿童划回来;第5步,如果左岸没有士兵,那么结束,否则转第1步.程序框图如图所示.。
人教A版高中数学必修三试卷第一章 算法初步训练题.docx

1a = 3b = a a b =+ b a b =- PRINT a ,b (第9题)i=1 s=0 WHILE i<=4 s=s*x+1 i=i+1 WEND PRINT s END (第8题)第一章 算法初步训练题(时间:85分钟 满分:100分)一、选择题(本大题共12小题,每小题3分,共36分)1.算法的三种基本结构是( )A .顺序结构、条件结构、循环结构B .顺序结构、循环结构、模块结构C .顺序结构、模块结构、条件结构D .模块结构、条件结构、循环结构2.用二分法求方程022=-x 的近似根的算法中要用哪种算法结构( )A .顺序结构B .条件结构C .循环结构D .以上都用3.给出一个算法bc ad d c ba -=,那么4231的值等于( )A .-2B .-1C .1D .24.将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( )A. B. C. D.5.下列给出的赋值语句中正确的是( ) A .4M = B .M M =- C .3B A == D .0x y +=6.给出以下四个问题,①x , 输出它的相反数. ②求面积为6的正方形的周长.③求三个数,,a b c 中输入一个数的最大数.④求函数1,0()2,0x x f x x x -≥⎧=⎨+<⎩的函数值. 其中不需要用条件语句来描述其算法的有 ( ) A. 1个 B. 2个 C. 3个 D. 4个7.用“辗转相除法”求得459和357的最大公约数是( )A .3B .9C .17D .518.当2=x 时,下面的程序段结果是 ( )A .3B .7C .15D .179.计算机执行下面的程序段后,输出的结果是( ) A .1,3 B .4,1 C .0,0 D .6,010.当3=a 时,下面的程序段输出的结果是( )A .9B .3C .10D .6a=b b=a c=b b=a a=c b=a a=b a=c c=b b=an=5 s=0 WHILE s<15 S=s + n n=n -1 WEND PRINT n END (第11题) IF 10a < THEN 2y a =* else y a a =* PRINT y (第10题) INPUT ”a,b,c=”;a,b,c IF b>a THEN t=a a=b b=t END IF IF c>a THEN t=a a=c c=t END IF IF c>b THEN t=b b=cc=t END IF PRINT a,b,c END (第18题) 11.右边程序执行后输出的结果是( )A.1- B .0 C .1 D .2 12. 右边程序运行后输出的结果为( ) A. 50B. 5C. 25D. 0 二、填空题(本大题共6小题,每小题4分,共24分)13.用“秦九韶算法”计算多项式12345)(2345+++++=x x x x x x f ,当x=2时的值的过程中,要经过 次乘法运算和 次加法运算.14. 二进制数111.11转换成十进制数是_________________.15.下列各数)9(85、)6(210、)4(1000、)2(111111中最小的数是___________.16.下图给出的是计算201614121++++ 的值的一个流程图,其中判断框内应填入的条件是____________。
人教A版高中数学必修三试卷 第一章 算法初步测试题 .doc
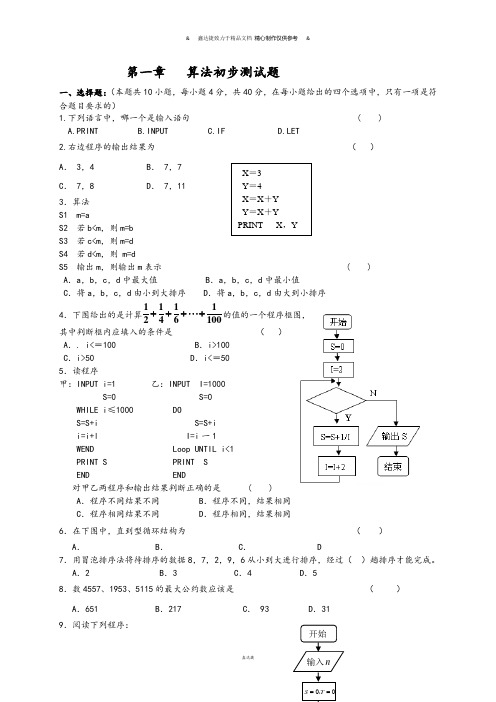
第一章 算法初步测试题一、选择题:(本题共10小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列语言中,哪一个是输入语句 ( ) A.PRINT B.INPUT C.IF D.LET2.右边程序的输出结果为 ( ) A . 3,4 B . 7,7 C . 7,8 D . 7,113.算法 S1 m=aS2 若b<m ,则m=b S3 若c<m ,则m=d S4 若d<m ,则 m=dS5 输出m ,则输出m 表示 ( ) A .a ,b ,c ,d 中最大值 B .a ,b ,c ,d 中最小值C .将a ,b ,c ,d 由小到大排序D .将a ,b ,c ,d 由大到小排序4.下图给出的是计算0101614121+⋅⋅⋅+++的值的一个程序框图, 其中判断框内应填入的条件是 ( )A .. i<=100B .i>100C .i>50D .i<=50 5.读程序甲:INPUT i=1 乙:INPUT I=1000 S=0 S=0 WHILE i ≤1000 DOS=S+i S=S+i i=i+l I=i 一1 WEND Loop UNTIL i<1 PRINT S PRINT SEND END对甲乙两程序和输出结果判断正确的是 ( ) A .程序不同结果不同 B .程序不同,结果相同 C .程序相同结果不同 D .程序相同,结果相同6.在下图中,直到型循环结构为 ()A .B .C . D7.用冒泡排序法将待排序的数据8,7,2,9,6从小到大进行排序,经过( )趟排序才能完成。
A .2 B .3 C .4 D .58.数4557、1953、5115的最大公约数应该是 ( ) A .651 B .217 C . 93 D .31 9.阅读下列程序:X =3 Y =4 X =X +Y Y =X +YPRINT X ,Ya=0 j=1WHILE j<=5 a=(a+j) mod 5 j=j+1 WEND PRINT a END(第13题)输入x ;if x <0, then y =32x π+;else if x >0, then y =52x π-;else y =0; 输出 y .如果输入x =-2,则输出结果y 为A .3+πB .3-πC .π-5D .-π-510.阅读右边的程序框,若输入的n 是100,则输出的 变量S 和T 的值依次是 ( ) A .2550,2500 B .2550,2550 C .2500,2500 D .2500,255011. 用秦九韶算法计算多项式654323567983512)(x x x x x x x f ++++-+=在4-=x 时的值时,3V 的值为 :A. -845B. 220C. -57D. 34 12. 用“辗转相除法”求得459和357的最大公约数是:A .3B .9C .17D .51 、填空题:(本大题共4小题,每小题5分,共20分 )13. 下列关于算法的说法,正确的是 。
人教A版高中数学必修三试卷安微师范大学附属中学高中第一章算法初步《1.1算法与程序框图》同步测试题.docx

高中数学学习材料鼎尚图文*整理制作《1.1 算法与程序框图(1)》同步测试题初稿:叶祥才(安徽师范大学附属中学) 修改:姚有胜(安徽省庐江中学) 审校:王冲(安徽省含山二中)一、选择题1.下列关于算法的描述正确的是( ).A.算法与求解一个问题的方法相同B.一个算法只能解决一个问题,不能重复使用C.算法过程要一步一步执行,每步执行的操作必须确切D.解决一类问题的算法只有一个考查目的:考查算法的概念.答案:C.解析:算法通常是指按照一定的规则解决某一类问题的明确的有限的步骤,明确性和有限性是算法的基本特征.解决某一个问题的算法可能不止一个.2.任何程序框图中都不可缺少的是( ).A.输入框B.处理框C.判断框D.起止框考查目的:考查程序框图的有关概念.答案:D.解析:程序框图主要由程序框和流程线组成.基本的程序框有起止框,输入、输出框,处理框,判断框,其中起止框是任何程序框图中不可缺少的.3.如图给出了一个算法程序框图,该算法程序框图的功能是( ).A.求三数中的最大数B.求三数中的最小数C.将按从小到大排列D.将按从大到小排列考查目的:考查对程序框图中条件结构的理解.答案:B.解析:通过框图可知,该程序框图的功能是求三个数中的最小数.二、填空题4.顺序结构是由______________组成的,这是任何一个算法都离不开的基本结构.考查目的:考查顺序结构的定义.答案:若干个依次执行的步骤.解析:顺序结构的概念.5.求实数x的绝对值的算法程序框图如图所示,则判断框①中可填 .考查目的:考查条件结构的应用.答案:x>0(或x>0? 或x≥0 或x≥0?).解析:利用绝对值的定义及条件结构的表示.6.执行如图所示的程序框图,输入,,,则输出的的值是________.考查目的:考查条件结构的应用.答案:68.解析:当输入,,时,不满足,因此执行:.由于,故执行.执行后,再执行一次后,的值为173-105=68,此时不成立,故输出68.三、解答题:7.如下算法:第一步,输入的值.第二步,若成立,则.第三步,否则,.第四步,输出的值.若输出的值为4,求输入的值.考查目的:考查分段函数类型的算法.答案:-2或4.解析:由所给的算法可知,该算法执行的功能是给定值,求分段函数的函数值.若,则;若,则,8.函数,写出求该函数的函数值的算法,并画出程序框图.考查目的:考查条件结构及分段函数程序框图的画法.答案:见解析.解析:算法如下:第一步,输入.第二步,如果,则.如果,则;如果,则.第三步,输出函数值.相应的程序框图如下图.《1.1 算法与程序框图(2)》同步测试题初稿:叶祥才(安徽师范大学附属中学) 修改:姚有胜(安徽省庐江中学) 审校:王冲(安徽省含山二中)一、选择题1.阅读下面的程序框图,运行相应的程序,则输出s的值为( ).A.-1B.0C.1D.3考查目的:条件结构与直到型循环结构的基本应用.答案:B.解析:第一次运行程序时i=1,s=3;第二次运行程序时,i=2,s=4;第三次运行程序时,i=3,s=1;第四次运行程序时,i=4,s=0,此时执行i=i+1后i=5,退出循环,输出s=0.2.阅读下面所示的程序框图,运行相应的程序,输出的s值等于( ) .考查目的:当型循环结构的基本应用.答案:-3.解析:可以列表如图,循环次数初始123s110-3k1234易知结果为-3.3.如果执行如图所示的程序框图,输入n=6,m=4,那么输出的p值为( ).A.720B.360C.240D.120考查目的:当型循环结构的应用.答案:B.解析:由框图可知:当n=6,m=4时,第一次循环:p=(6-4+1)×1=3,k=2.第二次循环:p=(6-4+2)×3=12,k=3.第三次循环:p=(6-4+3)×12=60,k=4.第四次循环:p=(6-4+4)×60=360,此时k=m,终止循环,输出p=360.二、填空题4.循环结构是指从某处开始,按照一定的条件 _____某些步骤的情况,这些步骤称为__ __;循环结构又分为_______ __和___ _____.考查目的:考查循环结构的概念.答案:反复执行,循环体,当型,直到型.解析:利用循环结构的概念.5.若某程序框图如图所示,则该程序运行后输出的k的值是__________.考查目的:考查直到型循环结构.答案:5.解析:初始值:k=2,执行“k=k+1”得k=3,a=43=64,b=34=81,a >b不成立;k=4,a=44=256,b=44=256,a>b不成立;k=5,a=45=1 024,b=54=625,a>b成立,此时输出k=5.6.如图的程序框图中,语句1将被执行的次数为________.考查目的:循环体执行次数的计算.答案:34.解析:执行.三、解答题7.对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据,具体如下表所示:为aii 1 2 3 4 5 6 7 8a40 41 43 43 44 46 47 48i在对上述统计数据的分析中,一部分计算见如图所示的程序框图(其中是这8个数据的平均数),求输出的S的值.考查目的:利用循环结构解决实际问题.答案:7.解析:∵=44,∴S=[(40-44)2+(41-44)2+…+(48-44)2]=7.8.写出求1×2×3×4×…×100的一个算法并画出程序框图.考查目的:利用循环结构解决累乘求值问题.答案:见解析.解析:数学中的累加、累乘、累差等重复性操作可以用循环结构来实现.循环结构分当型和直到型两种,二者的区别:前者是,当满足条件时执行循环体,而后者是“直到”条件满足时结束循环.第一步,设S的值为1.第二步,设i的值为2.第三步,如果i≤100执行第四步,否则转去执行第七步.第四步,计算S乘i并将结果赋给S.第五步,计算i加1并将结果赋给i.第六步,执行第三步.第七步,输出S的值并结束算法.根据自然语言描述,程序框图如下图.。
人教A版高中数学必修三试卷第一章算法初步§1.1习题课.docx

§1.1习题课课时目标1.理解并掌握画程序框图的规则.2.在具体问题的解决过程中,理解程序框图的三种基本逻辑结构.3.能正确选择并运用三种逻辑结构框图表示具体问题的算法.1.下列关于程序框图的描述①对于一个算法来说程序框图是唯一的;②任何一个框图都必须有起止框;③程序框图只有一个入口,也只有一个出口;④输出框一定要在终止框前.其中正确的有()A.1个B.2个C.3个D.4个答案 B解析②、③正确,对于一个算法来说,程序框图不唯一,与设计有关,故①错.输入输出的位置,不一定在开始和结束处,故④错.2.某程序框图如图所示,该程序运行后输出的k的值是()A.4 B.5答案 A解析 当k =0时,S =S =k =1, 当S =1时,S =1+21=k =2, 当S =3时,S =3+23=k =3,当S =11时,k =4,S =11+211>100,故k =4.3.如图是一个算法的程序框图,该算法所输出的结果是( )A.12B.23C.34D.45 答案 C解析 运行第一次的结果为n =0+11×2=12;第二次n =12+12×3=23;第三次n =23+13×4=34.此时i =4程序终止, 即输出n =34.4.阅读下边的程序框图,若输出s 的值为-7,则判断框内可填写( )A .i <3?B .i <4?答案 D解析 i =1,s =2;s =2-1=1,i =1+2=3; s =1-3=-2,i =3+2=5; s =-2-5=-7,i =5+2=7.因输出s 的值为-7,循环终止,故判断框内应填“i <6?”. 5.求边长为3,4,5的直角三角形的内切圆半径的算法为: 第一步 输入__________________; 第二步 计算r =a +b -c2;第三步 输出r .答案 a =3,b =4,c =56.根据下面的程序框图操作,使得当成绩不低于60分时,输出“及格”,当成绩低于60分时,输出“不及格”,则框1中填________,框2中填________.答案 是 否解析 由x ≥60与及格对应知1处填是,则2处填否.一、选择题1.一个完整的程序框图至少包含( ) A .终端框和输入、输出框 B .终端框和处理框 C .终端框和判断框D .终端框、处理框和输入、输出框 答案 A解析 一个完整的程序框图至少需包括终端框和输入、输出框. 2.下列程序框图表示的算法是( )A .输出c ,b ,aB .输出最大值C .输出最小值D .比较a ,b ,c 的大小 答案 B解析 根据程序框图可知,此图应表示求三个数中的最大数.3.用二分法求方程的近似根,精确度为δ,用直到型循环结构的终止条件是( ) A .|x 1-x 2|>δ B .|x 1-x 2|<δ C .x 1<δ<x 2 D .x 1=x 2=δ 答案 B解析 直到型循环结构是先执行、再判断、再循环,是当条件满足时循环停止,因此用二分法求方程近似根时,用直到型循环结构的终止条件为|x 1-x 2|<δ.4.阅读如图所示的程序框图,运行相应的程序,则输出的i 值等于( )A .2B .3C .4D .5 答案 CS=0→i =1→a =2 →S =2→i =2→a =8 →S =10→i =3→a =24 →S =34→i =4→输出i =4.5.如图给出的是计算12+14+16+…+1100的值的一个程序框图,其中判断框内应填入的条件是( )A .i ≥49?B .i ≥50?C .i ≥51?D .i ≥100? 答案 C解析 i =1时,S =0+12=12,i =2时,S =12+14,…,i =50时,S =12+14+16+…+1100,当i =51时结束程序,故选C.6.读如图所示的程序框图则循环体执行的次数为( )A .50B .49C .100D .99 答案 B解析 ∵i =i +2,∴当2+2n ≥100时循环结束此时n =49,故选B. 二、填空题7.直到型循环结构框图为________.答案 ②8.已知下列框图,若a =5,则输出b =________.答案 26解析 因a =5,所以5>5不成立, 判断框执行“否”,即b =52+1=26.9.执行如图所示的程序框图,若输入x =4,则输出y 的值为________.答案 -54解析 当输入x =4时, 计算y =12x -1,得y =1.不满足|y -x |<1.于是得x =1, 此时y =12-1=-12,不满足|-12-1|<1,此时x =-12,又推得y =-54.这样|y -x |=|-54+12|=34<1,执行“是”,所以输出的是-54.三、解答题10.已知点P 0(x 0,y 0)和直线l :Bx +By +C =0,写出求点P 0到直线l 的距离d 的算法并画出程序框图.解 (1)用数学语言来描述算法:第一步,输入点的坐标x 0,y 0,输入直线方程的系数即常数B ,B ,C ; 第二步,计算z 1=Bx 0+By 0+C ; 第三步,计算z 2=B 2+B 2;第四步,计算d =|z 1|z 2;第五步,输出d .(2)用程序框图来描述算法,如图:11.画出求满足12+22+32+…+i 2>106的最小正整数n 的程序框图. 解 程序框图如下:能力提升12.一队士兵来到一条有鳄鱼的深河的左岸.只有一条小船和两个小孩,这条船只能承载两个小孩或一个士兵.试设计一个算法,将这队士兵渡到对岸,并将这个算法用程序框图表示.解 第1步,两个儿童将船划到右岸;第2步,他们中一个上岸,另一个划回来;第3步,儿童上岸,一个士兵划过去;第4步,士兵上岸,让儿童划回来;第5步,如果左岸没有士兵,那么结束,否则转第1步.程序框图如图所示.13.某工厂2010年生产轿车200万辆,技术革新后预计每年的产量比上一年增加5%,问最早哪一年生产的轿车超过300万辆?试设计算法并画出相应的程序框图.解算法如下:第一步:n=2 010;第二步:a=200;第三步:T=0.05a;第四步:a=a+T;第五步:n=n+1;第六步:若a>300,输出n.否则执行第三步.程序框图:1.程序框图是用规定的图形、指向线及文字说明表示算法的图形,因此首要任务应是会画基本的程序框图并熟知它们的功能.2.画程序框图必须遵守一些共同的规则:(1)使用框图的符号要标准.(2)框图一般按从上到下、从左到右的顺序画.(3)除了判断框外,大多数框图符号只有一个进入点和一个退出点,判断框是唯一具有超过一个退出点的框图符号.(4)判断框有两种:一种是“是”与“否”两个分支的判断,而且有且仅有两个结果;另一种是多分支判断,有几种不同的结果,这种判断框中学阶段很少用到.(5)在图形符号内描述的语言要简练清楚.。
2020-2021人教版数学3章末综合测评1算法初步含解析

2020-2021学年人教A版数学必修3章末综合测评1算法初步含解析章末综合测评(一)算法初步(满分:150分时间:120分钟)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.下面对算法的描述正确的一项是()A.算法只能用自然语言来描述B.算法只能用图形语言来表示C.同一问题可以有不同的算法D.同一问题的算法不同,结果必然不同[答案]C2.执行如图所示的程序框图,若输出结果为1,则可输入的实数x值的个数为()A.1 B.2C.3 D.4B[根据题意,该框图的含义是:当x≤2时,得到函数y=x2-1;当x>2时,得到函数y=log2x,因此,若输出的结果为1时,若x ≤2,得到x 2-1=1,解得x =±错误!,若x >2,得到log 2x =1,无解,因此,可输入的实数x 的值可能为-错误!,错误!,共有2个.故选B.]3.下列算法语句正确的是( )A .输出语句PRINT A =4B .输入语句INPUT x =3C .赋值语句A =A *A +A -3D .赋值语句55=aC [输入语句、输出语句中输入、输出的是变量或数值,而不是等式.A 、B 均错;赋值语句格式是“变量=表达式”,D 错;C 对.]4.用辗转相除法,计算56和264的最大公约数时,需要做的除法次数是( )A .3B .4C .6D .7B [由辗转相除法264=56×4+40,56=40×1+16,40=16×2+8,16=8×2,即最大公约数为8,做4次除法.]5.下列各进制数中,最小的是( )A .1 002(3)B .210(6)C .1 000(4)D .111 111(2)A [1 002(3)=29,210(6)=78,1 000(4)=64,111 111(2)=63,故1002最小.](3)6.对于程序:试问,若输入m=-4,则输出的数为()A.9 B.-7C.5或-7 D.5D[由程序,先输入m,判断m>-4是否成立,因为m=-4,所以不成立,则执行m=1-m,最后输出结果为5。
人教A版高中数学必修三试卷第一章 算法初步 单元测试题.docx

桑水第一章 算法初步 单元测试题命题人:李军芳 印数:450(文) 时间:2013.01.073. 给出以下四个问题,①输入一个数x ,输出它的相反数.②求面积为6的正方形的周长.③求三个数a,b,c 中的最大数.④求函数0.10.2{)(≥-<+= x x x x x f 的函数值.其中不需要用条件语句来描述其算法的有 ( )A. 1个B. 2个C. 3个D. 4个4. 下面为一个求20个数的平均数的程序,在横线上应填充的语句为 ( )A .i>20B .i<20C .i>=20 S=0 i=1 DO INPUT x S=S+x i=i+1 LOOP UNTIL _____a=S/20PRINT aEND桑水D .i<=205.下面关于这个框图说明正确的是( )A .这是一个循环结构,属直到型B .这是一个当型循环结构C .这是一个条件结构D .这是一个条件结构与循环结构相混合的结构6. 将389 化成四进位制数的末位是 ( )A. 1B. 2C. 3D. 07. 下列各数中最小的数是 ( )A .)9(85B .)6(210C .)4(1000D .)2(1111118. 用秦九韶算法计算多项式1876543)(23456++++++=x x x x x x x f 当4.0=x 时的值时,需要做乘法和加法的次数分别是 ( )A. 6 , 6B. 5 , 6C. 5 , 5D. 6 , 59. 用秦九韶算法计算多项式654323567983512)(x x x x x x x f ++++-+=在4-=x 时的值时,()4-f 的值为 ( )A. -845B. 220C. -57D. 3410. 下左程序运行后输出的结果为 ( )A. 50B. 5C. 25D. 0a=0 j=1 WHILE j<=5 a=(a+j) MOD 5 j=j+1 WEND PRINT a END 第10题 x=1 y=1 WHILE x<=4 Z=0 WHILE y<=x+2 Z=Z+1 y=y+1 WEND PRINT Z x=x+1 y=1 WEND END 第11题桑水11. 上右程序运行后输出的结果为 ( )A. 3 4 5 6B. 4 5 6 7C. 5 6 7 8D. 6 7 8 9二、填空题.(每小题5分,10分)12. 下左程序运行后输出的结果为_________________________.13.上右程序输出的n 的值是_____________________.三、解答题: (注意:解答题必须要写出必要的文字说明或步骤)14. 用辗转相除法或者更相减损术求三个数 324 , 243 , 135 的最大公约数.15. 设计一个计算1+2+3+…+100的值的算法,并画出相应的程序框图.(要求用循环结构)x=5 y=-20 IF x<0 THEN x=y -3 ELSE y=y+3 END IF PRINT x -y ; y -x END 第12题 j=1 n=0 WHILE j<=11 j=j+1 IF j MOD 4=0 THEN n=n+1 END IF j=j+1 WEND PRINT n END 第13题桑水 16. 已知函数 ⎪⎩⎪⎨⎧=11-31-2x x x y ()()()101011≥<≤<x x x , 编写一程序求函数值.17.给出30个数:1,2,4,7,……,其规律是:第1个数是1,第2个数比第1个数大1, 第3个数比第2个数大2,第4个数比第3个数大3,依此类推.要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),(I )请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能;(II )根据程序框图写出程序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学学习材料
金戈铁骑整理制作
算法初步测试题(一)班级——姓名——
一、选择题:
1.下列语句中是算法的个数为()
①从济南到巴黎:先从济南坐火车到北京,再坐飞机到巴黎;
②统筹法中“烧水泡茶”的故事;
③测量某棵树的高度,判断其是否是大树;
④已知三角形的一部分边长和角,借助正余弦定理求得剩余的边角,再利用三角形的面
积公式求出该三角形的面积。
A.1 B.2 C.3 D.4
2.下列说法正确的是()
A.算法就是某个问题的解题过程;
B.算法执行后可以产生不同的结果;
C.解决某一个具体问题算法不同结果不同;
D.算法执行步骤的次数不可以为很大,否则无法实施。
3.给出以下四个问题, ()
①输入一个数x,输出它的相反数. ②求面积为6的正方形的周长.
③求三个数a,b,c中的最大数. ④判断一个数是否为质数
其中不需要用条件语句来描述其算法的有()A.1个B.2个C.3个D.4个
4.为解决四个村庄用电问题,政府投资在已建电厂与这四个村庄之间架设输电线路,现已知这四个村庄及电厂之间的距离如图所示(距离单位:公里)则能把电力输送到这四个村庄的输电线路的最短总长度应该是()
A.19.5 B.20.5 C.21.5 D.25.5
5.任何一个算法都必须有的基本结构是()
A.顺序结构B.条件结构C.循环结构D.三个都有
二、填空题:
6.有如下程序框图(如右图所示),则该程序框图表示的
算法的功能是。
7.下列关于算法的说法,正确的是 。
①求解某一类问题的算法是唯一的;
②算法必须在有限步操作之后停止;
③算法的每一步操作必须是明确的,不能有歧义或模糊;
④算法执行后一定产生确定的结果
三、解答题:
8.设计算法求100
991431321211⨯+⋅⋅⋅+⨯+⨯+⨯的值.要求画出程序框图。
9.如果你是老师,试设计一个在数学探究课上的教学方案,要求画出流程图.(开放型题,可以有不同的答案)
青年歌手电视大赛共有10名选手参加,并请了12名评委,在计算每位选手的平均分数
时,为了避免个别评委所给的极端分数的影响,必须去掉一个最高分和一个最底分后再求平均分.试设计一个算法,解决该问题,要求画出程序框图。
(假定分数采用10分制,即每位选手的分数最高分为10分,最底分为0分)。
10.中国网通规定:拨打市内电话时,如果不超过3分钟,则收取话费0.22元;如果通话时间超过3分钟,则超出部分按每分钟0.1元收取通话费,不足一分钟按以一分钟计算。
设通话时间为t (分钟),通话费用y (元),如何设计一个程序,计算通话的费用。
(一)参考答案
一.选择题 1 C 2 B 3 A 4 B 5 A
二、填空题
6.计算并输出使1×3×5×7…× >10 000成立的最小整数;7.②③④。
三、解答题
8.解析:这是一个累加求和问题,共99项相加,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.程序框图如下图所示
9、由于共有12位评委,所以每位选手会有12个
分数,我们可以用循环语句来完成这12个分数的输入,同时设计累加变量求出这12个分数的和,本问题的关键在于从这12个输入分数中找出最大数与最小数,以便从总分中减去这两个数。
由于每位选手的分数都介于0分和10分之间,去我们可以先假设其中的最大数为0,最小数为10,然后每次输入一个评委的分数,就进行一次比较,若输入的数大于0,就将
之代替最大数,若输入的数小于10,就用它代替最小数,依次下去,就能找出这12个数中的最大数与最小数,循环结束后,从总和中减去最大数与最小数,再除以10,就得到该选手最后的平均数.
程序框图:如上
10.解:算法分析:数学模型实际上为:y 关于t 的分段函数。
关系是如下:
⎪⎩
⎪⎨⎧∉>+-+∈>-+≤<=),3(),1]3([1.022.0),3(),3(1.022.0)30(,22.0Z t t t Z t t t t y
其中[t -3]表示取不大于t -3的整数部分。
算法步骤如下:
第一步:输入通话时间t ;
第二步:如果t ≤3,那么y = 0.22;否则判断t ∈Z 是否成立,若成立执行
y= 0.2+0.1× (t -3);否则执行y = 0.2+0.1×( [t -3]+1)。
第三步:输出通话费用c 。
