(文章)简单的三角恒等变换专题
《简单的三角恒等变换》三角函数简单的三角恒等变换

简单的三角恒等变换xx年xx月xx日•三角函数基本概念•三角恒等变换的基本法则•三角恒等变换的应用目录•常见三角恒等变换技巧•三角恒等变换的注意事项•练习题与解答01三角函数基本概念$\sin x = \frac{y}{r}$正弦函数$\cos x = \frac{x}{r}$余弦函数$\tan x = \frac{y}{x}$正切函数三角函数的定义周期性$2k\pi, k\in Z$振幅$|\sin x| \leq 1, |\cos x| \leq 1$相位$\sin(x+2k\pi) = \sin x$;$\cos(x+2k\pi) = \cos x$;$\tan(x+k\pi) = \tan x$正弦函数$y=|\sin x|$,波动曲线余弦函数$y=|\cos x|$,波动曲线正切函数$y=\tan x$,曲线不连续,无界01020302三角恒等变换的基本法则和差角公式公式二$\cos(x+y)=\cos x\cos y-\sin x\sin y$应用用于解决角度和的问题,如求两角和的正弦、余弦等。
公式一$\sin(x+y)=\sin x\cos y+\cos x\sin y$$\sin x\cosy=\frac{1}{2}(\sin(x+y)+\sin(x-y))$积化和差公式公式一$\cos x\siny=\frac{1}{2}(\sin(x+y)-\sin(x-y))$公式二用于将两角和的正弦与余弦变换成和差角的形式,方便后续计算。
应用公式一$\sin\frac{x}{2}=\pm\frac{1}{\s qrt{2}}(\cos x+1)^{1/2}$公式二$\cos\frac{x}{2}=\pm\frac{1}{\sqrt{2}}(\cos x-1)^{1/2}$应用用于计算半角的角度,适用于解三角形等问题。
半角公式03三角恒等变换的应用利用三角函数解直角三角形,得到直角三角形的三个边长。
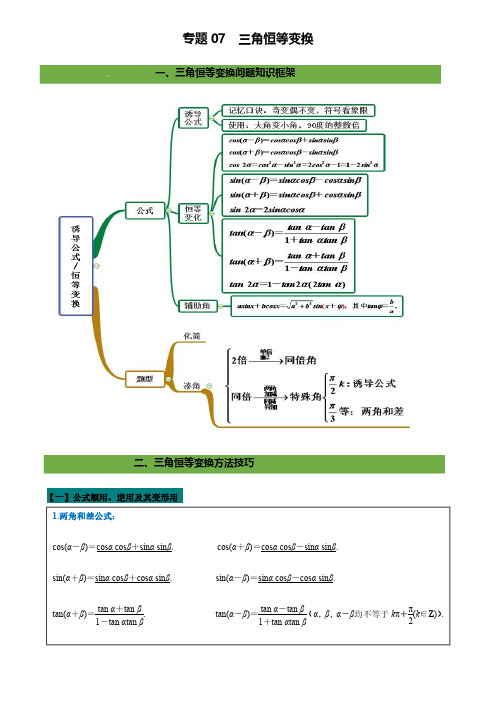
专题07:简单的三角恒等变换

专题07:简单的三角恒等变换1.降塞公式: 2l+cos2t/COS~CI=----------------------(1)2/C 、 -2I-COS2。
(2)Slrra=3,辅角公式 “sin 。
+bcosθ=√0^+P^sin(^+0)其中COsφ= '-,SF φ='>∣a 2+b 2'J"+",比如:____ . A=√12+(√3F(^==sinx+/=cosx)√12÷(√3)2√l 2+(√3)2=2(-SinX+ CoSX)=2(sinxcos-+cosxsin-)=2sin(x+-)2 23 3310常见数据:Sin15。
=cos75。
=6产,sin75。
=CoSI5。
=叱点,tanl5o =2-√3,tan75o =2+√3z考点01:降累公式1. 2cos2二→1的值是()12A.3B∙无C.D.2+322221 52 .已知CoSe=—一,一π<6<3π,则sin —=.522-考点02:SiMx 的降零公式及应用Csin800+1/、3∙()A.一立B.立C.-2D.2224 .函数/(x)=si112χ-g 是()A.周期为乃的偶函数B.周期为乃的奇函数C.周期为2%的偶函数D.周期为2万的奇函数考点03:Cos 2X 的降幕公式及应用5 .函数/(x )=cos2]χ的最小正周期为()y - sinx + V3cosx2.半角公式(符号的选择由匕所在的象限确定) 2A.2B.4C.2πD.4π6.已知函数/(%)=5111%与11(4+9-5/58$2(3乃+1)+35/^(不€砌.(1)求/(幻的单调递增区间;(2)求/(X)图像的对称轴方程和对称中心的坐标.考点04:SinXeoSX 的降吊公式及应用7 .化简求值:吟蓝票=一8 .(多选)已知函数/(x)=SinXCoSX-GCoS2x+C.函数启)的对称轴方程为“="+出%∈Z)D.函数於)的图象可由y=sin2x 的图象向左平移;个单位长度得到2126亚,则下列说法正确的是() 2 ITA. /(x) = sin(2x-y)B.函数<x )的最小正周期为加考点05: 9.求值: A. 0辅助角公式 5π rr . 5π cos √3sin —=1212B. -√2C.D. √210.求函数F (X )sin %+ cos X- - I 6B. √2的最大值( C.D. 1IL (多选)将函数/(x )=cos2x-sin2x 的图象向左平移小个单位后,所得图象关于》轴对称,则实数加的值可能为()π A.—8 3π B.— 8 5π C.— 8 lπ D.—— 8 12.(多选)己知。
专题07 三角恒等变换(学生版)
1.例题
【例
1】已知 0
2
, cos(
) 4
5. 5
(1)求 tan( ) 的值; 4
(2 )求 sin(2 ) 的值. 3
【例 2】已知△ABC 中, sin A cos A 7 ,则 tanA=
【例 2】已知函数 f(x)=
3sin
2x-π 6
+2sin2
x- π 12
(x∈R).
(1)求函数 f(x)的最小正周期;
(2)求使函数 f(x)取得最大值的 x 的集合.
2.巩固提升综合练习
【练习 1】当函数 y cos x 3 sin x 取得最大值时, tan x 的值是______
【练习 2】如果 f x sin x 2 cos(x ) 是奇函数,则 tan =
cos(α+β)=cosα cosβ-sinα sinβ.
sin(α-β)=sinα cosβ-cosα sinβ.
tan(α-β)= tan α-tan β(α,β,α-β均不等于 kπ+π(k∈Z)).
1+tan αtan β
2
2.二倍角公司
sin 2α=2sinα cosα; cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α; tan 2α= 2tan α . 1-tan2α
y0
为_____.
12.若
7
cos
2
cos
,则
tan
2
(
)
13.已知 cos( ) 6 ,则 sin 2 的值为
。
简单的三角恒等变换公式

简单的三角恒等变换公式
三角恒等变换是一种数学操作,用于在不改变一个三角形的形状的情况下改变它的位置或方向。
下面是几个常用的三角恒等变换公式:旋转:如果要将三角形旋转角度θ,则对于每个坐标 (x,y),可以使用以下公式:
x' = x * cosθ - y * sinθ
y' = x * sinθ + y * cosθ
平移:如果要将三角形平移到新的位置 (x',y'),则对于每个坐标 (x,y),可以使用以下公式:
x' = x + x0
y' = y + y0
缩放:如果要将三角形缩放比例为k,则对于每个坐标 (x,y),可以使用以下公式:
x' = k * x
y' = k * y
这些公式都可以使用单位矩阵来表示,例如旋转变换的单位矩阵如下:
[cosθ -sinθ]
[sinθ cosθ]。
三角恒等变换

专题三角恒等变换(一)一、诱导公式1、诱导公式(一~六)诱导公式一:sin(2)sin k απα+=,cos(2)cos k απα+=,tan(2)tan k απα+=,其中k Z ∈诱导公式二:sin()sin παα+=-,cos()cos παα+=-,tan()tan παα+=,其中k Z ∈诱导公式三:sin()sin αα-=-,cos()cos αα-=,tan()tan αα-=-,其中k Z ∈诱导公式四:sin()sin παα-=,cos()cos παα-=-,tan()tan παα-=-,其中k Z∈诱导公式五:sin cos 2παα⎛⎫-=⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭,其中k Z ∈诱导公式六:sin cos 2παα⎛⎫+= ⎪⎝⎭,cos sin 2παα⎛⎫+=- ⎪⎝⎭,其中k Z∈2、诱导公式口诀:“奇变偶不变,符号看象限”,意思是说角90k α⋅±(k 为常整数)的三角函数值:当k 为奇数时,正弦变余弦,余弦变正弦;当k 为偶数时,函数名不变,然后α的三角函数值前面加上当视α为锐角时原函数值的符号.3、用诱导公式进行化简时的注意点:(1)化简后项数尽可能的少;(2)函数的种类尽可能的少;(3)分母不含三角函数的符号;(4)能求值的一定要求值;(5)含有较高次数的三角函数式,多用因式分解、约分等.二、利用诱导公式求任意角三角函数值的步骤1、“负化正”:用公式一或三来转化.2、“大化小”:用公式一将角化为0°到360°间的角.3、“角化锐”:用公式二或四将大于90°的角转化为锐角.4、“锐求值”:得到锐角的三角函数后求值.三、利用诱导公式求值与求解解题策略1、条件求值问题的策略(1)条件求值问题,首先要仔细观察条件与所求式之间的角、函数名称及有关运算之间的差异及联系.(2)将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.2、给值求角问题,先通过化简已给的式子得出某个角的某种三角函数值,再结合特殊角的三角函数值逆向求角.3、观察互余、互补关系:如π3-α与π6+α,π3+α与π6-α,π4α与π4+α等互余,π3+θ与2π3θ,π4+θ与3π4-θ等互补,遇到此类问题,不妨考虑两个角的和,要善于利用角的变换来解决问题.题型一利用诱导公式给角求值【例1】cos 210︒的值等于()A .12B 32C .32D .22-【变式1-1】35πsin 6=()A .12B .12-C 32D .32【变式1-2】计算:5π7ππ2sin2cos tan 663⎛⎫+--= ⎪⎝⎭______.题型二利用诱导公式给值求值【例2】若()4sin ,5πα+=-且α是第二象限角,则cos α=()A .45-B .35-C .35D .45【变式2-1】设02πα⎛⎫∈ ⎪⎝⎭,,若3sin ,5α=则cos 2πα⎛⎫+= ⎪⎝⎭()A .35B .45C .35-D .45-【变式2-2】若()4sin 5πα+=-,则3cos 2πα⎛⎫-= ⎪⎝⎭()A .45-B .35-C .45D .35【变式2-3】设sin 25a ︒=,则sin 65cos115tan 205︒︒︒=()A 221a -B .221a -C .2a -D .2a题型三利用互余互补关系求值【例3】已知π3cos 35α⎛⎫-= ⎪⎝⎭,则πsin 6α⎛⎫+= ⎪⎝⎭()A .45±B .45C .45-D .35【变式3-1】已知π1sin 43α⎛⎫+= ⎪⎝⎭,则πcos 4α⎛⎫- ⎪⎝⎭的值为()A .13B.3C .13-D.3-【变式3-2】若1sin ,63a π⎛⎫+= ⎪⎝⎭则2cos 3a π⎛⎫+= ⎪⎝⎭()A .13B .13-C .79D .79-【变式3-3】已知cos 6πθ⎛⎫- ⎪⎝⎭=a (|a |≤1),则cos 56πθ⎛⎫+⎪⎝⎭+sin 23πθ⎛⎫- ⎪⎝⎭的值是________.【变式3-4】已知函数()π5π10πcos 2cos 2tan 26334π4πtan 2sin 233x x x f x x x ⎛⎫⎛⎫⎛⎫--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭.(1)化简()f x ;(2)若()0310f x =,求00π2πsin 2cos 263x x ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭的值.题型四利用诱导公式化简求值A .sin 4cos4-B .sin 4cos4--C .cos 4sin 4-D .sin 4cos 4+【变式4-1】(多选)已知角α满足sin cos 0αα⋅≠,则()()()sin πcos πsin cos k k k αααα+++∈Z 的取值可能为()A .2-B .1-C .2D .0【变式4-2】已知α是第四象限角,且cos α=()()sin cos cos sin 22πααππαα++-=⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭___________.【变式4-3】(1)化简:222cos(4)cos ()sin (3)sin(4)sin(5)cos ()θπθπθπθππθθπ+++-+--(2)已知()sin 3n f n π=(n ∈Z ),求(1)f +(2)f +(3)f +…+(2012)f 的值.【变式4-4】已知()()()()()3sin cos tan cos 222sin 2tan sin f πππααπαααπααππα⎛⎫⎛⎫⎛⎫+--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=---+.(1)化简()f α;(2)若31cos 25πα⎛⎫-=- ⎪⎝⎭,求()f α的值.题型五三角恒等式的证明【例5】(1)求证:tan(2)sin(2)cos(6)tan 33sin()cos()22παπαπααππαα----=-++;(2)设8tan()7m πα+=,求证1513sin()3cos()37720221sin()cos()77m m ππααππαα++-+=+--+.【变式5-1】求证:232sin()cos()12212sin ()ππθθπθ-+--+=tan(9)1tan()1πθπθ+++-.专题三角恒等变换(二)一、升(降)幂缩(扩)角公式利用余弦的二倍角公式变形可得:升幂公式:21cos 22cos αα+=,21cos 22sin αα-=降幂公式:21cos 2cos 2αα+=,21cos 2sin 2αα-=二、半角公式(只要求推导,不要求记忆)sin2a =cos2a =sin 1cos tan.21cos sin ααααα-===+以上三个公式分别称作半角正弦、余弦、正切公式,它们是用无理式表示的.sin 1cos tan ,tan 21cos 2sin αααααα-==+;2sin2sin 1cos 22tan 2sin cos 2sin cos 222αααααααα-===以上两个公式称作半角正切的有理式表示.三、积化和差与和差化积公式1、积化和差1sin cos [sin()sin()]2αβαβαβ=-++1cos sin )sin()]2αβαβαβ=+--1cos cos )cos()]2αβαβαβ=-++1sin sin [cos()cos()]2αβαβαβ=--+2、和差化积sin sin 2sincos 22x y x yx y +-+=sin sin 2cossin 22x y x yx y +--=cos cos 2cos cos22x y x yx y +-+=cos cos 2sin 22x y x yx y +--=-四、辅助角公式对于形如sin cos a x b x +的式子,可变形如下:sin cos a x b x +sin cos x x ⎫⋅⋅的平方和为1,故令cos ϕϕ==则sin cos a x b x +)sin cos cos sin x x ϕϕ+)x ϕ+其中ϕ角所在象限由,a b 的符号确定,ϕ角的值由tan baϕ=确定,或由sin ϕ=和cos ϕ=五、万能公式22tan2sin 1tan 2ααα=+;221tan 2cos 1tan 2ααα-=+;22tan2tan 1tan 2ααα=-六、三角函数化简“三看”原则七、三角恒等变换综合应用的解题思路(1)将()f x 化为sin cos a x b x +的形式;(2)构造)cos sin ()(x ba b x ba ab a x f ⋅++⋅++=222222(3)和角公式逆用,得())f x x ϕ=+(其中φ为辅助角);(4)利用())f x x ϕ=+研究三角函数的性质;(5)反思回顾,查看关键点、易错点和答题规范.题型一半角公式与万能公式的应用【例1】已知,02πα⎛⎫∈- ⎪⎝⎭,3sin 5α=-,则tan 2α=()A .3B .3-C .13D .13-【变式1-1】已知π3,π,sin 25αα⎛⎫∈= ⎪⎝⎭,则cos π2α⎛⎫-= ⎪⎝⎭()A.10B.10C.10-D.10【变式1-2】若3sin 5θ=,5π3π2θ<<,则tan cos 22θθ+=()A.3B .3C .3D .3-【变式1-3】已知()tan 3πα+=,则cos 22πα⎛⎫-= ⎪⎝⎭()A .35B .310C .34D 【变式1-4】若sin 11cos 2αα=+,则sin cos αα+的值为________.题型二积化和差与和差化积的应用【例2】利用和差化积公式,求下列各式的值:(1)sin15sin105︒+︒;(2)sin20sin40sin80︒+︒-︒;(3)cos40cos60cos80cos160︒+︒+︒+︒.【变式2-1】利用积化和差公式,求下列各式的值:(1)cos15cos75︒︒;(2)sin20sin40sin80︒︒︒.【变式2-2】下列关系式中正确的是()A .sin 5sin 32sin 8cos 2θθθθ+=B .cos3cos52sin 4sin θθθθ-=-C .1sin3sin5cos4cos 2θθθθ-=-D .()()1cos cos sin sin 2x y x y x y --+=⎡⎤⎣⎦【变式2-3】若1cos cos sin sin 2x y x y +=,2sin 2sin 23x y +=,则()sin +=x y ()A .23B .23-C .13D .13-【变式2-4】求值:cos 40cos80cos80cos160cos160cos 40︒︒︒︒︒++︒.【变式2-5】在ABC 中,若30B = ,则cos sin A C 的取值范围是()A .[]1,1-B .11,22⎡⎤-⎢⎥⎣⎦C .13,44⎡⎤-⎢⎥⎣⎦D .31,44⎡⎤-⎢⎥⎣⎦题型三辅助角公式及其应用【例3】将下列各式化成()sin A x ϕ+的形式:(1cos x x -;(2).444x x ππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭【变式3-1】求下列函数的最大值和最小值:(1)1cos 2y x x =;(2)sin cos y x x =-;(3)sin y x x =+;(4)sin 22y x x =.【变式3-2】(多选)若1sin cos()22x x x ϕ+=+,则ϕ的值可能为()A .6π-B .6πC .56πD .116π【变式3-3】已知πcos(63x -=,则πcos cos()3x x +-等于()A B .±C .-1D .1【变式3-4】已知函数2()cos 2cos f x x x x =+.(1)求函数()f x 的单调增区间;(2)求函数()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上的最大值与最小值,以及此时x 的取值.题型四三角恒等变换的化简问题【例4】化简4sin 24cos 24tan12cos12︒︒︒︒+=()A .1B CD .2【变式4-1】化简()()sin5cos51︒+︒︒=()A .2B .C .2D【变式4-2】若1cos sin 222αα=,则1sin cos 14ααπα++=⎛⎫+ ⎪⎝⎭()A .1B .12CD.【变式4-3】若2πθπ<<,tan 3θ=-=_________.题型五三角形中的三角恒等变换【例5】在ABC ∆中,若sin cos()1sin()cos 22A B A B ππ-=--,则这个三角形是()A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形【变式5-1】已知ABC ,角,,A B C 所对应的边分别为,,a b c ,且sin sin cos cos A B A B +=+,则ABC 是()A .直角三角形B .等边三角形C .钝角三角形D .锐角三角形【变式5-2】在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,()()2sin sin sin B C B C A +⋅-=.则△ABC的形状为()A .正三角形B .等腰直角三角形C .直角三角形D .等腰三角形。
简单的三角恒等变换

简单的三角恒等变换三角恒等变换是数学中非常重要的基础知识,它能够帮助我们解决很多与三角函数相关的问题。
在学习三角恒等变换的过程中,我们需要掌握一些基本的变换公式,这样才能灵活地运用它们来解决实际问题。
首先,我们来看正弦函数的恒等变换。
对于任意实数x,有如下公式:sin(x) = sin(x + 2πk) = sin(-x + 2πk)其中k为任意整数。
这意味着,在正弦函数中,每隔2π,函数的值会重复出现。
此外,我们还可以通过对称性质,得到以下两个恒等式:sin(π + x) = -sin(x)sin(π - x) = sin(x)这两个恒等式告诉我们当x逐渐增大或减小,正弦函数的值也会相应地发生变化。
接下来,我们来看余弦函数的恒等变换。
对于任意实数x,有如下公式:cos(x) = cos(x + 2πk) = cos(-x + 2πk)其中k为任意整数。
这表明在余弦函数中也存在着每隔2π重复的特征。
此外,我们还可以得到以下两个恒等式:cos(π + x) = -cos(x)cos(π - x) = -cos(x)这两个恒等式告诉我们,当x逐渐增大或减小,余弦函数的值也会相应地发生变化,并与正弦函数产生相反的变化。
最后,我们来看正切函数的恒等变换。
对于任意实数x,有如下公式:tan(x) = tan(x + πk)其中k为任意整数且x不为(π/2 + πk)。
这意味着正切函数也存在2π周期性。
此外,我们还可以得到以下两个恒等式:tan(π + x) = tan(x)tan(π/2 - x) = 1/tan(x)这两个恒等式告诉我们,正切函数在π/2和π处会出现无穷大和无穷小的特征,并且在这两个点附近的图像非常陡峭。
总之,三角恒等变换是非常重要的数学基础知识,它能够帮助我们解决非常多与三角函数相关的问题。
在学习的过程中,我们需要认真掌握各种基本变换公式,并能够正确地运用它们来解决实际问题。
希望读者能够通过学习,更好地掌握这一知识点。
专题5.5 三角恒等变换(解析版)

专题5.5三角恒等变换(一)两角和与差的正弦、余弦、正切公式1.C (α-β):cos(α-β)=cos αcos β+sin αsin β;C (α+β):cos(α+β)=cos αcos_β-sin_αsin β;S (α+β):sin(α+β)=sin αcos β+cos αsin β;S (α-β):sin(α-β)=sin_αcos_β-cos αsin β;T (α+β):tan(α+β)=tan α+tan β1-tan αtan β;T (α-β):tan(α-β)=tan α-tan β1+tan αtan β.2.变形公式:tan α±tan β=tan(α±β)(1∓tan αtan β);4sin(2cos sin πααα±=±.sin αsin β+cos(α+β)=cos αcos β,cos αsin β+sin(α-β)=sin αcos β,3.辅助角公式:函数f(α)=acos α+bsin α(a ,b 为常数),可以化为f(α)=a 2+b 2sin(α+φ)或f(α)=a 2+b 2cos(α-φ),其中φ可由a ,b 的值唯一确定.(二)二倍角的正弦、余弦、正切公式1.S 2α:sin 2α=2sin αcos α;C 2α:cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α;T 2α:tan 2α=2tan α1-tan 2α2.变形公式:(1)降幂公式:cos 2α=1+cos 2α2,sin 2α=1-cos 2α2,sin αcos α=12sin 2α.(2)升幂公式1+cos α=2cos 2α2;1-cos α=2sin 2α2;1+sin αα2+cos ;1-sin αα2-cos .(3)配方变形:1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)21±sin αsin α2±cos 1+cos α=2cos 2α2,1-cos α=2sin 2α2(4)sin 2α=2sin αcos αsin 2α+cos 2α=2tan α1+tan 2α;cos 2α=cos 2α-sin 2αcos 2α+sin 2α=1-tan 2α1+tan 2α.tanα2=sin α1+cos α=1-cos αsin α.(三)常见变换规律(1)角的变换:明确各个角之间的关系(包括非特殊角与特殊角、已知角与未知角),熟悉角的变换技巧,及半角与倍角的相互转化,如:2α=(α+β)+(α-β),α=(α+β)-β=(α-β)+β,40°=60°-20°=π2,α2=2×α4等.(2)名的变换:明确各个三角函数名称之间的联系,常常用到同角关系、诱导公式,把正弦、余弦化为正切,或者把正切化为正弦、余弦.一、单选题1.sin 40sin 50cos 40cos50︒︒-︒︒等于()A .1-B .1C .0D .cos10-︒【答案】C【解析】由两角和的余弦公式得:()()sin 40sin 50cos 40cos50cos 40cos50sin 40sin 50cos 4050cos900︒︒-︒︒=-︒︒-︒︒=-+=-=故选:C2.已知()5cos 2cos 22παπα⎛⎫-=+ ⎪⎝⎭,且()1tan 3αβ+=,则tan β的值为()A .7-B .7C .1D .1-【答案】D【解析】:因为()5cos 2cos 22παπα⎛⎫-=+ ⎪⎝⎭,所以sin 2cos αα=,所以sin tan 2cos ααα==,又()1tan 3αβ+=,所以()()()12tan tan 3tan tan 111tan tan 123αβαβαβααβα-+-=+-===-⎡⎤⎣⎦+++⨯.故选:D3.已知,αβ均为锐角,且1sin 2sin ,cos cos 2αβαβ==,则()sin αβ-=()A .35B .45C.3D .23【答案】A【解析】:因为1sin 2sin ,cos cos 2αβαβ==,所有22221sin cos 4sin cos 14ααββ+=+=,则2153sin 44β=,又,αβ均为锐角,所以sin β=cos β=所以sin αα==所以()3sin sin cos cos sin 5αβαβαβ-=-=.故选:A.4.已知()1sin 5αβ+=,()3sin 5αβ-=,则tan tan αβ的值为()A .2B .2-C .12D .12-【答案】B【解析】()()1sin sin cos cos sin 53sin sin cos cos sin 5αβαβαβαβαβαβ⎧+=+=⎪⎪⎨⎪-=-=⎪⎩,解得2sin cos 51cos sin 5αβαβ⎧=⎪⎪⎨⎪=-⎪⎩,所以tan sin cos 2tan cos sin ααββαβ==-.故选:B5.已知sin sin 13πθθ⎛⎫++= ⎪⎝⎭,则tan 6πθ⎛⎫+= ⎪⎝⎭()ABC .D .±22【答案】D【解析】sin sin()13πθθ++=,则1sin sin cos 122θθθ++=,即3sin 122θθ+=,故1sin cos 223θθ+=,所以sin 6πθ⎛⎫+= ⎪⎝⎭cos 63πθ⎛⎫+=± ⎪⎝⎭,所以tan 62πθ⎛⎫+=± ⎪⎝⎭故选:D6.下面公式正确的是()A .3sin cos 2πθθ⎛⎫+= ⎪⎝⎭B .2cos212cos θθ=-C .3cos sin 2πθθ⎛⎫+=- ⎪⎝⎭D .cos()sin 2πθθ-=【答案】D 【解析】对A ,3sin cos 2πθθ⎛⎫+=- ⎪⎝⎭,故A 错误;对B ,2cos 22cos 1θθ=-,故B 错误;对C ,3cos sin 2πθθ⎛⎫+= ⎪⎝⎭,故C 错误;对D ,cos()sin 2πθθ-=,故D 正确;故选:D7.已知2tan()5αβ+=,1tan()44πβ-=,则tan()4πα+的值为()A .16B .322C .2213D .1318【答案】B【解析】:因为2tan()5αβ+=,1tan()44πβ-=,所以()tan()tan 44ππααββ⎡⎤⎛⎫+=+-- ⎪⎢⎥⎝⎭⎣⎦()()tan tan 41tan tan 4παββπαββ⎛⎫+-- ⎪⎝⎭=⎛⎫++- ⎪⎝⎭213542122154-==+⨯.故选:B 8.设1cos1022a =-,22tan131tan 13b =+,c =,则a ,b ,c 大小关系正确的是()A .a b c <<B .c b a <<C .a c b <<D .b c a<<【答案】C【解析】()1cos10cos 6010cos 70sin 202a =︒=︒+︒=︒=︒,2222sin132tan13cos132sin13cos13sin 26sin 131tan 131cos 13b ︒︒︒===︒︒=︒︒+︒+︒,sin 25c =,因为函数sin y x =在0,2π⎛⎫⎪⎝⎭上是增函数,故sin 20sin 25sin 26<<,即a c b <<.故选:C.9.已知sin()63πα+=-,则2cos(2)3πα-=()A .23-B .13-C .23D .13【答案】B 【解析】:因为sin()6πα+=2cos 2cos 263παππα⎡⎤⎛⎫⎛⎫-=-⎪ ⎪⎢⎥⎝⎭⎣+⎭⎝⎦6cos 2πα⎪+⎛⎫=- ⎝⎭212n 6si πα⎡⎤⎛⎫=-- ⎪⎢⎥⎭⎣+⎝⎦21123⎡⎤⎛⎢⎥=--=- ⎢⎥⎝⎭⎣⎦故选:B 10.若11tan ,tan()72βαβ=+=,则tan =α()A .115B .112C .16D .13【答案】D【解析】:因为11tan ,tan()72βαβ=+=,所以()()()11tan tan 127tan =tan 111tan tan 3127αββααββαββ-+-+-===⎡⎤⎣⎦+++⨯.故选:D.11.已知3cos 16παα⎛⎫--= ⎪⎝⎭,则sin 26πα⎛⎫+= ⎪⎝⎭()A .13-B .13C.3-D.3【答案】B【解析】:因为3cos 16παα⎛⎫--= ⎪⎝⎭,即3cos cos sin sin 166ππααα⎛⎫-+= ⎪⎝⎭,即13cos sin 122ααα⎫-+=⎪⎪⎝⎭3sin 12αα-=1cos 123πααα⎫⎛⎫=+=⎪ ⎪⎪⎝⎭⎭,所以cos 3πα⎛⎫+= ⎪⎝⎭所以sin 2cos 2662πππαα⎛⎫⎛⎫+=-++ ⎪ ⎪⎝⎭⎝⎭2cos 22cos 133ππαα⎡⎤⎛⎫⎛⎫=-+=-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦21213⎡⎤⎢⎥=--=⎢⎥⎝⎭⎣⎦.故选:B 12.已知4sin 5α=,π5,π,cos ,213αββ⎛⎫∈=- ⎪⎝⎭是第三象限角,则()cos αβ-=()A .3365-B .3365C .6365D .6365-【答案】A【解析】由4sin 5α=,π,π2α⎛⎫∈ ⎪⎝⎭,可得3cos 5α=-由5cos ,13ββ=-是第三象限角,可得12sin 13β=-则()3541233cos cos cos sin sin 51351365αβαβαβ⎛⎫⎛⎫⎛⎫-=+=-⨯-+⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故选:A13.若sin 25α=,()sin 10βα-=,且,4απ⎡⎤∈π⎢⎥⎣⎦,3,2βππ⎡⎤∈⎢⎥⎣⎦,则αβ+的值是()A .54πB .74πC .54π或74πD .54π或94π【答案】B【解析】,,2,242ππαπαπ⎡⎤⎡⎤∈∴∈⎢⎥⎢⎥⎣⎦⎣⎦,又∵sin 2,2,,,242πππααπα⎡⎤⎡⎤=∴∈∈⎢⎥⎢⎥⎣⎦⎣⎦,∴cos 25α==-.又∵35,,,224πππβπβα⎡⎤⎡⎤∈∴-∈⎢⎥⎢⎥⎣⎦⎣⎦,∴()cos βα-==,于是()()()()cos cos 2cos 2cos sin 2sin αβαβααβααβα+=+-=---⎡⎤⎣⎦5105102⎛⎛⎫=---= ⎪ ⎪⎝⎭⎝⎭,易得5,24αβπ⎡⎤+∈π⎢⎥⎣⎦,则74αβπ+=.故选:B.14.)sin20tan50=()A .12B .2C D .1【答案】D【解析】原式()()()()sin20sin 50cos502sin 20sin 50602sin 20sin 9020cos50cos50cos 9050++===-2sin 20cos 20sin 401sin 40sin 40===.故选:D.15.若1cos ,sin(),0722ππααβαβ=+=<<<<,则角β的值为()A .3πB .512πC .6πD .4π【答案】A 【解析】∵0,022ππαβ<<<<,0αβπ∴<+<,由1cos 7α=,()sin αβ+=,得sin α=11cos()14αβ+=±,若11cos()14αβ+=,则sin sin[()]βαβα=+-sin()cos cos()sin αβααβα=+-+1110714=-<,与sin 0β>矛盾,故舍去,若11cos()14αβ+=-,则cos cos[()]βαβα=+-cos()cos sin()sin αβααβα=+++111147147=-⨯+⨯12=,又(0,)2πβ∈,3πβ∴=.故选:A.16.若7171212ππα<<,且7cos 268πα⎛⎫+=- ⎪⎝⎭,则5cos 12πα⎛⎫-=⎪⎝⎭()A .B .CD .14-【答案】A【解析】由27cos 212sin 6128ππαα⎛⎫⎛⎫+=-+=- ⎪ ⎪⎝⎭⎝⎭,得215sin 1216πα⎛⎫+= ⎪⎝⎭.因为7171212ππα<<,所以233122πππα<+<,所以sin 122πα⎛⎫⎛⎫+∈- ⎪ ⎪ ⎪⎝⎭⎝⎭,所以15sin 124πα⎛⎫+= ⎪⎝⎭所以5cos cos sin 1221212ππππααα⎛⎫⎛⎫⎛⎫⎛⎫-=-+=+=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭故选:A17.已知sin cos αα-=0απ≤≤,则sin 23πα⎛⎫-= ⎪⎝⎭()A B .34410-C .D 【答案】D【解析】:因为sin cos αα-=()22sin cos αα-=⎝⎭,即222sin 2sin cos cos 5αααα-+=,即21sin 25α-=,所以3sin 25α=,又sin cos 45πααα⎛⎫-=-=⎪⎝⎭,即2sin 42πα⎛⎫-= ⎪⎝⎭,因为0απ≤≤,所以3444πππα-≤-≤,所以044ππα<-≤,即42ππα<≤,所以22παπ<≤,所以4cos 25α==-,所以sin 2sin 2cos cos 2sin333πππααα⎛⎫-= ⎪⎝⎭23145252⎛⎫=⨯--⨯ ⎪⎝⎭故选:D18.若10,0,cos ,cos 2243423ππππβαβα⎛⎫⎛⎫<<-<<+=-= ⎪ ⎪⎝⎭⎝⎭,则cos 2βα⎛⎫+= ⎪⎝⎭()A B .C D .【答案】C 【解析】cos cos cos cos sin sin 2442442442βππβππβππβαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+--=+-++- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,因为0,022ππαβ<<-<<所以3,444πππα⎛⎫+∈ ⎪⎝⎭,,4242πβππ⎛⎫-∈ ⎪⎝⎭,因为1cos 43πα⎛⎫+= ⎪⎝⎭,cos 423πβ⎛⎫-= ⎪⎝⎭所以sin 4πα⎛⎫+ ⎪⎝⎭sin 42πβ⎛⎫-= ⎪⎝⎭则122cos 233βα⎛⎫+=+ ⎪⎝⎭C 19.已知π43cos sin 65αα⎛⎫-+= ⎪⎝⎭,则2πcos 3α⎛⎫+ ⎪⎝⎭的值是()A .45-B .45C .5-D .5【答案】A【解析】由πcos sin 6αα⎛⎫-+= ⎪⎝⎭ππ3πcos cossin sin sin sin 6623αααααα⎛⎫++=+=-=⎪⎝⎭,所以,π4cos 35α⎛⎫-= ⎪⎝⎭,所以,2πππ4cos cos πcos 3335ααα⎛⎫⎛⎫⎛⎫⎛⎫+=--=--=-⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:A.20.已知,2παπ⎛⎫∈ ⎪⎝⎭,且2sin 45πα⎛⎫+= ⎪⎝⎭,则cos()α-=()A .10B .10C .10-D .222110【答案】C【解析】因为,2παπ⎛⎫∈ ⎪⎝⎭,所以35,444πππα⎛⎫+∈ ⎪⎝⎭.又2sin 45πα⎛⎫+= ⎪⎝⎭,所以cos 45πα⎛⎫+==- ⎪⎝⎭,cos()cos cos cos cos sin sin 44444410ππππππααααα⎡⎤⎛⎫⎛⎫⎛⎫-==+-=+++=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦故选:C.二、多选题21.对于函数()sin 22f x x x =,下列结论正确的是()A .()f x 的最小正周期为πB .()f x 的最小值为2-C .()f x 的图象关于直线6x π=-对称D .()f x 在区间,26ππ⎛⎫-- ⎪⎝⎭上单调递增【答案】AB【解析】()1sin 222(sin 2cos 2)2sin(2)223f x x x x x x π=+=+=+,22T ππ==,A 正确;最小值是2-,B 正确;(2sin()0633f πππ-=-+=,C 错误;(,26x ππ∈--时,22(,0)33x ππ+∈-,232x ππ+=-时,()f x 得最小值2-,因此函数不单调,D 错误,故选:AB .22)A .222cos2sin 1212ππ-B .1tan151tan15+︒-︒C .cos 75︒︒D .cos15︒︒【答案】ABC【解析】A :222cos 2sin 2cos 12126πππ-==B :1tan15tan 45tan15tan 601tan151tan 45tan15+︒︒+︒==︒=-︒-︒︒C :cos 754sin15230︒︒=︒︒=︒=D :cos152sin(3015)2sin15︒︒=︒-︒=︒.故选:ABC23.已知函数2()sin 222x x xf x =-,则下列结论正确的有()A .()f x 的最小正周期为4πB .直线23x π=-是()f x 图象的一条对称轴C .()f x 在0,2π⎛⎫⎪⎝⎭上单调递增D .若()f x 在区间,2m π⎡⎤-⎢⎥⎣⎦上的最大值为12,则3m π≥【答案】BD【解析】:()21cos 1cos sin sin 222262x x x xf x x x π-⎛⎫=-=-=+- ⎪⎝⎭,所以()f x 的最小正周期为2,π故A 不正确;因为2362πππ-+=-,所以直线23x π=-是()f x 图象的一条对称轴,故B 正确;当02x π<<时,2+663x πππ<<,而函数sin y x =在2,63ππ⎛⎫⎪⎝⎭上不单调,故C 不正确;当2x m π-≤≤时,++366x m πππ-≤≤,因为()f x 在区间,2m π⎡⎤-⎢⎥⎣⎦上的最大值为12,即11sin 622x π⎛⎫+-≤ ⎪⎝⎭,所以sin 16x π⎛⎫+≤ ⎪⎝⎭,所以+62m ππ≥,解得3m π≥,故D 正确.故选:BD.24.已知函数22()cos cos sin (0)f x x x x x ωωωωω=+->的周期为π,当π[0]2x ∈,时,()f x 的()A .最小值为2-B .最大值为2C .零点为5π12D .增区间为π06⎡⎤⎢⎥⎣⎦,【答案】BCD【解析】22()cos cos sin (0)f x x x x x ωωωωω=+->2cos 2x xωω=+2sin 26x πω⎛⎫=+ ⎪⎝⎭,因为()f x 的周期为π,所以22ππω=,得1ω=,所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,当π[0]2x ∈,时,72,666x πππ⎡⎤+∈⎢⎥⎣⎦,所以1sin 2126x π⎛⎫-≤+≤ ⎪⎝⎭,所以12sin 226x π⎛⎫-≤+≤ ⎪⎝⎭,所以()f x 的最小值为1-,最大值为2,所以A 错误,B 正确,由()2sin 206f x x π⎛⎫=+= ⎪⎝⎭,72,666x πππ⎡⎤+∈⎢⎥⎣⎦,得26x ππ+=,解得512x π=,所以()f x 的零点为5π12,所以C 正确,由2662x πππ≤+≤,得06x π≤≤,所以()f x 的增区间为π06⎡⎤⎢⎣⎦,,所以D 正确,故选:BCD25.关于函数()cos 2cos f x x x x =-,下列命题正确的是()A .若1x ,2x 满足12πx x -=,则()()12f x f x =成立;B .()f x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增;C .函数()f x 的图象关于点π,012⎛⎫⎪⎝⎭成中心对称;D .将函数()f x 的图象向左平移7π12个单位后将与2sin 2y x =的图象重合.【答案】ACD 【解析】()1cos 2cos cos 222cos 222f x x x x x x x x ⎛⎫=-== ⎪ ⎪⎝⎭π2cos 23x ⎛⎫=+ ⎪⎝⎭,对于A ,若1x ,2x 满足12πx x -=,则()()()1222ππ2cos 2π2cos 233f x x x f x ⎡⎤⎛⎫=++=+= ⎪⎢⎥⎣⎦⎝⎭成立,故A 正确;对于B ,由ππ2π22π2π,3k x k k Z +≤+≤+∈,得:π5πππ,36k x k k +≤≤+∈Z ,即()f x 在区间π5π,36⎡⎤⎢⎣⎦上单调递增,故B 错误;对于C ,因为πππ2cos 2012123f ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,所以函数()f x 的图象关于点π,012⎛⎫⎪⎝⎭成中心对称,故C 正确;对于D ,将函数()f x 的图象向左平移7π12个单位后得到7π7ππ3π2cos 22cos 22sin 2121232y f x x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,其图象与2sin 2y x =的图象重合,故D 正确.故选:ACD 三、解答题26.求下列各式的值(1)cos54cos36sin54sin36⋅-⋅(2)sin7cos37cos(7)sin(37)⋅+-⋅-(3)ππcos sin 1212⋅(4)22ππsincos 88-【答案】(1)0;(2)12-;(3)14;(4)2-.【解析】(1)cos54cos36sin54sin36cos(5436)cos900⋅-⋅=+==.(2)sin7cos37cos(7)sin(37)sin7cos37cos7sin37⋅+-⋅-=⋅-⋅1sin(737)sin(30)2=-=-=-.(3)ππ1π1cossin 1212264⋅==.(4)22πππsin cos cos 8842-=-=-.27.已知3sin 5α=,其中2απ<<π.(1)求tan α;(2)若0,cos 2πββ<<=()sin αβ+的值.【答案】(1)34-(2)5-【解析】(1)由3sin 5α=可得4cos 5α=±,因为2απ<<π,故4cos 5α=-,进而sin 3tan cos 4ααα==-(2)π0,cos 2ββ<<=,故sin β==;()34sin =sin cos cos sin 55αβαβαβ++==28.已知角α为锐角,2πβαπ<-<,且满足1tan23=α,()sin 10βα-=(1)证明:04πα<<;(2)求β.【答案】(1)证明见解析(2)3.4πβ=【解析】(1)证明:因为1tan23α=,所以2122tan332tan 1tan 1441tan 129απαα⨯===<=--,因为α为锐角且函数tan y x =在0,2π⎛⎫⎪⎝⎭上单调递增,所以04πα<<(2)由22sin 3tan cos 4sin cos 1ααααα⎧==⎪⎨⎪+=⎩,结合角α为锐角,解得3sin 5α=,4cos 5α=,因为2πβαπ<-<,且()sin 10βα-=所以()cos βα-==()()()sin sin sin cos cos sin βαβααβααβα⎡⎤=+-=-+-⎣⎦3247225105102⎛=⨯-+⨯ ⎝⎭又5224πππαβπα<+<<+<,所以3.4πβ=29.已知α,β为锐角,π33sin 314α⎛⎫-=⎪⎝⎭,()11cos 14αβ+=-.(1)求cos α的值;(2)求角β.【答案】(1)17(2)π3【解析】(1)因为π0,2α⎛⎫∈ ⎪⎝⎭,所以ππ336πα⎛⎫-∈ ⎪⎝⎭-,,又π33sin 314α⎛⎫-=⎪⎝⎭所以π13cos 314α⎛⎫-== ⎪⎝⎭所以ππcos =cos +33αα⎡⎤⎛⎫- ⎪⎢⎥⎝⎭⎣⎦ππππ1cos cos sin sin =33337αα⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭(2)因为α,β为锐角,所以0αβ<+<π,则()sin 0αβ+>,因为()11cos 14αβ+=-,所以()sin 14αβ+==.又α为锐角,1cos 7α=,所以sin α==,故()()()sin sin sin cos cos sin βαβααβααβα=+-=+-+⎡⎤⎣⎦111714=+=因为β为锐角,所以π3β=.30.已知sincos22αα-=(1)求sin α的值;(2)若αβ,都是锐角,()3cos 5αβ+=,求sin β的值.【答案】(1)12【解析】(1)解:2221sin cos sin 2sin cos cos 1sin 2222222a αααααα⎛⎫-=-+=-= ⎪⎝⎭,1sin 2a =.(2)因为αβ,都是锐角,所以0αβ<+<π,()4sin 5αβ+==,13sin cos 22a a =⇒=,()()()43sin cos c 0s 13si o 55n sin sin 221αβααβααββα-=-+=+-=+-=⨯⨯⎡⎤⎣⎦31.已知tan ,tan αβ是方程23570x x +-=的两根,求下列各式的值:(1)()tan αβ+(2)()()sin cos αβαβ+-;(3)()cos 22αβ+.【答案】(1)12-(2)54(3)35【解析】(1)由题意可知:57tan tan ,tan tan 33αβαβ+=-=-()5tan tan 13tan 71tan tan 213αβαβαβ-++===--+(2)()()5sin sin cos cos sin tan tan 537cos cos cos sin sin 1tan tan 413αβαβαβαβαβαβαβαβ-+++====-++-(3)()22222211cos ()sin ()1tan ()34cos 221cos ()sin ()1tan ()514αβαβαβαβαβαβαβ-+-+-++====++++++。
专题3.4 三角恒等变换(解析版)

第三篇 三角函数与解三角形 专题3.4 三角恒等变换【考纲要求】1. 会用向量的数量积推导出两角差的余弦公式.2.能利用两角差的余弦公式推导出两角差的正弦、正切公式.3.能利用两角差的余弦公式推导出两角和的正弦、余弦、正切公式和二倍角的正弦、余弦、正切公式,了解它们的内在联系.4.能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆). 【命题趋势】三角恒等变换是三角变换的工具,主要考查利用两角和与差的三角公式、二倍角公式进行三角函数的化简与求值.可单独考查,也可与三角函数的知识综合考查. 【核心素养】本讲内容主要考查数学运算、逻辑推理的核心素养. 【素养清单•基础知识】1.两角和与差的正弦、余弦、正切公式 sin(α±β)=sin αcos β±cos αsin β. cos(α±β)=cos αcos β∓sin αsin β. tan(α±β)=tan α±tan β1∓tan αtan β.2.二倍角的正弦、余弦、正切公式 sin 2α=2sin αcos α.cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α. tan 2α=2tan α1-tan 2α.3.有关公式的逆用、变形(1)tan α±tan β=tan(α±β)(1∓tan αtan β). (2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2(3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2,sin α±cos α=2sin ⎝⎛⎭⎫α±π4.(4)a sin α+b cos α=a 2+b 2sin(α+φ)⎝⎛⎭⎫tan φ=b a ,a sin α+b cos α=a 2+b 2cos(α-φ)⎝⎛⎭⎫tan φ=a b .【素养清单•常用结论】 常见的几种角的变换 (1)α=(α+β)-β=(α-β)+β.(2)2α=(α+β)+α-β,2β=α+β-(α-β). (3)α+β2=α-β2-⎝⎛⎭⎫α2-β,α=2×α2. 【真题体验】1.【2019年高考全国Ⅱ卷理数】已知α∈(0,),2sin2α=cos2α+1,则sin α=( )A .B .C .D .【答案】B【解析】,,,又,,又,,故选B .【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查,中等难度,判断正余弦的正负,运算准确性是关键,题目不难,需细心,解决三角函数问题,研究角的范围后得出三角函数值的正负很关键,切记不能凭感觉.解答本题时,先利用二倍角公式得到正余弦关系,再利用角范围及正余弦平方和为1关系得出答案.2.【2019年高考江苏卷】已知,则的值是 .【答案】【解析】由,得,解得,或.,当时,上式当时,上式=综上,【名师点睛】本题考查三角函数的化简求值,渗透了逻辑推理和数学运算素养.采取转化法,利用分类讨论和转化与化归思想解题.由题意首先求得的值,然后利用两角和的正弦公式和二倍角公式将原问题转化为齐次式求值的问题,最后切化弦求得三角函数式的值即可.3.【2018年高考全国Ⅲ卷理数】若,则()A.B.C.D.【答案】B【解析】.故选B.【名师点睛】本题主要考查三角函数的求值,考查考生的运算求解能力,考查的核心素养是数学运算.4.【2018年高考全国卷II理数】若在是减函数,则的最大值是()A.B.C.D.【答案】A【解析】因为,所以由得,因此,从而的最大值为,故选A.【名师点睛】解答本题时,先确定三角函数单调减区间,再根据集合包含关系确定的最大值.函数的性质:(1).(2)周期(3)由求对称轴.(4)由求增区间;由求减区间.5.【2017年高考全国Ⅱ理数】函数()的最大值是.【答案】1【解析】化简三角函数的解析式:,由自变量的范围:可得:,当时,函数取得最大值1.【名师点睛】本题经三角函数式的化简将三角函数的问题转化为二次函数的问题,二次函数、二次方程与二次不等式统称“三个二次”,它们常结合在一起,有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析. 6.【2018年高考全国Ⅱ理数】已知,,则__________.【答案】【解析】因为,,所以所以,因此【名师点睛】本题主要考查三角恒等变换,考查考生分析问题、解决问题的能力,考查的核心素养是数学运算.7.【2017年高考江苏卷】若则.【答案】【解析】.故答案为.【考点】两角和的正切公式【名师点睛】三角函数求值的三种类型(1)给角求值:关键是正确选用公式,以便把非特殊角的三角函数转化为特殊角的三角函数.(2)给值求值:关键是找出已知式与待求式之间的联系及函数的差异.一般有如下两种思路:①适当变换已知式,进而求得待求式的值;②变换待求式,便于将已知式的值代入,从而达到解题的目的.(3)给值求角:实质是转化为“给值求值”,先求角的某一函数值,再求角的范围,进而确定角.8.【2019年高考浙江卷】设函数.(1)已知函数是偶函数,求的值;(2)求函数的值域.【答案】(1)或;(2).【解析】(1)因为是偶函数,所以,对任意实数x都有,即,故,所以.又,因此或.(2).因此,函数的值域是.【名师点睛】本题主要考查三角函数及其恒等变换等基础知识,同时考查运算求解能力.9.【2017年高考江苏卷】已知向量(1)若a∥b,求的值;(2)记,求的最大值和最小值以及对应的的值.【答案】(1);(2)时,取到最大值3;时,取到最小值.【解析】(1)因为,,a∥b,所以.若,则,与矛盾,故.于是.又,所以.(2).因为,所以,从而.于是,当,即时,取到最大值3;当,即时,取到最小值.【考法拓展•题型解码】 考法一 三角函数式的化简解题技巧:三角函数式的化简遵循的“三看”原则(1)一看式中各角:善于发现角之间的差别与联系,合理对角拆分,恰当选择三角公式,能求值的求出值,减少角的个数.(2)二看函数名称:看函数名称之间的差异,利用诱导公式、切弦互化、二倍角公式等实现名称的统一. (3)三看结构特征:分析结构特征,找到变形的方向,常见的有“遇到分式要通分”“整式因式分解”“二次式配方”等.【例1】 (1)已知0<θ<π,则(1+sin θ+cos θ)⎝⎛⎭⎫sin θ2-cos θ22+2cos θ=__________.(2)化简:(sin 2α+cos 2α-1)(sin 2α-cos 2α+1)sin 4α=__________.(3)化简:⎝ ⎛⎭⎪⎫1tan α2-tan α2·⎝⎛⎭⎫1+tan α·tan α2=__________. 【答案】(1)-cos θ (2)tan α (3)2sin α【解析】 (1)由θ∈(0,π)得0<θ2<π2,所以cos θ2>0,所以2+2cos θ=4cos 2θ2=2cos θ2.又(1+sin θ+cos θ)⎝⎛⎭⎫sin θ2-cos θ2 =⎝⎛⎭⎫2sin θ2cos θ2+2cos 2θ2·⎝⎛⎭⎫sin θ2-cos θ2 =2cos θ2⎝⎛⎭⎫sin 2θ2-cos 2θ2=-2cos θ2cos θ. 故原式=-2cos θ2cos θ2cosθ2=-cos θ.(2)(sin 2α+cos 2α-1)(sin 2α-cos 2α+1)sin 4α=sin 22α-(cos 2α-1)22sin 2α·cos 2α=sin 22α-cos 22α+2cos 2α-12sin 2α·cos 2α=-2cos 22α+2cos 2α2sin 2α·cos 2α=1-cos 2αsin 2α=2sin 2α2sin αcos α=sin αcos α=tan α. (3)原式=⎝ ⎛⎭⎪⎫cos α2sin α2-sin α2cos α2·⎝ ⎛⎭⎪⎫1+sin αcos α·sin α2cos α2=cos 2α2-sin 2α2sin α2cos α2·cos αcos α2+sin αsinα2cos αcos α2=2cos αsin α·cosα2cos αcosα2=2sin α. 考法二 三角函数式的求值答题模板:解三角函数求值问题的一般步骤 (1)给值(角)求值问题的一般步骤 ①化简条件式子或待求式子;②观察条件与所求之间的联系,从函数名称及角入手; ③将已知条件代入所求式子,化简求值. (2)给值求角问题的一般步骤 ①先求角的某一个三角函数值; ②确定角的范围;③根据角的范围写出所求的角.【例2】 (1)sin 50°(1+3tan 10°)=( ) A .-1 B .0 C .1 D .2【答案】C【解析】(1)sin 50°(1+3tan 10°)=sin 50°(1+tan 60°·tan 10°) =sin 50°·cos 60°cos 10°+sin 60°sin 10°cos 60°cos 10°=sin 50°·cos (60°-10°)cos 60°cos 10°=2sin 50°cos 50°cos 10°=sin 100°cos 10°=cos 10°cos 10°=1.(2)已知α为第二象限角,且sin 2α=-2425,则cos α-sin α的值为( )A .75B .-75C .15D .-15【答案】B【解析】由α为第二象限的角可知cos α<0,sin α>0,所以cos α-sin α<0,而(cos α-sin α)2=1-sin 2α=1+2425=4925,所以cos α-sin α=-75. (3)已知tan 2α=-22,且π4<α<π2,则2cos 2 α2-sin α-12sin ⎝⎛⎭⎫π4+α的值是( )A . 2B .- 2C .-3+2 2D .3-2 2【答案】C【解析】因为π4<α<π2,所以tan α>0,所以由tan 2 α=2tan α1-tan 2 α=-22可得tan α= 2.原式=2cos 2α2-1-sin α2⎝⎛⎭⎫sin π4cos α+cos π4sin α=cos α-sin αcos α+sin α=1-tan α1+tan α=1-21+2=-3+2 2.故选C .【例3】 (1)设α,β为钝角,且sin α=55,cos β=-31010,则α+β的值为( ) A .3π4B .5π4C .7π4D .5π4或7π4【答案】C【解析】因为α,β为钝角,sin α=55,cos β=-31010, 所以cos α=-255,sin β=1010,所以cos(α+β)=cos αcos β-sin αsin β=22>0. 又α+β∈(π,2π),所以α+β=7π4.(2)已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,则2α-β的值为__________.【答案】-3π4【解析】因为tan α=tan[(α-β)+β]=tan (α-β)+tan β1-tan (α-β)tan β=12-171+12×17=13>0,所以0<α<π2. 又因为tan 2α=2tan α1-tan 2α=2×131-⎝⎛⎭⎫132=34>0,所以0<2α<π2,所以tan(2α-β)=tan 2α-tan β1+tan 2αtan β=34+171-34×17=1.因为tan β=-17<0,所以π2<β<π,-π<2α-β<0,所以2α-β=-3π4.考法三 三角恒等变换与三角函数的综合问题 归纳总结三角恒等变换的综合应用主要是将三角恒等变换与三角函数的性质相结合,通过变换,将复杂的函数式化为y =A sin(ωx +φ)+b 的形式再研究性质.在研究性质时注意利用整体思想解决相关问题. 【例4】 设函数f (x )=sin ωx ·cos ωx -3cos 2ωx +32(ω>0)的图象上相邻最高点与最低点的距离为π2+4. (1)求ω的值;(2)若函数y =f (x +φ)⎝⎛⎭⎫0<φ<π2是奇函数,求函数g (x )=cos(2x -φ)在[0,2π]上的单调递减区间. 【答案】见解析【解析】 (1)f (x )=sin ωx ·cos ωx -3cos 2ωx +32=12sin 2ωx -3(1+cos 2ωx )2+32=12sin 2ωx -32cos 2ωx =sin ⎝⎛⎭⎫2ωx -π3.设T 为f (x )的最小正周期,由f (x )的图象上相邻最高点与最低点的距离为π2+4,得⎝⎛⎭⎫T 22+[2f (x )max ]2=π2+4.因为f (x )max=1,所以⎝⎛⎭⎫T 22+4=π2+4,整理得T =2π.又因为ω>0,T =2π2ω=2π,所以ω=12.(2)由(1)可知f (x )=sin ⎝⎛⎭⎫x -π3,所以f (x +φ)=sin ⎝⎛⎭⎫x +φ-π3.因为y =f (x +φ)是奇函数,所以sin ⎝⎛⎭⎫φ-π3=0.又因为0<φ<π2,所以φ=π3,所以g (x )=cos(2x -φ)=cos ⎝⎛⎭⎫2x -π3.令2k π≤2x -π3≤2k π+π,k ∈Z ,则k π+π6≤x ≤k π+2π3,k ∈Z ,所以函数g (x )的单调递减区间是⎣⎡⎦⎤k π+π6,k π+2π3,k ∈Z .又因为x ∈[0,2π],所以当k =0时,g (x )的单调递减区间为⎣⎡⎦⎤π6,2π3;当k =1时,g (x )的单调递减区间为⎣⎡⎦⎤7π6,5π3.所以函数g (x )在[0,2π]上的单调递减区间是⎣⎡⎦⎤π6,2π3,⎣⎡⎦⎤7π6,5π3. 【易错警示】易错点 化简求值时不能正确地确定函数值的符号【典例】 函数f (x )=6cos 2ωx2+3sin ωx -3(ω>0)在一个周期内的图象如图所示,A 为图象的最高点,B ,C为图象与x 轴的交点,且△ABC 为正三角形. (1)求ω的值及f (x )的值域;(2)若f (x 0)=835,且x 0∈⎝⎛⎭⎫-103,23,求f (x 0+1)的值.【错解】:(1)同正解(1). (2)f (x )=23sin ⎝⎛⎭⎫π4x +π3, f (x 0)=23sin ⎝⎛⎭⎫π4x 0+π3=835. 所以sin ⎝⎛⎭⎫π4x 0+π3=45, 所以cos ⎝⎛⎭⎫π4x 0+π3=±35. 所以f (x 0+1)=23sin ⎝⎛⎭⎫π4x 0+π3+π4=23×22·⎣⎡⎦⎤sin ⎝⎛⎭⎫π4x 0+π3+cos ⎝⎛⎭⎫π4x 0+π3=6⎝⎛⎭⎫45±35, 所以f (x 0+1)=765或f (x 0+1)=65.【错因分析】:一般情况下,当求出sin α的值再求cos α的值时,一定要根据题设条件得到α的取值范围,进而利用平方关系求值,本题中求出了sin ⎝⎛⎭⎫π4x 0+π3=45,但角度π4x 0+π3比较复杂,所以一般同学找不到它的取值范围.或嫌麻烦不愿去找,因而导致失分.【正解】:(1)f (x )=3+3cos ωx +3sin ωx -3=23sin ⎝⎛⎭⎫ωx +π3, 所以值域为[-23,23].因为BC =T 2=233×2=4,所以T =8=2πω,所以ω=π4.(2)f (x )=23sin ⎝⎛⎭⎫π4x +π3, f (x 0)=23sin ⎝⎛⎭⎫π4x 0+π3=835. 所以sin ⎝⎛⎭⎫π4x 0+π3=45,因为x 0∈⎝⎛⎭⎫-103,23, 所以π4x 0+π3∈⎝⎛⎭⎫-π2,π2,cos ⎝⎛⎭⎫π4x 0+π3=35. 所以f (x 0+1)=23sin ⎝⎛⎭⎫π4x 0+π3+π4=23×22·⎣⎡⎦⎤sin ⎝⎛⎭⎫π4x 0+π3+cos ⎝⎛⎭⎫π4x 0+π3=6⎝⎛⎭⎫45+35=765. 【误区防范】三角函数化简求值中应注意的几个问题(1)解题时注意观察角、名、结构等特征,注意利用整体思想解决相关问题.(2)运用公式时要注意公式成立的条件,要注意和、差、倍角的相对性,要注意升幂、降幂公式的灵活运用,要注意“1”的各种变形.(3)在三角求值时,往往要估计角的范围后再求值.特别是在(0,π)范围内,正弦值对应的角不唯一. 【跟踪训练】 已知cos 2θ=725,π2<θ<π,则2cos 2θ2-sin θ2sin ⎝⎛⎭⎫θ+π4=__________.【答案】2【解析】 原式=1+cos θ-sin θsin θ+cos θ.因为cos 2θ=725,π2<θ<π.π<2θ<2π,所以sin 2θ=-2425且cos θ<0<sin θ.因为(cos θ-sin θ)2=1-sin 2θ=4925且cos θ-sin θ<0,所以cos θ-sin θ=-75.又725=cos 2θ=(cos θ-sinθ)(cos θ+sin θ),所以cos θ+sin θ=-15,所以原式=1-75-15=2.【递进题组】1.化简2sin (π-α)+sin 2α2cos 2α2=( )A .sin αB .sin 2αC .2sin αD .sin α2【答案】C【解析】 原式=2sin α+2sin αcos α1+cos α=2sin α(1+cos α)(1+cos α)=2sin α.2.计算sin 20°cos 70°-cos 160°sin 70°的值为( ) A .0 B .-sin 50° C .1 D .-1【答案】C【解析】原式=sin 20°cos 70°+cos 20°sin 70°=sin(20°+70°)=1.3.(2018·全国卷Ⅱ)已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)=__________. 【答案】 -12【解析】 将两式平方相加得2+2sin(α+β)=1,所以sin(α+β)=-12.4.设θ为第二象限角,若tan ⎝⎛⎭⎫θ+π4=12,则sin θ+cos θ=__________. 【答案】 -105【解析】 因为tan ⎝⎛⎭⎫θ+π4=12, 所以tan θ=tan ⎣⎡⎦⎤⎝⎛⎭⎫θ+π4-π4= tan ⎝⎛⎭⎫θ+π4-tan π41+tan ⎝⎛⎭⎫θ+π4tan π4=12-11+12×1=-13,即sin θ=-13cos θ,又因为sin 2θ+cos 2θ=1,所以19cos 2θ+cos 2θ=1,cos 2θ=910,因为θ为第二象限角,所以cos θ=-31010,sin θ=-13cos θ=1010,sin θ+cos θ=-31010+1010=-105. 5.(2018·山东卷)设f (x )=23sin(π-x )sin x -(sin x -cos x )2. (1)求f (x )的单调递增区间;(2)把y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移π3个单位,得到函数y =g (x )的图象,求g ⎝⎛⎭⎫π6的值. 【答案】见解析【解析】 (1)f (x )=23sin 2x -(1-2sin x cos x )= 3(1-cos 2x )+sin 2x -1=sin 2x -3cos 2x +3-1= 2sin ⎝⎛⎭⎫2x -π3+3-1. 由2k π-π2≤2x -π3≤2k π+π2(k ∈Z ),得k π-π12≤x ≤k π+5π12(k ∈Z ),所以f (x )的单调递增区间是⎣⎡⎦⎤k π-π12,k π+5π12(k ∈Z ).(2)由(1)知f (x )=2sin ⎝⎛⎭⎫2x -π3+3-1,把y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到y =2sin ⎝⎛⎭⎫x -π3+3-1的图象,再把所得到的图象向左平移π3个单位,得到y =2sin x +3-1的图象,即g (x )=2sin x +3-1.所以g ⎝⎛⎭⎫π6=2sin π6+3-1= 3. 【考卷送检】 一、选择题1.已知sin 2α=13,则cos 2⎝⎛⎭⎫α-π4=( ) A .-13B .-23C .13D .23【答案】D【解析】 cos 2⎝⎛⎭⎫α-π4=1+cos ⎝⎛⎭⎫2α-π22=1+sin 2α2=23. 2.(2017·山东卷)函数y =3sin 2x +cos 2x 的最小正周期为( ) A .π2B .2π3C .πD .2π【答案】C【解析】 y =3sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6,其最小正周期为2π2=π.故选C . 3.(2018·全国卷Ⅰ)已知函数f (x )=2cos 2x -sin 2x +2,则( ) A .f (x )的最小正周期为π,最大值为3 B .f (x )的最小正周期为π,最大值为4 C .f (x )的最小正周期为2π,最大值为3 D .f (x )的最小正周期为2π,最大值为4【答案】B【解析】 因为函数f (x )=1+cos 2x -1-cos 2x 2+2=32cos 2x +52,所以f (x )的最小正周期为2π2=π,最大值为32+52=4.故选B . 4.(2019·绵阳中学月考)已知sin ⎝⎛⎭⎫2π3-α+sin α=435,则sin ⎝⎛⎭⎫α+7π6=( ) A .-45B .-35C .-25D .-15【答案】A【解析】 由题意得sin ⎝⎛⎭⎫2π3-α+sin α=32cos α+32sin α=3sin ⎝⎛⎭⎫α+π6=435,所以sin ⎝⎛⎭⎫α+π6=45,所以sin ⎝⎛⎭⎫α+7π6=-sin ⎝⎛⎭⎫α+π6=-45. 5.(2019·深圳中学期中)已知tan ⎝⎛⎭⎫α+π4=12,且-π2<α<0,则2sin 2α+sin 2αcos ⎝⎛⎭⎫α-π4=( ) A .-255B .-3510C .-31010D .255【答案】A【解析】 由tan ⎝⎛⎭⎫α+π4=tan α+11-tan α=12得tan α=-13.又-π2<α<0,故sin α=-1010.故2sin 2α+sin 2αcos ⎝⎛⎭⎫α-π4=2sin α(sin α+cos α)22(sin α+cos α)=22sin α=-255.6.已知sin ⎝⎛⎭⎫π6-α=cos ⎝⎛⎭⎫π6+α,则cos 2α=( ) A .1 B .-1 C .12D .0【答案】D【解析】 因为sin ⎝⎛⎭⎫π6-α=cos ⎝⎛⎭⎫π6+α,所以12cos α-32sin α=32cos α-12sin α,即⎝⎛⎭⎫12-32sin α=-⎝⎛⎭⎫12-32cos α,所以tan α=sin αcos α=-1,所以cos 2α=cos 2α-sin 2α=cos 2α-sin 2αsin 2α+cos 2α=1-tan 2αtan 2α+1=0.二、填空题7.tan ⎝⎛⎭⎫π4+α·cos 2α2cos 2⎝⎛⎭⎫π4-α的值为________.【答案】 1【解析】 原式=sin ⎝⎛⎭⎫π4+α·cos 2α2sin 2⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α=cos 2α2sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α=cos 2αsin 2⎝⎛⎭⎫π4+α=cos 2αsin ⎝⎛⎭⎫π2+2α=cos 2αcos 2α=1. 8.若锐角α,β满足(1+3tan α)(1+3tan β)=4,则α+β=________. 【答案】 π3【解析】 由(1+3tan α)(1+3tan β)=4可得tan α+tan β1-tan αtan β=3,即tan(α+β)= 3.又α+β∈(0,π),所以α+β=π3.9.已知α,β∈⎝⎛⎭⎫0,π2,tan(α+β)=9tan β,则tan α的最大值为________. 【答案】 43【解析】 因为α,β∈⎝⎛⎭⎫0,π2,所以tan α>0,tan β>0, 所以tan α=tan(α+β-β)=tan (α+β)-tan β1+tan (α+β)·tan β=8tan β1+9tan 2β=81tan β+9tan β≤82×3=43⎝⎛⎭⎫当且仅当1tan β=9tan β时等号成立,即(tan α)max =43.三、解答题10.(2018·浙江卷)已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过点P ⎝⎛⎭⎫-35,-45. (1)求sin(α+π)的值;(2)若角β满足sin(α+β)=513,求cos β的值.【答案】见解析【解析】 (1)由角α的终边过点P ⎝⎛⎭⎫-35,-45得sin α=-45,所以sin(α+π)=-sin α=45.(2)由角α的终边过点P ⎝⎛⎭⎫-35,-45得cos α=-35,由sin(α+β)=513得cos(α+β)=±1213.由β=(α+β)-α得cos β=cos(α+β)cos α+sin(α+β)sin α,所以cos β=-5665或cos β=1665.11.已知函数f (x )=sin 2x -sin 2⎝⎛⎭⎫x -π6,x ∈R . (1)求f (x )的最小正周期;(2)求f (x )在区间⎣⎡⎦⎤-π3,π4上的最大值和最小值. 【答案】见解析【解析】 (1)由已知,有f (x )=1-cos 2x 2-1-cos ⎝⎛⎭⎫2x -π32=12⎝⎛⎭⎫12cos 2x +32sin 2x -12cos 2x =34sin 2x -14cos 2x=12sin ⎝⎛⎭⎫2x -π6.所以f (x )的最小正周期T =2π2=π. (2)因为f (x )在区间⎣⎡⎦⎤-π3,-π6上是减函数,在区间⎣⎡⎦⎤-π6,π4上是增函数,且f ⎝⎛⎭⎫-π3=-14,f ⎝⎛⎭⎫-π6=-12,f ⎝⎛⎭⎫π4=34,所以f (x )在区间⎣⎡⎦⎤-π3,π4上的最大值为34,最小值为-12. 12.已知函数f (x )=3sin(ωx +φ)+2sin 2ωx +φ2-1(ω>0,0<φ<π)为奇函数,且相邻两对称轴间的距离为π2. (1)当x ∈⎣⎡⎦⎤-π2,π4时,求f (x )的单调递减区间; (2)将函数y =f (x )的图象沿x 轴方向向右平移π6个单位长度,再把横坐标缩短到原来的12(纵坐标不变),得到函数y =g (x )的图象.当x ∈⎣⎡⎦⎤-π12,π6时,求函数g (x )的值域. 【答案】见解析【解析】 (1)由题意得f (x )=3sin(ωx +φ)-cos ()ωx +φ=2sin ⎝⎛⎭⎫ωx +φ-π6,因为相邻两对称轴间的距离为π2,所以T =2πω=π,ω=2.又因为函数f (x )为奇函数,所以φ-π6=k π,k ∈Z ,φ=k π+π6,k ∈Z .因为0<φ<π,所以φ=π6,故函数f (x )=2sin 2x .令π2+2k π≤2x ≤3π2+2k π,k ∈Z ,得π4+k π≤x ≤3π4+k π,k ∈Z ,令k =-1,得-3π4≤x ≤-π4,因为x ∈⎣⎡⎦⎤-π2,π4,所以函数f (x )的单调递减区间为⎣⎡⎦⎤-π2,-π4. (2)由题意可得g (x )=2sin ⎝⎛⎭⎫4x -π3,因为x ∈⎣⎡⎦⎤-π12,π6,所以-2π3≤4x -π3≤π3,所以-1≤sin ⎝⎛⎭⎫4x -π3≤32,g (x )∈[-2,3],即函数g (x )的值域为[-2,3].13.(2019·洛阳统考)已知函数f (x )=sin 2ωx 2+12sin ωx -12(ω>0),x ∈R ,若f (x )在区间(π,2π)内没有零点,则ω的取值范围是( ) A .⎝⎛⎦⎤0,18 B .⎝⎛⎦⎤0,14∪⎣⎡⎭⎫58,1 C .⎝⎛⎦⎤0,58 D .⎝⎛⎦⎤0,18∪⎣⎡⎦⎤14,58 【答案】D【解析】 f (x )=sin 2ωx 2+12sin ωx -12=12sin ωx -12cos ωx =22sin ⎝⎛⎭⎫ωx -π4,因为π<x <2π,所以ωπ-π4<ωx -π4<2ωπ-π4,因为函数f (x )在区间(π,2π)内没有零点,所以⎩⎪⎨⎪⎧2π2ω≥π,f (π)·f (2π)≥0即⎩⎨⎧0<ω≤1,22sin ⎝⎛⎭⎫ωπ-π4≥0,22sin ⎝⎛⎭⎫2ωπ-π4≥0或⎩⎨⎧0<ω≤1,22sin ⎝⎛⎭⎫ωπ-π4≤0,22sin ⎝⎛⎭⎫2ωπ-π4≤0,则⎩⎪⎨⎪⎧0<ω≤1,2k +14≤ω≤2k +54,k +18≤ω≤k +58(k ∈Z )或⎩⎪⎨⎪⎧0<ω≤1,2k -34≤ω≤2k +14,k -38≤ω≤k +18(k ∈Z ),所以0<ω≤18或14≤ω≤58.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单的三角恒等变换专题
三角函数和代数、几何知识联系密切,它是研究其他各类知识的重要工具.高考题中与三角函数有关的问题,大都以恒等变形为研究手段.三角变换是运算、化简、求值、证明过程中不可缺少的解题技巧,要学会创设条件灵活运用三角公式,掌握运算,化简的方法和技能.
1.含有不同角或幂次不同的三角函数等式的证明
如果等式两边是含有不同角的三角函数式,那么可以从变化角入手,如果等式两边所含的三角函数的幂次不同,那么可以从变化次数入手.
例1 求证222(3cos4)tan cot 1cos4x x x x
++=
-. 分析:观察左、右两边式子间的差异,若选择“从左证到右”,则“切化弦”的方法势 在必行;若选择“从右证到左”,则倍角公式应是必用公式. 证法一:左边22442222sin cos sin cos cos sin sin cos x x x x x x x x
+=+= 222222
2211sin 2(sin cos )2sin cos 211sin 2sin 244x x x x x x x -+-== 22211sin 284sin 244cos 221cos 41cos 4(1cos 4)8
x x x x x x --+===--- 42(1cos4)2(3cos4)1cos41cos4x x x x
+++==--=右边. 证法二:右边2222(21cos4)2(22cos 2)2sin 22sin 2x x x x
+++== 2222222
22222(1cos 2)(sin cos )(cos sin )4sin cos 2sin cos x x x x x x x x x
+++-== 4422222(sin cos )tan cot 2sin cos x x x x x x
+==+=左边. 评析:切割化弦是三角变换的一种常用方法,若能把所给式子中的三角函数都化成同名、同角的三角函数,则此三角函数式的化简,实质上是代数式的变换.
2.含有差异角的三角函数式的求解
三角函数式中往往出现较多的差异角,注意观察角与角之间的和、差、倍、半、互补、互余等关系,运用角的变换,化多角为单角或减少未知角的数目,沟通条件角与结论角的联系,
使问题顺利获解.对角的变换:①可以通过诱导公式;②注意倍角的相对性,如α是2
α的倍角,3α是32
α的倍角等;③注意拆角、拼角技巧,例如2()()ααβαβ=++-,22αβαββ+-=-,πππ424αα⎛⎫+=-- ⎪⎝⎭
等.
例2 若π4cos 45x ⎛⎫-=- ⎪⎝⎭,5π7π44x <<,求2sin 22sin 1tan x x x -+. 分析:转化为已知一个角π4x ⎛⎫- ⎪⎝⎭
的三角函数值,求这个角的其余三角函数值的问题.这 样可以将所求式子化简,使其出现π4x ⎛⎫- ⎪⎝⎭
这个角的三角函数. 解:2s i n 22s i n 2s i n (c o s s i n )c o s s i n 2(c o s s i n )
1t a n c o s s i n c o s s i n x x x x x x x x x x
x x x x ---==+++ 1t a n πππs i n 2s i n 2t a n c o s 2t a n 1t a n 424x x x x x x x -⎛⎫⎛⎫⎛⎫==-=-- ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭. 2ππ[2c o s 1]t a n 44x x ⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭ 5π7π44x << ,3πππ24
x ∴-<-<-. 又π4cos 45x ⎛⎫-=- ⎪⎝⎭
, π3sin 45x ⎛⎫∴-= ⎪⎝⎭,π3tan 44x ⎛⎫-=- ⎪⎝⎭. ∴原式1632121254100⎛⎫⎛⎫=⨯-⨯-=- ⎪ ⎪⎝
⎭⎝⎭. 评析:本题采用的“凑角法”是解三角题的常用技巧,解题时首先要分析已知条件和结论中各种角之间的相互关系,并根据这种关系来选择公式.
3.给值求角的关键也是变角
把所求的角用含已知其值的角的式子表示,由所求的函数值结合该函数的单调区间求得角,但不要忽视对所求角的范围的讨论.即解决“给值求角”问题是由两个关键步骤构成:①把所求角用含已知角的式子表示;②由所得的函数值结合该函数的单调区间求得角.
例3 已知1tan()2αβ-=,1tan 7
β=-,且(0π)αβ∈,,,求2αβ-的值. 解:22()αβαββ-=-+ ,1tan()2
αβ-=
, 22t a n ()4t a n 2()1t a n ()3αβαβαβ-∴-==-- 从而tan(2)tan[2()]αβαββ-=-+4125tan 2()tan 372114125
1tan 2()tan 13721
αββαββ--+====--+⨯. 又[]tan()tan 1tan tan ()11tan()tan 3αββααββαββ-+=-+=
=<-- . 且0πα<<,π04α∴<<.π022
α∴<<. 又1tan 07
β=-<,且(0π)β∈,, ππ2β∴<<,ππ2
β-<-<-.
π20αβ∴-<-<.32π4
αβ∴-=-. 评析:本题通过变形转化为已知三角函数值求角的问题,关键在于对角的范围的讨论,注意合理利用不等式的性质,必要时,根据三角函数值,缩小角的范围,从而求出准确角.另外,求角一般都通过三角函数值来实现,但求该角的哪一种函数值,往往有一定的规律,若
(0π)α∈,,则求cos α.若ππ22α⎛⎫∈- ⎪⎝⎭
,,则求sin α等. 4.参变量的桥梁作用
根据三角函数式的结构,引入参变量,使参变量在解题过程中起到桥梁作用,通过参数代换,使繁难的式子变得简单、复杂的式子变得简明,使隐含的规律显露出来.
例4 求cos36cos72- 的值.
解:设cos36x = ,cos72y = ,
由2cos722cos 361=- ,得221y x =-.
又22cos3612sin 1812cos 72=-=- ,则212x y =-.
222()2()()x y x y x y x y ∴+=-=+-,
0x y +≠ ,12x y ∴-=,即1cos36cos722
-= . 评析:在三角函数求值问题中,通过引入参变量调节命题结构,把问题转化为对参变量的讨论.这种替换可以转化原问题的结构,简化解题过程.巧妙的变换,还可以收到事半功倍的效果.
5.借助方程思想证明等式
有关角度等式的证明问题,可以借助方程思想把其转化为已知三角函数值求角的问题 例5 若αβ,为锐角,且223sin 2sin 1αβ+=,3sin 22sin 20αβ-=,求证:π22
a β+=. 分析:由条件等式证明“角+角=角”的问题,一般转化为证明相应的三角函数值问题. 证明:已知两个等式可化为23sin cos2αβ=, ①
3sin cos sin 2ααβ=, ②
①÷②,得sin cos 2cos sin 2αβαβ
=,即cos cos 2sin sin 20αβαβ-=, c o s (2)α
β∴+=. π02α<< ,π02β<<,3π022
αβ∴<+<. π22
αβ∴+=. 评析:要证明两角相等,仅证明两个角的同名三角函数值相等是不够的,还必须要证明它们在同一单调区间内.。
