江苏省丹阳市第三中学九年级数学上册周周练(四)(附答案)$809120
九年级上数学周周练(4.1~4.3)含答案

周周练(4.1~4.3)(时间:45分钟 满分:100分)一、选择题(每小题4分,共28分)1.在比例尺为1∶5 000的地图上,量得甲、乙两地的距离为25 cm ,则甲、乙两地的实际距离是( ) A .1 250千米 B .125千米 C .12.5千米 D .1.25千米2.a ,b ,c ,d 是四条线段,下列各组中这四条线段成比例的是( ) A .a =2 cm ,b =5 cm ,c =5 cm ,d =10 cm B .a =5 cm ,b =3 cm ,c =10 cm ,d =6 cm C .a =30 cm ,b =2 cm ,c =0.8 cm ,d =2 cm D .a =5 cm ,b =0.02 cm ,c =7 cm ,d =0.3 cm 3.已知b a =513,则a -ba +b 的值是( )A.23 B.32 C.94 D.494.下列结论不正确的是( ) A .所有的矩形都相似 B .所有的正方形都相似C .所有的等腰直角三角形都相似D .所有的正八边形都相似5.一个多边形的边长分别为2,3,4,5,6,另一个和它相似的多边形的最长边长为24,则这个多边形的最短边长为( )A .6B .8C .12D .106.(上海中考)如图,已知在△ABC 中,点D ,E ,F 分别是边AB ,AC ,BC 上的点,DE ∥BC ,EF ∥AB ,且AD ∶DB =3∶5,那么CF ∶CB 等于( ) A .5∶8 B .3∶8 C .3∶5 D .2∶57.如图,已知DE ∥BC ,EF ∥AB ,现得到下列结论: ①AEEC =BFFC ;②AD BF =AB BC ;③EF AB =DE BC ;④CE CF =EA BF . 其中正确比例式的个数有( )A .4个B .3个C .2个D .1个二、填空题(每小题4分,共20分)8.若两个相似多边形的对应边分别为4 cm 和8 cm ,则它们的相似比为________. 9.若a b =c d =ef=2,且b +d +f =4,则a +c +e =________.10.(漳州中考)如图,AD ∥BE ∥CF ,直线l 1,l 2与这三条平行线分别交于点A ,B ,C 和点D ,E ,F ,ABBC =23,DE =6,则EF =________. 11.已知三个数:1,2,3,请你添上一个数,使它们能构成一个比例式,则这个数是____________(只填一个).12.北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH 为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9∶5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为________丈. 三、解答题(共52分)13.(8分)如图,已知点C 是线段AB 上的点,D 是AB 延长线上的点,且AD ∶BD =3∶2,AB ∶AC =5∶3,AC =3.6,求AD 的长.14.(12分)(1)已知a b =2,求a +bb ;(2)已知a b =52,求a -ba +b .15.(10分)小华的父亲计划修建一个矩形草坪,按1∶100的比例尺画出了草坪图(如图),他准备在草坪内栽种面积为0.02平方米的小矩形草皮,在草坪四周每隔50厘米种一株小杜鹃,你能帮助小华的父亲算算他需购买多少块小矩形草皮与多少株杜鹃吗?16.(10分)如图,在△ABC 中,EF ∥CD ,DE ∥BC. 求证:AF ·BD =AD ·FD.17.(12分)如图,矩形ABCD的长AB=30,宽BC=20.(1)如图1,若沿矩形ABCD四周有宽为1的环形区域,图中所形成的两个矩形ABCD与A′B′C′D′相似吗?请说明理由;(2)如图2,当x为多少时,图中的两个矩形ABCD与A′B′C′D′相似?参考答案1.D 2.B 3.D 4.A 5.B 6.A 7.B 8.1∶2 9.8 10.9 11.答案不唯一,如23 12.72 13.∵AB ∶AC =5∶3,AC =3.6,∴AB =53×3.6=6.∵AD ∶BD =3∶2,∴AB ∶AD =1∶3.∴AD =3×6=18. 14.(1)a +bb =3.(2)a -b a +b =37. 15.由于比例尺为1∶100,根据图纸,长为5×100=500(cm)=5(m),宽为3×100=300(cm)=3(m),5×3÷0.02=750(块),(3+5)×2÷0.5=32(株).答:需购买750块小矩形草皮,32株杜鹃. 16.证明:∵EF ∥CD ,∴AFFD =AEEC .∵DE ∥BC ,∴AD BD =AE EC .∴AF FD =ADBD .∴AF ·BD =AD ·FD. 17.(1)不相似,理由如下:AB =30,A ′B ′=28,BC =20,B ′C ′=18,而2830≠1820,故矩形ABCD 与矩形A ′B ′C ′D ′不相似.(2)若矩形ABCD 与A ′B ′C ′D ′相似,则A ′B ′AB =B ′C ′BC 或A ′B ′BC =B ′C ′AB .则30-2x 30=20-220或30-2x 20=20-230.解得x =1.5或9.故当x =1.5或9时,矩形ABCD 与矩形A ′B ′C ′D ′相似.。
九年级上册数学周末试卷【含答案】

九年级上册数学周末试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 若一个正方形的边长为a,则它的对角线长为()A. a/2B. a√2C. 2aD. a²2. 下列函数中,奇函数是()A. y = x²B. y = |x|C. y = x³D. y = x² + 13. 已知一组数据2,3,5,7,x,其平均数为4,则x的值为()A. 1B. 3C. 5D. 74. 在直角坐标系中,点P(2, -3)关于y轴的对称点坐标为()A. (-2, 3)B. (2, 3)C. (-2, -3)D. (3, -2)5. 若a > b > 0,则下列哪个选项是正确的?()A. a² > b²B. a b < bC. 1/a < 1/bD. a/b > b/a二、判断题(每题1分,共5分)6. 任何两个奇数之和都是偶数。
()7. 平行四边形的对角线互相平分。
()8. 二次函数y = ax² + bx + c的图像是一个抛物线。
()9. 任何两个实数的和、差、积、商(除数不为0)都是实数。
()10. 两条平行线的斜率一定相等。
()三、填空题(每题1分,共5分)11. 若一个三角形的两边长分别为5cm和12cm,且这两边的夹角为90°,则这个三角形的周长为____cm。
12. 若一个等差数列的首项为2,公差为3,则第10项为____。
13. 一次函数y = 2x 3的图像与y轴的交点坐标为____。
14. 若一组数据的标准差为4,则这组数据的方差为____。
15. 在直角坐标系中,点A(3, 4)到原点的距离为____。
四、简答题(每题2分,共10分)16. 简述勾股定理的内容。
17. 什么是等差数列?给出一个等差数列的例子。
18. 什么是函数的单调性?给出一个单调递增函数的例子。
新人教版九年级上册数学第4周周练(新课+复习)

1.函数y=-x2-4x+3图象顶点坐标是。
2.二次函数y=x2的图象向右平移3个单位,再向上平移两个单位长度,得到新的图象的函数表达式是。
3.一个正方形的面积为16cm2,当把边长增加x cm时,正方形面积为y cm2,则y 关于x的函数为。
4.下列说法错误的是()
A.二次函数y=3x2中,当x>0时,y随x的增大而增大
B.二次函数y=-6(x-1)2中,当x=1时,y有最大值0
C.a越大图象开口越小,a越小图象开口越大
D.不论a是正数还是负数,抛物线y=ax2(a≠0)的顶点一定是坐标原点
5.写出下来函数的开口、对称轴、顶点、极值、增减性
(1)y=3x2 (2)y=-x2+6x-8
6.已知二次函数的顶点坐标为原点,且其图象经过点(2,1),求此二次函数的解析式。
自变量x的取值范围是。
1、函数y=
x-2
2、6. 直线y=3x+b与y轴交点(0 ,–2),则这条直线不经过第象限.
3、y=kx+k的大致图象是()
A B C D
4、已知一次函数图象经过点(3 , 5) , (–4,–9)两点.
①求一次函数解析式.
②求图象和坐标轴交点坐标.
③求图象和坐标轴围成三角形面积.
④点(a , 2)在图象上,求a的值.。
九年级数学上册第四周周练

初三数学上册第四周周练出题人初三数学组审核初三数学组时间45分钟满分100分班级姓名分数一、选择题(每小题5分,满分15分)1.如图,小强和小明去测量一座古塔的高度,他们在离古塔60m的A处,用测角仪测得古塔顶的仰角为30°,已知测角仪高AD=1.5m,则古塔BE的高为()A.(20﹣1.5)m B.(20+1.5)m C.31.5m D.28.5m第1题图第2题2.如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,若AO=100cm,则墙角O到前沿BC的距离OE是()A.(60+100sinα)cm B.(60+100cosα)cmC.(60+100tanα)cm D.以上答案都不对3、如图,为测量一棵与地面垂直的树的高度,在距离树的底端点米的处,测得树顶的仰角为,则树的高度为( )A.米B.米C.米D.米二、填空题:1..如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60 m,则点A到对岸BC的距离是m.2.如图,防洪大堤的横断面是梯形,坝高AC=6米,背水坡AB的坡度i=1:2,则斜坡AB的长为米(精确到0.1米).3、如图,在Rt△ABC中,∠CAB=90°,AD是∠CAB的平分线,tanB=1/2,则CD:DB=______.4、小王在楼下点A处看到楼上点B处的小明的仰角是35度,那么点B处的小明看点A 处的小王的俯角等于度.5、阅读下面的材料,先完成阅读填空,再将要求答题:,,则①,,则;②,,则.③……观察上述等式,猜想:对任意锐角,都有.④三、计算:每题5分1、.2、cos60°-sin245°+tan230°+tan75°cot75°-tan45°四、解答题1.(15分)如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E….某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120m到达B处,测得∠CBN=70°.求河流的宽度CF.(结果精确到0.1m,参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)2.(15分)如图,在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A的仰角分别是30°和60°,已知测角仪器高CE=1.5米,CD=30米,求塔高AB.(保留根号)3.(15分)如图,某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B测得该岛在北偏东30°方向上,已知该岛周围16海里内有暗礁.(1)说明点B是否在暗礁区域内;(2)若继续向东航行有无触礁的危险?请说明理由.。
江苏省丹阳市第三中学九年级数学上册周周练(二)(无答案)

九年级数学周周练(二)一、选择题:(每小题3分)1.若⊙O的半径为5cm,点A到圆心O的距离为4cm,那么点A与⊙O的位置关系是()A. 点A在圆外 B. 点A在圆上 C. 点A在圆内 D. 不能确定2.下列说法:①长度相等的弧是等弧;②圆周角的度数等于圆心角度数的一半③相等的圆心角所对的弦相等;④方程x2+x+1=0的两个实数根之积为﹣1.你认为正确的共有()A.0个B.1个C.2个D.3个3.A,B,C是平面内的三点,AB=3,BC=3,AC=6,下列说法正确的是()A.可以画一个圆,使A,B,C都在圆上B.可以画一个圆,使A,B在圆上,C在圆外C.可以画一个圆,使A,C在圆上,B在圆外D.可以画一个圆,使B,C在圆上,A在圆内4.如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠OAC的度数是()A.35°B.55°C.65°D.70°5.如图,点A、B、P在⊙O上,且∠APB=50°.若点M是⊙O上的动点,要使△ABM为等腰三角形,则所有符合条件的点M有()A.1个B.2个C.3个D.4个6.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为()A.25°B.30°C.40°D.50°7.如图,⊙O的弦AB=6,M是AB上任意一点,且OM最小值为4,则⊙O的半径为()A.5 B.4 C.3 D.28.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为()A.15°B.28°C.29°D.34°二、填空题:(每小题3分)9.已知⊙O的半径为5cm,点A为线段OP的中点,当OP=6cm时,点A和⊙O的位置关系是。
10.已知直角三角形的两直角边分别为5,12,则它的外接圆半径R=.11.一条弦把圆分为2:3两部分,那么这条弦所对的圆周角的度数为.12.在直角坐标系中,⊙P、⊙Q的位置如图所示.在⊙P上且在⊙Q内部的格点坐标是。
九年级上数学周周练(2.1~2.4)含答案

周周练(2.1~2.4)(时间:45分钟 满分:100分)一、选择题(每小题4分,共32分)1.下列方程中,是一元二次方程的是( )A .x =2y -3B .2(x +1)=3C .x 2+3x -1=x 2+1D .x 2=92.x 2-6x =1左边配成一个完全平方式得( )A .(x -3)2=10B .(x -3)2=9C .(x -6)2=8D .(x -6)2=103.用公式法解-x 2+3x =1时,先求出a ,b ,c 的值,则a ,b ,c 依次为( )A .-1,3,1B .1,-3,-1C .-1,-3,-1D .1,-3,14.关于x 的方程3x 2-2x +m =0的一个根是-1,则m 的值为( )A .5B .-5C .1D .-15.方程x 2=0与3x 2=3x 的解为( )A .都是x =0B .有一个相同,且这个相同的解为x =0C .都不相同D .以上答案都不对6.方程(x -1)(x +3)=5的根为( )A .x 1=-1,x 2=-3B .x 1=1,x 2=-3C .x 1=-2,x 2=4D .x 1=2,x 2=-47.已知x =1是方程x 2-ax +1=0的根,化简a 2-2a +1-9-6a +a 2得( )A .1B .0C .-1D .28.现定义运算“★”,对于任意实数a ,b ,都有a ★b =a 2-3a +b ,如:3★5=32-3×3+5,若x ★2=6,则实数x 的值是( )A .-1B .4C .-1或4D .1或-4二、填空题(每小题4分,共16分)9.(厦门中考)方程x 2+x =0的解是x 1=0,x 2=________.10.(新余模拟)分式x 2-2x -3x +1值为0,则x =________. 11.(新疆中考)已知k >0,且关于x 的方程3kx 2+12x +k +1=0有两个相等的实数根,那么k 的值等于________.12.若xy ≠0,且x 2-2xy -8y 2=0,则x y =________.三、解答题(共52分)13.(20分)用适当的方法解下列方程:(1)2(x +3)2=8;(2)2x 2-4x +1=0;(3)x 2-5x -6=0;(4)x 2-22x =-18.14.(7分)先化简,再求值:m -33m 2-6m ÷(m +2-5m -2),其中m 是方程x 2+3x -1=0的根.15.(7分)已知△ABC 的两边长分别为2和3,第三边长是方程(x 2-2x)-5(x -2)=0的根,求△ABC 的周长.16.(8分)某种电脑病毒传播非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?17.(10分)(咸宁中考)已知关于x 的一元二次方程mx 2-(m +2)x +2=0.(1)证明:不论m 为何值,方程总有实数根;(2)m 为何整数时,方程有两个不相等的正整数根.参考答案1.D 2.A 3.D 4.B 5.B 6.D 7.B 8.C 9.-1 10.3 11.3 12.-2或413.(1)(x +3)2=4,x +3=±2.∴x 1=-5,x 2=-1.(2)2x 2-4x =-1,x 2-2x =-12.x 2-2x +1=-12+1. (x -1)2=12.x -1=±22. ∴x 1=1+22,x 2=1-22.(3)(x +1)(x -6)=0,x +1=0,或x -6=0.∴x 1=-1,x 2=6.(4)原方程可化为8x 2-42x +1=0,a =8,b =-42,c =1,b 2-4a c =0,x =42±016, ∴x 1=x 2=24.14.原式=m -33m (m -2)÷m 2-9m -2=m -33m (m -2)·m -2(m +3)(m -3)=13m (m +3)=13(m 2+3m ). ∵m 是方程x 2+3x -1=0的根,∴m 2+3m -1=0,即m 2+3m =1.∴原式=13(m 2+3m )=13. 15.原方程可化为x(x -2)-5(x -2)=0, ∴(x -5)(x -2)=0.∴x 1=5,x 2=2.∵三角形任意两边之和大于第三边,任意两边之差小于第三边,∴第三边的长x 的取值范围是1<x<5.∴x =2.∴△ABC 的周长为2+3+2=7.16.设每轮感染中平均一台电脑会感染x 台电脑,依题意,得1+x +(1+x)x =81.解得x 1=8,x 2=-10(舍去).(1+x)3=729>700.答:每轮感染中平均一台电脑会感染8台电脑,3轮感染后,被感染的电脑会超过700台.17.(1)证明:∵a =m ,b =-(m +2),c =2,∴Δ=b 2-4ac =(m +2)2-8m =m 2+4m +4-8m =m 2-4m +4=(m -2)2≥0.∴方程总有两个实数根.(2)方法1(公式法):∵x =-b ±b 2-4ac 2a =m +2±(m -2)22m =m +2±(m -2)2m ,∴x1=m+2+m-22m=1,x2=m+2-m+22m=2m.∵方程的两个实数根都是整数,∴2m是整数.∴m=±1或m=±2.∵方程有两个不相等的正整数根,∴m=1或2(舍去).∴m=1.方法2(因式分解法):∵mx2-(m+2)x+2=0,∴(x-1)(mx-2)=0.∴x-1=0或mx-2=0.∴x1=1,x2=2m.∵方程的两个实数根都是整数,∴2m是整数.∴m=±1或m=±2.∵方程有两个不相等的正整数根,∴m=1或2(舍去).∴m=1.。
苏科版九年级数学上册周周练试题.docx

初中数学试卷马鸣风萧萧一选择题(30分)1.用配方法解方程x 2-2x -1=0时,配方后得的方程为( ) A .(x +1)2=0B .(x -1)2=0C .(x +1)2=2D .(x -1)2=22.一元二次方程x 2+x -1=0 的根的情况为( ) A .有两个不相等的实数根 B .有两个相等的实数根 C .只有一个实数根D .没有实数根3.已知1x 、2x 是一元二次方程0142=+-x x 的两个根,则21x x ⋅等( )A .-4B .-1 C.1 D. 4 4.如图,AB 是⊙O 直径,∠AOC=130°,则∠D=( ) A.65° B .25°C .15°D .35° 5.在数轴上,点A 所表示的实数为3,点B 所表示的实数为a ,⊙A 的半径为2,下列说法中不正确的是( ) A .当a<5时,点B 在⊙A 内 B .当1<a<5时,点B 在⊙A 内 C .当a<1时,点B 在⊙A 外 D .当a>5时,点B 在⊙A 外6.如图,AB 是O ⊙的直径,点C 、D 在O ⊙上,110BOC ∠=°,AD OC ∥,则AOD ∠=( )A .70°B .60°C .50°D .40°7.下列说法正确的是( )A.经过三点可以作一个圆B.三角形的外心到这个三角形的三边距离相等C.等弧所对的圆心角相等D.相等的圆心角所对的弧相等8. 在平面直角坐标系xOy 中,以原点O 为圆心的圆过点A (13,0),直线y=kx ﹣3k+4与⊙O 交于B 、C 两点,则弦BC 的长的最小值为( )A.22B.24C.510D.3129.如图,正方形OABC 与正方形ODEF 是位似图形,O 为位似中心,相似比为1:2,点A 的坐标为(1,0),则E 点的坐标为( )OBD C AA .(2,0)B .(33,)22C.(2,2) D . (2,2)10.如图,AD 为等边△ABC 边BC 上的高,AB =4,AE =1,P 为高AD 上任意一点,则EP+BP 的最小值为( )。
苏科版九年级数学上册第4周周练试题(4A)
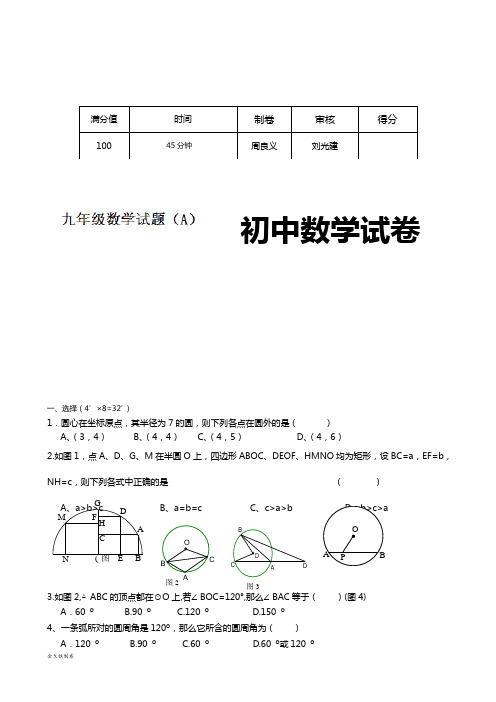
C OB 图2D A C O B 图3初中数学试卷一、选择(4’×8=32’)1.圆心在坐标原点,其半径为7的圆,则下列各点在圆外的是( ) A 、(3,4) B 、(4,4) C 、(4,5) D 、(4,6)2.如图1,点A 、D 、G 、M 在半圆O 上,四边形ABOC 、DEOF 、HMNO 均为矩形,设BC=a ,EF=b ,NH=c ,则下列各式中正确的是 ( ) A 、a>b>c B 、a=b=c C 、c>a>b D 、b>c>a3.如图2,△ABC 的顶点都在⊙O 上,若∠BOC=120°,那么∠BAC 等于( )(图4) A .60 º B.90 º C.120 º D.150 º 4、一条弧所对的圆周角是120º,那么它所含的圆周角为( ) A .120 º B.90 º C.60 º D.60 º或120 º满分值 时间制卷审核得分10045分钟周良义刘光建A (图111C F DE G N MHB · A B OPD ACOB 图75.如图3,AB 、AC 是⊙O 的弦,延长CA 到点D ,使AD=AB.若∠D=20 º,则∠BOC 等于( ) A .20 B.40 º C.80 º D.120 º 6.在半径为R 的圆内,长为R 的弦所对的圆周角为( )A .30 º B.60 º C.30 º或150 º D.120 º或607.如图4,⊙O 的直径为10cm ,弦AB 为8cm ,P 为弦AB 上的一动点,若OP 的长度为整数,则满足条件的点P 有( )A .2个B .3个C .4个D .5个8.已知方程x 2-6x+q=0可以配方成(x-p )2=7的形式,那么x 2-6x+q=2可以配方成下列的( )A 、(x-p )2=5B 、(x-p )2=9C 、(x-p+2)2=9D 、(x-p+2)2=5二、填空(4’×6=24’)9.已知⊙O 的半径r=2cm ,当OP= 时,点P 在⊙O 上;当OA=1cm 时,点A 在圆 ;当OB=4cm 时,点B 在圆 ;10.(1)如图,弦AB 把⊙O 分成2:7,∠AOB =_________°; (2)在⊙O 中,弦AB 的长恰好等于半径,AB 的度数为_______°.图611.如图6,P 是半径为5的⊙O 内一点,且OP=3,在过点P 的所有⊙O 的弦中,弦长为整数的弦的条数12.如图7,正方形ABCD 内接于⊙O ,点P 在AB 上,则∠DPC = .·O· P13.()()05422222=-+-+y x y x ,则=+22y x _________.14.已知关于x 的方程221(3)04x m x m --+=有两个不相等的实根,那么m 的最大整数是 三、解答题(共44分)15.(本题满分12分)用适当的方法解下列一元二次方程:(1)()1332+=+x x ; (2)01422=+-x x .16.(本题满分8分)在等腰△ABC 中,三边分别为a 、b 、c ,其中5a =,若关于x 的方程()2260x b x b +++-=有两个相等的实数根,求△ABC 的周长.17.(本题满分8分)小林准备进行如下操作实验:把一根长为cm 40的铁丝剪成两段,并把每一段各围成一个正方形.(1)要使这两个正方形的面积之和等于252cm ,小林该怎么剪?(2)小峰对小林说:“这两个正方形的面积之和不可能...等于244cm .”他的说法对吗?请说明理由.18.(本题满分8分)如图,⊙O 的半径OA 、OB 分别交弦CD 于点E 、F,且CE=DF.求证:△OEF 是等腰三角形.19.(本题满分8分)如图,圆柱形水管内原有积水的水平面宽CD=10cm1cm(EG=1cm),则此时水面宽AB为多少?DEACBFO。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学周周练(四)
一.选择题(共10小题30分)
1.下列说法中正确的是()
A.过三点一定可以作圆B.任意一个圆一定有内接三角形,并且只有一个内接三角形C.任意一个三角形一定有一个外接圆并且只有一个外接圆
D.三角形的外心到三角形各边的距离相等
2.下列每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是()A.B.C.D.
3.已知⊙O半径为3,M为直线AB上一点,若MO=3,则直线AB与⊙O的位置关系为()A.相切B.相交C.相切或相离D.相切或相交
4.如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于D,连接AD、OD(AC ≠AB),则能够判断图中∠B的余角(不再添加任何辅助线)的有()
A.1个B.2个C.3个D.4个
5.如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是()
A.线段AE的中垂线与线段AC的中垂线的交点
B.线段AB的中垂线与线段AC的中垂线的交点
C.线段AE的中垂线与线段BC的中垂线的交点
D.线段AB的中垂线与线段BC的中垂线的交点
6.如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是()
A.点(0,3)B.点(2,3)C.点(5,1)D.点(6,1)
7.如图,在平面直角坐标系中,⊙P与x轴相切于原点O,平行于y轴的直线交⊙P于M,N两点.若点M的坐标是(2,﹣1),则点N的坐标是()
A.(2,﹣4)B.(2,﹣4.5)C.(2,﹣5)D.(2,﹣5.5)
8.如图,AB是⊙0的直径,点D在AB的延长线上,过点D作⊙0的切线,切点为C,若∠A=25°,则∠D=()
A.60°B.65°C.50°D.40°
9.如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为()s时,BP与⊙O相切.
A.1 B.5 C.1或5 D.以上答案都不正确
10.如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为()A.4 B. C.6 D.
二.填空题(共8小题24分)
11.一个直角三角形两条直角边的长分别为6cm,8cm,则这个直角三角形的内心与外心之间的距离是cm.
12.如图,在Rt△ABC中,∠C=90°,O是AB上一点,⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是.
13.如图,AB是⊙0的直径,PB是⊙0的切线,PA交⊙0于点C, AB=3cm,PB=4cm,则BC=______cm.
14.若△ABC的周长为20cm,面积为32cm2,则△ABC的内切圆半径为.15.如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB 上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,
那么秒种后⊙P与直线CD相切.
16.将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接CD.连接BD,如图1,若α=80°,则∠BDC的度数为;
17.如图,在Rt△AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为.
18.如图,△ABC是等边三角形,边长为5,D为AC边上一动点,连接BD,⊙O为△ABD 的外接圆,过点A作AE∥BC交⊙O于E,连接DE,则DE的最小值为.
三.解答题(共5小题46分)(9+9+9+9+10)
19.如图,在△ABC中,∠C=90°,AC+BC=8,∠ACB的平分线交AB于点O,以O为圆心的⊙O与AC相切于点D.(1)求证:⊙0与BC相切;(2)当AC=2时,求⊙O的半径.
20.如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO 的延长线于点M,CM交⊙O于点D.(1)求证:AM=AC;(2)若AC=3,求MC的长.
21.AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.(1)求证:CE是⊙O的切线;(2)判断四边形AOCD是否为菱形?并说明理由.
22.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
23.如图,A(﹣5,0),B(﹣3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.(1)求点C的坐标;(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.。
