人教版数学七年级下册5.2平行线课时训练 (无答案)
新人教版七年级数学下册同步练习5.2平行线及其判定(练习卷+解析版)

新人教版七年级数学下册同步练习 5.2 平行线及其判定
参考答案与试题解析
一.选择题(共 10 小题,每小题 3 分,满分 30 分)
1.在同一平面内,不重合的两条直线的位置关系是( )
A.平行
B.相交
C.平行或相交
D.平行、相交或垂直
选:C.
2.直线 a、b、c 在同一平面内,
(1)如果 a⊥b,b⊥c,那么 a∥c;
B.有两条
C.不存在
D.有一条或不存在
解:①若点 P 在 OA 上,则不能画出与 OA 平行的直线,
②若点 P 不在 OA 上,则过点 P 有且只有一条直线与 OA 平行,
所以,这样的直线有一条或不存在.
故选 D.
4.下面推理正确的是( )
A.∵a∥b,b∥c,∴c∥d
B.∵a∥c,b∥d,∴c∥d
16.如图,EF⊥AB 于点 F,CD⊥AB 于点 D,E 是 AC 上一点,∠1=∠2,则图中互相平行 的直线有 2 对.
解:∵EF⊥AB,CD⊥AB, ∴∠EFA=∠CDA=90°, ∴EF∥CD, ∴∠1=∠EDC, ∵∠1=∠2, ∴∠EDC=∠2, ∴DE∥BC, 即图中互相平行的直线有 2 对, 故答案为:2.
(2)如果 a∥b,b∥c,c∥d,那么 a∥d;
(3)如果 a∥b,b⊥c,那么 a⊥c;
(4)如果 a 与 b 相交,b 与 c 相交,那么 a 与 c 相交.
在上述四种说法中,正确的个数为( )
A.1 个
B.2 个
C.3 个
D.4 个
解:直线 a、b、c 在同一平面内,
(1)如果 a⊥b,b⊥c,那么 a∥c;正确.
8.两条直线相交所成的四个角都相等时,这两条直线的位置关系是( )
5.2.2平行线的判定课时训练2022-2023学年人教版七年级下册数学

平行线的判定 练习题一、选择题1.如图,下列条件不能判定1l //2l 的是( )A 21∠=∠B 32∠=∠C 54∠=∠D ︒=∠+∠180432. 如图,在长方形ABCD 中,E=BG=F=12AD=13AB=2,E 、H 、G 在同一条直线上,则阴影部分的面积等于( )。
A.8 B.12 C.16 D.203.如图所示,下列条件中,不能判定AB ∥CD 的是( ) A.AB ∥EF,CD ∥EF B.∠5=∠A; C.∠1=∠4 D.∠2=∠3二、填空题4.若a,b,c 是三条直线,如果a ∥b,b ∥c,那么___________。
5.在同一平面内,若直线a 、b 、c ,满足b a ⊥,c a ⊥,则b 与c 的位置关系是 。
6.如图 ①,已知长方形纸带,∠DEF=20°,将纸带沿EF 折叠成图案②,再沿BF 折叠成图案③,则③中的∠CFE 的度数是__________。
7.将一副三角板摆放成如图所示的形状,图中1∠= 度.8.如图, 如果∠2=∠6,则______∥_______,如果∠9=_____,那么AD ∥BC;如果∠9=_____,那么AB ∥CD.三、解答题9.如图:在四边形ABCD 中,∠1=40°,∠2=40°,AD 与BC 平行吗?为什么?10.如图,已知,,试问EF 是否平行GH ,并说明理由。
11.如图,已知直线EF 和AB,CD 分别相交于K,H,且EG ⊥AB,∠CHF=60º,∠E=30°,试说明AB ∥CD.DG AEM ∠=∠21∠=∠12.如图,已知CDAB于D,EFAB于F,∠DGC=105°,∠BCG=75°,求∠1+∠2的度数.13.已知:如图⑿,CE 平分∠ACD,∠1=∠B,求证:AB∥CE14.如图:∠1=︒53,∠2=︒127,∠3=︒53,试说明直线AB与CD,BC与DE的位置关系。
人教版 数学七年级下册课时练 第五章 相交线与平行线 5.2.2 平行线的判定

人教版数学七年级下册第五章相交线与平行线5.2.2平行线的判定1.(2019·广西河池中考)如图,已知∠1=120°,要使a∥b,则∠2的大小是( D)A.60° B.80° C.100° D.120°2.(2019·四川南充顺庆区期末)如图,用直尺和三角尺作出直线AB,CD,得到AB∥CD的理由是__同位角相等,两直线平行__.3.(2019·湖北武汉武昌区模拟)如图,点B在DC上,BE平分∠ABD,∠ABE=∠C,试说明:BE∥AC.解:∵BE平分∠ABD,∴∠DBE=∠ABE.∵∠ABE=∠C,∴∠DBE=∠C.∴BE∥AC.4.(教材P15,习题5.2,T4改编)如图,根据题意填空:∵∠1=∠2(已知),∴__AB__∥__CD__.∵∠2=∠3(已知),∴__CD__∥__EF__.∴__AB__∥__EF__.5.(2019·甘肃金昌永昌期末)如图,在三角形ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.试判断DE与BC的位置关系,并说明理由.解:DE∥BC.理由如下:方法1:∵CD⊥AB,∴∠ADC=90°(垂直的定义),∴∠1+∠3=90°.∵∠1+∠2=90°(已知),∴∠3=∠2(同角的余角相等).∴DE∥BC(内错角相等,两直线平行).方法2:∵CD⊥AB,∴∠BDC=90°(垂直的定义),∴∠B+∠2=180°-∠BDC=180°-90°=90°.∵∠1+∠2=90°(已知),∴∠B=∠1(同角的余角相等).∴DE∥BC(同位角相等,两直线平行).6.(2019·山东潍坊模拟)在下列图形中,由∠1+∠2=180°不能得到AB∥CD的是( D)7.如图,DE是过三角形ABC的顶点A的直线.(1)当∠B=__∠DAB__时,DE∥BC,理由是__内错角相等,两直线平行__.(2)当∠B+__∠EAB__=180°时,DE∥BC,理由是__同旁内角互补,两直线平行__.8.(2019·宁夏石嘴山三中期中)如图,已知∠1=∠2,∠3+∠4=180°,试说明AB∥EF.解:∵∠1=∠2,∴AB∥CD.∵∠3+∠4=180°,∴CD∥EF.∴AB∥EF.9.如图,∠1=70°,∠2=110°,AB与ED平行吗?为什么?解:AB∥ED.理由如下:方法1:∵∠1=70°(已知),∠1=∠AOD(对顶角相等),∴∠AOD=70°(等量代换).∵∠2=110°(已知),∴∠2+∠AOD=180°.∴AB∥ED(同旁内角互补,两直线平行).方法2:∵∠1+∠COA=180°,∠1=70°,∴∠COA=180°-70°=110°.∵∠2=110°,∴∠COA=∠2,∴AB∥ED(同位角相等,两直线平行).方法3:∵∠1+∠BOD=180°,∠1=70°,∴∠BOD=180°-70°=110°.∵∠2=110°,∴∠BOD=∠2,∴AB∥ED(内错角相等,两直线平行).易错点不能正确识别截线与被截线,误判两直线平行10.(2019·安徽六安金寨期末)如图,下列条件不能判定AB∥FD的是( D)A.∠A+∠2=180°B.∠A=∠3C.∠1=∠4 D.∠1=∠A11.(2019·云南昆明五华区一模)如图所示,点E是AD延长线上的一点,如果添加一个条件,使BC∥AD,那么可添加的条件为( A)A.∠C+∠ADC=180°B.∠A+∠ACD=180°C.∠CBD=∠ADC D.∠C=∠CDA12.(2019·江苏南通海安期中)以下三种沿AB折叠的方法中,能判定纸带两条边线a,b互相平行的是( C)①如图1,展开后测得∠1=∠2;②如图2,展开后测得∠1=∠2且∠3=∠4;③如图3,测得∠1=∠2.A.①③B.①②③C.①②D.②③13.(2019·湖北鄂州梁子湖区期中)一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( B)A.第一次向右拐40°,第二次向左拐140°B.第一次向左拐40°,第二次向右拐40°C.第一次向左拐40°,第二次向右拐140°D.第一次向右拐40°,第二次向右拐40°14. (2019·湖南永州零陵区一模)如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是__20°__.15.如图,已知AC⊥AE,BD⊥BF,∠1=15°,∠2=15°,AE与BF平行吗?为什么?解:AE∥BF.理由如下:∵AC⊥AE,BD⊥BF(已知),∴∠EAC=∠FBD=90°(垂直的定义).∵∠1=∠2(已知),∴∠EAC+∠1=∠FBD+∠2(等式的性质),∴∠EAB=∠FBG,∴AE∥BF(同位角相等,两直线平行).16.(2019·河南濮阳期末)如图所示,已知BE平分∠ABD,DE平分∠CDB,且∠1与∠2互余,试判断直线AB,CD是否平行,并说明理由.解:AB∥CD.理由如下:∵∠1与∠2互余,∴∠1+∠2=90°.∵BE平分∠ABD,DE平分∠CDB,∴∠ABD=2∠1,∠CDB=2∠2,∴∠ABD+∠CDB=2(∠1+∠2)=180°.∴AB∥CD.17.如图所示,若MN⊥AB,垂足为Q,∠ABC=130°,∠FCB=40°,试判断直线MN与EF 的位置关系,并说明理由.解:MN∥EF.理由如下:方法1:延长AB交EF于点G,如图1所示.∵∠ABC=130°,∴∠GBC=180°-∠ABC=50°.又∵∠FCB=40°,∴∠BGC=180°-∠GBC-∠FCB=90°.∵MN⊥AB,∴∠AQN=90°,∴∠BGC=∠AQN,∴MN∥EF.方法2:延长CB交MN于点G,如图2所示.∵MN⊥AB,∴∠BQM=90°.∵∠ABC=130°,∴∠ABG=180°-∠ABC=50°,∴∠NGB=180°-∠ABG-∠BQM=40°.∵∠FCB=40°,∴∠NGB=∠FCB,∴MN∥EF.方法3:过点B作BG⊥AB,如图3所示.∵AB⊥MN,BG⊥AB,∴MN∥BG,∠ABG=90°.又∵∠ABC=130°,∴∠GBC=40°.∵∠FCB=40°,∴∠GBC=∠FCB.∴BG∥EF,∴MN∥EF.。
人教版数学七年级下册第五章5.2平行线及其判定课时同步训练

第五章 相交线与平行线5.2平行线及其判定5.2.2平行线的判定课前预习篇1. 判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.2. 判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.3.判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.典例剖析篇【例1】如图所示,已知∠A=∠B,点A ,C ,D 在同一条直线上,∠DCB=∠A+∠B,CE 是∠DCB 的平分线,试说明AB ∥CE 的理由.【解析】要证明AB ∥CE ,则要找到同位角或内错角相等的条件或找到同旁内角互补的条件.由条件CE 是∠DCB 的平分线可得∠DCE=∠ECB=21∠DCB ,又因为∠A=∠B ,∠DCB=∠A+∠B ,可得∠A=∠DCE 或∠B=∠ECB 从而得到AB ∥CE .解:因为CE 是∠DCB 的平分线, 所以∠DCE=∠ECB=21∠DCB . 因为∠DCB=∠A+∠B ,∠A=∠B ,所以∠A=∠DCE=21∠DCB , 所以AB ∥CE (同位角相等,两直线平行)(或者:所以∠B=∠ECB=21∠DCB ,所以AB ∥CE (内错角相等,两直线平行) 【例2】如图,直线EC 交直线PO 于点A ,交直线MN 于点C ,直线FC 交直线PQ 于点B ,交直线MN 于点C ,且90ECF ∠=°,如果50FBQ ∠=°, 要使PQ MN ∥,ECM ∠应该等于 .【答案】40°基础夯实篇1.两条直线被第三条直线所截,下列条件中,不能判断这两人条直线平行的的是 ( D )A 、同位角相等B 、内错角相等C 、同旁内角互补D 、同旁内角相等2.同一个平面内的4条直线满足a ⊥b,b ⊥c,c ⊥d,则下列式子正确的是( C )A .a ∥bB .b ⊥dC .a ⊥dD .b ∥c3.如图所示,点E 在AC 的延长线上,下列条件中能判断AB ∥CD 的是( B )A . ∠3=∠4B . ∠1=∠2C . ∠D=∠DCED . ∠D+∠ACD=180°4.如图所示,直线a ,b 被直线c 所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7 ③∠2+∠3=180°④∠4=∠7.其中能判定a ∥b 的序号是( A )A .①②B .①③C .①④D .③④5.(2009泉州)如图,不添加辅助线,请写出一个能判定E B ∥AC 的条件: ∠ACB=∠EBD 或 ∠EBA=∠A 等 .6.如图8,一个零件ABCD 需要AB 边与CD 边平行,现只有一个量角器,测得拐角∠ABC=100°,∠BCD=80°这个零件合格吗?____合格___填(“合格”或“不合格”)决胜中考篇7.如图,在三角形ABC 中,点E 在AC 上,点D ,G 在BC 上,点F 在AB 上,连接DE ,AD ,GF .完成下列填空.(1)若∠1=∠4,则 DE ∥ AC ( 内错角相等,两直线平行 ).(2)若∠1=∠ 5 ,则GF ∥ AD ( 同位角相等,两直线平行 ).(3)若∠BAC+∠ 3 =180,则DE ∥ AB ( 同旁内角互补,两直线平行 ) E D C B A 4321C B D A A B C D E8.如图9是由五个同样的三角形组成的图案,三角形的三个角分别为36°,72°,72°,则图中共有_5__ 对平行线.9.如图5-24,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA .(1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么? 解:(1)CD ∥AB因为CD ⊥MN ,AB ⊥MN ,所以CDN=∠ABM=90° 所以CD ∥AB(2)平行因为∠CDN=∠ABN=90°,∠FDC=EBA所以∠FDN=∠EBN所以FD ∥EB10.如图,已知∠1=∠2,∠3=∠4,试说明AB ∥EF .解:因为∠1=∠2,所以AB ∥CD (同位角相等,两直线平行).因为∠3=∠4,所以CD ∥EF (内错角相等,两直线平行)所以AB ∥EF (如果两条直线都与第三条直线平行,那么这两条直线平行)11.如图,已知直线1l ,2l 被直线3l 所截,∠1=45°,∠2=135°,试判1l ,2l 是否平行?并说明理由.解:平行.因为∠2=135°(已知),∠2+∠3=180°(平角定义),所以∠3=45°.因为∠1=45°,所以∠1=∠3,所以1l ∥2l (同位角相等,两直线平行).N M F E D C B A12.如图,试探索∠A,∠AEC,∠C之间具备什么关系时,AB∥CD?并说明理由.解:观察图形可以猜想:∠A+∠AEC+∠C=360°时,AB∥EF.理由如下:在E 点出现转折角,可以过点E作EF∥AB,则∠1+∠A=180°.因为∠A+∠AEC+∠C=∠A+∠1+∠2+∠C=360°,所以∠2+∠C=360°-180°=180°.所以EF∥CD(同旁内角互补,两直线平行)又因为EF∥AB,所以AB∥CD(如果两条直线都与第三条直线平行,那么这两条直线平行)13.如图,已知∠B= 25°,∠BCD =45°,∠CDE=30°,∠E =10°,试说明AB∥EF.解:如图,在∠BCD的内部作∠BCM =25°,在么CDE的内部作∠EDN =10°.因为∠B= 25°,∠E =10°(已知),所以∠B=∠BCM,∠E=∠EDN(等量代换).所以AB∥CM ,EF∥DN(内错角相等,两直线平行).又因为∠BCD =45°,∠CDE=30°(已知),所以∠DCM=20°,∠CDN=20°(等式的性质).所以∠DCM=∠CDN(等量代换).所以CM∥DN(内错角相等,两直线平行).因为AB∥CM,EF∥DN(已证),所以AB∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)。
人教版七年级数学 下册 第五章 5.2.2 平行线的判定 课时练
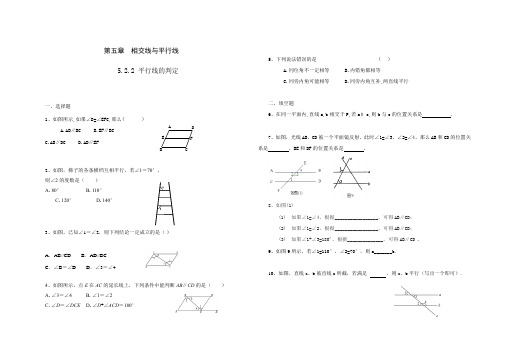
第五章 相交线与平行线5.2.2 平行线的判定一、选择题1、如图所示,如果∠D=∠EFC,那么( ) A.AD∥BC B.EF∥BC C.AB∥DC D.AD∥EF2、如图,梯子的各条横档互相平行,若∠1=70°, 则∠2的度数是( ) A .80°B .110°C .120°D .140°3、如图,已知∠1=∠2,则下列结论一定成立的是( )A .AB//CDB .AD//BC C .∠B =∠D D .∠3=∠44、如图所示,点E 在AC 的延长线上,下列条件中能判断AB ∥CD 的是( ) A .∠3=∠4B .∠1=∠2C .∠D =∠DCE D .∠D +∠ACD =180°5、下列说法错误的是 ( ) A.同位角不一定相等 B.内错角都相等C.同旁内角可能相等D.同旁内角互补,两直线平行二、填空题6、在同一平面内,直线a,b 相交于P,若a ∥c,则b 与c的位置关系是 .7、如图,光线AB 、CD 被一个平面镜反射,此时∠1=∠3,∠2=∠4,那么AB 和CD 的位置关系是 ,BE 和DF 的位置关系是 .8、如图(1)(1) 如果∠1=∠4,根据_________________,可得AB ∥CD ; (2) 如果∠1=∠2,根据_________________,可得AB ∥CD ; (3) 如果∠1+∠3=180º,根据______________,可得AB ∥CD . 9、如图9所示,若∠1=110°,∠2=70°,则a_______b .10、如图,直线a 、b 被直线c 所截,若满足 ,则a 、b 平行(写出一个即可).FE D CBA 21三、解答题11、如图所示,写出所有角满足的条件使AB∥EF,并说明理由.12、如图:已知∠2+∠D=180°,∠1=∠B,试说明:AB∥EF.13、已知:如图,∠A=∠F,∠C=∠D.求证:BD∥CE.14、(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由。
七年级数学下册 5.2.1 平行线课时训练(无答案)(新版)新人教版

第五章 相交线与平行线5.2.1平行线一、填空题1、在同一平面内,两条直线有 种位置关系,分别是 ,如果两条直线a 、b 不相交,那么这两条直线的位置关系一定是 ,记作 。
2、请举出一个生活中平行线的例子 。
3、过直线外一点画已知直线的平行线,能够画出 条直线与已知直线平行。
4、如果a//b ,b//c ,则a c ,根据是 。
5、如果MN//AB ,AC//MN ,则点C 在 上。
6、如图,在三角形ABC 中,∠A+∠B+∠C= ,D 、E 为AB 、AC 边上的两点,且DE//BC ,那么∠A+∠ADE+∠AED= ,说明∠B+∠C ∠ADE+∠二、选择题1、下列说法中错误的有( )个。
(1)两条不相交的直线叫做平行线(2)经过直线外一点,能够画出一条直线与已知直线平行,并且只能画出一条(3)如果a//b ,b//c ,则b//c(4)两条不平行的射线,在同一平面内一定相交A 、0B 、1C 、2D 、32、直线n m 、为空间内的两条直线,它们的位置关系是( )A 、平行B 、相交C 、异面D 、平行、相交或异面3、在同一平面内的三条直线,如果要使其中两条且只有两条平行,那么它们( )A 、有三个交点B 、只有一个交点C 、有两个交点D 、没有交点4、在同一平面内,直线n m 、相交于点O ,且n l //,则直线l 和m 的关系是( )A 、平行B 、相交C 、重合D 、以上都有可能5、两条射线平行是指( )A 、两条射线都是水平的B 、两条射线都在同一直线上且方向相同C 、两条射线方向相反D 、两条射线所在直线平行6、在平面内有两两相交的3条直线,如果最多有m 个交点,最少有n 个交点,那么mn =( ) A 、0 B 、1 C 、3 D 、6三、解答题1、作图在梯形ABCD 中,上底、下底分别为AD 、BC ,点M 为AB 中点,(1)过M 点作MN//AD 交CD 于N(2)MN 和BC 平行吗?为什么?(3)用适当的方法度量并比较NC 和ND 的大小关系B C2过P点作PQ//AB交AC与O,作PM//AC交AB于N。
七年级数学下册 第五章 相交线与平行线课时训练(无答

第五章 相交线与平行线一、选择题.1. 若三条直线交于一点,则共有对顶角(平角除外)( )A.六对B.五对C.四对D.三对 2.如图(16),如果AB ∥CD,那么图中相等的内错角是( ) A.∠1与∠5,∠2与∠6; B.∠3与∠7,∠4与∠8;C.∠5与∠1,∠4与∠8;D.∠2与∠6,∠7与∠33.下列语句:①三条直线只有两个交点,则其中两条直线互相平行; ②如果两条平行线被第三条截,同旁内角相等,那么这两条平行线都与第三条直线垂直; ③过一点有且只有一条直线与已知直线平行,其中( )A.①、②是正确的命题B.②、③是正确命题C.①、③是正确命题D.以上结论皆错4.下列与垂直相交的洗法:①平面内,垂直于同一条直线的两条直线互相平行; ②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;③平行内, 一条直线不可能与两条相交直线都垂直,其中说法错误个数有( )A.3个B.2个C.1个D.0个二、填空题1. 如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是_________.2.a 、b 、c 是直线,且a ∥b,b ⊥c,则a 与c 的位置关系是________.3.如图(11),MN ⊥AB,垂足为M 点,MN 交CD 于N,过M 点作MG ⊥CD,垂足为G,EF 过点N 点,且EF ∥AB,交MG 于H 点,其中线段GM 的长度是________到________的距离, 线段MN 的长度是________到________的距离,又是_______的距离,点N 到直线MG 的距离是___.G H N MF E D CBAFE O D C B A(11) (12)4.如图(12),AD ∥BC,EF ∥BC,BD 平分∠ABC,图中与∠ADO 相等的角有_______ 个,分别是___________.5.因为AB ∥CD,EF ∥AB,根据_________,所以_____________.6.命题“等角的补角相等”的题设__________,结论是__________.7.如图(13),给出下列论断:①AD ∥BC:②AB ∥CD;③∠A=∠C.以上其中两个作为题设,另一个作为结论,用“如果……,那么……”形式,写出一个你认为正确的命题是___________.D C B A FE ODC B A c l N M ba 2187654321D C B A (16)(13) (14) (15) 8.如图(14),直线AB 、CD 、EF 相交于同一点O,而且∠BOC=23∠AOC,∠DOF=13∠AOD,那么∠FOC=______度.9.如图(15),直线a 、b 被C 所截,a ⊥L 于M,b ⊥L 于N,∠1=66°,则∠2=________.三、解答题 1.如图(17),是一条河,C 河边AB 外一点:(1)过点C 要修一条与河平行的绿化带,请作出正确的示意图. (2)现欲用水管从河边AB,将水引到C 处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)2.如图(18),ABA ⊥BD,CD ⊥MN,垂足分别是B 、D 点,∠FDC=∠EBA.(1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?3、已知,如图,BCE 、AFE 是直线,AB ∥CD ,∠1=∠2,∠3=∠4。
人教版七年级数学下册 5.2.2 平行线的判定 课后练习
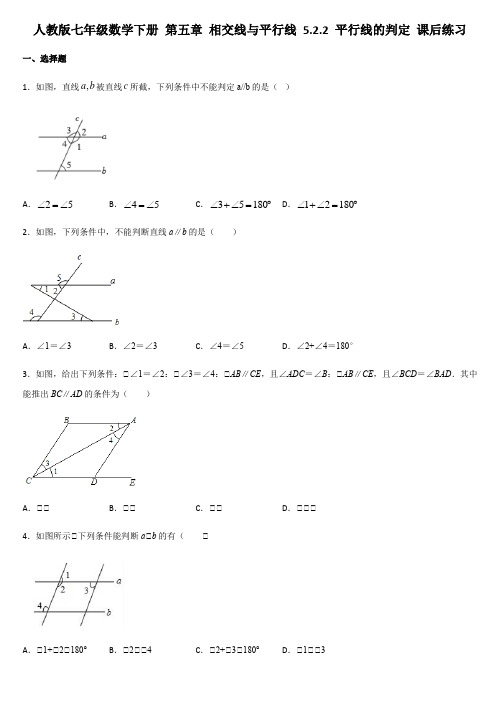
人教版七年级数学下册 第五章 相交线与平行线 5.2.2 平行线的判定 课后练习一、选择题1.如图,直线,a b 被直线c 所截,下列条件中不能判定a//b 的是( )A .25∠=∠B .45∠=∠C .35180∠+∠=︒D .12180∠+∠=︒2.如图,下列条件中,不能判断直线a ∥b 的是( )A .∠1=∠3B .∠2=∠3C .∠4=∠5D .∠2+∠4=180°3.如图,给出下列条件:①∠1=∠2:①∠3=∠4:①AB ∥CE ,且∠ADC =∠B :①AB ∥CE ,且∠BCD =∠BAD .其中能推出BC ∥AD 的条件为( )A .①①B .①①C .①①D .①①①4.如图所示①下列条件能判断a ①b 的有( ①A .①1+①2①180°B .①2①①4C .①2+①3①180°D .①1①①35.如图,下列不能判定DF ∥AC 的条件是( )A .∠A =∠BDFB .∠2=∠4C .∠1=∠3D .∠A +∠ADF =180°6.如图,下列条件:13241804523623∠=∠∠+∠=∠=∠∠=∠∠=∠+∠①,②,③,④,⑤中能判断直线12l l 的有( )A .5个B .4个C .3个D .2个7.如图,下列说法错误的是( )A .若a∥b,b∥c,则a∥cB .若∠1=∠2,则a∥cC .若∠3=∠2,则b∥cD .若∠3+∠5=180°,则a∥c 8.如图,下列条件中,不能判断AD ∥BC 的是( )A .∠FBC =∠DABB .∠ADC +∠BCD =180° C .∠BAC =∠ACE D .∠DAC =∠BCA9.如下图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5,能判定AB ∥CD 的条件为( )A .①②③④B .①②④C .①③④D .①②③10.如下图,在下列条件中,能判定AB//CD 的是( )A .∠1=∠3B .∠2=∠3C .∠1=∠4D .∠3=∠4第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题11.如图,不添加辅助线,请写出一个能判定DE ①BC 的条件___________.12.如图,现给出下列条件:①1B ∠∠=,②25∠∠=,③34∠∠=,④1D ∠∠=,⑤B BCD 180∠∠+=︒.其中能够得到AB//CD 的条件是_______.(只填序号)13.如图,添加一个你认为合适的条件______使//AD BC .14.已知:如图AB⊥BC ,BC⊥CD 且⊥1=⊥2,试说明:BE⊥CF .解:⊥AB⊥BC ,BC⊥CD (已知)⊥ = =90°( )⊥⊥1=⊥2(已知)⊥ = (等式性质)⊥BE⊥CF ( )15.如图,下列能判定//AB CD 的条件有_______个.①180B BAD ∠+∠=°;②12∠=∠;③34∠=∠;④5BAD ∠=∠.三、解答题16.如图,已知BE 平分ABC ∠,点D 在射线BA 上,且ABE BED ∠=∠.判断BC 与DE 的位置关系,并说明理由.17.综合与探究问题情境:如图,已知OC 平分AOB ∠,CD OA ⊥于点D ,E 为DC 延长线上一点,EF OB ⊥于点F ,EG 平分DEF ∠交OB 于点G ,180DEF AOB ∠+∠=︒.问题发现:(1)如图1,当90AOB ∠=︒时,12∠+∠=____________°;(2)如图2,当AOB ∠为锐角时,1∠与2∠有什么数量关系,请说明理由;拓展探究(3)在(2)的条件下,已知直角三角形中两个锐角的和是90°,试探究OC 和GE 的位置关系,并证明结论; (4)如图3,当AOB ∠为锐角时,若点E 为线段DC 上一点,EF OB ⊥于点F ,EH 平分DEF ∠交OA 于点H ,180DEF AOB ∠+∠=︒.请写出一个你发现的正确结论.18.如图,已知∠ABC=180°-∠A ,BD ⊥CD 于D ,EF ⊥CD 于E .(1)求证:AD ∥BC ;(2)若∠ADB=36°,求∠EFC 的度数.19.如图,AB ∥CD ,∠B =70°,∠BCE =20°,∠CEF =130°,请判断AB 与EF 的位置关系,并说明理由.20.如图,在ABC 中,D 是BC 边上的一点,45B ∠=︒,30BAD ∠=︒,将ABD △沿AD 折叠得到AED ,AE 与BC 交于点F .(1)求AFC ∠和EDF ∠的度数;(2)若32E C ∠∠=::,问:DE //AC 吗,请说明理由. 21.如图,已知∠A =70°,O 是AB 上一点,直线OD 与AB 的夹角∠BOD =82°,要使OD ∥AC ,直线OD 绕点O 按逆时针方向至少旋转多少度?22.如图,已知点E 、F 在直线AB 上,点G 在线段CD 上,ED 与FG 相交于点H ,∠C =∠EFG ,∠BFG =∠AEM ,求证:AB ∥CD .(完成下列填空)证明:∵∠BFG =∠AEM (已知)且∠AEM =∠BEC ( )∴∠BEC =∠BFG (等量代换)∴MC ∥ ( )∴∠C =∠FGD ( )∵∠C =∠EFG (已知)∴∠ =∠EFG ,(等量代换)∴AB ∥CD ( )23.如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+2)20,过点C作CB⊥x轴于点B.(1)求A、C两点坐标;(2)若过点B作BD∥AC交y轴于点D,且AE、DE分别平分∠CAB、∠ODB,如图2,求∠AED的度数.【参考答案】1.D 2.B 3.D 4.B 5.B 6.B 7.C 8.C 9.C 10.C∠=∠11.DAB B12.①①①13.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)14.①AB①BC,BC①CD(已知)①①ABC=①DCB=90°(垂直的定义)①①1=①2(已知)①①EBC =①FCB (等式性质)①BE①CF(内错角相等,两直线平行)15.116.解:BC∥DE;理由如下:∠,因为BE平分ABC所以∠ABE =∠CBE ,因为ABE BED ∠=∠,所以∠CBE =∠BED ,所以BC ∥DE .17.(1)∵CD OA ⊥,∴90AOB ∠=︒,∵180DEF AOB ∠+∠=︒,∴90DEF ∠=︒,∵OC 平分AOB ∠,EG 平分DEF ∠,∴∠1=12∠AOB=45︒,∠2=12∠DEF=45︒, ∴1290∠+∠=︒;故答案为:90;(2)1290∠+∠=︒.理由如下:∵OC ,EG 分别是AOB ∠,DEF ∠的平分线, ∴112DEF ∠=∠,122AOB ∠=∠, ∴112()2DEF AOB ∠+∠=∠+∠, ∵180DEF AOB ∠+∠=︒,∴1290∠+∠=︒;(3)OC 和EG 的位置关系为OC ∥GE .证明:∵EF OB ⊥于点F ,∴90EFG ∠=︒.∴190EGF ∠+∠=︒.∵1290∠+∠=︒,∴2EGF ∠=∠,∴OC ∥GE ;(4)答案不唯一,例如1290∠+∠=︒.理由如下:∵OC ,EH 分别是AOB ∠,DEF ∠的平分线, ∴112DEF ∠=∠,122AOB ∠=∠, ∴112()2DEF AOB ∠+∠=∠+∠, ∵180DEF AOB ∠+∠=︒,∴1290∠+∠=︒;18(1)证明:∵∠ABC=180°-∠A ,∴∠ABC+∠A=180°,∴AD ∥BC ;(2)∵AD ∥BC ,∠ADB=36°,∴∠DBC=∠ADB=36°,∵BD ⊥CD ,EF ⊥CD ,∴BD ∥EF ,∴∠DBC=∠EFC=36°19.AB ∥EF ,理由如下:∵AB ∥CD①∴∠B=∠BCD①∵∠B=70°①∴∠BCD=70°①∵∠BCE=20°①∴∠ECD=50°①∵CEF=130°①∴∠E+∠DCE=180°①∴EF∥CD①∴AB∥EF①20.解:(1)由折叠前后对应的角相等可知,∠BAD=∠DAF=30°,∴①BAF=①BAD+①DAF=30°+30°=60°,在①ABF中,由三角形内角和定理可知,①AFB=180°-①BAF-①B=180°-60°-45°=75°,∴①AFC=180°-①AFB=180°-75°=105°,在①ABD中,由三角形内角和定理可知,①ADB=180°-①BAD-①B=180°-30°-45°=105°,∴∠ADF=180°-①ADB=75°,由折叠前后对应的角相等可知,①ADE=①ADB=105°,∴①EDF=①ADE-①ADF=105°-75°=30°,故答案为:105°,30°;(2) DE//AC,理由如下:∵△ABD沿AD折叠得到△AED,∴∠B=∠E=45°,∵∠E:∠C=3:2,∴∠C=30°,∴∠C=∠EDF=30°,∴DE∥AC.21.解:解:∵OD'∥AC,∴∠BOD'=∠A=70°,∴∠DOD'=82°-70°=12°.故答案为:12°.22.证明:∵∠BFG=∠AEM(已知)且∠AEM=∠BEC(对顶角相等)∴∠BEC=∠BFG(等量代换)∴MC∥GF(同位角相等,两直线平行)∴∠C=∠FGD(两直线平行,同位角相等)∵∠C=∠EFG(已知)∴∠FGD=∠EFG,(等量代换)∴AB∥CD(内错角相等,两直线平行).故答案是:对顶角相等;GF;同位角相等,两直线平行;FGD;内错角相等,两直线平行.23.(1)∵(a+2)20∴a+2=0,b﹣2=0,∴a=﹣2,b=2,∴A(﹣2,0),C(2,2);(2)∵CB∥y轴,BD∥AC,∴∠CAB=∠5,∠ODB=∠6,∴∠CAB+∠ODB=∠5+∠6=90°,过点E作EF∥AC,如图∵BD∥AC∴BD∥EF∥AC,∵AE、DE分别平分∠CAB、∠ODB,∴∠1=∠3=12∠CAB,∠2=∠4=12∠ODB,∴∠AED=∠1+∠2=12(∠CAB+∠ODB)=45°∴∠AED的度数为45°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年人教版七年级下册数学5.2平行线线课时训练
一、选择题(每题四个选项中只有一个选项是正确的,共12题)
1.如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是()
A.平行B.相交C.垂直D.不能确定
2.如果a//b,b//c,那么a//c,这个推理的依据是( )
A.等量代换B.经过直线外一点,有且只有一条直线与已知直线平行
C.平行线的定义D.平行于同一直线的两直线平行
3.如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是()
A.∥1=∥3B.∥2+∥4=180°C.∥1=∥4D.∥3=∥4
4.下列说法错误的有()(1)相等的角是对顶角;(2)同旁内角互补;(3)同角或等角的余角相等;(4)平行于同一直线的两条直线互相平行;(5)垂直于同一条直线的两条直线互相平行;(6)过一点有且只有一条直线与已知直线平行;
A.5个B.2个C.3个D.4个
5.如图,直线a、b都与直线c相交,给出下列条件:(1)∥1=∥2;(2)∥3=∥6;(3)∥4+∥7=180°;(4)∥5+∥8=180°,
a b的是()
其中能判断//
A .(1)、(3)
B .(2)、(4)
C .(1)、(3)、(4)
D .(1)、(2)、(3)、(4)
6.如图,给出下面的推理:①因为B BEF ∠=∠,所以//AB EF ;②因为B CDE ∠=∠,所以//;AB CD ③因为
180DCE AEF ︒∠+∠=,
所以// AB EF ;④因为 180A AEF ︒∠+∠=,所以//AB EF .其中正确的推理是( )
A .①②③
B .①②④
C .①③④
D .②③④
7.如图,已知直线EF∥MN 垂足为F ,且∥1=140°,则当∥2等于( )时,AB∥CD .
A .50°
B .40°
C .30°
D .60°
8.如图,木工师傅在一块木板上画两条平行线,方法是:用角尺画木板边缘的两条垂线,这样画的理由有下列4种说法:其中正确的是( )
①同位角相等,两直线平行;
②内错角相等,两直线平行;
③同旁内角互补,两直线平行;
④平面内垂直于同一直线的两条直线平行.
A .①②③
B .①②④
C .①③④
D.①③
9.下列命题:①过一点有且只有一条直线与已知直线平行;②过一点有且只有一条直线与已知直线垂直;③
同旁内角互补;④垂直于同一条直线的两条直线垂直.其中的假命题有()
A.4 个B.3 个C.2 个D.1 个
10.对于同一平面内的三条直线a,b,c,给出下列5个论断:
①a∥b;②b∥c;③a∥c;④a∥b;⑤a∥c.
以其中两个论断作为题设,一个论断作为结论,组成一个你认为不正确的命题是()
A.已知①②则③B.已知②⑤则④C.已知②④则③D.已知④⑤则②
11.在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c 的距离为()
A.1cm B.3cm C.5cm或3cm D.1cm或3cm
12.下列说法中正确的个数有( )
①两条直线被第三条直线所截,内错角相等;
②在同一平面内不重合的两条直线有平行、相交和垂直三种位置关系;
③直线外一点到这条直线的垂线段的长度叫做点到直线的距离;
④在同一平面内,垂直于同一条直线的两条直线互相平行.
A.1个B.2个C.3个D.4个
二、填空题
13.在同一平面内,若直线a∥c,b∥c,则a_____b.
14.在间一平面内,有2019条互不重合的直线,l1,l2,l3,…,l2019,若l1∥l2,l2∥l3,l3∥l4,l4∥l5,以此类推,则l1和l2019的位置关系是_____.
15.如图,直线l与直线AB、CD分别相交于E、F,∥1=120°,当∥2=_____时,AB∥CD.
16.如图,对于下列条件:①∥B+∥BCD=180°;②∥1=∥2;③∥3=∥4;④∥D=∥5;其中一定能判定AB∥CD的条件有_____(填写所有正确条件的序号).
三、综合计算题
17.如图所示,一个四边形纸片ABCD,∥B=∥D=90o,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;并说明理由。
(2)如果∥C=130o,求∥AEB的度数.
18.将一幅三角板拼成如图所示的图形,过点C作CF平分∥DCE交DE于点F,
(1)求证:CF∥AB,
(2)求∥DFC的度数.
19.如图,∥1=30°,∥B=60°,AB∥AC.
(1)∥DAB+∥B等于多少度?(2)AD与BC平行吗?AB与CD平行吗?
20.如图,已知∥A = ∥C,∥E=∥F,试说明AB∥CD.。
