平行四边形综合提高练习题(同名10669)
平行四边形综合提高练习题
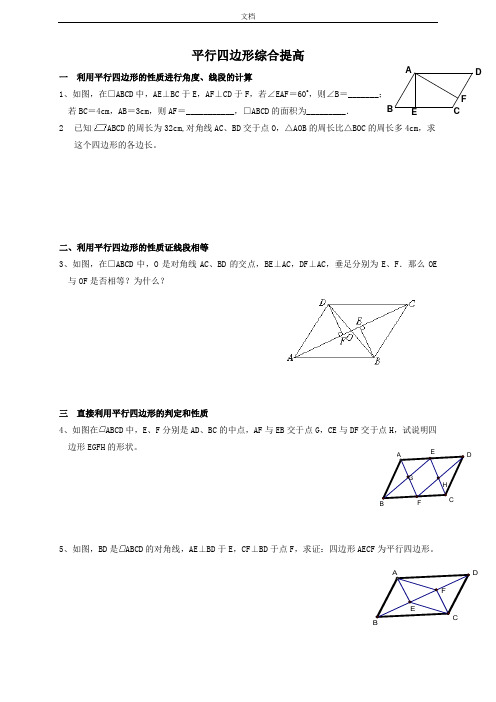
FEDCBA平行四边形综合提高一 利用平行四边形的性质进行角度、线段的计算1、如图,在□ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F ,若∠EAF =60o,则∠B =_______;若BC =4cm ,AB =3cm,则AF =___________,□ABCD 的面积为_________. 2 已知ABCD 的周长为32cm,对角线AC 、BD 交于点O ,△AOB 的周长比△BOC 的周长多4cm ,求这个四边形的各边长。
二、利用平行四边形的性质证线段相等3、如图,在□ABCD 中,O 是对角线AC 、BD 的交点,BE ⊥AC ,DF ⊥AC ,垂足分别为E 、F .那么OE 与OF 是否相等?为什么?三 直接利用平行四边形的判定和性质4、如图在ABCD 中,E 、F 分别是AD 、BC 的中点,AF 与EB 交于点G ,CE 与DF 交于点H ,试说明四边形EGFH 的形状。
5、如图,BD 是ABCD 的对角线,AE ⊥BD 于E ,CF ⊥BD 于点F ,求证:四边形AECF 为平行四边形。
HGABDCEABDCEF四 构造平行四边形解题6、如图2-33所示.Rt △ABC 中,∠BAC=90°,AD ⊥BC 于D ,BG 平分∠ABC ,EF ∥BC 且交AC 于F . 求证:AE=CF .7、已知,如图,AD 为△ABC 的中线,E 为AC 上一点,连结BE 交AD 于点F ,且AE=FE ,求证:BF=AC[能力提高]1、如图2-39所示.在平行四边形ABCD 中,△ABE 和△BCF 都是等边三角形. 求证:△DEF 是等边三角形.2、如图2-32所示.在ABCD 中,AE ⊥BC ,CF ⊥AD ,DN=BM .求证:EF 与MN 互相平分.FBC E D3、 如图2-34所示.ABCD 中,DE ⊥AB 于E ,BM=MC=DC .求证:∠EMC=3∠BEM .4 如图2-35所示.矩形ABCD 中,CE ⊥BD 于E ,AF 平分∠BAD 交EC 延长线于F .求证:CA=CF .[创新思维]1、以△ABC 的三条边为边在BC 的同侧作等边△ABP 、等边△ACQ 、等边△BCR , 求证:四边形PAQR 为平行四边形。
中考数学(平行四边形提高练习题)压轴题训练附答案

一、平行四边形真题与模拟题分类汇编(难题易错题)1.如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.(1)用尺规将图1中的△ABC分割成两个互补三角形;(2)证明图2中的△ABC分割成两个互补三角形;(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为、、的三角形,并计算图3中六边形DEFGHI的面积.②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.【答案】(1)作图见解析(2)证明见解析(3)①62;②6【解析】试题分析:(1)作BC边上的中线AD即可.(2)根据互补三角形的定义证明即可.(3)①画出图形后,利用割补法求面积即可.②平移△CHG到AMF,连接EM,IM,则AM=CH=BI,只要证明S△EFM=3S△ABC即可.试题解析:(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.(2)如图2中,延长FA到点H,使得AH=AF,连接EH.∵四边形ABDE,四边形ACGF是正方形,∴AB=AE,AF=AC,∠BAE=∠CAF=90°,∴∠EAF+∠BAC=180°,∴△AEF和△ABC是两个互补三角形.∵∠EAH+∠HAB=∠BAC+∠HAB=90°,∴∠EAH=∠BAC,∵AF=AC,∴AH=AB,在△AEH和△ABC中,∴△AEH≌△ABC,∴S△AEF=S△AEH=S△ABC.(3)①边长为、、的三角形如图4所示.∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,∴S六边形=17+13+10+4×5.5=62.②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,∵AM∥CH,CH⊥BC,∴AM⊥BC,∴∠EAM=90°+90°﹣x=180°﹣x,∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,∴∠EAM=∠DBI,∵AE=BD,∴△AEM≌△DBI,∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,∴△DBI和△ABC是互补三角形,∴S△AEM=S△AEF=S△AFM=2,∴S △EFM =3S △ABC =6.考点:1、作图﹣应用与设计,2、三角形面积2.已知:如图,在平行四边形ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,DF .(1)求证:△DOE ≌△BOF .(2)当∠DOE 等于多少度时,四边形BFDE 为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE =90°时,四边形BFED 为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE ≌△BOF (ASA );(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD 是平行四边形,进而利用垂直平分线的性质得出BE=ED ,即可得出答案.试题解析:(1)∵在▱ABCD 中,O 为对角线BD 的中点,∴BO=DO ,∠EDB=∠FBO ,在△EOD 和△FOB 中,∴△DOE ≌△BOF (ASA );(2)当∠DOE=90°时,四边形BFDE 为菱形,理由:∵△DOE ≌△BOF ,∴OE=OF ,又∵OB=OD ,∴四边形EBFD 是平行四边形, ∵∠EOD=90°,∴EF ⊥BD ,∴四边形BFDE 为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.3.如图①,四边形ABCD 是知形,1,2AB BC ==,点E 是线段BC 上一动点(不与,B C 重合),点F 是线段BA 延长线上一动点,连接,,,DE EF DF EF 交AD 于点G .设,BE x AF y ==,已知y 与x 之间的函数关系如图②所示.(1)求图②中y 与x 的函数表达式;(2)求证:DE DF ⊥;(3)是否存在x 的值,使得DEG △是等腰三角形?如果存在,求出x 的值;如果不存在,说明理由【答案】(1)y =﹣2x +4(0<x <2);(2)见解析;(3)存在,x =54或552-或32. 【解析】【分析】(1)利用待定系数法可得y 与x 的函数表达式;(2)证明△CDE ∽△ADF ,得∠ADF =∠CDE ,可得结论;(3)分三种情况:①若DE =DG ,则∠DGE =∠DEG ,②若DE =EG ,如图①,作EH ∥CD ,交AD 于H ,③若DG =EG ,则∠GDE =∠GED ,分别列方程计算可得结论.【详解】(1)设y =kx +b ,由图象得:当x =1时,y =2,当x =0时,y =4,代入得:24k b b +=⎧⎨=⎩,得24k b =-⎧⎨=⎩, ∴y =﹣2x +4(0<x <2);(2)∵BE =x ,BC =2∴CE =2﹣x , ∴211,4222CE x CD AF x AD -===-, ∴CE CD AF AD=, ∵四边形ABCD 是矩形,∴∠C =∠DAF =90°,∴△CDE ∽△ADF ,∴∠ADF =∠CDE ,∴∠ADF +∠EDG =∠CDE +∠EDG =90°,∴DE ⊥DF ;(3)假设存在x 的值,使得△DEG 是等腰三角形,①若DE =DG ,则∠DGE =∠DEG ,∵四边形ABCD 是矩形,∴AD ∥BC ,∠B =90°,∴∠DGE =∠GEB ,∴∠DEG =∠BEG ,在△DEF 和△BEF 中,FDE B DEF BEF EF EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△DEF ≌△BEF (AAS ),∴DE =BE =x ,CE =2﹣x ,∴在Rt △CDE 中,由勾股定理得:1+(2﹣x )2=x 2,x =54; ②若DE =EG ,如图①,作EH ∥CD ,交AD 于H ,∵AD ∥BC ,EH ∥CD ,∴四边形CDHE 是平行四边形,∴∠C =90°,∴四边形CDHE 是矩形,∴EH =CD =1,DH =CE =2﹣x ,EH ⊥DG ,∴HG =DH =2﹣x ,∴AG =2x ﹣2,∵EH ∥CD ,DC ∥AB ,∴EH ∥AF ,∴△EHG ∽△FAG ,∴EH HG AF AG =, ∴124222x x x -=--,∴125522x x ==(舍), ③若DG =EG ,则∠GDE =∠GED ,∵AD ∥BC ,∴∠GDE =∠DEC ,∴∠GED =∠DEC ,∵∠C =∠EDF =90°,∴△CDE ∽△DFE , ∴CE DE CD DF=, ∵△CDE ∽△ADF , ∴12DE CD DF AD ==, ∴12CE CD =, ∴2﹣x =12,x =32,综上,x =54或32. 【点睛】本题是四边形的综合题,主要考查了待定系数法求一次函数的解析式,三角形相似和全等的性质和判定,矩形和平行四边形的性质和判定,勾股定理和逆定理等知识,运用相似三角形的性质是解决本题的关键.4.如图,在平面直角坐标系中,直线DE 交x 轴于点E (30,0),交y 轴于点D (0,40),直线AB :y =13x +5交x 轴于点A ,交y 轴于点B ,交直线DE 于点P ,过点E 作EF ⊥x 轴交直线AB 于点F ,以EF 为一边向右作正方形EFGH .(1)求边EF 的长;(2)将正方形EFGH 沿射线FB 个单位的速度匀速平移,得到正方形E 1F 1G 1H 1,在平移过程中边F 1G 1始终与y 轴垂直,设平移的时间为t 秒(t >0). ①当点F 1移动到点B 时,求t 的值;②当G 1,H 1两点中有一点移动到直线DE 上时,请直接写出此时正方形E 1F 1G 1H 1与△APE 重叠部分的面积.【答案】(1)EF=15;(2)①10;②120;【解析】【分析】(1)根据已知点E(30,0),点D(0,40),求出直线DE的直线解析式y=-43x+40,可求出P点坐标,进而求出F点坐标即可;(2)①易求B(0,5),当点F1移动到点B时,1010=10;②F点移动到F'10t,F垂直x轴方向移动的距离是t,当点H运动到直线DE上时,在Rt△F'NF中,NFNF'=13,EM=NG'=15-F'N=15-3t,在Rt△DMH'中,43MHEM'=,t=4,S=12×(12+454)×11=10238;当点G运动到直线DE上时,在Rt△F'PK中,PKF K'=13,PK=t-3,F'K=3t-9,在Rt△PKG'中,PKKG'=31539tt--+=43,t=7,S=15×(15-7)=120.【详解】(1)设直线DE的直线解析式y=kx+b,将点E(30,0),点D(0,40),∴30040k bb+=⎧⎨=⎩,∴4340kb⎧=-⎪⎨⎪=⎩,∴y=﹣43x+40,直线AB与直线DE的交点P(21,12),由题意知F(30,15),∴EF=15;(2)①易求B(0,5),∴BF=10,∴当点F1移动到点B时,t=1010=10;②当点H 运动到直线DE 上时,F 点移动到F'的距离是10t , 在Rt △F'NF 中,NF NF '=13, ∴FN =t ,F'N =3t ,∵MH'=FN =t ,EM =NG'=15﹣F'N =15﹣3t ,在Rt △DMH'中,43MH EM '=, ∴41533t t =-, ∴t =4, ∴EM =3,MH'=4,∴S =1451023(12)11248⨯+⨯=; 当点G 运动到直线DE 上时,F 点移动到F'10,∵PF =10∴PF'10t ﹣10,在Rt △F'PK 中,13PK F K =',∴PK=t﹣3,F'K=3t﹣9,在Rt△PKG'中,PK KG'=31539tt--+=43,∴t=7,∴S=15×(15﹣7)=120.【点睛】本题考查一次函数图象及性质,正方形的性质;掌握待定系数法求函数解析式,利用三角形的正切值求边的关系,利用勾股定理在直角三角形中建立边之间的联系,准确确定阴影部分的面积是解题的关键.5.在ABC中,AD BC⊥于点D,点E为AC边的中点,过点A作//AF BC,交DE的延长线于点F,连接CF.()1如图1,求证:四边形ADCF是矩形;()2如图2,当AB AC=时,取AB的中点G,连接DG 、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).【答案】(1) 证明见解析;(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.【解析】【分析】(1)由△AEF≌△CED,推出EF=DE,又AE=EC,推出四边形ADCF是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF是矩形.(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.【详解】()1证明:∵//AF BC,∴AFE EDC∠=∠,∵E是AC中点,∴AE EC=,在AEF和CED中,AFE CDEAEF CEDAE EC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴AEF CED ≅,∴EF DE =,∵AE EC =,∴四边形ADCF 是平行四边形,∵AD BC ⊥, ∴90ADC ∠=,∴四边形ADCF 是矩形.()2∵线段DG 、线段GE 、线段DE 都是ABC 的中位线,又//AF BC ,∴//AB DE ,//DG AC ,//EG BC , ∴四边形ABDF 、四边形AGEF 、四边形GBDE 、四边形AGDE 、四边形GDCE 都是平行四边形.【点睛】考查平行四边形的判定、矩形的判定、三角形的中位线定理、全等三角形的判定和性质等知识,正确寻找全等三角形解决问题是解题的关键.6.如图1,在长方形纸片ABCD 中,AB=mAD ,其中m ⩾1,将它沿EF 折叠(点E. F 分别在边AB 、CD 上),使点B 落在AD 边上的点M 处,点C 落在点N 处,MN 与CD 相交于点P ,连接EP .设AM n AD=,其中0<n ⩽1.(1)如图2,当n=1(即M 点与D 点重合),求证:四边形BEDF 为菱形;(2)如图3,当12n =(M 为AD 的中点),m 的值发生变化时,求证:EP=AE+DP ; (3)如图1,当m=2(即AB=2AD),n 的值发生变化时,BE CF AM -的值是否发生变化?说明理由.【答案】(1)证明见解析;(2)证明见解析;(3)值不变,理由见解析.【解析】试题分析:(1)由条件可知,当n=1(即M 点与D 点重合),m=2时,AB=2AD ,设AD=a ,则AB=2a ,由矩形的性质可以得出△ADE ≌△NDF ,就可以得出AE=NF ,DE=DF ,在Rt △AED 中,由勾股定理就可以表示出AE 的值,再求出BE 的值就可以得出结论.(2)延长PM 交EA 延长线于G ,由条件可以得出△PDM ≌△GAM ,△EMP ≌△EMG 由全等三角形的性质就可以得出结论.(3)如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O ,通过证明△ABM ∽△KFE ,就可以得出EK KF AM AB =,即BE BK BCAM AB-=,由AB=2AD=2BC ,BK=CF 就可以得出BE CFAM -的值是12为定值. (1)∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°. ∵AB=mAD ,且n=2,∴AB=2AD .∵∠ADE+∠EDF=90°,∠EDF+∠NDF=90°,∴∠ADE=∠NDF . 在△ADE 和△NDF 中,∠A =∠N ,AD =ND ,∠ADE =∠NDF , ∴△ADE ≌△NDF (ASA ).∴AE=NF ,DE=DF . ∵FN=FC ,∴AE=FC .∵AB=CD ,∴AB-AE="CD-CF." ∴BE="DF." ∴BE=DE .Rt △AED 中,由勾股定理,得222AE DE AD =-,即2222AE AD AE AD ()=--,∴AE=34AD. ∴BE=2AD-34AD=54.∴554334ADBE AE AD ==. (2)如图3,延长PM 交EA 延长线于G ,∴∠GAM=90°. ∵M 为AD 的中点,∴AM=DM .∵四边形ABCD 是矩形,∴AB=CD ,AD=BC ,∠A=∠B=∠C=∠D=90°,AB ∥CD. ∴∠GAM=∠PDM .在△GAM 和△PDM 中,∠GAM =∠PDM ,AM =DM ,∠AMG =∠DMP , ∴△GAM ≌△PDM (ASA ).∴MG=MP .在△EMP 和△EMG 中,PM =GM ,∠PME =∠GME ,ME =ME , ∴△EMP ≌△EMG (SAS ).∴EG=EP . ∴AG+AE=EP .∴PD+AE=EP ,即EP=AE+DP .(3)12BE CF AM -=,值不变,理由如下: 如图1,连接BM 交EF 于点Q ,过点F 作FK ⊥AB 于点K ,交BM 于点O , ∵EM=EB ,∠MEF=∠BEF ,∴EF ⊥MB ,即∠FQO=90°. ∵四边形FKBC 是矩形,∴KF=BC ,FC=KB. ∵∠FKB=90°,∴∠KBO+∠KOB=90°.∵∠QOF+∠QFO=90°,∠QOF=∠KOB ,∴∠KBO=∠OFQ. ∵∠A=∠EKF=90°,∴△ABM ∽△KFE. ∴EK KF AM AB =即BE BK BC AM AB-=. ∵AB=2AD=2BC ,BK=CF ,∴12BE CF AM -=. ∴BE CFAM-的值不变.考点:1.折叠问题;2.矩形的性质;3.全等三角形的判定和性质;4.勾股定理;5.相似三角形的判定和性质.7.如图,在平面直角坐标系xOy 中,四边形OABC 的顶点A 在x 轴的正半轴上,OA=4,OC=2,点D 、E 、F 、G 分别为边OA 、AB 、BC 、CO 的中点,连结DE 、EF 、FG 、GD . (1)若点C 在y 轴的正半轴上,当点B 的坐标为(2,4)时,判断四边形DEFG 的形状,并说明理由.(2)若点C 在第二象限运动,且四边形DEFG 为菱形时,求点四边形OABC 对角线OB 长度的取值范围.(3)若在点C 的运动过程中,四边形DEFG 始终为正方形,当点C 从X 轴负半轴经过Y 轴正半轴,运动至X 轴正半轴时,直接写出点B 的运动路径长.【答案】(1)正方形(2)256OB <<(3)2π 【解析】分析:(1)连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形.(2)由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25,当点C 在x 轴上时,AC=6, 故可得结论; (3)根据题意计算弧长即可.详解:(1)正方形,如图1,证明连接OB ,AC ,说明OB ⊥AC ,OB=AC ,可得四边形DEFG 是正方形. (2)256OB <<如图2,由四边形DEFG 是菱形,可得OB=AC ,当点C 在y 轴上时,AC=25,当点C 在x 轴上时,AC=6, ∴256OB << ; (3)2π.如图3,当四边形DEFG 是正方形时,OB ⊥AC ,且OB=AC ,构造△OBE ≌△ACO ,可得B 点在以E (0,4)为圆心,2为半径的圆上运动.所以当C 点从x 轴负半轴到正半轴运动时,B 点的运动路径为2π .图1 图2 图3点睛:本题主要考查了正方形的判定,菱形的性质以及弧长的计算.灵活运用正方形的判定定理和菱形的性质运用是解题的关键.8.如图,在菱形ABCD 中,AB=6,∠ABC=60°,AH ⊥BC 于点H .动点E 从点B 出发,沿线段BC 向点C 以每秒2个单位长度的速度运动.过点E 作EF ⊥AB ,垂足为点F .点E 出发后,以EF为边向上作等边三角形EFG,设点E的运动时间为t秒,△EFG和△AHC的重合部分面积为S.(1)CE= (含t的代数式表示).(2)求点G落在线段AC上时t的值.(3)当S>0时,求S与t之间的函数关系式.(4)点P在点E出发的同时从点A出发沿A-H-A以每秒2个单位长度的速度作往复运动,当点E停止运动时,点P随之停止运动,直接写出点P在△EFG内部时t的取值范围.【答案】(1)6-2t;(2)t=2;(3)当<t≤2时,S=t2+t-3;当2<t≤3时,S=-t2+t-;(4)<t<.【解析】试题分析:(1)由菱形的性质得出BC=AB=6得出CE=BC-BE=6-2t即可;(2)由菱形的性质和已知条件得出△ABC是等边三角形,得出∠ACB=60°,由等边三角形的性质和三角函数得出∠GEF=60°,GE=EF=BE•sin60°=t,证出∠GEC=90°,由三角函数求出CE==t,由BE+CE=BC得出方程,解方程即可;(3)分两种情况:①当<t≤2时,S=△EFG的面积-△NFN的面积,即可得出结果;②当2<t≤3时,由①的结果容易得出结论;(4)由题意得出t=时,点P与H重合,E与H重合,得出点P在△EFG内部时,t的不等式,解不等式即可.试题解析:(1)根据题意得:BE=2t,∵四边形ABCD是菱形,∴BC=AB=6,∴CE=BC-BE=6-2t;(2)点G落在线段AC上时,如图1所示:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴∠ACB=60°,∵△EFG是等边三角形,∴∠GEF=60°,GE=EF=BE•sin60°=t,∵EF⊥AB,∴∠BEF=90°-60°=30°,∴∠GEB=90°,∴∠GEC=90°,∴CE==t,∵BE+CE=BC,∴2t+t=6,解得:t=2;(3)分两种情况:①当<t≤2时,如图2所示:S=△EFG的面积-△NFN的面积=××(t)2-××(-+2)2=t2+t-3,即S=t2+t-3;当2<t≤3时,如图3所示:S=t2+t-3-(3t-6)2,即S=-t2+t-;(4)∵AH=AB•sin60°=6×=3,3÷2=,3÷2=,∴t=时,点P与H重合,E与H重合,∴点P在△EFG内部时,-<(t-)×2<t-(2t-3)+(2t-3),解得:<t<;即点P在△EFG内部时t的取值范围为:<t<.考点:四边形综合题.9.已知一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,以线段AB为直角边在第二象限内左等腰直角三角形ABC,∠BAC=90°,如图1所示.(1)填空:AB= ,BC= .(2)将△ABC绕点B逆时针旋转,①当AC与x轴平行时,则点A的坐标是②当旋转角为90°时,得到△BDE,如图2所示,求过B、D两点直线的函数关系式.③在②的条件下,旋转过程中AC扫过的图形的面积是多少?(3)将△ABC向右平移到△A′B′C′的位置,点C′为直线AB上的一点,请直接写出△ABC扫过的图形的面积.【答案】(1):5;5;(2)①(0,﹣2);②直线BD的解析式为y=﹣x+3;③S=π;(3)△ABC扫过的面积为.【解析】试题分析:(1)根据坐标轴上的点的坐标特征,结合一次函数的解析式求出A、B两点的坐标,利用勾股定理即可解答;(2)①因为B(0,3),所以OB=3,所以AB=5,所以AO=AB-BO=5-3=2,所以A(0,-2);②过点C作CF⊥OA与点F,证明△AOB≌△CFA,得到点C的坐标,求出直线AC解析式,根据AC∥BD,所以直线BD的解析式的k值与直线AC的解析式k值相同,设出解析式,即可解答.③利用旋转的性质进而得出A,B,C对应点位置进而得出答案,再利用以BC为半径90°圆心角的扇形面积减去以AB为半径90°圆心角的扇形面积求出答案;(3)利用平移的性质进而得出△ABC扫过的图形是平行四边形的面积.试题解析:(1)∵一次函数y=x+3的图象与x轴、y轴分别交于A、B两点,∴A(-4,0),B(0,3),∴AO=4,BO=3,在Rt△AOB中,AB=,∵等腰直角三角形ABC,∠BAC=90°,∴BC=;(2)①如图1,∵B(0,3),∴OB=3,∵AB=5,∴AO=AB-BO=5-3=2,∴A(0,-2).当在x轴上方时,点A的坐标为(0,8),②如图2,过点C作CF⊥OA与点F,∵△ABC为等腰直角三角形,∴∠BAC=90°,AB=AC,∴∠BAO+∠CAF=90°,∵∠OBA+∠BAO=90°,∴∠CAF=∠OBA,在△AOB和△CFA中,,∴△AOB≌△CFA(AAS);∴OA=CF=4,OB=AF=3,∴OF=7,CF=4,∴C(-7,4)∵A(-4,0)设直线AC解析式为y=kx+b,将A与C坐标代入得:,解得:,则直线AC解析式为y=x,∵将△ABC绕点B逆时针旋转,当旋转角为90°时,得到△BDE,∴∠ABD=90°,∵∠CAB=90°,∴∠ABD=∠CAB=90°,∴AC∥BD,∴设直线BD的解析式为y=x+b1,把B(0,3)代入解析式的:b1=3,∴直线BD的解析式为y=x+3;③因为旋转过程中AC扫过的图形是以BC为半径90°圆心角的扇形面积减去以AB为半径90°圆心角的扇形面积,所以可得:S=;(3)将△ABC向右平移到△A′B′C′的位置,△ABC扫过的图形是一个平行四边形和三角形ABC,如图3:将C点的纵坐标代入一次函数y=x+3,求得C′的横坐标为,平行四边CAA′C′的面积为(7+)×4=,三角形ABC的面积为×5×5=△ABC扫过的面积为:.考点:几何变换综合题.10.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.(1)求矩形ABCD的边AD的长.(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)S=.【解析】试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.(2)由折叠可知AM=MP,在Rt△MPD中,∴∴y=-其中,0<x<3.(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.∴△PCN为等腰三角形,只可能NC=NP.过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,∴解得x=.(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.设MP=y,在Rt△ADM中,,即∴ y=.∴ S=考点:函数的性质、勾股定理.。
初中数学平行四边形提高题及常考题及培优题含解析

数学平行四边形提升题与常考题和培优题(含分析 )一.选择题(共12 小题)1.如图, DE 是△ ABC的中位线,过点 C 作 CF∥ BD 交 DE 的延伸线于点 F,则下列结论正确的选项是()A.EF=CF B.EF=DE C.CF< BD D.EF> DE2.如图,在△ ABC中,∠ ABC=90°,AB=8,BC=6.若 DE 是△ ABC的中位线,延长 DE 交△ ABC的外角∠ ACM 的均分线于点 F,则线段 DF 的长为()A.7B.8C.9D.103.如图,在△ ABC中, AB=4,BC=6,DE、DF 是△ ABC的中位线,则四边形B EDF 的周长是()A.5B.7C.8D.104.如图,在△ ABC中,点 D,E 分别是边 AB,AC的中点, AF⊥BC,垂足为点 F,∠ ADE=30°, DF=4,则 BF 的长为()A.4B.8C.2D.45.如图,将矩形纸片ABCD沿其对角线 AC 折叠,使点 B 落到点 B′的地点, AB′与 CD交于点 E,若 AB=8, AD=3,则图中暗影部分的周长为()A.11 B.16 C.19D.226.如图,在 ?ABCD中, AB=6,BC=8,∠ C 的均分线交 AD 于 E,交 BA 的延伸线于 F,则 AE+AF的值等于()A.2B.3C.4D.67.如图,平行四边形ABCD的周长是 26cm,对角线 AC 与 BD 交于点 O,AC⊥AB,E 是 BC中点,△AOD 的周长比△ AOB 的周长多 3cm,则 AE 的长度为()A.3cm B.4cm C.5cm D.8cm8.如图,在 ?ABCD中, AB=12,AD=8,∠ ABC的均分线交 CD 于点 F,交 AD 的延伸线于点 E,CG⊥BE,垂足为 G,若 EF=2,则线段 CG的长为()A.B.4C.2D.9.对于 ?ABCD的表达,正确的选项是()A.若 AB⊥ BC,则 ?ABCD是菱形B.若 AC⊥BD,则 ?ABCD是正方形C.若 AC=BD,则 ?ABCD是矩形 D.若 AB=AD,则 ?ABCD是正方形10.如图,在 ?ABCD中, BF均分∠ ABC,交 AD 于点 F,CE均分∠ BCD,交 AD 于点 E,AB=6,EF=2,则 BC长为()A.8B.10 C.12D.1411.如图,将 ?ABCD沿对角线 AC折叠,使点 B 落在 B′处,若∠ 1=∠ 2=44°,则∠B为()A.66°B.104°C.114°D.124°12.已知菱形 OABC在平面直角坐标系的地点以下图,极点A(5,0),OB=4,点 P 是对角线 OB 上的一个动点,D(0,1),当 CP+DP 最短时,点 P 的坐标为()A.(0,0) B.(1,)C.(,)D.(,)二.填空题(共12 小题)13.如图,在平行四边形ABCD中, AB=4,BC=5,∠ABC=60°,平行四边形 ABCD的对角线 AC、 BD交于点 O,过点 O 作 OE⊥ AD,则 OE=.14.如图,在△ ABC中,点 D、E、F 分别是边 AB、BC、CA 上的中点,且 AB=6cm,AC=8cm,则四边形 ADEF的周长等于cm.15.如图, ?ABCD中,∠ ABC=60°, E、 F 分别在 CD 和 BC的延伸线上, AE∥BD,EF⊥BC, EF=3,则 AB 的长是.16.有 3 个正方形以下图搁置,暗影部分的面积挨次记为S1,S2,则 S1:S2=.17.如图,在△ ABC中,∠ ACB=90°, M 、N 分别是 AB、 AC的中点,延伸BC至点 D,使 CD= BD,连结 DM、DN、MN.若 AB=6,则 DN=.18.如图,在 ?ABCD中, E 为边 CD 上一点,将△ ADE沿 AE 折叠至△ AD′E处,AD′与 CE交于点 F.若∠ B=52°,∠ DAE=20°,则∠ FED′的大小为.19.如图,在 Rt△ABC中,∠ B=90°,AB=4,BC>AB,点 D 在 BC上,以 AC 为对角线的平行四边形ADCE中, DE的最小值是.20.如图,把平行四边形 ABCD折叠,使点 C 与点 A 重合,这时点 D 落在 D1,折痕为 EF,若∠ BAE=55°,则∠ D1AD= .21.如图,△ APB中, AB=2,∠ APB=90°,在 AB 的同侧作正△ ABD、正△ APE和正△ BPC,则四边形 PCDE面积的最大值是.22.如图,已知菱形 ABCD的边长 2,∠ A=60°,点 E、 F 分别在边 AB、AD 上,若将△ AEF沿直线 EF折叠,使得点 A 恰巧落在 CD边的中点 G 处,则 EF= .23.如图,在菱形 ABCD中,过点 B 作 BE⊥AD,BF⊥CD,垂足分别为点E, F,延伸 BD 至 G,使得 DG=BD,连结 EG, FG,若 AE=DE,则=.24.如图,在正方形ABCD中,对角线 AC 与 BD 订交于点 O,E 为 BC上一点,CE=5,F 为 DE 的中点.若△ CEF的周长为 18,则 OF的长为.三.解答题(共16 小题)25.如图,四边形 ABCD是平行四边形, AE 均分∠ BAD,交 DC的延伸线于点E.求证: DA=DE.26.如图,已知△ ABC,AD 均分∠ BAC交 BC于点 D,BC的中点为 M ,ME∥AD,交 BA 的延伸线于点 E,交 AC 于点F.( 1)求证: AE=AF;( 2)求证: BE= (AB+AC).27.已知:如图,矩形ABCD的对角线 AC、 BD 订交于点 O,CE∥DB,交 AB 的延伸线于点 E.求证: AC=EC.28.如图,平行四边形ABCD中, BD⊥ AD,∠ A=45°,E、F 分别是 AB、CD上的点,且 BE=DF,连结 EF交 BD 于 O.(1)求证: BO=DO;(2)若 EF⊥ AB,延伸 EF交 AD 的延伸线于 G,当 FG=1时,求 AE的长.29.如图,在四边形ABCD中,∠ ABC=90°, AC=AD, M ,N 分别为 AC,CD的中点,连结 BM,MN,BN.(1)求证: BM=MN;(2)∠ BAD=60°,AC均分∠ BAD,AC=2,求 BN 的长.30.在平行四边形 ABCD中, E 是 AD 上一点, AE=AB,过点 E 作直线 EF,在EF 上取一点 G,使得∠ EGB=∠EAB,连结 AG.(1)如图①,当 EF与 AB 订交时,若∠ EAB=60°,求证: EG=AG+BG;(2)如图②,当 EF与 CD订交时,且∠ EAB=90°,请你写出线段 EG、AG、BG 之间的数目关系,并证明你的结论.31.如图,四边形 ABCD为平行四边形,∠ BAD的角均分线 AE 交 CD于点 F,交BC的延伸线于点 E.(1)求证: BE=CD;(2)连结 BF,若 BF⊥AE,∠ BEA=60°,AB=4,求平行四边形 ABCD的面积.32.如图, ?ABCD中, AB=2,AD=1,∠ ADC=60°,将 ?ABCD沿过点 A 的直线 l 折叠,使点 D 落到 AB 边上的点 D′处,折痕交 CD边于点 E.(1)求证:四边形 BCED′是菱形;(2)若点 P 是直线 l 上的一个动点,请计算 PD′+PB 的最小值.33.如图,在 ?ABCD中,连结 BD,在 BD 的延伸线上取一点E,在 DB的延伸线上取一点 F,使 BF=DE,连结 AF、 CE.求证: AF∥CE.34.如图,在 ?ABCD中, E 是 BC的中点,连结 AE并延伸交 DC的延伸线于点 F.(1)求证: AB=CF;(2)连结 DE,若 AD=2AB,求证: DE⊥AF.35.如图, ?ABCD的对角线 AC、BD 订交于点 O,EF过点 O 且与 AB、CD分别相交于点 E、 F,连结 EC.(1)求证: OE=OF;(2)若 EF⊥ AC,△ BEC的周长是 10,求 ?ABCD的周长.36.如图,在 ?ABCD中, E、 F 分别为边 AD、BC的中点,对角线 AC 分别交 BE,DF于点 G、H.求证: AG=CH.37.如图,分别以Rt△ ABC的直角边 AC 及斜边 AB 向外作等边△ ACD及等边△ABE,已知:∠ BAC=30°,EF⊥AB,垂足为 F,连结 DF.(1)试说明 AC=EF;(2)求证:四边形 ADFE是平行四边形.38.如图,BD 是△ ABC的角均分线,它的垂直均分线分别交A B,BD,BC于点 E,F,G,连结 ED,DG.( 1)请判断四边形EBGD的形状,并说明原因;( 2)若∠ ABC=30°,∠ C=45°,ED=2 ,点 H 是 BD 上的一个动点,求HG+HC 的最小值.39.如图 1,已知点 E,F,G,H 分别是四边形 ABCD各边 AB,BC, CD,DA 的中点,依据以下思路能够证明四边形 EFGH是平行四边形:( 1)如图 2,将图 1 中的点 C 挪动至与点 E 重合的地点, F,G,H 还是 BC,CD,DA 的中点,求证:四边形CFGH是平行四边形;(2)如图 3,在边长为 1 的小正方形构成的 5× 5 网格中,点 A,C,B 都在格点上,在格点上画出点 D,使点 C 与 BC,CD,DA 的中点 F,G,H 构成正方形 CFGH;(3)在( 2)条件下求出正方形 CFGH的边长.40.我们给出以下定义:按序连结随意一个四边形各边中点所得的四边形叫中点四边形.(1)如图 1,四边形 ABCD中,点 E,F,G,H 分别为边 AB,BC,CD,DA 的中点.求证:中点四边形 EFGH是平行四边形;(2)如图 2,点 P 是四边形 ABCD内一点,且知足 PA=PB,PC=PD,∠ APB=∠CPD,点 E,F,G,H 分别为边 AB, BC,CD,DA 的中点,猜想中点四边形EFGH的形状,并证明你的猜想;(3)若改变( 2)中的条件,使∠ APB=∠CPD=90°,其余条件不变,直接写出中点四边形 EFGH的形状.(不用证明)数学平行四边形提升题与常考题和培优题(含分析 )参照答案与试题分析一.选择题(共12 小题)1.( 2016?厦门)如图, DE是△ ABC的中位线,过点 C 作 CF∥BD 交 DE的延伸线于点 F,则以下结论正确的选项是()A.EF=CF B.EF=DE C.CF< BD D.EF> DE【剖析】第一依据三角形的中位线定理得出AE=EC,而后依据 CF∥BD 得出∠ ADE=∠ F,既而依据AAS 证得△ ADE≌△ CFE,最后依据全等三角形的性质即可推出EF=DE.【解答】解:∵ DE是△ ABC的中位线,∴E为 AC中点,∴AE=EC,∵CF∥BD,∴∠ ADE=∠F,在△ ADE和△ CFE中,∵,∴△ ADE≌△ CFE(AAS),∴DE=FE.应选 B.【评论】本题考察了三角形中位线定理和全等三角形的判断与性质,解答本题的重点是依据中位线定理和平行线的性质得出 AE=EC、∠ ADE=∠F,判断三角形的全等.2.(2016?陕西)如图,在△ ABC中,∠ ABC=90°,AB=8,BC=6.若 DE 是△ ABC 的中位线,延伸DE 交△ ABC的外角∠ ACM 的均分线于点F,则线段 DF 的长为()A.7B.8C.9D.10【剖析】依据三角形中位线定理求出DE,获得 DF∥BM,再证明 EC=EF= AC,由此即可解决问题.【解答】解:在 RT△ABC中,∵∠ ABC=90°,AB=8,BC=6,∴ AC===10,∵DE是△ABC的中位线,∴ DF∥BM,DE= BC=3,∴∠ EFC=∠ FCM,∵∠ FCE=∠ FCM,∴∠ EFC=∠ ECF,∴EC=EF= AC=5,∴DF=DE+EF=3+5=8.应选 B.【评论】本题考察三角形中位线定理、等腰三角形的判断和性质、勾股定理等知识,解题的重点是灵巧应用三角形中位线定理,掌握等腰三角形的判断和性质,属于中考常考题型.3.(2016?贵宾)如图,在△ ABC中, AB=4,BC=6,DE、 DF是△ ABC的中位线,则四边形 BEDF的周长是()A.5B.7C.8D.10【剖析】由中位线的性质可知DE=,DF=,DE∥BF,DF∥ BE,可知四边形 BEDF为平行四边形,从而可得周长.【解答】解:∵ AB=4, BC=6, DE、DF 是△ ABC的中位线,∴DE= =2,DF==3,DE∥BF, DF∥BE,∴四边形 BEDF为平行四边形,∴四边形 BEDF的周长为: 2× 2+3× 2=10,应选 D.【评论】本题主要考察了三角形中位线的性质,利用中位线的性质证得四边形BEDF为平行四边形是解答本题的重点4.(2016?葫芦岛)如图,在△ ABC中,点 D,E 分别是边 AB,AC的中点, AF⊥BC,垂足为点 F,∠ ADE=30°,DF=4,则 BF 的长为()A.4B.8C.2D.4【剖析】先利用直角三角形斜边中线性质求出AB,再在 RT△ ABF 中,利用30角所对的直角边等于斜边的一半,求出AF 即可解决问题.【解答】解:在 RT△ABF中,∵∠ AFB=90°,AD=DB,DF=4,∴AB=2DF=8,∵AD=DB, AE=EC,∴ DE∥BC,∴∠ ADE=∠ABF=30°,∴ AF= AB=4,∴ BF===4 .应选 D.【评论】本题考察三角形中位线性质、含 30 度角的直角三角形性质、直角三角形斜边中线性质、勾股定理等知识,解题的重点是灵巧应用这些知识解决问题,属于中考常考题型.5.( 2017?河北一模)如图,将矩形纸片ABCD沿其对角线 AC折叠,使点 B 落到点 B′的地点,AB′与 CD 交于点 E,若 AB=8,AD=3,则图中暗影部分的周长为()A.11 B.16 C.19D.22【剖析】第一由四边形 ABCD为矩形及折叠的特征,获得B′C=BC=AD,∠B′=∠B=∠D=90°,∠ B′EC=∠DEA,获得△ AED≌△ CEB′,得出 EA=EC,再由暗影部分的周长为 AD+DE+EA+EB′+B′C+EC,即矩形的周长解答即可.【解答】解:∵四边形ABCD为矩形,∴ B′C=BC=AD,∠ B′=∠B=∠D=90°∵∠ B′EC=∠DEA,在△ AED和△ CEB′中,,∴△ AED≌△ CEB′(AAS);∴EA=EC,∴暗影部分的周长为AD+DE+EA+EB′+B′C+EC,=AD+DE+EC+EA+EB′+B′C,=AD+DC+AB′+B′C,=3+8+8+3,=22,应选 D.【评论】本题主要考察了图形的折叠问题,全等三角形的判断和性质,及矩形的性质.熟记翻折前后两个图形能够重合找出相等的角是解题的重点.6.(2016?泰安)如图,在 ?ABCD中, AB=6,BC=8,∠C 的均分线交 AD 于 E,交BA 的延伸线于 F,则 AE+AF的值等于()A.2B.3C.4D.6【剖析】由平行四边形的性质和角均分线得出∠F=∠FCB,证出 BF=BC=8,同理:DE=CD=6,求出 AF=BF﹣AB=2,AE=AD﹣DE=2,即可得出结果.【解答】解:∵四边形 ABCD是平行四边形,∴AB∥CD,AD=BC=8,CD=AB=6,∴∠ F=∠DCF,∵ CF均分∠ BCD,∴∠ FCB=∠DCF,∴∠ F=∠FCB,∴BF=BC=8,同理: DE=CD=6,∴AF=BF﹣AB=2,AE=AD﹣DE=2,∴AE+AF=4;应选: C.【评论】本题考察了平行四边形的性质、等腰三角形的判断;娴熟掌握平行四边形的性质,证明三角形是等腰三角形是解决问题的重点.7.( 2016?绵阳)如图,平行四边形 ABCD的周长是 26cm,对角线 AC 与 BD 交于点 O,AC⊥AB, E 是 BC 中点,△ AOD的周长比△ AOB 的周长多 3cm,则 AE 的长度为()A.3cm B.4cm C.5cm D.8cm【剖析】由?ABCD的周长为 26cm,对角线 AC、BD 订交于点 O,若△ AOD 的周长比△ AOB的周长多 3cm,可得 AB+AD=13cm,AD﹣AB=3cm,求出 AB 和 AD的长,得出 BC的长,再由直角三角形斜边上的中线性质即可求得答案.【解答】解:∵ ?ABCD的周长为 26cm,∴AB+AD=13cm,OB=OD,∵△ AOD的周长比△ AOB 的周长多 3cm,∴( OA+OD+AD)﹣( OA+OB+AB)=AD﹣AB=3cm,∴AB=5cm,AD=8cm.∴BC=AD=8cm.∵AC⊥AB,E 是BC中点,∴ AE= BC=4cm;应选: B.【评论】本题考察了平行四边形的性质、直角三角形斜边上的中线性质.娴熟掌握平行四边形的性质,由直角三角形斜边上的中线性质求出AE 是解决问题的重点.第 17 页(共 56 页)8.(2016?济南)如图,在 ?ABCD中, AB=12,AD=8,∠ ABC的均分线交 CD 于点F,交 AD 的延伸线于点 E,CG⊥BE,垂足为 G,若 EF=2,则线段 CG的长为()A.B.4C.2D.【剖析】先由平行四边形的性质和角均分线的定义,判断出∠ CBE=∠CFB=∠ABE=∠E,从而获得 CF=BC=8,AE=AB=12,再用平行线分线段成比率定理求出 BE,而后用等腰三角形的三线合一求出 BG,最后用勾股定理即可.【解答】解:∵∠ ABC的均分线交 CD 于点 F,∴∠ ABE=∠CBE,∵四边形 ABCD是平行四边形,∴DC∥AB,∴∠ CBE=∠CFB=∠ABE=∠E,∴CF=BC=AD=8,AE=AB=12,∵ AD=8,∴DE=4,∵DC∥AB,∴,∴,∴EB=6,∵CF=CB,CG⊥BF,∴ BG= BF=2,在 Rt△BCG中, BC=8, BG=2,依据勾股定理得, CG===2,应选: C.【评论】本题是平行四边形的性质,主要考察了角均分线的定义,平行线分线段成比率定理,等腰三角形的性质和判断,勾股定理,解本题的重点是求出AE,记着:题目中出现平行线和角均分线时,极易出现等腰三角形这一特色.9.(2016?河北)对于 ?ABCD的表达,正确的选项是()A.若 AB⊥ BC,则 ?ABCD是菱形B.若 AC⊥BD,则 ?ABCD是正方形C.若 AC=BD,则 ?ABCD是矩形 D.若 AB=AD,则 ?ABCD是正方形【剖析】由菱形的判断方法、矩形的判断方法、正方形的判断方法得出选项A、B、D 错误, C 正确;即可得出结论.【解答】解:∵ ?ABCD中, AB⊥BC,∴四边形 ABCD是矩形,不必定是菱形,选项 A 错误;∵ ?ABCD中, AC⊥BD,∴四边形 ABCD是菱形,不必定是正方形,选项 B 错误;∵?ABCD中, AC=BD,∴四边形 ABCD是矩形,选项 C 正确;∵?ABCD中, AB=AD,∴四边形 ABCD是菱形,不必定是正方形,选项 D 错误;应选: C.【评论】本题考察了平行四边形的性质、菱形的判断方法、矩形的判断方法、正方形的判断方法;娴熟掌握矩形、菱形、正方形的判断方法是解决问题的重点.10.( 2016?丹东)如图,在 ?ABCD中, BF均分∠ ABC,交 AD 于点 F,CE均分∠BCD,交 AD 于点 E,AB=6,EF=2,则 BC长为()A.8B.10 C.12D.14【剖析】由平行四边形的性质和角均分线得出∠ABF=∠AFB,得出 AF=AB=6,同理可证 DE=DC=6,再由 EF的长,即可求出BC的长.【解答】解:∵四边形 ABCD是平行四边形,∴AD∥BC,DC=AB=6,AD=BC,∴∠ AFB=∠FBC,∵ BF均分∠ ABC,∴∠ ABF=∠FBC,则∠ ABF=∠AFB,∴AF=AB=6,同理可证: DE=DC=6,∵EF=AF+DE﹣AD=2,即 6+6﹣AD=2,解得: AD=10;应选: B.【评论】本题主要考察了平行四边形的性质、等腰三角形的判断;娴熟掌握平行四边形的性质,证出 AF=AB是解决问题的重点.11.(2016?河北)如图,将 ?ABCD沿对角线 AC折叠,使点 B 落在 B′处,若∠ 1=∠ 2=44°,则∠ B 为()A.66°B.104°C.114°D.124°【剖析】由平行四边形的性质和折叠的性质得出∠ ACD=∠ BAC=∠B′AC,由三角形的外角性质求出∠ BAC=∠ACD=∠B′AC=∠1=22°,再由三角形内角和定理求出∠B 即可.【解答】解:∵四边形 ABCD是平行四边形,∴AB∥CD,∴∠ ACD=∠BAC,由折叠的性质得:∠ BAC=∠B′AC,∴∠ BAC=∠ACD=∠B′AC=∠ 1=22°,∴∠ B=180°﹣∠ 2﹣∠ BAC=180°﹣44°﹣22°=114°;应选: C.【评论】本题考察了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;娴熟掌握平行四边形的性质,求出∠BAC的度数是解决问题的重点.12.(2016?咸宁)已知菱形 OABC在平面直角坐标系的地点以下图,极点A(5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点 P 的坐标为()A.(0,0) B.(1,)C.(,)D.(,)【剖析】如图连结 AC,AD,分别交 OB 于 G、P,作 BK⊥ OA 于 K.第一说明点 P 就是所求的点,再求出点 B 坐标,求出直线 OB、 DA,列方程组即可解决问题.【解答】解:如图连结 AC,AD,分别交 OB 于 G、P,作 BK⊥ OA 于 K.∵四边形 OABC是菱形,∴AC⊥OB,GC=AG,OG=BG=2 ,A、 C 对于直线 OB 对称,∴PC+PD=PA+PD=DA,∴此时 PC+PD最短,在 RT△ AOG中, AG===,∴ AC=2,∵OA?BK= ?AC?OB,∴ BK=4, AK==3,∴点 B 坐标( 8,4),∴直线 OB分析式为 y=x,直线 AD 分析式为 y=﹣x+1,由解得,∴点 P坐标(,).应选 D.【评论】本题考察菱形的性质、轴对称﹣最短问题、坐标与图象的性质等知识,解题的重点是正确找到点 P 地点,建立一次函数,列出方程组求交点坐标,属于中考常考题型.二.填空题(共12 小题)13.( 2017?新城区校级模拟)如图,在平行四边形 ABCD 中, AB=4,BC=5,∠ABC=60°,平行四边形 ABCD的对角线 AC、 BD交于点 O,过点 O 作 OE⊥AD,则OE=.【剖析】作 CF⊥AD 于 F,由平行四边形的性质得出∠ ADC=∠ABC=60°,CD=AB=4,OA=OC,求出∠DCF=30°,由直角三角形的性质得出 DF= CD=2,求出CF= DF=2,证出OE是△ ACF的中位线,由三角形中位线定理得出OE 的长即可.【解答】解:作 CF⊥AD 于 F,以下图:∵四边形 ABCD是平行四边形,∴∠ ADC=∠ABC=60°,CD=AB=4,OA=OC,第 22 页(共 56 页)∴DF= CD=2,∴CF= DF=2 ,∵CF⊥AD,OE⊥AD, CF∥OE,∵OA=OC,∴OE是△ ACF的中位线,∴OE= CF= ;故答案为:.【评论】本题考察了平行四边形的性质、直角三角形的性质、勾股定理、三角形中位线定理等知识;娴熟掌握平行四边形的性质,证出 OE 是三角形的中位线是解决问题的重点.14.( 2016?张家界)如图,在△ ABC中,点 D、E、F 分别是边 AB、 BC、CA上的中点,且 AB=6cm, AC=8cm,则四边形 ADEF的周长等于 14 cm.【剖析】第一证明四边形 ADEF是平行四边形,依据三角形中位线定理求出DE、EF即可解决问题.【解答】解:∵ BD=AD, BE=EC,∴ DE= AC=4cm,DE∥AC,∵ CF=FA,CE=BE,∴ EF= AB=3cm,EF∥AB,∴四边形 ADEF是平行四边形,∴四边形 ADEF的周长 =2( DE+EF)=14cm.故答案为 14.【评论】本题考察三角形中位线定理、平行四边形的判断和性质等知识,解题的重点是出现中点想到三角形中位线定理,记着三角形中位线平行于第三边且等于第三边的一半,属于中考常考题型.15.( 2017 秋?海宁市校级月考)如图,?ABCD中,∠ ABC=60°,E、F 分别在 CD 和 BC的延伸线上, AE∥BD,EF⊥ BC,EF=3,则 AB 的长是.【剖析】依据直角三角形性质求出CE长,利用勾股定理即可求出AB 的长.【解答】解:∵四边形 ABCD是平行四边形,∴AB∥DC,AB=CD,∵ AE∥BD,∴四边形 ABDE是平行四边形,∴AB=DE=CD,即 D 为 CE中点,∵ EF⊥BC,∴∠ EFC=90°,∵ AB∥CD,∴∠ DCF=∠ABC=60°,∴∠ CEF=30°,∵ EF=3,∴ CE==2 ,∴AB= ,故答案为:.【评论】本题考察了平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,本题综合性比较强.16.(2017?河北区模拟)有 3 个正方形以下图搁置,暗影部分的面积挨次记为S1,S2,则 S1:S2= 4:9.【剖析】设大正方形的边长为 x,再依据相像的性质求出 S1、S2与正方形面积的关系,而后进行计算即可得出答案.【解答】解:设大正方形的边长为x,依据图形可得:∵= ,∴= ,∴=,∴ S1=S正方形ABCD,∴S1= x2,∵= ,∴=,∴S2= S正方形ABCD,∴S2= x2,∴S1:S2= x2: x2=4:9.故答案是: 4:9.【评论】本题考察了正方形的性质,用到的知识点是正方形的性质、相像三角形的性质、正方形的面积公式,重点是依据题意求出 S1、S2与正方形面积的关系.17.(2016?随州)如图,在△ ABC中,∠ ACB=90°,M 、N 分别是 AB、AC的中点,延伸 BC至点 D,使 CD= BD,连结 DM、DN、MN.若 AB=6,则 DN= 3 .【剖析】连结 CM,依据三角形中位线定理获得NM=CB,MN∥ BC,证明四边形 DCMN 是平行四边形,获得 DN=CM,依据直角三角形的性质获得CM= AB=3,等量代换即可.【解答】解:连结 CM,∵ M、N 分别是 AB、AC的中点,∴NM= CB,MN ∥BC,又 CD= BD,∴MN=CD,又 MN∥BC,∴四边形 DCMN 是平行四边形,∴DN=CM,∵∠ ACB=90°,M 是 AB 的中点,∴CM= AB=3,∴DN=3,故答案为: 3.【评论】本题考察的是三角形的中位线定理、直角三角形的性质、平行四边形的判断和性质,掌握三角形的中位线平行于第三边,而且等于第三边的一半是解题的重点.18.( 2016?武汉)如图,在 ?ABCD中,E 为边 CD上一点,将△ ADE沿 AE 折叠至△AD′E处,AD′与 CE交于点 F.若∠ B=52°,∠DAE=20°,则∠ FED′的大小为 36° .【剖析】由平行四边形的性质得出∠D=∠ B=52°,由折叠的性质得:∠ D′=∠D=52°,∠EAD′=∠DAE=20°,由三角形的外角性质求出∠ AEF=72°,与三角形内角和定理求出∠ AED′=108,°即可得出∠ FED′的大小.【解答】解:∵四边形ABCD是平行四边形,∴∠ D=∠ B=52°,由折叠的性质得:∠ D′=∠D=52°,∠ EAD′=∠DAE=20°,∴∠ AEF=∠D+∠ DAE=52°+20°=72°,∠ AED′=180﹣°∠ EAD′﹣∠ D′=108,°∴∠ FED′=108﹣°72°=36°;故答案为: 36°.【评论】本题考察了平行四边形的性质、折叠的性质、三角形的外角性质以及三角形内角和定理;娴熟掌握平行四边形的性质和折叠的性质,求出∠ AEF和∠ AED′是解决问题的重点.19.( 2016?东营)如图,在Rt△ABC 中,∠ B=90°,AB=4,BC> AB,点 D 在 BC 上,以 AC为对角线的平行四边形ADCE中, DE的最小值是4.【剖析】第一证明 BC∥AE,当 DE⊥BC 时, DE 最短,只需证明四边形ABDE是矩形即可解决问题.【解答】解:∵四边形 ADCE是平行四边形,∴BC∥AE,∴当 DE⊥BC时, DE最短,此时∵∠ B=90°,∴AB⊥BC,∴DE∥AB,∴四边形 ABDE是平行四边形,∵∠ B=90°,∴四边形 ABDE是矩形,∴DE=AB=4,∴DE的最小值为4.故答案为 4.【评论】本题考察平行四边形的性质、垂线段最短等知识,解题的重点是找到DE的地点,学会利用垂线段最短解决问题,属于中考常考题型.20.( 2016?常德)如图,把平行四边形 ABCD折叠,使点 C 与点 A 重合,这时点 D 落在 D1,折痕为 EF,若∠ BAE=55°,则∠ D1AD= 55° .【剖析】由平行四边形的性质和折叠的性质得出∠D1∠,得出∠1AE=BAD D AD=∠BAE=55°即可.【解答】解:∵四边形 ABCD是平行四边形,∴∠ BAD=∠C,由折叠的性质得:∠ D1AE=∠ C,∴∠ D1AE=∠ BAD,∴∠ D1AD=∠ BAE=55°;故答案为: 55°.【评论】本题考察了平行四边形的性质、折叠的性质;由平行四边形和折叠的性质得出∠ D1AE=∠BAD 是解决问题的重点.21.(2016?常州)如图,△ APB中,AB=2,∠ APB=90°,在 AB 的同侧作正△ ABD、正△ APE和正△ BPC,则四边形 PCDE面积的最大值是1.【剖析】先延伸 EP交 BC于点 F,得出 PF⊥BC,再判断四边形 CDEP为平行四边形,依据平行四边形的性质得出:四边形 CDEP的面积 =EP×CF=a× b= ab,最后依据 a2+b2=4,判断ab 的最大值即可.【解答】解:延伸 EP交 BC于点 F,∵∠ APB=90°,∠ APE=∠BPC=60°,∴∠ EPC=150°,∴∠ CPF=180°﹣150°=30°,∴PF均分∠BPC,又∵ PB=PC,∴PF⊥BC,设 Rt△ABP中, AP=a, BP=b,则CF= CP= b,a2+b2=22=4,∵△ APE和△ ABD都是等边三角形,∴AE=AP,AD=AB,∠ EAP=∠ DAB=60°,∴∠ EAD=∠PAB,∴△ EAD≌△ PAB(SAS),∴ED=PB=CP,同理可得:△ APB≌△ DCB(SAS),∴EP=AP=CD,∴四边形 CDEP是平行四边形,∴四边形 CDEP的面积 =EP×CF=a×b=ab,又∵( a﹣b)2=a2﹣2ab+b2≥ 0,∴2ab≤a2+b2=4,∴ab≤1,即四边形 PCDE面积的最大值为1.故答案为: 1【评论】本题主要考察了等边三角形的性质、平行四边形的判断与性质以及全等三角形的判断与性质,解决问题的重点是作协助线结构平行四边形的高线.22.( 2016?盐城)如图,已知菱形 ABCD的边长 2,∠ A=60°,点 E、F 分别在边AB、AD 上,若将△ AEF沿直线 EF折叠,使得点 A 恰巧落在 CD边的中点 G 处,则EF=.【剖析】延伸 CD,过点 F 作 FM⊥CD于点 M,连结 GB、 BD,作 FH⊥AE 交于点H,由菱形的性质和已知条件得出∠ MFD=30°,设 MD=x,则 DF=2x, FM= x,得出 MG=x+1,由勾股定理得出(x+1)2+(x)2=(2﹣2x)2,解方程得出 DF=0.6,AF=1.4,求出 AH= AF=0.7,FH=,证明△ DCB是等边三角形,得出BG⊥CD,由勾股定理求出BG=,设BE=y,则GE=2﹣y,由勾股定理得出()2+y2=(2﹣y)2,解方程求出 y=0.25,得出 AE、 EH,再由勾股定理求出 EF即可.【解答】解:延伸 CD,过点 F 作 FM⊥CD于点 M ,连结 GB、BD,作 FH⊥ AE交于点 H,以下图:∵∠ A=60°,四边形 ABCD是菱形,∴∠ MDF=60°,∴∠ MFD=30°,设 MD=x,则 DF=2x, FM= x,∵DG=1,∴ MG=x+1,∴( x+1)2 +(x)2=(2﹣2x)2,∴DF=0.6, AF=1.4,∴ AH= AF=0.7,FH=AF?sin∠ A=1.4×=,∵CD=BC,∠ C=60°,∴△DCB是等边三角形,∵G 是 CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG= ,设 BE=y,则 GE=2﹣ y,∴()2+y2=(2﹣y)2,解得: y=0.25,∴ AE=1.75,∴ EH=AE﹣AH=1.75﹣0.7=1.05,∴EF===.故答案为:.【评论】本题考察了菱形的性质、翻折变换的性质、勾股定理、等边三角形的判断与性质等知识;本题综合性强,难度较大,运用勾股定理得出方程是解决问题的重点.23.( 2016?丽水)如图,在菱形ABCD中,过点 B 作 BE⊥AD,BF⊥CD,垂足分别为点 E,F,延伸 BD 至 G,使得 DG=BD,连结 EG,FG,若 AE=DE,则=.【剖析】连结AC、EF,依据菱形的对角线相互垂直均分可得AC⊥BD,依据线段垂直均分线上的点到线段两头点的距离相等可得AB=BD,而后判断出△ABD 是等边三角形,再依据等边三角形的三个角都是60°求出∠ADB=60°,设EF 与BD 订交于点 H,AB=4x,而后依据三角形的中位线平行于第三边而且等于第三边的一半求出 EH,再求出 DH,从而获得 GH,利用勾股定理列式求出 EG,最后求出比值即可.【解答】解:如图,连结 AC、 EF,在菱形 ABCD中, AC⊥BD,∵BE⊥AD,AE=DE,∴ AB=BD,又∵菱形的边 AB=AD,∴△ABD是等边三角形,∴∠ ADB=60°,设 EF与 BD 订交于点 H, AB=4x,∵AE=DE,∴由菱形的对称性, CF=DF,∴ EF是△ ACD的中位线,∴DH= DO= BD=x,在 Rt△EDH中, EH= DH= x,∵DG=BD,∴ GH=BD+DH=4x+x=5x,在 Rt△EGH中,由勾股定理得, EG===2x,所以,==.故答案为:.【评论】本题考察了菱形的性质,等边三角形的判断与性质,勾股定理,三角形的中位线平行于第三边而且等于第三边的一半,难点在于作协助线结构出直角三角形以及三角形的中位线.24.(2016?青岛)如图,在正方形 ABCD中,对角线 AC与 BD 订交于点 O,E 为BC上一点, CE=5,F 为 DE 的中点.若△ CEF的周长为 18,则 OF的长为.【剖析】先依据直角三角形的性质求出 DE 的长,再由勾股定理得出 CD 的长,从而可得出 BE的长,由三角形中位线定理即可得出结论.【解答】解:∵ CE=5,△ CEF的周长为 18,∴CF+EF=18﹣5=13.∵F为 DE的中点,∴DF=EF.∵∠ BCD=90°,∴CF= DE,∴EF=CF= DE=6.5,∴DE=2EF=13,∴CD===12.∵四边形 ABCD是正方形,∴BC=CD=12,O 为 BD 的中点,∴OF是△ BDE的中位线,∴OF= (BC﹣CE)= (12﹣5)= .故答案为:.【评论】本题考察的是正方形的性质,波及到直角三角形的性质、三角形中位线定理等知识,难度适中.三.解答题(共16 小题)25.( 2016?北京)如图,四边形 ABCD是平行四边形, AE均分∠ BAD,交 DC 的延伸线于点 E.求证: DA=DE.【剖析】由平行四边形的性质得出 AB∥ CD,得出内错角相等∠ E=∠ BAE,再由角均分线证出∠ E=∠DAE,即可得出结论.【解答】证明:∵四边形 ABCD是平行四边形,∴AB∥CD,∴∠ E=∠BAE,∵AE均分∠BAD,∴∠BAE=∠DAE,∴∠ E=∠DAE,∴DA=DE.【评论】本题考察了平行四边形的性质、平行线的性质、等腰三角形的判断;娴熟掌握平行四边形的性质,证出∠ E=∠ DAE是解决问题的重点.26.( 2016?淄博)如图,已知△ ABC,AD 均分∠ BAC交 BC于点 D, BC的中点为M, ME∥ AD,交 BA 的延伸线于点 E,交 AC于点 F.(1)求证: AE=AF;(2)求证: BE= (AB+AC).【剖析】(1)欲证明 AE=AF,只需证明∠ AEF=∠ AFE即可.(2)作 CG∥EM,交 BA的延伸线于 G,先证明 AC=AG,再证明 BE=EG即可解决问题.【解答】证明:(1)∵ DA 均分∠ BAC,∴∠ BAD=∠CAD,∵ AD∥EM,∴∠ BAD=∠AEF,∠ CAD=∠AFE,∴∠ AEF=∠AFE,∴ AE=AF.(2)作 CG∥EM,交 BA 的延伸线于 G.∵EF∥CG,∴∠ G=∠ AEF,∠ ACG=∠ AFE,∵∠ AEF=∠AFE,∴∠ G=∠ ACG,∴AG=AC,∵ EM∥ CG,∴= ,∵ BM=CM,∴BE=EG,∴BE= BG= (BA+AG)= (AB+AC).【评论】本题考察三角形中位线定理、角均分线的性质、等腰三角形的判断和性质等知识,解题的重点是增添协助线,结构等腰三角形,以及三角形中位线,属于中考常考题型.27.( 2017 春?泉山区校级月考)已知:如图,矩形 ABCD的对角线 AC、BD 订交于点 O,CE∥DB,交 AB的延伸线于点 E.求证: AC=EC.【剖析】先由矩形的对角线相等得出 AC=DB,再证明四边形 CDBE是平行四边形,得出对边相等 DB=CE,即可得出 AC=CE.【解答】证明:∵四边形 ABCD是矩形,∴AC=DB, AB∥DC,∴DC∥BE,又∵ CE∥ DB,∴四边形 CDBE是平行四边形,∴DB=CE,第 36 页(共 56 页)∴AC=CE.【评论】本题考察了矩形的性质以及平行四边形的判断与性质;娴熟掌握矩形的性质和证明平行四边形是解决问题的重点.28.( 2016?梅州)如图,平行四边形 ABCD中,BD⊥AD,∠A=45°,E、 F 分别是AB、CD上的点,且 BE=DF,连结 EF交 BD于 O.(1)求证: BO=DO;(2)若 EF⊥ AB,延伸 EF交 AD 的延伸线于 G,当 FG=1时,求 AE的长.【剖析】(1)由平行四边形的性质和 AAS证明△ OBE≌△ ODF,得出对应边相等即可;(2)证出 AE=GE,再证明 DG=DO,得出 OF=FG=1,即可得出结果.【解答】(1)证明:∵四边形 ABCD是平行四边形,∴ DC∥AB,∴∠ OBE=∠ODF.在△ OBE与△ ODF中,∴△ OBE≌△ ODF(AAS).∴BO=DO.(2)解:∵ EF⊥AB,AB∥ DC,∴∠ GEA=∠GFD=90°.∵∠ A=45°,∴∠G=∠ A=45°.∴AE=GE∵BD⊥AD,。
平行四边形综合训练拔高题

平行四边形综合训练拔高题一.选择题(共15小题)1.如图,▱ABCD中,AC.BD为对角线,BC=3,BC边上的高为2,则阴影部分的面积为()A.3 B.6 C.12 D.242.已知平行四边形一边长为10,一条对角线长为6,则它的另一条对角线α的取值范围为()A.4<α<16 B.14<α<26C.12<α<20 D.以上答案都不正确3.在▱ABCD中,AB=3,BC=4,当▱ABCD的面积最大时,下列结论正确的有()①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.A.①②③B.①②④C.②③④D.①③④4.某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE的长为1100m,则隧道AB的长度为()A.3300m B.2200m C.1100m D.550m5.如图,在矩形ABCD中,P、R分别是BC和DC上的点,E、F分别是AP和RP 的中点,当点P在BC上从点B向点C移动,而点R不动时,下列结论正确的是()A.线段EF的长逐渐增长B.线段EF的长逐渐减小C.线段EF的长始终不变D.线段EF的长与点P的位置有关6.如图,DE是△ABC的中位线,且△ADE的周长为20,则△ABC的周长为()A.30 B.40 C.50 D.无法计算7.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为()A.4S1B.4S2C.4S2+S3D.3S1+4S38.如图,▱ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=BC,连接OE.下列结论:①∠CAD=30°;②S▱ABCD=AB•AC;③OB=AB;④OE=BC,成立的个数有()A.1个 B.2个 C.3个 D.4个9.如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,若AE=4,AF=6,平行四边形ABCD的周长为40.则平行四边形ABCD的面积为()A.24 B.36 C.40 D.4810.如图所示,▱ABCD中,两条对角线AC、BD相交于点O,AF⊥BD于F,CE ⊥BD于E,则图中全等三角形的对数共有()A.5对 B.6对 C.7对 D.8对11.若▱ABCD的对称中心在坐标原点,AD∥x轴,若A的坐标为(﹣1,2),则点C的坐标为()A.(1,﹣2)B.(2,﹣1)C.(1,﹣3)D.(2,﹣3)12.如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66°B.104°C.114° D.124°13.如图,在▱ABCD中,AB=6,BC=8,∠C的平分线交AD于E,交BA的延长线于F,则AE+AF的值等于()A.2 B.3 C.4 D.614.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为()A.11+B.11﹣C.11+或11﹣D.11+或1+15.如图,▱ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为()A.13 B.17 C.20 D.26二.解答题(共6小题)16.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.17.在▱ABCD中,∠ADC的平分线交直线BC于点E、交AB的延长线于点F,连接AC.(1)如图1,若∠ADC=90°,G是EF的中点,连接AG、CG.①求证:BE=BF.②请判断△AGC的形状,并说明理由;(2)如图2,若∠ADC=60°,将线段FB绕点F顺时针旋转60°至FG,连接AG、CG.那么△AGC又是怎样的形状.(直接写出结论不必证明)18.在平行四边形ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.若平行四边形ABCD的面积为,求AG的长.19.如图,已知▱ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.(1)若M为AG中点,且DM=2,求DE的长;(2)求证:AB=CF+DM.20.如图,已知▱ABCD中,DE⊥BC于点E,DH⊥AB于点H,AF平分∠BAD,分别交DC、DE、DH于点F、G、M,且DE=AD.(1)求证:△ADG≌△FDM.(2)猜想AB与DG+CE之间有何数量关系,并证明你的猜想.21.已知:如图,平行四边形ABCD中,E、F分别是边BC和AD上的点,且BE=DF.求证:AE=CF.平行四边形综合训练拔高题参考答案一.选择题(共15小题)1.A;2.B;3.B;4.B;5.C;6.B;7.A;8.C;9.D;10.C;11.A;12.C;13.C;14.D;15.B;二.解答题(共6小题)16.;17.;18.;19.;20.;21.;。
平行四边形综合提高练习题

FEDCB A平行四边形综合提高一 利用平行四边形的性质进行角度、线段的计算1、如图,在□ABCD 中,AE⊥BC 于E,AF ⊥CD 于F,若∠EAF=60o,则∠B=_______;若BC =4cm,AB =3cm,则AF =___________,□A BCD 的面积为_________. 2已知A BC D的周长为32c m,对角线A C、BD 交于点O,△AO B的周长比△BOC 的周长多4cm,求这个四边形的各边长。
二、利用平行四边形的性质证线段相等3、如图,在□AB CD 中,O 是对角线AC、BD的交点,BE ⊥AC ,DF ⊥AC ,垂足分别为E 、F .那么O E与OF 是否相等?为什么?三 直接利用平行四边形的判定和性质4、如图在A BC D中,E、F分别是AD 、BC 的中点,AF 与EB 交于点G,CE 与DF 交于点H ,试说明四边形EGFH 的形状。
5、如图,B D是A BCD 的对角线,AE ⊥BD于E,CF ⊥B D于点F ,求证:四边形AEC F为平行四边形。
四 构造平行四边形解题HGADCEABDCEF6、如图2-33所示.Rt △A BC 中,∠BAC=90°,AD ⊥BC 于D,BG 平分∠A BC ,E F∥BC 且交AC 于F. 求证:AE=CF.7、已知,如图,AD 为△AB C的中线,E 为A C上一点,连结BE 交AD 于点F ,且AE=FE,求证:BF=AC[能力提高]1、如图2-39所示.在平行四边形AB CD 中,△ABE 和△B CF都是等边三角形.求证:△DEF 是等边三角形.2、如图2-32所示.在ABC D中,AE⊥B C,CF ⊥AD,DN =BM .求证:EF 与MN 互相平分.3、 如图2-34所示.ABCD 中,DE ⊥AB 于E,BM =MC=DC .求证:∠EM C=3∠BEM .4 如图2-35所示.矩形AB CD 中,C E⊥BD 于E ,AF 平分∠BAD 交E C延长线于F .求证:CA=CF.FBC E D[创新思维]1、以△ABC 的三条边为边在BC 的同侧作等边△ABP 、等边△ACQ 、等边△BCR , 求证:四边形P AQR 为平行四边形。
(完整word)平行四边形综合提高练习题.doc

平行四边形综合提高一利用平行四边形的性质进行角度、线段的计算1、如图,在□ABCD中, AE⊥ BC于 E, AF⊥CD于 F,若∠ EAF=60o,则∠ B= _______;若 BC= 4cm,AB= 3cm,则AF= ___________,□ ABCD的面积为 _________.A DFB E C2已知 ABCD的周长为 32cm,对角线 AC、 BD交于点 O,△ AOB的周长比△ BOC的周长多 4cm,求这个四边形的各边长。
二、利用平行四边形的性质证线段相等3、如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF⊥AC,垂足分别为E、F.那么OE与OF是否相等?为什么?三直接利用平行四边形的判定和性质4、如图在ABCD中, E、 F 分别是 AD、 BC的中点, AF 与 EB交于点 G,CE与 DF交于点 H,试说明四边形EGFH的形状。
AEDGHB FC5、如图, BD是ABCD的对角线, AE⊥ BD于 E, CF⊥BD于点 F,求证:四边形A ECF为平行四边形。
A DFEC B四构造平行四边形解题6、如图 2-33 所示. Rt △ABC中,∠ BAC=90°, AD⊥BC于 D,BG平分∠ ABC, EF∥ BC且交 AC于 F.求证: AE=CF.7、已知,如图,AD为△ ABC的中线, E 为 AC上一点,连结BE交 AD于点 F,且 AE=FE,求证: BF=ACB [ 能力提高 ]AEFD C1.如图 2-39 所示.在平行四边形ABCD中,△ ABE和△ BCF都是等边三角形.求证:△DEF是等边三角形.2、如图 2-32 所示.在ABCD中,AE⊥ BC,CF⊥ AD,DN=BM.求证: EF 与 MN互相平分.3、如图 2-34 所示.ABCD中, DE⊥ AB于 E, BM=MC=DC.求证:∠ EMC=3∠ BEM.4 如图 2-35 所示.矩形ABCD中, CE⊥ BD于 E, AF 平分∠ BAD交 EC延长线于F.求证: CA=CF.[ 创新思维 ]1、以△ ABC的三条边为边在BC的同侧作等边△ABP、等边△ ACQ、等边△ BCR,求证:四边形PAQR为平行四边形。
(完整版)平行四边形提高题练习
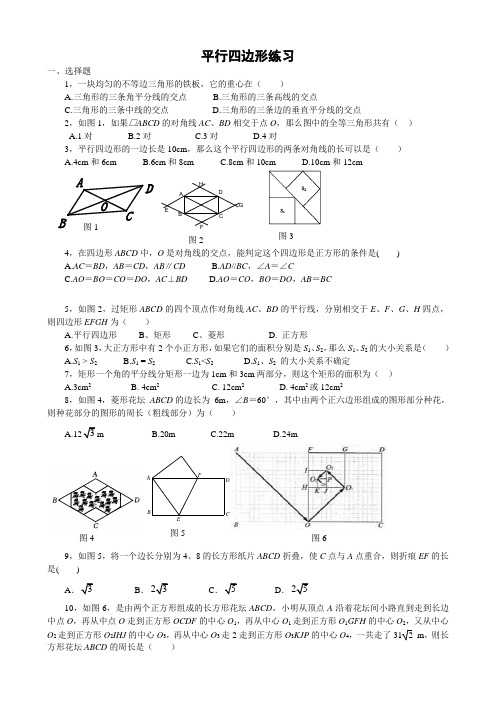
平行四边形练习一、选择题1,一块均匀的不等边三角形的铁板,它的重心在( )A.三角形的三条角平分线的交点B.三角形的三条高线的交点C.三角形的三条中线的交点D.三角形的三条边的垂直平分线的交点2,如图1,如果□ABCD 的对角线AC 、BD 相交于点O ,那么图中的全等三角形共有( )A.1对B.2对C.3对D.4对3,平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是( )A.4cm 和6cmB.6cm 和8cmC.8cm 和10cmD.10cm 和12cm4,在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( )A.AC =BD ,AB =CD ,AB ∥CDB.AD //BC ,∠A =∠CC.AO =BO =CO =DO ,AC ⊥BDD.AO =CO ,BO =DO ,AB =BC5,如图2,过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线,分别相交于E 、F 、G 、H 四点,则四边形EFGH 为( )A.平行四边形 B 、矩形 C 、菱形 D. 正方形6,如图3,大正方形中有2个小正方形,如果它们的面积分别是S 1、S 2,那么S 1、S 2的大小关系是( )A.S 1 > S 2B.S 1 = S 2C.S 1<S 2D.S 1、S 2 的大小关系不确定7,矩形一个角的平分线分矩形一边为1cm 和3cm 两部分,则这个矩形的面积为( )A.3cm 2B. 4cm 2C. 12cm 2D. 4cm 2或12cm 28,如图4,菱形花坛 ABCD 的边长为 6m ,∠B =60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )A.123mB.20mC.22mD.24m9,如图5,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则折痕EF 的长是( )A .3B .23C .5D .2510,如图6,是由两个正方形组成的长方形花坛ABCD ,小明从顶点A 沿着花坛间小路直到走到长边中点O ,再从中点O 走到正方形OCDF 的中心O 1,再从中心O 1走到正方形O 1GFH 的中心O 2,又从中心O 2走到正方形O 2IHJ 的中心O 3,再从中心O 3走2走到正方形O 3KJP 的中心O 4,一共走了31 2 m ,则长方形花坛ABCD 的周长是( )图6 图4 F EDC B A 图5 图3 AD C B HE FG 图2O A B D C 图1A.36 mB.48 mC.96 mD.60 m二、填空题(每题3分,共30分)11,如图7, 若将四根木条钉成的矩形木框变形为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角的值等于___.12,如图8,过矩形ABCD 的对角线BD 上一点K 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMKP 的面积S 1与矩形QCNK 的面积S 2的大小关系是S 1 S 2(填“>”或“<”或“=”).13,如图9,四边形ABCD 是正方形,P 在CD 上,△ADP 旋转后能够与△ABP ′重合,若AB =3,DP =1,则PP ′=___.14,已知菱形有一个锐角为60°,一条对角线长为6cm ,则其面积为___cm 2.15,如图10,在梯形ABCD 中,已知AB ∥CD ,点E 为BC 的中点, 设△DEA 的面积为S 1,梯形ABCD 的面积为S 2,则S 1与S 2的关系为___.16,如图11,四边形ABCD 的两条对角线AC 、BD 互相垂直,A 1B 1C 1D 1四边形ABCD 的中点四边形.如果AC =8,BD =10,那么四边形A 1B 1C 1D 1的面积为___.17,如图12,□ABCD 中,点E 在边AD 上,以BE 为折痕,将△ABE 向上翻折,点A 正好落在CD 上的点F ,若△FDE 的周长为8,△FCB 的周长为22,则FC 的长为___.18,将一张长方形的纸对折,如图13所示,可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到 条折痕,如果对折n 次,可以得到 条折痕.三、解答题(共40分)19,如图1,4,等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于D ,折痕分别交边AB 、BC 于点F 、E ,若AD =2,BC =8.求BE 的长.…… 第一次对折 第二次对折 第三次对折图13图11A 1B 1C 1D 1 D A B C D A B C EF 图12 D C BA 图7 图9 图8K NM Q C BF E D C B A 图14图10 E D C B A20,在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD 分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有___组;(2)请在图15的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的饿两条直线有什么规律?21,如图16,已知四边形ABCD 是平行四边形,∠BCD 的平分线CF 交边AB 于F ,∠ADC 的平分线DG 交边AB 于G .(1)线段AF 与GB 相等吗?(2)请你在已知条件的基础上再添加一个条件,使得△EFG 为等腰直角三角形,并说明理由.1.七巧板是我们祖先的一项创造,被誉为“东方魔板”,如图是一副七巧板,若已知S △BIC =1,请你根据七巧板制作过程的认识,解决下列问题: A B C D A B C D D CB A 图15 A BCDEF 图17图16 O F D B E C A· 图18(1)求一只蚂蚁从点A 沿A →B →C →H →E 所走的路线的总长。
(必考题)初中八年级数学下册第十八章《平行四边形》提高卷(答案解析)

一、选择题1.如图,在ABC ∆中,D 是AB 上一点,,AD AC AE CD =⊥于点E ,点F 是BC 的中点,若10BD =,则EF 的长为( )A .8B .6C .5D .4C 解析:C【分析】首先根据AD AC =可得△ACD 为等腰三角形,再由AE CD ⊥结合“三线合一”性质可得E 为CD 的中点,从而得到EF 为△CBD 的中位线,最终根据中位线定理求解即可. 【详解】∵AD AC =,∴△ACD 为等腰三角形,∵AE CD ⊥,∴E 为CD 的中点,(三线合一)又∵点F 是BC 的中点,∴EF 为△CBD 的中位线, ∴152EF BD ==, 故选:C .【点睛】 本题考查等腰三角形三线合一的性质以及中位线的性质,准确判断出中位线是解题关键. 2.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( )A .8B .16C .82D .162解析:A【分析】根据勾股定理,可得正方形的边长,进而可得正方形的面积.【详解】∵正方形ABCD 中,对角线4AC =,∴AB 2+BC 2=AC 2,∴2AB 2=42,∴AB 2=8.故选:A .【点睛】本题主要考查的是正方形的性质,勾股定理,熟练掌握勾股定理是解题的关键.3.下列命题中,错误的是()A.一组对边平行的四边形是梯形;B.两组对边分别相等的四边形是平行四边形;C.对角线相等的平行四边形是矩形;D.一组邻边相等的平行四边形是菱形.A解析:A【分析】根据梯形,平行四边形,矩形,菱形的判定进行判断即可.【详解】解:A、一组对边平行,另一组对边不平行的四边形是梯形,故错误,符合题意;B、两组对边分别相等的四边形是平行四边形,正确,不符合题意;C、对角线相等的平行四边形是矩形,正确,不符合题意;D、一组邻边相等的平行四边形是菱形,正确,不符合题意;故选:A.【点睛】主要考查梯形,平行四边形,矩形,菱形的判定,注意梯形的定义应从两组对边的不同位置关系分别考虑.4.下列命题中,正确的命题是()A.菱形的对角线互相平分且相等B.顺次联结菱形各边的中点所得的四边形是矩形C.矩形的对角线互相垂直平分D.顺次连结矩形各边的中点所得的四边形是正方形B解析:B【分析】根据菱形的性质、矩形的性质、中点四边形的定义逐一判断即可.【详解】解:A. 菱形的对角线互相平分,但不相等,该命题错误;B. 顺次联结菱形各边的中点所得的四边形是矩形,该命题正确;C. 矩形的对角线互相平分,但是不垂直,该命题错误;D. 顺次连结矩形各边的中点所得的四边形是菱形,该命题错误;故选:B.【点睛】本题考查特殊四边形的判定和性质,掌握菱形的性质、矩形的性质、中点四边形的定义是解题的关键.5.如图,把一张长方形纸片沿对角线折叠,若△EDF是等腰三角形,则∠BDC()A .45ºB .60ºC .67.5ºD .75ºC解析:C【分析】 由翻折可知:△BDF ≌△BCD ,所以∠EBD=∠CBD ,∠E=∠C=90°,由于△EDF 是等腰三角形,易证∠ABF=45°,所以∠CBD=12∠CBE=22.5°,从而可求出∠BDC=67.5°. 【详解】解:由翻折的性质得,∠DBC=∠EBD ,∵矩形的对边AD ∥BC ,∠E=∠C=90°,∴∠DBC=∠ADB ,∴∠EBD=∠ADB ,∵△EDF 是等腰三角形,∠E=90°,∴△EDF 是等腰直角三角形,∴∠DFE=45°,∵∠EBD+∠ADB=∠DFE ,∴∠DBF=12∠DFE=22.5°, ∴∠CBD =22.5°,∴∠BDC=67.5°,故选:C .【点睛】本题考查等腰三角形,涉及矩形的性质,全等三角形的判定与性质等知识,需要学生灵活运用所学知识.6.如图,已知在正方形ABCD 中,E 是BC 上一点,将正方形的边CD 沿DE 折叠到DF ,延长EF 交AB 于点G ,连接DG .现有如下4个结论:①AG =GF ;②AG 与EC 一定不相等;③45GDE ∠=︒;④BGE △的周长是一个定值.其中正确的个数为( )A .1B .2C .3D .4C解析:C【分析】根据HL 证明△ADG ≌△FDG ,根据角的平分线的意义求∠GDE ,根据GE=GF+EF=EC+AG ,确定△BGE 的周长为AB+AC.【详解】根据折叠的意义,得△DEC ≌△DEF ,∴EF=EC ,DF=DC ,∠CDE=∠FDE ,∵DA=DF ,DG=DG ,∴Rt △ADG ≌Rt △FDG ,∴AG=FG ,∠ADG=∠FDG ,∴∠GDE=∠FDG+∠FDE =12(∠ADF+∠CDF ) =45°, ∵△BGE 的周长=BG+BE+GE ,GE=GF+EF=EC+AG ,∴△BGE 的周长=BG+BE+ EC+AG=AB+AC ,是定值,∴正确的结论有①③④,故选C.【点睛】本题考查了正方形中的折叠变化,直角三角形的全等及其性质,角的平分线,三角形的周长,熟练掌握折叠的全等性是解题的关键.7.如图,正方形ABCD 的对角线相交于点O ,正方形OMNQ 与ABCD 的边长均为a ,OM 与CD 相交于点E ,OQ 与BC 相交于点F ,且满足DE CF ,则两个正方形重合部分的面积为( )A .212aB .214aC .218a D .2116a B 解析:B【分析】由正方形OMNQ 与ABCD 得∠DOC=∠MOQ=90°可推出∠DOE=∠COF 由AC ,BD 是正方形ABCD 的对角线求得∠ODE=∠OCF=45°,可证△DOE ≌△COF (AAS ),利用面积和差S 四边形FOEC = S △EOC +S △DOE =S △DOC =214a 即可. 【详解】∵正方形OMNQ 与ABCD ,∴∠DOC=∠MOQ=90°,∴∠DOE+∠EOC =90º,∠EOC+∠COF=90º,∴∠DOE=∠COF ,又AC ,BD 是正方形ABCD 的对角线,∴∠ODE=∠OCF=45°,∵DE CF =,∴△DOE ≌△COF (AAS ),∴S 四边形FOEC =S △EOC +S △COF = S △EOC +S △DOE =S △DOC ,∵S △DOC =2ABCD 11=44S a 正方形, ∴S 四边形FOEC =214a . 故选择:B .【点睛】 本题考查正方形的性质,全等三角形的判定与性质,掌握正方形的性质,全等三角形的判定与性质是解题关键.8.如图,Rt Rt ABC BAD △≌△,BC 、AD 交于点E ,M 为斜边的中点,若CMD α∠=,AEB β∠=.则α和β之间的数量关系为( )A .2180βα-=︒B .60βα-=︒C .180αβ+=︒D .2βα=A解析:A【分析】根据题意可得,CAB DBA ABC BAD ∠=∠∠=∠,再由直角三角形斜边的中线等于斜边的一半,可证CM DM AM BM ===,继而证明()AMC BMD SSS △≌△,解得1802AMC BMD CAM ∠=∠=︒-∠,最后根据三角形内角和180°定理,分别解得αβ、与CAM ∠的关系,整理即可解题.【详解】Rt Rt ABC BAD △≌△,CAB DBA ABC BAD ∴∠=∠∠=∠M 是AB 的中点,11,22CM AB DM AB ∴== CM DM AM BM ∴===∴∠CAM=∠MCA ,Rt Rt ABC BAD △≌△AC BD ∴=()AMC BMD SSS △≌△1802AMC BMD CAM ∴∠=∠=︒-∠CMD α∴=∠180AMC BMD =︒-∠-∠1802(1802)CAM =︒-⨯︒-∠4180CAM =∠-︒90ABC BAD CAM ∠=∠=︒-∠,AEB β=∠=180BAD ABC ︒-∠-∠180(90)(90)CAM CAM =︒-︒-∠-︒-∠2CAM =∠2180βα∴-=︒故选:A .【点睛】本题考查全等三角形的判定与性质、直角三角形斜边中线的性质、等腰三角形的性质、三角形内角和180°等知识,是重要考点,难度较易,掌握相关知识是解题关键. 9.如图,长方形纸片ABCD ,点E ,M ,N 分别在边AB ,BC ,AD 上,将纸片分别沿EN ,EM 对折,使点A 落在点'A 处,点B 落在点'B 处,若''30A EB ∠=︒,则NEM ∠的度数为( )A .70︒B .75︒C .80︒D .85︒B解析:B【分析】 先由翻折的性质得到'AEN A EN ∠=∠,'BEM B EM ∠=∠,由图可得''''A EN B EM NEM A EB ∠+∠=∠+∠,然后根据180AEN NEM MEB ∠+∠+∠=︒,得到2''180NEM A EB ∠+∠=︒,进而可求出NEM ∠的度数.【详解】由翻折的性质可知:'AEN A EN ∠=∠,'BEM B EM ∠=∠,由图知:''''A EN B EM NEM A EB ∠+∠=∠+∠,又∵180AEN NEM MEB ∠+∠+∠=︒,∴''180A EN B EM NEM ∠+∠+∠=︒,∴2''180NEM A EB ∠+∠=︒,又∵''30A EB ∠=︒,∴75NEM ∠=︒.故选:B .【点睛】本题主要考查的是翻折的性质,掌握翻折的性质是解题的关键.10.矩形不一定具有的性质是( )A .对角线互相平分B .是轴对称图形C .对角线相等D .对角线互相垂直参考答案D解析:D【分析】根据矩形的性质即可判断.【详解】解:∵矩形的对角线线段,四个角是直角,对角线互相平分,∴选项A 、B 、C 正确,故选:D .【点睛】本题考查矩形的性质,解题的关键是记住矩形的性质.二、填空题11.如图,在平行四边形ABCD 中,2AD CD =,F 是AD 的中点,CE AB ⊥,垂足E 在线段AB 上.下列结论①DCF ECF ∠=∠;②EF CF =;③3DFE AEF ∠=∠;④2BEC CEF S S <中,一定成立的是_________.(请填序号)②③④【分析】如图延长EF 交CD 的延长线于H 作EN ∥BC 交CD 于NFK ∥AB 交BC 于K 利用平行四边形的性质全等三角形的判定和性质一一判断即可解决问题【详解】解:如图延长EF 交CD 的延长线于H 作EN ∥解析:②③④【分析】如图延长EF 交CD 的延长线于H .作EN ∥BC 交CD 于N ,FK ∥AB 交BC 于K .利用平行四边形的性质,全等三角形的判定和性质一一判断即可解决问题.【详解】解:如图,延长EF 交CD 的延长线于H .作EN ∥BC 交CD 于N ,FK ∥AB 交BC 于K . ∵四边形ABCD 是平行四边形,∴AB ∥CH ,∴∠A=∠FDH ,在△AFE 和△DFH 中,A FDH AFE HFD AF DF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AFE ≌△DFH ,∴EF=FH ,∵CE ⊥AB ,AB ∥CH ,∴CE ⊥CD ,∴∠ECH=90°,∴CF=EF=FH ,故②正确,∵DF=CD=AF ,∴∠DFC=∠DCF=∠FCB ,∵∠FCB >∠ECF ,∴∠DCF >∠ECF ,故①错误,∵FK ∥AB ,FD ∥CK ,∴四边形DFKC 是平行四边形,∵AD=2CD ,F 是AD 中点,∴DF=CD ,∴四边形DFKC 是菱形,∴∠DFC=∠KFC ,∵AE ∥FK ,∴∠AEF=∠EFK ,∵FE=FC ,FK ⊥EC ,∴∠EFK=∠KFC ,∴∠DFE=3∠AEF ,故③正确,∵四边形EBCN 是平行四边形,∴S △BEC =S △ENC ,∵S △EHC =2S △EFC ,S △EHC >S △ENC ,∴S △BEC <2S △CEF ,故④正确,故正确的有②③④.故答案为②③④.【点睛】本题考查平行四边形的性质、全等三角形的判定和性质、直角三角形斜边的中线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.12.如图,在菱形ABCD 中,6AC =,5AB =,点E 是直线AB ,CD 之间任意一点,连接AE ,BE ,DE ,CE ,则EAB 和ECD 的面积之和是______.12【分析】连接BD 根据菱形对角线的性质利用勾股定理计算BD 的长根据两平行线的距离相等所以△EAB 和△ECD 的面积和等于菱形ABCD 面积的一半再利用菱形面积等于对角线积的一半计算可得结论【详解】如图解析:12【分析】连接BD ,根据菱形对角线的性质,利用勾股定理计算BD 的长,根据两平行线的距离相等,所以△EAB 和△ECD 的面积和等于菱形ABCD 面积的一半,再利用菱形面积等于对角线积的一半计算可得结论.【详解】如图,连接BD 交AC 于O ,∵四边形ABCD 是菱形,∴AC ⊥BD ,OA=12AC=12×6=3, ∵AB =5,由勾股定理得:224AB OA -=,∴BD=2OB=8,∵AB ∥CD , ∴△EAB 和△ECD 的高的和等于点C 到直线AB 的距离,∴△EAB 和△ECD 的面积和=12×ABCD S 菱形=12×12×AC×BD=168=124⨯⨯. 故答案为:12.【点睛】本题考查菱形的性质,三角形的面积,平行线的性质,熟知平行线的距离相等,得△EAB 和△ECD 的高的和等于点C 到直线AB 的距离是解题的关键.13.在Rt ABC 中,∠C =90°,点D 是AB 边的中点,若AB =8,则CD =______.4【分析】根据直角三角形斜边上的中线等于斜边的一半可以得【详解】∵D 是AB 的中点∴∴故答案为:4【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质熟记性质是解题的关键解析:4.【分析】根据直角三角形斜边上的中线等于斜边的一半可以得2AB CD =.【详解】∵90C ∠=︒,D 是AB 的中点,∴2AB CD =, ∴118422CD AB ==⨯=. 故答案为:4.【点睛】 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,熟记性质是解题的关键.14.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是______________.30°【分析】根据矩形的性质得到AD∥BC∠DCB=90°根据平行线的性质得到∠F=∠ECB=20°根据三角形的外角的性质得到∠ACG=∠AGC=∠GAF+∠F=2∠F=40°于是得到结论【详解】解解析:30°【分析】根据矩形的性质得到AD∥BC,∠DCB=90°,根据平行线的性质得到∠F=∠ECB=20°,根据三角形的外角的性质得到∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,于是得到结论.【详解】解:∵四边形ABCD是矩形,∴AD∥BC,∠DCB=90°,∴∠F=∠ECB∵∠ECB=20°,∴∠F=∠ECB=20°,∵∠GAF=∠F,∴∠GAF=∠F=20°,∴∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,∴∠ACB=∠ACG+∠ECB=60°,∴∠ACD=90°﹣∠ACB=90°﹣60°=30°,故答案为:30°.【点睛】本题考查了矩形的性质,用到的知识点为:矩形的对边平行;两直线平行,内错角相等;三角形的一个外角等于和它不相邻的两个内角的和.15.正三角形ABC中,已知AB=6,D是直线AC上的动点,CE⊥BD于点E,连接AE,则AE长的取值范围是_______________.≤AE≤【分析】取BC中点O利用勾股定理以及直角三角形的性质分别求得AO和OE再利用三角形三边关系即可求解【详解】解:取BC中点O连接OAOE∵△ABC正三角形且AB=6∴AO⊥BCBO=OC=BC解析:333≤AE≤333【分析】取BC 中点O ,利用勾股定理以及直角三角形的性质分别求得AO 和OE ,再利用三角形三边关系即可求解.【详解】解:取BC 中点O ,连接OA 、OE ,∵△ABC 正三角形,且AB=6,∴AO ⊥BC ,BO=OC=12BC=12AB=3, ∴22226333AB BO -=-=,在△OAE 中,OA-OE<AE< OA+OE ,当O 、A 、E 在同一直线上时,取等号,∴OA-OE ≤AE ≤OA+OE , ∴333≤AE 333≤, 故答案为:333≤AE 333≤.【点睛】本题考查了等边三角形的性质,直角三角形的性质,三角形三边的关系,注意,直角三角形斜边上的中线等于斜边的一半.16.如图,在四边形ABCD 中,AC a =,BD b =,且AC BD ⊥顺次连接四边形ABCD 各边的中点,得到四边形1111D C B A ,再顺次连接四边形1111D C B A 各边中点,得到四边形2222A B C D …如此进行下去,得到四边形n n n n A B C D ,下列结论正确的有__________.①四边形2222A B C D 是矩形;②四边形4444A B C D 是菱形;③四边形5555A B C D 的周长是4a b +.②③【分析】利用三角形的中位线的性质证明四边形是矩形四边形是菱形四边形是矩形四边形是菱形从而可得到规律序号n 是奇数时四边形是矩形当序号n 是偶数时四边形是菱形再探究n 是奇数时四边形的周长即可解决问题【解析:②③【分析】利用三角形的中位线的性质证明四边形1111D C B A 是矩形,四边形2222A B C D 是菱形,四边形3333A B C D 是矩形,四边形4444A B C D 是菱形,从而可得到规律,序号n 是奇数时四边形是矩形,当序号n 是偶数时四边形是菱形,再探究n 是奇数时四边形的周长即可解决问题.【详解】解: 1111,,,A B C D 分别是,,,AB BC CD DA 的中点,1111111111//,,//,,22A B AC A B AC C D AC C D AC ∴== 11//,A D BD 11111111//,,A B C D A B C D ∴=∴ 四边形1111D C B A 是平行四边形,,AC BD ⊥ 11//,A B AC 11//,A D BD1111,A B A D ∴⊥∴ 四边形1111D C B A 是矩形,1111,AC B D ∴=如图,2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点,∴ 2211221111,,22A B AC A D B D == 四边形2222A B C D 是平行四边形, 2222,A B A D ∴=∴ 四边形2222A B C D 是菱形,故①不符合题意,2222,A C B D ∴⊥同理可得:四边形3333A B C D 是矩形,四边形4444A B C D 是菱形,故②符合题意,······总结规律:四边形n n n n A B C D , 当序号n 是奇数时四边形是矩形,当序号n 是偶数时四边形是菱形,111111111111,,2222A B C D AC a A D B C BD b ====== ∴ 四边形1111D C B A 的周长为,a b +如图, 四边形1111D C B A 是矩形,四边形2222A B C D 是菱形,2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点,222222112211,,,A C B D A C A D B D A B ∴⊥==由中位线的性质同理可得:33332233332211111111,,22242224A DBC BD a a D C A B A C b b ===⨯====⨯= 所以四边形3333A B C D 的周长为()1,2a b + 由规律可得:四边形5555A B C D 是矩形, 同理可得:四边形5555A B C D 的周长是()11.224a b a b +⨯+=故③符合题意. 故答案为②③.【点睛】本题考查三角形的中位线的性质,中点四边形,菱形的判定与性质,矩形的判定与性质,解题的关键是学会从特殊到一般,探究规律,利用规律解决问题.17.已知:如图,把长方形纸片ABCD 沿EF 折叠,使D C 、分别落在D C ''、的位置,若65EFB ︒∠=,则AED '∠的度数为_________.【分析】由长方形纸片可得再求解由折叠的性质求解结合平角的定义可得答案【详解】解:长方形纸片由折叠可得:故答案为:【点睛】本题考查的是矩形与折叠平行线的性质简单题解题的关键是理解折叠的性质 解析:50︒【分析】由长方形纸片ABCD ,65EFB ∠=︒可得//,AD BC 再求解,DEF ∠ 由折叠的性质求解,D EF '∠ 结合平角的定义可得答案.【详解】 解: 长方形纸片ABCD ,65EFB ∠=︒,//,AD BC ∴65DEF EFB ∴∠=∠=︒,由折叠可得:65D EF DEF '∠=∠=︒,180180656550.AED D EF DEF ''∴∠=︒-∠-∠=︒-︒-︒=︒故答案为:50.︒【点睛】本题考查的是矩形与折叠,平行线的性质,简单题,解题的关键是理解折叠的性质. 18.如图,在正方形ABCD 中,有面积为4的正方形EFGH 和面积为2的正方形PQMN 、点E F P Q 、、、分别在边AB BC CD AD 、、、上,点M N 、在边HG 上,且组成的图形为轴对称图形,则正方形ABCD 的面积为__________.【分析】连接交于交于交于依据轴对称图形的性质即可得到的长进而得到正方形的面积【详解】解:如图连接交于交于交于正方形中有面积为4的正方形和面积为2的正方形又组成的图形为轴对称图形为对称轴为等腰直角三角 解析:279242【分析】连接BD ,交PQ 于R ,交HG 于S ,交EF 于K ,依据轴对称图形的性质,即可得到BD 的长,进而得到正方形ABCD 的面积.【详解】解:如图,连接BD ,交PQ 于R ,交HG 于S ,交EF 于K ,正方形ABCD 中,有面积为4的正方形EFGH 和面积为2的正方形PQMN , 2EH EF ∴==,2MQ QP ==, 又组成的图形为轴对称图形, BD ∴为对称轴, BEF ∴∆、DPQ ∆为等腰直角三角形,四边形EKSH 、四边形MSRQ 为矩形, 112EK BK EF ∴===,11222DR QR PQ ===,2KN EH ==,2RS MQ ==, 1312223222BD ∴=+++=+, ∴正方形ABCD 的面积22113279(32)222242BD ==⨯+=+, 故答案为:279242+.【点睛】本题主要考查了轴对称图形,轴对称图形是针对一个图形而言的,是一种具有特殊性质图形,被一条直线分割成的两部分沿着对称轴折叠时,互相重合;轴对称图形的对称轴可以是一条,也可以是多条甚至无数条.19.如图,在平行四边形ABCD 中,BF 平分∠ABC ,交AD 于点F ,CE 平分∠BCD ,交AD 于点E ,AB =8,EF =1,则BC 长为__________.15【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB 得出AF=AB=8同理可得DE=DC=8再由EF 的长即可求出BC 的长【详解】解:∵四边形ABCD 是平行四边形∴AD ∥BCDC=AB=8A解析:15【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB ,得出AF=AB=8,同理可得DE=DC=8,再由EF 的长,即可求出BC 的长.【详解】解:∵四边形ABCD 是平行四边形,∴AD ∥BC ,DC=AB=8,AD=BC ,∴∠AFB=∠FBC ,∵BF 平分∠ABC ,∴∠ABF=∠FBC,则∠ABF=∠AFB,∴AF=AB=8,同理可证:DE=DC=8,∵EF=AF+DE-AD=1,即8+8-AD=1,解得:AD=15;故答案为:15.【点睛】本题主要考查了平行四边形的性质、等腰三角形的判定;熟练掌握平行四边形的性质,证出AF=AB是解决问题的关键.20.如图,正方形ABCD中,点E,F分别在BC和AB上,BE=2,AF=2,BF=4,将△BEF绕点E顺时针旋转,得到△GEH,当点H落在CD边上时,F,H两点之间的距离为______.【分析】根据旋转的可证明△BEF≌△CHE作FM⊥CD于M分别求出FMMH的长利用勾股定理即可求解【详解】∵将△BEF绕点E顺时针旋转得到△GEH点H落在CD边上∵BE=2AF=2BF=4∴GH=B解析:10【分析】根据旋转的可证明△BEF≌△CHE,作FM⊥CD于M,分别求出FM,MH的长,利用勾股定理即可求解.【详解】∵将△BEF绕点E顺时针旋转,得到△GEH,点H落在CD边上,∵BE=2,AF=2,BF=4∴GH=BF=EC=4,222425+=∴在Rt△HEC中,()22-=2542∴BE=CH又∵∠B=∠C=90°,BF=CE=4∴△BEF≌△CHE作FM⊥CD于M,故四边形AFMD是矩形,∴DM=AF=2,MH=CM-CH=2,FM=AD=6∴FH=22+=26210故答案为:210.【点睛】此题主要考查正方形的性质与全等三角形的判定与性质,解题的关键是熟知勾股定理、正方形的性质、矩形的性质及全等三角形的判定定理.三、解答题21.如图,四边形ABCD是矩形,对角线AC与BD相交于点O,∠AOD=60°,AD=2,求AC的长度.解析:4【分析】根据矩形的性质和等边三角形的性质,可以得到OA的长,从而可以求得AC的长.【详解】解:∵四边形ABCD是矩形,∴OA=OC=OB=OD,∵∠AOD=60°,AD=2,∴△AOD是等边三角形,∴OA=OD=2,∴AC=2OA=4,即AC的长度为4.【点睛】本题考查了矩形的性质,等边三角形的判定与性质,熟记性质并判断出△AOB是等边三角形是解题的关键.22.如图,过ABCD 对角线AC 与BD 的交点E 作两条互相垂直的直线,分别交边AB 、BC .CD 、DA 于点P 、M 、Q 、N .(1)求证:PBE QDE ≅△△;(2)顺次连接点P 、M 、Q 、N ,求证:四边形PMQN 是菱形.解析:(1)见解析;(2)见解析.【分析】(1)由ASA 证PBE QDE ≅△△即可;(2)由全等三角形的性质得出EP EQ =,同理可得EM EN =,根据对角线互相平分的四边形是平行四边形得四边形PMQN 是平行四边形,再由对角线互相垂直的平行四边形是菱形,即可得出结论.【详解】(1)证明:四边形ABCD 是平行四边形,EB ED ∴=,//AB CD ,EBP EDQ ∴∠=∠,在PBE △和QDE △中,EBP EDQ EB ED BEP DEQ ∠=∠⎧⎪=⎨⎪∠=∠⎩,()PBE QDE ASA ∴≅△△;(2)证明:如图所示:PBE QDE ≅△△,EP EQ ∴=,同理可得EM EN =,∴四边形PMQN 是平行四边形,PQ MN ⊥,∴四边形PMQN 是菱形.【点睛】本题考查了平行四边形的判定与性质,菱形的判定,全等三角形的判定与性质;熟练掌握菱形的判定和平行四边形的判定与性质,证明三角形全等是解题的关键.23.如图,已知点E 是ABCD 的边CD 延长线上的一点;连接AE ,BD ,且//AE BD ;过点E 作EF BC ⊥,交BC 的延长线于点F ,连接DF ;求证:DF DE =解析:见解析【分析】根据平行四边形的性质可得AB CD =,//AB CD ,然后结合题意利用两组对边分别平行的四边形是平行四边形可判定四边形ABDE 是平行四边形,然后利用平行四边形的性质和直角三角形斜边中线等于斜边一半证明求解.【详解】证明:∵四边形ABCD 是平行四边形,∴AB CD =,//AB CD ,又∵//AE BD∴四边形ABDE 是平行四边形;∴AB DE =,即CD DE =;又EF BC ⊥于点F ;∴∠EFC=90°∴在Rt CEF △中,点D 是斜边CE 的中点∴DF DE =.【点睛】本题考查平行四边形的性质和判定以及直角三角形斜边中线等于斜边的一半,掌握相关性质定理正确推理论证是解题关键.24.如图,平行四边形ABCD 中,,AP BP 分别平分DAB ∠和CBA ∠,交于DC 边上点P , 2.5AD =.(1)求线段AB 的长.(2)若3BP =,求ABP △的面积.解析:(1)5;(2)6【分析】(1)证出AD=DP=2.5,BC=PC=2.5,得出DC=5=AB ,即可求出答案;(2)根据平行四边形性质得出AD ∥CB ,AB ∥CD ,推出∠DAB+∠CBA=180°,求出∠PAB+∠PBA=90°,在△APB 中求出∠APB=90°,由勾股定理求出AP ,从而求得△ABP 的面积.【详解】解:(1)∵AP 平分∠DAB ,∴∠DAP=∠PAB ,∵四边形ABCD 是平行四边形,∵AB ∥CD ,∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP 是等腰三角形,∴AD=DP=2.5,同理:PC=CB=2.5,即AB=DC=DP+PC=5;(2)∵四边形ABCD 是平行四边形,∴AD ∥CB ,AB ∥CD ,∴∠DAB+∠CBA=180°,又∵AP 和BP 分别平分∠DAB 和∠CBA ,∴∠PAB+∠PBA=12(∠DAB+∠CBA )=90°, 在△APB 中,∠APB=180°-(∠PAB+∠PBA )=90°;在Rt △APB 中,AB=5,BP=3,∴,∴△APB 的面积=4×3÷2=6.【点睛】本题考查了平行四边形的性质,平行线的性质,等腰三角形的性质和判定,三角形的内角和定理,勾股定理等知识点的综合运用.25.如图,BD 为ABC 的角平分线,E 为AB 上一点,BE BC =,连结DE . (1)求证:BDC BDE ≅△△;(2)若7AB =,2CD =,90︒∠=C ,求ABD △的面积.解析:(1)证明见解析;(2)7【分析】(1)根据角平分线的性质可得DBC DBE ∠=∠,再根据已知条件BE BC =,BD BD =,即可证明;(2)根据(1)中结果,得2DE CD ==,90DEB C ∠=∠=︒,即可求得ABD △的面积.【详解】(1)∵BD 平分ABC ∠,∴DBC DBE ∠=∠,∴在BDC 和BDE 中,BD BD =,DBC DBE ∠=∠,BE BC =,∴BDC ≌BDE ;(2)∵BDC ≌BDE ,∴2DE CD ==,90DEB C ∠=∠=︒, ∴1172722ABD S AB DE =⋅=⨯⨯=△. 【点睛】本题考查了角平分线的性质、全等三角形的证明和性质、三角形面积等知识,解题的关键是熟练掌握运用以上知识点.26.如图,在ABC 中,AB AC =,10BC =.(1)尺规作图:(要求:保留作图痕迹,不写作法)①作BAC ∠的平分线交BC 于点D ;②作边AC 的中点E ,连接DE ;(2)在(1)所作的图中,若12AD =,则DE 的长为__________.解析:(1)①见解析;②见解析;(2)6.5(1)①以A 为圆心,小于AB 的长度为半径画圆,交AB 、AC 于两个点,再分别以这两个点为圆心,一样的半径画弧,交于一点,连接这个点与点A ,即可得到BAC ∠的平分线,再画出它与BC 的交点D ;②作线段AC 的垂直平分线,即可找到线段AC 的中点E ,连接DE ;(2)由等腰三角形“三线合一”的性质得152BD BC ==,AD BC ⊥,用勾股定理求出AB 的长,再根据中位线的性质得到DE 的长.【详解】解:(1)①如图所示:②如图所示:(2)∵AB AC =,AD 平分BAC ∠,∴152BD BC ==,AD BC ⊥, 在Rt ABD △中,2213AB AD BD =+=, ∵E 、D 分别是AC 和BC 的中点,∴1 6.52DE AB ==, 故答案是:6.5.【点睛】 本题考查等腰三角形的性质,中位线的定理,以及角平分线和垂直平分线的作法,解题的关键是熟练掌握这些几何的性质定理以及作图方法.27.(问题提出)小颖发现某座房屋的侧面是一种特殊的五边形,她决定好好研究一下它的特点,并计算它(问题探究)定义:如图()1,我们把满足,,90AB AE CB DE C D ︒==∠=∠=的五边形ABCDE 叫做屋形.其中,AB AE 叫做脊,,BC DE 叫做腰,CD 叫做底.性质:边:屋形的腰相等,脊相等;角:①屋形腰与底的夹角相等;②脊与腰的夹角相等;对角线:①②屋形有两组对角线分别相等,且其中一组互相平分.对称性:屋形是以底的垂直平分线为对称轴的轴对称图形;(1)请直接填写屋形对角线的性质①;(2)请你根据定义证明“屋形的脊与腰的夹角相等”;己知:如图,五边形ABCDE 是屋形.求证:证明:(问题解决)(3)如图,在屋形ABCDE 中,若5,8,6AB BC CD ===,试求出屋形ABCDE 的面积.解析:(1)屋形有一条对角线与底平行且相等;(2)见解析;(3)60【分析】(1)根据屋形的特点可得结论;(2)连接BE ,证明四边形BCDE 为平行四边形,再根据+CBE ABE DEB AEB ∠=∠+得出结论;(3)连接BE ,过A 作AH BE ⊥,先利用勾股定理得出AH 的值,再利用三角形和矩形的面积公式求解即可.【详解】解:(1)屋形有一条对角线与底平行且相等(2)求证:屋形的脊与腰夹角相等证明:连接BEAB AE =,ABE AEB ∴∠=∠,C D ∠=∠,//BC DE ∴,又BC DE =,∴四边形BCDE 为平行四边形,90CBE DEB ︒∴∠=∠=∵ABE AEB ∠=∠,∴+CBE ABE DEB AEB ∠=∠+,ABC AED ∴∠=∠.【问题解决】连接BE ,过A 作AH BE ⊥,5AB =,5AE ∴=,,AH BE AB AE ⊥=,142BH EH BE ∴===, 2222543AH AB BH ∴=--=,∴BE=2BH=6,183122ABE S ∆∴=⨯⨯=, BCDE 8648S =⨯=矩,481260+=,∴屋形ABCDE 的面积为60.【点睛】本题考查了平行四边形的判定与性质及勾股定理,解题的关键是正确作出辅助线. 28.如图,已知四边形ABCD 是平行四边形,E 是AB 延长线上一点且BE AB =,连接CE ,BD .(1)求证:四边形BECD 是平行四边形(2)连接DE ,若4AB BD ==,22DE =,求BECD 的面积.解析:(1)见解析;(2)47BECD S =菱形 【分析】(1)根据四边形ABCD 是平行四边形,得到AB CD =,//AB CD ,再根据BE AB =,得到BE CD =,利用一组对边平行且相等的四边形BECD 是平行四边形去判定.(2)先利用已知条件证四边形BECD 是菱形,再在Rt BOE △中,利用勾股定理求BO ,进而求BC ,则可求菱形面积.【详解】解:(1)∵四边形ABCD 是平行四边形,∴AB CD =,//AB CD ,又∵BE AB =,∴BE CD =,//BE CD ,∴四边形BECD 是平行四边形.(2)如图,连接DE ,交BC 于点O ,∵4AB BD ==,BE AB =,∴4BD BE ==,由(1)得四边形BECD 是平行四边形,∴BECD 是菱形,∴DE BC ⊥,∵DE =∴12OE DE ==,在Rt BOE △中,BO === ∴2BC BO ==∴1122BECD S BC DE =⋅=⨯=菱形 【点睛】 本题考查了平行四边形、菱形性质和判定的综合应用,熟练掌握相关知识是解答此题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形综合提高一利用平行四边形的性质进行角度、线段的计算1、如图,在□ABCD中,AE⊥BC于E,AF⊥CD于F,若∠EAF=60o,则∠B=_______;若BC=4cm,AB=3cm,则AF=___________,□ABCD的面积为_________.2已知ABCD的周长为32cm,对角线AC、BD交于点O,△AOB的周长比△BOC的周长多4cm,求这个四边形的各边长。
二、利用平行四边形的性质证线段相等3、如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF⊥AC,垂足分别为E、F.那么OE与OF是否相等?为什么?三直接利用平行四边形的判定和性质4、如图在ABCD中,E、F分别是AD、BC的中点,AF与EB交于点G,CE与DF交于点H,试说明四边形EGFH的形状。
5、如图,BD是ABCD的对角线,AE⊥BD于E,CF⊥BD于点F,求证:四边形AECF为平行四边形。
四构造平行四边形解题6、如图2-33所示.Rt△ABC中,∠BAC=90°,AD⊥BC于D,BG平分∠ABC,EF∥BC且交AC于F.求证:AE=CF.7、已知,如图,AD为△ABC的中线,E为AC上一点,连结BE交AD于点F,且AE=FE,求证:BF=AC[能力提高]1、如图2-39所示.在平行四边形ABCD中,△ABE和△BCF都是等边三角形.求证:△DEF是等边三角形.2、如图2-32所示.在ABCD中,AE⊥BC,CF⊥AD,DN=BM.求证:EF与MN互相平分.3、如图2-34所示.ABCD中,DE⊥AB于E,BM=MC=DC.求证:∠EMC=3∠BEM.4 如图2-35所示.矩形ABCD中,CE⊥BD于E,AF平分∠BAD交EC延长线于F.求证:CA=CF.[创新思维]1、以△ABC 的三条边为边在BC 的同侧作等边△ABP 、等边△ACQ 、等边△BCR , 求证:四边形PAQR 为平行四边形。
2.如图2-40所示.ABCD 中,AF 平分∠BAD 交BC 于F ,DE ⊥AF 交CB 于E .求证:BE=CF .3、已知:如图4-12, ABCD 中,AE ⊥BD ,CF ⊥BD ,M ,N 分别是AD ,BC 的中点. 求证:四边形MENF 是平行四边形.4.已知:如图4-23,P 是等边△ABC 一点,PD ∥AB ,PE ∥BC ,PF ∥AC .求证:PD+PE+PF 为定值.5.在等腰△ABC 中,AB =AC ,点D 是直线BC 上一点,DE ∥AC 交直线AB 于E ,DF ∥AB 交直线AC 于点F ,解答下列各问:(1)如图1,当点D 在线段BC 上时,有DE +DF =AB ,请你说明理由;(6分)(2)如图2,当点D 在线段BC 的延长线上时,请你参考(1)画出正确的图形,并写出线段DE 、AF BCDE P AFEADF 、AB 之间的关系并加以证明.(图1) (图2)6.如图2-38所示.DE ⊥AC ,BF ⊥AC ,DE=BF ,∠ADB=∠DBC .求证:四边形ABCD 是平行四边形.7、已知:如图,在□ ABCD 中,AE ⊥AD 交BD 于E .若CD=DE 21,求证:∠ADB=21∠BDC8、已知:如图4-21,在 ABCD 中,△ABE 和△BCF 都是等边三角形.求证:△DEF 是等边三角形.1.如图,已知四边形ABCD 为平行四边形,AE⊥BD 于E ,CF⊥BD 于F . (1)求证:BE=DF ;(2)若 M 、N 分别为边AD 、BC 上的点,且DM=BN ,试判断四边形MENF 的形状(不必说明理由).DCA BE2.如图所示,▱AECF的对角线相交于点O,DB经过点O,分别与AE,CF交于B,D.求证:四边形ABCD是平行四边形.3.如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.(1)求证:△ABE≌△CDF;(2)若AC与BD交于点O,求证:AO=CO.4.已知:如图,在△ABC中,∠BAC=90°,DE、DF是△ABC的中位线,连接EF、AD.求证:EF=AD.5.如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.6.如图,已知,▱ABCD中,AE=CF,M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形.7.如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:四边形AECF是平行四边形.8.在▱ABCD中,分别以AD、BC为边向作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.9.如图所示,DB∥AC,且DB=AC,E是AC的中点,求证:BC=DE.10.已知:如图,在梯形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P自点A向D以1cm/s 的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ 截梯形为两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?11.如图:已知D、E、F分别是△ABC各边的中点,求证:AE与DF互相平分.12.已知:如图,在▱ABCD中,对角线AC交BD于点O,四边形AODE是平行四边形.求证:四边形ABOE、四边形DCOE都是平行四边形.13.如图,已知四边形ABCD中,点E,F,G,H分别是AB、CD、AC、BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分.14.如图:▱ABCD中,MN∥AC,试说明MQ=NP.15.已知:如图所示,平行四边形ABCD的对角线AC,BD相交于点O,EF经过点O并且分别和AB,CD相交于点E,F,点G,H分别为OA,OC的中点.求证:四边形EHFG是平行四边形.16.如图,已知在▱ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在△ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证:AF=CE;(2)如果AC=EF,且∠ACB=135°,试判断四边形AFCE是什么样的四边形,并证明你的结论.18.如图平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2(1)求证:D是EC中点;(2)求FC的长.19.如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠E FB=60°,DC=EF.(1)求证:四边形EFCD是平行四边形;(2)若BF=EF,求证:AE=AD.20.如图,四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点.(1)请判断四边形EFGH的形状?并说明为什么;(2)若使四边形EFGH为正方形,那么四边形ABCD的对角线应具有怎样的性质?21.(2008•)如图,△ACD、△ABE、△BCF均为直线BC同侧的等边三角形.(1)当AB≠AC时,证明:四边形ADFE为平行四边形;(2)当AB=AC时,顺次连接A、D、F、E四点所构成的图形有哪几类?直接写出构成图形的类型和相应的条件.22.如图,以△ABC的三边为边,在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,那么,四边形AFED是否为平行四边形?如果是,请证明之,如果不是,请说明理由.23.(2007•)在△ABC中,AB=AC,点P为△ABC所在平面一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.请直接应用上述信息解决下列问题:当点P分别在△ABC(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.24.(2006•)如图1,P为Rt△ABC所在平面任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE.探究:(1)请猜想与线段DE有关的三个结论;(2)请你利用图2,图3选择不同位置的点P按上述方法操作;(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明;如果你认为你写的结论是错误的,请用图2或图3加以说明;(注意:错误的结论,只要你用反例给予说明也得分)(4)若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE 有关的结论(直接写答案).25.(2005•)在一次数学实践探究活动中,小强用两条直线把平行四边形ABCD分割成四个部分,使含有一组对顶角的两个图形全等;(1)根据小强的分割方法,你认为把平行四边形分割成满足以上全等关系的直线有_________ 组;(2)请在图中的三个平行四边形中画出满足小强分割方法的直线;(3)由上述实验操作过程,你发现所画的两条直线有什么规律?26.如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P 从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.(1)求CD的长;(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.27.已知平行四边形的三个顶点的坐标分别为O(0,0)、A(2,0)、B(1,1),则第四个顶点C的坐标是多少?28.已知平行四边形ABCD的周长为36cm,过D作AB,BC边上的高DE、DF,且cm,,求平行四边形ABCD的面积.29.如图,在平面直角坐标系中,已知O为原点,四边形ABCD为平行四边形,A、B、C的坐标分别是A(﹣3,),B(﹣2,3),C(2,3),点D在第一象限.(1)求D点的坐标;(2)将平行四边形ABCD先向右平移个单位长度,再向下平移个单位长度所得的四边形A1B1C1D1四个顶点的坐标是多少?(3)求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积?30.如图所示.▱ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.第10题图平行四边形及特殊平行四边形1.下列说法不正确...的是( ) A .一组邻边相等的矩形是正方形 B .对角线相等的菱形是正方形C .对角线互相垂直的矩形是正方形D .有一个角是直角的平行四边形是正方形 2.(2010 )下列说法中,你认为正确的是( )A .四边形具有稳定性B .等边三角形是中心对称图形C .任意多边形的外角和是360oD .矩形的对角线一定互相垂直3.(2010 )下列命题中正确的是( )A .对角线相等的四边形是菱形B .对角线互相垂直的四边形是菱形C .对角线相等的平行四边形是菱形D .对角线互相垂直的平行四边形是菱形 4.(2010襄樊)菱形的周长为8cm ,高为1cm ,则菱形两邻角度数比为( ) A .3:1B .4:1C .5:1D .6:15.(2010回族自治区)点A 、B 、C 是平面不在同一条直线上的三点,点D 是平面任意一点,若A 、B 、C 、D 四点恰能构成一个平行四边形,则在平面符合这样条件的点D 有 ( ) A .1个 B .2个C .3个D .4个6.(2010 江津)四边形ABCD 的对角线互相平分,要使它成为矩形,那么需要添加的条件是( ) A .AB CD =B .AD BC =C .AB BC =D .AC BD =7. (2010 )已知四边形ABCD ,有以下四个条件:①//AB CD ;②AB CD =;③//BC AD ;④BC AD =.从这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法种数共有( )A .6种B .5种C .4种D .3种8.(2010)如图6,在□ABCD 中,AB=6,AD=9,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG⊥AE,垂足为G ,BG=24,则ΔCEF 的周长为( ) A .8 B .9 C .10 D .1114题图GFEDCBA 9.(2010)如图,在菱形ABCD 中,DE⊥AB,3cos 5A =,BE=2,则tan∠DBE 的值是( ) A .12B .2 CD10.(2010 荷泽) 如图,菱形ABCD 中,∠B=60°,AB =2㎝,E 、F 分别是BC 、CD 的中点,连结AE 、EF 、AF ,则△AEF 的周长为( ) A .32㎝B .33㎝C .34㎝D .3㎝11.(2010) 矩形ABCD 中,E 、F 、M 为AB 、BC 、CD 边上的点, 且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则EM 的长为( ) A .5 B .25 C .6 D .2612.(2010聊城)如图,点P 是矩形ABCD 的边AD 的一个动点,矩形的两条边AB 、BC 的长分别为3和4,那么点P 到矩形的两条对角线AC 和BD 的距离之和是( ) A .125B .65C .245D .不确定13.若菱形两条对角线的长分别为6和8,则这个菱形的周长为( )A .20B .16C .12D . 1014.(2010 )已知:如图,在正方形ABCD 外取一点E ,连接AE ,BE ,DE .过点A 作AE 的垂线交ED 于点P .若1AE AP ==,PB①△APD ≌△AEB ;②点B 到直线AE; ③EB ED ⊥;④1APD APB S S ∆∆+=+4ABCD S =正方形 其中正确结论的序号是( )A .①③④ B.①②⑤ C.③④⑤ D .①③⑤15.(2010 )如图,将一正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;...,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( ) A .669 B .670 C .671 D . 672第15题A BCDMNA 'B '20题16.(2010)正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示,点G 在线段DK 上,正方形BEFG 的边长为4,则DEK ∆的面积为( ) A .10B .12C .14D .1617.(2010綦江县)如图,在ABCD 中,分别以AB 、AD 为边向外作等边△ABE、△ADF,延长CB 交AE 于点G ,点G 在点A 、E 之间,连结CG 、CF ,则以下四个结论一定正确的是( ) ①△CDF≌△EBC②∠CDF=∠EAF③△ECF 是等边三角形④CG⊥AEA .只有①② B.只有①②③ C .只有③④ D .①②③④18.(2010)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是( ).A .2+10B .2+210C .12D .1819.(2010)如图,已知矩形纸片ABCD ,点E 是AB 的中点,点G 是BC 上的一点,∠BEG>60°,现沿直线EG 将纸片折叠,使点B 落在纸片上的点H 处,连接AH ,则与∠BEG 相等的角的个数为( )A .4B .3C .2D .120.(2010)如图(上页),四边形ABCD 是边长为9的正方形纸片,将其沿MN 折叠,使点B 落在CD 边上的B '处,点A 对应点为A ',且C B '=3,则AM 的长是( ) A .1.5 B .2 C .2.25 D .2.521.(2010)如图(上页)是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知B AGCDHE第19题图②34yx第21题图第27题A BDOE 大正方形面积为49,小正方形面积为4,若用x ,y 表示直角三角形的两直角边(x y >),下列四个说法:①2249x y +=,②2x y -=,③2449xy +=,④9x y +=.其中说确的是( ) A .①② B. ①②③ C. ①②④ D. ①②③④22.(2010)如图,四边形ABCD 中,AB//CD ,要使四边形ABCD 为平行四边形,则可添加的条件为 .(填一个即可).23(2010荆州)如图,在平行四边形ABCD 中,∠A=130°,在AD 上取DE=DC ,则∠ECB 的度数是 .24.(2010 )如图,P 是菱形ABCD 对角线BD 上一点,PE⊥AB 于点E ,PE =4cm ,则点P 到BC 的距离是_____cm.25.(2010)如图,在□ABCD 中,AE =EB ,AF =2,则FC 等于_____.26.(2010)如图,在□ABCD 中,对角线AC 、BD 相交于点O ,如果AC=14,BD=8,AB=x ,那么x 的取值围是 .27.(2010)如图,已知菱形ABCD 的一个角︒=∠80BAD ,对角线AC 、BD 相交于点O ,点E 在AB 上,且BO BE =,则EOA ∠= 度.28.(2010)过□ABCD 对角线交点O 作直线m ,分别交直线AB 于点E ,交直线CD 于点F ,若AB=4,AE=6,则DF 的长是 .29.(2010 )如图,已知正方形ABCD 的边长为3,E 为CD 边上一点, 1DE =.以点A 为中心,把△ADE 顺时针旋转90︒,得△ABE ',连接EE ',则EE '的长等于 .30.(2010)如图,边长为6的正方形ABCD 绕点B 按顺时针方向旋转30°后得到正方形EBGF ,EF 交CD 于点H ,则FH 的长为______(结果保留根号)。
