中考几何专题复习-手拉手模型-旋转全等型
完整word版中考专题复习几何题用旋转构造手拉手模型

中考专题复习——几何题用旋转构造“手拉手”模型一、教学目标:,归纳掌握其基本特征.1.了解并熟悉“手拉手模型”,利用旋转构造全等解决相关问题.2.借助“手拉手模型”举一反三,解决求定值,定角,最值等一类问题.3.二、教学重难点:,学会用旋转构造全等.1.挖掘和构造“手拉手模型”用旋转构造全等的解题方法最优化选择.2.三、教学过程:D 1.复习旧知EH为等边三角形,从中你能得出师:如图,△ABD,△BCE GF哪(1)△ABE CAB 4)△BFG为等边三角形CFB (3)些结论?DBFDBC≌△(2)△ABG≌△生:△≌△EGB (……)BH平分∠AHCB,F,四点共圆(8G7=6DGH)(5△AGB∽△()∠DHA60°()H,,这两个全等的三角形除了对应边相等,对应角相等外,与△DBC师:我们再来重点研究△ABE 还有什么共同特征呢?.B,即同一个顶点B生:它们有同一个字母经过怎样的图形运动得到?看作由△ABE师:我们也可以把△DBC 60°得到.生:绕点B顺时针旋转2.引入新课,谁可以将这个模型的师:其实我们可以给这两个全等的三角形赋予一个模型,叫“手拉手模型”特征再做进一步的简化归纳呢?生:对应边相等.师:我们可以称之为“等线段”.生:有同一个顶点..师:我们可以称之为“共顶点”师:等线段,共顶点的两个全等三角形,我们一般可以考虑哪一种图形运动?生:旋转.“手拉手模型”可以归纳为:等线段,共顶点,一般用旋转.师:3.小题热身3图1图2图.=____BECAD于,则AF°,AB=AD,AE⊥BD于E,BC⊥4511.如图,△BAD中,∠BAD=.=______AECE=4,则ABC△和△BED均为等边三角形,ADE三点共线,若BE=2,2.如图2,.=_______=5,则EFBEEAF=45°,=3,DF,正方形3.如图3ABCD中,∠题,这里面有“手拉手模型”吗?请你找出其中的“等线段,共顶点”.2师:我们来看第1,第BCD.C逆时针旋转90°得△AC,BC,共顶点是C,△ACF绕点生:题1中,等线段是.60°得△CBEB,△ABD绕点D顺时针旋转,共顶点是题2中,等线段是AB,BC 题,这里有“手拉手模型”吗?师:我们再来看第3 生:没有.师:那其中有没有“等线段,共顶点”呢?.,共顶点是A生:等线段是AD,AB 师:我们可否利用旋转来构造“手拉手模型”呢?90°.AE旋转,绕点A逆时针旋转生:将90°,你是如何思考的?师:为什么是逆时针旋转逆AE,那么将ADAB绕点A逆时针旋转90°即为全等的三角形,生:我准备构造一个和△ABE GD,证明全等.AG时针旋转90°可得,连接师:说的不错,谁能再来归纳一下,借助“手拉手模型”,用旋转构造全等的方法吗?“共顶点”的线段,将其旋转.生:先找有没有“等线段,共顶点”,再找其中一条师:旋转角度如何确定,方向怎么选择?生:选择其中一个三角形,将“共顶点”的线段旋转.旋转角为两条“等线段”间的夹角.方向应与所选择的起始“等线段”旋转到另一条“等线段”时的方向一致.师:非常棒,可以说,你已经掌握了这节课的精髓.但是,很多题目中只是隐含了“手拉手模型”的一些条件,剩余的需要我们自己去构造,可以如何构造呢?.步骤1:先找有没有“等线段,共顶点”“共顶点”的线段旋转.:选择其中一个三角形,将其中经过2步骤.:旋转方向与这个三角形的“等线段”旋转到另一条“等线段”的方向一致,旋转角为“等步骤3 线段”间的夹角.师:这道题还有一个要注意的地方,你发现了吗?F三点共线.G,D,生:连接GD后,要证明4.例题精讲A度数.,求∠ADC,DC=3,BD=5:等边△例1ABC中,AD =4 师:这里有没有隐含的“手拉手模型”?D要构造全等,该怎样旋转?CB生:将△ADC绕点A顺时针旋转60°.师:你是怎么想的,还有其他做法吗?A,A为“共顶点”,我选择的旋转线段生:我发现AB=AC E也要绕,所以△ADC60是AD,因为AC绕点A顺时针旋转°到AB D°.点A顺时针旋转60°.也可将△ADB绕点A逆时针旋转60BC【解答】≌△也为等边三角形.易证△AEBBE,DE.则△ADE绕点将ADA顺时针旋转60°到AE,连接°AEB=∠ADC=150BE=DC=4,根据勾股定理逆定理,可证∠BED=90°,则∠,∴ADCCOD=?AOB?2:如图,△ABO和△CDO均为等腰直角三角形,例DA的长度为OD BC试求以AD、、OC+BOC=90?.若△的面积为1,三边长的三角形的面积.O师:由于线段分散,如何通过图形变换,使这些线段能构成一个三角CB形?即是以△BCE,即可使OC,OD共线,再通过证明确定O生:将OD绕点逆时针旋转90°至OE 的长度为三边长的三角形.、BCOC+ODAD、【解答】D.易证OE,连接BE如图,将OD 绕点O逆时针旋转90°至A OD+、OCBCBCEADOAD△≌△OBE,=BE,∴△即是以AD、E.=22=SOEOC长度为三边长的三角形.又∵=,∴S BOC△BCE△O CB5.自主练习DA ACBABC=∠,CD=3,∠1.如图,在四边形ABCD中,AD=4 .45°,则BD的长为_________=∠ADC=,并写出解决方法.师:请找出隐含的“手拉手模型”BC绕点ADA.方法是将CA生:“等线段”是和BA,“共顶点”是°.顺时针旋转90A E为边,向外做正方,以ABC2.如图,在△中,BC=2,ABAC=2 .BE形ACDE,连接,则BE最大值为_________D师:请找出隐含的“手拉手模型”,并写出解决方法.A.EA,“共顶点”是A生:“等线段”是CA和C A逆时针旋转90°.方法是将AB绕点B师:你为何要逆时针旋转,你准备旋转哪个三角形?°.也绕点生:△ABC,因为AC是逆时针旋转90°到AE,所以ABA逆时针旋转90是等边三角形,BCB上,AB=1,=2,△ACDA3.如图,点在⊙D面积的最大值.求△BCD ,并写出解决方法.师:请找出隐含的“手拉手模型”A C.CA和CD,“共顶点”是“等线段”是生:BC°.C逆时针旋转60方法是将CA绕点附:自主练习解答E≌△EACAD1.如图,将绕点A顺时针旋转90°至AE,易证△°,DAB,可得CE=BD,又∵∠=90=45°,∴∠CDEEDA DA2222+3CDCDEDECD=3,=24,则Rt△中,CE=+DE=241 =(42)CB41 DB,∴=41∴CE=,≌△EAFCAB,易证△°至绕点如图,将2.ABA逆时针旋转90AF E.由三,∴ABAFBAFRt2BCEF 可得==.△中,==2BF2=D4. BEBF+EFBE角形三边关系易知,≤,∴最小值为F ABC.CBDE,过点E作EF⊥C3.如图,将CB绕点逆时针旋转60°至CE,连接D,=3,CBA≌CED 则DE=1,EF△于作F于,过点DDG⊥CBG.易证E边上的高,可证作DGDG<DE+EF.过E A S,.=,当D,EF三点共线时,DGDE+EF即高的最大值为1+3BCDmax△ GCBF13 3×(×=21+)=+12DEABFC.。
2020年中考备考专题复习讲义------手拉手模型(PDF版无答案)

手拉手模型类型一、旋转型全等1.等边三角形条件:如图1,△OAB ,△OCD 均为等边三角形.结论:①△OAC ≌△OBD ;②∠AEB =60°;③EO 平分∠AED .④O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:如图2,∵△OAB ,△OCD 均为正△∴OA=OB ,OC =OD ,∠AOB =∠COD =60°∴∠AOB+∠BOC =∠COD+∠BOC ∴∠AOC=∠BOD ∴△OAC ≌△OBD∴∠OAC=∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO=120°∴∠AEB =60°作OM 、ON 分别⊥AC 、BD 于点M 、N∵S △OAC =S △OBD ,AC =BD∴OM =ON∴EO 平分∠AED ∴∠OEA =∠OED =∠OBA =∠OCD =60°∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆;点E 为△OBC 的费马点(仅图2)2.等腰直角三角形条件:如图3,△OAB ,△OCD 均为等腰直角三角形.结论:①△OAC ≌△OBD ;②∠AEB =90°;③EO 平分∠AED.④O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:如图4,∵△OAB ,△OCD 均为等腰Rt △∴OA=OB ,OC =OD ,∠AOB =∠COD =90°∴∠AOB+∠BOC =∠COD+∠BOC ∴∠AOC=∠BOD ∴△OAC ≌△OBD ∴∠OAC=∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO=90°∴∠AEB =90°作OM 、ON 分别⊥AC 、BD 于点M 、N∵S △OAC =S △OBD ,AC =BD ∴OM =ON ∴EO 平分∠AED∴∠OEA =∠OED =∠OBA =∠OCD =45°∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆(四边形OMEN 是正方形)OB DAC EO BD A C E图1OB DACE OBD ACE图3O B DA CE N M 图2OBD A CEN M 图43.任意等腰三角形条件:如图5,△OAB ,△OCD 均为等腰三角形,OA=OB ,OC=OD ,∠AOB=∠COD.结论:①△OAC ≌△OBD ;②∠AEB=∠AOB ;③EO 平分∠AED.④O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:证明:如图6,∵OA=OB ,OC=OD ,∠AOB=∠COD∴∠AOB+∠BOC =∠COD+∠BOC∴∠AOC=∠BOD ∴△OAC ≌△OBD∴∠OAC=∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO∴∠AEB =∠AOB作OM 、ON 分别⊥AC 、BD 于点M 、N∵S △OAC =S △OBD ,AC =BD ∴OM =ON∴EO 平分∠AED∴∠OEA =∠OED =∠OBA =∠OCD∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆模型二、旋转型相似1.一般情况条件:如图7,CD //AB ,将△OCD 旋转至右图位置.结论:①△OCD ∽△OAB ,△OAC ∽△OBD ;②延长AC 交BD 于点E ,则∠BEC=∠BOA.③O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆证明:∵CD //AB ,旋转∴△OCD ∽△OAB ,∠COD =∠AOB∴∠COD -∠COB =∠AOB -∠COB ,OC :OA =OD :OB ∴∠AOC =∠BOD ∴△OAC ∽△OBD∴∠OAC =∠OBD∴∠BAE+∠ABE=∠OAB -∠OAC+∠ABO+∠OBD=∠OAB+∠ABO ∴∠BEC=∠BOA=∠DOC ∴O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆2.特殊情况条件:如图9,CD //AB ,∠AOB=90°,将△OCD 旋转至右图位置.结论:右图中①△OCD ∽△OAB ,△OAC ∽△OBD ;②连接AC ,BD 交于点E ,则∠BEC =∠BOA ;③BD AC =OD OC =OBOA =tan ∠OCD ;④BD ⊥AC ;⑤连接AD ,BC ,则AD 2+BC 2=AB 2+CD 2;⑥S 四边形ABCD =12AC ·BD (对角线互相垂直的四边形).⑦O 、A 、B 、E 四点共圆,O 、D 、C 、E 四点共圆(证明可参考以上方法)O BDA CE OBD A CE图5OB D ACOB D ACE 图9OB D AC OBD AC图7E O B DACENM 图6OBD AC图8E中考真题1.[2019·滨州]如图,在△OAB 和△OCD 中,OA =OB ,OC =OD ,OA >OC ,∠AOB =∠COD =40°,连接AC ,BD 交于点M ,连接OM .下列结论:①AC =BD ;②∠AMB =40°;③OM 平分∠BOC ;④MO 平分∠BMC .其中正确的个数为()DBCAMOA .4B .3C .2D .12.[2018·东营]如图,点E 在△DBC 的边DB 上,点A 在△DBC 内部,∠DAE =∠BAC =90°,AD =AE ,AB =AC .给出下列结论:①BD =CE ;②∠ABD +∠ECB =45°;③BD ⊥CE ;④BE 2=2(AD 2+AB 2)﹣CD 2.其中正确的是()DBCAEA .①②③④B .②④C .①②③D .①③④3.[荆门]如图,点A ,B ,C 在一条直线上,△ABD ,△BCE 均为等边三角形,连接AE 和CD ,AE 分别交CD ,BD 于点M ,P ,CD 交BE 于点Q ,连接PQ ,BM ,下面结论:①△ABE ≌△DBC ;②∠DMA =60°;③△BPQ 为等边三角形;④MB 平分∠AMC ,其中结论正确的有()CDB MAEQPA .1个B .2个C .3个D .4个4.[2016·贺州]如图,在△ABC 中,分别以AC 、BC 为边作等边三角形ACD 和等边三角形BCE ,连接AE 、BD 交于点O ,则∠AOB 的度数为.DC AEBO5.[2018·包头]如图,在Rt △ACB 中,∠ACB =90°,AC =BC ,D 是AB 上的一个动点(不与点A ,B 重合),连接CD ,将CD 绕点C 顺时针旋转90°得到CE ,连接DE ,DE 与AC 相交于点F ,连接AE .下列结论:①△ACE ≌△BCD ;②若∠BCD =25°,则∠AED =65°;③DE 2=2CF ·CA ;④若AB =32,AD =2BD ,则AF =53.其中正确的结论是.(填写所有正确结论的序号)D CA EBF6.[柳州]如图,在△ABC 中,分别以AC ,BC 为边作等边△ACD 和等边△BCE .设△ACD 、△BCE 、△ABC 的面积分别是S 1、S 2、S 3,现有如下结论:①S 1:S 2=AC 2:BC 2;②连接AE ,BD ,则△BCD ≌△ECA ;③若AC ⊥BC ,则S 1·S 2=34S 32.其中结论正确的序号是.DCA EB7.[2019·宜宾]如图,△ABC 和△CDE 都是等边三角形,且点A 、C 、E 在同一直线上,AD 与BE 、BC 分别交于点F 、M ,BE 与CD 交于点N .下列结论正确的是(写出所有正确结论的序号).①AM =BN ;②△ABF ≌△DNF ;③∠FMC +∠FNC =180°;④1MN =1AC +1CEA DCF EBMN8.[2019·襄阳]如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点C ,点D 在AB 上,∠BAC =∠DEC =30°,AC 与DE 交于点F ,连接AE ,若BD =1,AD =5,则CF EF=.D CAEBF9.[2017·包头]如图,在△ABC 与△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,且点D 在AB 上,点E 与点C 在AB 的两侧,连接BE ,CD ,点M 、N 分别是BE 、CD 的中点,连接MN ,AM ,AN .下列结论:①△ACD ≌△ABE ;②△ABC ∽△AMN ;③△AMN 是等边三角形;④若点D 是AB 的中点,则S △ABC =2S △ABE .其中正确的结论是.(填写所有正确结论的序号)DC AE BMN10.[烟台]如图,△ABC 与△AEF 中,AB =AE ,BC =EF ,∠B =∠E ,AB 交EF 于D .给出下列结论:①∠AFC =∠C ;②DE =CF ;③△ADE ∽△FDB ;④∠BFD =∠CAF 其中正确的结论是.D CABFE11.[鄂州]在平面内正方形ABCD 与正方形CEFH 如图放置,连DE ,BH ,两线交于M .求证:(1)BH =DE .(2)BH ⊥DE .M DHFECBA12.[莱芜]如图,△ABC 是等腰直角三角形,∠ACB =90°,分别以AB ,AC 为直角边向外作等腰直角△ABD 和等腰直角△ACE ,G 为BD 的中点,连接CG ,BE ,CD ,BE 与CD 交于点F .(1)判断四边形ACGD 的形状,并说明理由.(2)求证:BE =CD ,BE ⊥CD .DCHEBFGA13.[2019·无锡]如图,在Rt △ABC 中,AC =BC =4,∠ACB =90°,正方形BDEF 的边长为2,将正方形BDEF 绕点B 旋转一周,连接AE 、BE 、CD .(1)请找出图中与△ABE 相似的三角形,并说明理由;(2)求当A 、E 、F 三点在一直线上时CD 的长;(3)设AE 的中点为M ,连接FM ,试求FM 长的取值范围.DCAEBFBA备用题C。
初中必会几何模型(口诀突破):手拉手模型(或旋转型)

初中必会几何模型(口诀突破):手拉手模型(或旋转型)教材知识:三角形全等知识中,教材对全等三角形的图形变换概括为三种:平移型、翻折型、旋转型。
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.归纳模型:三种变换中以旋转型为考试的热点和难点,这种变换我们往往也称为手拉手模型。
因为这种图形变换都是以等腰三角形的顶点为旋转点,进行适当旋转而成。
然后,连接对应点构造新的三角形,证明三角形全等即可解决。
划重点,上口诀:等腰图形有旋转,辨清共点旋转边。
关注三边旋转角,全等思考边角边。
模型变换:如图,△ABC是等腰三角形、△ADE是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE=a。
结论:连接BD、CE,则有△BAD≌△CAE。
模型证明:图②图③同理可证。
模型分析:(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形。
(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型。
(3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现。
模型实例:如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:(1)AG与CE是否相等?(2)AG与CE之间的夹角为多少度?问题解答:模型实练:如图,在直线AB的同一侧作△ABD和△BCE,△ABD和△BCE都是等边三角形、连接AE、CD,二者交点为H.求证:(1)△ABE≌△DBC;(2)AE=DC;(3)∠DHA=60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB(6)连接GF,GF∥AC;(7)连接HB,HB平分∠AHC.。
(完整word版)用旋转构造“手拉手”模型

中考专题复习——几何题用旋转构造“手拉手”模型一、教学目标:1.了解并熟悉“手拉手模型”,归纳掌握其基本特征.2.借助“手拉手模型”,利用旋转构造全等解决相关问题.3.举一反三,解决求定值,定角,最值等一类问题.二、教学重难点:1.挖掘和构造“手拉手模型”,学会用旋转构造全等.2.用旋转构造全等的解题方法最优化选择.三、教学过程:1.复习旧知师:如图,△ABD ,△BCE 为等边三角形,从中你能得出哪些结论?生:(1)△ABE ≌△DBC (2)△ABG ≌△DBF (3)△CFB ≌△EGB (4)△BFG 为等边三角形(5)△AGB ∽△DGH (6)∠DHA =60°(7)H ,G ,F ,B 四点共圆 (8)BH 平分∠AHC …… 师:我们再来重点研究△ABE 与△DBC ,这两个全等的三角形除了对应边相等,对应角相等外,还有什么共同特征呢?生:它们有同一个字母B ,即同一个顶点B .师:我们也可以把△DBC 看作由△ABE 经过怎样的图形运动得到? 生:绕点B 顺时针旋转60°得到.2.引入新课师:其实我们可以给这两个全等的三角形赋予一个模型,叫“手拉手模型”,谁可以将这个模型的特征再做进一步的简化归纳呢? 生:对应边相等.师:我们可以称之为“等线段”. 生:有同一个顶点.师:我们可以称之为“共顶点”.师:等线段,共顶点的两个全等三角形,我们一般可以考虑哪一种图形运动? 生:旋转.师: “手拉手模型”可以归纳为:等线段,共顶点,一般用旋转.H GF E DCBA3.小题热身图1 图2 图31.如图1,△BAD中,∠BAD=45°,AB=AD,AE⊥BD于E,BC⊥AD于C,则AF=____BE.2.如图2,△ABC和△BED均为等边三角形,ADE三点共线,若BE=2,CE=4,则AE=______.3.如图3,正方形ABCD中,∠EAF=45°,BE=3,DF=5,则EF=_______.师:我们来看第1,第2题,这里面有“手拉手模型”吗?请你找出其中的“等线段,共顶点”.生:题1中,等线段是AC,BC,共顶点是C,△ACF绕点C逆时针旋转90°得△BCD.题2中,等线段是AB,BC,共顶点是B,△ABD绕点D顺时针旋转60°得△CBE.师:我们再来看第3题,这里有“手拉手模型”吗?生:没有.师:那其中有没有“等线段,共顶点”呢?生:等线段是AD,AB,共顶点是A.师:我们可否利用旋转来构造“手拉手模型”呢?生:将AE旋转,绕点A逆时针旋转90°.师:为什么是逆时针旋转90°,你是如何思考的?生:我准备构造一个和△ABE全等的三角形,AB绕点A逆时针旋转90°即为AD,那么将AE逆时针旋转90°可得AG,连接GD,证明全等.师:说的不错,谁能再来归纳一下,借助“手拉手模型”,用旋转构造全等的方法吗?生:先找有没有“等线段,共顶点”,再找其中一条“共顶点”的线段,将其旋转.师:旋转角度如何确定,方向怎么选择?生:选择其中一个三角形,将“共顶点”的线段旋转.旋转角为两条“等线段”间的夹角.方向应与所选择的起始“等线段”旋转到另一条“等线段”时的方向一致.师:非常棒,可以说,你已经掌握了这节课的精髓.但是,很多题目中只是隐含了“手拉手模型”的一些条件,剩余的需要我们自己去构造,可以如何构造呢?步骤1:先找有没有“等线段,共顶点”.步骤2:选择其中一个三角形,将其中经过“共顶点”的线段旋转.步骤3:旋转方向与这个三角形的“等线段”旋转到另一条“等线段”的方向一致,旋转角为“等线段”间的夹角.师:这道题还有一个要注意的地方,你发现了吗?生:连接GD后,要证明G,D,F三点共线.4.例题精讲例1:等边△ABC中,AD=4,DC=3,BD=5,求∠ADC度数.师:这里有没有隐含的“手拉手模型”?要构造全等,该怎样旋转?生:将△ADC绕点A顺时针旋转60°.师:你是怎么想的,还有其他做法吗?生:我发现AB=AC,A为“共顶点”,我选择的旋转线段是AD,因为AC绕点A顺时针旋转60°到AB,所以△ADC也要绕点A顺时针旋转60°.也可将△ADB绕点A逆时针旋转60°.【解答】将AD绕点A顺时针旋转60°到AE,连接BE,DE.则△ADE也为等边三角形.易证△AEB≌△ADC,∴BE=DC=4,根据勾股定理逆定理,可证∠BED=90°,则∠AEB=∠ADC=150°例2:如图,△ABO和△CDO均为等腰直角三角形,∠AOB=∠COD=90︒.若△BOC的面积为1,试求以AD、BC、OC+OD的长度为三边长的三角形的面积.师:由于线段分散,如何通过图形变换,使这些线段能构成一个三角形?生:将OD绕点O逆时针旋转90°至OE,即可使OC,OD共线,再通过证明确定△BCE即是以AD、BC、OC+OD的长度为三边长的三角形.【解答】如图,将OD绕点O逆时针旋转90°至OE,连接BE.易证△OAD≌△OBE,AD=BE,∴△BCE即是以AD、BC、OC+OD 长度为三边长的三角形.又∵OC=OE,∴S△BCE=2S△BOC=2.EAOBCDDC BOABBDCBA5.自主练习1.如图,在四边形ABCD 中,AD =4,CD =3,∠ABC =∠ACB =∠ADC =45°,则BD 的长为 _________. 师:请找出隐含的“手拉手模型”,并写出解决方法.生:“等线段”是CA 和BA ,“共顶点”是A .方法是将AD 绕点A 顺时针旋转90°.2.如图,在△ABC 中,BC =2,AB =2,以AC 为边,向外做正方形ACDE ,连接BE ,则BE 最大值为_________. 师:请找出隐含的“手拉手模型”,并写出解决方法.生:“等线段”是CA 和EA ,“共顶点”是A . 方法是将AB 绕点A 逆时针旋转90°.师:你为何要逆时针旋转,你准备旋转哪个三角形?生:△ABC ,因为AC 是逆时针旋转90°到AE ,所以AB 也绕点A 逆时针旋转90°. 3.如图,点A 在⊙B 上,AB =1,BC =2,△ACD 是等边三角形,求△BCD 面积的最大值.师:请找出隐含的“手拉手模型”,并写出解决方法. 生:“等线段”是CA 和CD ,“共顶点”是C . 方法是将CA 绕点C 逆时针旋转60°.附:自主练习解答1. 如图,将AD 绕点A 顺时针旋转90°至AE ,易证△EAC ≌△DAB ,可得CE =BD ,又∵∠EDA =45°,∴∠CDE =90°,CD =3,DE =42,则Rt △CDE 中,CE 2=CD 2+DE 2=32+ (42)2=41∴CE =41,∴DB =412.如图,将AB 绕点A 逆时针旋转90°至AF ,易证△EAF ≌△CAB ,可得EF =BC =2.Rt △BAF 中,AF =AB =2,∴BF =2.由三角形三边关系易知,BE ≤EF +BF ,∴BE 最小值为4.EDCBAADC BDFEBCDA3.如图,将CB绕点C逆时针旋转60°至CE,连接DE,过点E作EF⊥CB 于F,过点D作DG⊥CB于G.易证△CBA≌CED,则DE=1,EF=3,过E作DG边上的高,可证DG<DE+EF.当D,E,F三点共线时,DG=DE+EF.即高的最大值为1+3,S△BCDmax=12×2×(1+3)=1+ 3FEDCBAGEFABCD。
初中数学九大几何模型
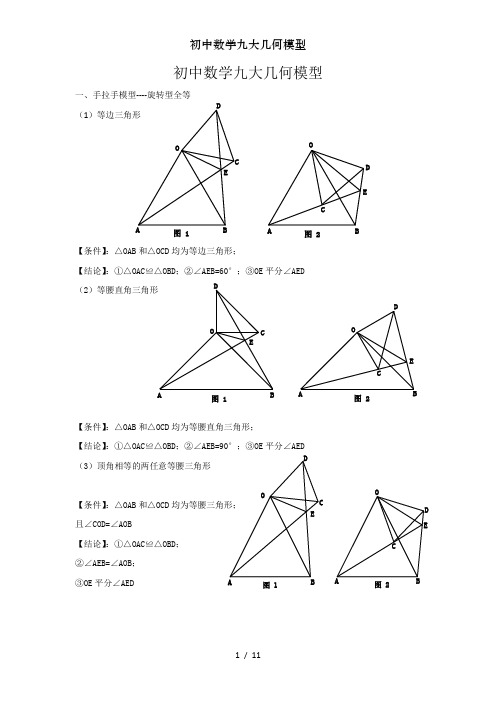
初中数学九大几何模型一、手拉手模型----旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OACDE图 2OABC DEOABCD E图 1图 2二、模型二:手拉手模型----旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90°将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型-90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21S S =-OB COACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4(2)全等型-120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE ;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=证明提示:①可参考“全等型-90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
几何模型之——“手拉手”及其经典考题

几何模型之——“手拉手”及其经典考题几何模型之——“手拉手”及其经典考题一、“手拉手”全等模型如图,△ABC与△ADE都是等腰三角形,AB=AC,AD=AE.∠BAC=∠DAE.结论:△BAD≌△CDE.二、模型分析手拉手模型常和旋转结合,在考试中作为几何综合题目出现。
三、模型实例例1.如图,△ABC与△EDC都为等腰直角三角形,连接AE、BD,相交于点F.问:(1)AE与BD是否相等?(2)AE与BD之间的夹角为多少度?例2.如图,直线AB的同一侧作△ABD和△BCE都为等边三角形,连接AE交DB于点G、连接CD交BE于点F,AE与CD交于点H.求证:(1)△ABE≌△DBC;(2)AE=DC;(3)∠DHA=60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)连接GF,GF∥AC;(7)连接HB,HB平分∠AHC。
四、精选练习1.如图,在△ABC中,AC=CB,∠ACB=90°,D为AC延长线上一点,点E在BC上,且AE=BD.(1)求证:CD=CE;(2)若∠BAE=30°,求∠ABD度数.2.如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于点F.求证:(1)AE=DC;(2)∠AFD=60°;(3)连接FB,FB平分∠AFC。
3.在线段AE同侧作等边△CDE(∠ACE<120°),点F,G分别是线段BE和AD的中点.求证:△CFG是等边三角形.4.将等腰Rt△ABC和等腰Rt△ADE按图①方式放置,∠A=90°,AD边与AB边重合,AB=2AD=4。
将△ADE绕点A逆时针方向旋转一个角度(0°<>180°),BD的延长线交CE于P.(1)如图②,证明:BD=CE,BD⊥CE;(2)如图③,在旋转的过程中,当AD⊥BD时,求出CP的长.。
初中数学经典几何模型05-手拉手模型构造全等三角形(含答案)

初中数学经典几何模型专题05 手拉手模型构造全等三角形【专题说明】两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
【知识总结】【基本模型】一、等边三角形手拉手-出全等图1 图2图3 图4二、等腰直角三角形手拉手-出全等两个共直角顶点的等腰直角三角形,绕点C旋转过程中(B、C、D不共线)始终有①△BCD≌△ACE;②BD⊥AE(位置关系)且BD=AE(数量关系);③FC平分∠BFE;图1图2图3图41、如图,点C在线段AB上,△DAC和△DBE都是等边三角形,求证:△DAB≌△DCE;DA∥EC.2、已知:△ACB和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°,连结AE,BD交于点O,AE与DC交于点0,AE与DC交于点M,BD与AC交于点N.3、已知,在△ABC中,AB=AC,点P平面内一点,将AP绕A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ、CP,⑴若点P在△ABC内部,求证BQ=CP;⑵若点P在△ABC外部,以上结论还成立吗?4、如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.若AB=√2,AG=1,则EB=________________.5、已知正方形ABCD和正方形AEFG有一个公共点,点G、E分别在线段AD、AB上,若将正方形AEFG 绕点A按顺时针方向旋转,连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长度始终相等?并说明理由。
6、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠BDC=45°;④BE2=2(AD2+AB2)其中结论正确的个数是_______【基础训练】1、已知△ABC为等边三角形,点D为直线BC上一动点(点D不与点B,点C重合).以AD为边作等边三角形ADE,连接CE.如图1,当点D在边BC上时,求证:△ABD≌△ACE;直接判断结论BC=DC+CE是否成立(不需要证明);如图2,当点D在边BC的延长线上时,其他条件不变,请写出BC、DC、CE之间存在的数量关系,并写出证明过程.2、如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点.若DE=13,BD=12,求线段AB的长.3、如图,点A、B、C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM.下面结论:△ABE≌△DBC;∠DMA=60°;△BPQ为等边三角形;MB平分∠AMC.其中正确的有____________4、如图1,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.求证:BE=AD;用含α的式子表示∠AMB的度数;当α=90°时,取AD、BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.【巩固提升】1、已知△ABC和△BDE都是等腰直角三角形,∠ACB=∠BED=90°,AB=2BD,连接CE.(1)如图1,若点D在AB边上,点F是CE的中点,连接BF.当AC=4时,求BF的长;(2)如图2,将图1中的△BDE绕点B按顺时针方向旋转,使点D在△ABC的内部,连接AD,取AD 的中点M,连接EM并延长至点N,使MN=EM,连接CN.求证:CN⊥CE.2、如图,△ABC中AB=AC=5,tan∠ACB=,点D为边BC上的一动点(不与点B、C重合),将线段AD绕点A顺时针旋转得AE,使∠DAE=∠BAC,DE与AB交于点F,连接BE.(1)求BC的长;(2)求证∠ABE=∠ABC;(3)当FB=FE时,求CD的长.3、如图1,在△ABC中,∠ACB=90°,AC=BC,D为AB上一点,连接CD,将CD绕点C顺时针旋转90°至CE,连接AE.(1)求证:△BCD≌△ACE;(2)如图2,连接ED,若CD=2,AE=1,求AB的长;(3)如图3,若点F为AD的中点,分别连接EB和CF,求证:CF⊥EB.4、如图,△ABC和△EDC都是等腰直角三角形,C为它们的公共直角顶点,连接AD、BE,点F为线段AD的中点,连接CF.(1)如图1,当D点在BC上时,试判断线段BE、CF的关系,并证明你的结论;(2)如图2,把△DEC绕C点顺时针旋转一个锐角,其他条件不变时,请探究BE、CF的关系并直接写出结论.5、如图1,在△ABC中,AB=AC,∠BAC=90°,D、E分别是AB、AC边的中点.将△ABC绕点A顺时针旋转a角(0°<a<180°),得到△AB′C′(如图2),连接DB',EC'.(1)探究DB'与EC'的数量关系,并结合图2给予证明;(2)填空:①当旋转角α的度数为时,则DB'∥AE;②在旋转过程中,当点B',D,E在一条直线上,且AD=时,此时EC′的长为.6、如图,∠AOB=120°,OC平分∠AOB,∠MCN=60°,CM与射线OA相交于M点,CN与直线BO相交于N点.把∠MCN绕着点C旋转.(1)如图1,当点N在射线OB上时,求证:OC=OM+ON;(2)如图2,当点N在射线OB的反向延长线上时,OC与OM,ON之间的数量关系是(直接写出结论,不必证明)专题05 手拉手模型构造全等三角形答案【专题说明】两个具有公共顶点的相似多边形,在绕着公共顶点旋转的过程中,产生伴随的全等或相似三角形,这样的图形称作共点旋转模型;为了更加直观,我们形象的称其为“手拉手”模型。
初中数学几何模型之——手拉手模型,跟我学-应对中考轻松自如
初中数学几何模型之——手拉手模型,跟我学-应对中考轻松自
如
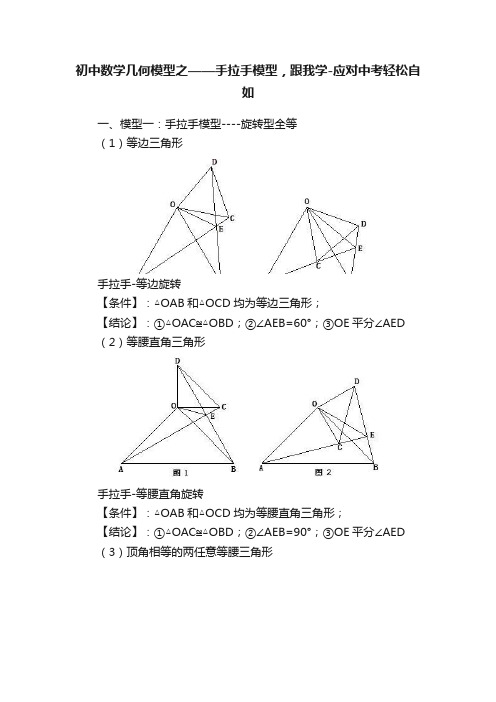
一、模型一:手拉手模型----旋转型全等
(1)等边三角形
手拉手-等边旋转
【条件】:△OAB和△OCD均为等边三角形;
【结论】:①△OAC≌△OBD;②∠AEB=60°;③OE平分∠AED
(2)等腰直角三角形
手拉手-等腰直角旋转
【条件】:△OAB和△OCD均为等腰直角三角形;
【结论】:①△OAC≌△OBD;②∠AEB=90°;③OE平分∠AED
(3)顶角相等的两任意等腰三角形
手拉手-等腰旋转
【条件】:△OAB和△OCD均为等腰三角形;且∠COD=∠AOB
【结论】:①△OAC≌△OBD;②∠AEB=∠AOB;③OE平分∠AED
二、模型二:手拉手模型----旋转型相似
(1)一般情况
【条件】:CD∥AB,将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA
(2)特殊情况
【条件】:CD∥AB,∠AOB=90° 将△OCD旋转至右图的位置
【结论】:①右图中△OCD∽△OAB→→→△OAC∽△OBD;
②延长AC交BD于点E,必有∠BEC=∠BOA;
③BD/AC=OD/OC=OB/OA=tan∠OCD;
④BD⊥AC;
⑤连接AD、BC,必有AD2+BC2=AB2+CD2;
⑥S△BCD=1/2AC×BD。
