初中几何经典模型总结(手拉手模型)
经典手拉手模型12个结论,你知道几个?

经典手拉手模型12个结论,你知道几个?展开全文初中经典几何模型--手拉手模型说明手拉手模型是学习初中几何模型中的第3个(第1个模型是三线八角模型、第2个是内外角平分线模型),手拉手算是最常见的模型了,在很多全等或者相似的题目当中都会用到,大家对这个模型并不陌生,但大家对构造手拉手模型的应用却不是很熟练(如费马点问题),今天我们就手拉手的结论进行总结,以及以中考压轴题为例讲解手拉手模型的应用。
1手拉手-全等手拉手的12个结论,我以等边三角形为母题进行解析(因为等边最特殊)第1、2个结论:△AOD≌△COB、AD=CB第3个结论:∠AGC=60°(定值)第4、5个结论:OM=ON、△OMN是等边三角形第6个结论:MN//AB第7个结论:PO是∠APB的角平分线第8个结论:存在多组三角形相似注:三角形相似在这里由非常多,就不一一例举了,在这个模型中考相似居多的是母子型、8字形、A字形,且省略了证明的思路。
第9个结论:存在3组4点共圆注:四点共圆的方法证明方式是利用对角互补第10个结论:存在3组的线段和数量关系注:在四边形OMGN中,满足的线段关系是:GO=GM+GN;在四边形OGDB中,满足的线段关系是:GB=GO+GD。
第11结论:OG平方=DG·CG第12个结论:注:两个等边三角形在运动时,有些结论是能够保持不变的~~~ 2手拉手-相似经典模型注:(图1-15-3的类型可以等腰直角三角形)一定得记住以上3种手拉手-相似模型,只有对这3种类型熟练掌握,对于一些压轴题才能更好的突破,下面我会通过2道小例题进行介绍和说明:例1-2018宁德二模例2-孙超老师出题3手拉手-练习例1-2016年广东解:例2-2017年淮安坚持是一种品质,优秀是一种习惯;不忘初心,成就学生梦想;为孩子们节约更多的时间成本;通过《课前导学》,帮助学生养成预习的习惯;通过《精彩课堂》,帮助学生高效复习和总结;初中的学习生活很短,也很有意义;希望能够陪着你慢慢成长,畅游知识海洋。
初中必会几何模型(口诀突破):手拉手模型(或旋转型)

初中必会几何模型(口诀突破):手拉手模型(或旋转型)教材知识:三角形全等知识中,教材对全等三角形的图形变换概括为三种:平移型、翻折型、旋转型。
一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等.归纳模型:三种变换中以旋转型为考试的热点和难点,这种变换我们往往也称为手拉手模型。
因为这种图形变换都是以等腰三角形的顶点为旋转点,进行适当旋转而成。
然后,连接对应点构造新的三角形,证明三角形全等即可解决。
划重点,上口诀:等腰图形有旋转,辨清共点旋转边。
关注三边旋转角,全等思考边角边。
模型变换:如图,△ABC是等腰三角形、△ADE是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE=a。
结论:连接BD、CE,则有△BAD≌△CAE。
模型证明:图②图③同理可证。
模型分析:(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形。
(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型。
(3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现。
模型实例:如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:(1)AG与CE是否相等?(2)AG与CE之间的夹角为多少度?问题解答:模型实练:如图,在直线AB的同一侧作△ABD和△BCE,△ABD和△BCE都是等边三角形、连接AE、CD,二者交点为H.求证:(1)△ABE≌△DBC;(2)AE=DC;(3)∠DHA=60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB(6)连接GF,GF∥AC;(7)连接HB,HB平分∠AHC.。
中考数学相似三角形中的重要模型手拉手模型

相似三角形中的重要模型-手拉手模型相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。
手拉手模型相似是手拉手模型当中相对于手拉手全等模型较难的一种模型,在实际的应用和解题当中出现时,对于同学们来说,都比较困难。
而深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“手拉手”模型(旋转模型)。
手拉手相似证明题一般思路方法:①由线段乘积相等转化成线段比例式相等;②分子和分子组成一个三角形、分母和分母组成一个三角形;③第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等; ④第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。
模型1.“手拉手”模型(旋转模型)【模型解读与图示】“手拉手”旋转型定义:如果将一个三角形绕着它的项点旋转并放大或缩小(这个顶点不变),我们称这样的图形变换为旋转相似变换,这个顶点称为旋转相似中心,所得的三角形称为原三角形的旋转相似三角形。
1)手拉手相似模型(任意三角形)条件:如图,∠BAC=∠DAE=α,A DA E kA BA C==; 结论:△ADE ∽△ABC ,△ABD ∽△ACE ;E CkB D=.2)手拉手相似模型(直角三角形)条件:如图,90A O BC OD ∠=∠=︒,O C O D kO AO B==(即△COD ∽△AOB );结论:△AOC ∽△BOD ;B DkA C=,AC ⊥BD ,12A B C DS A B C D=⨯.3)手拉手相似模型(等边三角形与等腰直角三角形)条件:M 为等边三角形ABC 和DEF 的中点; 结论:△BME ∽△CMF ;B EC F条件:△ABC 和ADE 是等腰直角三角形; 结论:△ABD ∽△ACE.例1.(2022·山西·寿阳县九年级期末)问题情境:如图1所示,在△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,在图1中将ADE 绕A 点顺时针旋转一定角度,得到图2,然后将BD 、CE 分别延长至M 、N ,使DM =12BD ,EN =12CE ,得到图3,请解答下列问题:(1)猜想证明:若AB =AC ,请探究下列数量关系:①在图2中,BD 与CE 的数量关系是_________. ②在图3中,猜想∠MAN 与∠BAC 的数量关系,并证明你的猜想;(2)拓展应用:其他条件不变,若AB ,按上述操作方法,得到图4,请你继续探究:∠MAN 与∠BAC的数量关系?AM 与AN 的数量关系?直接写出你的猜想.例2.(2022•新乡中考模拟)在△ABC中,CA=CB=m,在△AED中,DA=DE=m,请探索解答下列问题.【问题发现】(1)如图1,若∠ACB=∠ADE=90°,点D,E分别在CA,AB上,则CD与BE的数量关系是,直线CD与BE的夹角为;【类比探究】(2)如图2,若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图2所示的位置,则CD 与BE之间是否满足(1)中的数量关系?说明理由.【拓展延伸】(3)在(1)的条件下,若m=2,将△AED绕点A旋转过程中,当B,E,D三点共线.请直接写出CD的长.例3.(2022·山东·九年级课时练习)【问题发现】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D为斜边BC上一点(不与点B,C重合),将线段AD绕点A顺时针旋转90°得到AE,连接EC,则线段BD与CE的数量关系是______,位置关系是______;【探究证明】如图2,在Rt△ABC和Rt△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,将△ADE绕点A旋转,当点C,D,E在同一条直线上时,BD与CE具有怎样的位置关系,说明理由;【拓展延伸】如图3,在Rt△BCD中,∠BCD=90°,BC=2CD=4,过点C作CA⊥BD于A.将△ACD绕点A顺时针旋转,点C的对应点为点E.设旋转角∠CAE为α(0°<α<360°),当C,D,E在同一条直线上时,画出图形,并求出线段BE的长度.例4.(2022·山东·东营市一模)【提出问题】(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.【类比探究】(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.【拓展延伸】(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.例5.(2022•长垣市一模)在△AB=AC,点D为AB边上一动点,∠CDE=∠BAC=α,CD=ED,连接BE,EC.(1)问题发现:如图①,若α=60°,则∠EBA=,AD与EB的数量关系是;(2)类比探究:如图②,当α=90°时,请写出∠EBA的度数及AD与EB的数量关系并说明理由;(3)拓展应用:如图③,点E为正方形ABCD的边AB上的三等分点,以DE为边在DE上方作正方形DEFG,点O为正方形DEFG的中心,若OA=,请直接写出线段EF的长度.例6.(2022·成都市·九年级课时练习)一次小组合作探究课上,老师将两个正方形按如图所示的位置摆放(点E 、A 、D 在同一条直线上),发现B ED G=且B ED G⊥.小组讨论后,提出了下列三个问题,请你帮助解答:(1)将正方形A E F G 绕点A 按逆时针方向旋转(如图1),还能得到B E D G=吗?若能,请给出证明,请说明理由;(2)把背景中的正方形分别改成菱形A E F G 和菱形A B C D ,将菱形A E F G 绕点A 按顺时针方向旋转(如图2),试问当E A G ∠与B A D ∠的大小满足怎样的关系时,B ED G=;(3)把背景中的正方形分别改写成矩形A E F G 和矩形A B C D ,且23AE AB AGAD==,2A Ea=,2A Bb=(如图3),连接D E ,B G .试求22D E B G+的值(用a ,b 表示).课后专项训练1.如图,在△ABC与△ADE中,∠ACB=∠AED=90°,∠ABC=∠ADE,连接BD、CE,若AC:BC=3:4,则BD:CE为()A.5:3B.4:3C.√5:2D.2:√32.如图,△ABC∽△ADE,∠BAC=∠DAE=90°,AB与DE交于点O,AB=4,AC=3,F是DE的中点,连接BD,BF,若点E是射线CB上的动点,下列结论:①△AOD∽△FOB,②△BOD∽△EOA,③∠FDB+∠FBE=90°,④BF=56AE,其中正确的是()A.①②B.③④C.②③D.②③④3、如图,正方形A B C D的边长为8,线段C E绕着点C逆时针方向旋转,且3C E=,连接B E,以B E为边作正方形B E F G,M为A B边的中点,当线段F M的长最小时,ta n E C B∠=______.4.(2022•虹口区期中)如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)求证:△ABC∽△ADE;(2)判断△ABD与△ACE是否相似?并证明.5.(2023·浙江·九年级课时练习)在△ABC中,AB=AC,∠BAC=α,点P为线段CA延长线上一动点,连接PB,将线段PB绕点P逆时针旋转,旋转角为α,得到线段PD,连接DB,DC.(1)如图1,当α=60°时,求证:P A=DC;(2)如图2,当α=120°时,猜想P A和DC的数量关系并说明理由.(3)当α=120°时,若AB=6,BP D到CP的距离.6.(2022·重庆·九年级课时练习)观察猜想(1)如图1,在等边A B C中,点M 是边B C 上任意一点(不含端点B 、C ),连接A M ,以A M 为边作等边A M N,连接C N ,则A B C ∠与A C N ∠的数量关系是______. (2)类比探究:如图2,在等边A B C中,点M 是B C 延长线上任意一点(不含端点C ),(1)中其它条件不变,(1)中结论还成立吗?请说明理由. (3)拓展延伸:如图3,在等腰A B C中,B AB C=,点M 是边B C 上任意一点(不含端点B 、C ),连接A M ,以A M 为边作等腰A M N,使顶角A M NA B C∠=∠.连按C N .试探究A B C ∠与A C N ∠的数量关系,并说明理由.7.(2022·江苏·九年级课时练习)【问题发现】如图1,在Rt △ABC 中,∠BAC =90°,AB =AC ,D 为斜边BC 上一点(不与点B ,C 重合),将线段AD 绕点A 顺时针旋转90°得到AE ,连接EC ,则线段BD 与CE 的数量关系是______,位置关系是______;【探究证明】如图2,在Rt △ABC 和Rt △ADE 中,∠BAC =∠DAE =90°,AB =AC ,AD =AE ,将△ADE 绕点A 旋转,当点C ,D ,E 在同一条直线上时,BD 与CE 具有怎样的位置关系,说明理由;【拓展延伸】如图3,在Rt △BCD 中,∠BCD =90°,BC =2CD =4,过点C 作CA ⊥BD 于A .将△ACD 绕点A 顺时针旋转,点C 的对应点为点E .设旋转角∠CAE 为α(0°<α<360°),当C ,D ,E 在同一条直线上时,画出图形,并求出线段BE 的长度.8.(2022·山东·九年级课时练习)如图,A B C和A D E是有公共顶点直角三角形,90B A C D A E ∠=∠=︒,点P 为射线B D ,C E 的交点.(1)如图1,若A B C和A D E是等腰直角三角形,求证:C PB D⊥;(2)如图2,若30A D EA B C ∠=∠=︒,问:(1)中的结论是否成立?请说明理由.(3)在(1)的条件下,4A B =,3A D =,若把A D E 绕点A 旋转,当90E A C ∠=︒时,请直接写出P B 的长度9.(2023·广东·深圳市九年级期中)(1)如图1,Rt △ABC 与Rt △ADE ,∠ADE =∠ABC =90°,12A BA DB CD E==,连接BD ,CE .求证:5B DC E=.(2)如图2,四边形ABCD ,∠BAD =∠BCD =90°,且12A B A D=,连接BC ,BC 、AC 、CD 之间有何数量关系?小明在完成本题中,如图3,使用了“旋转放缩”的技巧,即将△ABC 绕点A 逆时针旋转90°,并放大2倍,点B 对应点D .点C 落点为点E ,连接DE ,请你根据以上思路直接写出BC ,AC ,CD 之间的关系. (3)拓展:如图4,矩形ABCD ,E 为线段AD 上一点,以CE 为边,在其右侧作矩形CEFG ,且12A B C EB CE F==,AB=5,连接BE,BF.求BE的最小值.510.(2023·绵阳市·九年级专题练习)在△ABC中,AB=AC,∠BAC=α,点P是△ABC外一点,连接BP,将线段BP绕点P逆时针旋转α得到线段PD,连接BD,CD,AP.观察猜想:的值为,直线CD与AP所成的较小角的度数为°;(1)如图1,当α=60°时,C DA P的值及直线CD与AP所成的较小角的度数;类比探究:(2)如图2,当α=90°时,求出C DA P拓展应用:(3)如图3,当α=90°时,点E,F分别为AB,AC的中点,点P在线段FE的延长线上,点A,D,P三点在一条直线上,BD交PF于点G,CD交AB于点H. 若CD=2BD的长.11.(2023·湖北·九年级专题练习)在A B C和A D E中,B A B C∠=∠=,点=,D A D E=,且A B C A D EαE在A B C的内部,连接EC,EB,EA和BD,并且90∠+∠=︒.A C E AB Eα=︒时,线段BD与CE的数量关系为__________,线段EA,EB,EC的【观察猜想】(1)如图①,当60数量关系为__________.α=︒时,(1)中的结论是否依然成立?若成立,请给出证明,若不成立,【探究证明】(2)如图②,当90请说明理由;【拓展应用】(3)在(2)的条件下,当点E在线段CD上时,若B C=B D E的面积.12.(2023··广西一模)如图,A C B△和D C E均为等腰直角三角形,,.现将D C E绕点C旋转.∠=∠=︒==A CB DC E A C B CD CE C90,(1)如图1,若,,A D E三点共线,A D=B到直线C E的距离;(2)如图2,连接,A EB D,点F为线段B D的中点,连接C F,求证:A E C F⊥;(3)如图3,若点G在线段A B上,且8,==,在A C G内部有一点O,请直接写出A C A G22O C A G++的最小值.13.(2022•南山区校级一模)(1)【问题发现】如图①,正方形AEFG 的两边分别在正方形ABCD 的边AB 和AD 上,连接CF .填空:①线段CF 与DG 的数量关系为 ;②直线CF 与DG 所夹锐角的度数为 .(2)【拓展探究】如图②,将正方形AEFG 绕点A 逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.(3)【解决问题】如图③,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,AB =AC =10,O 为AC 的中点.若点D 在直线BC 上运动,连接OE ,则在点D 的运动过程中,线段OE 长的最小值为 (直接写出结果).14、某校数学活动小组在一次活动中,对一个数学问题作如下探究:(1)问题发现:如图1,在等边A B C 中,点P 是边B C 上任意一点,连接A P ,以A P 为边作等边A P Q,连接CQ ,BP 与CQ 的数量关系是________; (2)变式探究:如图2,在等腰A B C中,A BB C=,点P 是边B C 上任意一点,以A P 为腰作等腰A P Q,使A PP Q=,A P QA B C∠=∠,连接C Q ,判断A B C ∠和A C Q ∠的数量关系,并说明理由;(3)解决问题:如图3,在正方形A D B C 中,点P 是边B C 上一点,以A P 为边作正方形A P E F ,Q 是正方形A P E F 的中心,连接C Q .若正方形A P E F 的边长为5,2C Q =A DBC 的边长.15、如图,四边形ABCD 和四边形AEFG 都是正方形,C ,F ,G 三点在一直线上,连接AF 并延长交边CD 于点M .(1)求证:△MFC ∽△MCA ;(2)求证△ACF ∽△ABE ; (3)若DM =1,CM =2,求正方形AEFG 的边长.16、已知,ABC 中,AB =AC ,∠BAC =2α°,点D 为BC 边中点,连接AD ,点E 为线段AD 上一动点,把线段CE绕点E顺时针旋转2α°得到线段EF,连接FG,FD.(1)如图1,当∠BAC=60°时,请直接写出B F的值;(2)如图2,当∠BAC=90°时,(1)中的结论是A E否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;(3)如图3,当点E在AD上移动时,请直接写出点E运动到什么位置时D F的值最小.最小值是多少?(用含α的三角函数表示)D C。
中考数学几何专题——手拉手模型一

手拉手模型一、手拉手模型1.手的判别:人站在等腰三角形顶角的位置,张开双臂,左手边的腰为左手,右手边的腰为右手。
2.手拉手模型的定义:两个等顶角的等腰三角形组成的图形,且顶角的顶点为公共顶点。
(顶角相等、等腰三角形、共顶点)条件模型结论特殊结论△ABC与△CDE是等腰三角形,且∠ACB=∠DCE (1)D ACD@D BCE (SSS)(2)AD=BE(左手拉左手,右手拉右手)(3)ÐBHA=ÐBCA(4)HC平分ÐAHE△ABC与△CDE是等腰直角三角形,且∠ACB=∠DCE=90°(5)S D BCD=S D ACE(6)BD2+AE2=AB2+DE2正方形ACBP与正方形CEQD是正方形△ABC 与△CDE是等边三角形(5)D ACM@D BCND DCM@D ECN(6) CM=CN(7)D CMN是等边三角形(8)MN∥AE,CD∥AB, CB∥DE(9) BH+CH=AHDH+CH=EH二、手拉手模型的变形:(两三角形相似,且对应角共顶点)条件模型结论D BAC∽D DAE,且ÐDAE=ÐBAC (1)D BAD∽D CAE(两边对应成比例且夹角相等) (2)BDCE=BACA(3) ÐBHC=ÐBAC【巩固练习】1、如图所示,若△ABC、△ADE都是正三角形,试比较线段BD与线段CE的大小.2、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是()3、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:(1)说明四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,四边形ADEF是菱形?(4)当△ABC满足什么条件时,四边形ADEF是正方形?(5)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?4、问题情境:如图1,已知△ABC和△DCE中,∠ACB=∠DCE=90°,AC=BC=2,CD=CE=1,点D在AC 边上,点E 在BC 延长线上。
手拉手模型的结论

手拉手模型的结论
1,手拉手模型可以看作是一个等腰三角形经过顺时针旋转到另一个地方得到另一个三角形,旋转过程中可能有缩放,这样形成的几何图形。
2,可以看作△ADE绕着顶点A顺时针旋转到△ABC位置(有比例放大),也可以看作是△ABC从头顶按顺时针旋转到△ADE。
用旋转的思路可以方便地理解哪一只手对应到哪一只手,因为解题思路通常是做左手拉左手,右手拉右手的辅助线。
3,全等三角形动点问题,化动为静,分类讨论,解题方法。
4,全等三角形之截长补短法,像AB+CD=EF这类题目。
5,全等三角形模型之倍长中线法,三种添加辅助线的方法,口诀突破。
6,旋转是初中三大几何模型之一,在平面内,将一个图形绕着某个定点按照某个方向旋转一定的角度,这个定点为旋转中心,转动的角度为旋转角,当旋转角为60°时可以得到等边三角形,当旋转角为90°时可以得到等腰直角三角形。
初中数学几何模型之手拉手模型复习整理

初中数学几何模型手拉手模型模型巧记:1.等角共点推等角.(有两条短手臂和两条长手臂)2.相同图形在一起,要把边角边想起.什么是手拉手?321ECA B D 如图所示,△ABC 和△BED 都是等边三角形,∴BE=BD(我们称为短手臂)BC=AB(我们称为长手臂)又∵∠1=∠2=60°(三角形均为等边三角形)∴∠1+∠3=∠2+∠3(等角共点推等角)∴∠ABE=∠CBD在△ABE 和△CBD 中, ቐBE =BD∴∠ABE=∠CBDBC =AB∴△ABE ≌△CBD(SAS)模型讲解结论: 如图所示,AB=AC,AD=AE,∠BAC=∠DAE.(1)则△ABD ≌△ACE.(2)BD 和CE 的夹角∠BFE=∠BAC=∠DAE.图1ED C BA 图2FA B C DE 解:(1)证明如下: ∵∠BAC=∠DAE ∴∠BAC-∠DAC=∠DAE-∠DAC ∴∠BAD=∠CAE∴在△ABD 和△ACE 中ቐAD =AE ∠BAD=∠CAEAB =AC∴ △ABD ≌△ACE(SAS)有长手臂和短手臂有共点的相等的角(这里就满足手拉手的条件了,有长手臂和短手臂,也有共点的等角)结论: 如图所示,AB=AC,AD=AE,∠BAC=∠DAE.(1)则△ABD ≌△ACE.(2)BD 和CE 的夹角∠BFE=∠BAC=∠DAE.图2FA B CDE解: (2)由1得, △ABD ≌△ACE ∴∠1=∠2,(全等三角形对应角相等) 又∵∠3=∠4(对顶角相等) 在三角形中内角和为180° ∴∠1+∠4+∠BAC=180° ∴∠2+∠3+∠BFE=180° ∴∠BFE=∠BAC(等量代换)∴ ∠BFE=∠BAC=∠DAE 4321结论1: 如图所示,等边△ABC和等边△CDE,△BCD≌△ACE,∠BFA=60°.结论图1FEDCBA你发现图中的手拉手模型了吗?结论图1FEDCBA结论2: 如图所示,等腰Rt △ABC 和等腰Rt △CDE,则△BCD ≌△ACE,∠BFA=90°.F 结论图2E D C B A F结论图2ED C B A你发现图中的手拉手模型了吗?如图,△ACB 和△DCE 均为等边三角形,点A,D,E 在同一条直线上,连结BE,则∠AEB 的度数为______.模型练习1E DBCA 60°大手拉小手,等边等角全等找.如图,△ABC 和△ADE 都是等腰直角三角形,CE 和BD 相交于点M,则BD 和CE 的数量关系是_______.BD=CE.模型练习2MDEA C B如图,△ABC 中,AB=AC,∠BAC=40°,将△ABC 绕点A 按逆时针方向旋转100°得到△ADE,连结BD,CE 相交于点F ,则BD 与CE 的数量关系是________.BD=CE.100°模型练习340°FEDCB A如图,△ABC 和△CDE 均为等边三角形,点A,D,E 在同一条直线上,连结BE,若∠CAE=25°,则∠EBC 的度数为_____.25°模型练习4EDBCA如图所示,B,D,E 在同一条直线上,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=_______.55°1模型练习532EDC BA如图,在△ABC 中,∠ABC=45°,AD,BE 分别为BC,AC 边上的高,AD,BE 相交于点F ,连结CF ,则有下列结论:①BF=AC;②∠FCD=45°.③若BF=2EC,则△FDC 的周长等于AB 的长.其中正确的有_______.①②③模型练习6FE D CBA如图,在△AOB 和△COD 中,OA=OB,OC=OD,OA<OC,∠AOB=∠COD=36°.连结AC,BD 交于点M,连结OM.有下列结论:①∠AMB=36°.②AC=BD.③OM平分∠AOD.④MO 平分∠AMD.其中正确的结论有________.①②④模型练习7M DBOAC已知△AOB 和△MON 都是等腰直角三角形(22OA <OM =ON ),∠AOB=∠MON=90°.(1)如图1,连结AM,BN,求证:△AOM ≌△BON.图1MNBOA图1MNBOA(2)若将△MON 绕点O 顺时针旋转.①如图2,当点N 恰好在AB 边上时,求证:BN 2+AN 2=2ON 2.②当点A,M,N 在同一条直线上时,若OB=4,ON=3,请直接写出线段BN 的长.图2MNBOAJ图3.1MNBO AJAO BNM图3.246+32246−322。
初中数学全等三角形手拉手模型

∵ቐ∠ABE = ∠EBC
= BC
∴△ABE≌△DBC(SAS)
过B点分别向AE和DC作垂线,垂足为点M,N
∵BM,BN分别为△ABE和△DBC对应边上的高
∴BM=BN
在Rt△BMF和Rt△BNF中
BF =
∵ቊ
BM =
∴Rt△BMF≌Rt△BNF(HL)
手拉手模型-等边三角形
为右手顶点。
B(左手)
(头 )
(头)
B(左手
)
C(右手 )
C(右手)
手拉手模型基于
“ASA全等判定”
2、手拉手模型-模型分析
二、“手拉手模型”的基本构图:
常见变形:
手拉手模型-等边三角形
例1、如图在直线ABC的同一侧作两个等边三角形△ABD与△BCE,连结AE与CD.
证明:(1)△ ≌△ (2) = (3)与之间的夹角为60°(4)△ ≌△ (5)△ ≌△ (6)
∴AE=DC
(3)延长AE分别交BD于点N,CD于H
由(1)可知,∠BDC=∠BAE
又∵∠ANB=∠HND(对顶角相等)
∴180°-( ∠BDC + ∠HND )=
180°-(∠BAE + ∠ANB )
即∠DHN=∠ABD=60°
∴ 与的夹角为60°
(4)过点B分别向AE和DC所在直
变式1-4.
D
如果两个等边三角形△ABD和△BCE,连接AE与CD,证明:
1. △ABE≌△DBC
2. AE=DC
3. AE与DC的夹角为60°
4. AE与DC的交点设为H,BH平分∠AHC
【解析】①利用角度的和差关系证明∠ABE=∠DBC,且AB=DB,BC=BE
初中数学九大几何模型-初中几何九大模型-初中九大几何模型
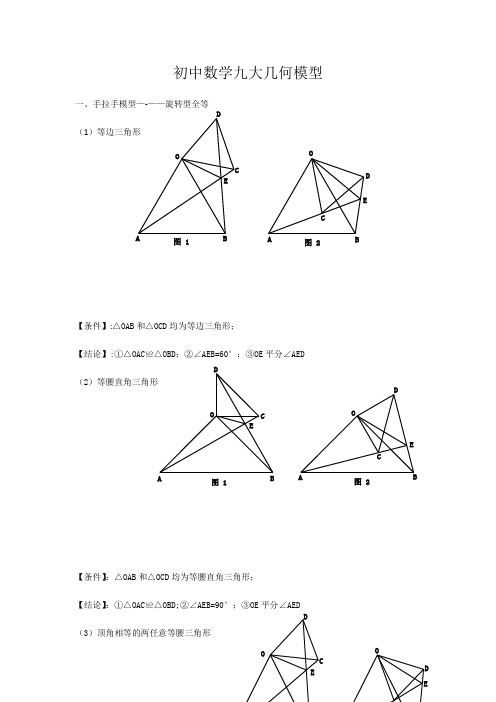
初中数学九大几何模型一、手拉手模型—-——旋转型全等(1)等边三角形【条件】:△OAB 和△OCD 均为等边三角形;【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED(2)等腰直角三角形【条件】:△OAB 和△OCD 均为等腰直角三角形;【结论】:①△OAC ≌△OBD;②∠AEB=90°;③OE 平分∠AED(3)顶角相等的两任意等腰三角形OAB C DE图 1OABCD E图 2OABCDE图 1OABCDE图 2OCDEOD E【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED二、模型二:手拉手模型--——旋转型相似 (1)一般情况【条件】:CD ∥AB , 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA;OAB COABCDEOB CDEOA CD③===OAOBOC OD AC BD tan ∠OCD ;④BD ⊥AC; ⑤连接AD 、BC ,必有2222CD AB B C AD +=+;⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型 (1)全等型—90°【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB【结论】:①CD=CE;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 21S S S =+= 证明提示:①作垂直,如图2,证明△CDM ≌△CEN②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE —OD=2OC ;③2△OCD △OCE OC 21S S =-(2)全等型—120°【条件】:①∠AOB=2∠DCE=120°;②OC 平分∠AOB【结论】:①CD=CE;②OD+OE=OC ;③2△OCE △OCD △DCE OC 43S S S =+=AOBCDE 图 1A OBCDEM N 图 2A OBCDEF图 3A O BCDEMN 图 4证明提示:①可参考“全等型—90°”证法一;②如右下图:在OB 上取一点F ,使OF=OC ,证明△OCF 为等边三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中几何经典模型总结(手拉手模型)
模型可以让同学更快的进入到几何之中,产生兴趣。
也是近来学习初中几何不可或缺的一种重要方法。
下面给大家介绍一种经典几何模型---手拉手模型,这也是历年数学中考常考的几何压轴题型之一。
手拉手模型的概念:1、手的判别:判断左右:将等腰三角形顶角顶点朝上,正对读者,读者左边为左手顶点,右边为右手顶点。
2、手拉手模型的定义:定义: 两个顶角相等且有共顶点的等腰三角形形成的图形。
(左手拉左手,右手拉右手)例如:3、手拉手模型的重要结论三个固定结论:结论
1:△ABC≌△AB'C'(SAS)BC=B'C'(左手拉左手等于右手拉右手)结论2:∠BOB'=∠BAB'(用四点共圆证明)结论3: AO平分∠BOC'(用四点共圆证明)例题解析:类型一共顶点的等腰直角三角形中的手拉手例1:已知:如图△ABC 和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°.求证:BD=CE.分析:
要证BD=CE可转化为证明△BAE≌△CAD,由已知可证AB=AC,AE=AD,∠BAC=∠EAD=90°,因为∠BAC
∠CAE=∠EAD ∠CAE,即可证∠BAE=∠CAD,符合SAS,即得证.解答:证明:∵△ABC与△AED均为等腰直角三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=90°,∴∠BAC
∠CAE=∠EAD ∠CAE,即∠BAE=∠CAD,在△BAE与
△CAD中,AB=AC,∠BAE=∠CAD,
AE=AD∴△BAE≌△CAD(SAS),∴BD=CE.类型二共顶点的等边三角形中的手拉手例2:图1、图2中,点B为线段AE上一点,△ABC与△BED都是等边三角形。
(1)如图1,求证:AD=CE;(2)如图2,设CE与AD交于点F,连接BF.①求证:∠CFA=60°;②求证:CF BF=AF.分析:(1)如图1,利用等边三角形性质得:BD=BE,AB=BC,
∠ABC=∠DBE=60°,再证∠ABD=∠CBE,根据SAS证明
△ABD≌△CBE得出结论;(2)①如图2,利用(1)中的全等得:∠BCE=∠DAB,根据两次运用外角定理可得结论;②如图3,作辅助线,截取FG=CF,连接CG,证明
△CFG是等边三角形,并证明△ACG≌△BCF,由线段的和得出结论.解答:证明:(1)如图1,∵△ABC与△BED都是等边三角形,∴BD=BE,AB=BC,∠ABC=∠DBE=60°,
∴∠ABC ∠CBD=∠DBE ∠CBD,即∠ABD=∠CBE,在
△ABD和△CBE中,AB=AC∠ABD=∠CBEBD=BE,
∴△ABD≌△CBE(SAS),∴AD=CE,(2)①如图2,由(1)得:△ABD≌△CBE,∴∠BCE=∠DAB,∵∠ABC=∠BCE
∠CEB=60°,∴∠ABC=∠DAB ∠CEB=60°,
∵∠CFA=∠DAB ∠CEB,∴∠CFA=60°,②如图3,在AF上取一点G,使FG=CF,连接CG,∵∠AFC=60°,
∴△CGF是等边三角形,∴∠GCF=60°,CG=CF,∴∠GCB ∠BCE=60°,∵∠ACB=60°,∴∠ACG ∠GCB=60°,
∴∠ACG=∠BCE,∵AC=BC,∴△ACG≌△BCF,
∴AG=BF,∵AF=AG GF,∴AF=BF CF.类型三共顶点正方形中的手拉手例3:如图,两个正方形ABCD与DEFG,连结CE、AG,二者相交于点H。
求:(1)AG=CE (2)AG与CE 之间的夹角为多少度?(3)HD平分∠AHE分析:(1)由四边形ABCD与DEFG是正方形,可得AD=CD,
∠ADC=∠GDE=90°,进而得出∠ADG=∠CDE,DG=DE,然后由SAS即可判定△ADG≌△CDE,根据全等三角形的性质则可证得AG=CE;(2)根据全等三角形的性质和角的关系即可得出夹角是90°;(3)根据全等三角形的性质和三角形的面积解答即可.解答:(1)∵ABCD和DEFG是正方形,∴AD=CD,DG=DE,且∠ADC=∠GDE=90°,
∴∠ADG=∠CDE,在△ADG与△CDE中,
AD=CD∠ADG=∠CDEDG=DE,∴△ADG≌△CDE(SAS),∴AG=CE;(2)CE与DG交点为O,∵△ADG≌△CDE,
∴∠DEC=∠AGD,∵∠DEC ∠DOE=90°,∴∠AGD
∠DOE=90°=∠AGD ∠GOH,∴∠GHE=90°;(3)过点D作MD⊥AG,DN⊥CE,∵△ADG≌△CDE,
∴S△DCE=S△ADG,∴12×CE×DN=12×AG×DM,
∴DM=DN,且MD⊥AG,DN⊥CE,∴DH平分∠AHE。
