动态分析法时间数列分析法
合集下载
统计学基础-时间数列分析
• （二）平均发展水平 • 概念：根据时间数列中各个不同时期发展水平加以平均而得到
的平均数。又叫序时平均数或动态平均数。
总量指标时间数列序时平均数的计算 • 计算 相对指标时间数列序时平均数计算
平均指标时间数列序时平均数计算
二、时间数列的水平分析指标
• （二）平均发展水平 • 1.总量指标时间数列序时平均数的计算 • （1)由时期数列计算序时平均数
• 基期 • 不同 • 分类
逐期增长量：是本期水平比上一期水平增长的绝对数量。
累计增长量：是本期水平比某一固定时期水平增长的绝对 数量，说明某一段时期内总的增长量。
二、时间数列的水平分析指标
• （三）增长量 • 年距增长量=报告期水平-上年同期发展水平
各期逐期增长量之和等于相应时期的累计增长量 • 关系
• 影响现象变动的因素： • 1.长期趋势：现象在相当长的时期内持续发展变化的趋势，它
是由各个时期普遍、持续、决定性的基本因素所左右，是各期 发展水平沿着一个方向上升或者下降的趋势变动。 • 2.季节变动：现象因受自然条件和社会因素的影响，在一年或 更短的时间内所产生的具有周期性、规律性的重复变动。
四、时间数列的变动趋势分析
（一）时间数列变动趋势分析的意义
社会经济现象的发展变化，是许多因素共同作用的结果。这
些因素起推动和制约作用，彼此之间的关系也错综复杂。为了分
析时间数列的发展变化规律，必须把影响时间数列的各种因素分
开，找出它们的变动规律。 长期趋势
基本因素 季节变动
分类
循环变动
偶然因素：不规则变动
• （一）发展速度和增长速度 • 2.增长速度
概念：表明现象增长程度的相对指标，说明报告期水平比基 期水平增加的程度。
的平均数。又叫序时平均数或动态平均数。
总量指标时间数列序时平均数的计算 • 计算 相对指标时间数列序时平均数计算
平均指标时间数列序时平均数计算
二、时间数列的水平分析指标
• （二）平均发展水平 • 1.总量指标时间数列序时平均数的计算 • （1)由时期数列计算序时平均数
• 基期 • 不同 • 分类
逐期增长量：是本期水平比上一期水平增长的绝对数量。
累计增长量：是本期水平比某一固定时期水平增长的绝对 数量，说明某一段时期内总的增长量。
二、时间数列的水平分析指标
• （三）增长量 • 年距增长量=报告期水平-上年同期发展水平
各期逐期增长量之和等于相应时期的累计增长量 • 关系
• 影响现象变动的因素： • 1.长期趋势：现象在相当长的时期内持续发展变化的趋势，它
是由各个时期普遍、持续、决定性的基本因素所左右，是各期 发展水平沿着一个方向上升或者下降的趋势变动。 • 2.季节变动：现象因受自然条件和社会因素的影响，在一年或 更短的时间内所产生的具有周期性、规律性的重复变动。
四、时间数列的变动趋势分析
（一）时间数列变动趋势分析的意义
社会经济现象的发展变化，是许多因素共同作用的结果。这
些因素起推动和制约作用，彼此之间的关系也错综复杂。为了分
析时间数列的发展变化规律，必须把影响时间数列的各种因素分
开，找出它们的变动规律。 长期趋势
基本因素 季节变动
分类
循环变动
偶然因素：不规则变动
• （一）发展速度和增长速度 • 2.增长速度
概念：表明现象增长程度的相对指标，说明报告期水平比基 期水平增加的程度。
第七章.时间序列(平均发展水平)
1950-1998年中国水灾受灾面积(单位：千公顷）
二、时间数列的种类
按数列中所排列指标的表现形式不同分为：
绝对数数列
时期数列 （总量指标数列） 时点数列
相对数数列 （相对指标数列）
平均数数列 （平均指标数列）
时期序列与时点序列的区别
如果数列中变量反映现象在各段时期内发展过程的总量， 即为时期序列。 其特点是：第一，数列中各变量值可以累计相加。 第二，变量值大小随时间长短而变动。 第三，数据的取得一般采用连续登记的方法。 如果数列中变量反映现象在某一时点上所处的状态，即为 时点序列。 其特点是：第一，数列中变量值不能相加。 第二，变量值大小与时间长短没有直接关系。 第三，数据的取得一般采用间断登记的方法。
【例】某商业企业2006年第二季度某商品库存 资料如下，求第二季度的月平均库存额 时间 库存量(百件) 3月末 4月末 5月末 6月末 66 72 64 68
解：第二季度的月平均库存额为：
66 68 72 64 2 67.67 百件 a 2 4 1
※间隔不相等 时，采用加权序时平均法
构成要素：
现象所属的时间
反映现象发展水平的指标数值
研究的目的
1、描述社会经济现象的发展状况和 结果; 2、研究社会经济现象的发展速度、 发展趋势和平均水平，探索社会经济 现象发展变化的规律，并据以对未来 进行统计预测；
3、利用不同的但互相联系的时间数 列进行对比分析或相关分析。
要素一：时间t
年份 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988
②该企业第二季度的月平均劳动生产率：
a 10000 12 .6 14 .6 16 .3 3 c 2200 b 2000 2000 2200 4 1 2 2 6904 .76 元 人
第六章 时间数列分析
例如，某企业资料如表6-9,求平均职工人数及平均固定资产 额。
表6-9 某企业上半年统计资料
月 份 1月 2月 3月 4月 5月 6月 7月 月初职工数 （人） 124 126 124 122 126 128 124 月初固定资产额（万元） 60 60 61 64 64 70 70 其计算公式为：平均数=（期初数+期末数）/2 在这里，可将本月期初数当作上月期末数，因为本月初与上 月末这两个时点一般是同一数值。同理，可将本月期末数当作上 月期初数。因此，各月平均数如下： 1月平均人数 = （124+126）/2 = 125(人) 2月平均人数 = （126+124）/2 = 125(人) 3月平均人数 = （124+122）/2 = 123(人) 4月平均人数 = （122+126）/2 = 124(人) 5月平均人数 = （126+128）/2 = 127(人) 6月平均人数 = （128+124）/2 = 126(人)
表6-8 某企业六月份职工平均人数计算表
日期
日数f
人数a
af
1～8 9～15 16～25 26～30 合 计
8 7 10 5 30
500 510 520 516 —
4000 3570 5200 2580 15350
af 15350 511.7 512人 a 30 f （2）间断时点数列序时平均数的计算 ①间隔相等间断时点数列序时平均数的计算 首先将期初值加期末值除以2得出本期平均值，然后将各时 段平均值相加除以间隔期数则得该时点数列的序时平均数。
表6-5 某商场销售资料（单位：万元）
时 间 平均销售额
一季度 800
二季度 850
统计学第八章时间数列
2020/1/19
增长速度growth rate 表明现象的增长程度
某现 基象 期报 水 告 平 报期 告 基的 期 期 基 增 水 水 期 长 平 平 发 水 量 展 平 1速
环比增长速度=环比发展速度-1 定基增长速度=定基发展速度-1
2020/1/19
增 1长 的 % 绝 环 对 逐 比 期 增 1 值 增 0 长 0上 长 1速 0 期 量 0度 水平
n 1
n 1
（5）间隔不相等不连续时点的时点数列
2020/1/19
aa1 2a2t1a2 2a3t2an12 antn1 t1t2tn1
增长量和平均增长量 •增长量growth amount
总量指标报告期水平与基期水平之差，表明 该指标在一定时期内增加或减少的绝对数量。
社会经济现象以若干年为周期的 涨落起伏相同或基本相同的一种 波浪式的变动
随机变动（I）
客观社会经济现象由于天灾、人 祸、战乱等突发事件或偶然因素 引起是无周期性波动
2020/1/19
一般模型 加法模型
Y=T+S+C+I
乘法模型 Y=T×S×C×I
分解方法
加法模型 T=Y-（S+C+I）
乘法模型
2020/1/19
✓水平法（几何平均法）
n
X
n
Xi
i1
n
an a0
适用：水平指标的平均发展速度计算
2020/1/19
✓方程法（累计法）
a 0 x a 0 x 2 a 0 x 3 a 0 x n a i
xx2x3xnai a0
适用：侧重于考察中长期间的累计总量
平均增长速度 = 平均发展速度-100% 表明现象在一个较长时期中逐期平均增长变化的程度
统计学基础第五章动态数列分析
统计学基础第五章动态数列分析【教学目的】1.区分不同种类的动态数列2.熟练掌握计算平均发展水平的各种方法3.掌握发展速度、增长速度的种类，运用它们之间的数量关系进行动态指标的相互推算4.理解趋势的意义，运用长期趋势测定方法对长期趋势进行测定5.计算季节比率，并且深刻理解季节比率的经济含义【教学重点】1.总量指标动态数列的种类和特点2.动态比较指标和动态平均指标的计算3.动态数列的分析方法【教学难点】1.绝对数时间数列中的时点数列平均指标的计算2.相对数、平均数时间数列动态平均指标的计算3.动态数列分析方法中的季节变动分析方法【教学时数】教学学时为12课时【教学内容参考】第一节动态数列的意义和种类一、动态数列的概念将某一个统计指标在不同时间上的各个数值，按时间先后顺序排列，就形成了一个动态数列，也叫做时间数列。
动态数列一般由两个基本要素构成：一是被研究现象所属的时间；二是反映该现象的统计指标数值。
通过编制和分析动态数列，首先可以从现象的量变过程中反映其发展变化的方向、程度和趋势，研究其质量变化的规律性。
其次，通过对动态数列资料的研究，可以对某些社会经济现象进行预测。
第三，利用动态数列，可以在不同地区或国家之间进行对比分析。
编制和分析动态数列具有非常重要的作用，这种方法已成为对社会经济现象进行统计分析的一种重要方法。
【案例】下面图表列举了我国2004～2007年若干经济指标的动态数列。
表5-1 我国2004-2007年若干经济指标二、动态数列的种类按照构成动态数列的基本要素———统计指标的表现形式不同，动态数列可分为绝对数动态数列、相对数动态数列和平均数动态数列三种类型。
其中绝对数动态数列是基本的数列，相对数和平均数动态数列是派生数列。
(一)绝对数动态数列在这种动态数列中，统计指标值表现为总量指标。
根据指标值的时间特点，又可分为时期数列和时点数列。
国内生产总值就是时期数列，年底人口数就是时点数列。
1.时期数列时期数列中，每一指标值反映在一段时期内发展的结果，即“过程总量”。
第七章 时间数列分析
二、时间序列的种类
㈠总量指标时间序列 ㈡相对指标时间序列 ㈢平均指标时间序列
（三）平均数时间序列：把一系列同类平均数按时间顺序排列 而成的数列，反映现象一般水平的发展变化过程．
A、种类：静态、动态两种。 B、各期指标数值不可直接相加。
某地积累率及职工年平均工资资料 时间 2002 2003 2004 2005 积累率% 23.76 26.39 24.21 27.81 平均工资（元） 2200 2450 3010 3280
法也有所不同。
（1）时期序列的序时平均数。时期序列中的各观察值可以相 加，形成一段时期内的累计总量，所以时期序列的序时平均 数可直接用各时期的指标值之和除以时期项数来计算。
a1 a 2
an -1 a n
a
a1 a2 L an a n
a
i 1
n
i
n
根据表中的国内生产总值序列，计算2002—2006年的年平 均国内生产总值。
总规模和总水平及其发展变化的情况 。
A、种类：时期指标时期数列；时点指标时点数列。 B、时点：“某一瞬间”日、 月（季、年）初、末。 C、间隔：相邻两个时点之间的时间跨度 f；
我国国内生产总值等时间数列 2004 2005 2006 2007 136515 182321 210871 257306 129988 130756 131448 132129
年份 GDP （亿元） 年末人口数 （万人） 人均GDP （元/人） 职工平均工资 (元)
2002 102398 128045 7997 12422 9371 2003a 116694 129227 14040 a 简单算术平均法, ai:各期发展水平；n:时期项数 n 10502 2004 136515 129988 16024 102398 116694 136515 182321 210871 2005 13926 149759 .8(亿元） 182321 130756 18405 5 16084 2006 210871 131448 21001
统计学原理第四章动态数列
第三节 动态数列速度分析指标
动态数列的速度分析指标，也即反映国 民经济速度的主要指标有发展速度 增 发展速度、增 发展速度 长速度、平均发展速度 平均增长速度。 平均发展速度和平均增长速度 长速度 平均发展速度 平均增长速度 其中发展速度是最基本的速度分析指标。
一、发展速度和增长速度 （一）发展速度
(2)由时点数列计算序时平均数。 1 根据连续时点数列计算序时平均数。 a 对连续变动的连续时点数列求序时平均数。 简单算术平均数
∑a a=
n
b 对非连续变动的连续时点数列求序时平均数。 加权算术平均数
∑ af a= ∑f
2 根据间断时点数列计算序时平均数。 a 对间隔相等的间隔时点数列求序时平均数。 简单算术平均数 某企业1998年第二季度商品库存额 某企业 年第二季度商品库存额
这种计算方法称为“首末折半法 首末折半法”。 首末折半法
b 对间隔不等的间隔时点数列求序时平均数。 a1 + a2 a2 + a3 an−1 + an f1 + f2 +L+ fn−1 2 2 a= 2
∑f
i =1
n−1
i
某农场某年生猪存栏数
1月1日 3月1日 8月1日 10月1日 12月31日 日期 月 日 月 日 月 日 月 日 月 日 生猪存栏数(头 1200 1250 1460 生猪存栏数 头) 1420 1400
特点： (1)数列中各个指标的数值是可以相加的，即相 加具有一定的经济意义。 (2)数列中每一个指标数值的大小与所属的时期 长短有直接的联系。 (3)数列中每个指标的数值，通常是通过连续不 断的登记而取得的。
2、时点数列 在绝对数动态数列中，如果各项指标都是反映某 种现象在某一时点（瞬间）上所处的数量水平， 这种绝对数动态数列就称为时点数列。 特点： (1)数列中各个指标的数值是不能相加的，相加 不具有实际经济意义。 (2)数列中每一个指标数值的大小与其时间间隔 长短没有直接联系。 (3)数列中每个指标的数值，通常是通过一定时 期登记一次而取得的。
时间数列分析
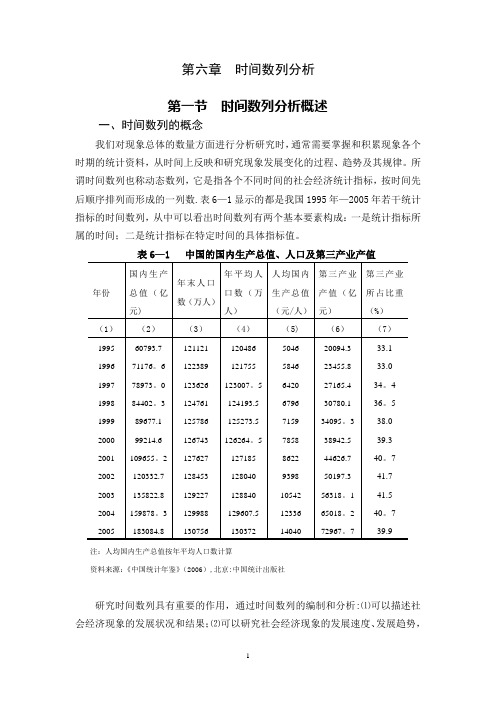
第六章时间数列分析第一节时间数列分析概述一、时间数列的概念我们对现象总体的数量方面进行分析研究时，通常需要掌握和积累现象各个时期的统计资料，从时间上反映和研究现象发展变化的过程、趋势及其规律。
所谓时间数列也称动态数列，它是指各个不同时间的社会经济统计指标，按时间先后顺序排列而形成的一列数.表6—1显示的都是我国1995年—2005年若干统计指标的时间数列，从中可以看出时间数列有两个基本要素构成：一是统计指标所属的时间；二是统计指标在特定时间的具体指标值。
表6—1 中国的国内生产总值、人口及第三产业产值注：人均国内生产总值按年平均人口数计算资料来源：《中国统计年鉴》（2006）,北京:中国统计出版社研究时间数列具有重要的作用，通过时间数列的编制和分析:⑴可以描述社会经济现象的发展状况和结果；⑵可以研究社会经济现象的发展速度、发展趋势，探索现象发展变化的规律,并据以进行统计预测；⑶分析长期趋势、季节变动和循环变动等了解和分析社会现象发展变化的规律性。
二、时间数列的种类时间数列按照其指标的性质，可以分为总量指标、相对指标和平均指标时间数列等三大类型。
总量指标时间数列也称绝对数时间数列，是基本的时间数列，相对指标和平均指标时间数列都是在总量指标时间数列的基础上派生出来的。
㈠总量指标时间数列总量指标时间数列是指把一系列同类的总量指标按时间先后顺序排列起来形成的时间数列。
它反映社会经济现象在各个时期达到的绝对水平及其变化发展的状态。
表6—1中的国内生产总值、年末人口和第三产业产值都属于总量指标时间数列。
按照总量指标所反映的内容的不同，可以分为总体单位总量和总体标志总量两种。
年末人口数是总体单位总量指标，而国内生产总值和第三产业产值是总体标志总量指标.根据总量指标反映的社会经济现象所属的时间不同，又可将总量指标时间数列分为时期数列和时点数列。
下面来讨论时期数列和时点数列的特点.⒈时期序列各项指标都是反映某种现象在一段时期内发展过程的总量,该时间数列称为时期序列。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（二）平均增长量
1.概念 2.计算 3.预测公式 若现象在一定时期内的逐期增长量大体相
同 ，其平均增长量可作为预测的依据，其一般公 式为
aˆ tk a t k
第三节 动态数列的速度指标 （现象发展的速度）
一、发展速度和增长速度 （一）发展速度 （二）增长速度 二、平均发展速度和平均增长速度 （一） 概念 （二）计算（平均发展速度的计算）
Ⅰ.由时期数列计算序时平均数
a a1 a2 an a
n
n
① 总量指标动态数列 序时平均数的计算（Ⅱ）
Ⅱ.由时点数列计算序时平均数：
由时点数列计算序时平均数，实际上是按照一定条件 推算出来的近似值。这个条件就是假定在相邻时点之间现 象是均匀变动的。
时点间连断续时时点点间 间间 间隔 隔隔 隔不 相不 相等 等等 等（ （（ （DCBA）） ））
第二年 65 112.1 130.0 109.9 120.7 60.4 111.9 125.3 62.6
第三年 74 113.8 148.0 109.9 132.6 66.3 111.9 140.2 70.1
第四年 78 105.4 156.0 109.9 145.6 72.9 111.9 156.9 78.5
1.时距扩大法
例如：现将某工厂1998年各月总产值和职工人数资料列 表如下：
月份 1
2
3
4
5
6
7
8
9
10
11
12
1
总产值 40.5 35.0 42.0 41.5 40.4 45.4 46.0 48.4 49.0 51.0 50.5 54.2 ----
(C)在掌握间隔相等间断时点资料时
a
a1 2
a2
a3
an 2
a1
an 2
n 1
ai
i2
n 1
n 1
例（D）
已知某地区1997年各时点的人口数资料如下：
1月1日
6月1日
8月1日 12月31日
21.3万人 21.35万人 21.36万人 21.5万人 试计算该地区该年人口的月平均数。
例：(2)
某贸易企业1998年第一季度各月份商品流转速度资 料如下:
一月
二月
三月
平均
商 品 销 售 额 120
143
289
184
（a）
平均库存额
60
65
85
70
（b）
商品流转次数 2.0
2.2
3.4
2.63
（c）
试计算企业第一季度的月平均商品流转次数及季
度流转次数。
二、增长量和平均增长量
（一）增长量 1.概念 2.分类 3.年距增长量
平均指标动
态数列动 静态 态平 平均 均指 指标 标动 动态 态数 数列 列
三、编制时间数列的要求
基本原则—保证动态数列中各指标数值的可比性
1.时间长短应统一； 2.总体范围应统一； 3.计算要统一； 4.经济内容要一致。
必须指出：对可比性的理解不能绝对化。比如有 时为了特殊目的，也可以把时期长短不同的指标编 成动态数列。
上年 第 一 第 二 第 三 第 四 年平
末
季末 季末 季末 季末 均
零售企业数 （b） 职工人数
（a） 每企业职工 人数（c）
250 1400 5.6
256 1408 5.5
255 1479 5.8
304 1520 5.0
320 1536 4.8
275 1469 5.3
试计算该年月平均每网点职工人数。
一、发展水平和平均发展水平
（一）发展水平 1.概念 2.种类
（二）平均发展水平 1.概念 2.计算 （序时平均数的计算方法）
①总量指标动态数列序时平均数的计算—基本方法 Ⅰ.由时期数列计算序时平均数 Ⅱ.由时点数列计算序时平均数： ②相对指标或平均指标动态数列序时平均数的计算
—派生方法
① 总量指标动态数列 序时平均 数的计算（Ⅰ）
a0
n为间隔年数
M 1 n M 1 n
增长 下降
3.两种方法有何区别及使用范围
①区别
从速度看 几何平均法
n
x
yn
yn
高次方程法
2
xx
3
x
xn
a 0 yn an a n 高次方程法 a0 x a0 x2 a0 x3 a0 xn a a
作趋势预测，为社会经济服务；
②研究各种现象之间的内在联系和依存关系；
③系统积累资料的方法之一。
二、时间数列的种类
A、数值统计
动态数列总相量对指指标标动动态态数数列列时 时 —点 期 有数 数 六列 列 种区 形别 式DCB、 、 、数 相 时值 加 间大 运 关小 算 系
第五年 80 102.6 160.0 109.9 160.0 80.0 111.9 175.7 87.8
五年
355
-
710.0
-
668.9 334.6
-
710.0 355.0
合计
第四节 长期趋势和季节变动 （现象发展的趋势）
一、影响动态数列变动的主要因素 二、长期趋势的分析 三、季节变动的分析 四、不规则变动的分析
例（C）
假定某企业1997年第三季度各时点的职工人数资 料如下 ：
6月30日 7月31日 8月31日 9月30日
1200人
1260人
1254人
试求第三季度的月平均人数。
1290人
解：月平均人数
12001260 12601254 12541290
a
2
2
2
1253(人）
4 1
Ⅱ.由时点数列计算序时平均数：(C)
②预测公式 若某种现象在一定时期内的各环比发展（或增长）
速度大体相同，则可依次作为预测的依据。预测模型为：
k
atk at x
2.高次方程法（累积法）
n
x
n 1
x
x3
2
x
x
a
0
a0
计算
用试根法计算近似值 x 2 x1 f x1 f x1 查《累积法平均增长速度查对表》 M a 100%
一、影响动态数列变动的主要因素
四个部分（分量）长季期节趋波势动（（TS））
不循规环则波变动动（（C）I）合并 成循 环波 动— 不规 则变 动的 分量 （I C）
动态数列各期发展水平 y=T·S·IC
二、长期趋势的分析
（一）长期趋势的概念 （二）长期趋势的测定（T）
1.时距扩大法： 2.移动平均法： 3. 数学模型法： ① 直线修匀法（直线趋势配合法） ②曲线修匀法（曲线趋势配合法）
Ⅱ.由时点数列计算序时平均数：(A)
（A）在掌握间隔相等的连续时点资料时
a a1 a2 an a
n
n
例（B）
某单位人事部门对本单位在册职工人数有如下记录：
1月1日 1月11日 1月16日 1月25日 2月5日
218人 调出18人 调入6人 调入9人 调出4人 问：1月份该单位职工在册人数是多少？ 解：日平均在册人数
动态分析指标平平发增均均展长增发速速长展度度量速度
平均增长速度
水平指标—现象发展的水平分析 速度指标—现象发展的速度分析
第二节 动态数列的水平指标 （现象发展的水平）
一、发展水平和平均发展水平
（一）发展水平 （二）平均发展水平
二、增长量和平均增长量
（一）增长量 （二）平均增长量
第五章 动态分析法 —时间数列分析法
第一节 时间数列的一般问题
第二节 动态数列的水平指标 （现象发展的水平）
第三节 动态数列的速度指标 （现象发展的速度）
第四节 长期趋势和季节变动 （现象发展的趋势）
第一节 时间数列的一般问题
一、时间数列的意义
1.概念： 2.构成： 3.作用：
二、时间数列的种类 三、编制时间数列的要求（原则）
（一）发展速度
1.概念
发展速度是表明现象发展程度的相对指标，是两个时
期发展水平指标对比的结果，
即发展速度
报告期水平 基期水平
a1 a0
2.分类：
环比发展速度 由于采用的基期不同，发展速度可分为 定基发展速度
（二）增长速度
1.概念 增长速度是表明现象增长程度的相对指标，
是报告期增长量对比基期水平而得。
2.分类： 由于采用的基期不同，增长速度可分为
环比增长速
度
定基增长速度
3.在统计实务中，为消除季节变动的影响，还使 用年距发展速度和年距增长速度。
4. 为 进 一 步 对 比 分 析 现 象 的 增 长 情 况 ， 需 运 用 “增长1%的绝对值指标”指标。
3.年距发展速度和年距增长速度
年距发展速度
1.几何平均法（水平法）
① 计算公式
xG n a1 a2 a3 an n an n R (R表示总发展速度）
a0 a1 a2
a n1 a0
或xG n x1 x2 x3 xn n x n R (x表示环比发展速度）
结果的计算
用对数表计算
用《水平法平均增长速度查对表》
最末一年的定基发展速度 各年定基发展速度的总和 最末一年的定基发展水平 各年发展水平的总和
② ②适用现象 几何平均法—以年发展水平表现的国家长期
计划指标，如：产量、产值、商品的销售额等指标 。
高次方程法—以若干年累积数表现的国家
1.概念 2.计算 3.预测公式 若现象在一定时期内的逐期增长量大体相
同 ，其平均增长量可作为预测的依据，其一般公 式为
aˆ tk a t k
第三节 动态数列的速度指标 （现象发展的速度）
一、发展速度和增长速度 （一）发展速度 （二）增长速度 二、平均发展速度和平均增长速度 （一） 概念 （二）计算（平均发展速度的计算）
Ⅰ.由时期数列计算序时平均数
a a1 a2 an a
n
n
① 总量指标动态数列 序时平均数的计算（Ⅱ）
Ⅱ.由时点数列计算序时平均数：
由时点数列计算序时平均数，实际上是按照一定条件 推算出来的近似值。这个条件就是假定在相邻时点之间现 象是均匀变动的。
时点间连断续时时点点间 间间 间隔 隔隔 隔不 相不 相等 等等 等（ （（ （DCBA）） ））
第二年 65 112.1 130.0 109.9 120.7 60.4 111.9 125.3 62.6
第三年 74 113.8 148.0 109.9 132.6 66.3 111.9 140.2 70.1
第四年 78 105.4 156.0 109.9 145.6 72.9 111.9 156.9 78.5
1.时距扩大法
例如：现将某工厂1998年各月总产值和职工人数资料列 表如下：
月份 1
2
3
4
5
6
7
8
9
10
11
12
1
总产值 40.5 35.0 42.0 41.5 40.4 45.4 46.0 48.4 49.0 51.0 50.5 54.2 ----
(C)在掌握间隔相等间断时点资料时
a
a1 2
a2
a3
an 2
a1
an 2
n 1
ai
i2
n 1
n 1
例（D）
已知某地区1997年各时点的人口数资料如下：
1月1日
6月1日
8月1日 12月31日
21.3万人 21.35万人 21.36万人 21.5万人 试计算该地区该年人口的月平均数。
例：(2)
某贸易企业1998年第一季度各月份商品流转速度资 料如下:
一月
二月
三月
平均
商 品 销 售 额 120
143
289
184
（a）
平均库存额
60
65
85
70
（b）
商品流转次数 2.0
2.2
3.4
2.63
（c）
试计算企业第一季度的月平均商品流转次数及季
度流转次数。
二、增长量和平均增长量
（一）增长量 1.概念 2.分类 3.年距增长量
平均指标动
态数列动 静态 态平 平均 均指 指标 标动 动态 态数 数列 列
三、编制时间数列的要求
基本原则—保证动态数列中各指标数值的可比性
1.时间长短应统一； 2.总体范围应统一； 3.计算要统一； 4.经济内容要一致。
必须指出：对可比性的理解不能绝对化。比如有 时为了特殊目的，也可以把时期长短不同的指标编 成动态数列。
上年 第 一 第 二 第 三 第 四 年平
末
季末 季末 季末 季末 均
零售企业数 （b） 职工人数
（a） 每企业职工 人数（c）
250 1400 5.6
256 1408 5.5
255 1479 5.8
304 1520 5.0
320 1536 4.8
275 1469 5.3
试计算该年月平均每网点职工人数。
一、发展水平和平均发展水平
（一）发展水平 1.概念 2.种类
（二）平均发展水平 1.概念 2.计算 （序时平均数的计算方法）
①总量指标动态数列序时平均数的计算—基本方法 Ⅰ.由时期数列计算序时平均数 Ⅱ.由时点数列计算序时平均数： ②相对指标或平均指标动态数列序时平均数的计算
—派生方法
① 总量指标动态数列 序时平均 数的计算（Ⅰ）
a0
n为间隔年数
M 1 n M 1 n
增长 下降
3.两种方法有何区别及使用范围
①区别
从速度看 几何平均法
n
x
yn
yn
高次方程法
2
xx
3
x
xn
a 0 yn an a n 高次方程法 a0 x a0 x2 a0 x3 a0 xn a a
作趋势预测，为社会经济服务；
②研究各种现象之间的内在联系和依存关系；
③系统积累资料的方法之一。
二、时间数列的种类
A、数值统计
动态数列总相量对指指标标动动态态数数列列时 时 —点 期 有数 数 六列 列 种区 形别 式DCB、 、 、数 相 时值 加 间大 运 关小 算 系
第五年 80 102.6 160.0 109.9 160.0 80.0 111.9 175.7 87.8
五年
355
-
710.0
-
668.9 334.6
-
710.0 355.0
合计
第四节 长期趋势和季节变动 （现象发展的趋势）
一、影响动态数列变动的主要因素 二、长期趋势的分析 三、季节变动的分析 四、不规则变动的分析
例（C）
假定某企业1997年第三季度各时点的职工人数资 料如下 ：
6月30日 7月31日 8月31日 9月30日
1200人
1260人
1254人
试求第三季度的月平均人数。
1290人
解：月平均人数
12001260 12601254 12541290
a
2
2
2
1253(人）
4 1
Ⅱ.由时点数列计算序时平均数：(C)
②预测公式 若某种现象在一定时期内的各环比发展（或增长）
速度大体相同，则可依次作为预测的依据。预测模型为：
k
atk at x
2.高次方程法（累积法）
n
x
n 1
x
x3
2
x
x
a
0
a0
计算
用试根法计算近似值 x 2 x1 f x1 f x1 查《累积法平均增长速度查对表》 M a 100%
一、影响动态数列变动的主要因素
四个部分（分量）长季期节趋波势动（（TS））
不循规环则波变动动（（C）I）合并 成循 环波 动— 不规 则变 动的 分量 （I C）
动态数列各期发展水平 y=T·S·IC
二、长期趋势的分析
（一）长期趋势的概念 （二）长期趋势的测定（T）
1.时距扩大法： 2.移动平均法： 3. 数学模型法： ① 直线修匀法（直线趋势配合法） ②曲线修匀法（曲线趋势配合法）
Ⅱ.由时点数列计算序时平均数：(A)
（A）在掌握间隔相等的连续时点资料时
a a1 a2 an a
n
n
例（B）
某单位人事部门对本单位在册职工人数有如下记录：
1月1日 1月11日 1月16日 1月25日 2月5日
218人 调出18人 调入6人 调入9人 调出4人 问：1月份该单位职工在册人数是多少？ 解：日平均在册人数
动态分析指标平平发增均均展长增发速速长展度度量速度
平均增长速度
水平指标—现象发展的水平分析 速度指标—现象发展的速度分析
第二节 动态数列的水平指标 （现象发展的水平）
一、发展水平和平均发展水平
（一）发展水平 （二）平均发展水平
二、增长量和平均增长量
（一）增长量 （二）平均增长量
第五章 动态分析法 —时间数列分析法
第一节 时间数列的一般问题
第二节 动态数列的水平指标 （现象发展的水平）
第三节 动态数列的速度指标 （现象发展的速度）
第四节 长期趋势和季节变动 （现象发展的趋势）
第一节 时间数列的一般问题
一、时间数列的意义
1.概念： 2.构成： 3.作用：
二、时间数列的种类 三、编制时间数列的要求（原则）
（一）发展速度
1.概念
发展速度是表明现象发展程度的相对指标，是两个时
期发展水平指标对比的结果，
即发展速度
报告期水平 基期水平
a1 a0
2.分类：
环比发展速度 由于采用的基期不同，发展速度可分为 定基发展速度
（二）增长速度
1.概念 增长速度是表明现象增长程度的相对指标，
是报告期增长量对比基期水平而得。
2.分类： 由于采用的基期不同，增长速度可分为
环比增长速
度
定基增长速度
3.在统计实务中，为消除季节变动的影响，还使 用年距发展速度和年距增长速度。
4. 为 进 一 步 对 比 分 析 现 象 的 增 长 情 况 ， 需 运 用 “增长1%的绝对值指标”指标。
3.年距发展速度和年距增长速度
年距发展速度
1.几何平均法（水平法）
① 计算公式
xG n a1 a2 a3 an n an n R (R表示总发展速度）
a0 a1 a2
a n1 a0
或xG n x1 x2 x3 xn n x n R (x表示环比发展速度）
结果的计算
用对数表计算
用《水平法平均增长速度查对表》
最末一年的定基发展速度 各年定基发展速度的总和 最末一年的定基发展水平 各年发展水平的总和
② ②适用现象 几何平均法—以年发展水平表现的国家长期
计划指标，如：产量、产值、商品的销售额等指标 。
高次方程法—以若干年累积数表现的国家