统计曲线表
几种常见的统计图表

R
W
扇形图(sector diagram)
概念:以一个圆面积为100%,用圆内 各扇形面积所占的百分比来表示各 部分所占的构成比例 适用资料:构成比资料 绘制要点: ①每3.6o为1%,用3.6乘以百分数即为 请问:如何表示 所占扇形的度数。用量角器画出. 扇形内各部分所 ②从相当于时钟12点或9点的位置开始 顺时针方向绘图. ③每部分用不同线条或颜色表示,并在 图上标出百分比,下附图例说明. ④当比较不同资料的百分构成时,可以 画两个相等大小的圆,在每个圆的 下面写明标题,并用相同的图例表 示同一个构成部分. 应用:描述各部分的百分构成.
展变化或一种现象随另一种现象变迁的情况 2、适用资料:连续性资料。 3、绘制要点: ①坐标轴:横轴表示时间或组段,纵轴表示频数或频率。 纵轴坐标可以不从0开始,因此在看图时要注意纵轴的 起点坐标。 ②数据点画在组段中间位置。相邻的点用直线连接,不要 用平滑的曲线连接。无数据的组段用虚线连接。直线 不能任意外延。 ③同一张折线图上不要画太多条曲线,否则不易分清。当 有两条或两条以上曲线在同一张折线图上时,须用不 同颜色或不同的图形形式加以区分,并附图例加以说 明。 4、应用:反映事物的连续的动态变化规律。
190 180 170 160 150 40 45 50 ©Û ¤ 55 Ç ª± (cm)
ì ß É µ (cm)
Í 10.Ä ³ 20Ë Ä Ç Ä É µ · Ç Û ± Ä ¶ Ï ¼ ± Ø ê Ð ê ì ß Í ©ª¤³ Ø ³
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 5 10 15 20 25 30
9% 18% 43%
ô · « ² È Ï ä Æ
ü ³ ° ¡ Î Ï ¼ ° ¾ ¡ È ° ë Ô ° ¡ Ì Ð ¼ ° ü Ë
SPSS常用统计图

4
198.4
22.67
13
209.5
28.49
5
199.4
6
199.9
7
200.9
8
201.1
9
201.4
据建文立件第数,1步
执行
Graph sSca
tter/do
例:绘制质量控制图
并采用措施来及时纠正某些不良趋势。
• SPSS中质量控制图包括:
• 均值-极差控制图(均值-标准差控制图)、
个值-移动极差控制图、不合格品率和不合
格品控制图、缺陷数和单位缺陷数控制图4
种。我们仅以均值-极差控制图为例。
• 执行GraphControl命令,弹出对话框:
第35页,共65页。
用来直观表示数据是否服从特定分布
描述一组或几组数据随另一序列性变量变化的趋势。
描述与时间相关的变量随着时间变化的趋势。
第4页,共65页。
2 条图
• 条图用于描述定类或定序变量的分布,有3种条图:简 单条图、分组条图、分段条图。
条图
简单条图
分组条图
第5页,共65页。
分段条图
简单条图
• 从菜单选择“GraphsBars”弹出Bar Charts对话框
简单Pareto图
分段Pareto图
图中数据表示
观测量分类描述 变量描述模式 观测值描述模式
例(超市.sav)
类别
甲地区 营业额
乙地区 营业额
食品
5660
4000
生活用品
2148
1500
家电
12400 14000
办公用品
645
700
1.绘制甲地区Pareto图
96芯中继段测试表格(自动曲线)

55 0.063
0.063 0.019
56 0.054
0.054 0.017
57 0.063
0.063 0.019
58 0.063
0.063 0.019
59 0.056
0.056 0.017
60 0.065
0.065 0.020
61 0.056
0.056 0.017
62 0.070
0.070 0.021
95 0.054
0.054 0.016
96 0.062
0.062 0.019
中继段: 澄县古徵街公园光交-烟草局机房
波长: 1310nm
配盘序号
光纤长度(km) 0.306
接头编号
1# 2#
光纤接头衰减统计表
中继段纤长: 0.306 km 通道(光纤)
平均衰减 总衰减 3# 4# 5# 6# 7# (db/km) (db)
63 0.057
0.057 0.017
64 ห้องสมุดไป่ตู้.058
0.058 0.018
65 0.051
0.051 0.016
66 0.051
0.051 0.016
67 0.065
0.065 0.020
68 0.065
0.065 0.020
69 0.057
0.057 0.018
70 0.051
0.051 0.016
71 0.050
0.050 0.015
72 0.058
0.058 0.018
73 0.061
0.061 0.019
74 0.054
0.054 0.016
75 0.064
0.064 0.020
应用统计学第2章--统计表统计图

接收区间——各组上限值组成的一列区域 功能:返回各组的频数。
②使用【工具】→“数据分析”→“直方图”功 能
其它数值数据统计图
统计图可以形象、直观、生动、简洁地显示数 据的特征。 常用的统计图有以下几种: 1.折线图 ——通常用来描述时间序列数据,用以表示某 些指标的变化趋势。 制作折线图时应正确选择坐标轴轴的刻度。对 同样的统计资料,延伸或压缩某一坐标轴可能 传达不同的甚至是误导的印象。
0—9 10—19 20—29 30—39 40—49 50—59 60—69 70—79 80—89 90以上
未分组数据的茎叶图
• 用于显示未分组的原始数据的分布
• 由“茎”和“叶”两部分构成,其图形是由数字 组成的
• 以该组数据的高位数值作树茎,低位数字作树叶 • 对于n(20≤n≤300)个数据,茎叶图最大行数不超
标签下选“平滑线”复选框,就将折线图转换 为曲线图。
⑵经济管理中几种常见的频数分布曲线
①正态分布曲线 ——这是客观事物数量特征上表现得最为普遍的
一类频数分布曲线。 如人的身高、体重、智商,钢的含碳量、抗拉强
度,某种农作物的产量等等。
正态分布曲线
②偏态曲线
——按其长尾拖向哪一方又可分为右偏(正偏)和 左偏(负偏)两类。
排序是把数据从小到大(或从大到小)进行排列。 (2) 茎叶图
茎叶图就是将数据分成几组(称为茎),每组中数 据的值(称为叶)放置在每行的右边。结果可以显示出数 据是如何分布的,以及数据中心在哪里。
为了制作茎叶图,可以将整数作为茎,把小数(叶) 化整。例如,数值5.40,它的茎(行)是5,叶是4;数值 4.30,它的茎(行)是4,叶是3。也可以将数据的十位数 作为茎,个位数作为叶。
恩格尔曲线与恩格尔系数

• • •
• •
工程经济学
五:恩格尔的调查 自19世纪以来,收入与商品消费之间的关系就被 经济学家所研究。抽样家庭的支出数据经常被收集, 以探求其中的规律。
1853年,经济学家恩格(Engel)尔调查了伯根地区153户家 庭在不同消费项目上的支出情况
年收入 出项目 食 服 品 装 $225—300 62.0 16.0 17.0 年收入 $450—600 55.0 18.0 17.0 7.5 2.5 100.0 年收入 $750—10000 50.0 18.0 17.0 11.5 3.5 100.0
工程经济学
恩格尔曲线
• 恩格尔曲线可以用收入弹性来表示。恩格尔通过把统计调查数据资料 列表,指出一个家庭在食品和其他项目上的开支取决于它的收入和总 的消费开支。随着收入的增加,用于食品的支出部分将下降;用于住 宅和衣服方面的支出将基本保持不变;而用于其他商品的支出会增加。 这种分析的结果被称为恩格尔定律。
房租、照明、燃料
服务(教育、法律、健康) 4.0 旅游和娱乐 总 计 1.0 100.0
工程经济学 六:广泛应用
• • 国际上常常用恩格尔系数来衡量一个国家和地区人民生活水平的状况。 根据联合国粮农组织提出的标准,恩格尔系数在59%以上为贫困,50-59%为 温饱,40-50%为小康,30-40%为富裕,低于30%为最富裕。在中国运用这一 标准进行国际和城乡对比时,要考虑到那些不可比因素,如消费品价格比价 不同、居民生活习惯的差异、以及由社会经济制度不同所产生的特殊因素。 对于这些横截面比较中的不可比问题,在分析和比较时应做相应的剔除。另 外,在观察历史情况的变化时要注意,恩格尔系数反映的是一种长期的趋势, 而不是逐年下降的绝对倾向。它是在熨平短期的波动中求得长期的趋势。
报表曲线图统计测试用例
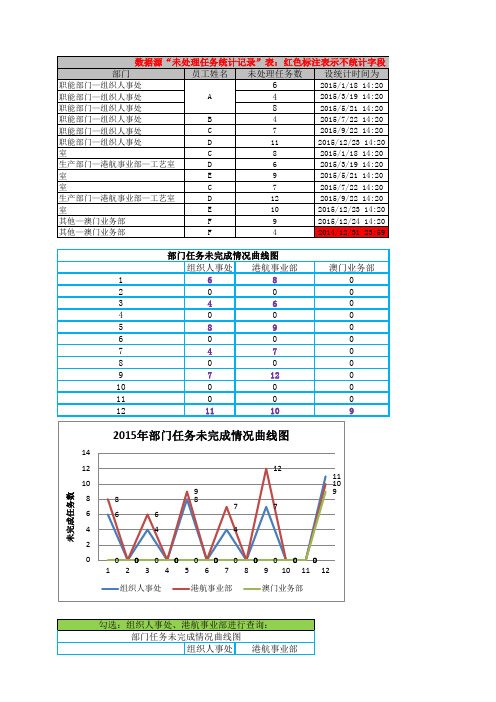
职能部门—组织人事处 职能部门—组织人事处 职能部门—组织人事处 生产部门—港航事业部—水工一室 生产部门—港航事业部—工艺室 生产部门—港航事业部—水工一室 生产部门—港航事业部—水工一室 生产部门—港航事业部—工艺室 生产部门—港航事业部—水工一室 其他—澳门业务部 其他—澳门业务部 B C D C D E C D E F F 4 7 11 8 6 9 7 12 10 9 4 2015/7/22 14:20 2015/9/22 14:20 2015/12/23 14:20 2015/1/18 14:20 2015/3/19 14:20 2015/5/21 14:20 2015/7/22 14:20 2015/9/22 14:20 2015/12/23 14:20 2015/12/24 14:20 2014/12/31 23:59
1 2 3 4 5 6 7 8 9 10 11 12
部门任务未完成情况曲线图 组织人事处 港航事业部 6 8 0 0 4 6 0 0 8 9 0 0 4 7 0 0 7 12 0 0 0 0 11 10
澳门业务部 0 0 0 0 0 0 0 0 0 0 0 9
2015年部门任务未完成情况曲线图
14 12 10 未完成任务数 8 6
6 0 4 0 8 0 4 0 7 0 0 11
8 0 6 0 9 0 7 0 12 0 0 10
2015年部门任务未完成情况曲线图
14
概率分布与统计图表
心,左右对称。 2. 在 在 处取得概率密度函数的最大值, 处有拐点,表现为 钟形曲线。即正
对称。即态分布以均数为中
态曲线在横轴上方均数处最高。
2018/10/26
6
3. 正态分布有两个参数,即均数µ 和标准差σ。
µ 是位置参数,σ是变异度参数(形状参数)。常用
N(µ ,σ2)表示均数为μ ,标准差为σ的正态分布;用
( 2)
2018/10/26
16
( 3)
查附表1,标准正态分布曲线下左侧面积为0.10所对应
的Z值为-1.28,所以80%的8岁男孩身高值集中在
X 1.28S 区间内,即116.9cm~129.2cm
2018/10/26
17
练习:
查附表,求标准正态分布曲线下的面积。 (-∞,-1.96),( -∞ ,-2.58), (-1.96,1.96),(-1,1),( -∞ ,0.00)。
,
S=4.79 cm ,估计(1)该地8岁男孩身高在130 cm以上者占该地8岁 男孩总数的百分比;(2)身高界于120cm~128cm者占该地8岁男孩
总数的比例;(3)该地80%男孩身高集中在哪个范围?
先做标准化变化:
理论上该地8岁男孩身高在130 cm以上者占该地8岁男孩 总数的7.21%。
2018/10/26 15
分析:正常人的血红蛋白过高过低均为异常,要制
定双侧正常值范围。
该指标的95%医学参考值范围为
2018/10/26 21
例4 某地调查110名正常成年男子的第一秒肺通 气量,得均数为4.2 L,标准差为0.7 L ,试估计该地 正常成年男子第一秒肺通气量的95%参考值范围。
分析:正常人的第一秒肺通气量近似正态分布,且只
恩格尔曲线
恩格尔曲线1、名称由来:恩格尔曲线表示消费者在每一收入水平对某种商品的需求量。
由消费者的收入---消费曲线可以推导出消费者的恩格尔曲线。
它是以德国十九世纪后期统计学家恩格尔的名字命名的。
正常商品中,恩格尔曲线由左下朝右上倾斜,表明随着收入的增加,X的消费量也随之增加;而劣质商品则相反,随着收入的增加,商品的消费量下降。
恩格尔一直致力于研究家庭收入和各项支出之间的关系,在1857年,他提出了著名的恩格尔定律,即随着收入的上升,食品在总支出中的比重是下降的。
从统计结果来看,世界各地小至家庭,大至国家基本上都遵循这一定律,因此我们常常将恩格尔系数即食品在总开支中的比重作为衡量经济发展水平的一个指标。
通常认为,恩格尔系数超过50%的经济尚处于维持温饱的生计经济,而小于30%的则是富裕经济。
当然,这一标准并不是绝对的,个别经济在一定时期内可能会出现经济发展与恩格尔系数相背离的情况。
恩格尔还发现,随着收入提高,衣着,住房在总开支中的比重基本维持不变,而奢侈品,教育,娱乐,储蓄等比重是上升的。
恩格尔曲线可以用收入弹性来表示。
恩格尔通过把统计调查数据资料列表,指出一个家庭在食品和其他项目上的开支取决于它的收入和总的消费开支。
随着收入的增加,用于食品的支出部分将下降;用于住宅和衣服方面的支出将基本保持不变;而用于其他商品的支出会增加。
这种分析的结果被称为恩格尔定律。
2、不同商品的恩格尔曲线形状(1)必需品恩格尔曲线呈上凹型,表明必需品的需求量增加数量随着收入的增加而变得越来越少;(2)奢侈品恩格尔曲线呈下凹型,表明奢侈品的需求量增加数量随着收入的增加而增加得越来越快;(3)低档商品恩格尔曲线的斜率是负的,表明低档商品的需求量随收入的增加而减少.3、恩格尔曲线和需求曲线恩格尔曲线描述收入增加与商品需求量变动之间的关系.它反映在商品价格和其它因素不变时收入的变化引起需求量怎样的变化。
恩格尔曲线是一条联系收入变化和X消费量变化的曲线。
标准正态分布曲线
标准正态分布曲线标准正态分布曲线是统计学中一个非常重要的概念,它描述了许多自然现象和人类行为的分布规律。
标准正态分布曲线又称为正态分布曲线,是以高斯函数为基础的一种连续概率分布。
在实际应用中,标准正态分布曲线有着广泛的应用,可以用来描述各种随机变量的分布情况,为我们提供了重要的统计学工具。
标准正态分布曲线的形状是一个钟形曲线,两头低,中间高,呈对称分布。
它的横轴是随机变量的取值,纵轴是对应的概率密度。
标准正态分布曲线的均值为0,标准差为1。
这个特殊的性质使得标准正态分布曲线在统计学中有着重要的地位,许多统计学方法都是基于对正态分布的假设进行推导和应用的。
标准正态分布曲线在实际应用中有着广泛的用途。
首先,在自然科学领域,许多自然现象和实验数据都服从正态分布。
例如,身高、体重、智力水平等人类特征,以及温度、压力、光强等物理量,都可能服从正态分布。
其次,在社会科学领域,许多人类行为和心理特征也可以用正态分布来描述。
比如,考试成绩、收入水平、心理测试得分等都可能服从正态分布。
因此,对于这些数据的分析和处理,常常需要用到正态分布的理论和方法。
在统计学中,标准正态分布曲线也是许多重要统计方法的基础。
比如,假设检验、参数估计、方差分析等方法都是基于对正态分布的假设进行推导和应用的。
因此,对于这些方法的正确理解和应用,需要对正态分布曲线有着深入的认识。
在实际应用中,我们常常需要对标准正态分布曲线进行一些计算和推断。
比如,给定一个数值,我们需要求出它在标准正态分布曲线下的累积概率,或者给定一个概率,我们需要求出对应的数值。
这些计算通常需要使用正态分布表或者统计软件来进行。
对于这些计算方法的正确掌握,可以帮助我们更好地理解和应用标准正态分布曲线。
总之,标准正态分布曲线是统计学中一个非常重要的概念,它描述了许多自然现象和人类行为的分布规律。
在实际应用中,标准正态分布曲线有着广泛的应用,可以用来描述各种随机变量的分布情况,为我们提供了重要的统计学工具。
成绩分段统计人数曲线图
分数
12
56
78
23
89
43
26
45
65
34Hale Waihona Puke 56353
23
34
23
56
45
65
34
56
第一步、得到分数段,比如[0,30]为30段,(30,40]为40段,(40,50]为50段,依次类推,则在“分数”列旁边增加“分数段”列,并在相应行的单元格中输入公式:=IF(A3<=30,30,IF(A3<=40,40,IF(A3<=50,50,IF(A3<=60,60,IF(A3<=70,70,IF(A3<=80,80,IF(A3<=90,90,IF(A3<=100,100)))))))),得到如下结果
分数
分数段
12
30
56
60
78
80
23
30
89
90
43
50
26
30
45
50
65
70
34
40
56
60
35
40
3
30
23
30
34
40
23
30
56
60
45
50
65
70
34
40
56
60
第二步:统计各段人数。选中“分数段”整列,在“插入”菜单栏中选择“数据透视表”,生成如下内容的透视表:
行标签
计数项:分数段
30
6
40
4
50
3
60
4
70
2
80
1
90
