浅谈悬索桥的稳定性
悬索桥

2014-11-25 建筑资料商城专家一见解:因为悬索桥的主体结构做到了没有弯矩,只承受拉力。
这几乎是效率最高的结构体系。
简单说,拿筷子做类比。
随便一用力就可以把筷子掰断,这就是筷子在受弯;但几乎很少有人能够把筷子拉断,这就是筷子在受拉。
几乎所有的材料,受拉的效能都要远远高于受弯的效能。
(具体的分析,可以参照这个回答:为什么对木棍,铁棒等,折断比拉断更容易)再举个例子,想想一下晾衣服。
受弯的例子就是晾衣杆,木头的、竹子的、金属的,这些杆子都要有足够的直径,否则很容易就被衣服压断了;受拉的例子则是晾衣绳,很细的一根绳子,所用的材料比木杆子少得多,晾上衣服之后下垂的弧度很大,但一般情况下很难被拉断。
与轴心拉压相比,受弯是一个效率极低的承载方式。
一定程度上,提高结构效能就是尽量的把受弯转化为受拉或者受压。
如果同时能够做到尽量减轻结构自重,那就更完美了。
拱结构就是转化为受压的例子,而悬索桥则是转化为受拉的例子。
a 图就是最普通的梁式桥,完全依靠受弯承载。
这种形式非常常见,地铁、高架、小型公路桥梁,几乎全部是这样的。
右边是它的截面的应力分布,上下表面大,中间位置几乎为零。
也就是说,整个截面的应力并不是平均分配的,而是存在一个“水桶效应”,尽管中间位置几乎没有应力,但是,只要上下边缘达到了极限,整个截面就离破坏不远了。
上下边缘处的应力就是这个水桶最短的那块木板。
既然中间截面几乎为零,那么为什么不把它们省略呢?于是,就有了 b 图这种开孔梁。
截面中间部位应力很小的那些地方被省去,减轻了自重。
拉压应力集中在上下边缘处。
把这个趋势进一步扩大,也就是把原来的梁式结构进一步格构化,去掉应力小的部位,保留最基本的部位,我们就得到了 c 图的这种桁架结构。
d 图是它的大致内力分布,红色受拉,蓝色受压。
它的截面分布更加合理,上弦杆件受压,下弦杆件受拉,中间没用的部位全是空的。
著名的南京长江大桥就是这样的结构形式。
如果把这个最优化的趋势做到极致,那就达到了 e 图这种的悬索结构。
悬索桥索塔稳定性全过程分析

悬索桥索塔稳定性全过程分析段瑞芳;钱登潮;赵宝俊【摘要】As the core component for load-bearing, the mechanical property of the pylon therefore becomes one of the most crucial factors in bridge design.In order to analyze the stability of main towers of the suspension bridges, finite element model of a suspension bridge including its tower and the whole bridge has been created by the software ANSYS to do some contrastive analysis of stability under 2 cases (free standing tower and tower on finished stage).5 major stability-influential factors: nonlinear factors, initial imperfections, constraint conditions, pylon rigidity and static wind load are chosen for the simulation.The researching results indicate that the influences of initial imperfections, pylon rigidity and static wind load to stability of the towers are relatively small while the influence of constraint conditions is quite significant.Furthermore, the varying amplitude of the stability-safety factor keeps decreasing with increase of the elastic restrained stiffness of main cables on the tower top and finally becomes stable at a constant value.%作为悬索桥受力体系中的重要承重构件,索塔的受力性能也成为悬索桥设计中至关重要的一环.为了分析悬索桥主塔的稳定性问题,采用有限元法,建立了索塔及全桥的有限元模型,并对裸塔和成桥阶段索塔工况下的两类稳定性进行对比分析,主要考虑非线性因素、初始缺陷、索塔刚度、约束条件和静风荷载五种因素进行分析计算.研究结果表明,初始缺陷、索塔刚度及静风荷载对索塔的稳定性影响较小;约束条件对索塔稳定性的影响十分明显,塔顶主缆的弹性约束刚度越大,稳定安全系数的变幅越小,最后趋于一个定值.【期刊名称】《武汉理工大学学报(交通科学与工程版)》【年(卷),期】2017(041)002【总页数】6页(P224-228,233)【关键词】悬索桥;索塔;稳定性;非线性;影响因素【作者】段瑞芳;钱登潮;赵宝俊【作者单位】陕西交通职业技术学院西安 710018;温州市公路管理处温州325027;陕西省交通建设集团公司西安 710075【正文语种】中文【中图分类】U443.38由于索塔高度的增加和索塔截面的薄壁化等皆弱化了索塔结构的刚度,使得其稳定分析成为控制悬索桥安全的主要因素之一.通过分析计算和实验探索,很多学者都对稳定性问题进行了深入研究,并取得了丰硕的成果.在悬索桥的设计验算中,对成桥状态的索塔稳定性进行安全储备估算时,由于主缆的约束作用在相关规范中并未提及,若不计其约束作用则会降低计算的准确性[1].文献[2-3]指出,索塔稳定问题的关键是计算索塔杆件的临界荷载和自由长度,在评估索塔稳定性的时候,必须考虑其与受拉主缆缆力相关的工作特点.文献[4-5]提出在实际工程的稳定性分析中,还需要考虑风压及其他横向荷载的影响.文献[6-7]研究了主塔的稳定性与边界条件密切相关.但是由于问题自身复杂程度较高,特别是当构件存在诸如初始缺陷及其他非线性因素影响时,对于结构稳定全过程计算分析的求解工作量和难度也大大增加[8],因此,对结构进行考虑初始缺陷的非线性分析,即进行第二类稳定性计算求解其极限承载力是十分必要的.文中在分析索塔的稳定性时,就从两类稳定性计算出发,对不同工况下索塔的稳定性做了详细对比计算,且分析了不同因素对其稳定性的影响程度并总结得出相关结论,可为类似结构的初步设计提供参考建议.文中研究的依托工程为一正在修建的地锚式悬索桥,桥梁总长960 m,主跨为628 m的简支钢箱加劲梁悬索桥,主缆边跨为166 m,中跨垂跨比为1∶10.索塔部分为钢筋混凝土结构,受力形式上为柔性的刚构式塔.塔柱之间设3道横梁,塔柱截面为矩形的空心薄壁形式,索塔材料均采用强度等级为C50的混凝土.模型采用三维梁单元Beam188模拟塔柱及横向联系梁,模拟主缆对索塔约束作用时采用Combin14弹簧单元.在计算塔顶的弹簧约束作用时,需要借助全桥模型求解,以便能准确地数值模拟出主缆对索塔的纵向约束作用,故同时建立全桥的有限元分析模型,其中主缆和吊杆采用Link10杆单元、索塔和加劲梁采用Beam188梁单元、索夹采用质量单元Mass21进行模拟,建立有限元模型见图1~2.对于索塔结构进行稳定性分析时的荷载组合,根据索塔在施工过程中经历的阶段,按照表1进行组合.其中对于风荷载的计算,依托工程所在位置为海拔1 898 m,根据文献[9]中相关规定,按百年一遇风速26.3 m/s考虑,此时直接作用在索塔上的纵向静风荷载为15.28 kN/m,作用在索塔上的横向静风荷载为18.462 kN/m.经计算得索塔纵向及横向各阶次稳定安全系数及其失稳模态类型,见表2~5.不论是索塔的纵向还是横向稳定性,其裸塔阶段失稳破坏的形式均以纵向失稳破坏为主.但是索塔在成桥阶段时,随着主缆约束作用的增强,纵向稳定性有明显提升,使得索塔的一阶失稳模态由纵向失稳变为横向失稳,与塔顶自由的情况通过计算比较,纵向稳定性有明显提升,同时验证了主缆的纵向约束作用是非常显著的.合理计入施工过程中可能出现的偏差,而后按照其失稳模态将初始缺陷施加到索塔的有限元模型中,计算过程中,裸塔时将其自重和所受的纵向(横向)静风荷载按倍数放大进行加载,成桥时将塔身自重、主缆传递的荷载、加劲梁荷载和所受的纵向(横向)静风荷载均按倍数放大进行加载,同时进行非线性稳定分析,求解其极限承载力[10-11].综合考虑其材料与几何非线性因素进行双重非线性分析,通过循环迭代完成分析后,可得到此状态下索塔的荷载—位移曲线,见图3~6.结果表明,合理计入施工误差后,同时考虑双重非线性因素的影响,计算可得索塔的第二类稳定安全系数在第一类稳定安全系数的12%~31%倍之间,且均为索塔底部混凝土发生受压破坏.5.1 不同非线性的影响因素分别考虑几何非线性、材料非线性及双重非线性因素的影响,不考虑索塔可能存在的初始缺陷,经计算可得裸塔及成桥状态索塔的稳定安全系数,结果见图7~8.由图7~8可知,当考虑双重非线性因素的影响时,虽然索塔的稳定安全系数低于仅考虑任何单一非线性因素时的计算结果,但仍可满足结构对稳定安全性的要求,与考虑材料非线性因素影响时相似,索塔的稳定安全系数为横向高于纵向.5.2 初始缺陷的影响将索塔的几何初始缺陷施加在有限元模型中,并计入双重非线性因素的影响,通过有限元计算软件ANSYS进行第二类稳定分析,计算结果见图9.随着初始缺陷的增大,索塔的稳定性也在逐渐降低,但整体变化不大,最大只有5%的变化幅值.索塔在裸塔状态时各向的稳定安全系数,总体上要高于索塔在成桥状态对应方向的稳定安全系数.5.3 约束条件的影响为得到在不同塔顶弹簧刚度下索塔的纵向稳定屈曲特征值,直接或间接作用于索塔的纵向静风荷载依然采用百年一遇的静阵风风速26.3 m/s,通过对不同的塔顶约束弹簧刚度C1进行取值,可得到对应的索塔纵向稳定安全系数及失稳方向,结果见表6.由表6可知,塔顶弹簧的影响十分明显,即主缆对索塔的约束作用是非常显著的.成桥状态不考虑主缆约束时,索塔的纵向稳定安全系数为5.579,稳定安全性相对较低,约为裸塔状态安全系数的1/4,且均为纵向失稳,说明随着施工过程的推进,索塔所受荷载逐渐增大,使得索塔的稳定安全系数随之减小.继续将弹簧刚度放大,增至约2.45×107 N/m时索塔的纵向稳定安全系数为29.265,且已趋于稳定,这时由于主缆的纵向弹性约束作用,索塔的稳定安全性得到显著提升.5.4 索塔刚度的影响通过修改索塔的相对刚度,可得到索塔相对刚度和索塔纵向(横向)第一类稳定及第二类稳定安全系数的关系,见图10~17.图10~11的工况为裸塔纵向,图12~13为成桥纵向,图14~15为裸塔横向,图16~17为成桥横向.不论是纵向抑或横向,索塔的稳定安全系数均与其刚度成正比,各相对刚度之间的稳定安全系数近乎呈线性关系,这与欧拉公式所阐述的内容也是完全可以对应的,且阶数越高其变化率亦越大.对索塔进行第二类稳定性分析可知,索塔的第二类稳定安全系数也与索塔刚度成正相关.但是由于在变化截面刚度时往往针对截面尺寸进行改变,在施工时,较大的截面尺寸也就需要较多的材料,故在对索塔的稳定性进行设计计算时,不仅要考虑安全性的要求,还要综合考虑其经济性,使设计方案达到最优.5.5 静风荷载的影响在计算风荷载对索塔纵向稳定性的影响时,依然选择裸塔状态和成桥状态两个阶段.在进行成桥稳定性计算时,还需要计算风荷载作用在主缆和加劲梁时,主缆和加劲梁传递给索塔的风荷载,见表7.将表7中的荷载数据和对应的边界条件施加在有限元模型中,对索塔纵向和横向进行2类稳定分析,结果见图18~21.图18~19工况为索塔纵向,图20~21为索塔横向.不论是对于裸塔状态还是成桥状态,静风荷载对索塔纵(横)向稳定性的影响都非常小.随着风速的增加,直接或间接作用于索塔的荷载都会出现较大的增幅,对索塔形成相对比较大的侧向扰动,此时索塔纵向的两类稳定安全系数均略有减小,但下降率极其微小,说明静风荷载对其纵向稳定性的影响不大.文中在总结对索塔稳定性已有研究的基础上,运用有限元分析软件ANSYS对一中空截面的受压杆件和某在建地锚式悬索桥的索塔进行了分析,分别从纵向和横向两个方向出发,就裸塔和成桥状态两个工况对其两类稳定性进行了详细分析计算,并通过修改不同影响因素的参数计算了其对索塔稳定性的影响程度.通过模拟计算,得出以下结论:1) 相同工况下,横桥向索塔的第一类稳定安全系数普遍略小于同阶次纵向索塔的第一类稳定安全系数,虽然相差最大仅有1.6%,仍可说明对索塔横向的稳定性进行验算是十分必要的.在进行索塔的设计时,应增强其横向刚度,提高结构稳定性.2) 通过计入初始缺陷和双重非线性因素对索塔进行了极限承载力分析,得到索塔的第二类稳定安全系数在第一类稳定安全系数的0.12~0.31倍之间,且失稳时均为索塔底部混凝土材料发生受压破坏.3) 初始缺陷、索塔刚度及静风荷载对索塔的稳定性影响较小;考虑双重非线性因素的影响时,索塔的稳定安全系数低于考虑任何单一非线性因素影响的计算结果;约束条件对索塔稳定性的影响十分明显,特别是塔顶主缆的弹性约束作用,主缆的约束刚度越大,稳定安全系数的变幅越小,最后趋于一个定值.【相关文献】[1]许世展,高传明,贺拴海,等.悬索桥主塔纵向稳定的实用计算[J].长安大学学报(自然科学版),2005(1):41-43.[2]曾华,李德寅.悬索桥桥塔的稳定及桥式比选[J].国外桥梁,1995(1):40-48.[3]张琴.大跨度悬索桥索塔非线性稳定分析[J].山西建筑,2012(5):196-198.[4]刘恩吉.悬索桥桥塔纵向稳定性分析[J].世界桥梁,2009(2):45-47.[5]中华人民共和国交通部.公路桥梁抗风设计规范:JTG/T D60—01—2004[S].北京:人民交通出版社,2004.[6]孟凡超.公路桥涵设计手册:悬索桥[M].北京:人民交通出版社,2011.[7]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.[8]李国豪.桥梁结构稳定与震动[M].北京:中国铁道出版社,2002.[9]张琴.大跨度悬索桥索塔非线性稳定分析[J].山西建筑,2012(5):196-198.[10]刘恩吉.悬索桥桥塔纵向稳定性分析[J].世界桥梁,2009(2):45-47.[11]宋凯.自锚式悬索桥主塔稳定计算方法及影响因素分析[J].城市道桥与防洪,2013(7):73-75.。
悬索桥的结构原理、力学性能及建造方法

悬索桥的结构原理、力学性能及建造方法一、原理悬索桥中最大的力是悬索中的张力和塔架中的压力。
由于塔架基本上不受侧向的力,它的结构可以做得相当纤细,此外悬索对塔架还有一定的稳定作用。
假如在计算时忽视悬索的重量的话,那么悬索形成一个双曲线。
这样计算悬索桥的过程就变得非常简单了。
老的悬索桥的悬索一般是铁链或联在一起的铁棍。
现代的悬索一般是多股的高强钢丝。
二、结构悬索桥的构造方式是19世纪初被发明的,许多桥梁使用这种结构方式。
现代悬索桥,是由索桥演变而来。
适用范围以大跨度及特大跨度公路桥为主,当今大跨度桥梁全采用此结构。
是大跨径桥梁的主要形式。
悬索桥是以承受拉力的缆索或链索作为主要承重构件的桥梁,由悬索、索塔、锚碇、吊杆、桥面系等部分组成。
悬索桥的主要承重构件是悬索,它主要承受拉力,一般用抗拉强度高的钢材(钢丝、钢缆等)制作。
由于悬索桥可以充分利用材料的强度,并具有用料省、自重轻的特点,因此悬索桥在各种体系桥梁中的跨越能力最大,跨径可以达到1000米以上。
1998年建成的日本明石海峡桥的跨径为1991米,是目前世界上跨径最大的桥梁。
悬索桥的主要缺点是刚度小,在荷载作用下容易产生较大的挠度和振动,需注意采取相应的措施。
三、性能按照桥面系的刚度大小,悬索桥可分为柔性悬索桥和刚性悬索桥。
柔性悬索桥的桥面系一般不设加劲梁,因而刚度较小,在车辆荷载作用下,桥面将随悬索形状的改变而产生S 形的变形,对行车不利,但它的构造简单,一般用作临时性桥梁。
刚性悬索桥的桥面用加劲梁加强,刚度较大。
加劲梁能同桥梁整体结构承受竖向荷载。
除以上形式外,为增强悬索桥刚度,还可采用双链式悬索桥和斜吊杆式悬索桥等形式,但构造较复杂。
桥面支承在悬索(通常称大揽)上的桥称为悬索桥。
英文为Suspension Bridge,是“悬挂的桥梁”之意,故也有译作“吊桥”的。
“吊桥”的悬挂系统大部分情况下用“索”做成,故译作“悬索桥”,但个别情况下,“索”也有用刚性杆或键杆做成的,故译作“悬索桥”不能涵盖这一类用桥。
三塔悬索桥的缆索体系及其抗风稳定性

Absr c :Ba e a c s h e — o r us e i n rd - iho Hi wa i ge,whih i ta t s d on a e of t r e t we s p nso b i ge Ta z u gh y Brd c s o rt n z v rw ih t em a n s a 08 ,t x m p e t p ta a e s s e a d ve he Ya gt e Ri e t h i p n of1 0 m wo e a l swih s a i lc bl y t m n do l a l s t m , r s e tv l ub e c b e ys e e p c i e y,we e de i ne r s g d. Th s r c u a d a c c a a t rs is, t e e t u t r l yn mi h r c e itc h
关 键词 : 三塔 悬 索桥 ; 空间缆 索体 系; 面双缆 体 系; 力特性 ; 平 动 空气静 力稳 定性 ; 气动 力稳 定性 空
中图分类 号 : 4. 5 U4 8 2 文0 1 0 —3 3 2 1 ) 40 3 —5
Ke r :t r e t we u p n i rdg y wo ds h e — o r s s e son b i e;s a il a l y t m ; d ubl a l y t m ; d na i p ta c b e s s e o e c be s se y m c c r c e itc ha a t rs is;a r t tc s a lt e os a i t biiy;a r dy m i t biiy e o na c s a lt
大跨度自锚式悬索桥稳定性研究

第3 5卷
第 7期
2008年 7 月
湖 南 大 学 学 报 (自 然 科 学 版 ) Jun l f u a nvri ( aua Si cs o ra o nnU ie t N trl c ne) H sy e
V0 . 5, . 13 No 7
和在 根 据 实桥 按 比例制 作 的全桥 试 验模 型上 进 行超 载 试 验 , 明 了本 文 理论 分 析 的结论 是 证
正确 的 .
关 键词 : 型试验 ; 模 自锚 式悬 索桥 ; 挠度 理论 ; 结构稳 定性 ; 限承载 力 极
中 图分 类 号 : 4 . U4 6 1 文献标 识码 : A
b t ft e e t o d ,we ebu l.By a a y i he e u to ,t o lwi g c ncu inswe e o t i d:i s o h o h s wo la s r i t n l zng t q a ins he f l o n o l so r b ane ti
2. l g fC v l g n e i g,Hu a iv,Ch n s a Hu a 4 0 8 Ch n ; o e C l e o i i En i e r n n n Un a gh , n n 1 0 2, i a
3. p fB ig gn eig o t wetJat n i De to rd eEn ier ,S uh s ioo gUnv,C e g u,Sc u n 61 0 1, in ) n hnd ih a 0 3 Ch a Ab t a t Ba e n d fe to h o y,t if r n ile u to s,d s rb n h ea ins p e we n t e s r c : s d o elc i n t e r he dfe e ta q a in e c i i g t e r lto hi sb t e hed —
三塔悬索桥钢中塔弹塑性稳定性分析
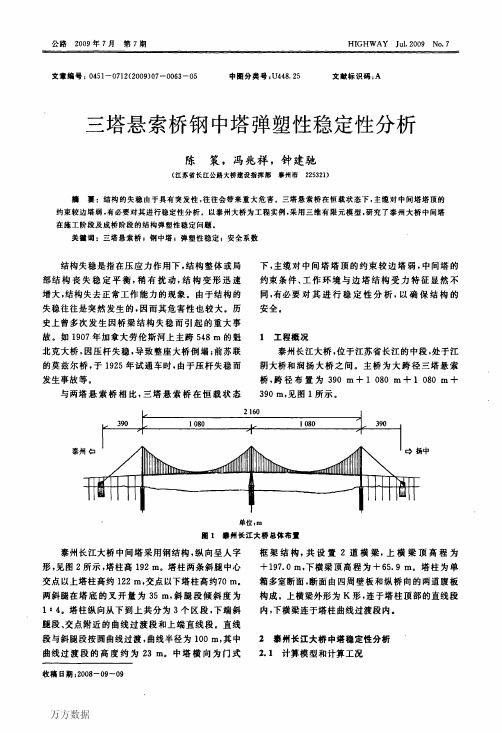
万方数据
圈5工况3~工况5临界失穗时MIs嚣圈
2009年第7期
陈策等:三塔悬索桥钢中塔弹塑性稳定性分析
工况
3 4 5
裹2 中塔整体失稳形式和极限承载力
失稳形式
极限承载力
kN
设计轴力 kN
稳定安全 系数
顺桥向弯曲 5.67×10s 顺桥向弯曲 2.95X10s 横桥向弯曲 5.26×105
1.89×105 1.77XlOs 1.89X105
3.0 L7 2.8
工况4对应的中塔纵向整体稳定计算为最不利 工况,由于模型的边界条件为塔底固结,塔顶自由, 实桥存在主缆对中塔的纵向约束,中塔结构在成桥 阶段在一跨满载一跨空载作用下,其稳定安全系数 为1.7,成桥状态中塔的名义等代刚度较独塔状态 增加了77%,由于塔的整体稳定临界荷载与塔的刚 度成正比,若根据成桥状态中塔的名义等代刚度,对 临界荷载及稳定安全系数进行修正,则中塔纵向极 值点失稳稳定安全系数约为3.0。工况5对应中塔 横向整体稳定计算为最不利工况,中塔横向极值点 失稳稳定安全系数为2.8。对于一般桥梁结构,可 认为当非线性计算的稳定安全系数大于2.5时的结 构,是足够安全的。
泰州长江大桥钢中塔塔柱的垂直精度设计要求 纵横向均不大于1/10 000,在上述3种荷载工况下, 中塔顶部截面存在较大的端弯矩,由此等效换算得 到的偏心较大,故忽略安装初始偏心的影响,只考虑 中塔初曲率和塔顶端弯矩的影响。实际偏心距取由 塔顶弯矩换算得到的偏心距,再加上1/10 000的初 曲率,按最不利偏心位置布置荷载。 2.3.4计算结果及分析
悬索桥的结构优化探讨

悬索桥的结构优化探讨悬索桥作为一种重要的交通工程结构,具有较大的跨度和优良的结构效果。
它的独特之处在于悬索桥主梁由悬挂在主塔上的钢索和主梁构成,这种设计使得悬索桥能够适应大跨度和高负载的要求。
然而,随着科技的发展和对桥梁质量、经济性的要求不断提高,对悬索桥结构的优化也成为一个研究热点。
首先,悬索桥的结构优化需要考虑的因素众多。
其中包括桥梁的载荷情况、悬索索的材料、主塔和主梁的设计。
在设计悬索桥时,必须充分考虑预期的交通负荷、运行速度以及气候和地质条件等。
此外,悬索索的材料选择也非常重要,它们必须具备高强度和耐久性,以承受桥梁的巨大受力。
主塔和主梁的设计也需要考虑到桥梁的整体稳定性和安全性。
对于悬索桥结构的优化,一种重要的措施是减轻桥梁的自重。
过重的桥梁可能会导致主塔和主梁过度受力,从而减小桥梁的使用寿命。
为了解决这个问题,可以通过采用新的材料或结构设计来减轻桥梁的自重。
例如,在主梁的设计中,可以采用空腹梁或中空箱梁结构,以减少材料的使用量。
此外,钢材和复合材料等新材料的应用也可以降低桥梁的自重,提高整体的经济性和可持续性。
除了减轻自重外,悬索桥的结构优化还包括提高桥梁的刚度和稳定性。
这对于桥梁的正常使用和运行非常重要。
在悬索桥的设计中,可以通过在主塔和主梁之间增加横向钢结构,或在悬索索之间加装补强杆件等方法来提高桥梁的刚度和稳定性。
此外,优化悬索桥的结构还可以通过合理设计桥面防腐层以及加装减震器等措施,来提高桥梁的耐久性和安全性。
悬索桥结构优化的另一个重要方面是降低桥梁的建设和维护成本。
悬索桥作为一种大型工程结构,其建设和维护所需的成本是一笔巨大的开支。
因此,通过合理的结构设计和施工方法,可以降低悬索桥的建设和维护成本。
例如,在桥梁的施工中可以采用更加精确的测量和施工技术,以减少材料浪费和人力成本。
此外,优化桥梁的结构设计,选择合适的材料和施工方式,也可以降低桥梁维护的难度和成本。
总的来说,悬索桥的结构优化是一个复杂而综合的问题。
悬索桥的拉压平衡分析

悬索桥的拉压平衡分析悬索桥,作为一种古老而又充满魅力的桥梁结构,一直以来都吸引着人们的目光。
它以悬挂在两个支柱之间的主悬索为主要承载构件,通过悬索和斜拉索的相互作用,实现了桥梁的稳定和平衡。
本文将从拉压平衡的角度,探讨悬索桥的结构特点和力学原理。
悬索桥的主要特点是悬挂在两个支柱之间的主悬索,它承担了桥梁荷载的大部分重量。
主悬索的形状通常呈现出一种悬垂的曲线,这是因为悬索在自重和荷载作用下会发生弯曲。
悬索桥的拉压平衡依赖于主悬索的稳定性,因此主悬索的设计和施工是悬索桥工程中最为关键的环节之一。
在拉压平衡分析中,我们首先需要考虑主悬索的受力情况。
主悬索上的每一点都承受着来自两个方向的力,即向下的重力和向上的张力。
由于主悬索的形状是悬垂曲线,所以在任何一点上,张力的方向都沿着切线方向。
这意味着主悬索上的张力可以通过切线力的合成得到。
而切线力的合成又可以通过积分计算来求解。
除了主悬索上的拉力,悬索桥还需要考虑斜拉索的作用。
斜拉索是连接主悬索和桥面的关键构件,它的作用是将主悬索上的拉力传递到桥面上。
斜拉索的设计需要考虑到两个方面的因素:一是斜拉索的角度,二是斜拉索的张力。
斜拉索的角度决定了主悬索上的拉力在垂直方向上的分量大小,而斜拉索的张力则决定了桥面上的受力情况。
在悬索桥的拉压平衡分析中,还需要考虑到其他一些因素。
例如,主悬索和斜拉索的材料强度、桥面的自重、风荷载等等。
这些因素都会对悬索桥的结构和力学性能产生影响,需要在设计和施工过程中进行综合考虑。
总的来说,悬索桥的拉压平衡分析是一项非常复杂而又重要的工作。
它需要考虑到主悬索和斜拉索的受力情况,以及其他一些因素的影响。
只有在拉压平衡得到良好的控制和平衡时,悬索桥才能够保持结构的稳定和安全。
因此,在悬索桥的设计和施工中,拉压平衡分析是一个不可或缺的环节,需要专业的工程师和技术人员进行深入研究和探索。
悬索桥作为一种独特的桥梁结构,不仅具有实用性,还具有观赏性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浅谈悬索桥的稳定性
摘要随着桥梁事业不断发展,悬索桥的应用也越来越广泛,所以其稳定性也显得尤为重要。
而在现实中的风荷载及各种桥梁上的活荷载(主要指车辆)都将影响悬索桥的稳定性。
现就悬索桥在荷载作用下的稳定性有关问题进行简单的讨论。
关键词悬索桥;风荷载;活荷载;稳定性
悬索桥,又名吊桥(suspension bridge)指的是以通过索塔悬挂并锚固于两岸(或桥两端)的缆索(或钢链)作为上部结构主要承重构件的桥梁。
悬索桥由悬索、索塔、锚碇、吊杆、桥面系等部分组成。
悬索桥的主要承重构件是悬索,它主要承受拉力,一般用抗拉强度高的钢材(钢丝、钢绞线、钢缆等)制作。
由于悬索桥可以充分利用材料的强度,并具有用料省、自重轻的特点,因此悬索桥在各种体系桥梁中的跨越能力最大,跨径可以达到1000m以上。
悬索桥的主要缺点是刚度小,在荷载作用下容易产生较大的挠度和振动,需注意采取相应的措施。
其缆索几何形状由力的平衡条件决定,一般接近抛物线。
从缆索垂下许多吊杆,把桥面吊住,在桥面和吊杆之间常设置加劲梁,同缆索形成组合体系,以减小活载所引起的挠度变形。
相对于其它桥梁结构悬索桥可以使用比较少的物质来跨越比较长的距离。
悬索桥可以造得比较高,容许船在下面通过,在造桥时没有必要在桥中心建立暂时的桥墩,因此悬索桥可以在比较深的或比较急的水流上建造。
悬索桥比较灵活,因此它适合大风和地震区的需要,比较稳定的桥在这些地区必须更加坚固和沉重。
按照桥面系的刚度大小,悬索桥可分为柔性悬索桥和刚性悬索桥。
柔性悬索桥的桥面系一般不设加劲梁,因而刚度较小,在车辆荷载作用下,桥面将随悬索形状的改变而产生S形的变形,对行车不利,但它的构造简单,一般用作临时性桥梁。
刚性悬索桥的桥面用加劲梁加强,刚度较大。
加劲梁能同桥梁整体结构承受竖向荷载。
除以上形式外,为增强悬索桥刚度,还可采用双链式悬索桥和斜吊杆式悬索桥等形式,但构造较复杂。
桥梁结构的失稳现象可以分为以下几类:1)个别构件的失稳,例如压杆的失稳和梁的侧倾;2)部分结构或整个结构的失稳;3)构件的局部失稳,而局部失稳常常会导致整个结构体系的失稳。
风荷载作用下:悬索桥的加劲梁视为一个机翼,可用航空学和空气动力学的有关研究和理论分析。
悬索桥的结构风振有有限振动和发散振动。
有限振动包括涡激振和颤振。
涡激振,是在风速比较小的有限度的风速范围内由卡曼涡流引起的振动;而颤振是由风的乱流引起的一种不规则振动,它的振幅随风速增大而增大,这时结构断面发生弯曲与扭转耦合,可能产生灾害性的振幅。
发散振动是风速超过某一数值后,振幅急剧增大的一种破坏振动。
它包括有:竖向弯曲振动,扭转振动和弯扭联合振动3种形式。
对大跨悬索桥的非线性静风稳定性研究考虑了以下3种效应的影响:1)非线性位移相关风载;2)几何非线性;3)材料非线性。
风静动力系数为有效攻角的函数,而有效攻角随主梁变形而变化,所以位移相关风载是非线性的;通过采用几何刚度矩阵可以考虑侧向弯扭屈曲、扭转发散及弯扭耦合失稳;采用塑性铰理论进行材料非线性分析。
使用有限元法建立风致静力失稳的分析模型,建模过程中同时考虑了非线性位移相关风载、几何非线性及材料非线性。
大跨度悬索桥的结构刚度主要来自于主缆,因此提高结构整体刚度的着眼点应放在主缆上。
通过调整主缆同加劲梁的相对位置和增加特定的水平和横向的辅助索可以达到提高结构抗扭刚度和扭转振动频率的目的。
各种模型的比较结果为:
1)节段模型试验在临界风速时,呈现出竖向与扭转综合振动的失稳;
2)在均匀气流中,全桥模型试验仅在略高节段模型中的临界风速时,出现发散性的失稳;
3)紊流中的全桥模型试验,观察到不规则的竖向振动,其振幅随紊流的增大而加大,但并无失稳或扭振。
综上所诉悬索桥的坚固性不强,在大风情况下交通必须暂时被中断。
活荷载(这主要指车辆荷载):在桥梁上的活载较多,这里只考虑车辆行驶时对悬索桥的作用。
悬索桥在车辆荷载作用下,主要为挠曲线振动。
车辆荷载高速通过桥梁时,其作用的位置和荷载的大小随时间不停地发生变化,进而引起桥梁结构的振动。
在做了各种原型与模型的相似模型试验后,可知加劲梁在车辆的作用下会产生拉力,需用铰支座将其固定;悬索桥的主塔较高,塔身大多采用翻模法分段浇筑,在主塔连结板的部位要注意预留钢筋及模板支撑预埋件。
对于索鞍孔道顶部的混凝土要在主缆架设完成后浇筑,以方便索鞍及缆索的施工。
利用大跨度悬索桥的挠度理论,建立了自锚式悬索桥加劲梁在恒载、恒载与活载及活载下的变形与荷载的平衡方程。
对所建立的方程进行分析后,得到了如下结论:自锚式悬索桥加劲梁在恒载状态设计时,应按受横向荷载作用的压弯梁验算面内稳定性,但是活载作用下不存在面内稳定问题。
通过对润扬单跨双铰简支梁箱梁悬索桥模型的抽样及试验,得出车辆对箱梁的受力特点如下:
1)由测试截面应力值及其沿梁宽分布图可知,从整体上看,钢箱梁各部位在各种不利车辆荷载工况下的应力水平都比较低,远低于材料的屈服应力;
2)受剪力滞效应和桥面横坡的影响,箱梁两侧和中央处的应力(绝对值)较梁宽四分点处的应力要略大一些,因此在车辆作用下的受力状态更为不利;
3)对于大跨度缆索承重梁桥而言,车辆荷载的集中程度是导致顶板应力增大的重要因素之一。
因此必须对通过大桥的挂车、超重车等进行限制与评估;
4)有车辆荷载作用位置的不同导致钢箱梁各部位均出现不容程度的拉压应力交替现象,因此对于钢箱梁这种焊接结构而言,其疲劳破坏值也值得引起重视。
参考文献
[1]杨咏昕,葛耀君,项海帆.改善大跨度悬索桥抗风稳定性能的实践和探索.
[2]单富文,李云飞,陈洁余,朱祖楞著.悬索曲线理论及其运用.长沙:湖南科学技术出版社,1983.
[3]陈仁富.竖向荷载作用下的悬索桥非线性力素分析.成都:西南交通大学硕士学位论文,1987.
[4]王浩,李爱群,郭彤,赵耕文.车载作用下大跨度悬索桥钢箱梁受力状态的实验研究.。
