百校大联考全国名校联盟2018届高三联考(三)理数试题
2018年5月2018届高三第三次全国大联考(新课标Ⅲ卷)理数卷
理科数学试题 第1页（共6页） 理科数学试题 第2页（共6页）绝密★启用前|2018年第三次全国大联考【新课标Ⅲ卷】理科数学（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。
写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．已知全集U =R ，集合}043|{2≤--=x x x A ，{|||0}B x x =>，则以下结论成立的是 A ．A B =RB ．=B A ]4,0(C ．()U AB A =ðD ．}0{=B A2．已知复数z 满足14i 1z z -=-+，其中i 为虚数单位，则在复平面内，复数z 对应的点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知椭圆C ：22221(0)x ya b a b+=>>的左、右焦点分别为1F ，2F ，过点1F 作长轴的垂线与椭圆C 的一个交点为P ，若43tan 12=∠F PF ，则椭圆C 的离心率为 A ．21B ．31C ．41D ．514．若执行如图所示的程序框图，则输出的结果为A ．122018-B ．222018-C ．122019-D ．222019-5．已知甲、乙、丙、丁四人在某次高考模拟考试后交流各自的数学考试情况，甲说：“我分数肯定最低”；乙说：“我肯定不是最低分的那个人”；丙说：“我不会最低，但也不可能得最高分”；丁说：“那只有我是最高分了”.考试公布结果后，发现四人的分数各不相同，且仅有一人没有说对，则四人中得最高分的是A ．甲B ．乙C ．丙D ．丁6．《九章算术》卷五《商功》中有如下问题：今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何？问题中“刍甍”指的是底面为矩形的屋脊状的几何体，如图1，该几何体可由图2中的八边形ABCDEFGH 沿BG ，CF 向上折起，使得AH 与DE 重合而成，设网格纸上每个小正方形的边长为1，则此“刍甍”中EF 与平面BCFG 所成角的正弦值为A ．515 B ．552 C ．510D ．557．已知曲线e xy =，直线1=x 及)0(1<+=k kx y 围成的封闭图形的面积大于e ，则实数k 的取值范围为理科数学试题 第3页（共6页） 理科数学试题 第4页（共6页）A ．)0,4(-B ．)0,4[-C ．)4,(--∞D ．]4,(--∞8．若不等式组⎪⎩⎪⎨⎧≥+≤--≥+-102201y x y x y x 表示的平面区域为Ω，则区域Ω的内切圆半径为A ．532-B ．352-C ．252-D ．522-9．已知函数)sin()(ϕω+=x A x f （0,0A ω>>）的部分图象与坐标轴交于点Q P M ,,，如图，其中)0,21(-Q ，32PQ OP =-，且PMQ ∠为钝角，则A 的取值范围为A ．)36,0(B ．),36(+∞ C ．)2,0(D ．)2,36( 10．关于函数xx x f ln 21)(2-=有如下说法，其中正确的是A ．函数()f x 的定义域为),0(+∞B ．1x =是函数()f x 的零点C ．函数()f x 在定义域内为减函数D ．函数()f x 在定义域内不存在极值点11．某校高三（1）班周二的课表安排如下，其中上午有四节课，下午有三节课，现需要对课表进行重新调整，将其中的历史改成数学，其他科目既不增加也不减少，且调整后两节数学课不连续（如数学安排在第4，第5节也符合要求），语文课不能安排在第1节，则不同的安排方法种数为A ．48C ．612D ．82812．已知双曲线)0,0(12222>>=-b a by a x 的离心率为2，1F ，2F 分别是双曲线的左、右焦点，点)0,(a M -，),0(b N ，点P 为线段MN 上的动点，若12PF PF ⋅取得最小值和最大值时，12PF F △的面积分别为1S ，2S ，则=21S S A ．21B ．31 C ．41 D ．51 第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分）13．若向量(1,2)=a ，(1,)λ=-b ，|2|+=a b ，则=λ ． 14．如图是一个几何体的三视图，则该几何体的外接球的表面积为 ．15．在ABC △中，4A π∠=，P 为BC 边上一点，且2=AP ，若PAB PAC ∠=∠2，则PC PB 11+的最大值为 ． 16．若关于x 的不等式12e e 2e 2x x m x +-+>+（其中e 为自然对数的底数，0,x m >∈Z ）恒成立，则m 的最大值为 ．三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分12分）已知数列}{n a满足11=a ，131+=+n n n a a a （n *∈N ）．（1）求数列}{n a 的通项公式；（2）令nn n a b 2=，n S 为数列}{n b 的前n 项和，若0)23(11≥-⋅-+n n S n λ有解，求实数λ的取值范围．18．（本小题满分12分）如图，几何体PDBAC 中，⊥PA 平面ABC ，ABC △为正三角形，BDC △为等腰直角三角形，理科数学试题 第5页（共6页） 理科数学试题 第6页（共6页）BDC ∠为直角，平面⊥BDC 平面ABC ，2==AC PA ，M 为PB 的中点．（1）求证：//DM 平面ABC ； （2）求二面角C DM B --的余弦值．19．（本小题满分12分）如图是某市2017年12个月高层住宅网签情况的统计图：（1）求该市2017年高层住宅月成交均价的平均数；（2）利用（1）中计算的平均数，若当月成交均价高于月成交均价的平均数时，则视为价格上升，反之为下降；若当月成交套数高于月成交套数的平均数时，则视为成交量上升，反之为下降．若从全年中任选两个月，记所选两个月价格上升且成交量下降的个数为ξ，求随机变量ξ的分布列和期望（月成交套数的平均数约为3537套）；（3）在（2）的条件下，补充完整下列的22⨯列联表，并分析该市在2017年12个月中高层住宅月成交套数与月成交均价的升降是否有关？附：))()()(()(22d b c a d c b a bc ad n K ++++-=，其中d c b a n +++=.20．（本小题满分12分）在抛物线C ：2ax y =（0>a ）上取两点),(11n m A ，),(22n m B ，且412=-m m ，过点B A ,分别作抛物线C 的切线，两切线交于点)3,1(-P ． （1）求抛物线C 的方程；（2）设直线l 交抛物线C 于N M ,两点，记直线OM ，ON （其中O 为坐标原点）的斜率分别为,OM ON k k ，且2-=⋅ON OM k k ，若OMN △的面积为32，求直线l 的方程.21．（本小题满分12分）已知函数21()(1)e 2x f x ax x =--()a ∈R ． （1）讨论函数)(x f 的单调性；（2）若对任意实数]1,0[,,321∈x x x ，都有)()()(321x f x f x f ≥+，求实数a 的取值范围． 请考生在第22、23两题中任选一题作答．注意：只能做所选定的题目.如果多做，则按所做的第一个题目计分．22．（本小题满分10分）选修4－4：坐标系与参数方程已知曲线1C 的参数方程为sin x y ϕϕ⎧=⎪⎨=⎪⎩（ϕ为参数），以直角坐标系xOy 的原点O 为极点，x 轴的正半轴为极轴，建立极坐标系，曲线2C 的极坐标方程为32=ρ． （1）将曲线1C 的参数方程化为极坐标方程；（2）射线4θπ=（0≥ρ）与曲线1C ，2C 分别交于P ，Q 两点，曲线1C 与极轴的交点为A ，求PAQ △的面积．23．（本小题满分10分）选修4－5：不等式选讲已知函数x x x f 2|23|)(-+=．（1）若3)(<x f ，求满足条件的实数x 的值所组成的集合A ； （2）若A ∈μλ,，求证：1||||||2-+>μλλμ．。
2018年3月2018届高三第一次全国大联考(新课标Ⅲ卷)理数卷(全解全析)
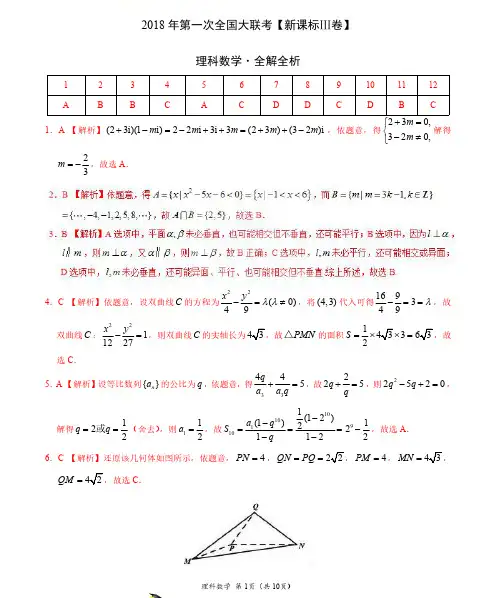
2018年第一次全国大联考【新课标Ⅲ卷】理科数学·全解全析123456789101112ABBCACDDCDBC1．A 【解析】(23i)(1i)22i 3i 3(23)(32)i mm m m m +-=-++=++-，依题意，得230,320,m m +=⎧⎨-≠⎩解得23m =-，故选A ．4．C 【解析】依题意，设双曲线C 的方程为22(0)49x y λλ-=≠，将(4,3)代入可得169349λ-==，故双曲线C ：2211227x y -=，则双曲线C 的实轴长为PMN △的面积132S =⨯=，故选C ．5．A 【解析】设等比数列{}n a 的公比为q ，依题意，得33445q a a q +=，故225q q+=，则22520q q -+=，解得122q q ==或（舍去），则112a =，故101091101(12)(1)1221122a q Sq --===---，故选A．6．C 【解析】还原该几何体如图所示，依题意，4PN =，QN PQ ==4PM =，MN =QM =C ．7．D 【解析】运行该程序，12,2,,22S n a A ====，14,2S =继续运行，13,,44n a A ===，38,4S =继续运行，14,,88n a A ===，716,8S =继续运行，15,,1616n a A ===，153216S =，由题意观察各选项，可知选D ．9．C 【解析】方法一：记函数()f x 的最小正周期为T ，依题意，2M =，3(222T ππ=--，故4T =π，故2142ωπ==π，故1()2sin()2f x x ϕ=+，将(,2)2A π-代入1()2sin()2f x x ϕ=+中，得()1(2222k k ϕππ⨯-+=+π∈Z ，则32()4k k ϕπ=+π∈Z ，又0ϕ<<π，故34ϕπ=，即13()2sin()24f x x π=+，当[6,4]x ∈-π-π时，()f x 的最大值为2，最小值为，故所求最值之和为2-，故选C.方法二：记函数()f x 的最小正周期为T ，依题意，2M =，3()222T ππ=--，故4T =π，则求函数()f x 在[6,4]-π-π上的最值之和可以转化为求函数()f x 在[2,4]ππ上的最值之和，根据题图，可知函数()f x 在[2,4]ππ上的最大值为2，最小值在(2,0)-中取得，故函数()f x 在[6,4]-π-π上的最值之和(0,2)∈，观察各选项可知选C.学科*网10．D 【解析】将该三棱锥补形为一长方体，其中底面长为2，宽为1，高为2，由三棱锥四个顶点均为长方体的顶点，可知长方体的外接球即为三棱锥的外接球，设长方体外接球的直径为R 2，则9221)2(2222=++=R ，解得23=R ，即长方体外接球的半径为23，故所求球的体积为3439(322π⨯=π．11．B 【解析】设椭圆方程为λ=+4922x y （0>λ），直线l 的方程为1-=my x ，联立方程消去x 得036918)49(22=-+-+λmy y m ，设),(),,(2211y x B y x A ，则根据根与系数的关系，得4918221+=+m my y ，12293694y y m λ-=+.由点C 在椭圆内，得41>λ，所以120y y <，又OAC △与OBC △的面积之比为1:3，可得213y y -=，则491822221+=-=+m m y y y ，所以49922+-=m my ，则OAB OAC OBC S S S =+△△△49||18||2||21||||21||||21222121+==-=⨯⨯+⨯⨯=m m y y y y OC y OC ||4||918m m +=，又12492||4||9=⨯≥+m m ，所以183122OAB OAC OBC S S S =+≤=△△△，当且仅当||4||9m m =，即23m =±时取等号，故OAB △面积的最大值为23，故选B．13．22680【解析】依题意，2128n=，解得7n =，故7(23)x -的展开式的通项公式为777177C (2)(3)C 2(3)r r r r rr r r T x x ---+=-=-，令73r -=，解得4r =，故3x 的系数为4347C 2(3)=22680-.16．343-【解析】因为131n n a a n --=+，所以1111333n n a a n -=++，考虑构造等比数列，由111111((1)]24324n n a n a n --+=---，得111(124113(1)24n n a n a n --+=---，所以11{()}24n a n -+是一个公比为13的等比数列，将22512a =-代入2133a a -=中，解得1374a =-，故1111(10()243n n a n --+=-⨯，即111110()243n n a n -=+-⨯，又()12111111110(110()243243n n n n a a n n ----=+-⨯---⨯11120(0(2)23n n -=+⨯>≥，1233725230,0,041236=a a a =-<-<=>，所以n S 的最小值为123725344123a a +=--=-.17．（本小题满分12分）【解析】（I ）因为27cos 7cos 7cos B b C c B =+，且3a =，所以9cos 7cos 7cos a B b C c B =+，即9sin cos 7sin cos 7sin cos A B B C C B =+,即()9sin cos 7sin 7sin A B B C A =+=，又sin 0A ≠，所以7cos 9B =，（2分）又22214a c b +-=及余弦定理得cos 7ac B =，则7379c ⨯=，解得3c =；由22214a c b +-=，3a =，3c =，得2b =.（6分）（II ）因为7cos 9B =，所以sin 9B ==.又由余弦定理，得2222222331cos 22233b c a A bc +-+-===⨯⨯，则sin 3A ==，（10分）所以227142102sin()sin cos cos sin 393927A B A B A B -=-=-⨯.（12分）18．（本小题满分12分）【解析】（I ）填写表格如下：空气质量指数3(μg/m )[)0,50[)50,100[)100,150[)150,200[]200,250天数4080502010（3分）故X 的分布列为：X01234P11001401001270100148010012101001（9分）（III ）依题意，任取1天空气质量指数在150以上（含150）的概率为320，由二项分布知识可知，3~(5,)20Y B ，故()335204E Y =⨯=.（12分）19．（本小题满分12分）【解析】（I ）如图，连接PD .因为90MPA ∠=，且MPA ∠是二面角A BC D --的平面角，故平面ABC ⊥平面BCDE .（2分）因为AB AC =，P 为线段BC 的中点，故AP BC ⊥，因为平面ABC 平面BCDE BC =，AP ⊂平面ABC ，故AP ⊥平面BCDE ，因为DE ⊂平面BCDE ，故AP DE ⊥.（4分）因为1,2,3BE BC CD ===，所以DE EP DP ===，故222DE EP DP +=，即DE EP ⊥，因为AP EP P = ，所以DE ⊥平面APE .（6分）由0,0,AD DE ⎧⋅=⎪⎨⋅=⎪⎩m m 得30,220,x ty z x z --+=⎧⎨-=⎩令,x t =可得2,y z t ==，故(,2,)t t =m ；（10分）又(0,0,1)=n 为平面ABC 的一个法向量，平面ADE 与平面ABC 所成角的平面角的余弦值为14，所以14=，解得7t =（负值舍去），故7AP =.（12分）20．（本小题满分12分）【解析】（I ）因为曲线962-+-=x x y 与x 轴相切，令0962=-+-=x x y ，得3=x ，所以曲线962-+-=x x y 与x 轴相切于点)0,3(.（1分）设圆C 的标准方程为：222)()(r b y a x =-+-，则依题意，得⎪⎩⎪⎨⎧-==-+-=1)()3(3222a b r b a a ，（2分）解得⎪⎩⎪⎨⎧===223r b a ，（4分）∴所求圆C 的标准方程为：4)2()3(22=-+-y x ．（5分）设),(),,(2211y x N y x M ，则根据根与系数的关系，得221146kk x x ++=+，22119k x x +=.（8分）因为3ON OM =，所以123x x =，所以12322(1)k x k +=+，221212232933[]2(1)1k x x x k k +===++.（10分）解得433±=k ，所以直线l的方程为34y x +=或34y x -=．（12分）21．（本小题满分12分）【解析】（I ）依题意，得22111()(0)px f 'x x x px px -=-=>；（2分）当0p <时，10px -<，此时21()0px f 'x px -=>，故()f x 在(0,)+∞上单调递增；（4分）当0p >时，当1(0,x p ∈时，()0f 'x <，故()f x 在1(0,)p 上单调递减；当1(,)x p∈+∞时，()0f 'x >，故()f x 在1(,)p+∞上单调递增.（6分）（II ）依题意，得e (ln 1)xm x x ≥+-，（8分）令()e (ln 1)xh x x x =+-，下面求函数()h x 的最小值，1()(ln 1)e 1x h'x x x =+-+，令1()ln 1m x x x =+-，结合（I ）中结论可知，()1ln 1m x x x=+-在[]1,e 上单调递增，故()()10m x m ≥=，故1ln 10x x+-≥在[]1,e 上恒成立.（10分）故()1(ln 1)e 110x h'x x x=+-+≥>，故()()e ln 1xh x x x =+-在[]1,e 上单调递增.故min [()](1)1e h x h ==-，故1e m ≥-.综上所述，实数m 的取值范围为[)1e,-+∞.（12分）22．（本小题满分10分）选修4-4：坐标系与参数方程（II ）设曲线C 上一点)sin ,cos 3(θθP ，则点P 到直线l 的距离11|2sin cos 3|+--=θθd |2cos()2|6θπ+-=，（8分）可知当cos()16θπ+=-时，d 取得最大值，且为22，即直线m 与直线l 之间的最大距离为22．（10分）23．（本小题满分10分）选修4-5：不等式选讲【解析】（I ）3)1(|42||)42(||42|||2222++=++=++--≥+++-a a a a x a x a x a x ，（2分）由33)1(2≥++a ，得3|42|||2≥+++-a x a x ，即3)(≥x f ．（4分）（II ）当1-=a 时，21,2()|1||2|3,2121,1x x f x x x x x x --<-⎧⎪=-++=-≤≤⎨⎪+>⎩.（7分）作出函数)(x f 的图象及直线5y =如图：可知所围成的图形为梯形，令5)(=x f ，得3-=x 或2，（9分）则所求图形的面积为822)53(=⨯+．（10分）。
2018年3月2018届高三第一次全国大联考(新课标Ⅲ卷)理数卷(正式考试版)
绝密★启用前|学易教育教学研究院命制 2018年第一次全国大联考【新课标卷III 】 理科数学（考试时间：120分钟 试卷满分：150分） 注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。
2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
写在本试卷上无效。
3．回答第Ⅱ卷时，将答案写在答题卡上。
写在本试卷上无效。
4．考试结束后，将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题（本大题共12个小题,每小题5分,共60分．在每小题给出的四个选项中,只有一个选项是符合题目要求的）1．已知集合12{|}3A x x=∈∈+Z N ，2{|450}B x x x =--≤，则A B = （ ） A ．{1,0,1,3}- B ．{1,0,1,2}- C ．{1,0,1}- D ．{0,1,2,3}2．已知i 是虚数单位，复数i z a =+()a ∈R ，且满足13i1z z -=+，则||z =（ ）ABCD ．33．若()()2,3,,6m ==a b ，且()+⋅=+a b a a b a ，则m =（ ）A ．12B ．2C ．4D ．94．函数3()e e x x f x x -=--的大致图象是（ ）A B C D 5．如图，在半径为4的大圆中有三个小半圆123,,O O O ，其半径分别为1，2，1，若在大圆内随机取一点，则此点取自阴影部分的概率是（ ）A ．14B ．38C ．58D ．7166．已知锐角ABC △BC ，且3AB =，4AC =，则BC =（ ） AB ．6C ．5 D7．执行如下图所示的程序框图（算法流程图），输出的结果是（ ）A ．4B ．12C ．84D ．1688．把函数())4f x x π=-的图象上每个点的横坐标扩大到原来的4倍，再向左平移3π，得到函数()g x 的图象，则函数()g x 的一个单调递增区间为（ ）A ．175[,]66ππ-- B ．57[,]66ππ- C ．24[,]33ππ-D ．719[,]66ππ 9．在1220172016(2)x+的展开式中，5x 项的系数为（ ）A ．252B ．264C ．512D ．53210．《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，将底面为矩形，一棱垂直于底面的四棱锥称之为“阳马”，已知某“堑堵”与某“阳马”组合而成的几何体的三视图中如图所示，已知该几何体的体积为x =（ ） A ．1 BC ．2 D．11．过抛物线C ：24y x =上一点(4,4)P 作两条直线分别与抛物线相交于点,A B 两点，连接AB ，若直线AB 的斜率为1，且直线,PA PB 与坐标轴都不垂直，则直线,PA PB 的斜率倒数之和为（ ）A ．12B ．1C ．2D ．312．已知函数2()f x x m =+与函数1()ln 3g x x x =--1([,2])2x ∈的图象上至少存在一对关于x 轴对称的点，则实数m 的取值范围是（ ）A ．5[ln 2,2]4+B ．5[2ln 2,ln 2]4-+C ．5[ln 2,2ln 2]4+-D ．[2ln 2,2]-第II 卷本试卷包括必考题和选考题两部分．第13题～第21题为必考题,每个试题考生都必须作答．第22题～第23题为选考题,考生根据要求作答．二、填空题（本大题共4小题,每小题5分,共20分）132，则该正六棱锥的外接球的表面积为___________．14．已知双曲线22221(0,0)x y a b a b-=>>的左右焦点分别关于两条渐近线的对称点重合，则双曲线的离心率为___________．15．已知x ，y 满足约束条件135250430x x y x y ≤-⎧⎪-+≥⎨⎪+-≥⎩，记z mx y =+（0m >）的最大值为()m Ω，若7()5m Ω≤，则实数m 的最小值为___________． 16．如图，在边长为2的菱形ABCD 中，3B π∠=，AEMF 是以A 为圆心，1为半径的扇形，点M 为圆弧 EF上任意一点，MN AB ．设MAF θ∠=，则当 EMMN +取得最小值时，θ=___________． 三、解答题（本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤） 17．（本小题满分12分）已知n S 为公差不为零的等差数列{}n a 的前n 项和，515S =，且248a a a 、、成等比数列．（1）求数列{}n a 的通项公式；。
2018届高三大联考数学试卷(3)
绝密★启用前2018届高三大联考(3)数 学 试试卷总分：150分 考试时间：120分钟本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 参考公式：如果事件A 、BP （A +B ）=P （A ）+P （B S =4πR 2 如果事件A 、B 相互独立，那么 其中RP （A ·B ）=P （A ）·P （B 球的体积公式如果事件A 在一次试验中发生的概率是P ，V =34πR 3那么n 次独立重复试验中恰好发生k其中R 表示球的半径P n (k )= C k n P k (1－P )n－k第Ⅰ卷（选择题 共60分）注意事项：1.答第Ⅰ卷前，考生务必将密封线内的内容填写完整.2.每小题选出答案后，用钢笔或圆珠笔将答案填写在第Ⅱ卷卷头处.3.本卷共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项符合题目要求.一、选择题：（本大题共12小题,每小题5分,共60分.） 1．已知函数f （x ）满足f （x+1）=23+f （x ）（x ∈R ），且f （0）=1. 则数列{()}f n （n N *∈）前20项的和为 ( ) A ．335 B ．315 C ．325 D ．3051．解析：A 由f （n+1）-f （n ）=23得,数列{()}f n （n N *∈）是首项为f (1)=23+f(0)=25 公差为23的等差数列, ∴s 20=20335232192025=⨯⨯+⨯ , 故选A . 2. 若向量),sin ,(cos ),sin ,(cos ββαα==则与一定满足 （ ）A. b a 与的夹角等于βα-B. （)()-⊥+C.a ∥bD. b a ⊥2．解析：B （)sin sin ,cos (cos )sin sin ,cos (cos )()βαβαβαβα--⋅++=-⋅+=cos 2α-β2cos+sin 2α-sin 2β=1-1=0,故b a 与一定满足B ，而对于A 、B 、C 只有加条件才成立，故选B 。
5月2018届高三第三次全国大联考(江苏卷)数学卷(全解全析)
程
中
得
x12 a2
y12 b2
1
x22
a2
y22 b2
1
,
两式
相
减,
化
简
得
y1 y2 2b2 x1 x2 a2
, 又 因 为 A, B, D, F
四点共线, 所以
数学 第 3 页（共 14 页） 3
原创精品资源学科网独家享有版权，侵权必究！
20 c4
2
32
63
6
23
cos( 2 ) cos(2 ) 1 2sin2 ( ) 7 ．学科~网
3
3
69
10．【答案】 7
【解析】法 1：设 an 表示该女子第 n 天所织的布的尺数,则数列{an} 是以 3 为首项, 2 为公比的等比数列,
设
Sn
是数列{an} 的前
n
2018 年第三次全国大联考【江苏卷】
数学 I·全解全析
1．【答案】 {x | 1 x 3} (或用区间表示为 (1 , 3] )
2
2
22
【解析】由题意,得 A {x | 2x 1 0} {x | x 1} , B {x | 2x2 x 3 0} {x | 1 x 3} ,所以
2
2
A B {x | 1 x 3}．
2
2
ቤተ መጻሕፍቲ ባይዱ
2．【答案】 3 4i
【解析】由题意,得 z (4 3i) 1 i (4 3i)(i) 3 4i ,所以 z 3 4i ． 1 i
3．【答案】 8
【解析】由题意,得 x 12 14 16 a 20 16 ,解得 a 18 ,所以 s2 1 (42 22 02 22 42 ) 1 40 8 ．
普通高等学校2018届高三招生全国统一考试仿真卷(三)数学(理)试题含答案
绝密 ★ 启用前2018年普通高等学校招生全国统一考试仿真卷理科数学（三）本试题卷共2页，23题（含选考题）。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项：1、答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后，请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．若集合{}|11A x x =-<<，{}|02B x x =<<，则A B =（ ） A ．{}|11x x -<< B ．{}|12x x -<< C ．{}|02x x <<D ．{}|01x x <<2．设复数12i z =+（是虚数单位），则在复平面内，复数2z 对应的点的坐标为（ ） A ．()3,4- B ．()5,4C ．()3,2-D ．()3,43．()()6221x x -+的展开式中4x 的系数为（ ） A ．-160B ．320C ．480D ．6404．某几何体的三视图如图所示，则该几何体的表面积为（ ）A ．52π+B ．42π+C ．44π+D ．54π+5．过双曲线221916x y -=的右支上一点P ，分别向圆1C ：()2254x y ++=和圆2C ：()2225x y r -+=（0r >）作切线，切点分别为M ，N ，若22PM PN -的最小值为58，则r =（ ） A ．BCD ．6()f x 的最小正周期大于，则ω的取值范围为（ ）A ．1,12⎛⎫ ⎪⎝⎭ B ．()0,2 C ．()1,2 D ．[)1,27．在ABC △中，内角A ，B ，C 的对边分别为，，，若函数()()3222113f x x bx a c ac x =+++-+无极值点，则角B 的最大值是（） ABCD 8．公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”，刘徽得到了圆周率精确到小数点后两位的近似值3．14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为（ ）（参考数据：sin150.2588≈，sin7.50.1305≈）A ．12B ．20C ．24D ．489．设π02x <<，则“2cos x x <”是“cos x x ＜”的（ ） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件10．欧阳修的《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆盖其口，徐以杓酌油沥之，自钱孔入，而钱不湿”，可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为3cm 的圆面，中间有边长为1cm 的正方形孔．现随机向铜钱上滴一滴油（油滴的大小忽略不计），则油滴落入孔中的概率为（ ）ABC ．19D11．已知()cos23,cos67AB =︒︒，()2cos68,2cos22BC =︒︒，则ABC △的面积为（ ） A ．2BC ．1D．212．已知定义在R 上的可导函数()f x 的导函数为()f x '，对任意实数均有()()()10x f x xf x '-+>成立，且()1e y f x =+-是奇函数，则不等式()e 0x xf x ->的解集是（ ） A ．(),e -∞B ．()e,+∞C ．(),1-∞D ．()1,+∞第Ⅱ卷本卷包括必考题和选考题两部分。
推荐-全国大联考(湖南专用)2018届高三第三次联考数学试卷(理科) 精品
全国大联考(湖南专用)2018届高三第三次联考数学试卷（理科）第Ⅰ卷 (选择题 共50分)一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若复数z 满足i (1+2i) z = 5，则z 等于（ ）A ．2－iB ．－2+iC ．－2－iD ．－1－2i1． 设f ：x →x 2是集合A 到集合B 的映射，若B ＝｛1,2｝，则A ∩B 等于（ ）（A ）Φ （B ）｛1｝ （C ）Φ或｛2｝ （D ）Φ或｛1｝ 2．设某等差数列的首项为a (a ≠0)，第二项为b ．则这个数列中有一项为0的充要条件是（ ）A ．a －b 是正整数B ．a+b 是正整数C ．b a b -是正整数 D ．ba a-是正整数 3．在△ABC 中，若sin A = cos Bcos C ，则tan C+tan B 的值为（ ） A ．－1 B ．1 C ．－2 D ．24．如图，一条螺旋线是用以下方法画成：△ABC 是边长为1的正三角形，曲线CA 1，A 1A 2，A 2A 3分别以A 、B 、C 为圆心，AC 、BA 1、CA 2为半径画的圆弧，曲线CA 1A 2A 3称为螺旋线旋转一圈．然后又以A 为圆心AA 3为半径画圆弧……这样画到第n 圈，则所得螺旋线的长度l n 为（ ）A ．(3n 2+n)πB ．(3n 2－n+1) πC ．()2n n32π+ D ．()21n n 32π+- 5．已知α∈(0，2π)，且cos α= a ，则关于x 的不等式sin x ≤ a 的解集可以用区间表示为（ ）A ．[2k π－α+2π，2k π+α+2π] (k ∈Z) B ．[2k π－α+2π，2k π+α+23π] (k ∈Z) C ．[2k π－α，2k π+α] (k ∈Z) D ．[2k π+α+2π，2k π－α+25π] (k ∈Z) 6．已知11n 23a n -=(n ∈ N*)，记数列{a n }的前n 项和为S n ，则使S n >0的n 的最小值为（ ）A ．10B ．11C ．12D ．137．已知函数f (x) = 3sin ()ϕω+x ，g(x) = 3cos ()ϕω+x ．若对任意x ∈R 都有⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛+x 6f x 6f ππ，则g (6π)的值为 （ ）A ．0B ．3C ．－3D ．3或－38．数列{a n }的前n 项和为S n ，且2n 1n n a S 2S +=+，1a 2-=则数列{a n }的首项为（ ）A ．1或一2B ．土1C ．土2D ．2或－19．已知数列{a n }、{b n }的前n 项和分别为A n 、B n ，记n n n n n n n b a A b B a c ⋅-⋅+⋅= (n ≥1)，则数列{c n }的前10项和为（ ） A ．A 10+B 10 B ．2B A 1010+ C ． A 10·B 10 D ．1010B A ⋅ 10．已知定义在R 上的减函数f (x)，对任意t ∈R ，总有f (－1+t)+f (－1－t)= 2．若m+n<－2，则（ ）A ．f (m)－f (n)>2B ．f (m) + f (n)>2C ．f (m)－f (n)<2D ．f (m) + f (n)<2第Ⅱ卷 (非选择题 共100分)二、填空题：本大题共5小题，每小题4分，共20分．把答案填在题中的横线上． 11．设随机变量的分布列为P(ξ=k) = ak (k=1，2，…，n)，则a=____________.12．5cos 5sin 355cos 2-的值是__________________. 13．已知cos β= a ，sin α= 4sin(α+β)，则tan(α+β) =_______________. 14．在公差为d (d≠0)的等差数列{a n }中，若S n 是数列{a n }的前n 项和，则数列1020S S -，2030S S -，3040S S -也成等差数列，且公差为l00d ．类比上述结论，相应地在公比为q(q≠1)的等比数列{b n }中，若T n 是数列{b n }的前n 项积，则有_________________________________________________________________.15．如图，某人从A 出发沿道路逆时针行走再回到A ，且所走过 的路线是一个矩形，则不同的走法有________种；若从B 出发 按同样要求回到B ，则不同的走法有__________种.三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程及演算步骤． 16．(本小题满分12分) 已知tan A 与tan (4π－A)是方程0q px x 2=++的两根，若3tan A=2tan (4π－A)，求p 与q 的值．17．(本小题满分12分) 已知函数f (x) = cos (x ω+a) (0<ω<2π)的图象向右平移a 个单位后得到的图象关于点(a+1，0)对称，且f (x)在[ωa-，1]上是单调函数，f(x)的图象关于点(4，0)对称，求f (x)的表达式．18．(本小题满分14分) 已知函数()()()1n 3nnn r 1n 2rrn 1n 22n n 21n 1n 20n x 1x 1x x x x f C C C C C -+-+--++-+-+-= ，其中n ∈N*，求函数f (x)的极大值和极小值．19．(本小题满分14分) 已知函数()x b b 242ax x f 22-+-=，()()2a x 1x g ---= (a ，b ∈R)．(1) 当b=0时，若f (x)在[2，+∞)上单调递增，求a 的取值范围；(2) 当a 为整数时，若存在x 0使得f (x 0)是f (x)的最大值，g (x 0)是g(x)的最小值，求a ，b 的值．20．(本小题满分14分) 设数列{a n }满足：若n=2k －1 (k ∈N*)，a n = n ；若n=2k (k ∈N*)，a n = a k . (1) 求a 2+a 4+a 6+a 8+a 10+a 12+a 14+a 16；(2) 若n n 212321n a a a a a S +++++=- ，求证：S n = 4 n －1+S n －l (n ≥2)；(3) 证明：n n 21411S 1S 1S 1-<+++ ．21．(本小题满分14分) 在平面直角坐标系内，已知三个点列{A n }，{B n }，{C n }，其中A n (n ，an )，B n (n ，b n )，C n (n －1，0)，n n 1n n C B //A A +，且点列{B n }在斜率为6的直线上．(1) 试用a 1，b 1与n 表示a n (n ≥2)；(2) 设a 1= a ，b 1=－a ，在a 6与a 7两项中至少有一项是数列{a n }的最小项，试求a 的取值范围； (3)设n ∈N*，在(2)的条件下，证明：数列{a n }中，最小项为a 6与最小项为a 7的概率相等．2018届高三数学试卷（理科）参考答案一、选择题1．C 2．D 3．B 4．A 5．D 6．B 7．A 8．A 9．C 10．B 二、填空题11．()1n n 2+ 12．1 13．4a a 12--± 14．1020T T ，2030T T ，3040T T 也成等比数列，且公比为q l 0015．30，94 提示： 2．D ba a1n -=-是正整数．故选D ． 3．B tan C+tan B=()1Asin B C sin =+. 4．A ()()ππn n 3n 332132l 2n +=++++=． 5．D 根据诱导公式可知，cos α = a ，于是结合正弦线或者正弦曲线可知，所求解选D ． 6．B 由通项公式，a 1+a 2+…+a 10 =0，n ≥1l 时，a n >0，S n 开始大于0，故n 最小为11． 7．A f 2 (x)+g 2 (x)=9，由已知6x π=是函数f (x)图象的对称轴，f(6π)=3或f(6π)=－3，g(6π)=0，故选A ．8．A a l = 2 (a l +a 2)+a 12得 a l =1或－2．9．C 当n ≥2时，1n 1n n n n B A B A c ---=，故c l +c 2 +…+c 10= A l0B l0． 10．B 由已知得f[－1+(n+1)]+f[－1－(n+1)]=2，即f (－2－n)=2－f(n)，由于 m <－2一n ，所以 f (m)>f(－2－n)=2－f(n)，即 f m)+f(n)>2． 11．()1n n 2+ 由a (1+2+…+n)=1，可得．12．1 原式= ()5cos 5sin 3560cos 2--=1．13．4a a 12--±sin α= sin [(α+β)－β]=…= 4sin(α+β) 可化为()=-=+4cos sin tan βββα4a a 12--±．15．30，94 横边、竖边各取一条与点A 所在的横边、竖边可组成一个矩形，有6×5=30种；当B 为矩形顶点时有5×6=30种，当B 在横边上（不为顶点）时有5×2×4=40种，当B 在纵边上(不为顶点)时有6×1×4=24种，共有30+40+24—94种．16．解：设t=tan A ，则tan(4π一A)=t1t1+- …………………………………2分 由已知得3t=2t1t 1+-，解得t=31或t=－2，…………………………………5分当t=31时，tan(4π一A)=21， 此时p=－[tan A+tan(4π一A)]=65-， q=tan A·tan(4π一A)=61………8分当t=－2时，tan(4π－A)=－3，此时p=5，q=6．…………………………………………………………11分 由以上讨论知：p=65-，q=61；或p=5，q=6．………………………12分17．解：由题设y=cos[ω(x －a)+α]的图象关于点(a+l ，0)对称， 则cos[ω(a+1－a)+α]=0，即 2k ππαω+=+(k ∈Z)．……………………3分又f (x) =cos(ωx+α)在[ωa-，1]上是单调函数，令t=ωx+α，则g(t)= cos t 在[0，ω+α]上是单调函数， ∴0<2k ππαω+=+≤π，∴0<k+21≤1． ∵k ∈Z ，∴k=0，于是 ω+α=2π………………………………………8分又f (x) =cos(ωx+α)的图象关于点(4，0)对称， ∴4ω+α2m ππ+= (m ∈Z)，∴πωm 3=(m ∈Z)． ……………… 11分 ∵0<ω<2π，∴3πω=，∴f(x)=cos(6x 3ππ+)．……………………………12分18．解：由已知可得 ()()n1n 2x 1x x f -=- ……………2分 所以()()()()[]x 1n 31n 2x 1x x 'f 1n 2n 2----=--………………………… 4分令()0x 'f =，得x l =0，x 2=1n 31n 2--，x 3=1．………………………… 5分 从而x l < x 2< x 3．当n 为偶数时，f(x)的增减表如下：从而f(x)在x=0时无极值；在x=1n 31n 2--时取得极大值()1n 31n 3n 1n 2--⋅-；在x=1时取极小值0．………………………………………………………9分 当n 为奇数时f(x)的增减表如下：从而f(x)在x=0时无极值；在x=1n 31n 2--时取得极大值()1n 31n 3n 1n 2--⋅-；在x=1时无极值． ……………………………………………………14分 19．解：(1)当b=0时，f(x)= ax 2－4x ，若a=0，则f (x)=－4x ，则f(x)在[2，+∞)上递减，不合题意． 则知a ≠0，要使f(x)在[2，+∞)上单调递增，则知：a ≥1………………………………………………………6分 (2) 若a=0，f (x)=－22b b 24-+x ，则f (x)无最大值，由知a ≠0．要使f(x)有最大值，必须 ⎩⎨⎧≥-+<0b b 240a 2即a<0且1－5≤b ≤1+5 此时ab b 24x x 20-+==，f (x)取最大值．又g (x)取最小值时，a x x 0==，依题意有ab b 24a 2-+=∈Z∴()51b 5b b 24a 222≤--=-+=，又a<0，a ∈Z ，则a=－1，此时b =－1或3．…………………………………………14分 20．(1)解：a 2+a 4+a 6+a 8+a 10+a 12+a 14+a 16 =22．……………………4分 (2) n n 212321n a a a a a S +++++=-= (1231n a a a -+++ )+(n 242a a a +++ ) =[1+3+5+…+(2n －1)]+( 12321n a a a a -++++ )=1n 1n n S 22121--+⨯-+= 4n －1+S n －1 (n ≥2)．………………8分(3) 由(2)并累加得 ()2431444S S n1n 21n +=++++=- ， ∴n n n 43243S 1<+=， ∴⎪⎭⎫⎝⎛++++<+++-1n 2n 21414141143S 1S 1S 1 n 411-=…14分 21．解：(1) 1n n A A +=(1，a n+l －a n )，n n C B =(－1，－b n )，又∵ n n 1n n C B //A A +，∴ 1×(－b n )=－1×(a n+l －a n )，即b n = a n+l －a n ∵ 点列{B n }在斜率为6的直线上，∴()n1n b b n1n -+-+=6，∴ b n+1－b n =6， 即数列{b n }是首项为b 1，公差为6的等差数列， ∴ b n = b 1+6(n —1)，故a n = a 1+(a 2－a 1)+(a 3－a 2)+…+(a n －a n －1)= a l +b l +b 2+…+b n －1= 3 n 2+(b 1－9)n+6+a 1－b 1 (n ≥2)． …………………………5分 (2) 由a 1= a ，b 1=－a ，及(1)，得a n =3n 2－(a+9)n+6+2a ，因为二次函数f(x) = 3x 2－(a+9)x+6+2a 是开口向上，对称轴为直线69a x +=的抛物线，在a 6与a 7两项中至少有一项是数列{a n }的最小项，则21569a 211≤+≤， ∴ 24≤a ≤36．……………………………………………………………9分 (3)证明：∵ a n+1－a n =6n －(a+6)，又 30≤a +6≤42，若 6n ≤30，即n≤5时。
5月2018届高三第三次全国大联考(江苏卷)数学卷(参考答案)
数学 I·参考答案
1． {x | 1 x 3} (或用区间表示为 (1 , 3] )
2
2
22
3． 8
5． 3 7． 1
2 9． 7
9 11． 3
13． x2 y2 1 72 36
15．（本小题满分 14 分）
2． 3 4i 4． 1
3 6． 5 8． 2 2
故当 x 8 时, V (x) 有最大值,最大值为V (x)max V (8) 1536 ． 即当该框架的底面宽为 8 分米时，长方体框架所占的空间体积最大，最大值为 1536 立方分米．（14 分） 18．（本小题满分 16 分）
【解析】（1）设等比数列{an} 的公比为 q ,则 an a1 qn1 ．（2 分）
分）
22
3
当且仅当 x 12 x ,即 x 8 时,V (x) 有最大值,（13 分） 2
最大值为 V (x)max 1536 ．
即当该框架的底面宽为 8 分米时，长方体框架所占的空间体积最大，最大值为 1536 立方分米．（14 分）
法 2：因为 V (x) 6x2 (12 x) 72x2 6x3(0 x 12),
yM
y1
2
y2
(x1
x2 ) 6
p 2
,
所以
x0
y02 2p
p 8
,即
N( p 8
,
p) 2
．（12
分）
数学 第 4 页（共 11 页）
数学 第 2 页（共 11 页） 2
原创精品资源学科网独家享有版权，侵权必究！