必修四第一章综合练习题
必修四第一章 三角函数 精选练习题(有答案和解析)

必修四第一章 三角函数精选练习题一、选择题1.在0°~360°的范围内,与-510°终边相同的角是( ) A .330° B .210° C .150° D .30°B [因为-510°=-360°×2+210°,因此与-510°终边相同的角是210°.] 2.cos 420°的值为( ) A .12 B .-12C .32D .-32A [cos 420°=cos(360°+60°)=cos 60°=12,故选A.]3.已知角θ的终边上一点P (a ,-1)(a ≠0),且tan θ=-a ,则sin θ的值是( ) A .±22 B .-22 C .22 D .-12B [由题意得tan θ=-1a =-a , 所以a 2=1, 所以sin θ=-1a 2+(-1)2=-22.] 4.一个扇形的弧长与面积的数值都是6,这个扇形中心角的弧度数是( ) A .1 B .2 C .3 D .4C [设扇形的半径为r ,中心角为α,根据扇形面积公式S =12lr 得6=12×6×r ,所以r =2, 所以α=l r =62=3.]5.已知sin θ+cos θ=43,θ∈⎝ ⎛⎭⎪⎫0,π4,则sin θ-cos θ的值为( ) A .23 B .13 C .-23 D .-13 C [∵已知sin θ+cos θ=43,θ∈⎝ ⎛⎭⎪⎫0,π4,∴1+2sin θcos θ=169,∴2sin θcos θ=79,故sin θ-cos θ=-(sin θ-cos θ)2 =-1-2sin θ·cos θ =-23,故选C.]6.函数y =tan(sin x )的值域是( ) A .⎣⎢⎡⎦⎥⎤-π4,π4B .⎣⎢⎡⎦⎥⎤-22,22C .[]-tan 1,tan 1D .[]-1,1C [sin x ∈[-1,1],又-π2<-1<1<π2,且y =tan x 在⎝ ⎛⎭⎪⎫-π2,π2上是增函数,所以y min =tan(-1)=-tan 1,y max =tan 1.]7.将函数y =sin ⎝ ⎛⎭⎪⎫x -π3的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移π3个单位,得到的图象对应的解析式为( )A .y =sin 12xB .y =sin ⎝ ⎛⎭⎪⎫12x -π2C .y =sin ⎝ ⎛⎭⎪⎫12x -π6D .y =sin ⎝ ⎛⎭⎪⎫2x -π6 C [函数y =sin ⎝ ⎛⎭⎪⎫x -π3的图象上所有点的横坐标伸长到原来的2倍可得y =sin ⎝ ⎛⎭⎪⎫12x -π3,再将所得的图象向左平移π3个单位,得到函数y =sin ⎣⎢⎡⎦⎥⎤12⎝⎛⎭⎪⎫x +π3-π3=sin ⎝ ⎛⎭⎪⎫12x -π6.] 8.函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π4在⎣⎢⎡⎦⎥⎤0,π2上的单调递增区间是( ) A .⎣⎢⎡⎦⎥⎤0,π8B .⎣⎢⎡⎦⎥⎤π8,π2C .⎣⎢⎡⎦⎥⎤0,3π8D .⎣⎢⎡⎦⎥⎤3π8,π2C [令2k π-π2≤2x -π4≤2k π+π2(k ∈Z )得k π-π8≤x ≤k π+3π8(k ∈Z ),k =0时,x∈⎣⎢⎡⎦⎥⎤-π8,3π8,又x ∈⎣⎢⎡⎦⎥⎤0,π2, ∴x ∈⎣⎢⎡⎦⎥⎤0,3π8,故选C.]9.已知函数y =A sin(ωx +φ)(A >0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )A .y =2sin ⎝ ⎛⎭⎪⎫2x -π4B .y =2sin ⎝ ⎛⎭⎪⎫2x -π4或y =2sin ⎝ ⎛⎭⎪⎫2x +3π4 C .y =2sin ⎝ ⎛⎭⎪⎫2x +3π4D .y =2sin ⎝ ⎛⎭⎪⎫2x -3π4C [由图可知A =2,4⎝ ⎛⎭⎪⎫π8+π8=2πω得ω=2,且2×⎝ ⎛⎭⎪⎫-π8+φ=π2+2k π(k ∈Z )∴φ=2k π+3π4(k ∈Z ), 又∵|φ|<π, ∴φ=3π4,故选C.]10.如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为P 0(2,-2),角速度为1,那么点P 到x 轴的距离d 关于时间t 的函数图象大致为( )C [∵P 0(2,-2),∴∠P 0Ox =π4.按逆时针转时间t 后得 ∠POP 0=t ,∠POx =t -π4. 此时P 点纵坐标为2sin ⎝ ⎛⎭⎪⎫t -π4,∴d =2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫t -π4.当t =0时,d =2,排除A ,D ; 当t =π4时,d =0,排除B.]11.设α是第三象限的角,且⎪⎪⎪⎪⎪⎪cos α2=-cos α2,则α2的终边所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 B [∵α是第三象限的角, ∴π+2k π<α<3π2+2k π,k ∈Z . ∴π2+k π<α2<3π4+k π,k ∈Z . ∴α2在第二或第四象限. 又∵⎪⎪⎪⎪⎪⎪cos α2=-cos α2,∴cos α2<0.∴α2是第二象限的角.]12.化简1+2sin (π-2)·cos (π-2)得( )A .sin 2+cos 2B .cos 2-sin 2C .sin 2-cos 2D .±cos 2-sin 2 C [1+2sin (π-2)·cos (π-2) =1+2sin 2·(-cos 2) =(sin 2-cos 2)2, ∵π2<2<π,∴sin 2-cos 2>0. ∴原式=sin 2-cos 2.]13.同时具有下列性质的函数可以是( ) ①对任意x ∈R ,f (x +π)=f (x )恒成立; ②图象关于直线x =π3对称; ③在⎣⎢⎡⎦⎥⎤-π6,π3上是增函数.A .f (x )=sin ⎝ ⎛⎭⎪⎫x 2+π6B .f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6C .f (x )=cos ⎝ ⎛⎭⎪⎫2x +π3D .f (x )=cos ⎝ ⎛⎭⎪⎫2x -π6B [依题意知,满足条件的函数的周期是π,图象以直线x =π3为对称轴,且在⎣⎢⎡⎦⎥⎤-π6,π3上是增函数.对于A 选项,函数周期为4π,因此A 选项不符合;对于C 选项,f ⎝ ⎛⎭⎪⎫π3=-1,但该函数在⎣⎢⎡⎦⎥⎤-π6,π3上不是增函数,因此C 选项不符合;对于D 选项,f ⎝ ⎛⎭⎪⎫π3≠±1,即函数图象不以直线x =π3为对称轴,因此D 选项不符合.综上可知,应选B.]14.已知函数f (x )=-2tan(2x +φ)(|φ|<π),若f ⎝ ⎛⎭⎪⎫π16=-2,则f (x )的一个单调递减区间是( )A .⎝ ⎛⎭⎪⎫3π16,11π16B .⎝ ⎛⎭⎪⎫π16,9π16C .⎝ ⎛⎭⎪⎫-3π16,5π16D .⎝ ⎛⎭⎪⎫π16,5π16 A [由f ⎝ ⎛⎭⎪⎫π16=-2得-2tan ⎝ ⎛⎭⎪⎫π8+φ=-2,所以tan ⎝ ⎛⎭⎪⎫π8+φ=1,又|φ|<π,所以φ=π8,f (x )=-2tan ⎝ ⎛⎭⎪⎫2x +π8, 令k π-π2<2x +π8<k π+π2,k ∈Z 得 k π2-5π16<x <k π2+3π16,k ∈Z .可得f (x )的单调递减区间是⎝ ⎛⎭⎪⎫k π2-5π16,k π2+3π16,k ∈Z ,令k =1,可得f (x )的一个单调递减区间是⎝ ⎛⎭⎪⎫3π16,11π16.]二、填空题15.对于锐角α,若tan α=34,则cos 2α+2sin 2α=________. 6425 [由题意可得:cos 2α+2sin 2α=cos 2α+4sin αcos αcos 2α+sin 2α=1+4tan α1+tan 2α=6425.]16.已知sin α=13,且α是第二象限角,那么cos(3π-α)的值为________. 223[cos(3π-α)=-cos α=-(-1-sin 2α)=1-⎝ ⎛⎭⎪⎫132=223.] 17.函数y =3-tan x 的定义域是________.⎝ ⎛⎦⎥⎤k π-π2,k π+π3(k ∈Z ) [作出三角数线如图,由函数可知3-tan x ≥0中tan x ≤3,而3对应角为π3,由图中阴影部分可得定义域为⎝ ⎛⎦⎥⎤k π-π2,k π+π3(k ∈Z ).]18.函数y =tan ⎝ ⎛⎭⎪⎫2x -π4的定义域为________.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ≠3π8+k π2,k ∈Z[2x -π4≠π2+k π,即x ≠3π8+k π2,k ∈Z .]19.若函数y =sin(ωx +φ)(ω>0)的部分图象如图所示,则ω=________.4 [观察图象可知函数y =sin(ωx +φ)的半个周期为π4, 所以2πω=π2,ω=4.]20.已知函数f (x )=sin(ωx +φ)(ω>0),若将f (x )的图象向左平移π3个单位长度所得的图象与将f (x )的图象向右平移π6个单位长度所得的图象重合,则ω的最小值为________.4 [由条件可知,图象变换后的解析式分别为y =sin ⎝ ⎛⎭⎪⎫ωx +ωπ3+φ和y =sin ⎝ ⎛⎭⎪⎫ωx -ωπ6+φ,由于两图象重合,所以ωπ3+φ=-ωπ6+φ+2k π(k ∈Z ). 即ω=4k (k ∈Z ),由ω>0,∴ωmin =4.]21.一扇形的圆心角为2弧度,记此扇形的周长为C ,面积为S ,则C -1S 的最大值为________.4 [由已知可得弧长l =2r ,周长C =4r ,面积S =12×lr =r 2,∴C -1S =4r -1r 2=-1r 2+4r =-⎝ ⎛⎭⎪⎫1r -22+4,故C -1S 的最大值为4.] 22.已知角α终边上一点P 的坐标为⎝ ⎛⎭⎪⎫sin 5π6,cos 5π6,则角α的最小正值是________.5π3 [角α终边上一点P 的坐标为⎝ ⎛⎭⎪⎫sin 5π6,cos 5π6,即⎝ ⎛⎭⎪⎫12,-32, tan α=-3212=-3,且α为第四象限角,所以角α的最小正值是5π3.]23.函数y =2+cos x2-cos x(x ∈R )的最大值为________.3 [由题意有y =42-cos x-1,因为-1≤cos x ≤1,所以1≤2-cos x ≤3,则43≤42-cos x ≤4,由此可得13≤y ≤3,于是函数y =2+cos x 2-cos x (x ∈R )的最大值为3.]24.对于函数f (x )=⎩⎨⎧sin x ,sin x ≤cos x ,cos x ,sin x >cos x ,给出下列四个命题:①该函数是以π为最小正周期的周期函数;②当且仅当x =π+k π(k ∈Z )时,该函数取得最小值-1; ③该函数的图象关于x =5π4+2k π(k ∈Z )对称; ④当且仅当2k π<x <π2+2k π(k ∈Z )时,0<f (x )≤22. 其中正确命题的序号是________. ③④ [作出函数f (x )的图象如图所示:由图象可知f (x )为周期函数,T =2π,①错误;当x =2k π+π或x =2k π+3π2时,取最小值-1,故②错误;x =π4+2k π(k ∈Z )和x =5π4+2k π(k ∈Z )都是该图象的对称轴,故③正确; 当2k π<x <π2+2k π(k ∈Z )时,f (x )图象在x 轴上方且f (x )max =22. 故0<f (x )≤22.故④正确.]三、解答题25.已知sin(π-α)·cos(-8π-α)=60169,且α∈⎝ ⎛⎭⎪⎫π4,π2,求sin α与cos α的值.[解] 由已知条件可得sin αcos α=60169,∴(sin α+cos α)2=1+2sin αcos α=1+120169=289169, (sin α-cos α)2=1-2sin αcos α=1-120169=49169. ∵x ∈⎝ ⎛⎭⎪⎫π4,π2,∴sin α>cos α, ∴⎩⎪⎨⎪⎧sin α+cos α=1713,sin α-cos α=713,解方程组得sin α=1213,cos α=513.26.(1)已知角α的终边经过点P (4,-3),求2sin α+cos α的值; (2)已知角α的终边经过点P (4a ,-3a )(a ≠0),求2sin α+cos α的值; (3)已知角α终边上一点P 到x 轴的距离与到y 轴的距离之比为3∶4,求2sin α+cos α的值.[解] (1)∵α终边过点P (4,-3),∴r =|OP |=5,x =4,y =-3, ∴sin α=y r =-35,cos α=x r =45, ∴2sin α+cos α=2×⎝ ⎛⎭⎪⎫-35+45=-25.(2)∵α终边过点P (4a ,-3a )(a ≠0), ∴r =|OP |=5|a |,x =4a ,y =-3a . 当a >0时,r =5a ,sin α=y r =-35, cos α=x r =45, ∴2sin α+cos α=-25;当a <0时,r =-5a ,∴sin α=y r =35, cos α=x r =-45, ∴2sin α+cos α=25.综上,2sin α+cos α=-25或25. (3)当点P 在第一象限时,sin α=35, cos α=45,2sin α+cos α=2; 当点P 在第二象限时,sin α=35, cos α=-45,2sin α+cos α=25;当点P 在第三象限时,sin α=-35, cos α=-45,2sin α+cos α=-2; 当点P 在第四象限时,sin α=-35, cos α=45,2sin α+cos α=-25.27.是否存在角α,β,α∈⎝ ⎛⎭⎪⎫-π2,π2,β∈(0,π),使等式sin(3π-α)=2cos ⎝ ⎛⎭⎪⎫π2-β,3cos(-α)=-2cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由.[解] 假设存在角α,β满足条件,则{sin α=2sin β, ①3cos α=2cos β, ② 由①2+②2得sin 2α+3cos 2α=2. ∴cos 2α=12, ∴cos α=22.∵α∈⎝ ⎛⎭⎪⎫-π2,π2,∴α=±π4.当α=π4时,代入②得:cos β=32, ∵0<β<π,∴β=π6,代入①可知成立; 当α=-π4时,代入②得cos β=32,∵0<β<π,∴β=π6,此时代入①式不成立,故舍去. ∴存在α=π4,β=π6满足条件.28.已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫2x +π3+1. (1)求函数f (x )的最大值,并求取得最大值时x 的值; (2)求函数f (x )的单调递增区间.[解] (1)当2x +π3=2k π+π2,则x =k π+π12(k ∈Z )时,f (x )max =3. (2)当2k π-π2≤2x +π3≤2k π+π2,即k π-5π12≤x ≤k π+π12时,函数f (x )为增函数.故函数f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤k π-5π12,k π+π12(k ∈Z ). 29.如图是函数y =A sin(ωx +φ)+k (A >0,ω>0,|φ|<π2)的一段图象.(1)求此函数解析式;(2)分析一下该函数是如何通过y =sin x 变换得来的? [解] (1)由图象知A =-12-⎝ ⎛⎭⎪⎫-322=12,k =-12+⎝ ⎛⎭⎪⎫-322=-1,T =2×⎝ ⎛⎭⎪⎫2π3-π6=π,∴ω=2πT =2.∴y =12sin(2x +φ)-1. 当x =π6,2×π6+φ=π2,∴φ=π6. ∴所求函数解析式为y =12sin ⎝ ⎛⎭⎪⎫2x +π6-1.(2)把y =sin x 向左平移π6个单位得到y =sin ⎝ ⎛⎭⎪⎫x +π6,然后纵坐标保持不变、横坐标缩短为原来的12倍,得到y =sin ⎝ ⎛⎭⎪⎫2x +π6,再横坐标保持不变,纵坐标变为原来的12倍,得到y =12sin ⎝ ⎛⎭⎪⎫2x +π6,最后把函数y =12sin ⎝ ⎛⎭⎪⎫2x +π6的图象向下平移1个单位,得到y=12sin ⎝ ⎛⎭⎪⎫2x +π6-1的图象.30.已知函数f (x )=A sin(ωx +φ)⎝ ⎛⎭⎪⎫A >0,ω>0,|φ|<π2的图象在y 轴上的截距为1,它在y 轴右侧的第一个最大值点和最小值点分别为(x 0,2)和(x 0+3π,-2).(1)求f (x )的解析式;(2)将f (x )的图象上的所有点的横坐标缩短到原来的13倍(纵坐标不变),然后再将所得的图象向右平移π3个单位,得到函数g (x )的图象,写出函数g (x )的解析式,并用五点作图的方法画出g (x )在长度为一个周期的闭区间上的图象.[解] (1)由f (x )=A sin(ωx +φ)在y 轴上的截距为1,最大值为2,得1=2sin φ,所以sin φ=12.又|φ|<π2,所以φ=π6.由题意易知T =2[(x 0+3π)-x 0]=6π, 所以ω=2πT =13, 所以f (x )=2sin ⎝ ⎛⎭⎪⎫x 3+π6.(2)将f (x )的图象上的所有点的横坐标缩短到原来的13倍(纵坐标不变),得到y =2sin ⎝ ⎛⎭⎪⎫x +π6的图象;再把所得图象向右平移π3个单位,得到g (x )=2sin ⎝ ⎛⎭⎪⎫x -π3+π6=2sin ⎝ ⎛⎭⎪⎫x -π6的图象.列表:。
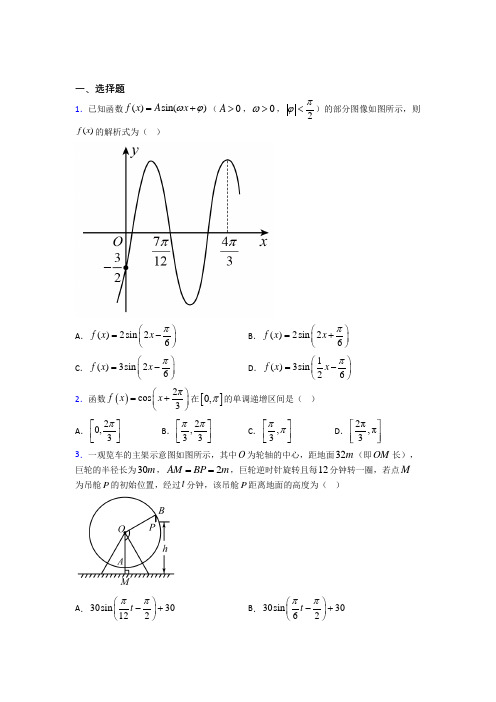
高一必修四第一章单元测试题有答案

三角函数单元测试卷一、 选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合要求的,把正确答案的代号填在括号内.) 1.0sin300的值是( )A12 B 12- C 2 D 2-2.已知 3cos 5α=-,α为第二象限角,则sin α=( )A 45-B 45C 25±D 45±3.已知0cos cos30θ=,则θ=( )A 030B 0036030k ⋅+()k Z ∈C 0036030()k k Z ⋅±∈D 0018030()k k Z ⋅+∈ 4.若θ为第一象限角,则2θ所在的象限是( ) A 第一,二象限 B 第二,三象限 C 第一,三象限 D 第二,四象限>5.函数cos()4y x π=-的递增区间是( )A 32,2,44k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B 52,2,44k k k Z ππππ⎡⎤--∈⎢⎥⎣⎦ C 52,2,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D 32,2,44k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦6.函数5sin(2)6y x π=+图象的一条对称轴方程是( )A 12x π=-B 0x =C 6x π=D 3x π=7.函数()sin(2)3f x x π=-的图像向左平移3π个单位,再将图象上各点的横坐标压缩为原来的12,那么所得图象的函数表达式为( )A sin y x =B 2sin(4)3y x π=+C sin(4)3y x π=+D sin()3y x π=+8.函数()tan f x x =的周期为( ) A 2π B π C2π D 4π @9.1sin cos 5αα+=,α为第四象限角,则tan α=( )A 34B 34-C 43D 43- 10.已知函数()f x 是R 上的奇函数且(1)2,(3)()f f x f x =+=则(8)f =( ) A 2 B -2 C 0 D 111.设0ω>,函数sin()23y x πω=++的图像向右平移23π个单位后与原图像重合,则ω的最小值为( )A 2πB πC 2D 312.已知函数f (x )=f (x ),且当)2,2(ππ-∈x 时,f (x )=x +sin x ,设a =f (1),b =f (2),c =f (3),则( )A a<b<cB b<c<aC c<b<aD c<a<b二、填空题(本大题共4小题,每小题5分,共20分,把最简单结果填在题后的横线上) ?13.比较大小 )413tan(π- )517tan(π-14.计算911cos tan()46ππ+-=___________15. 已知θ是第二象限角,则24sin sin cos θθθ-可化简为______________16.已知()sin()(0),()(),363f x x f f πππωω=+>=且()f x 在区间(,)63ππ内有最大值,无最小值,则ω的最小值为_________三、解答题(本大题共6小题,满分70分,解答应写出必要的文字说明、证明过程或演算步骤.)17.(10分) 已知3tan =α,计算ααααsin 3cos 5cos 2sin 4+- 的值 。
(word完整版)高一数学必修四第一章测试题

宣威市第九中学第一次月考高一数学试卷本试卷分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,时间120分钟.第Ⅰ卷(选择题 共60分)一.选择题(每小题5分,共60分) 1.与32︒-角终边相同的角为( )A .36032k k Z ︒︒⋅+∈, B. 360212k k Z ︒︒⋅+∈, C .360328k k Z ︒︒⋅+∈, D. 360328k k Z ︒︒⋅-∈, 2. 半径为1cm ,中心角为150o 的弧长为( )A .cm 32B .cm 32πC .cm 65D .cm 65π3.点A(x,y)是300°角终边上异于原点的一点,则yx值为( ) A.3 B. - 3 C. 33 D. -334.下列函数中属于奇函数的是( )A. y=cos(x )2π+B. sin()2y x π=- C. sin 1y x =+ D.cos 1y x =-5.要得到函数x y sin =的图象,只需将函数⎪⎭⎫ ⎝⎛-=3sin πx y 的图象 ( )A. 向左平移3π B. 向右平移3π C. 向左平移32π D. 向右平移32π6. 已知点(sin cos tan )P ααα-,在第一象限,则在[02π],内α的取值范围是( ) A.π3π5ππ244⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭U ,, B.ππ5ππ424⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭U ,, C.π3π53ππ2442⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭U ,, D.ππ3ππ424⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭U ,,7. 函数2sin(2)6y x π=+的一条对称轴是( )A. x = 3πB. x = 4πC. x = 2πD. x = 6π8. 函数)32sin(π-=x y 的单调递增区间是( )A .5,1212k k ππππ⎡⎤-++⎢⎥⎣⎦ Z k ∈ B .52,21212k k ππππ⎡⎤-++⎢⎥⎣⎦ Z k ∈ C .5,66k k ππππ⎡⎤-++⎢⎥⎣⎦Z k ∈ D .52,266k k ππππ⎡⎤-++⎢⎥⎣⎦Z k ∈9.已知函数sin()(0,)2y x πωϕωϕ=+><的部分图象如图所示,则此函数的解析式为( ) A .sin(2)2y x π=+ B .sin(2)4y x π=+C .sin(4)2y x π=+ D .sin(4)4y x π=+ 10.在函数22sin ,sin ,sin(2),cos()323x y x y x y x y ππ===+=+中,最小正周期为π的函数的个数是( )A. 1个B. 2个C. 3个D.4个11.设()f x 是定义域为R ,最小正周期为32π的函数,若cos ,(0)(),2sin ,(0)x x f x x x ππ⎧-≤<⎪=⎨⎪≤<⎩ 则15()4f π-等于( )B. 1C. 0D.12.设a 为常数,且1>a ,[0,2x ∈π],则函数1sin 2cos )(2-+=x a x x f 的最大值为( ).A.12+aB.12-aC.12--aD.2a第Ⅱ卷(非选择题 共90分)二、填空题(每小题5分,共20分)13. 设角α的终边过点(4,3)P t t -(,0)t R t ∈>且,则2sin cos αα+=14. 函数1y tan 34x π⎛⎫=- ⎪⎝⎭的定义域为15.求使sin α>成立的α的取值范围是 16 关于函数f(x)=4sin ⎪⎭⎫⎝⎛+3π2x (x ∈R),有下列论断:①函数y=f(x)的表达式可改写为y=4cos(2x-π6); ②函数y=f(x)的最小正周期为2π;③函数y=f(x)的图象关于点⎪⎭⎫⎝⎛-0 6π,对称; ④函数y=f(x)的图象可由y=4sin2x 向左平移3π个单位得到. 其中正确的是 .(将你认为正确的论断的序号都填上) 一、选择题(每小题5分,共60分)二、填空题(每小题5分,共20分)13、 14、 15、 16、三、解答题(共70分,解答应写出文字说明,证明过程或演算步骤) 17. (本小题满分10分)(1) ;(2)已知=αsin 21-,且α是第四象限角,求αcos 、αtan 的值.18.(本小题满分12分)已知51cos sin =+θθ,其中θ是ABC ∆的一个内角. (1)求θθcos sin 的值;(2)判断ABC ∆是锐角三角形还是钝角三角形; (3)求θθcos sin -的值.19.(本小题满分12分)已知tan 1tan 1αα=--,求(1)21sin sin cos ααα+的值;(2)设222sin ()sin (2)sin()322()cos ()2cos()f πθθθθθθπ++π-+--=π+--,求()3f π的值.20.(本小题满分12分)已知函数()2sin sin f x x x =+,02x π≤≤. 若方程m x f =)(有两个不同的实数根,求实数m 的取值范围.21(本小题满分12分)已知函数a x x +-=)62sin(2)(f π.(1)求函数f(x)的最小正周期; (2)求函数f(x)的单调递减区间;(3)若]2,0[x π∈时,f(x)的最小值为-2,求a 的值.22.(本小题满分12分)函数)2||,0,0)(sin(πϕωϕω<>>+=A x A y 的一段图象如图所示,根据图象求:(1))(x f 的解析式;(2)函数)(x f 的图象可以由函数sin ()y x x R =∈ 的图象经过怎样的变换得到?。
必修四第一章测试题

高一数学必修4第一章《三角函数》单元测试卷班级 ______学号 _______姓名 成绩__________. 一、选择题(本大题共10小题,每小题5分,共50分) 1、sin 210=AB. C .12D .12- ( )2、已知角α的终边经过点P (m 4-,m 3)(0≠m ),则α+αcos sin 2的值是 ( ) A 1或1- B.52或52- C. 1或52- D. 1-或52 3、若扇形的周长是16cm ,圆心角是2弧度,则扇形的面积是 (单位2cm ) ( ) A .16B .32C .8D .644、已知A={第一象限角},B={锐角},C={小于90°的角},那么A 、B 、C 关系是 ( )A .B=A ∩CB .B ∪C=CC .A CD .A=B=C5、已知角α的余弦线是单位长度的有向线段;那么角α的终边 ( )A .在x 轴上B .在直线y x =C .在y 轴上D .在直线y x =或y x =-上 6、为了得到函数2sin(),36x y x R π=+∈的图像,只需把函数2sin ,y x x R =∈的图像上所有的点 ( )A .向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) B .向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) C .向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) D .向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)7、如图,曲线对应的函数是 ( )A .y=|sin x |B .y=sin|x |C .y=-sin|x |D .y=-|sin x |8、已知x x f 3cos )(cos =,则)(s i n x f 等于 ( )A . x 3sinB .x 3cosC .x 3cos -D .x 3sin -二、填空题(本大题共4小题,每小题5分,共20分) 9、若2cos 3α=,α是第四象限角,则sin(2)sin(3)cos(3)απαπαπ-+---=________ 10、不等式0tan 31≥+x 的解集是 . 11、已知sin 2cos 5,tan 3sin 5cos ααααα-=-+那么的值为_______12、设()f x 是定义域为R ,周期为32π的函数,若()()cos 02sin 0x x f x xx ππ⎧⎛⎫-≤≤ ⎪⎪⎝⎭=⎨⎪≤≤⎩则154f π⎛⎫-= ⎪⎝⎭________三、解答题(本大题共3小题,共30分)13、已知()2,A a -是角α终边上的一点,且sin α=,求cos α,αtan 的值.;14、求函数y=2sin (3π―2x ),),0(π∈x 的单调增区间和对称中心点.15、已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的图象过点(0,1),在相邻两最值点()0,2x ,()003,202x x ⎛⎫+-> ⎪⎝⎭上()f x 分别取得最大值和最小值.(1)求()f x 的解析式;(2)若函数()()g x af x b=+的最大和最小值分别为6和2,求,a b 的值.(3)如果在任意两个偶数内()f x 至少能同时取得最大值A 和最小值A -,那么正整数ω的最小值是多少?。
高一数学必修四第一章综合能力检测

第一章综合能力检测一、选择题(本大题共12个小题,每小题5分,共60分) 1.下列等式成立的是( ) A .sin π3=12 B .cos 5π6=-12 C .sin(-7π6)=12 D .tan 2π3= 3答案:C解析:sin π3=32,cos 5π6=-32,tan 2π3=-3, sin(-7π6)=12.2.函数y =45sin(2x +π3)的图像( ) A .关于原点对称 B .关于点(-π6,0)对称 C .关于y 轴对称 D .关于直线x =π6对称 答案:B3.如果sin(π+A )=-12,那么cos(32π-A )的值是( ) A .-12 B.12 C .-32 D.32答案:A解析:由sin(π+A )=-12,得sin A =12,则cos(32π-A )=-sin A =-12.4.函数y =sin(ωx +φ)(x ∈R ,ω>0,0≤φ<2π)的部分图像如图,则( )A .ω=π2,φ=π4 B .ω=π3,φ=π6 C .ω=π4,φ=π4 D .ω=π4,φ=5π4 答案:C解析:依图像可知,T 4=3-1=2,∴T =8,ω=2πT =π4.将点(1,1)代入y =sin(π4x +φ)中,得1=sin(π4+φ).∴π4+φ=π2,∴φ=π4.5.设0≤x ≤2π,使sin x ≥12且cos x <22同时成立的x 值是( ) A.π6≤x ≤5π6 B.π6≤x ≤74π C.5π6≤x ≤74π D.π4<x ≤56π答案:D解析:由正弦曲线得sin x ≥12时,x ∈[π6,56π];由余弦曲线得cos x <22时,x ∈(π4,74π),∴sin x ≥12且cos x <22时,x ∈(π4,56π].6.若函数y =sin(2x +θ)的图像向左平移π6个单位后恰好与y =sin2x 的图像重合,则θ的最小正值是( )A.4π3B.π3 C.5π6 D.5π3答案:D解析:将y =sin(2x +θ)的图像左移π6个单位得y =sin[2(x +π6)+θ]=sin(2x +π3+θ),故π3+θ=2k π,k ∈Z ,因此θ的最小正值为5π3.7. [2011·陕西卷]设函数f (x )(x ∈R )满足f (-x )=f (x ),f (x +2)=f (x ),则y =f (x )的图像可能是( )答案:B解析:由f (-x )=f (x )得,f (x )为偶函数,所以图像关于y 轴对称. 又f (x +2)=f (x )得f (x )的周期为2,故选B.8. 令a =sin(π-1),b =sin2,c =cos1,则它们的大小顺序是( ) A .a >b >c B .b >a >c C .c >b >a D .c >a >b 答案:B解析:c =sin(π2+1),且π>π2+1>π-1>2>π2,又y =sin x 在[π2,π]上是减函数,∴sin(π2+1)<sin(π-1)<sin2,即c <a <b .9.已知f (x )=cos2x -1,g (x )=f (x +m )+n ,则使g (x )为奇函数的实数m ,n 的可能取值为( )A .m =π2,n =-1 B .m =π2,n =1 C .m =-π4,n =-1 D .m =-π4,n =1答案:D解析:显然n =1, ∴g (x )=cos(2x +2m ).∵g (x )为奇函数,∴cos2m =0,∴2m =k π+π2. 经检验D 符合条件.10.已知f (x )=sin(2x +φ)的一个单调区间是[π3,5π6],则φ的一个值是( )A .-π6 B.π6 C .-π2 D.π2答案:A解析:排除法,若φ=±π2,f (x )=±cos2x 不合题意,若φ=π6,也不适合题意,故选A.11.下列命题正确的个数是( ) ①函数y =sin|x |不是周期函数;②函数y =tan x 在定义域内是增函数; ③函数y =|cos 2x +12|的周期是π2; ④函数y =sin(5π2+x )是偶函数. A .0 B .1 C .2 D .3答案:B解析:用排除法将错误说法淘汰.对于①,从其图像可以说明其不是周期函数;对于②,∵0<π,而tan0=tanπ,∴y =tan x 在定义域内不是增函数;对于③,y =|cos2(x +π2)+12|=|12-cos2x |≠|cos2x +12|,因此π2不是y =|cos2x +12|的周期;对于④,f (x )=sin(5π2+x )=sin(2π+π2+x )=cos x ,显然是偶函数.12. [2011·辽宁卷]已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图像如图,则f (π24)=( )A. 2+ 3B. 3C. 33D. 2- 3答案:B解析:由图像可知:T 2=3π8-π8=π4,即T =π2. 所以ω=2.由图像知,图像过点(3π8,0), 所以0=A tan(2×3π8+φ), 即34π+φ=k π(k ∈Z ).所以φ=k π-3π4(k ∈Z ),又|φ|<π2, 所以φ=π4,再由图像过点(0,1), 所以A =1,则f (x )=tan(2x +π4), 故f (π24)=tan(2×π24+π4)=tan π3= 3.二、填空题(本大题共4个小题,每小题5分,共20分) 13.函数y =sin(π6-2x )的单调递减区间是________. 答案:[k π-π6,k π+π3],k ∈Z解析:∵y =sin(π6-2x )=-sin(2x -π6),∴令2k π-π2≤2x -π6≤2k π+π2,k ∈Z ,∴k π-π6≤x ≤k π+π3,k ∈Z .14.y =lg(cos x -sin x )的定义域是________. 答案:(2k π-34π,2kx +π4)(k ∈Z )解析:由cos x -sin x >0知,cos x >sin x ,由单位圆知2k π-34π<x <2k π+π4.15.如下图是函数y =A sin(ωx +φ)+k (|φ|<π2)在一个周期内的图像,那么这个函数的一个解析式是______.答案:y =3sin(2x +π3)-1解析:由图可知A =3,k =-1,ω=2,且当x =-π6时,sin(2x +φ)=0,又|φ|<π2,故φ=π3.16.已知函数f (x )=2sin ωx (ω>0)在区间[-π3,π4]上的最小值是-2,则ω的最小值是________.答案:32解析:函数f (x )=2sin ωx (ω>0)在区间[-π3,π4]上的最小值是-2,则ωx 的取值范围是[-ωπ3,ωπ4],∴-ωπ3≤-π2,或ωπ4≥3π2,∴ω≥32,即ω的最小值等于32.三、解答题(本大题共6个小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤)17. (本小题满分10分)设tan(α+8π7)=a , 求sin (15π7+α)+3cos (α-13π7)sin (20π7-α)-cos (α+22π7)的值. 解:原式=sin (π+8π7+α)+3cos (α+8π7-3π)sin (4π-8π7-α)-cos (α+8π7+2π) =-sin (8π7+α)-3cos (α+8π7)-sin (8π7+α)-cos (α+8π7) =tan (8π7+α)+3tan (8π7+α)+1=a +3a +1. 18. (本小题满分12分)[2011·浙江卷]已知函数f (x )=A sin(π3x +φ),x ∈R ,A >0,0<φ<π2,y =f (x )的部分图像如图所示,P 、Q 分别为该图像的最高点和最低点,点P 的坐标为(1,A ).求f (x )的最小正周期及φ的值. 解:(1)由题意得,T =2ππ3=6.因为P (1,A )在y =A sin(π3x +φ)的图像上, 所以sin(π3+φ)=1. 又因为0<φ<π2, 所以φ=π6.19.(本小题满分12分)函数f (x )=A sin(ωx +φ),x ∈R (其中A >0,ω>0,0<φ<π2)的图像与x 轴的交点中,相邻两个交点之间的距离为π2,且图像上一个最低点为M (2π3,-2).(1)求f (x )的解析式;(2)当x ∈[π12,π2]时,求f (x )的值域. 解:(1)由最低点为M (2π3,-2)得A =2.由x 轴上相邻两个交点之间的距离为π2得T 2=π2,即T =π, ∴ω=2πT =2ππ=2.由点M (2π3,-2)在图像上得2sin(2×2π3+φ)=-2, 即sin(4π3+φ)=-1, 故4π3+φ=2k π-π2,k ∈Z ,∴φ=2k π-116π. 又φ∈(0,π2),∴φ=π6,故f (x )=2sin(2x +π6). (2)∵x ∈[π12,π2],∴2x +π6∈[π3,7π6], 当2x +π6=π2,即x =π6时,f (x )取得最大值2; 当2x +π6=7π6,即x =π2时,f (x )取得最小值-1, 故f (x )的值域为[-1,2].20.(本小题满分12分)[2011·福建卷]已知等比数列{a n }的公比q =3,前3项和S 3=133.(1)求数列{a n }的通项公式;(2)若函数f (x )=A sin(2x +φ)(A >0,0<φ<π)在x =π6处取得最大值,且最大值为a 3,求f (x )的解析式.解:(1)由q =3,S 3=133得a 1(1-33)1-3=133,解得a 1=13.所以a n =13×3n -1=3n -2. (2)由(1)知a n =3n -2,所以a 3=3. 因为函数f (x )的最大值为3,所以A =3. 因为当x =π6时,f (x )取得最大值,所以sin(2×π6+φ)=1,又0<φ<π,故φ=π6.所以函数f (x )的解析式为f (x )=3sin(2x +π6).21.(本小题满分12分)已知函数f (x )=sin(ωx +φ)(ω>0,0≤φ≤π)为偶函数,且其图像上相邻的一个最高点和最低点之间的距离为4+π2.(1)求函数f (x )的表达式;(2)若sin α+f (α)=23,求2sin 2(3π-α)tan (3π+α)的值. 解:(1)∵f (x )为偶函数,∴sin(-ωx +φ)=sin(ωx +φ),即2sin ωx cos φ=0恒成立,∴cos φ=0,又0≤φ≤π,∴φ=π2.又其图像上相邻的一个最高点和最低点之间的距离为4+π2,设其最小正周期为T ,则T 2=4+π2-22=π.∴T =2π,∴ω=1,∴f (x )=cos x .(2)∵原式=2sin 2αtan α=2sin αcos α,又sin α+cos α=23,∴1+2sin αcos α=49,∴2sin αcos α=-59,即原式=-59.22.(本小题满分12分)设函数f (x )=2sin(2x +π4)+2.(1)用“五点法”作出函数f (x )在一个周期内的简图;(2)求函数f (x )的周期、最大值、最小值及当函数取最大值和最小值时相应的x 值的集合;(3)求函数f (x )的单调递增区间;(4)说明函数f (x )的图像可以由y =sin x (x ∈R )的图像经过怎样的变换而得到.解:(1)列表:函数图像如下图:(2)周期T =π,f (x )max =2+2,此时x ∈{x |x =k π+π8,k ∈Z }.f (x )min =2-2,此时x ∈{x |x =k π+58π,k ∈Z }.(3)函数f (x )的单调递增区间为:[k π-38π,k π+π8](k ∈Z ).(4)先将y =sin x (x ∈R )的图像向左平移π4个单位长度,然后将所得图像上各点的横坐标缩小为原来的12(纵坐标不变),再将所得图像上各点的纵坐标伸长为原来的2倍(横坐标不变),最后将所得图像向上平移2个单位长度,就可得到f(x)=2sin(2x+π4)+2的图像.。
第一章1-3单元练习1必修四

第一章1-3单元练习11、下列各角中,与角330°的终边相同的有是A .510°B .150°C .-150°D .-390°3、如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为A .5.0sin 1B .sin 0.5C .2sin 0.5D .tan 0.55、已知α是第二象限角, 则2α是A, 第一象限角 B, 第一、三象限角 C, 第二、四象限角 D, 锐角7、已知α角的正弦线和余弦线是符号相反、长度相等的有向线段,则α的终边在A.第一象限角的平分线上B.第四象限角的平分线上C.第二、四象限角的平分线上D.第一、三象限角的平分线上9、已知奇函数()[]上为,在01-x f 单调减函数,又α,β为锐角三角形内角,则A. f (cos α)>f (cos β)B. f (sin α)>f (sin β)C. f (sin α)<f (cos β) f (sin α)>f (cos β)11、已知1sin cos ,(0,)5αααπ+=∈,则tan α的值为A .-43或-34B .43或34C .-43D .-3413、如果点(2sin cos ,cos )P θθθ位于第三象限,那么角θ所在象限是A、第一象限 B 、第二象限 C 、第三象限 D 、第四象限15、若θ为第一象限角,则能确定为正值的是 A.2sin θ B.cos 2θ C.tan 2θD. cos 2θ17、角θ为第一或第二象限角的等价条件是A .sin 0θ>B 。
|sin |sin θθ=C 。
cos tan 0θθ>D 。
θ为锐角或钝角 19、为则若)12(sin ,2cos )(cos πf x x f =21.A B. 21- C. 23- D.2321、若角0600的终边上有一点()a ,4-,则a 的值是A .34B .34-C .34±D .323、已知α是第二象限角,下列四个不等式①2cos 2sin 2tan ααα>> ②2tan 2cos 2sin ααα>>③2sin 2cos 2tan ααα>> ④2sin 2tan 2cos ααα>>可能成立的是A .①②B .①③C .②③D .③④25、在[0,2π]上满足21sin ≥x 的x 的取值范围是 A.⎥⎦⎤⎢⎣⎡6,0π B.⎥⎦⎤⎢⎣⎡ππ65,6 C.⎥⎦⎤⎢⎣⎡ππ32,6 D.⎥⎦⎤⎢⎣⎡ππ,6527、若不等式a x >--1)32sin(π对于任意的实数x 都成立,则实数a 的取值范围是A .(-2,+∞)B .),2[+∞]2,(-∞ D .(-∞,-2)29、 设()f x 为偶函数,且(0,1)x ∈时,()2f x x =-+,则列说法正确的是 A,0(0.5)(30)f f < B,0(sin 0.5)(sin30)f f <C,(sin1)(cos1)f f < D,(sin 2)(cos 2)f f >31、一个扇形的弧长与面积都是5,则该扇形的圆心角为_________ 33、如图,已知∠AOy=30°,∠BOx=45°,终边落在阴影部分 (含边界)的角的集合是___________________________35、若角α与角β的终边关于y 轴对称,则+=αβ______ 37、=-++)425tan(325cos 625sin πππ39、与02002-终边相同的最小正角是________41、1024°是第_______象限角;1712π是第_______象限角43、已知53sin +-=m m θ,)2(524cos πθπθ<<+-=m m,则θtan =____45、sin 2(3x π-)+ sin 2(6x π+)=________47、已知角α为第二象限角,则化简cos sin 49、已知1sin()2πα+=,求角α=__________51、x 是三角形的一个内角,且sinx+cosx=15-,则tanx 的值是______53、化简:0sin(2)cos()cos(180)sin(3)sin()2παπαπαπαα-+----=55、已知角x 的终边过点P (1,3)(1)求sin(π-x)-sin(2π+x)的值 (2)写出角x 的集合S57、 已知tan α=求sin α 及 cos α59、已知sin 3cos x x =,计算2222cos cos sin x x x +-61、已知)2cos(2)sin(απαπ-=-,求下列各式的值(1)ααααcos 3sin 5cos 2sin 4+-(2)αααα22cos cos sin sin -⋅-63、化简:︒+︒︒︒+790cos 250sin 430cos 290sin 2165、已知33)6cos(=-a π,求)6(sin )65cos(2ππ--+a a 的值67、 (1)化简11sin(2)cos()cos()cos()229cos()sin(3)sin()sin()2πππαπαααππαπαπαα-++-----+, (2)化简44661sin cos 1sin cos αααα----69、解不等式sin cos x x >71、求函数22sin cos y x x =-+的最大值及相应的x 的值.。
(典型题)高中数学必修四第一章《三角函数》检测卷(包含答案解析)(1)
一、选择题1.已知函数()sin()f x A x ωϕ=+(0A >,0>ω,2πϕ<)的部分图像如图所示,则()f x 的解析式为( )A .()2sin 26f x x π⎛⎫=- ⎪⎝⎭B .()2sin 26f x x π⎛⎫=+ ⎪⎝⎭C .()3sin 26f x x π⎛⎫=-⎪⎝⎭D .1()3sin 26f x x π⎛⎫=-⎪⎝⎭ 2.函数()2cos 3⎛⎫=+ ⎪⎝⎭πf x x 在[]0,π的单调递增区间是( ) A .20,3π⎡⎤⎢⎥⎣⎦B .2,33ππ⎡⎤⎢⎥⎣⎦C .,3ππ⎡⎤⎢⎥⎣⎦D .2π,π33.一观览车的主架示意图如图所示,其中O 为轮轴的中心,距地面32m (即OM 长),巨轮的半径长为30m ,2AM BP m ==,巨轮逆时针旋转且每12分钟转一圈,若点M 为吊舱P 的初始位置,经过t 分钟,该吊舱P 距离地面的高度为( )A .30sin 30122t ππ⎛⎫-+⎪⎝⎭B .30sin 3062t ππ⎛⎫-+⎪⎝⎭C .30sin 3262t ππ⎛⎫-+⎪⎝⎭D .30sin 62t ππ⎛⎫-⎪⎝⎭ 4.已知函数()sin 26f x x π⎛⎫=-⎪⎝⎭,若方程()35f x =的解为1x ,2x (120x x π<<<),则()12sin x x -=( )A .35B .45-C .D .5.将函数()sin 25f x x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度后得到函数()y g x =的图象,对于函数()y g x =有以下四个判断: ①该函数的解析式为2sin 210y x π⎛⎫=+ ⎪⎝⎭; ②该函数图象关于点,02π⎛⎫⎪⎝⎭对称; ③该函数在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增; ④该函数在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增. 其中,正确判断的序号是( ) A .②③B .①②C .②④D .③④6.已知函数()()cos f x x ωϕ=+(0>ω,0πϕ-<<)的图象关于点,08π⎛⎫⎪⎝⎭对称,且其相邻对称轴间的距离为23π,将函数()f x 的图象向左平移3π个单位长度后,得到函数()g x 的图象,则下列说法中正确的是( )A .()f x 的最小正周期23T π= B .58πϕ=-C .()317cos 248πx g x ⎛⎫=- ⎪⎝⎭D .()g x 在0,2π⎡⎤⎢⎥⎣⎦上的单调递减区间为,82ππ⎡⎤⎢⎥⎣⎦7.筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用.假设在水流量稳定的情况下,简车上的每一个盛水筒都做逆时针匀速圆周运动.现将筒车抽象为一个几何图形,如图所示,圆O 的半径为4米,盛水筒M 从点0P 处开始运动,0OP 与水平面的所成角为30,且每分钟恰好转动1圈,则盛水筒M 距离水面的高度H (单位;m )与时间t (单位:s )之间的函数关系式的图象可能是( )A .B .C .D .8.下列结论正确的是( ) A .sin1cos1< B .2317cos cos 54ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭C .()()tan 52tan 47->-D .sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭9.使函数()3)cos(2)f x x x θθ=+++是偶函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .6π B .3π C .23π D .56π 10.已知函数()[][]sin cos cos sin f x x x =+,其中[]x 表示不超过实数x 的最大整数,则( )A .()f x 是奇函数B .π2π33f f ⎛⎫⎛⎫<⎪ ⎪⎝⎭⎝⎭C .()f x 的一个周期是πD .()f x 的最小值小于011.如图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.某摩天轮最高点距离地面高度为120m ,转盘直径为110m 设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要20min .游客甲坐上摩天轮的座舱,开始转动t min 后距离地面的高度为H m ,则在转动一周的过程中,高度H 关于时间t 的函数解析式是( )A .()55cos 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭B .()55sin 65020102H t t ππ⎛⎫=-+≤≤ ⎪⎝⎭C .()55cos 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭D .()55sin 65020102H t t ππ⎛⎫=++≤≤ ⎪⎝⎭12.已知函数()()()3cos 0g x x ωϕω=+>在7,6ππ⎛⎫ ⎪⎝⎭上具有单调性,且满足04g π⎛⎫= ⎪⎝⎭,()3g π=,则ω的取值共有( ) A .6个B .5个C .4个D .3个二、填空题13.已知3()tan 1f x a x x =+(a ,b 为实数),且3(lg log 10)5f =,则(lglg3)f =____________.14.已知定义在R 上的函数()f x 满足:()()2f x f x π+=,且当[]0,x π∈时,()sin f x x =.若对任意的(],x m ∈-∞,都有()2f x ≤,则实数m 的取值范围是______. 15.如图,某公园要在一块圆心角为3π,半径为20m 的扇形草坪OAB 中修建一个内接矩形文化景观区域CDEF ,若//EF AB ,则文化景观区域面积的最大值为______2m .16.若函数f (x )=2sin(ωx +φ)(ω>0,0<φ<π)的图象经过点,26π⎛⎫⎪⎝⎭,且相邻两条对称轴间的距离为2π,则4f π⎛⎫⎪⎝⎭的值为________. 17.设函数()y f x =的定义域为D ,若对任意的1x ∈D ,总存在2x ∈D ,使得()()121f x f x ⋅=,则称函数()f x 具有性质M .下列结论:①函数3y x x =-具有性质M ; ②函数35x x y =+具有性质M ;③若函数()[]8log 2,0,y x x t =+∈具有性质M ,则510t =; ④若3sin y x a =+具有性质M ,则5a =. 其中正确结论的序号是____________.18.函数251612()sin (0)236x x f x x x x ππ-+⎛⎫=--> ⎪⎝⎭的最小值为_______. 19.关于函数()4sin(2)(),3f x x x R π=+∈有下列命题:①由12()()0f x f x ==可得12x x -必是π的整数倍;②()y f x =的图象关于点(,0)6π-对称;③()y f x =的表达式可改写为4cos(2);6y x π=-④()y f x =的图象关于直线6x π=-对称.其中正确命题的序号是_________.20.将函数()sin (0)f x x ωω=>的图象向右平移6π个单位长度,得到函数()y g x =的图像,若()y g x =是偶函数,则ω的最小值为________.三、解答题21.已知函数()12sin 26x f x π⎛⎫=+⎪⎝⎭,x ∈R .(1)用“五点法”画出函数()f x 一个周期内的图象; (2)求函数()f x 在[],ππ-内的值域; (3)若将函数()f x 的图象向右平移6π个单位长度,得到函数()g x 的图象,求函数()g x 在[],ππ-内的单调增区间.22.函数()sin()f x A x ωϕ=+(0,0,[0,2))A ωϕπ>>∈的图象如图所示:(1)求()f x 的解析式; (2)()f x 向左平移12π个单位后得到函数()g x ,求()g x 的单调递减区间;(3)若,2x ππ⎡⎤∈-⎢⎥⎣⎦且()32f x ≥,求x 的取值范围.23.已知向量a =(cosωx -sinωx ,sinωx),b =(-cosωx -sinωx,2cosωx).设函数f(x)=a b ⋅+λ(x ∈R)的图象关于直线x =π对称,其中ω,λ为常数,且ω∈1,12⎛⎫⎪⎝⎭.(1)求函数f(x)的最小正周期; (2)若y =f(x)的图象经过点,04π⎛⎫⎪⎝⎭,求函数f(x)在区间30,5π⎡⎤⎢⎥⎣⎦上的取值范围 24.已知函数()()()f x g x h x =,其()22g x x =,()h x =_____. (1)写出函数()f x 的一个周期(不用说明理由); (2)当,44x ππ⎡⎤∈-⎢⎥⎣⎦时,求函数()f x 的最大值和最小值. 从①cos 4x π⎛⎫+⎪⎝⎭,②2sin 24x π⎛⎫- ⎪⎝⎭这两个条件中任选一个,补充在上面问题中并作答, 注:如果选择多个条件分别解答.按第一个解答计分. 25.已知sin(3)(),cos x f x x R xπ-=∈(1)若α为第三象限角,且3sin 5α=-,求()f α的值. (2)若,34x ππ⎡⎤∈-⎢⎥⎣⎦,且21()2()1cos g x f x x =++,求函数()g x 的最小值,并求出此时对应的x 的值.26.函数()cos()(0)f x x ωφω=+>的部分图像如图所示.(1)求()f x 的表达式; (2)若[1,2]x ∈,求()f x 的值域;(3)将()f x 的图像向右平移112个单位后,再将所得图像横坐标伸长到原来的2倍,纵坐标不变,得到函数()y g x =的图像,求()g x 的单调递减区间.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】 本题首先可根据33π44T 求出ω,然后根据当43x π=时函数()f x 取最大值求出ϕ,最后代入30,2⎛⎫- ⎪⎝⎭,即可求出A 的值. 【详解】因为4π7π3π3124,所以33π44T ,T π=,因为2T πω=,所以2ω=,()sin(2)f x A x ϕ=+,因为当43x π=时函数()sin(2)f x A x ϕ=+取最大值,所以()42232k k Z ππϕπ⨯+=+∈,()26k k Z πϕπ=-+∈,因为2πϕ<,所以6πϕ=-,()sin 26f x A x π⎛⎫=- ⎪⎝⎭,代入30,2⎛⎫- ⎪⎝⎭,3sin 26A π⎛⎫-=- ⎪⎝⎭,解得3A =,()3sin 26f x x π⎛⎫=- ⎪⎝⎭, 故选:C. 【点睛】关键点点睛:本题考查根据函数图像求函数解析式,对于()sin()f x A x ωϕ=+,可通过周期求出ω,通过最值求出A ,通过代入点坐标求出ϕ,考查数形结合思想,是中档题.2.C解析:C 【分析】先求出函数的单调增区间,再给k 取值即得解. 【详解】 令22223+<+<+ππk πx πk π(k ∈Z ) ∴42233+<<+ππk πx k π(k ∈Z ), 所以函数的单调递增区间为4[2,2]33ππk πk π++(k ∈Z ), 当1k =-时,5233ππx -<<- 当0k =时,433x ππ<<又∵[]0,x π∈, 故选:C 【点睛】方法点睛:求三角函数()cos()f x A wx ϕ=+的单调区间,一般利用复合函数的单调性原理解答:首先是对复合函数进行分解,接着是根据复合函数的单调性原理分析出分解出的函数的单调性,最后根据分解函数的单调性求出复合函数的单调区间.3.B解析:B 【分析】先通过计算得出转动的角速度,然后利用三角函数模型表示在转动的过程中点B 的纵坐标满足的关系式,则吊舱到底面的距离为点B 的纵坐标减2. 【详解】如图所示,以点M 为坐标原点,以水平方向为x 轴,以OM 所在直线为y 轴建立平面直角坐标系.因为巨轮逆时针旋转且每12分钟转一圈,则转动的角速度为6π每分钟, 经过t 分钟之后,转过的角度为6BOA t π∠=,所以,在转动的过程中,点B 的纵坐标满足:3230sin 30sin 322662y t t ππππ⎛⎫⎛⎫=--=-+ ⎪ ⎪⎝⎭⎝⎭则吊舱距离地面的距离30sin 32230sin 306262h t t ππππ⎛⎫⎛⎫=-+-=-+ ⎪ ⎪⎝⎭⎝⎭. 故选:B . 【点睛】建立三角函数模型解决实际问题的一般步骤: (1)审题:审清楚题目条件、要求、理解数学关系; (2)建模:分析题目变化趋势,选择合适的三角函数模型; (3)求解:对所建立的数学模型进行分析研究,从而得到结论.4.B解析:B 【分析】求出函数()f x 在(0,)π上的对称轴,然后由正弦函数性质得1223x x π+=,这样12sin()x x -化为2222sin(2)sin 2cos(2)336x x x πππ⎛⎫-=+=- ⎪⎝⎭,而已知条件为23sin(2)65x π-=,再由正弦函数性质确定226x π-的范围,从而由平方关系求得结论.【详解】函数()sin 26f x x π⎛⎫=-⎪⎝⎭的对称轴满足:()262x k k Z πππ-=+∈,即()23k x k Z ππ=+∈,令0k =可得函数在区间()0,π上的一条对称轴为3x π=,结合三角函数的对称性可知1223x x π+=,则:1223x x π=-,()122222sin sin 2sin 2cos 2336x x x x x πππ⎛⎫⎛⎫⎛⎫-=-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,由题意:0πx <<,则112666x πππ-<-<,23sin 265x π⎛⎫-= ⎪⎝⎭,120x x π<<<,则2226x πππ<-<,由同角三角函数基本关系可知:24cos 265x π⎛⎫-=- ⎪⎝⎭, 故选:B . 【点睛】关键点点睛:本题考查正弦函数的性质,考查平方关系.解题时根据自变量的范围求得此范围内函数的对称轴,从而得出两个变量12,x x 的关系,可化双变量为单变量,再根据函数值及函数性质确定出单变量的范围,从而求得结论.注意其中诱导公式的应用,目的是把求值式与已知条件中的角化为一致.5.A解析:A 【分析】根据函数平移变换得sin 2y x =,再根据正弦函数的性质依次讨论即可得答案. 【详解】解:由函数sin 25y x π⎛⎫=+ ⎪⎝⎭的图象平移变换的性质可知: 将sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后 解析式为sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,选项①错误; 令2x k =π,k Z ∈,求得2k x =π,k Z ∈, 故函数的图象关于点,02k ⎛⎫⎪⎝⎭π对称, 令1k =,故函数的图象关于点,02π⎛⎫⎪⎝⎭对称,选项②正确; 则函数的单调递增区间满足:222()22k x k k Z ππππ-≤≤+∈,即()44k x k k Z ππππ-≤≤+∈,令0k =可得函数的一个单调递增区间为,44ππ⎡⎤-⎢⎥⎣⎦,选项③正确,④错误.故选:A. 【点睛】本题考查三角函数平移变换,正弦型函数的单调区间,对称中心等,考查运算求解能力,解题的易错点在于平移变换时,当1ω≠时,须将ω提出,平移只针对x 进行平移,具体的在本题中,sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度之后得sin 2sin 2105y x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦,而不是sin 2sin 251010y x x πππ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,是中档题. 6.D解析:D 【分析】首先根据三角函数的性质,可知相邻对称轴间的距离是半个周期,判断A ;再求函数的解析式,判断B ;根据平移规律得到函数()g x ,判断C ;最后根据函数()g x 的解析式,利用整体代入的方法求函数的单调递减区间. 【详解】相邻对称轴间的距离是半个周期,所以周期是43π,故A 不正确; 243T ππω==,解得:32ω=,()f x 的图象关于点,08π⎛⎫⎪⎝⎭对称,3,282k k Z ππϕπ∴⨯+=+∈,解得:5,16k k Z πϕπ=+∈ 0πϕ-<<, 1116πϕ∴=-,故B 不正确; ()311cos 216f x x π⎛⎫=- ⎪⎝⎭,向左平移3π个单位长度后得()31133cos cos 2316216g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 故C 不正确; 当02x π≤≤时,3339,2161616x πππ⎡⎤-∈-⎢⎥⎣⎦,当3390,21616x ππ⎡⎤-∈⎢⎥⎣⎦时,函数单调递减,即 ,82x ππ⎡⎤∈⎢⎥⎣⎦,故D 正确. 故选:D 【点睛】关键点点睛:本题的关键是根据三角函数的性质求得函数()f x 的解析式,第四个选项是关键,需根据整体代入的方法,先求33216x π-的范围,再确定函数的单调递减区间. 7.D解析:D 【分析】先根据题意建立坐标系,写出盛水筒M 距离水面的高度H 与时间t 之间的函数关系式,再根据关系式即可判断. 【详解】解:以O 为圆心,过点O 的水平直线为x 轴,建立如图所示的平面直角坐标系:0306xOP π∠==,OP ∴在()t s 内转过的角为:26030t t ππ=, ∴以x 轴正半轴为始边,以OP 为终边的角为:306t ππ-,P ∴点的纵坐标为:4sin 306t ππ⎛⎫-⎪⎝⎭, H ∴与t 之间的函数关系式为:4sin 2306H t ππ⎛⎫=-+⎪⎝⎭, 当sin 1306t ππ⎛⎫-= ⎪⎝⎭时,max 426H =+=, 当sin 1306t ππ⎛⎫-=-⎪⎝⎭时,max 422H =-+=-, 对A ,B ,由图像易知max min H H =-,故A ,B 错误; 对C ,max min H H <-,故C 错误; 对D ,max min H H >-,故D 正确. 故选:D. 【点睛】关键点点睛:本题解题的关键是理解题意,根据题意写出H 与t 之间的函数关系式.8.D解析:D 【分析】利用正弦函数的单调性可判断AD 选项的正误;利用正切函数的单调性可判断C 选项的正误;利用余弦函数的单调性可判断B 选项的正误. 【详解】对于A 选项,因为正弦函数sin y x =在0,2π⎛⎫⎪⎝⎭上单调递增, 且01122ππ<-<<,则sin1sin 1cos12π⎛⎫>-=⎪⎝⎭,A 选项错误; 对于B 选项,因为余弦函数cos y x =在()0,π上为减函数,23233cos cos cos 555πππ⎛⎫-== ⎪⎝⎭,1717cos cos cos 444πππ⎛⎫-== ⎪⎝⎭, 3045πππ<<<,则3cos cos 54ππ<,即2317cos cos 54ππ⎛⎫⎛⎫-<- ⎪ ⎪⎝⎭⎝⎭,B 选项错误; 对于C 选项,当900x -<<时,正切函数tan y x =单调递增, 因为9052470-<-<-<,所以,()()tan 52tan 47-<-,C 选项错误;对于D 选项,因为正弦函数sin y x =在,02π⎛⎫- ⎪⎝⎭上单调递增,因为021018πππ-<-<-<,所以,sin sin 1810ππ⎛⎫⎛⎫->- ⎪ ⎪⎝⎭⎝⎭,D 选项正确. 故选:D. 【点睛】思路点睛:解答比较函数值大小问题,常见的思路有两个: (1)判断各个数值所在的区间; (2)利用函数的单调性直接解答.9.B解析:B 【解析】1())cos(2))cos(2))2sin(2)26f x x x x x x πθθθθθ=+++=+++=++,由于()f x 为偶函数,则(0)2sin()26f πθ=+=±,sin()1,662k πππθθπ+=±+=+,3k πθπ=+,当0k =时,3πθ=,()2sin(2)2sin(2)362f x x x πππ=++=+2cos2x =,当[0,]4x π∈时,2[0,]2x π∈,()2cos2f x x =为减函数,符合题意,所以选B.10.D解析:D 【分析】利用奇函数的性质判断A ,分别求3f π⎛⎫⎪⎝⎭和23f π⎛⎫⎪⎝⎭判断大小,取特殊值验证的方法判断C ,分区间计算一个周期内的最小值,判断选项D 。
数学必修四第一章复习题

z)(k k 223.k 22∈⎥⎦⎤⎢⎣⎡++πππz)(k 43k ,4k ∈⎥⎦⎤⎢⎣⎡++ππππz)(k 4k ,4k ∈⎥⎦⎤⎢⎣⎡+-ππππ1.下列函数中,最小正周期为π的是( ) A .cos 4y x = B .sin 2y x = C .sin 2x y = D .co s4x y =2.下列函数中,在区间[0,]2π上为减函数的是( )A .cos y x =B .sin y x =C .tan y x =D .sin ()3y x π=-3.半径为πcm ,中心角为120o 的弧长为 ()A .cm 3πB .cm 32πC .cm 32π D .cm 322π4.α是第二象限角,P (x , 5 ) 为其终边上一点,且cos α=42x ,则sin α的值为 ( )A .410 B .46 C .42 D .-4105.已知函数)cos()(,2sin)(x x g x x f -=+=ππ,则 ( )A .()f x 与()g x 都是奇函数B .()f x 与()g x 都是偶函数C .()f x 是奇函数,()g x 是偶函数D .()f x 是偶函数,()g x 是奇函数 6、函数)23cos(x y -=π的单调递减区间是( )7、已知函数1)2sin()(--=ππx x f ,则下列命题正确的是( )A .)(x f 是周期为1的奇函数B .)(x f 是周期为2的偶函数C .)(x f 是周期为1的非奇非偶函数D .)(x f 是周期为2的非奇非偶函数8、函数)292cos(π-=x y 是( )A .奇函数非偶函数B .偶函数非奇函数C .非奇非偶函数D .既是奇函数又是偶函数 9.函数x2sin 2y=的奇偶数性为( ).A. 奇函数B. 偶函数 C .既奇又偶函数 D. 非奇非偶函数 10.函数y=sin2x 的单调减区间是( )A. B.C. []z)(k k 23,k 2∈+ππππ+D.1. 函数y=2cosx-1的单调递减区间是__________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修四第一章基础强化训练题1、已知角α的终边过点P (-4,3) ,则 的值是 ( )A. - 1B. 1C.D.2、已知cosα=﹣,α是第三象限的角,则sinα=( ) A .﹣ B . C .﹣ D .3、31sin 6π⎛⎫-⎪⎝⎭的值是( ) A.12 B. 12- C. 32 D. 32-4、已知,且为第四象限角,则( )A. B. C. D.5、半径为cm π,中心角为060动点扇形的弧长为( )A. 23cm πB. 3cm πC. 23cm πD. 223cm π 6、已知角α终边经过点3122P ⎛⎫⎪⎪⎝⎭,则cos α=( ) A.12 B. 32 C. 33 D. 12±7、点A(x,y)是300°角终边上异于原点的一点,则yx值为( ) 33 C. 33 D. -338、α是第二象限角,则2α是( ) A. 第一象限角 B. 第二象限角C. 第一象限角或第三象限角D. 第一象限角或第二象限角 9、若()3sin 5πα+=, α是第三象限的角,则sincos22sin cos 22παπαπαπα++-=---( ) A.12 B. 12- C. 2 D. 2-10、若3sin 45πα⎛⎫-= ⎪⎝⎭,则()sin 2πα+= ( ) A. 725-B. 725C. 15-D. 1511、将表的分针拨慢10分钟,则分针转过的角的弧度数是( ) A.3π B. 6π C. 3π- D. 6π- 12、()cos 570-︒= ( )A.12 B. 12- C. 3- D. 313、已知角α的终边经过点()3,4P ,则角α的正弦值为( )A.34 B. 43 C. 35 D. 45 14、已知α是锐角,则2α是()A. 第一象限角B. 第二象限角C. 小于180的正角D. 第一或第二象限角 15、的值为( )A. B. C. D.16、与角终边相同的角是 ( )A.B. C.D.17、已知2cos 23sin ,,2πθθθπ⎛⎫=∈ ⎪⎝⎭,则θ的终边经过点()A .()2,2-B .()1,2-C .()1,3-D .()2,1-18、化简0sin600的值是( ) A.12 B. 12- C. 33-19、13cos 6π⎛⎫⎪⎝⎭的值是( ) 33—12 D. 1220、函数()()sin f x A x ωϕ=+ (其中A >0,2πϕ<)的图象如图所示,为了得到()f x 的图象,则只需将g(x)=sin2x 的图象()A. 向右平移6π个长度单位B. 向左平移6π个长度单位C. 向右平移3π个长度单位D. 向左平移3π个长度单位 21、对于函数,下列说法正确的是( )A. 函数图像关于点对称B. 函数图像关于直线对称C. 将它的图像向左平移个单位,得到的图像D. 将它的图像上各点的横坐标缩小为原来的倍,得到的图像22、为了得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图像,可以将函数cos2y x =的图像() A. 向左平移512π个单位 B. 向右平移512π个单位C. 向右平移6π个单位 D. 向左平移6π个单位 23、为得到函数πsin 23y x ⎛⎫=-+ ⎪⎝⎭的图像,只需将函数()sin 2y x =-的图像( ) A. 向右平移π3个单位B. 向左平移π3个单位C. 向右平移π6个长度单位 D. 向左平移π6个长度单位 24、1tan ,1cos ,1sin 的大小关系是()A.1cos 1sin 1tan >>B.1sin 1cos 1tan >> C.1tan 1sin 1cos >>D.1tan 1cos 1sin >> 25、将函数cos2y x =的图象向左平移2π个单位,得到函数()y f x =的图象,则下列说法正确的是( ) A. ()y f x =是奇函数 B. ()y f x =的周期为2π C. ()y f x =的图象关于直线2x π=对称 D. ()y f x =的图象关于点,02π⎛⎫-⎪⎝⎭的对称 26、函数()()sin f x A x ωϕ=+(0A >,0ω>,2πϕ<)的部分图象如图所示,则,ωϕ的值分别为( )A. 2,0B. 2,4π C. 2,3π- D. 2,6π27、将函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭图象上的每个点的纵坐标不变,横坐标缩短为原来的一半,再将所得图象向左平移12π个单位得到函数()g x 的图象,在()g x 图像的所有对称轴,离远点最近的对称轴为( ) A. 24x π=- B. 4x π= C. 524x π= D. 12x π=28、函数()()cos f x x ωϕ=+的部分图象如图所示,则()f x 的单调递减区间为( )A. 13,44k k ππ⎛⎫-+ ⎪⎝⎭,Z k ∈ B. 132,244k k ππ⎛⎫-+ ⎪⎝⎭,Z k ∈C. 13,44k k ⎛⎫-+ ⎪⎝⎭,Z k ∈ D. 132,244k k ⎛⎫-+ ⎪⎝⎭,Z k ∈ 29、将函数()sin 6f x x π⎛⎫=+ ⎪⎝⎭的图象上各点的纵坐标不变,横坐标扩大到原来的2倍,所得图象的一条对称轴方程可以是( ) A. 12x π=-B. 12x π=C. 3x π=D. 23x π=30、由函数的图象,变换得到函数的图象,这个变换可以是( )A. 向左平移B. 向右平移C. 向左平移D. 向右平移 31、已知α是第二象限角,(5P x 为其终边上一点,且2cos x α=,则x 等于( ) 332- D. 332、cos 26x y π⎛⎫=-⎪⎝⎭()x ππ-≤≤的值域为( ) A. 11,22⎡⎤-⎢⎥⎣⎦ B. [-1,1]C. 1,12⎡⎤-⎢⎥⎣⎦ D. 13,22⎡-⎢⎣⎦33、已知已知sin π325α⎛⎫+=⎪⎝⎭,α∈π0,2⎛⎫⎪⎝⎭,则sin(π+α)等于__________ 34、已知角θ的终边经过点(),2P x ,且1cos 3θ=,则x =__________. 35、已知扇形的周长是10cm ,面积是42cm ,则扇形的半径是________. 36、26sin3π=_____________.37、________.38、已知函数()cos 2cos2,3f x x x π⎛⎫=+- ⎪⎝⎭其中x ∈R,给出下列四个结论: ①函数()f x 是最小正周期为π的奇函数;②函数()f x 图象的一条对称轴是直线x =2π3; ③函数()f x 图象的一个对称中心为5π,0;12⎛⎫⎪⎝⎭④函数()f x 的单调递增区间为[kπ+π6,kπ+2π3],k ∈Z. 其中正确的结论序号是_____ 39、函数的值域为__________.40、若点P 在角的终边上,且|OP|=2,则点P 的坐标是________.41、已知函数()2cos 2f x x π⎛⎫=+⎪⎝⎭,且()13f a -=,则()f a 的值为________.42、已知tanα是关于x 的方程2210x x --=的一个实根,且α是第三象限角. (1)求2sin cos sin cos αααα-+的值;(2)求cos sin αα+的值.43、计算与化简(I )计算:;(II )化简:.44、已知为第三象限角,.(1)化简(2)若,求的值.45、已知函数()()sin (0,0,)2f x A x A πωϕωϕ=+>><的部分图象如图所示.(1)求函数()f x 的解析式;(2)如何由函数2sin y x =的通过适当图象的变换得到函数()f x 的图象,写出变换过程;(3)若142f α⎛⎫=⎪⎝⎭,求sin 6πα⎛⎫- ⎪⎝⎭的值.46、(10分)已知1tan 3α=,求下列各式的值: (1)sin 3cos sin cos αααα+-;(2)2cos sin 2αα-.47、已知α是第二象限角,1tan(270)5α-︒=. (1)求sin α和cos α的值;(2)求sin(180)cos(360)tan(270)sin(180)tan(270)ααααα︒-︒--+︒-︒--︒的值.48、已知4sin 5α=,α为第二象限.求cos α,tan α的值. 49、计算与化简 (I )计算:112029sin cos tan 634πππ⎛⎫⎛⎫⎛⎫+-+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; (II )化简:()()()()3tan cos 2sin 2cos sin ππαπααπαπα⎛⎫--- ⎪⎝⎭--+. 50、已知sin (3π+θ)=12,求cos(3)cos(4)cos [cos()1]cos(2)cos(3)cos()πθθπθπθθππθθ+-++-+++-的值.51、已知角α的终边经过点P (-4a ,3a )(a ≠0),求sin α+cos α-tan α的值. 52、已知sinα=,求cosα,tanα的值. 53、已知函数的部分图象如图所示.(1)求的解析式;(2)求的单调递增区间.54、已知()23sin 2sin (0)2xf x x ωωω=->的最小正周期为π.(1)若()3f x =-,求tan x ; (2)若5,612ππθ⎡⎤∈⎢⎥⎣⎦,()35f θ=,求3f πθ⎛⎫+ ⎪⎝⎭的值.55、已知函数()4sin 16f x x π⎛⎫=+- ⎪⎝⎭。
(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值。
56、已知函数()4sin 16f x x π⎛⎫=+- ⎪⎝⎭。
(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间,64ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值。
参考答案1、【答案】D2、【答案】C3、【答案】A4、【答案】B5、【答案】A6、【答案】B7、【答案】B8、【答案】C9、【答案】B 10、【答案】A 11、【答案】A 12、【答案】C 13、【答案】D 14、【答案】C 15、【答案】A 16、【答案】C 17、【答案】D 18、【答案】D 19、【答案】A 20、【答案】B 21、【答案】B 22、【答案】B 23、【答案】C 24、【答案】A 25、【答案】C 26、【答案】D 27、【答案】A 28、【答案】D 29、【答案】D 30、【答案】B 31、【答案】D 32、【答案】C33、【答案】4-5 34、【答案】2 35、【答案】4cm 36、【答案】337、【答案】 38、【答案】②③④ 39、【答案】[2,10] 40、【答案】(-1,) 41、【答案】13- 42、【答案】(1)2sin cos 1sin cos 2αααα-=+;(2)sin cos 2αα+=-.试题解析:∵2210x x --=,∴121,12x x =-=,∴1tan 2α=-或tan 1α=,又α是第三象限角, 所以tan 1α= (1)2sin cos 2tan 12111sin cos tan 1112αααααα--⨯-===+++.(2)∵22sin tan 1cos sin cos 1ααααα⎧==⎪⎨⎪+=⎩且α是第三象限角,∴2sin 22cos 2αα⎧=-⎪⎪⎨⎪=-⎪⎩, ∴sin cos 2αα+=-43、【答案】(I )0;(II )1. (I )3120292sin cos tan sin cos tan 634634ππππππ⎛⎫⎛⎫⎛⎫+-+=-++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭111022⎛⎫=-+-+= ⎪⎝⎭(II )原式()()sin cos tan cos cos cos 1cos sin sin xxx x x x x x x--===--44、【答案】(1)(2)45、【答案】(1)()2sin 26f x x π⎛⎫=+⎪⎝⎭(2)见解析(3)78解:(1)()2sin 26f x x π⎛⎫=+⎪⎝⎭. (2)法1:先将2sin y x =的图象向左平移6π个单位,再将所得图象纵坐标不变,横坐标压缩为原来的12倍,所得图象即为()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图象.法2:先将2sin y x =的图象纵坐标不变,横坐标压缩为原来的倍,再将所得图象向左平移12π个单位,…,所得图象即为()2sin 26f x x π⎛⎫=+ ⎪⎝⎭的图象.(3)由12sin 22sin 446262f ααπαπ⎛⎫⎛⎫⎛⎫=⋅+=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 得:1sin 264απ⎛⎫+=⎪⎝⎭, 而217sin cos 12sin 1632688ππαπαα⎛⎫⎛⎫⎛⎫-=+=-+=-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.46、【答案】(1)5-(2)31047、【答案】(1)∵1tan(270)5α-︒=,∴11tan 5α-=,得tan 5α=-.∴222tan 25sin 261tan ααα==+, 2211cos 261tan αα==+.∵α是第二象限角,∴52626sin αα==. (2)原式26cos α=-= 48、【答案】34,53--.49、【答案】(I )0;(II )1.50、【答案】sin (3π+θ)=-sin θ,∴sin θ=-12. 51、【答案】当a>0,1120,当a<0,192052、【答案】或53、【答案】(1);(2)单调递增区间为.54、【答案】(1)3(2)933+. 2sin 2cos cos 2sin 6363x x ππππ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭433+=所以2sin 21336f πππθθ⎡⎤⎛⎫⎛⎫+=++-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦933+. 55、【答案】(1)T=2π;(2)f(x)621,最小值为-1. 试题分析:(1)利用2T πω=即可得周期;(2)根据x 的范围求出x 6π+的范围,利用正弦函数的图象即可得最值.试题解析:(1)、2T π=. (2)、由题意可知50x 612ππ≤+≤,所以50sin(x )sin 612ππ≤+≤62+所以f(x)621,最小值为-1.56、【答案】(1)T=2π;(2)f(x)621,最小值为-1.。
