最小二乘一次完成算法(程序)
各类最小二乘算法

β N −1 H* = N 0
β N −2
β 2( N −1) WN = 0
β 2( N −2)
0 ⋱ 1
三、递推算法 ∵
k θ(k ) = ∑ β i =1
∧
2(k −i) h (i )h T (i )
2随着采样次数的增多数据量不断增加ls估计有可能出现所谓的数据饱和现象导致递推算法不能接近参数真二关于数据饱和现象的分析所谓数据饱和现象就是随着时间的推移采集到的数据越来越多新数据所提供的信息被淹没在老数据的海洋之中
Ⅴ 各种最小二乘类参数辨识算法 §1 概 述
最小二乘类参数辨识算法(一次完成算法、递推算法) 最小二乘类参数辨识算法 (一次完成算法 、 递推算法 ) 是一种 最基本和常用的参数估计方法。但研究和应用表明, 最基本和常用的参数估计方法。 但研究和应用表明, 这一算 法仍存在明显的不足。 法仍存在明显的不足。 一、LS 算法的主要不足之处 1、当模型噪声为有色噪声时,LS 估计不再是无偏估计、一致 、当模型噪声为有色噪声时, 估计不再是无偏估计、 估计。 估计。 2、随着采样次数的增多,数据量不断增加,LS估计有可能出 、随着采样次数的增多,数据量不断增加, 估计有可能出 现所谓的“数据饱和”现象, 现所谓的“数据饱和”现象,导致递推算法不能接近参数真 值。
于是有: 于是有:
α P ( k ) P − 1 ( k − 1) = I − P ( k ) h ( k ) h T ( k )
则:
ˆ θ ( k ) = P ( k ) H * T Z * = P ( k ) α H * −1T Z * −1 + h ( k ) z ( k ) k k k k
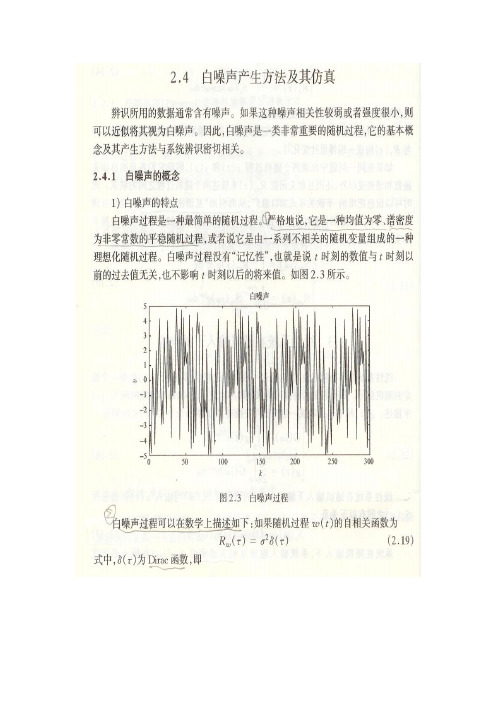
白噪声
-0.0156 0.9219 0.5703 0.4531 -0.2500 -0.4844
0.1016 -0.3672 0.8047 -0.1328 0.2188 0.3359
-0.9531 -0.7188 0.6875 -0.8359
0.0234 0.1406 0.8438 0.0820 0.4922 0.9609
0.7852 0.7266 0.3750 0.2578 0.5508 0.3164
0.9023 0.4336 0.6094 0.6680 0.0234 0.1406
0.8438 0.0820 0.4922 0.9609 0.7852 0.7266
0.0234 0.1406 0.8438 0.0820
。
1编程如下:
A=6;x0=1;M=255;f=2; N=100;%初始化;
x0=1;M=255;
fork=1:N %乘同余法递推100次;
x2=A*x0;%分别用x2和x0表示xi+1和xi-1;
x1=mod (x2,M);%取x2存储器的数除以M的余数放x1(xi)中;
白噪声
如果一个零均值、平稳随机过程的谱密度为常数,我们称之为白噪声(由白色光联想∞,τ=0
0,τ≠0
3 ,其中, 为Dirac函数,即 =
且
4 无记忆性,即t时刻的数值与t时刻以前的过去值无关,也不影响t时刻以后的将来值。从另一意义上说,即不同时刻的随机信号互不相关。
Columns 31 through 40
-1 1 -1 1 1 1 1 -1 -1 -1
Columns 41 through 50
_最小二乘法

,
• 线性模型 y = X θ + e 线性模型: 式中: 维输出向量; 维噪声向量; 式中: y 为n维输出向量;e 为n维噪声向量;θ 为m 维输出向量 维噪声向量 维参数向量; 维测量矩阵。 维参数向量;X 为 n × m 维测量矩阵。
足够大,当 只要 α 足够大 当 k > m 后,初值 P (0)、 0) 初值 θ ( 对估计的影响可以忽略. 对估计的影响可以忽略
LS法和 法和RLS法的比较 法和 法的比较
• • • LS法是一次完成算法,适于离线辩识,要记忆全部测 法是一次完成算法,适于离线辩识, 法是一次完成算法 量数据; 量数据; RLS法是递推算法,适于在线辩识和时变过程,只需 法是递推算法, 法是递推算法 适于在线辩识和时变过程, 要记忆n+1步数据; 步数据; 要记忆 步数据 RLS 法用粗糙初值时,如若 N 较小时,估计精度不 法用粗糙初值时, 较小时, 如 LS 法。
以上三式构成一组递推最小二乘估计算式 ^ ^ • 物理意义:新的参数估计 θ N +1是对上次老的估计 θ N 进行 物理意义: 修正而得出的。 修正而得出的。
初值选取方式
• 初值选取一般有两种方法可以考虑 初值选取一般有两种方法可以考虑: 1、先取一批数据,求取 θ ( N ) , P(N)做初值 、先取一批数据 求取 做初值,N>m 做初值
第四章线性系统参数估计的最小二乘法
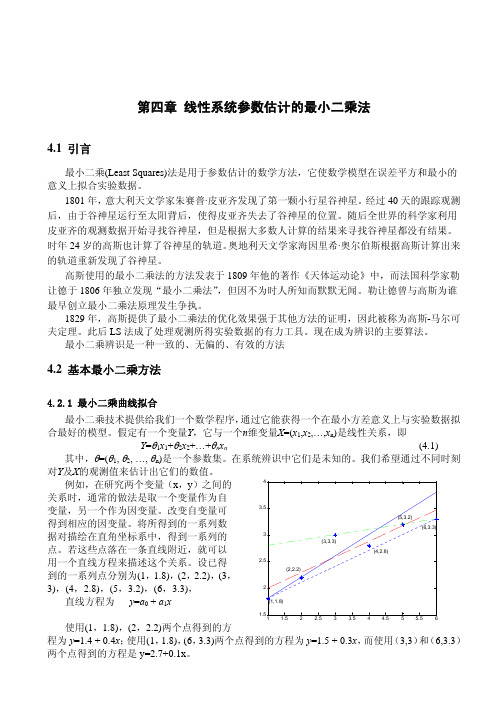
下面讨论更为一般的情况。 假设在t1, t2, …, tm时刻对Y及X的观测值序列已经被我们获得,并且用
y(i), x1(i), x2(i), x3(i), … i = 1,2, …, m 来表示这些观测数据。显然,可以用 m 个方程组来表示量测数据与估计值之间的关系
⎧ y(1) = θ1x1(1) +θ 2 x2 (1) +L+θ n xn (1)
从图中可看到,前两条线都仅能满足两个点的要求,而对其它点的误差都很大,其 6 个点的 误差平方累计分别为 0.49 和 0.42。第三条线能满足三个点的要求,但误差平方累计更大,为 1.58。 显然我们需要找到一条更为理想的直线来取得较小的误差。例如图中的红色短划线,它的方程 为 y=1.697 + 0.294x,误差平方累计为 0.25。这条线是怎样得到的呢?它是用最小二乘法得到的。
z
−2
,在其输入端加入 M 序列输入后
所得到的输出输入数据见下表,请利用这些数据辨识出系统的传递函数的系数。
k
1
2
3
4
5
6
7
8
9
10
输入 u
1
0
1
1
0
0
1
1
1
0
输出 y -0.45 -0.01
1.15
2.56
1.92
-0.30 -0.80 0.91 2.92 2.40
解: 已知系统阶数 n=2,有 4 个未知数。将式(4.4)展开 y(k) = −a1 y(k −1) − a2 y(k − 2) + b0u(k) + b1u(k −1) 根据要求,观测次数 N>2n+1,取 N 为 6,k=3
桥梁颤振导数自由振动识别的分段扩阶最小二乘迭代算法

道位移 和速 度 的时 程及 初 始信 息。Sra 基 于 ID a r k T
(ba i i e D ma ) Irhm Tm o i 法 , 出 了 MID( df dJ利用模型 自由振动 的位移 b h T m i 法 , am m D n 响应 , 可以一次识别 出全部的颤振导数 。Bo n h r j n和 wo Jkb e a o sn对 C H C vr n eBokHak l tx B M( oai c l n e Mar )法 a c i 和 C S Co o e S et m) P ( rs Pw r pc u 法进行 了考证 , B M法 s r CH 识别精度较 高。 。项海 帆 、 明、 顾 陈艾 荣 、 张若雪 、 丁泉 顺等 发展 了用 于识别 1 8个颤振导数 的总体最小二乘 法¨ , 利用跟踪技术将结构模态从 噪声模态 中检 出, 有效地提高了抗噪能力 。文献[ 1 在文献[0 的基础 1] 1] 上提出了加权整体最 小二乘法 , 同一 风速下 多次 自 将 由振动记录作为一个 整体 , 在整体残差 平方 和最小 的 意 义上 , 同时 对 该 风 速 下 多 次 竖 向 和扭 转 振 动 响应 时 程 进行 非线 性最 小二 乘拟 合 。文 献 [2 建 立 一个 联 系 1] 复模态与物理坐标 的二次泛 函, 泛 函以颤 振导数为 该 自变量, 通过使泛函极小 , 自动搜索到颤振导数 的正确 值, 避免了复模 态参数识别误差 的进 一步扩大 。文献 [3 提出了一种识别 颤振 导数的迭代法 , 用模态参 】] 先 数将 自由振动响应 以解析解形式表达 , 利用迭代法 , 使 准则 函数极 小 , 获得 模 态 参 数 的最 优 估 计 值 , 由模 态 再 参数提取颤振导数 , 可称为解析解拟合法¨ 。
最小二乘法

第3章 线性动态模型参数辨识-最小二乘法3.1 辨识方法分类根据不同的辨识原理,参数模型辨识方法可归纳成三类: ① 最小二乘类参数辨识方法,其基本思想是通过极小化如下准则函数来估计模型参数:min )()ˆ(ˆ==∑=θθLk k J 12ε 其中)(k ε代表模型输出与系统输出的偏差。
典型的方法有最小二乘法、增广最小二乘法、辅助变量法、广义最小二乘法等。
② 梯度校正参数辨识方法,其基本思想是沿着准则函数负梯度方向逐步修正模型参数,使准则函数达到最小,如随机逼近法。
③ 概率密度逼近参数辨识方法,其基本思想是使输出z 的条件概率密度)|(θz p 最大限度地逼近条件0θ下的概率密度)|(0θz p ,即)|()ˆ|(0m a x θθz p z p −−→−。
典型的方法是极大似然法。
3.2 最小二乘法的基本概念● 两种算法形式 ① 批处理算法:利用一批观测数据,一次计算或经反复迭代,以获得模型参数的估计值。
② 递推算法:在上次模型参数估计值)(ˆ1-k θ的基础上,根据当前获得的数据提出修正,进而获得本次模型参数估计值)(ˆk θ,广泛采用的递推算法形式为() ()()()~()θθk k k k d z k =-+-1K h其中)(ˆk θ表示k 时刻的模型参数估计值,K (k )为算法的增益,h (k -d ) 是由观测数据组成的输入数据向量,d 为整数,)(~k z 表示新息。
● 最小二乘原理定义:设一个随机序列)},,,(),({L k k z 21∈的均值是参数θ 的线性函数E{()}()T z k k θ=h其中h (k )是可测的数据向量,那么利用随机序列的一个实现,使准则函数21()[()()]LT k J z k k θθ==-∑h达到极小的参数估计值θˆ称作θ的最小二乘估计。
● 最小二乘原理表明,未知参数估计问题,就是求参数估计值θˆ,使序列的估计值尽可能地接近实际序列,两者的接近程度用实际序列与序列估计值之差的平方和来度量。
系统辨识方法之最小二乘法

综述最小二乘法的系统辨识姓名:费冬妹学号:2010108102 专业:控制理论与控制工程摘要:在研究一个控制系统过程中,建立系统的模型十分必要。
因此,系统辨识在控制系统的研究中起到了至关重要的作用。
本文主要介绍了系统辨识的最小二乘方法,最小二乘法的一次完成过程进行了推导,最小二乘法的一次完成的缺陷在于对于有色噪声并没有很好的辨识效果。
其中系统辨识在工程中的应用非常广泛,系统辨识的方法有很多种,最小二乘法是一种应用极其广泛的系统辨识方法,阐述了动态系统模型的建立及其最小二乘法在系统辨识中的应用,并通过实例分析说明了最小二乘法应用于系统辨识中的重要意义。
关键词:系统辨识、最小二乘法一、系统辨识的定义系统辨识、状态估计和控制理论是现代控制理论三个相互渗透的环节。
1962年,L.A.zadeh给出“辨识”的定义为:系统辨识是在对输入和输出观测的基础上,在指定的一类系统中,确定一个与被识别的系统等价的系统。
[1]最先提出了系统辨识的定义。
随着科技的发展,数学建模对科学研究及指导及生产都有非常重要的意义。
给一个系统建立数学模型是一个比较复杂的工作,其中关键的一个环节是系统辨识。
系统辨识就是研究如何利用系统的输入、输出信号建立系统的数学模型。
[7]系统数学模型是系统输入、输出及其相关变量间的数学关系式,它描述系统输入、输出及相关变量之间相互影响、变化的规律性。
换句话说,系统辨识就是从系统的运算和实验数据建立系统的模型(模型结构和参数)。
系统辨识的三要素:数据、模型类和准则。
系统辨识的基本原理:在输入输出的基础上,从一类系统中确定一个与所测系统等价的系统。
[2]二、最小二乘法的引出最小二乘法是1795年高斯在预测星体运行轨道最先提出的,它奠定了最小二乘估计理论的基础.到了20世纪60年代瑞典学者Austron把这个方法用于动态系统的辨识中,在这种辨识方法中,首先给出模型类型,在该类型下确定系统模型的最优参数。
我们可以将所研究的对象按照对其了解的程度分成白箱、灰箱和黑箱。
基于matlab的最小二乘法仿真

基于Matlab的最小二乘法的仿真摘要:任何待研究的对象都可以看成是一个系统。
系统的数学模型是系统本质特征的数学抽象,是建立系统状态参数之间以及与外作用之间最主要的相互作用、相互制约的数学表达式。
系统辨识是研究建立系统数学模型的理论与方法它研究的领域非常广阔,包括自动控制、航天、航空、天文学、海洋、医学、生物学、生态学以及省会经济学等众多领域。
本文主要介绍了系统辨识中最经典的数据处理方法最小二乘法,并将matlab用在最小二乘法的数据处理中。
The Simulation Of Least Square Method Using Matlab关键字:最小二乘法 matlabAbstract:the object of study for any can be as a system. Themathematical model of the system is the system of mathematics abstract nature, it is to establish the system state between the parameters of the function and between the most main, the interaction between a restraint mathematical expressions.System identification is research to establish a system of mathematical model theory and method of the field of study it is very wide, including automatic control, aerospace, aviation,astronomy, Marine, medicine, biology, ecology and provincial capital economics, etc. This paper mainly introduces the identification of the most classic of system data processing method, and the least square method with matlab in least square method of data processing.Key word:Least square method matlab引言最小二乘法是一种以选用误差平方和最小为准则,来最佳拟合出符合实验数据约最优参数估计的数学方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《系统辨识与建模》(MATLAB编程)
信研0701 孙娅萍2007000694
编程第四次作业
仿真模型参数为:a=[-1.5 0.7];b=[1.0 0.5],由下式递推产生502组数据,并形成如下矩阵:
z(k)=1.5z(k–1)-0.7z(k–2)+1.0u(k–1)+0.5u(k–2)+v(k)
试用一次完成最小二乘法辨识系统模型。
程序部分:
%************************************************************%
% ***** 二阶系统的最小二乘一次完成算法辨识程序*****%
% 系统辨识的输入信号u是6阶的M序列,长度是500;
L = 500;
u = load('u.txt'); u2 = load('u2.txt'); u1 = load('u1.txt');
z = zeros(1,L+1);
for k = 3 : (L+1)
% 理想输出作为系统观测值
z(k) = 1.5 * z(k-1) - 0.7 * z(k-2) + u(k-1) + 0.5 * u(k-2);
end
% 绘制输入信号和输出观测值的图形
figure(1)
i = 1 : 1 : L;
subplot(2,1,1)
plot(i,u)
k = 1 : 1 : (L+1);
subplot(2,1,2)
plot(k,z)
z = z'
z1 = load('z1.txt'); z2 = load('z2.txt'); z3 = load('z3.txt');
Na = 2; Nb = 2; % 定义Na、Nb;
for i = 1 : (Na+Nb)
if ((i == 1))
H = -1 * z2;
end
if (i == 2)
H = -1 * z1;
end
if (i == (Na+1))
H = u2;
end
if (i ==(Na+2))
H = u1;
end
if ( i == 1)
HL = H;
else
HL = [HL,H];
end
end% 给样本矩阵HL赋值;
ZL = z3; % 给样本矩阵ZL赋值;
HL
% 计算参数Cita
C1 = HL'* HL;
C2 = inv(C1);
C3 = HL' * ZL
C = C2 * C3;
Cita = C'
程序运行结果:
估计值:Cita = -1.5000 0.7000 1.0004 0.4995
真值:Cita = -1.5 0.7 1 0.5。
