数据结构-第7章 图---1. 基本概念
离散数学 7-1图概念7-2路与回路

例如
路:v1e2v3e3v2e3v3e4v2e6v5e7v3 迹:v5e8v4e5v2e6v5e7v3e4v2 通路:v4e8v5e6v2e1v1e2v3
学习本节要熟悉如下术语(22个): 路、 路的长度、 回路、 迹、 通路、 圈、 割点、
连通、连通分支、 连通图、 点连通度、
点割集、
边割集、 割边、 边连通度、 可达、 弱分图、
单侧连通、 强连通、 弱连通、 强分图、 单侧分图 掌握5个定理,一个推论。
7-2 路与回路
路
无向图的连通性
7-1 图的基本概念
图的定义
点的度数
特殊的图 图同构
三、特殊的图
1、多重图 定义7-1.4:含有平行边的图称为多重图。 2、简单图:不含平行边和环的图称为简单图。 3、完全图 定义7-1.5:简单图G=<V,E>中,若每一对结点 间均有边相连,则称该图为完全图。 有n个结点的无向完全图记为Kn。 无向完全图:每一条边都是无向边 不含有平行边和环 每一对结点间都有边相连
3、图的分类:
①无向图:每条边均为无向边的图称为无向图。 ②有向图:每条边均为有向边的图称为有向图。
③混合图:有些边是无向边,有些边是有向边的图称
为混合图。
v1 (孤立点) v5 V1’ v1 环
v2
v4 v3 (a)无向图
V2’
V3’ (b)有向图 V4’
v2
v4 v3 ( c ) 混合图
4、点和边的关联:如ei=(u,v)或ei=<u,v>称u, v与ei关联。 5、点与点的相邻:关联于同一条边的结点称为邻 接点。
大学计算机基础07数据结构与算法资料PPT课件

7.1 算 法 7.2 数据结构的基本概念 7.3 线性表及其顺序存储结构 7.4 栈和队列 7.5 线性链表 7.6 树与二叉树 7.7 查找与排序技术
第7章 数ST PART OF THE OVERALL OVERVIEW, PLEASE SUMMARIZE THE CONTENT
例7.2 有5个人坐在一起, 问第5个人的岁数,他说比第4个人大2岁。 问第4个人的岁数,他说比第3个人大2岁。 问第3个人的岁数,他说比第2个人大2岁。 问第2个人的岁数,他说比第1个人大2岁。 问第1个人的岁数,他说是10岁。 请问第5个人多大。
27.07.2020
11
第7章 数据结构与算法
这个问题可以用递归方法解决。递归过程如下: age(5)=age(4)十2 age(4)=age(3)十2 age(3)=age(2)十2 age(2)=age(1)十2 age( l)=10
27.07.2020
14
第7章 数据结构与算法
2.算法的空间复杂度 算法的空间复杂度是指执行这个算法所需要的内存空间。 类似算法的时间复杂度,空间复杂度作为算法所需存储空 间的度量。
27.07.2020
15
第7章 数据结构与算法
7.2 数据结构的基本概念 数据结构主要研究三个问题:
(1)数据集合中各数据元素之间所固有的逻辑关 系,即数据的逻辑结构;
现实世界中存在的一切个体都可以是数据元素(简称元 素)。
例如: 春、夏、秋、冬; 26、56、65、 73、26、…; 父亲、儿子、女儿。
数据元素之间的关系可用前后件关系 例如, “春”是“夏”前件,“夏”是“春”的后件。
27.07.2020
18
第7章图_数据结构

v4
11
2013-8-7
图的概念(3)
子图——如果图G(V,E)和图G’(V’,E’),满足:V’V,E’E 则称G’为G的子图
2 1 4 3 5 6 3 5 6 1 2
v1 v2 v4 v3 v2
v1 v3 v4
v3
2013-8-7
12
图的概念(4)
路径——是顶点的序列V={Vp,Vi1,……Vin,Vq},满足(Vp,Vi1),
2013-8-7 5
本章目录
7.1 图的定义和术语 7.2 图的存储结构
7.2.1 数组表示法 7.2.2 邻接表 ( *7.2.3 十字链表 7.3.1 深度优先搜索 7.3.2 广度优先搜索 7.4.1 图的连通分量和生成树 7.4.2 最小生成树
*7.2.4 邻接多重表 )
7.3 图的遍历
连通树或无根树
无回路的图称为树或自由树 或无根树
2013-8-7
18
图的概念(8)
有向树:只有一个顶点的入度为0,其余 顶点的入度为1的有向图。
V1 V2
有向树是弱 连通的
V3
V4
2013-8-7
19
自测题
7. 下列关于无向连通图特性的叙述中,正确的是
2013-8-7
29
图的存贮结构:邻接矩阵
若顶点只是编号信息,边上信息只是有无(边),则 数组表示法可以简化为如下的邻接矩阵表示法: typedef int AdjMatrix[MAXNODE][MAXNODE];
*有n个顶点的图G=(V,{R})的邻接矩阵为n阶方阵A,其定 义如下:
1 A[i ][ j ] 0
【北方交通大学 2001 一.24 (2分)】
《数据结构》第二版严蔚敏课后习题作业参考答案(1-7章)

《数据结构》第二版严蔚敏课后习题作业参考答案(1-7章)【第一章绪论】1. 数据结构是计算机科学中的重要基础知识,它研究的是如何组织和存储数据,以及如何通过高效的算法进行数据的操作和处理。
本章主要介绍了数据结构的基本概念和发展历程。
【第二章线性表】1. 线性表是由一组数据元素组成的数据结构,它的特点是元素之间存在着一对一的线性关系。
本章主要介绍了线性表的顺序存储结构和链式存储结构,以及它们的操作和应用。
【第三章栈与队列】1. 栈是一种特殊的线性表,它的特点是只能在表的一端进行插入和删除操作。
本章主要介绍了栈的顺序存储结构和链式存储结构,以及栈的应用场景。
2. 队列也是一种特殊的线性表,它的特点是只能在表的一端进行插入操作,而在另一端进行删除操作。
本章主要介绍了队列的顺序存储结构和链式存储结构,以及队列的应用场景。
【第四章串】1. 串是由零个或多个字符组成的有限序列,它是一种线性表的特例。
本章主要介绍了串的存储结构和基本操作,以及串的模式匹配算法。
【第五章数组与广义表】1. 数组是一种线性表的顺序存储结构,它的特点是所有元素都具有相同数据类型。
本章主要介绍了一维数组和多维数组的存储结构和基本操作,以及广义表的概念和表示方法。
【第六章树与二叉树】1. 树是一种非线性的数据结构,它的特点是一个节点可以有多个子节点。
本章主要介绍了树的基本概念和属性,以及树的存储结构和遍历算法。
2. 二叉树是一种特殊的树,它的每个节点最多只有两个子节点。
本章主要介绍了二叉树的存储结构和遍历算法,以及一些特殊的二叉树。
【第七章图】1. 图是一种非线性的数据结构,它由顶点集合和边集合组成。
本章主要介绍了图的基本概念和属性,以及图的存储结构和遍历算法。
【总结】1. 数据结构是计算机科学中非常重要的一门基础课程,它关注的是如何高效地组织和存储数据,以及如何通过算法进行数据的操作和处理。
本文对《数据结构》第二版严蔚敏的课后习题作业提供了参考答案,涵盖了第1-7章的内容。
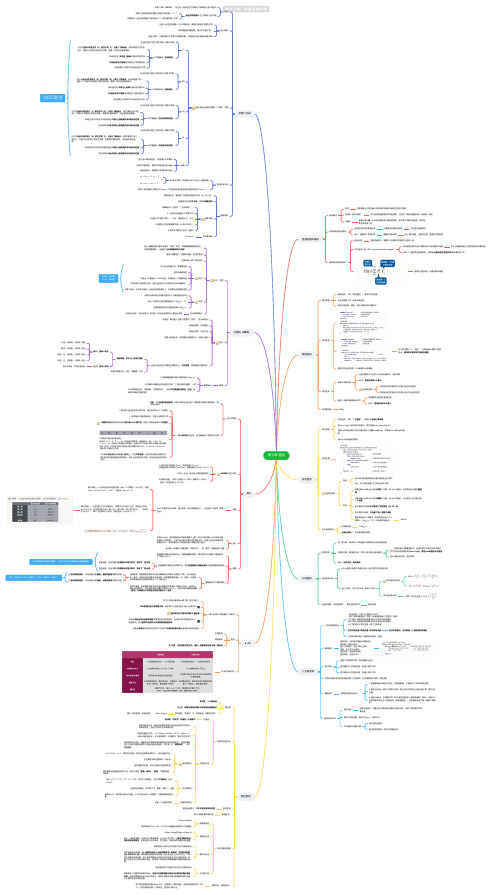
王道数据结构 第七章 查找思维导图-高清脑图模板
每次调整的对象都是“最小不平衡子树”
插入操作
在插入操作,只要将最小不平衡子树调整平衡,则其他祖先结点都会恢复平衡
在A的左孩子的左子树中插入导致不平衡
由于在结点A的左孩子(L)的左子树(L)上插入了新结点,A的平衡因子由1增
至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。
LL
将A的左孩子B向右上旋转代替A成为根节点 将A结点向右下旋转成为B的右子树的根结点
RR平衡旋转(左单旋转)
而B的原左子树则作为A结点的右子树
在A的左孩子的右子树中插入导致不平衡
由于在结点A的左孩子(L)的右子树(R)上插入了新结点,A的平衡因子由1增
LR
至2,导致以A为根的子树失去平衡,需要两次旋转操作,先左旋转再右旋转。
将A的左孩子B的右子树的根结点C向左上旋转提升至B结点的位置
本质:永远保证 子树0<关键字1<子树1<关键字2<子树2<...
当左兄弟很宽裕时,用当前结点的前驱、前驱的前驱来填补空缺 当右兄弟很宽裕时,用当前结点的后继、后继的后继来填补空缺
兄弟够借。若被删除关键字所在结点删除前的关键字个数低于下限,且与此结点 右(或左)兄弟结点的关键字还很宽裕,则需要调整该结点、右(或左)兄弟结 点及其双亲结点及其双亲结点(父子换位法)
LL平衡旋转(右单旋转)
而B的原右子树则作为A结点的左子树
在A的右孩子的右子树中插入导致不平衡
由于在结点A的右孩子(R)的右子树(R)上插入了新结点,A的平衡因子由-1
减至-2,导致以A为根的子树失去平衡,需要一次向左的旋转操作。
RR
将A的右孩子B向左上旋转代替A成为根节点 将A结点向左下旋转成为B的左子树的根结点
《数据结构》填空作业题(答案)

《数据结构》填空作业题答案第1章绪论(已校对无误)1.数据结构包括数据的逻辑结构、数据的存储结构和数据的运算三方面的内容。
2.程序包括两个内容:数据结构和算法。
3. 数据结构的形式定义为:数据结构是一个二元组: Data Structure =(D,S)。
4. 数据的逻辑结构在计算机存储器内的表示,称为数据的存储结构。
5. 数据的逻辑结构可以分类为线性结构和非线性结构两大类。
6. 在图状结构中,每个结点的前驱结点数和后继结点数可以有多个。
7. 在树形结构中,数据元素之间存在一对多的关系。
8. 数据的物理结构,指数据元素在计算机中的标识(映象),也即存储结构。
9. 数据的逻辑结构包括线性结构、树形结构和图形结构 3种类型,树型结构和有向图结构合称为非线性结构。
10. 顺序存储结构是把逻辑上相邻的结点存储在物理上连续的存储单元里,结点之间的逻辑关系由存储单元位置的邻接关系来体现。
11. 链式存储结构是把逻辑上相邻的结点存储在物理上任意的存储单元里,节点之间的逻辑关系由附加的指针域来体现。
12. 数据的存储结构可用4种基本的存储方法表示,它们分别是顺序存储、链式存储、索引存储和散列存储。
13. 线性结构反映结点间的逻辑关系是一对一的,非线性结构反映结点间的逻辑关系是一对多或多对多。
14. 数据结构在物理上可分为顺序存储结构和链式存储结构。
15. 我们把每种数据结构均视为抽象类型,它不但定义了数据的表示方式,还给出了处理数据的实现方法。
16. 数据元素可由若干个数据项组成。
17. 算法分析的两个主要方面是时间复杂度和空间复杂度。
18. 一个算法的时间复杂度是用该算法所消耗的时间的多少来度量的,一个算法的空间复杂度是用该算法在运行过程中所占用的存储空间的大小来度量的。
19. 算法具有如下特点:有穷性、确定性、可行性、输入、输出。
20. 对于某一类特定的问题,算法给出了解决问题的一系列操作,每一操作都有它的确切的定义,并在有穷时间内计算出结果。
第7章图(上)-数据结构简明教程(第2版)-微课版-李春葆-清华大学出版社
图 的 基 本 概 念
【例7.1】 一个图G1=(V1,E1),其中:
V1={0,1,2,3,4}
7.1
E1={(0,1),(1,2),(2,3),(3,4),(2,4),(0,3)}
另一个图G2=(V2,E2),其中:
图
的
V2={0,1,2,3,4}
的
因为图中每条边分别作为两个相邻点的度各计一次。
基
本
概
念
【例7.2】一个无向图中有16条边,度为4的顶点有3个,度为
3的顶点有4个,其余顶点的度均小于3,则该图至少有( )个顶点。
A.10
B.11
C.12
D.13
7ห้องสมุดไป่ตู้1
设该图有n个顶点,图中度为i的顶点数为ni(0≤i≤4),
图 的 基
n4=3,n3=4。 要使顶点数最少,该图应是连通的,即n0=0,
本 概 念
n=n4+n3+n2+n1+n0=7+n2+n1,即n2+n1=n-7。 度之和=4×3+3×4+2×n2+n1=24+2n2+n1≤24+2(n2+n1)
=24+2×(n-7)=10+2n。
而度之和=2e=32,所以有10+2n≥32,即n≥11。
7.1
(4)子图
设有两个图G=(V,E)和G'=(V',E'),若V'是V的子集,即 V' V,且E'是E的子集,即E' E,则称G'是G的子图。
(1≤k≤m),若该图是有向图,则<ik-1,ik>∈E(G),
数据结构第七章课后习题答案 (1)
7_1对于图题7.1(P235)的无向图,给出:(1)表示该图的邻接矩阵。
(2)表示该图的邻接表。
(3)图中每个顶点的度。
解:(1)邻接矩阵:0111000100110010010101110111010100100110010001110(2)邻接表:1:2----3----4----NULL;2: 1----4----5----NULL;3: 1----4----6----NULL;4: 1----2----3----5----6----7----NULL;5: 2----4----7----NULL;6: 3----4----7----NULL;7: 4----5----6----NULL;(3)图中每个顶点的度分别为:3,3,3,6,3,3,3。
7_2对于图题7.1的无向图,给出:(1)从顶点1出发,按深度优先搜索法遍历图时所得到的顶点序(2)从顶点1出发,按广度优先法搜索法遍历图时所得到的顶点序列。
(1)DFS法:存储结构:本题采用邻接表作为图的存储结构,邻接表中的各个链表的结点形式由类型L_NODE规定,而各个链表的头指针存放在数组head中。
数组e中的元素e[0],e[1],…..,e[m-1]给出图中的m条边,e中结点形式由类型E_NODE规定。
visit[i]数组用来表示顶点i是否被访问过。
遍历前置visit各元素为0,若顶点i被访问过,则置visit[i]为1.算法分析:首先访问出发顶点v.接着,选择一个与v相邻接且未被访问过的的顶点w访问之,再从w 开始进行深度优先搜索。
每当到达一个其所有相邻接的顶点都被访问过的顶点,就从最后访问的顶点开始,依次退回到尚有邻接顶点未曾访问过的顶点u,并从u开始进行深度优先搜索。
这个过程进行到所有顶点都被访问过,或从任何一个已访问过的顶点出发,再也无法到达未曾访问过的顶点,则搜索过程就结束。
另一方面,先建立一个相应的具有n个顶点,m条边的无向图的邻接表。
数据结构-第7章图答案
7.3 图的遍历 从图中某个顶点出发游历图,访遍图中其余顶点, 并且使图中的每个顶点仅被访问一次的过程。 一、深度优先搜索 从图中某个顶点V0 出发,访问此顶点,然后依次 从V0的各个未被访问的邻接点出发深度优先搜索遍 历图,直至图中所有和V0有路径相通的顶点都被访 问到,若此时图中尚有顶点未被访问,则另选图中 一个未曾被访问的顶点作起始点,重复上述过程, 直至图中所有顶点都被访问到为止。
void BFSTraverse(Graph G, Status (*Visit)(int v)) { // 按广度优先非递归遍历图G。使用辅助队列Q和访问标志数组 visited。 for (v=0; v<G.vexnum; ++v) visited[v] = FALSE; InitQueue(Q); // 置空的辅助队列Q for ( v=0; v<G.vexnum; ++v ) if ( !visited[v]) { // v尚未访问 EnQueue(Q, v); // v入队列 while (!QueueEmpty(Q)) { DeQueue(Q, u); // 队头元素出队并置为u visited[u] = TRUE; Visit(u); // 访问u for ( w=FirstAdjVex(G, u); w!=0; w=NextAdjVex(G, u, w) ) if ( ! visited[w]) EnQueue(Q, w); // u的尚未访问的邻接顶点w入队列Q
4。邻接多重表
边结点
mark ivex
顶点结点
ilink
jvex
jlink
info
data
firstedge
#define MAX_VERTEX_NUM 20 typedef emnu {unvisited, visited} VisitIf; typedef struct Ebox { VisitIf mark; // 访问标记 int ivex, jvex; // 该边依附的两个顶点的位置 struct EBox *ilink, *jlink; // 分别指向依附这两个顶点的下一条 边 InfoType *info; // 该边信息指针 } EBox; typedef struct VexBox { VertexType data; EBox *firstedge; // 指向第一条依附该顶点的边 } VexBox; typedef struct { VexBox adjmulist[MAX_VERTEX_NUM]; int vexnum, edgenum; // 无向图的当前顶点数和边数 } AMLGraph;
《数据结构》第 7 章 图
v3
v4 v5 v4
v3
v5 v4
v3
v5 v4
v3
v5 v4
v3
v5
注
一个图可以有许多棵不同的生成树。 所有生成树具有以下共同特点: 生成树的顶点个数与图的顶点个数相同; 生成树是图的极小连通子图; 一个有 n 个顶点的连通图的生成树有 n-1 条边; 生成树中任意两个顶点间的路径是唯一的; 在生成树中再加一条边必然形成回路。 含 n 个顶点 n-1 条边的图不一定是生成树。
A1 = {< v1, v2>, < v1, v3>, < v3, v4>, < v4, v1>} v1 v2
有向图
v3
v4
制作:计算机科学与技术学院 徐振中
数据结构 边:若 <v, w>∈VR 必有<w, v>∈VR,则以 无序对 (v, w) 代表这两个有序对,表示 v 和 w 之 间的一条边,此时的图称为无向图。 G2 = (V2, E2) V2 = {v1, v2, v3, v4, v5}
第七章 图
E2 = {(v1, v2), (v1, v4), (v2, v3), (v2, v5) , (v3, v4), (v3, v5)} v1
G2
v3
v2
无向图
v4
v5
制作:计算机科学与技术学院 徐振中
数据结构
第七章 图
例:两个城市 A 和 B ,如果 A 和 B 之间的连线的涵义是 表示两个城市的距离,则<A, B> 和 <B, A> 是相同的, 用 (A, B) 表示。 如果 A 和 B 之间的连线的涵义是表示两城市之 间人口流动的情况,则 <A, B> 和 <B, A> 是不同的。 北京 <北京,上海> (北京,上海) <上海,北京> <北京,上海> 北京 上海 上海
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.1.2 图的基本术语
4、稠密图、稀疏图 当一个图接近完全图时,则称为稠密图。 相反,当一个图含有较少的边数(即当e<<n(n1))时,则称为稀疏图。
7.1.2 图的基本术语
5、子图
设有两个图G=(V,E)和G'=(V',1E'),若V'是V 的子集,即V'∈V,且E'是E的子集,即E' ∈E
1
2
0
两个强连通分量
3
7.1.2 图的基本术语
在一个非强连通中找强连通分量的方法。
① 在图中找有向环。
② 扩展该有向环:如果某个顶点到该环中任一顶点有 路径,并且该环中任一顶点到这个顶点也有路径, 则加入这个顶点。
一个非强连通图 1
3个强连通分量 1
2
0
2
0
3
4
5
3
4
5
7.1.2 图的基本术语
10、生成树、生成森林: 一个连通图(无向图)的生成树是一个极小连通 子图,它含有图中全部n个顶点和只有足以构 成一棵树的n-1条边,称为图的生成树。
a
b
c
d
(a) 有向图G1
7.1.1 图的定义
【例2】设有无向图G2,形式化定义是: G2=(V2 ,E2) V2={a,b,c,d} E2={(a,b), (a,c), (b,c), (c,d)}
a
d
b
c
(b) 无向图G2
7.1.1 图的定义
图抽象数据类型: ADT Graph{
数据对象:具有相同特性的元素集合 数据关系:R {VR}
无若向图图中:G任中若意的从两极顶个大点顶连i点到通都顶子连点图通j有称,路为则径G称的,为连则连通称通分顶图量点,i 和。否j则是称连为通非的连。通图。
显然,任何连通图的连通分量只有一个,即本
身,而非连通图有多个连通分量。
1
1
2
0
3 一个连通图
2
0
3
一个非连通图
两个连通分量
7.1.2 图的基本术语
1
1
2
0
3 一个连通图
2
0
3 图的生成树
7.1.2 图的基本术语
关于无向图的生成树的几个结论: 一棵有n个顶点的生成树有且仅有n-1条边; 如果一个图有n个顶点和小于n-1条边,则是非 连通图; 如果多于n-1条边,则一定有环; 有n-1条边的图不一定是生成树。
7.1.2 图的基本术语
有向图的生成森林是这样一个子图,由若干棵 有向树组成,含有图中全部顶点,但是只有足 够构成若干棵有向树的边。
7.1.2 图的基本术语
2、顶点的度、入度和出度
无向图:以顶点i为端点的边数称为该顶点的
度。
1
顶点1的度为3
有向图:以顶点i2为终点3 的入0 边的数目,称为
该 称顶为2点该的顶入点13 度的出。0 度以。顶一点个i为4(顶b)始点点顶顶的的点点入00出的 的度边入出与度度的出为为数12度目的,和
7.1.1 图的定义
在图G中,如果代表边的顶点对是无序的,则称 G为无向图。用圆括号序偶表示无向边。
1
(0,1)
2
3
0
4
7.1.1 图的定义
如果表示边的顶点对是有序的,则称G为有向图 。用尖括号序偶表示有向边。
1
<0,1>
230
4
7.1.1 图的定义
【例1】设有有向图G1,形式化定义是: G1=(V1 ,E1) V1={a,b,c,d} E1={<a,b>,<a,c>, <c,d> ,<d,a>,<d,b>}
9、强连通图和强连通分量
有向图:若从顶点i到顶点j有路径,则称从顶 点i到j是连通的。
若图G中的任意两个顶点i和j都连通,即从顶点
i到j和从顶点j到i都存在路径,则称图G是强连
通图。 1
1
2
0
2
0
3 一个强连通图
3 一个非强连通图
7.1.2 图的基本术语
9、强连通图和强连通分量 有向图G中的极大强连通子图称为G的强连通 分量。显然,强连通图只有一个强连通分量, 即本身。非强连通图有多个强连通分量。
VR { x, y | P(x, y),xyV}
操作集合:创建、插入、删除、遍历等 }
7.1.2 图的基本术语
1、端点和邻接点 无向图:若存在一条边(i,j) →顶点i和顶点 j为端点,它们互为邻接点。 有向图:若存在一条边<i,j> →顶点i为起始 端点(简称为起点),顶点j为终止端点(简称 终点),它们互为邻接点。
,则称G'是G的子图。 2
3
0
1
2
3
0
4
4 1
2
3
0
4
7.1.2 图的基本术语
6、路径和路径长度 在一个图G=(V,E)中,从顶点i到顶点j的一条 路径(i,i1,i2,…,im,j)。 所有的(ix,iy) ∈E(G),或者<ix,iy> ∈E(G)
7.1.2 图的基本术语
6、路径和路径长度 路径长度是指一条路径上经过的边的数目。 若一条路径上除开始点和结束点可以相同外, 其余顶点均不相同,则称此路径为简单路径。
12
3
5
2
0
6
3
7.1 图
1、图的定义与相关术语 图是多对多的网状结构,记为G=(V,E); 邻接点、路径与回路、顶点的度、生成树; 2、与树结构的区别: 图是多对多关系,树是一对多关系 3、图的类型: 无向图/有向图/完全图/子图/连通图(连通图、 连通分量针对无向图,强连通图、强连通分量针 对有向图) 4、顶点在图中的位置:人为排序编号
7.1.2 图的基本术语
3、完全图 无向图:每两个顶点之间都存在着一条边,称 为完全无向图, 包含有n(n-1)/2条边。 有向图:每两个顶点之间都存在着方向相反的 两条边,称为完全有向图,包含有n(n-1)条边。
1
2
0
1
2
0
3 完全无向图:n=4,e=n(n-1)/2=6
3 完全有向图:n=4,e=n(n-1)=12
有向树是只有一个顶点的入度为0 ,其余顶点 的入度均为1的有向图。
a
b
a
d
e
c
d
cb
e
(a) 有向图
(b) 生成森林
7.1.2 图的基本术语
11、权和网
图中每一条边都可以附带有一个对应的数值, 这种与边相关的数值称为权。
权可以表示从一个顶点到另一个顶点的距离或 花费的代价。ຫໍສະໝຸດ 边上带有权的图称为带权图,也称作网。
7.1 图的定义 7.2 图的存储结构 7.3 图的遍历 7.4 图的连通性问题 7.5 有向无环图及其应用 7.6 最短路径
7.1.1 图的定义
图(Graph)是一种网状数据结构。
G由顶点集合V(G)和边集合E(G)构成,其形式化
定义为:G=(V,E)。
1
2
3
0
4
说明:对于n个顶点的图,对每个顶点连续编号 ,即顶点的编号为0~n-1。通过编号唯一确定一 个顶点。
1
0→ 1的一条简单
2
0
路径,长度为2
3
7.1.2 图的基本术语
7、回路或环
若一条路径上的开始点与结束点为同一个顶点 ,则此路径被称为回路或环。
开始点与结束点相同的简单路径被称为简单回 路或简单环。
1
(0,2,1,0)就是一
2
0
条简单回路,其长度
为3。
3
7.1.2 图的基本术语
8、连通、连通图和连通分量
为该顶点的度。
4
顶点0的度为1+2=3
(a)
7.1.2 图的基本术语
顶点1的度为3
1
2
3
0
1 230
4
4
顶点0的入度为1
(a)
(b) 顶点0的出度为2
顶点0的度为1+2=3
7.1.2 图的基本术语
若一个图中有n个顶点和e条边,每个顶点的度 为di(0≤i≤n-1),则有:
e= 1
2
n1 i0
di
