青岛二中高一数学同步专练(人教A版2019必修1)-专题5.1 任意角和弧度制
高一数学(必修一)《第五章-任意角和弧度制》练习题及答案解析-人教版

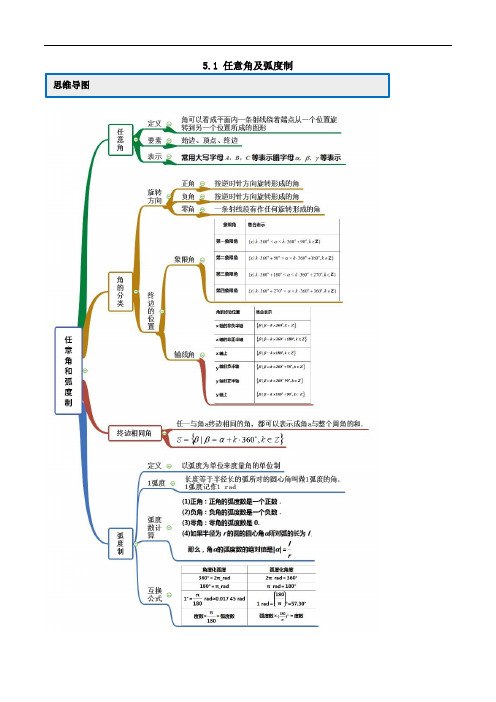
高一数学(必修一)《第五章 任意角和弧度制》练习题及答案解析-人教版班级:___________姓名:___________考号:___________一、多选题1.已知扇形的周长是12,面积是8,则扇形的圆心角的弧度数可能是( ) A .1 B .4C .2D .3二、单选题2.终边与直线y x =重合的角可表示为( ) A .45180,k k Z ︒︒+⋅∈ B .45360,k k Z ︒︒+⋅∈ C .135180,k k Z ︒︒+⋅∈ D .225360,k k Z ︒︒+⋅∈3.下列角中与116π-终边相同的角是( ) A .30-︒B .40-︒C .20︒D .390︒4.下列说法正确的是( )A .长度等于半径的弦所对的圆心角为1弧度B .若tan 0α≥,则()2k k k Z ππαπ≤≤+∈C .若角α的终边过点()()3,40P k k k ≠,则4sin 5α D .当()224k k k Z ππαπ<<+∈时,则sin cos αα<5.已知一个母线长为1的圆锥的侧面展开图的圆心角等于240︒,则该圆锥的侧面积为( )A B .881πCD .23π6.《掷铁饼者》取材于希腊的现实生活中的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中具有表现力的瞬间(如图).现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”,掷铁饼者的手臂长约为4πm肩宽约为8πm ,“弓”所在圆的半径约为5m 41.414≈和1.732)( )A .1.012mB .1.768mC .2.043mD .2.945m三、填空题7.6730'︒化为弧度,结果是______.8.已知扇形的周长为20cm ,面积为92cm ,则扇形的半径为________.9.折扇最早出现于公元五世纪的中国南北朝时代,《南齐书》上说:“褚渊以腰扇障日.”,据《通鉴注》上的解释,“腰扇”即折扇.一般情况下,折扇可以看作从一个圆面中剪下的扇形制作而成,设扇形的弧长为l ,扇形所在的圆的半径为r ,当l 与r 的比值约为2.4时,则折扇看上去的形状比较美观.若一把折扇所在扇形的半径为30cm ,在保证美观的前提下,此折扇所在扇形的面积是_______2cm .10.设地球半径为R ,地球上北纬30°圈上有A ,B 两点,点A 在西经10°,点B 在东经110°,则点A 和B 两点东西方向的距离是___________.四、解答题11.将下列各角化成360,,0360k k βαα=+⋅︒∈︒≤<︒Z 的形式,并指出它们是第几象限的角:(1)1320︒;(2)315-︒;(3)1500︒;(4)1610-︒.12.根据角度制和弧度制的转化,已知条件:1690α=︒(1)把α表示成2k πβ+的形式[)()Z,02k βπ∈∈,;(2)求θ,使θ与α的终边相同,且()4,2θππ∈--.13.已知一扇形的圆心角是72°,半径为20,求扇形的面积. 14.已知一扇形的圆心角为α,半径为R ,弧长为l. (1)若α=60°,R =10 cm ,求扇形的弧长l ;(2)已知扇形的周长为10 cm ,面积是4 cm 2,求扇形的圆心角;(3)若扇形周长为20 cm ,当扇形的圆心角α为多少弧度时,则这个扇形的面积最大? 15.已知扇形的周长为c ,当扇形的圆心角为多少弧度时,则扇形的面积最大.16.某商场共有三层楼,在其圆柱形空间内安装两部等长的扶梯Ⅰ、Ⅱ供顾客乘用,如图,一顾客自一楼点A 处乘Ⅰ到达二楼的点B 处后,沿着二楼地面上的弧BM 逆时针步行至点C 处,且C 为弧BM 的中点,再乘Ⅱ到达三楼的点D 处,设圆柱形空间三个楼面圆的中心分别为半径为8m ,相邻楼层的间距为4m ,两部电梯与楼面所成角的正弦值均为13.(1)求此顾客在二楼地面上步行的路程; (2)求异面直线AB 和CD 所成角的余弦值.17.某地政府部门欲做一个“践行核心价值观”的宣传牌,该宣传牌形状是如图所示的扇形环面(由扇形OAD 挖去扇形OBC 后构成的).已知2OA =米,OB x =米()02x <<,线段BA 、线段CD 与弧BC 、弧AD 的长度之和为6米,圆心角为θ弧度.(1)求θ关于x 的函数解析式;(2)记该宣传牌的面积为y ,试问x 取何值时,则y 的值最大?并求出最大值.参考答案与解析1.AB【分析】利用扇形的弧长与面积公式建立方程组求解,再利用圆心角公式.【详解】设扇形的半径为r ,弧长为l ,面积为S ,圆心角为α,则212l r +=,182S lr ==解得2r =和8l =或4r =和4l ,则4lrα==或1.故C ,D 错误. 故选:AB . 2.A【分析】根据终边相同的角的概念,简单计算即可.【详解】终边与直线y x =重合的角可表示为45180,k k Z +⋅∈. 故选:A. 3.D【分析】由角度制与弧度制的互化公式得到113306π-=-︒,结合终边相同角的表示,即可求解. 【详解】由角度制与弧度制的互化公式,可得113306π-=-︒ 与角330-︒终边相同的角的集合为{|330360,}A k k Z αα==-︒+⋅︒∈ 令2k =,可得390α=︒所以与角330α=-︒终边相同的角是390α=︒. 故选:D. 4.D【分析】利用弧度制、三角函数值的正负、三角函数的定义和三角函数线的应用逐一判断选项即可. 【详解】对于A ,长度等于半径的弦所对的圆心角为3π弧度,A 错误; 对于B ,若tan 0α≥,则()2k k k ππαπ≤<+∈Z ,B 错误;对于C ,若角α的终边过点()()3,40P k k k ≠,则4sin 5α=±,C 错误;对于D ,当()224k k k ππαπ<<+∈Z 时,则sin cos αα<,D 正确.故选D.5.D【分析】根据扇形的圆心角、弧长和半径的关系以及扇形的面积求解. 【详解】解:将圆心角240︒化为弧度为:43π,设圆锥底面圆的半径为r 由圆心角、弧长和半径的公式得:4213r ππ=⨯,即23r =由扇形面积公式得:22133S ππ=⨯⨯=所以圆锥的侧面积为23π. 故选:D. 6.B【分析】由题意分析得到这段弓形所在的弧长,结合弧长公式求出其所对的圆心角,双手之间的距离,求得其弦长,即可求解.【详解】如图所示,由题意知“弓”所在的弧ACB 的长54488l ππππ=++=,其所对圆心角58524ππα==则两手之间的距离()522sin 1.768m 44AB AD π==⨯⨯≈.故选:B .7.38π【解析】根据角度制与弧度制的关系180π︒=,转化即可. 【详解】180π︒= 1180π︒∴=36730'67.567.51808ππ︒∴︒==⨯=故答案为:38π 【点睛】本题主要考查了弧度制与角度制的转化,属于容易题. 8.9cm【分析】由题意设扇形的半径为r cm ,弧长为l cm ,由扇形的周长、面积可得1(202)92r r -=,解出r 后,验证即可得解.【详解】设扇形的半径为r cm ,弧长为l cm ,圆心角为θ ∵220l r +=,∴202l r =-∴192lr =,即1(202)92r r -=,解得1r =或9r = 当1r =时,则18l =,则181821l r θπ===>,不合题意,舍去; 当9r =时,则2l =,则229l r θπ==<,符合题意. 故答案为:9cm.【点睛】本题考查了扇形弧长及面积公式的应用,考查了运算求解能力,属于基础题. 9.1080【分析】首先求出弧长,再根据扇形面积公式计算可得;【详解】解:依题意30r =cm , 2.4lr=所以 2.472l r ==cm ,所以117230108022S lr ==⨯⨯=2cm ;故答案为:108010 【分析】求出,O A O B ''的长度,确定AO B ∠'的大小,再由弧长公式求得A,B 两地的东西方向的距离. 【详解】如图示,设O '为北纬30°圈的圆心,地球球心为O则60AOO '∠= ,故AO '=,即北纬30°R由题意可知2π1203AO B '∠==故点A 和B 两点东西方向的距离即为北纬30°圈上的AB 的长故AB 的长为2π3R =11.(1)132********︒=︒⨯+︒,第三象限; (2)()315360145-︒=︒⨯-+︒,第一象限; (3)1500360460︒=︒⨯+︒,第一象限; (4)()16103605190-︒=︒⨯-+︒,第三象限.【分析】先将各个角化为指定形式,根据通过终边相同的角的概念判断出角所在象限.【详解】(1)132********︒=︒⨯+︒,因为240︒的角终边在第三象限,所以1320︒是第三象限角; (2)()315360145-︒=︒⨯-+︒,因为45︒的角终边在第一象限,所以315-︒是第一象限角; (3)1500360460︒=︒⨯+︒,因为60︒的角终边在第一象限,所以1500︒是第一象限角; (4)()16103605190-︒=︒⨯-+︒,因为190︒的终边在第三象限,所以1610-︒是第三象限角. 12.(1)254218α=⨯π+π; (2)4718θπ=-.【分析】(1)先把角度数化成弧度数,再表示成符合要求的形式. (2)由(1)可得252,(Z)18k k θππ=+∈,再按给定范围求出k 值作答. (1)依题意,169251690169081801818παπππ=︒=⨯==+ 所以254218α=⨯π+π. (2)由(1)知252,(Z)18k k θππ=+∈,而(4,2)θππ∈--,则25422,()18k k Z ππππ-<+<-∈,解得2k =- 所以254741818θ=-π+π=-π. 13.80π【分析】先求出弧长,再利用扇形的面积公式直接求解. 【详解】设扇形弧长为l ,因为圆心角272721805ππ︒⨯==rad 所以扇形弧长2·2085l r παπ⨯=== 于是,扇形的面积S =12l ·r =12×8π×20=80π. 14.(1)103π;(2)12;(3)=10,=2l α 【分析】(1)根据扇形的弧长公式进行计算即可.(2)根据扇形的周长公式以及面积公式建立方程关系进行求解 (3)根据扇形的扇形公式结合基本不等式的应用进行求解即可. 【详解】(1)α=60°=rad ,∴l =α·R =×10=(cm).(2)由题意得解得 (舍去),故扇形圆心角为. (3)由已知得,l +2R =20.所以S =lR = (20-2R )R =10R -R 2=-(R -5)2+25,所以当R =5时,则S 取得最大值25 此时l =10,α=2.【点睛】本题主要考查扇形的弧长公式和面积公式的应用,根据相应的弧长公式和面积公式建立方程关系是解决本题的关键.15.当扇形的圆心角为2rad 时,则扇形的面积最大.【解析】设扇形的半径为r ,弧长为l ,利用周长公式,求得2l c r =-,代入扇形的面积公式,结合二次函数的性质,即可求解.【详解】设扇形的半径为r ,弧长为l 则2l r c +=,即2(0)2c l c r r =-<<由扇形的面积公式12S lr =,代入可得222111(2)()22416c S c r r r cr r c =-=-+=--+当4c r =时,则即22cl c r =-=时,则面积S 取得最小值此时2l rad r α==,面积的最小值为2c 16.【点睛】本题主要考查了扇形的周长,弧长公式,以及扇形的面积公式的应用,其中解答中熟记扇形的弧长公式和面积公式,准确运算是解答的关键,着重考查了推理与运算能力,属于基础题. 16.(1)2πm【分析】(1)过点B 作一楼地面的垂线,垂足为B ',则B '落在圆柱底面圆上,结合题意计算出1BO M ∠的大小,再利用扇形的弧长公式即可得出结果.(2)建立空间直角坐标系,求出异面直线AB 和CD 的方向向量,再由异面直线所成角的向量公式代入即可得出答案. (1)如图,过点B 作一楼地面的垂线,垂足为B ',则B '落在圆柱底面圆上 连接B A ',则B A '即为BA 在圆柱下底面上的射影 故BAB '∠即为电梯Ⅰ与楼面所成的角,所以1sin 3BAB '∠=.因为4BB AM '==,所以AB '=在AOB '中8OA OB ='=,所以AOB '是等腰直角三角形 连接1O ,B ,1O M ,则1π2BO M AOB '∠=∠= 因为BC CM =,所以BC 的长为π82π4⨯= 故此顾客在二楼地面上步行的路程为2π m . (2)连接2OO ,由(1)可知所在直线两两互相垂直.以O 为原点OB ',OA 和2OO 的方向分别为x ,y ,z 轴的正方向,建立空间直角坐标系,如图所示,则()8,0,4B ()0,8,0A 与()C 和()D -,所以()8,8,4AB =- ()4CD =-. 设异面直线AB 和CD 所成角为θ,则·42cos cos ,=9AB CD AB CD AB CDθ==故异面直线AB 和CD 17.(1)22(02)2x x x θ+=<<+; (2)当12x =时,则y 的值最大,最大值为94.【分析】(1)根据弧长公式和周长列方程得出θ关于x 的函数解析式;(2)根据面积公式求出y 关于x 的函数表达式,根据二次函数性质可得y 的最大值. (1)根据题意,弧BC 的长度为x θ米,弧AD 的长度2AD θ=米2(2)26x x θθ∴-++=∴22(02)2x x x θ+=<<+. (2)依据题意,可知2211222OAD OBC y S S x θθ=-=⨯-扇扇 化简得:22y x x =-++ 02x <<∴当12x =,则2max 1192224y ⎛⎫=-++= ⎪⎝⎭.∴当12x =时,则y 的值最大,且最大值为94.。
2020年人教A版高中数学必修第一册5.1 任意角及弧度制(解析版)
5.1 任意角及弧度制运用一 基础概念理解【例1】(2019·湖南高一期末)下列说法正确的是( ) A.小于90︒的角是锐角B.钝角是第二象限的角C.第二象限的角大于第一象限的角D.若角α与角β的终边相同,则,απβ=+∈k k Z 【答案】B【解析】A :负角不是锐角,比如“30-︒”的角,故错误; B :钝角范围是“90180α︒<<︒”,是第二象限的角,故正确; C :第二象限角取“91︒”,第一象限角取“361︒”,故错误; D :当角α与角β的终边相同,则2,k k Z απβ=+∈.故选:B. 【触类旁通】1.已知A ={第一象限角},B ={锐角},C ={小于90°的角},那么A ,B ,C 的关系是( ) A.B =A ∩C B.B ∪C =C C.A ⊆B ∩C D.A =B =C【答案】B【解析】∵A ={第一象限角}={α|k ⋅360∘<α<k ⋅360∘+90∘,k ∈Z};B ={锐角}={α|0∘<α<90∘};C ={小于90°的角}={α|α<90∘}.∴B ∪C ={小于90°的角}=C ,即B ⊂C ,且B ⊂A ,则B 不一定等于A ∩C ,A 不一定是C 的子集,三集合不一定相等, 由集合间的关系可得B ∪C =C .故选B .运用二 终边相同的角【例2】(1)如果α=−21∘,那么与终边相同的角可以表示为 A.{β|β=k ⋅360∘+21∘,k ∈Z } B.{β|β=k ⋅360∘−21∘,k ∈Z } C.{β|β=k ⋅180∘+21∘,k ∈Z }D.{β|β=k ⋅180∘−21∘,k ∈Z } (2)终边在直线y =-x 上的所有角的集合是( )A .{α|α=k ·360°+135°,k ∈Z}B .{α|α=k ·360°-45°,k ∈Z}C .{α|α=k ·180°+225°,k ∈Z}D .{α|α=k ·180°-45°,k ∈Z}(3)(2019春•南京期中)若角α=m•360°+60°,β=k•360°+120°,(m,k∈Z),则角α与β的终边的位置关系是()A.重合B.关于原点对称C.关于x轴对称D.关于y轴对称【答案】(1)B(2)D(3)D【解析】根据终边相同的角相差360∘的整数倍,故与角α有相同终边的角为k⋅360∘+α(k∈Z),所以α=−21∘,表示为k⋅360∘−21∘(k∈Z),故选B.(2)直线y=﹣x过原点,它是第二、四象限角的平分线所在的直线,故在0°~360°范围内终边在直线y=﹣x上的角有两个:135°,315°.因此,终边在直线y=﹣x上的角的集合S={α|α=135°+k•360°,k∈Z}∪{α|α=315°+k•360°,k∈Z}={α|α=135°+2k•180°,k∈Z}∪{α|α=135°+(2k+1)•180°,k∈Z}={α|α=135°+k•180°,k∈Z}.或者表示为S={α|α=k·180°-45°,k∈Z}.故选:D.(3)α的终边和60°的终边相同,β的终边与120°终边相同,∵180°﹣120°=60°∴角α与β的终边的位置关系是关于y轴对称,故选:D.【触类旁通】1.与角-1 560°终边相同的角的集合中,最小正角是________,最大负角是________.【答案】240°-120°【解析】根据终边相同的角相差360°的整数倍,故与﹣1560°终边相同的角可表示为:{α|α=k•360°﹣1560°,k∈Z}.则当k=4时,α=4×360°﹣1560°=﹣120°,此时为最大的负角.当k=5时,α=5×360°﹣1560°=240°,此时为最小的正角.故答案为:240°,﹣120°2.(2018春•武功县期中)下列各组角中,终边相同的角是()A.﹣398°,1042°B.﹣398°,142°C.﹣398°,38°D.142°,1042°【答案】A【解析】由题意,﹣398°=322°﹣2×360°,1042°=322°+2×360°,142°,38°;这四个角中,终边相同的角是﹣398°和1042°.故选:A.3.已知α=﹣30°,若α与β的终边关于直线x﹣y=0对称,则β=;若α与β的终边关于y轴对称,则β=;若α与β的终边关于x轴对称,则β=.【答案】见解析【解析】如图,设α=﹣30°所在终边为OA,则关于直线x﹣y=0对称的角β的终边为OB,终边在OB上的最小正角为120°,故β=120°+k•360°,k∈Z;关于y轴对称的角β的终边为OC,终边在OC上的最小正角为210°,故β=210°+k•360°,k∈Z;关于x轴对称的角β的终边为OD,终边在OD上的最小正角为30°,故β=30°+k•360°,k∈Z.故答案为:120°+k •360°,k ∈Z ;210°+k •360°,k ∈Z ;30°+k •360°,k ∈Z .运用三 角所在象限【例3】(1)(2019·湖南高一期末)179︒是() A .第一象限角B .第二象限角C .第三象限角D .第四象限角(2)(2019春•北碚区校级期中)已知α为第二象限角,则所在的象限是( ) A .第一或第二象限 B .第二或第三象限 C .第一或第三象限 D .第二或第四象限【答案】(1)B (2)C【解析】(1)1791801︒︒︒=-,所以179︒表示第二象限角,故选B . (2)∵α是第二象限角,∴k •360°+90°<α<k •360°+180°,k ∈Z , 则k •180°+45°<<k •180°+90°,k ∈Z ,令k =2n ,n ∈Z 有n •360°+45°<<n •360°+90°,n ∈Z ;在一象限;k =2n +1,n ∈z ,有n •360°+225°<<n •360°+270°,n ∈Z ;在三象限;故选:C .【触类旁通】1.(2018•徐汇区校级模拟)若α是第二象限的角,则的终边所在位置不可能是( ) A .第一象限 B .第二象限 C .第三象限D .笫象限【答案】C【解析】∵α是第二象限角,∴90°+k •360°<α<180°+k •360°,k ∈Z . 则30°+k •120°<<60°+k •120°,k ∈Z .当k =0时,30°<<60°,α为第一象限角;2α3α当k =1时,150°<<180°,α为第二象限角;当k =2时,270°<<300°,α为第四象限角.由上可知,的终边所在位置不可能是第三象限角.故选:C .2.(2019秋•宜城市校级月考)如果α是第三象限角,则是( )A .第一象限角B .第一或第二象限角C .第一或第三象限角D .第二或第四象限角【答案】C【解析】∵α是第三象限角,∴180°+k •360°<α<270°+k •360°,k ∈Z , ∴﹣135°﹣k •180°<﹣<﹣90°﹣k •180°,∴﹣是第一或第三象限角.故选:C .运用四 弧度制的理解【例4】(2019春•历城区校级月考)下列命题中,真命题的是( ) A .1弧度是一度的圆心角所对的弧 B .1弧度是长度为半径的弧 C .1弧度是一度的弧与一度的角之和D .1弧度是长度等于半径长的弧所对的圆心角的大小 【答案】D【解析】根据弧度的定义知:长度等于半径长的弧所对的圆心角叫做1弧度的角. 故选:D .2α-【触类旁通】1.(2019春•静安区期末)下列选项中,错误的是( ) A .“度”与“弧度”是度量角的两种不同的度量单位B .一度的角是周角的,一弧度的角是周角的 C .根据弧度的定义,180度一定等于π弧度D .不论是用角度制还是弧度制度量角,它们与圆的半径长短有关 【答案】D【解析】“度”与“弧度”是度量角的两种不同的度量单位,判断正确;一度的角是周角的,一弧度的角是周角的,满足两种角的度量定义,正确; 根据弧度的定义,180度一定等于π弧度,满足两种角的度量关系,正确; 不论是用角度制还是弧度制度量角,它们与圆的半径长短有关,不正确;故选:D .运用五 角度与弧度的转化【例5-1】(2019春•微山县校级月考)将下列弧度转化为角度:角度化为弧度: (1)12π= ; (2)136π= ;(3)512π-= . (4)36︒= rad ;(5)105-︒= rad . 【答案】:15°,390°,﹣75°,.【解析】∵π=180°, ∴;;;36°=36×;.【例5-2】(2019·榆林市第二中学高一期末)下列各角与3π终边相同的角是( ) A .43π B .53π C .43π-D .53π-【答案】D 【解析】与3π终边相同的角可表示为()23k k Z πβπ=+∈,当1k =-时,53πβ=- 136012π136012π故选D【触类旁通】1.1 920°的角化为弧度数为( )A.163B.323C.163π D.323π【答案】D【解析】∵1°=π180rad ,∴1 920°=1 920×π180rad =323π rad.2.(2019·上海市三林中学高一月考)与角136π终边相同的最小正角大小是_________ 【答案】6π 【解析】所有与角136π终边相同的角是α =132,6k k Z ππ+∈ ,令1k =- 即得到最小的正角,即6π。
青岛二中高一数学同步专练(人教A版2019必修1)-第八讲 函数的最值
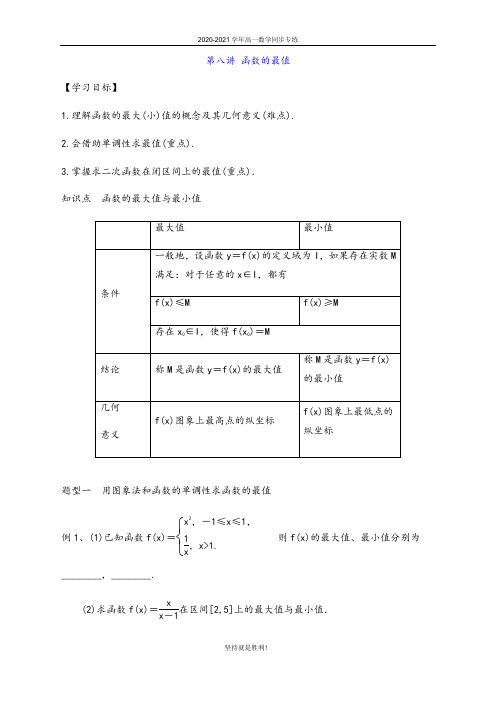
第八讲 函数的最值【学习目标】1.理解函数的最大(小)值的概念及其几何意义(难点).2.会借助单调性求最值(重点).3.掌握求二次函数在闭区间上的最值(重点). 知识点 函数的最大值与最小值题型一 用图象法和函数的单调性求函数的最值例1、(1)已知函数f(x)=⎩⎨⎧x 2,-1≤x≤1,1x ,x>1.则f(x)的最大值、最小值分别为________,________.(2)求函数f(x)=xx -1在区间[2,5]上的最大值与最小值.(1)解析 作出函数f(x)的图象(如图).由图象可知,当x =±1时,f(x)取最大值为f(±1)=1.当x =0时,f(x)取最小值f(0)=0,故f(x)的最大值为1,最小值为0. 答案 1 0(2)解 任取2≤x 1<x 2≤5, 则f(x 1)=x 1x 1-1,f(x 2)=x 2x 2-1, f(x 2)-f(x 1)=x 2x 2-1-x 1x 1-1=x 1-x 2(x 2-1)(x 1-1), ∵2≤x 1<x 2≤5,∴x 1-x 2<0,x 2-1>0,x 1-1>0, ∴f(x 2)-f(x 1)<0,∴f(x 2)<f(x 1). ∴f(x)=xx -1在区间[2,5]上是单调减函数. ∴f(x)max =f(2)=22-1=2,f(x)min =f(5)=55-1=54.规律方法1.图象法求最值的步骤2.利用函数的单调性求最值的两个易错点(1)求函数的最值时应首先求函数的定义域,在定义域内进行.(2)求函数在闭区间上的最值,易出现的失误是不判断函数的单调性而直接将两端点值代入,认为是函数的最值. 【训练1】 已知函数f(x)=x +1x.(1)求证f(x)在[1,+∞)上是增函数; (2)求f(x)在[1,4]上的最大值及最小值. (1)证明 设1≤x 1<x 2,则f(x 1)-f(x 2)=(x 1+1x 1)-(x 2+1x 2)=(x 1-x 2)·x 1x 2-1x 1x 2.∵1≤x 1<x 2,∴x 1-x 2<0,x 1x 2>1, ∴x 1x 2-1>0,∴f(x 1)-f(x 2)<0,即f(x 1)<f(x 2). ∴f(x)在[1,+∞)上是增函数.(2)解 由(1)可知,f(x)在[1,4]上递增, ∴当x =1时, f(x)min =f(1)=2, 当x =4时, f(x)max =f(4)=174. 综上所述,f(x)在[1,4]上的最大值是174,最小值是2.题型二 函数最值的实际应用例2、某公司生产一种电子仪器的固定成本为20 000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)=⎩⎨⎧400x -12x 2(0≤x≤400),80 000 (x >400).其中x 是仪器的月产量.(1)将利润表示为月产量的函数f(x);(2)当月产量为何值时,公司所获利润最大?最大利润为多少元?(总收益=总成本+利润)解 (1)设月产量为x 台,则总成本为20 000+100x ,从而f(x)=⎩⎨⎧-12x 2+300x -20 000(0≤x≤400),60 000-100x (x >400).(2)当0≤x≤400时,f(x)=-12(x -300)2+25 000;∴当x =300时,f(x)max =25 000,当x >400时,f(x)=60 000-100x 是减函数, f(x)<60 000-100×400<25 000. ∴当x =300时 ,f(x)max =25 000.即每月生产300台仪器时利润最大,最大利润为25 000元. 规律方法 求解实际问题的四个步骤(1)读题:分为读懂和深刻理解两个层次,把“问题情景”译为数学语言,找出问题的主要关系(目标与条件的关系).(2)建模:把问题中的关系转化成函数关系,建立函数解析式,把实际问题转化成函数问题.(3)求解:选择合适的数学方法求解函数.(4)评价:对结果进行验证或评估,对错误加以改正,最后将结果应用于现实,作出解释或预测.特别提醒:求解实际问题的步骤也可认为分成“设元——列式——求解——作答”四个步骤.【训练2】某水厂蓄水池有水450吨,水厂每小时向蓄水池注水80吨,同时蓄水池又向居民小区供水,t小时内供水量为8020t吨.现在开始向池中注水并同时向居民供水,多少小时后蓄水池中水量最少?解设t小时后,池中水量为y吨,则y=450+80t-8020t=4(20t-10)2+50,当20t=10,即t=5时,y=50,min所以5小时后蓄水池中水量最少,最少为50吨.题型三二次函数的最值【探究1】(1)求函数y=x2-2x+2的单调区间.(2)求函数y=-x2-2x+2的单调区间.解(1)函数y=x2-2x+2是开口向上,对称轴为x=1的抛物线,故其单减区间是(-∞,1),单增区间是(1,+∞).(2)函数y=-x2-2x+2的图象是开口向下,对称轴为x=-1的抛物线,故其单减区间是(-1,+∞),单增区间是(-∞,-1).【探究2】函数f(x)=x2-2x+2在区间[-1,0],[-1,2],[2,3]上的最大值和最小值分别是什么?解函数f(x)=x2-2x+2的图象开口向上,对称轴为x=1,(1)因为f(x)在区间[-1,0]上单调递减,所以f(x)在区间[-1,0]上的最大值为f(-1)=5,最小值为f(0)=2;(2)因为f(x)在区间[-1,1]上单调递减,在[1,2]上单调递增,则f(x)在区间[-1,2]上的最小值为f(1)=1,又因为f(-1)=5,f(2)=2,f(-1)>f(2),所以f(x)在区间[-1,2]上的最大值为f(-1)=5.(3)因为f(x)在区间[2,3]上单调递增,所以f(x)在区间[2,3]上的最小值为f(2)=2,最大值为f(3)=5.【探究3】 已知函数f(x)=x 2-ax +1,(1)求f(x)在[0,1]上的最大值;(2)当a =1时,求f(x)在闭区间[t ,t +1](t ∈R)上的最小值. 解 (1)因为函数f(x)=x 2-ax +1的图象开口向上,其对称轴为x =a2,所以区间[0,1]的哪一个端点离对称轴远,则在哪个端点取到最大值, 当a 2≤12,即a≤1时,f(x)的最大值为f(1)=2-a ; 当a 2>12,即a>1时,f(x)的最大值为f(0)=1. (2)当a =1时,f(x)=x 2-x +1,其图象的对称轴为x =12.①当t≥12时,f(x)在[t ,t +1]上是增函数,∴f(x)min =f(t)=t 2-t +1;②当t +1≤12,即t≤-12时,f(x)在上是减函数,∴f(x)min =f(t +1)=t 2+t +1;③当t<12<t +1,即-12<t<12时,函数f(x)在⎣⎢⎡⎦⎥⎤t ,12上单调递减,在⎣⎢⎡⎦⎥⎤12,t +1上单调递增,所以f(x)min =f⎝⎛⎭⎪⎫12=34.规律方法含参数的二次函数最值问题的解法解决含参数的二次函数的最值问题,首先将二次函数化为y=a(x+h)2+k的形式,再依a的符号确定抛物线开口的方向,依对称轴x=-h得出顶点的位置,再根据x的定义区间结合大致图象确定最大或最小值.对于含参数的二次函数的最值问题,一般有如下几种类型:(1)区间固定,对称轴变动(含参数),求最值;(2)对称轴固定,区间变动(含参数),求最值;(3)区间固定,最值也固定,对称轴变动,求参数.通常都是根据区间端点和对称轴的相对位置进行分类讨论.课堂小结1.函数的最值与值域、单调性之间的联系(1)对一个函数来说,其值域是确定的,但它不一定有最值,如函数y=1x.如果有最值,则最值一定是值域中的一个元素.(2)若函数f(x)在闭区间[a,b]上单调,则f(x)的最值必在区间端点处取得,即最大值是f(a)或f(b),最小值是f(b)或f(a).2.二次函数在闭区间上的最值探求二次函数在给定区间上的最值问题,一般要先作出y=f(x)的草图,然后根据图象的增减性进行研究.特别要注意二次函数的对称轴与所给区间的位置关系,它是求解二次函数在已知区间上最值问题的主要依据,并且最大(小)值不一定在顶点处取得.。
新高考高中数学必修一-任意角和弧度制同步测试题(含解析)

人教A 版(2019)必修第一册 5.1 任意角和弧度制一、单选题1.已知第二象限角α的终边上一点()sin ,tan P ββ,则角β的终边在 A .第一象限 B .第二象限C .第三象限D .第四象限2.“角A 小于2π”是“角A 是第一象限角”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件3.下列选项中,满足αβ<的是( ) A .1α=,2β=︒ B .1α=,60β=-︒ C .225α=︒,4β= D .180α=︒,πβ=4.下列各组的两个角中,终边不相同的一组角是( ) A .-56°与664° B .800°与-1360° C .150°与630° D .-150°与930°5.角α和β满足关系:2()k k αππβ=+-∈Z ,则角α与β的终边( ) A .关于x 轴对称 B .关于y 轴对称C .关于原点对称D .以上答案都不对6.将一条闭合曲线放在两条平行线之间,无论这条闭合曲线如何运动,只要它与两平行线中的一条直线只有一个交点,就必与另一条直线也只有一个交点,则称此闭合曲线为等宽曲线,这两条平行直线间的距离叫等宽曲线的宽比.如圆所示就是等宽曲线.其宽就是圆的直径.如图所示是分别以A 、B 、C 为圆心画的三段圆弧组成的闭合曲线Γ(又称莱洛三角形),下列关于曲线Γ的描述中,正确的有( ) (1)曲线Γ不是等宽曲线;(2)曲线Γ是等宽曲线且宽为线段AB 的长; (3)曲线Γ是等宽曲线且宽为弧AB 的长; (4)在曲线Γ和圆的宽相等,则它们的周长相等; (5)若曲线Γ和圆的宽相等,则它们的面积相等.A .1个B .2个C .3个D .4个7.半径为1cm ,圆心角为120︒的扇形的弧长为( ) A .1cm 3B .2cm 3C .cm 3πD .2cm 3π8.已知()1,4k k k πθααπ⎧⎫∈=+-⋅∈⎨⎬⎩⎭Z ,则角θ的终边所在的象限是( )A .第一象限B .第二象限C .第一或第二象限D .第三或第四象限9.如图所示的时钟显示的时刻为4:30,此时时针与分针的夹角为()0ααπ<≤.若一个半径为1的扇形的圆心角为α,则该扇形的面积为( )A .2πB .4π C .8π D .16π10.已知扇形的圆心角为120°,半径为3,则扇形面积为( ) A .2π B .3πC .154π D .52π11.下列说法:①终边相同的角必相等;①锐角必是第一象限角;①小于90︒的角是锐角;①第二象限的角必大于第一象限的角;①若角α的终边经过点(0,3)M -,则角α是第三或第四象限角,其中错误的是( ) A .①①①B .①①①C .①①①①D .①①①①{}|4590,B k k Z ββ==︒+⋅︒∈,则( )A .AB =∅ B .B①AC .A①BD .A B =二、填空题13.已知本次数学考试总时间为2小时,你在奋笔疾书沙沙答题,分针滴答滴答忙着转圈.现在经过了1小时,则此时分针转过的角的弧度数是 _______.14.已知角2020α=-︒,则与α终边相同的最小正角是______.15.大于360-︒且终边与角75︒重合的负角是________.16.已知扇形的周长为16cm ,面积为162cm ,则扇形的圆心角α的弧度数为___________.三、解答题17.已知扇形的周长为20cm ,求扇形面积的最大值,并求此时圆心角的弧度数.18.一扇形的周长为20cm ,当扇形的圆心角α等于多少弧度时,这个扇形面积最大,并求此扇形的最大面积.19.用弧度制表示顶点在原点,始边重合于x 轴的非负半轴,终边落在阴影部分内的角的集合(包括边界,如图7-1-7所示).20.把下列各角化为2(02,)k k πααπ+<∈Z 的形式且指出它是第几象限角,并写出与它终边相同的角的集合. (1)463π-; (2)1485-︒;21.分别写出当角α在第四象限时,角2α的所在象限.参考答案:1.C根据第二象限横纵坐标的正负值判断得sin 0,tan 0,ββ<⎧⎨>⎩再判断角β的象限即可.【详解】因为点()sin ,tan P ββ在第二象限,所以有sin 0,tan 0,ββ<⎧⎨>⎩所以β是第三象限角.故选:C本题考查各象限三角函数值的正负.属于基础题. 2.D利用特殊值法结合充分、必要条件的定义判断可得出结论. 【详解】若角A 小于2π,取4A π=-,此时,角A 不是第一象限角,即“角A 小于2π”⇒“角A 是第一象限角”;若角A 是第一象限角,取24A ππ=+,此时,2A π>,即“角A 小于2π”⇐/“角A 是第一象限角”. 因此,“角A 小于2π”是“角A 是第一象限角”的既不充分也不必要条件.故选:D. 3.C先判断出B ,D 不满足αβ<;然后利用角度制与弧度制的互化,判断出C 正确. 【详解】解:对于选项B ,有αβ>, 对于D ,有αβ=; 对于A ,因为1801()2π=︒>︒,所以满足αβ>, 对于C ,因为18044()225π=⨯︒>︒,满足αβ<.故选:C . 4.C利用终边相同的两个角符合的规律逐一判断各选项即可得解. 【详解】因终边相同的两个角总是相差360的整数倍,对于A ,664(56)7202360--==⋅,即角-56°与664°终边相同,A 不正确; 对于B ,800(1360)21606360--==⋅,即角800°与-1360°终边相同,B 不正确; 对于C ,6301504801360120-==⋅+,即角150°与630°终边不相同,C 正确; 对于D ,930(150)10803360--==⋅,即角-150°与930°终边相同,D 不正确, 所以角150°与630°终边不相同. 故选:C 5.B根据终边相同角的定义判断可得; 【详解】解:因为角α和β满足关系:2()k k αππβ=+-∈Z , 因为β与πβ-的终边关于y 轴对称, 而2()k k αππβ=+-∈Z 与πβ-的终边相同, 所以角α与β的终边关于y 轴对称 故选:B 6.B若曲线Γ和圆的宽相等,设曲线Γ的宽为1,则圆的半径为12,根据定义逐项判断即可得出结论. 【详解】若曲线Γ和圆的宽相等,设曲线Γ的宽为1,则圆的半径为12, (1)根据定义,可以得曲线Γ是等宽曲线,错误; (2)曲线Γ是等宽曲线且宽为线段AB 的长,正确; (3)根据(2)得(3)错误;(4)曲线Γ的周长为1326ππ⨯⨯=,圆的周长为122ππ⨯=,故它们的周长相等,正确; (5)正三角形的边长为1,则三角形对应的扇形面积为2166ππ⨯=,正三角形的面积1112S =⨯⨯,则一个弓形面积6S π=则整个区域的面积为3(62ππ= 而圆的面积为2124ππ⎛⎫= ⎪⎝⎭,不相等,故错误;综上,正确的有2个, 故选:B.本题主要考查新定义,理解“等宽曲线”得出等边三角形是解题的关键. 7.D利用扇形弧长公式直接计算即可. 【详解】圆心角120︒化为弧度为23π, 则弧长为221cm 33ππ⨯=. 故选:D.8.C利用终边相同的角的概念,对当k 是奇数和偶数进行分类讨论,即可得解. 【详解】由已知,()1,4k k k πθααπ⎧⎫∈=+-⋅∈⎨⎬⎩⎭Z ,当()2k m m =∈Z 时,24m πθπ=+,即角θ的终边在第一象限;当()21k m m =+∈Z 时,324m πθπ=+,即角θ的终边在第二象限. 所以角θ的终边在第一或第二象限. 故选:C 9.C求出α的值,利用扇形的面积公式可求得扇形的面积. 【详解】由图可知,1284παπ=⨯=,所以该扇形的面积212481S ππ=⨯⨯=.故选:C. 10.B把圆心角化为弧度,然后由面积公式计算. 【详解】 21203π︒=.2123323S ππ=⨯⨯=. 故选:B . 11.C①取特殊角:0︒与360︒进行判断;①根据锐角的范围直接判断; ①取负角进行否定; ①取特殊角进行否定; ①取特殊角进行否定. 【详解】①终边相同的角必相等错误,如0︒与360︒终边相同,但不相等; ①锐角的范围为(0,90)︒︒,必是第一象限角,正确; ①小于90︒的角是锐角错误,如负角;①第二象限的角必大于第一象限的角错误,如120︒是第二象限角,390︒是第一象限角; ①若角α的终边经过点(0,3)M -,则角α是终边在y 轴负半轴上的角,故①错误. 其中错误的是①①①①. 故选C .(1)要证明一个命题为真命题,需要严格的证明;要判断一个命题为假命题,举一个反例就可以了.(2)角的概念的辨析题中,通常可以取特殊角来否定结论. 12.D考虑A 中角的终边的位置,再考虑B 中角的终边的位置,从而可得两个集合的关系. 【详解】. 45180,k k Z α=︒+⋅︒∈ 表示终边在直线y x =上的角,135180,k k Z α=︒+⋅︒∈ 表示终边在直线y x =-上的角,而4590,k k Z β=︒+⋅︒∈ 表示终边在四条射线上的角,四条射线分别是射线,0;,0;,0;,0y x x y x x y x x y x x =≥=-≤=≤=-≥ , 它们构成直线y x =、直线y x =-,故A B =. 故选:D.本题考查终边相同的角,注意180k α⋅︒+的终边与α 的终边的关系是重合或互为反向延长线,而90k α⋅︒+的终边与α 的终边的关系是重合或互为反向延长线或相互垂直,本题属于中档题. 13.2π-先明确1小时是60分钟,得到分针转过的角度,再算出弧度数. 【详解】因为1小时是60分钟,分针正好转过一周360-, 所以转过的角的弧度数是2π-. 故答案为:2π-本题主要考查弧度制,还考查了理解辨析的能力,属于基础题. 14.140°先求出与α终边相同角的集合,再通过解不等式进行求解即可. 【详解】与2020α=-︒终边相同的角的集合为{}2020360,k k Z θθ=-︒+⋅︒∈, 令20203600k -︒+⋅︒>︒,解得10118k >,故当6k =时,140θ=︒满足条件. 故答案为:140° 15.285-︒根据终边相同的角的概念进行判断. 【详解】大于360-︒且终边与角75︒重合的负角是285-︒. 故答案为:285-︒本题考查终边相同的角,属于基础题. 16.2设扇形圆心角为α,半径为r ,列方程组求出α的值.【详解】解:由扇形的周长为16cm ,面积为216cm ,可设扇形圆心角为α,且(0,2)απ∈,半径为r , 则22161162r r r αα+=⎧⎪⎨⋅=⎪⎩, 解得24r α=⎧⎨=⎩所以2α=.故答案为:2.17.面积最大值为225cm ,此时圆心角弧度数为2设扇形的半径为R ,弧长为l ,依题意有220l R +=,利用扇形面积公式12S lR =扇形,利用基本不等式即可求得答案.【详解】解:设扇形的半径为R ,弧长为l ,则220l R +=.()()()210112021025222R R S lR R R R R -+⎡⎤==-⋅=-⋅=⎢⎥⎣⎦扇形(当且仅当5R =时取等号). S 扇形最大值为25,此时5R =,10l =.故扇形圆心角的弧度数2l Rα==. 所以扇形面积最大值为225cm ,此时圆心角弧度数为2.18.2α=弧度,最大面积225cm设扇形的半径为r ,得出弧长为202,010r r -<<,确定扇形面积函数式,利用二次函数的性质,求出面积最大时半径和弧长的值,即可得出结论【详解】设扇形的半径为r ,其周长为20,则扇形弧长为202r -,且2020,010r r ->∴<<, 扇形面积221(202)10(5)252S r r r r r =-=-+=--+, 当=5r ,1025α==时,S 取最大值为25, 所以圆心角为2弧度时,扇形面积最大为25.本题考查扇形面积、弧长公式的应用、以及二次函数的最值,合理设元是解题的关键,考查计算求解能力,属于基础题.19.(1)522,612k k k ππαπαπ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ; (2)3322,44k k k ππαπαπ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ; (3),62k k k ππαπαπ⎧⎫+≤≤+∈⎨⎬⎩⎭Z .将角度化成弧度,结合任意角概念表示出来即可.【详解】对图(1),可看作5,612ππ⎡⎤-⎢⎥⎣⎦范围内的角,结合任意角概念,可表示为522,612k k k ππαπαπ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ; 对图(2),可看作33,44ππ⎡⎤-⎢⎥⎣⎦范围内的角,结合任意角概念,可表示为3322,44k k k ππαπαπ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ; 对图(3),可看作由,62ππ⎡⎤⎢⎥⎣⎦的范围角,经过旋转半圈整数倍形成的角,故可表示为,62k k k ππαπαπ⎧⎫+≤≤+∈⎨⎬⎩⎭Z .20.(1)第二象限角,终边相同的角的集合为22,3k k πββπ⎧⎫=+∈⎨⎬⎩⎭Z ∣;(2)第四象限角.终边相同的角的集合为72,4k k πββπ⎧⎫=+∈⎨⎬⎩⎭Z ∣;(3)第四象限角,终边相同的角的集合为{2(820),}k k ββππ=+-∈Z ∣.利用与角α终边相同的角的集合的结论,即可得出结果.【详解】(1)4628233πππ-=-⨯+,它是第二象限角,终边相同的角的集合为22,3k k πββπ⎧⎫=+∈⎨⎬⎩⎭Z ∣. (2)714855*********ππ-︒=-⨯︒+︒=-⨯+,它是第四象限角.终边相同的角的集合为72,4k k πββπ⎧⎫=+∈⎨⎬⎩⎭Z ∣. (3)2042(820)ππ-=-⨯+-,而382022πππ<-<. 所以20-是第四象限角,终边相同的角的集合为{2(820),}k k ββππ=+-∈Z ∣. 21.答案见解析由终边相同的角和象限角的定义进行判断即可【详解】(1)当角α在第一象限时,即22,2k k k Z ππαπ<<+∈,则,24k k k Z απππ<<+∈, 当2k n =(n Z ∈)时,22,24n n n Z απππ<<+∈,则2α为第一象限的角, 当21k n =+(n Z ∈)时,(21)(21),24n n n Z απππ+<<++∈,即522,24n n n Z αππππ+<<+∈,则角2α为第三象限的角, 综上,角2α在第一或第三象限; (2)当角α在第二象限时,即22,2k k k απ+π<<π+π∈Z ,则,422k k k αππ+π<<+π∈Z , 当2k n =(n Z ∈)时,22,422n n n Z παπππ+<<+∈,则 2α为第一象限的角,当21k n =+(n Z ∈)时,(21)(21),422n n n Z παπππ++<<++∈,即5322,422n n n Z παπππ+<<+∈,则 2α为第三象限的角, 综上,角2α在第一或第三象限; (3)当角α在第三象限时,即322,2k k k Z πππαπ+<<+∈,则3,224k k k Z παπππ+<<+∈, 当2k n =(n Z ∈)时,322,224n n n Z παπππ+<<+∈,则2α为第二象限的角, 当21k n =+(n Z ∈)时,3(21)(21),224n n n Z παπππ++<<++∈,即3722,224n n n Z παπππ+<<+∈,则2α为第四象限的角, 综上,角2α在第二或第四象限; (4)当角α在第四象限时,即3222,2k k k Z ππαππ+<<+∈,则3,42k k k Z παπππ+<<+∈, 当2k n =(n Z ∈)时,322,42n n n Z παπππ+<<+∈,则2α为第二象限的角, 当21k n =+(n Z ∈)时,3(21)(21),42n n n Z παπππ++<<++∈,即 7222,42n n n Z παπππ+<<+∈,则2α在第二或第四象限, 综上,角2α在第二或第四象限。
2020-2021学年高一数学课时同步练习第五章第1节任意角和弧度制

第五章 三角函数 第1节 任意角和弧度制一、基础巩固1.(2020·南昌县莲塘第二中学期末)下面与角233π终边相同的角是( ) A .43π B .3π C .53π D .23π 【答案】C 【解析】解:因为235633πππ=+.所以233π与53π的终边相同.2.(2020·山东省五莲县第一中学月考)300-化为弧度是( ) A .43π-B .53π-C .23π-D .56π-【答案】B 【解析】300530023603ππ-=-⨯=-3.(2020·辽宁大连·高一期末)若42ππα<<,则点()cos sin ,sin tan P αααα--位于( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】C 【解析】由42ππα<<知:cos sin 1tan ααα<<<∴cos sin 0αα-<,sin tan 0αα-< 故,P 位于第三象限4.(2020·山西平城·大同一中高一月考)已知扇形的周长为12cm ,圆心角为4rad ,则此扇形的面积为( ). A .8cm 2 B .10cm 2C .12cm 2D .14cm 2【答案】A【解析】解:设扇形的半径为r cm , ∵扇形的周长为12cm ,圆心角为4rad , ∴2412r r +=,得2r,∴此扇形的面积214282S =⨯⨯=(cm 2)5.(2019·新疆高一期末)若sin cos 0αα⋅>,则角α的终边在( ) A .第一、二象限 B .第一、三象限 C .第一、四象限 D .第二、四象限【答案】B【解析】由sin cos 0αα⋅>可得sin α>0,cos α>0⎧⎨⎩ 或sin α<0,cos α<0⎧⎨⎩当sin α>0cos α>0⎧⎨⎩时,角α的终边位于第一象限,当sin α<0cos α<0⎧⎨⎩时,角α的终边位于第三象限. 6.(2020·河南商丘·月考(理))中央电视台每天晚上的“焦点访谈”是时事、政治性较强的一个节目,其播出时间是在晚上看电视节目人数最多的“黄金时间”,即晚上7点与8点之间的一个时刻开始播出,这一时刻是时针与分针重合的时刻,以高度显示“聚焦”之意,比喻时事、政治的“焦点”,则这个时刻大约是( ) A .7点36分 B .7点38分C .7点39分D .7点40分【答案】B【解析】设7点t 分()060t <<时针OA 与分针OB 重合. 在7点时,时针OC 与分针OD 所夹的角为210︒, 时针每分钟转0.5︒,分针每分钟转6︒,则分针从OD 到达OB 需旋转6t ︒,时针从OC 到达OA 需旋转0.5t ︒, 于是60.5210t t ︒=︒+︒,解得2383811t =≈(分)7.(2020·安徽省泗县第一中学开学考试)已知角α终边过点P (1,-1),则tan α的值为( ) A .1B .-1C .22D .-22【答案】B【解析】因为角α终边过点P (1,-1), 所以由正切函数定义知1tan 1α-==-1. 8.(2020·天水市第一中学期中)如果1弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( ) A .B .sin0.5C .2sin0.5D .tan0.5【答案】A【解析】设圆的半径为r ,则有sin0.51r ⋅=,可得1sin 0.5r =,所以这个圆心角所对的弧长为11sin 0.5r ⋅=,故选A .9.(2020·广东高一期末)下列说法正确的是( ) A .终边相同的角一定相等 B .831-︒是第二象限角C .若角α,β的终边关于x 轴对称,则360αβ+=︒D .若扇形的面积为35π,半径为2,则扇形的圆心角为310π 【答案】D【解析】A :1,361︒︒两个角的终边相同,但是这两个角不相等,故本说法错误;B :8313360249︒︒-︒=-⨯+,而180249270︒︒︒<<,所以831-︒是第三象限角,故本说法错误;C :当1,1αβ︒︒==-时,两个角的终边关于x 轴对称,而0360αβ+=︒≠︒,故本说法错误;D :设扇形的弧长为l ,因为扇形的面积为35π,半径为2,所以有3132525l l ππ=⨯⇒=,因此扇形的圆心角为3210l π=. 10.(2020·湖北黄冈·高一月考)“圆材埋壁”是《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,学会一寸,锯道长一尺,问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知道大小,用锯取锯它,锯口深一寸,锯道长一尺,问这块圆柱形木材的直径是多少?现有圆柱形木材一部分埋在墙壁中,截面如图所示,已知弦1AB =尺,弓形高1CD =寸,则阴影部分面积约为(注: 3.14π≈,5sin22.513︒≈,1尺=10寸)()A.6.33平方寸B.6.35平方寸C.6.37平方寸D.6.39平方寸【答案】A【解析】连接OC,设半径为r,5AD=寸,则1OD r=-在直角三角形OAD中,222OA AD OD=+即()22251r r=+-,解得13r=则5sin13AOC∠=,所以22.5AOC∠=则222.545AOB∠=⨯=所以扇形OAB的面积21451316966.333608Sππ⨯⨯===三角形OAB的面积211012602S=⨯⨯=所以阴影部分面积为1266.3360 6.33S S-=-=11.(2020·安徽高三月考(文))达芬奇的经典之作《蒙娜丽莎》举世闻名,画中女子神秘的微笑,数百年来让无数观赏者入迷,现将画中女子的嘴唇近似的看作一个圆弧,设嘴角A、B间的圆弧长为l、嘴角间的距离为d、圆弧所对的圆心角为θ(θ为弧度角),则l、d和θ所满足的恒等关系为()A.sin2=dlθθB.2sin2=dlθθC.cos2=dlθθD.2cos2=dlθθ【答案】B【解析】设该圆弧所对应的圆的半径为r ,则2sin2r d θ=,⋅=r l θ,两式相除得2sin2=dlθθ 12.(2020·永州市第四中学高一月考)点P 从(1,0)点出发,沿单位圆221x y +=逆时针方向运动π3弧长到达Q 点,则Q 点坐标为( )A .13,2⎛⎫ ⎪ ⎪⎝⎭B .31,2⎛⎫-- ⎪ ⎪⎝⎭C .13,2⎛⎫-- ⎪ ⎪⎝⎭D .3,21⎛⎫- ⎪ ⎪⎝⎭【答案】A【解析】由题意可知1r =, 根据三角函数的定义可知1cos32x r π==,3sin 3y r π==, 所以点Q 的坐标是13,22⎛⎫⎪ ⎪⎝⎭.13.(2020·广东梅州·高三其他(理))在很多地铁的车厢里,顶部的扶手是一根漂亮的弯管,如下图所示.将弯管形状近似地看成是圆弧,已知弯管向外的最大突出(图中CD )有15cm ,跨接了6个坐位的宽度(AB ),每个座位宽度为43cm ,估计弯管的长度,下面的结果中最接近真实值的是( )A .250cmB .260cmC .295cmD .305cm【答案】B【解析】如图所示,AB 为弯管,AB 为6个座位的宽度,则643258AB cm =⨯=15CD cm =设弧AB 所在圆的半径为r ,则222()r r CD AC =-+22(15)129r =-+解得562r cm ≈129sin 0.23562AOD ∠=≈ 可以近似地认为sin x x ≈,即0.23AOD ∠≈ 于是0.46AOB ∠≈,AB 长5620.46258.5≈⨯≈所以260cm 是最接近的,其中选项A 的长度比AB 还小,不可能, 因此只能选B ,260或者由cos 0.97x ≈,sin 20.4526x x π≈⇒<所以弧长5622946π<⨯≈.14.(2020·河南项城市第三高级中学高一月考)设2α是第一象限角,且cos cos αα=-,则α是第( )象限角 A .一 B .二C .三D .四【答案】B【解析】∵2α是第一象限角,∴360903602k k α︒<<︒+︒,k Z ∈, ∴720180720k k α︒<<︒+︒,k Z ∈,∴α为第一象限角或第二象限角或终边在y 轴正半轴上的轴线角,∵cos cos αα=-,∴cos 0α<,∴α是第二象限角.15.(2020·上海高三专题练习)如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M 和N 是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周,点M ,N 在大圆内所绘出的图形大致是( )A .B .C .D .【答案】A【解析】如图所示:由题意可知,小圆1O 总与大圆O 相内切,且小圆1O 总经过大圆的圆心O , 设某时刻两圆相切于点A ,此时动点M 所处的位置为点M ', 则大圆圆弧MA 与小圆M 转过的圆弧相等,以切点A 在如图上运动为例,记直线OM 与此时小圆1O 的交点为1M , 记0,2AOM πθ⎛⎫∠=∈ ⎪⎝⎭,则1111OM O M OO θ∠=∠=, 所以111111M O A M OO OM O ∠=∠+∠2θ=,所以大圆圆弧MA 的长为11l θθ=⨯=,小圆圆弧1AM 的长为2122l θθ=⨯=, 所以12l l =,所以小圆的圆弧1AM 与圆弧AM '的长相等,所以点1M 与点M '重合,即动点M 在线段MO 上运动, 同理可知,此时点N 在与MO 垂直的线段上运动,点A 在其它位置类似可得,M 、N 的轨迹为互相垂直的线段. 观察四个选项可知,只有选项A 符合.16.(多选题)(2020·全国高一课时练习)下列与412︒角的终边相同的角是( ) A .52︒ B .778︒ C .308-︒ D .1132︒【答案】ACD【解析】因为41236052=︒︒+︒,所以与412︒角的终边相同角为36052,k k Z β=⨯︒+︒∈, 当1k =-时,308β=-︒, 当0k =时,52β=︒, 当2k =时,772β=︒, 当3k =时,1132β=︒, 当4k =时,1492β=︒, 综上,选项A 、C 、D 正确.17.(多选题)已知α是第三象限角,则2α可能是( ) A .第一象限角 B .第二象限角C .第三象限角D .第四象限角【答案】BD【解析】因为α是第三象限角,所以3222k k πππαπ+<<+,k Z ∈, 3224k k παπππ∴+<<+,k Z ∈, 当k 为偶数时,2α是第二象限角;当k 为奇数时,2α是第四象限角 18.(多选题)(2019·全国高一课时练习)(多选)下列说法正确的是( ) A .“度”与“弧度”是度量角的两种不同的度量单位 B .1的角是周角的1360,1rad的角是周角的12π C .1rad 的角比1的角要大D .用弧度制度量角时,角的大小与圆的半径有关【答案】ABC【解析】由题意,对于A 中,“度”与“弧度”是度量角的两种不同的度量单位,所以是正确的; 对于B 中,周角为360,所以1的角是周角的1360,周角为2π弧度,所以1rad 的角是周角的12π是正确的;对于C 中,根据弧度制与角度制的互化,可得1801rad 1π=>,所以是正确;对于D 中,用弧度制度量角时,角的大小与圆的半径无关的,所以D 项是错误的. 19.(多选题)(2020·重庆高一月考)设α是第三象限角,则2α所在象限是( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】BD 【解析】α是第三象限角,360180360270k k α∴⋅︒+︒<<⋅︒+︒,k Z ∈,则180901801352k k α⋅︒+︒<<⋅︒+︒,k Z ∈,令2k n =,n Z ∈ 有360903601352n n α⋅︒+︒<<⋅︒+︒,n Z ∈;在二象限;21k n =+,n z ∈,有3602703603152n n α⋅︒+︒<<⋅︒+︒,n Z ∈;在四象限;二、拓展提升1.(2020·浙江课时练习)若点(2,3)(0)P m m m -<在角α的终边上,求sin ,cos ,tan ααα的值. 【解析】由题意,知点(2,3)(0)P m m m -<在第二象限,且r =.故3sinm r α-=== 2cosm r α===33tan 22m m α-==-. 2.(2020·全国高一课时练习)已知如图.(1)写出终边落在射线OA 、OB 上的角的集合; (2)写出终边落在阴影部分(包括边界)的角的集合.【解析】(1)终边落在射线OA 上的角的集合是{}210360,k k Z αα=+⋅∈, 终边落在射线OB 上的角的集合{}300360,k k Z αα=+⋅∈;(2)终边落在阴影部分(含边界)的角的集合是{}210360300360,k k k Z αα+⋅≤≤+⋅∈.3.(2020·全国高一课时练习)写出终边在直线3y x =上的角的集合. 【解析】直线33y x =的倾斜角为6πα=,所以终边在直线33y x =上的角为=2,6k k Z πβπ+∈或7=2,6k k Z πβπ+∈, =2(21),66k k k Z ππβπππ++=++∈,综合得终边在直线33y x=上的角为=,6k k Z πβπ+∈, 所以终边在直线33y x =上的角的集合为{|=,}6k k Z πββπ+∈.4.(2020·南昌县莲塘第二中学期末)已知扇形的圆心角所对的弦长为2,圆心角为2弧度. (1)求这个圆心角所对的弧长; (2)求这个扇形的面积.【解析】∵扇形的圆心角所对的弦长为2,圆心角α=2弧度,∴扇形半径为1sin1r =. (1)这个圆心角所对的弧长为122sin1sin1l r α==⨯=. (2)扇形面积为21121122sin1sin1sin 1S lr ==⨯⨯=.。
山东省青岛市第二高级中学高一数学理模拟试题含解析

山东省青岛市第二高级中学高一数学理模拟试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,v3的值为()A.27 B.11C.109 D.36参考答案:D略2. 为了得到函数f(x)=log2(﹣2x+2)的图象,只需把函数f(x)=log2(﹣2x)图象上所有的点( )A.向左平移2个单位长度B.向右平移2个单位长度C.向左平移1个单位长度D.向右平移1个单位长度参考答案:D考点:函数的图象与图象变化.专题:函数的性质及应用.分析:先将函数f(x)=log2(﹣2x+2)化成y=log2[﹣2(x﹣1)],然后和函数y=log2(﹣2x)比较看x的变化.解答:解:函数f(x)=log2(﹣2x+2)化成y=log2 [﹣2(x﹣1)],和函数y=log2(﹣2x)相比,x 的变化是减1,根据左加右减,所以将函数y=log2(﹣2x)的图象向右平移1个单位得到f(x)=log2(﹣2x+2)的图象.故选D.点评:本题考查了图象在x轴方向上的平移变换,一般是先研究x的变化,需要先将函数式适当变形再来判断,根据“左加右减”进行3. 已知a>0,b>0且ab=1,则函数f(x)=a x与g(x)=﹣log b x的图象可能是()A.B.C.D.参考答案:B【考点】对数函数的图象与性质.【分析】推导出g(x)=﹣log b x=log x, =a,由此利用指数函数、对数函数的图象和性质能求出结果.【解答】解:g(x)=﹣log b x=log x,∵a>0,b>0且ab=1,∴当a>1时, =a>1,此时函数f(x)=a x的图象过点(0,1),图象在x轴上方,是增函数,g(x)=﹣log b x的图象过点(1,0),图象在y轴左侧,是增函数,B满足条件;当0<a<1时,=a∈(0,1),此时函数f(x)=a x的图象过点(0,1),图象在x轴上方,是增减数,g(x)=﹣log b x的图象过点(1,0),图象在y轴左侧,是减函数,都不满足条件.故选:B.4. 集合,集合,Q=则P与Q的关系是()A.P=QB.P QC.D.参考答案:C5. 在平面上,,,,若,则的取值范围是( )A. B. C. D.参考答案:D6. 在边长为1的等边三角形△ABC的BC边上任取一点D,使成立的概率为()A.B. C. D.参考答案:B7. 已知()A B C D参考答案:B8. 函数y=﹣x2﹣4mx+1在[2,+∞)上是减函数,则m的取值范围是()A.[﹣1,+∞)B.(﹣∞,1)C.(﹣∞,﹣1] D.(1,+∞)参考答案:A【考点】二次函数的性质.【分析】求出二次函数的对称轴,利用函数的单调性列出不等式求解即可.【解答】解:函数y=﹣x2﹣4mx+1开口向下,对称轴为:x=﹣2m,在[2,+∞)上是减函数,可得:﹣2m≤2,解得m≥﹣1.故选:A.【点评】本题考查二次函数的简单性质的应用,考查计算能力.9. 设,下列关系正确的是()A. B.C. D.参考答案:A略10. (5分)若直角坐标平面内的两不同点P、Q满足条件:①P、Q都在函数y=f(x)的图象上;②P、Q关于原点对称,则称点对[P,Q]是函数y=f(x)的一对“友好点对”(注:点对[P,Q]与[Q,P]看作同一对“友好点对”).已知函数f(x)=,则此函数的“友好点对”有()对.A.0 B. 1 C. 2 D.3参考答案:B考点:函数的图象;分段函数的应用.专题:函数的性质及应用.分析:根据题意可知只须作出函数(x>0)的图象关于原点对称的图象,确定它与函数y=﹣x2﹣4x(x≤0)交点个数即可.解答:由题意得:函数f(x)=“友好点对”的对数,等于函数(x>0)的图象关于原点对称的图象,与函数y=﹣x2﹣4x(x≤0)交点个数在同一坐标系中做出函数(x>0)的图象关于原点对称的图象,与函数y=﹣x2﹣4x(x≤0)的图象如下图所示:由图象可知,两个图象只有一个交点. 故选B点评: 本题考查的知识点是函数的图象,分段函数,新定义,其中将“友好点对”的对数转化为对应图象交点个数是解答的关键.二、 填空题:本大题共7小题,每小题4分,共28分11. 函数的图像过定点.参考答案:(1,2)当时,,所以过定点。
高中数学必修第一册《5-1任意角和弧度制》课时同步训练试题

故选: .
【点睛】
本题考查了角度所在象限,意在考查学生的计算能力和转化能力.
5.C
【分析】
首先根据图形计算出矢 ,弦 ,再带入弧田面积公式即可.
【详解】
如图所示:
因为 , , 为等边三角形.
所以 ,矢 ,弦 .
.
故选:C
【点睛】
本题主要考查扇形面积公式,同时考查学生对题意的理解,属于中档题.
所以 ,
所以扇形的面积为 .
【点睛】
本题主要考查弧长公式和扇形面积公式,还考查了运算求解的能力,属于中档题.
16.(1) (2) 80π(3) 2,最大值为100cm2
【解析】
(1)设扇形圆心角的弧度数为θ(0<θ<
2π),弧长为l,半径为r,
依题意有
①代入②得r2-5r+4=0,解之得r1=1,r2=4.
对于C选项,锐角是第一象限角,故C选项正确.
对于D选项, 中角的范围不一样,所以D选项错误.
故选:BC
【点睛】
本小题主要考查角的范围比较,考查集合交集、并集和集合相等的概念,属于基础题.
8.BD
【分析】
用不等式表示第三象限角α,再利用不等式的性质求出 满足的不等式,从而确定 的终边所在的象限.
【详解】
∴l=40-2r,∴S= lr= ×(40-2r)r=(20-r)r=-(r-10)2+100.
∴当半径r=10cm时,扇形的面积最大.
这个最大值为100cm2,这时θ= = =2rad.
15.(1) ;(2)
【分析】
(1)由弦 的长等于半径,得到 ,然后利用扇形的弧长公式求解.
(2)由弦 的长等于半径的 倍,先求 ,进而得到 ,然后利用扇形的面积公式求解.
2021-2022年高一数学人教版A版(2019)必修第一册同步练习题5-1 任意角和弧度制含答案

2021-2022年高一数学人教版A版(2019)必修第一册同步练习题5-1 任意角和弧度制【含答案】一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.把一条射线绕着端点按顺时针方向旋转240°所形成的角是( )A.120°B.-120°C.240°D.-240°【答案】D【解析】按顺时针方向旋转形成的角是负角,排除A、C;又由题意知旋转的角度是240°,排除B.故选D.2.给出下列四个结论:①-15°角是第四象限角;②185°角是第三象限角;③475°角是第二象限角;④-350°角是第一象限角.其中正确的个数为( )A.1 B.2C.3 D.4【答案】D【解析】①-15°角是第四象限角;②因为180°<185°<270°,所以185°角是第三象限角;③因为475°=360°+115°,90°<115°<180°,所以475°角是第二象限角;④因为-350°=-360°+10°,所以-350°角是第一象限角.所以四个结论都是正确的.3.集合A={α|α=k·90°-36°,k∈Z},B={β|-180°<β<180°},则A∩B=( )A.{-36°,54°}B.{-126°,144°}C.{-126°,-36°,54°,144°}D.{-126°,54°}【答案】C【解析】令k =-1,0,1,2,则A ,B 的公共元素有-126°,-36°,54°,144°. 4.已知角α=45°,β=315°,则角α与β的终边( ) A .关于x 轴对称 B .关于y 轴对称 C .关于直线y =x 对称 D .关于原点对称【答案】A【解析】因为β=315°=360°-45°,所以315°角与-45°角的终边相同,所以α与β的终边关于x 轴对称.5.若α与β终边相同,则α-β的终边落在( ) A .x 轴的非负半轴上 B .x 轴的非正半轴上 C .y 轴的非负半轴上 D .y 轴的非正半轴上 【答案】A【解析】∵α=β+k ·360°,k ∈Z ,∴α-β=k ·360°,k ∈Z ,∴其终边在x 轴的非负半轴上. 6.(多选)已知角2α的终边在x 轴的上方,那么角α可能是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角 【答案】AC【解析】因为角2α的终边在x 轴的上方,所以k ·360°<2α<k ·360°+180°,k ∈Z ,则有k ·180°<α<k ·180°+90°,k ∈Z.故当k =2n ,n ∈Z 时,n ·360°<α<n ·360°+90°,n ∈Z ,α为第一象限角;当k =2n +1,n ∈Z 时,n ·360°+180°<α<n ·360°+270°,n ∈Z ,α为第三角限角.故选A 、C.7.若角α与角x +4π有相同的终边,角β与角x -4π有相同的终边,那么α与β间的关系为( ) A .α+β=0B .α-β=0C .α+β=2k π(k ∈Z)D .α-β=2π+2k π(k ∈Z) 【答案】D【解析】∵α=x +4π+2k 1π(k 1∈Z),β=x -4π+2k 2π(k 2∈Z),∴α-β=2π+2(k 1-k 2)π(k 1∈Z ,k 2∈Z).∵k 1∈Z ,k 2∈Z ,∴k 1-k 2∈Z.∴α-β=2π+2k π(k ∈Z). 8.已知某机械采用齿轮传动,由主动轮M 带着从动轮N 转动(如图所示),设主动轮M 的直径为150 mm ,从动轮N 的直径为300 mm ,若主动轮M 顺时针旋转2π,则从动轮N逆时针旋转( )A.8π B .4π C.2π D .π【答案】B【解析】设从动轮N 逆时针旋转θ rad ,由题意,知主动轮M 与从动轮N 转动的弧长相等,所以θπ⨯=⨯230022150,解得θ=4π,选B. 二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)9.若α满足180°<α<360°,5α与α有相同的始边,且又有相同的终边,则α=________. 【答案】270°【解析】∵5α=α+k ·360°,k ∈Z ,∴α=k ·90°,k ∈Z. 又∵180°<α<360°,∴α=270°.10.集合{α|k ·180°≤α≤k ·180°+45°,k ∈Z}中角表示的范围(用阴影表示)是图中的________(填序号).【答案】②【解析】集合{α|k ·180°≤α≤k ·180°+45°,k ∈Z}中,当k 为偶数时,此集合与{α|0°≤α≤45°}表示终边相同的角,位于第一象限;当k 为奇数时,此集合与{α|180°≤α≤225°}表示终边相同的角,位于第三象限.所以集合{α|k ·180°≤α≤k ·180°+45°,k ∈Z}中角表示的范围为图②所示.11.(2020·浙江高一课时练习)一条铁路在转弯处呈圆弧形,圆弧的半径为2km ,一列火车以30km /h 的速度通过,10s 间转过_______弧度.【答案】124【解析】10s 间列车转过的弧长为10130(km)360012⨯=,转过的角1112224α==(弧度). 故答案为:12412.已知圆的一段弧长等于该圆外切正三角形的边长,则这段弧所对圆心角的弧度数的绝对值为______;若圆弧长等于其所在圆的内接正方形的周长,那么这段弧所对圆心角的弧度数的绝对_____. 【答案】23 42【解析】设圆半径为r ,这段弧所对圆心角的弧度数为θ,则圆外切正三角形的边长为23r ,∴23||23rθ==2r ,周长为42r ,即圆弧长为42r ,∴42||42rrθ==. 三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)13.已知α,β都是锐角,且α+β的终边与-280°角的终边相同,α-β的终边与670°角的终边相同,求角α,β的大小.【解析】由题意可知,α+β=-280°+k ·360°,k ∈Z , ∵α,β都是锐角,∴0°<α+β<180°. 取k =1,得α+β=80°.①∵α-β=670°+k ·360°,k ∈Z ,α,β都是锐角, ∴-90°<α-β<90°.取k =-2,得α-β=-50°.② 由①②,得α=15°,β=65°.14.如图,点A 在半径为1且圆心在原点的圆上,且∠AOx =45°,点P 从点A 处出发,以逆时针方向沿圆周匀速旋转.已知点P 在1秒内转过的角度为θ(0°<θ<180°),经过2秒钟到达第三象限,经过14秒钟又回到出发点A ,求θ,并判断θ所在的象限.【解析】根据题意知,14秒钟后,点P 在角14θ+45°的终边上,所以45°+k ·360°=14θ+45°,k ∈Z.又180°<2θ+45°<270°, 即67.5°<θ<112.5°,∴67.5°<71800k <112.5°.又k ∈Z ,∴k =3或4,∴所求的θ的值为75400或77200.∵0°<75400<90°,90°<77200<180°,∴θ在第一象限或第二象限.15.已知扇形AOB 的圆心角α为23π,半径长R 为6,求: (1)弧AB 的长; (2)扇形所含弓形的面积. 【解析】(1)l =α·R =23π×6=4π, 所以弧AB 的长为4π. (2)S 扇形OAB =12lR =12×4π×6=12π. 如图所示,过点O 作OD ⊥AB ,交AB 于点D ,23π=120°,所以∠AOD =60°,∠DAO =30°, 于是有S △OAB =12×AB ×OD =12×2×6cos 30°×3=3所以弓形的面积为S 扇形OAB -S △OAB =12π-3所以弓形的面积是12π-316.(2020·浙江高一课时练习)如图,3dm ,宽为1dm 的长方形在桌面上作无滑动翻滚,翻滚到第四次时被小木块挡住,此时长方形的底边与桌面所成的角为6π,求点A 走过的路程及走过的弧所在扇形的总面积.【解析】如图:在扇形1ABA 中,圆心角为2π, 弧长()131dm 22l AB πππ=⨯=+=,面积()21112dm 22S AB πππ=⨯⨯=⨯⨯=. 在扇形12ACA 中,圆心角为2π, 弧长()211dm 222l A C πππ=⨯=⨯=,面积()221111dm 2244S A C πππ=⨯⨯=⨯⨯=, 在扇形23A DA 中,圆心角为263ππππ--=,弧长()3233dm 333l A D πππ=⨯==, 面积()232131323dm 22S A D ππ===. 综上,点A 走过的路程()()1239233dm 26l l l l ππππ+=++=++=, 点A 走过的弧所在扇形的总面积()21237dm 424ππππ=++=++=S S S S。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题5.1 任意角和弧度制知识储备1.角的概念的推广(1)定义:角可以看成平面内的一条射线绕着端点从一个位置旋转到另一个位置所成的图形.(2)分类⎩⎨⎧按旋转方向不同分为正角、负角、零角.按终边位置不同分为象限角和轴线角.(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S ={β|β=α+k ·360°,k ∈Z}. 2.弧度制的定义和公式(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad. (2)公式姓名:__________________ 班级:______________ 得分:_________________ 注意事项:本试卷满分100分,考试时间45分钟,试题共16题.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共8小题,每小题5分,共40分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.把一条射线绕着端点按顺时针方向旋转240°所形成的角是( )A.120°B.-120°C.240°D.-240°【答案】D【解析】按顺时针方向旋转形成的角是负角,排除A、C;又由题意知旋转的角度是240°,排除B.故选D.2.给出下列四个结论:①-15°角是第四象限角;②185°角是第三象限角;③475°角是第二象限角;④-350°角是第一象限角.其中正确的个数为( )A.1 B.2C.3 D.4【答案】D【解析】①-15°角是第四象限角;②因为180°<185°<270°,所以185°角是第三象限角;③因为475°=360°+115°,90°<115°<180°,所以475°角是第二象限角;④因为-350°=-360°+10°,所以-350°角是第一象限角.所以四个结论都是正确的.3.集合A={α|α=k·90°-36°,k∈Z},B={β|-180°<β<180°},则A∩B=( ) A.{-36°,54°} B.{-126°,144°}C.{-126°,-36°,54°,144°} D.{-126°,54°}【答案】C【解析】令k=-1,0,1,2,则A,B的公共元素有-126°,-36°,54°,144°. 4.已知角α=45°,β=315°,则角α与β的终边( )A.关于x轴对称B.关于y轴对称C.关于直线y=x对称D.关于原点对称【答案】A【解析】因为β=315°=360°-45°,所以315°角与-45°角的终边相同,所以α与β的终边关于x轴对称.5.若α与β终边相同,则α-β的终边落在( )A.x轴的非负半轴上B.x轴的非正半轴上C.y轴的非负半轴上D.y轴的非正半轴上【答案】A【解析】∵α=β+k·360°,k∈Z,∴α-β=k·360°,k∈Z,∴其终边在x轴的非负半轴上.6.(多选)已知角2α的终边在x轴的上方,那么角α可能是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角【答案】AC【解析】因为角2α的终边在x轴的上方,所以k·360°<2α<k·360°+180°,k∈Z,则有k·180°<α<k·180°+90°,k∈Z.故当k=2n,n∈Z时,n·360°<α<n·360°+90°,n∈Z,α为第一象限角;当k=2n+1,n∈Z时,n·360°+180°<α<n·360°+270°,n∈Z,α为第三角限角.故选A、C.7.若角α与角x +4π有相同的终边,角β与角x -4π有相同的终边,那么α与β间的关系为( ) A .α+β=0B .α-β=0C .α+β=2k π(k ∈Z)D .α-β=2π+2k π(k ∈Z) 【答案】D 【解析】∵α=x +4π+2k 1π(k 1∈Z),β=x -4π+2k 2π(k 2∈Z),∴α-β=2π+2(k 1-k 2)π(k 1∈Z ,k 2∈Z).∵k 1∈Z ,k 2∈Z ,∴k 1-k 2∈Z.∴α-β=2π+2k π(k ∈Z). 8.已知某机械采用齿轮传动,由主动轮M 带着从动轮N 转动(如图所示),设主动轮M 的直径为150 mm ,从动轮N 的直径为300 mm ,若主动轮M 顺时针旋转2π,则从动轮N 逆时针旋转( ) A.8π B .4π C.2π D .π【答案】B【解析】设从动轮N 逆时针旋转θ rad ,由题意,知主动轮M 与从动轮N 转动的弧长相等,所以θπ⨯=⨯230022150,解得θ=4π,选B. 二、填空题(本大题共4小题,每小题5分,共20分.不需写出解答过程,请把答案直接填写在横线上)9.若α满足180°<α<360°,5α与α有相同的始边,且又有相同的终边,则α=________.【答案】270°【解析】∵5α=α+k·360°,k∈Z,∴α=k·90°,k∈Z.又∵180°<α<360°,∴α=270°.10.集合{α|k·180°≤α≤k·180°+45°,k∈Z}中角表示的范围(用阴影表示)是图中的________(填序号).【答案】②【解析】集合{α|k·180°≤α≤k·180°+45°,k∈Z}中,当k为偶数时,此集合与{α|0°≤α≤45°}表示终边相同的角,位于第一象限;当k为奇数时,此集合与{α|180°≤α≤225°}表示终边相同的角,位于第三象限.所以集合{α|k·180°≤α≤k·180°+45°,k∈Z}中角表示的范围为图②所示.11.(2020·浙江高一课时练习)一条铁路在转弯处呈圆弧形,圆弧的半径为2km,一列火车以30km/h的速度通过,10s间转过_______弧度.【答案】1 24【解析】10s间列车转过的弧长为10130(km)360012⨯=,转过的角1112224α==(弧度).故答案为:1 2412.已知圆的一段弧长等于该圆外切正三角形的边长,则这段弧所对圆心角的弧度数的绝对值为______;若圆弧长等于其所在圆的内接正方形的周长,那么这段弧所对圆心角的弧度数的绝对_____.【答案】【解析】设圆半径为r,这段弧所对圆心角的弧度数为θ,则圆外切正三角形的边长为r,∴||θ==;,周长为,即圆弧长为,∴||θ==三、解答题(本大题共4小题,共40分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)13.已知α,β都是锐角,且α+β的终边与-280°角的终边相同,α-β的终边与670°角的终边相同,求角α,β的大小.【解析】由题意可知,α+β=-280°+k·360°,k∈Z,∵α,β都是锐角,∴0°<α+β<180°.取k=1,得α+β=80°.①∵α-β=670°+k·360°,k∈Z,α,β都是锐角,∴-90°<α-β<90°.取k=-2,得α-β=-50°.②由①②,得α=15°,β=65°.14.如图,点A在半径为1且圆心在原点的圆上,且∠AOx=45°,点P从点A处出发,以逆时针方向沿圆周匀速旋转.已知点P在1秒内转过的角度为θ(0°<θ<180°),经过2秒钟到达第三象限,经过14秒钟又回到出发点A,求θ,并判断θ所在的象限.【解析】根据题意知,14秒钟后,点P在角14θ+45°的终边上,所以45°+k·360°=14θ+45°,k∈Z.又180°<2θ+45°<270°, 即67.5°<θ<112.5°,∴67.5°<71800⋅k <112.5°.又k ∈Z ,∴k =3或4,∴所求的θ的值为75400或77200.∵0°<75400<90°,90°<77200<180°,∴θ在第一象限或第二象限. 15.已知扇形AOB 的圆心角α为23π,半径长R 为6,求: (1)弧AB 的长;(2)扇形所含弓形的面积. 【解析】(1)l =α·R =23π×6=4π, 所以弧AB 的长为4π. (2)S 扇形OAB =12lR =12×4π×6=12π. 如图所示,过点O 作OD ⊥AB ,交AB 于点D ,23π=120°,所以∠AOD =60°,∠DAO =30°,于是有S △OAB =12×AB ×OD=12×2×6cos 30°×3=所以弓形的面积为S 扇形OAB -S △OAB =12π-.所以弓形的面积是12π-916.(2020·,宽为1dm 的长方形在桌面上作无滑动翻滚,翻滚到第四次时被小木块挡住,此时长方形的底边与桌面所成的角为6π,求点A 走过的路程及走过的弧所在扇形的总面积.【解析】如图:在扇形1ABA 中,圆心角为2π,弧长()1dm 22l AB πππ=⨯==,面积()21112dm 22S AB πππ=⨯⨯=⨯⨯=.在扇形12A CA 中,圆心角为2π, 弧长()211dm 222l AC πππ=⨯=⨯=,面积()221111dm 2244S AC πππ=⨯⨯=⨯⨯=, 在扇形23A DA 中,圆心角为263ππππ--=,弧长)32dm 33l A D ππ=⨯==,面积()232112dm 2332S A D π=⨯⨯=⨯=.综上,点A 走过的路程(()1239dm 26l l l l πππ+=++=++=, 点A 走过的弧所在扇形的总面积()21237dm 424ππππ=++=++=S S S S。
