广东省茂名市2013届高三第二次高考模拟数学文试题 Word版含答案
2013广东高考文科数学试卷及答案(高清版)

2013年普通高校招生全国统一考试广东省高考数学答案1-5 DAADC 6-10 BCBCD 11 [)()1,00,-+∞; 1214; 13 1,1,3,3; 14 (2,1); 1516. 解:(1)cos cos 31264f A A A ππππ⎛⎫⎛⎫=+===⎪ ⎪⎝⎭⎝⎭,解得2A = (2)43042cos 2cos 2sin 336217f πππαπααα⎛⎫⎛⎫⎛⎫+=++=+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即15sin 17α= 2842cos 2cos 3665f ππβπββ⎛⎫⎛⎫-=-+== ⎪ ⎪⎝⎭⎝⎭,即4cos 5β=因为0,2παβ⎡⎤,∈⎢⎥⎣⎦,所以8cos 17α==,3sin 5β== 所以8415313cos()cos cos sin sin 17517585αβαβαβ+=-=⨯-⨯=- 17. 解:(1)依题意得,10(20.020.030.04)1a +++=,解得0.005a = (2)这100名学生语文成绩的平均分为:550.05650.4750.3850.2950.0573⨯+⨯+⨯+⨯+⨯=(分)(3)数学成绩在[50,60)的人数为:1000.055⨯=数学成绩在[60,70)的人数为:11000.4202⨯⨯= 数学成绩在[70,80)的人数为:41000.3403⨯⨯=数学成绩在[80,90)的人数为:51000.2254⨯⨯=所以数学成绩在[50,90)之外的人数为:100520402510----= 18. 解:(1)证明:因为AB ⊥平面PAD , 所以PH AB ⊥因为PH 为△PAD 中AD 边上的高 所以PH AD ⊥因为AB AD A = 所以PH ⊥平面ABCD (2)连结BH ,取BH 中点G ,连结EG因为E 是PB 的中点, 所以//EG PH因为PH ⊥平面ABCD 所以EG ⊥平面ABCD则1122EG PH == 111332E BCFBCF V S EG FC AD EG -∆=⋅=⋅⋅⋅⋅=12 P ABCH FE D G M(3)证明:取PA 中点M ,连结MD ,ME 因为E 是PB 的中点所以1//2ME AB = 因为1//2DF AB = 所以//ME DF =所以四边形MEDF 是平行四边形 所以//EF MD 因为PD AD = 所以MD PA ⊥ 因为AB ⊥平面PAD , 所以MD AB ⊥ 因为PA AB A = 所以MD ⊥平面PAB所以EF ⊥平面PAB19. 解:(1)当1n =时,1121T S =-因为111T S a ==,所以1121a a =-,求得11a =(2)当2n ≥时,221112[2(1)]2221n n n n n n n S T T S n S n S S n ---=-=----=--+所以1221n n S S n -=+-① 所以1221n n S S n +=++② ②-①得 122n n a a +=+ 所以122(2)n n a a ++=+,即1222n n a a ++=+(2)n ≥求得123a +=,226a +=,则21222a a +=+ 所以{}2n a +是以3为首项,2为公比的等比数列所以1232n n a -+=⋅所以1322n n a -=⋅-,*n ∈N20. 解:(1)因为椭圆1C 的左焦点为1(1,0)F -,所以1c =,点(0,1)P 代入椭圆22221x y a b +=,得211b=,即1b =,所以2222a b c =+=所以椭圆1C 的方程为2212x y +=.(2)直线l 的斜率显然存在,设直线l 的方程为y kx m =+,2212x y y kx m ⎧+=⎪⎨⎪=+⎩,消去y 并整理得222(12)4220k x kmx m +++-= 因为直线l 与椭圆1C 相切,所以2222164(12)(22)0k m k m ∆=-+-= 整理得22210k m -+=①24y x y kx m⎧=⎨=+⎩,消去y 并整理得222(24)0k x km x m +-+= 因为直线l 与抛物线2C 相切,所以222(24)40km k m ∆=--= 整理得1km =②综合①②,解得2k m ⎧=⎪⎨⎪=⎩或2k m ⎧=-⎪⎨⎪=⎩所以直线l的方程为2y x =或2y x =--21. 解:(1)令2()23(1)6g x x a x a =-++229(1)4893093(31)(3)a a a a a a ∆=+-=-+=--① 当103a <≤时,0∆≥,方程()0g x =的两个根分别为1334a x +=,2x =所以()0g x >的解集为33(()a ++-∞+∞ 因为12,0x x >,所以D A B ==33()a +++∞ ②当113a <<时,0∆<,则()0g x >恒成立,所以D A B ==(0,)+∞综上所述,当103a <≤时,D =3333(0,()44a a +-+++∞; 当113a <<时,D =(0,)+∞ (2)2()66(1)66()(1)f x x a x a x a x '=-++=--,令()0f x '=,得x a =或1x =① 当103a <≤时,由(1)知D =12(0,)(,)x x +∞ 因为2()23(1)6(3)0g a a a a a a a =-++=->,(1)23(1)6310g a a a =-++=-≤ 所以1201a x x <<<≤,所以(),()f x f x '随x 的变化情况如下表:所以()f x 的极大值点为x a =,没有极小值点 ②当113a <<时,由(1)知D =(0,)+∞ 所以(),()f x f x '随x 的变化情况如下表:所以()f x 的极大值点为x a =,极小值点为1x = 综上所述,当103a <≤时,()f x 有一个极大值点x a =,没有极小值点; 当113a <<时,()f x 有一个极大值点x a =,一个极小值点1x =。
广东省茂名市2013届高三第二次高考模拟语文试题 Word版含答案

绝密★启用前试卷类型:A茂名市2013年第二次高考模拟考试语文试卷本试卷共8页,24小题,满分150分。
考试用时150分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上,将条形码横贴在答题卡右上角“条形码贴”。
2.选择题每小题选出答案后,用2b铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 作答选做题时,请先用2b铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5. 考生必须保持答题卡的整洁,考试结束后,将试卷和答题卡一并交回。
一、本大题4小题,每小题3分,共12分。
1.下列词语中加点的字,每对读音都不相同的一组是A.旋.律/琴弦.醇.厚/谆.谆告诫埋.怨/隐姓埋.名B.箴.言/斟.酌拜谒./殚精竭.虑折.本/大打折.扣C.覆辙./掣.肘寒暄./喧.宾夺主传.记/传.奇小说D.包庇./媲.美谙.熟/万马齐暗.忖度./度.德量力2.下面语段中划线的词语,使用不恰当的一项是王莽新政很像19世纪欧洲才出现的空想社会主义的那套东西:全国实行公有制,计划经济,生产资料(田地)平均分配,这些政令合起来看,就像一个惊天地泣鬼神的大棋局,王莽是一位高瞻远瞩的棋手,在下一盘很大很大的棋。
那些空想社会主义的创始人当年要是了解到王莽的大棋局,一定为之汗颜。
但是,各地豪强纷纷率众起兵,反抗王莽的新政。
公元23年,王莽被攻入长安城的起义军杀死,他想要建立一个人人富足的理想社会,可惜到头来只是一个昙花一现。
A.惊天地泣鬼神 B.高瞻远瞩 C.汗颜 D.昙花一现3.下列句子中,没有语病的一项是A.今年是国务院确定的《重大节假日免收小型客车通行费》后的第一个春节假日,长、短途自驾游客大量增加,出现了第一轮的旅游高潮。
2013茂名二模(文数)【含答案--全WORD--精心排版】

茂名市2013年第二次高考模拟考试数学试卷(文科)本试卷共4页,21小题, 满分150分。
考试用时120分钟。
参考公式: 锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高. 一、选择题。
(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 已知集合22{1},{log 0}A x x B x x =>=>,则A B = ( )A .{1}x x <-B .{0}x x >C .{1}x x >D .{}1x 1>-< x x2. 已知,x y R ∈,i 是虚数单位,且1xi y i -=-+,则(1)x y i ++的值是( ) A .2 B .2i - C .4- D .2i3. 函数1()23f x x x =-+-的定义域是( ) A .[2,)+∞ B .[2,3) C .(,3)(3,)-∞⋃+∞ D .()[2,3)3,⋃+∞4. 设双曲线22221x y a b-=(0,0a b >>)的虚轴长为2 ,焦距为23, 则双曲线的渐近线方程为( )A. 12y x =±B. 22y x =± C. 2y x =± D. 2y x =± 5. 将函数sin(6)4y x π=+的图像上各点向右平移8π个单位,则得到新函数的解析式为( )A. sin(6)2y x π=-B. sin(6)4y x π=+C. 5sin(6)8y x π=+D. sin(6)8y x π=+6. 若向量,,a b c满足a //b ,且0b c = ,则()2a b c += ( )A .4B .3C .2D .07. 已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1, 则该几何体的体积为( ) A. 3242π-B. 243π-C. 24π-D. 242π- 8. 为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B(如图),要测量A ,B 两点的距离,测量人员 在岸边定出基线BC ,测得BC=50m ,105ABC ∠=,45BCA ∠=就可以计算出A,B 两点的距离为( )A . 502m B. 503m C. 252m D.2522m 9. 已知椭圆221169x y +=及以下3个函数:①()f x x =②()sin f x x =③()cos f x x =;其中函数图像能等分该椭圆面积的函数个数有( )A. 1个B. 2个C. 3个D. 0个10. 设函数()f x 的定义域均为D ,若存在非零实数l 使得对于任意x M ∈(M D ⊆),有x l D +∈,且()()f x l f x +≥,则称()f x 为M 上的l 高调函数。
【2013茂名二模】广东省茂名市2013届高三第二次高考模拟理综试题_Word版含答案

广东省茂名市2013届高三第二次高考模拟理综试题13.下列说法正确的是A.牛顿首先测出万有引力恒量GB.布朗运动是指液体分子的无规则运动C.气体自发的扩散运动总是向着更为无序的方向进行D.扩散现象不能在固体中发生14.下列四幅图的有关说法,错误的是r时,分子间不存在引力和斥力A.分子间距为B.水面上的单分子油膜,在测量油膜直径d大小时可把他们当做球形处理C.食盐晶体中的钠,氯离子按一定规律分布,具有空间上的周期性D.猛推木质推杆,密闭的气体温度升高,压强变大,外界对气体做正功15.如图小车向右做加速直线运动,物块贴在小车左壁相对静止。
当小车的加速度增大时,下列说法正确的是A.物块受到的弹力不变B.物块受到的摩擦力不变C.物块受到四个力的作用D.物块受到的合外力为零16.如图电子枪射出的电子束进入示波管,在示波管正下方有竖直放置的通顺时针电流的环形导线,则示波管中的电子束将A.向上偏转B.向下偏转C.向纸外偏转D .向纸里偏转17.下列说法正确的是A .铀核裂变的核反应是:He Th U 422349023892+→B .He 42核由两个中子和两个质子组成C .n P Al He 103015271342+→+是α衰变方程D .氢原子吸收一个光子从低能级跃迁到高能级,氢原子的电势能增加了18.如图所示,带电粒子从A 开始沿虚线穿过竖直放置的平行板电容器,则粒子A .带负电B .做加速运动C .机械能增加D .电势能增大19.“天宫一号”绕地球的运动可看做匀速圆周运动,转一周所用的时间约90分钟。
下列说法正确的是A .“天宫一号”离地面的高度比地球同步卫星离地面的高度小B .“天宫一号”的线速度比地球同步卫星的线速度小C .“天宫一号” 的向心加速度比地球同步卫星向心加速度大D .当宇航员刘洋站立于“天宫一号”内不动时,她受力平衡20.如图所示为理想变压器,原、副线圈匝数比为2:1,原线圈接交流电压tV u π100sin 220=,图中电压表和电流表为理想电表,1R 为负温度系数的热敏电阻(当温度升高时阻值减小),则正确的是A .交流电的频率为Hz 50B .电压表示数是V 110C .当1R 处温度降低时,电压表示数不变D .当1R 处温度降低时,电压表示数变大21.我国“蛟龙号”在某次试验时,深潜器内的显示屏上显示出了从水面开始下潜到最后返回水面的10min 内全过程的深度曲线(a )和速度图像(b ),则正确的有A .(a )图中3h 代表本次下潜最大深度为m 360B .全过程中最大加速度是2/025.0s mC .潜水员感到失重体验发生在0-1min 和8-10min 内D .整个潜水器在8-10min 时间段内机械能守恒34.(18分)(1)验证“力的平行四边形法则”实验如图所示,A 为固定橡皮的图钉,O 为橡皮筋与细绳的结点,OB 、OC 为细绳子,图乙是在白纸上根据实验结果画出的图。
2013广东高考数学(文科)真题及详细答案

2013广东高考数学(文科)真题及详细答案一、 选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合{}{}22|20,,|20,S x x x x R T x x x x R =+=∈=-=∈,则S T = ( )A. {}0B. {}0,2C. {}2,0-D. {}2,0,2-【答案】A ;【解析】由题意知{}0,2S =-,{}0,2T =,故{}0S T = ;2. 函数()lg 11x y x +=-的定义域是( )A. ()1,-+∞B. [)1,-+∞C. ()()1,11,-+∞D. [)()1,11,-+∞【答案】C ;【解析】由题意知1010x x +>⎧⎨-≠⎩,解得1x >-且1x ≠,所以定义域为()()1,11,-+∞ ;3. 若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是( )A. 2B. 3C. 4D. 5 【答案】D ;【解析】因为()34i x yi i +=+,所以34xi y i -=+,根据两个复数相等的条件得:3y -=即3y =-,4x =,所以x yi +43i =-,x yi +的模224(3)5=+-=;4. 已知51sin 25πα⎛⎫+=⎪⎝⎭,那么cos α=( ) A. 25- B. 15- C.15D.25【答案】C ; 【解析】51sin sin ()co s ()co s()co s 22225ππππααααα⎛⎫⎡⎤+=+=-+=-==⎪⎢⎥⎝⎭⎣⎦; 5. 执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是( )A. 1B. 2C. 4D. 7【答案】D ;【解析】1i =时,1(11)1s =+-=;2i =时,1(21)2s =+-=;3i =时,2(31)4s =+-=;4i =时,4(41)7s =+-=;图1 图26. 某三棱锥的三视图如图2所示,则该三棱锥的体积是( )A.16B. 13C. 23D. 1【答案】B ;【解析】由三视图可看出该三棱锥的底面为直角边为1的等腰直角三角形,高为2, 所以该三棱锥的体积111112323V =⋅⋅⋅⋅=; 7. 垂直于直线1y x =+且与圆221x y +=相切于第Ⅰ象限的直线方程是( )A. 20x y +-= B. 10x y ++= C. 10x y +-= D. 20x y ++=【答案】A ;【解析】设所求直线为l ,因为l 垂直直线1y x =+,故l 的斜率为1-,设直线l 的方程为y x b =-+,化为一般式为0x y b +-=;因为l 与圆相切221x y +=相切,所以圆心(0,0)到直线l 的距离12b -==,所以2b =±,又因为相切与第一象限,所以0b >,故2b =,所以l 的方程为20x y +-=;8. 设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( )A. 若//,//l l αβ,则//αβB. 若,l l αβ⊥⊥,则//αβC. 若,//l l αβ⊥,则αβ//D. 若,l αβα⊥//,则l β⊥【答案】B ; 【解析】若α与β相交,且l 平行于交线,则也符合A ,显然A 错;若,//l l αβ⊥,则αβ⊥,故C 错;,l αβα⊥//,若l 平行交线,则//l β,故D 错;9. 已知中心在原点的椭圆C 的右焦点为()1,0F ,离心率等于12,则C 的方程是( )A.22134xy+= B.22143xy+= C.22142xy+= D.22143xy+=【答案】D ;【解析】由焦点可知()1,0F 可知椭圆焦点在x 轴上,由题意知11,2c c a==,所以222,213a b ==-=,故椭圆标准方程为22143xy+=;10. 设a 是已知的平面向量且0a ≠ ,关于向量a的分解,有如下四个命题:① 给定向量b ,总存在向量c ,使a b c =+;② 给定向量b 和c ,总存在实数λ和μ,使a b c λμ=+;③ 给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使a b c λμ=+;④ 给定正数λ和μ,总存在单位向量b 和单位向量c ,使a b c λμ=+.上述命题中的向量b ,c 和a在同一平面内且两两不共线,则真命题的个数是( )A. 1B. 2C. 3D. 4【答案】D ;【解析】因为单位向量(模为1的向量,方向不确定)和一个不为零的实数可以表示任何一个向量,由题意可知A,B,C,D 均正确;二、 填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11~13题)11. 设数列{}n a 是首项为1,公比为2-的等比数列,则1234a a a a +++=____________; 【答案】15;【解析】由题意知11a =,22a =-,34a =,48a =-,所以;1234a a a a +++124815=+++=;12. 若曲线2ln y ax x =-在点()1,a 处的切线平行于x 轴,则a =_____________;【答案】12;【解析】因为2ln y ax x =-,所以12y a x x'=-,因为曲线2ln y ax x =-在点()1,a 处的切线平行于x 轴,所以1210x y a ='=-=,所以12a =;13. 已知变量,x y 满足约束条件30111x y x y -+≥⎧⎪-≤≤⎨⎪≥⎩,则z x y =+的最大值是_____________;【答案】5;【解析】作出可行域可得直角梯形的四个顶点分别为(1,1),(1,2),(1,1),(1,4)--,代入可知z 的最大值为145z =+=;(二)选做题(14~15题,考生只能从中选做一题)14. (坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=,以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为___________________; 【答案】22(1)1x y -+=;【解析】因为曲线C 的极坐标方程为2cos ρθ=;所以2cos 2cos 1cos 2x ρθθθ===+① ,sin 2sin cos sin 2y ρθθθθ===②;①可变形得:cos 21x θ=-③,②可变形得:sin 2y θ=;由22sin 2cos 21θθ+=得:22(1)1x y -+=;15. (几何证明选讲选做题)如图3,在矩形A B C D 中,3A B =,3B C =,B E A C ⊥,垂足为E ,则E D =___________; 【答案】212;【解析】因为在矩形A B C D 中,3A B =,3B C =,B E AC ⊥,所以030B C A ∠=,所以03co s 3032C E C B =⋅=;在CDE 中,因为60E C D ∠=,由余弦定理得:()22222033331212co s 603232224D EC E CD CE C D ⎛⎫=+-⋅⋅⋅=+-⨯⨯⨯=⎪ ⎪⎝⎭,所以212C D =;三、 解答题:本大题共6小题,满分80分. 解答须写出文字说明和演算步骤.16. (本小题满分12分)已知函数()2co s ,12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若3co s 5θ=,3,22πθπ⎛⎫∈⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【答案与解析】 (1)22co s 2co s21331242f ππππ⎛⎫⎛⎫=-==⨯=⎪ ⎪⎝⎭⎝⎭;(2)因为3co s 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,所以234sin 155θ⎛⎫=--=-⎪⎝⎭;2co s 2co s 2co s co s sin sin 6612333f ππππππθθθθθ⎛⎫⎛⎫⎛⎫⎛⎫-=--=-=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭314332462525210⎛⎫-=⨯-⨯= ⎪ ⎪⎝⎭;17. (本小题满分12分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下: 分组(重量) [)80,85[)85,90[)90,95[)95,100频数(个)5102015(1) 根据频数分布表计算苹果的重量在[)90,95的频率;(2) 用分层抽样的方法从重量在[)80,85和[)95,100的苹果中共抽取4个,其中重量在[)80,85的有几个?(3) 在(2)中抽出的4个苹果中,任取2个,求重量在[)80,85和[)95,100中各有一个的概率;【答案与解析】(1)重量在[)90,95的频率200.450==;(2)若采用分层抽样的方法从重量在[)80,85和[)95,100的苹果中共抽取4个,则重量在[)80,85的个数541 515=⨯=+;(3)设在[)80,85中抽取的一个苹果为x,在[)95,100中抽取的三个苹果分别为,,a b c,从抽出的4个苹果中,任取2个共有(,),(,),(,),(,),(,),(,)x a x b x c a b a c b c6种情况,其中符合“重量在[)80,85和[)95,100中各有一个”的情况共有(,),(,),(,)x a x b x c种;设“抽出的4个苹果中,任取2个,求重量在[)80,85和[)95,100中各有一个”为事件A,则事件A的概率31()62P A==;18.(本小题满分14分)如图4,在边长为1的等边三角形A B C中,,D E分别是,A B A C上的点,A D A E=,F是B C的中点,A F与D E交于点G. 将A B F∆沿A F折起,得到如图5所示的三棱锥A B C F-,其中22B C=.(1)证明:D E B C F//平面;(2)证明:C F A B F⊥平面;(3)当23A D=时,求三棱锥F D E G-的体积F D E GV-.图4 图5(1)证明:在图4中,因为A B C是等边三角形,且A D A E=,所以A D A EA B A C=,//D E B C;在图5中,因为//D G B F,//G E F C,所以平面D G E//平面B C F,所以D E B C F//平面;(2)证明:在图4中,因为因为A B C是等边三角形,且F是B C的中点,所以A F B C⊥;在图5中,因为在B F C 中,12,22B F FC B C ===,所以222B F FC B C +=,B FC F ⊥,又因为A F C F ⊥,所以C F A B F ⊥平面;(3)因为,A F C F A F B F ⊥⊥,所以A F ⊥平面B C F ,又因为平面D G E //平面B C F ,所以A F ⊥平面D G E ;所以11111113333232336324F D EG D G E V S F G D G G E F G -=⋅⋅=⋅⋅⋅⋅=⋅⋅⋅⋅= ; 19. (本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足2*1441,n n S a n n N +=--∈,且2514,,a a a 构成等比数列;(1) 证明:2145a a =+;(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<.(1)证明:因为2*1441,n n S a n n N +=--∈,令1n =,则212441S a =--,即22145a a =+,所以2145a a =+;(2)当2n ≥时,()()221144441411n n n n n a S S a n a n -+⎡⎤=-=------⎣⎦2214n n a a +=--,所以221(2)n n a a +=+,因为{}n a 各项均为正数,所以12n n a a +=+;因为2514,,a a a 构成等比数列,所以22145a a a ⋅=,即2222(24)(6)a a a +=+,解得23a =,因为2145a a =+,所以11a =, 212a a =+ ,符合12n n a a +=+,所以12n n a a +=+对1n =也符合,所以数列{}n a 是一个以11a =为首项,2d =为公差的等差数列,1(1)221n a n n =+-⋅=-;(3)因为111111()(21)(21)22121n n a a n n n n +==-+--+,所以12231111111111111()()()21323522121n n a a a a a a n n ++++=-+-+⋅⋅⋅+--+111111111112133521212121212n n n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅-=-=< ⎪ ⎪-+++⎝⎭⎝⎭; 所以对一切正整数n ,有1223111112n n a a a a a a ++++<.20. (本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=的距离为322. 设P 为直线l 上的点,过点P 作抛物线C 的两条切线,P A P B ,其中,A B 为切点.(1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l 上的定点时,求直线A B 的方程; (3) 当点P 在直线l 上移动时,求A F B F ⋅的最小值. 【答案与解析】(1)因为抛物线焦点()()0,0F c c >到直线:20l x y --=的距离为322所以23222c d --==,又因为0c >,所以解得1c =,抛物线的焦点坐标为(0,1),所以抛物线C 的方程为24x y =;(2)因为抛物线的方程为24x y =,即214y x =,所以12y x '=,设过()00,P x y 点的切线l '与抛物线的切点坐标为21(,)4m m ,所以直线l '的斜率2001142y mk m x m-==-,解得210004m x x y =+-或220004m x x y =--;不妨设A 点坐标为2111(,)4m m ,B 点坐标为2221(,)4m m ,因为2004x y -2200004(2)48x x x x =--=-+ 20(2)40x =-+>,所以12m m ≠;221212012111144()42A B m m k m m x m m -==+=-;所以直线A B 的方程为210111()42y m x x m -=-,代入整理得:012y x =;(3)A 点坐标为2111(,)4m m ,B 点坐标为2221(,)4m m ,F 点坐标为()0,1,因为0020x y --=;所以221000004(2)4m x x y x x =+-=+-+,222000004(2)4m x x y x x =--=--+,1202m m x +=,12048m m x =-;因此A FB F ⋅=2222222222112212111*********m m m m m m ⎛⎫⎛⎫⎛⎫⎛⎫+-⋅+-=+⋅+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()2222222212121212121211111111()1()2144164164m m m m m m m m m m m m ⎛⎫⎛⎫⎡⎤=++=+++=++-+ ⎪ ⎪⎣⎦⎝⎭⎝⎭()22220000001139(48)22(48)12692()16422x x x x x x ⎡⎤=-+--+=-+=-+⎣⎦,所以当032x =时,A F B F ⋅取最小值92;21. 设函数()()32f x x kx x k R =-+∈.(1) 当1k =时,求函数()f x 的单调区间;(2) 当0k <时,求函数在[,]k k -上的最小值m 和最大值M . 【答案与解析】(1) 因为()32f x x kx x =-+,所以2()321f x x k x '=-+;当1k =时,2212()3213()033f x x x x =-+=-+>,所以()fx 在R 上单调递增;(2) 因为2()321f x x kx '=-+,22(2)4314(3)k k ∆=--⨯⨯=-;① 当0∆≤时,即30k -≤<时,()0f x '≥,()f x 在R 上单调递增,此时无最小值和最大值;② 当0∆>时,即3k <-时,令()0f x '=,解得22223363k k k k x +-+-==或22223363k k k k x ----==;令()0f x '>,解得233k k x --<或233k k x +->;令()0f x '<,解得223333k k k k x --+-<<;因为223033k k k kk +-+<=<-,2232333k k k kk k --->=>作()f x 的最值表如下:xk 23,3k k k ⎛⎫-- ⎪ ⎪⎝⎭233k k --2233,33k k k k ⎛⎫--+- ⎪ ⎪⎝⎭233k k +-23,3k k k ⎛⎫+-- ⎪⎪⎝⎭k -()f x '+-+()f xk极大值极小值32k k--。
茂名市高三第二次高考模拟数学文试题(含答案)

广东省茂名市2014届高三第二次高考模拟数学(文)试题本试卷分选择题和非选择题两部分,满分 150分,考试时间120分钟。
意事项:1. 答卷前,考生要务必填写答题卷上的有关项目。
2. 选择题每小题选出答案后,用 2B 铅笔把答案的序号填在答题卡相应的位置上。
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内的相应位置上;如 需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效。
4. 考生必须保持答题卷的整洁.考试结束后,将答题卷交回。
1参考公式:锥体的体积公式是 V =」Sh ,3rrrr A . z =-1 — iB . z =-1+iC.z =2D .z已知复数z=1 — i 「、2 )(i 为虚数单位),z 为z 的共轭复数,则下列结论正确的是( ”的否定是5. A . x 0 R, X 0 + 2x 0 +2> 0 2 C. —X R, x + 2x+2> 0 B. D. X o R, _x R, 已知数列{a n }的前n 项和为S n ,且a 6=1,则S H 的值为( ) A . 11 B . 10 对某商店一个月内每天的顾客人数进行统计, 样本的中位数、众数、极差分别是( 2 X 0 + 2x 0 +2》0 2x + 2X+2W 0 C. 12 得到样本的茎叶图(如右图 ) D . 所示), 则该A . 47, 45, 56 B. 46, 45, 53 3 1 2 4 4 8 9C . 46, 45, 56 D. 45, 47, 53 4 5 55577889 00 1 14 7 9 设m 、n 是两条不同的直线, a , 3是两个不同的平面,下列命题正确的 6 ns 阁i A . m // a , n // P 且 a // P ,则川//以 B. m 丄a , n 丄P 且。
丄P,m 丄nC. m 丄□, n U P , m 丄 n.则a 丄B D. m Ua , n Ua , m / P,n // 0 , a // 07 5是(6. 2已知圆(X — a ) 2+ y =1与直线y=x 相切于第三象限,则 a 的值是() B .2C. -2D.其中S 是锥体的底面积.h 是锥体的高。
2013茂名一模(文数)含答案--全WORD--精心排版

茂名市201 3年第一次高考模拟考试数学试卷(文科)第一部分选择题(共50分)一、选择题(本大题共1 0小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知{}2,0,1P =-,{}|11Q x x =-≤≤,则PQ =( )A .{}2,0,1- B .{}0,1 C .∅ D .{}02.气象台预报“茂名市明天降雨的概率是80%”,下列理解正确的是( )A .茂名市明天将有80%的地区降雨B .茂名市明天将有80%的时间降雨C .明天出行不带雨具肯定要淋雨D .明天出行不带雨具淋雨的可能性很大 3.计算:2(1)i i +=( )A .-2B .2C .2iD .-2i4.已知双曲线221(0)5x y m m -=>的右焦点F(3,o),则此双曲线的离心率为( ) A .6 B .322 C .32 D .345.已知向量(1,2),(2,1)a x b =-=,则a b ⊥的充要条件是( ) A .12x =-B .1x =-C .5x =D .x =06.函数121()()2xf x x =-的零点个数为( )A .0B .1C .2D .37.某程序框图如图所示,该程序运行后,输出的x 值为31,则a 等于( ) A .0 B .1 C .2 D .38.若某一几何体的正视图与侧视图均为边长是1的正方形,且其体积为12,则该几何体的俯视图可以是( )9.函数1()ln()f x x x=-的图象是( )10.设向量12(,)a a a =,12(,)b b b =,定义一运算:12121122(,)(,)(,)a b a a b b a b a b ⊗=⊗=。
已知1(,2)2m =,11(,sin )n x x =。
点Q 在()y f x =的图像上运动,且满足OQ m n =⊗ (其中O 为坐标原点),则()y f x = 的最大值及最小正周期分别是( ) A .1,2π B .1,42π C .2,π D .2,4π第二部分 非选择题(共100分)二、填空题(本大题共5小题,第14、15小题任选一道作答,多选的按第14小题给分,共20分) (一)必做题:第1 1至1 3题为必做题,每道试题考生都必须作答。
平面向量 Word版(含答案)
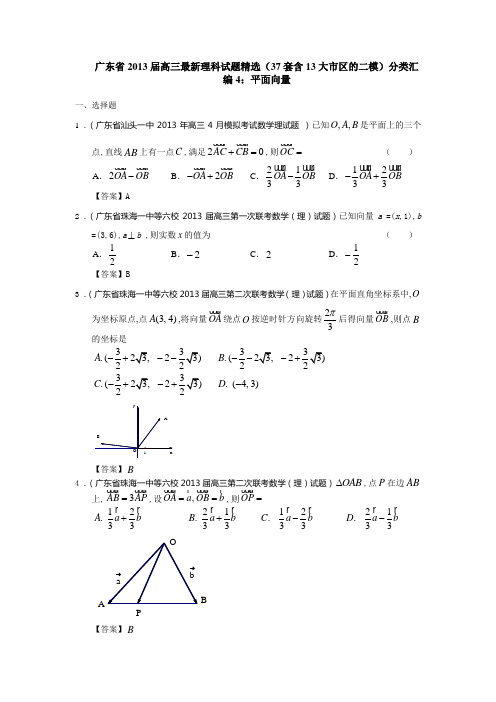
广东省2013届高三最新理科试题精选(37套含13大市区的二模)分类汇编4:平面向量一、选择题1 .(广东省汕头一中2013年高三4月模拟考试数学理试题 )已知,,O A B 是平面上的三个点,直线AB 上有一点C ,满足20AC CB += ,则OC =( )A .2OA OB - B .2OA OB -+C .2133OA OB -D .1233OA OB -+【答案】A2 .(广东省珠海一中等六校2013届高三第一次联考数学(理)试题)已知向量a =(x ,1),b=(3,6),a ⊥b ,则实数x 的值为 ( )A .12B .2-C .2D .21-【答案】B3 .(广东省珠海一中等六校2013届高三第二次联考数学(理)试题)在平面直角坐标系中,O 为坐标原点,点(3,4)A ,将向量OA 绕点O 按逆时针方向旋转23π后得向量OB ,则点B 的坐标是3.(22A -+--3.(22B ---+3.(22C -+-+ .(4,3)D -【答案】B4 .(广东省珠海一中等六校2013届高三第二次联考数学(理)试题)OAB ∆,点P 在边AB 上,3AB AP = ,设,OA a OB b ==,则OP =12.33A a b + 21.33B a b + .C 1233a b - .D 2133a b -PBA【答案】B5 .(广东省肇庆市2013届高三上学期期末统一检测数学(理)试题)定义空间两个向量的一种运算sin ,⊗=⋅<>a b a b a b ,则关于空间向量上述运算的以下结论中,①⊗=⊗a b b a ,②()()λλ⊗=⊗a b a b ,③()()()+⊗=⊗+⊗a b c a c b c , ④若1122(,),(,)x y x y ==a b ,则1221x y x y ⊗=-a b . 恒成立的有 ( )A .1个B .2个C .3个D .4个【答案】B 解析: ①恒成立; ② ()λ⊗=a b sin ,λ⋅<>a b a b ,()λ⊗=a b sin ,λ⋅<>a b a b ,当0<λ时,()()λλ⊗=⊗a b a b 不成立;③当,,a b c 不共面时,()()()+⊗=⊗+⊗a b c a c b c 不成立,例如取,,a b c 为两两垂直的单位向量,易得()+⊗=a b c ()()2⊗+⊗=a c b c ;④由sin ,⊗=⋅<>a b a b a b ,cos ,=⋅<>a b a b a b ,可知2222()()⊗+=⋅ a b a b a b,2()⊗=a b 222222222112212121221()()()()()x y x y x x y y x y x y ⋅-=++-+=- a b a b ,故1221x y x y ⊗=-a b 恒成立.6 .(广东省肇庆市2013届高三上学期期末统一检测数学(理)试题)已知向量(1,cos ),(1,2cos )θθ=-=a b 且⊥a b ,则cos 2θ等于( )A .1-B .0C .12D .2【答案】B 解析:212cos 0cos 20θθ⊥⇔-+=⇔=a b .7 .(广东省汕头市东山中学2013届高三第二次模拟考试数学(理)试题(详解))在平行四边形ABCD 中,AE →=13AB →,AF →=14AD →,CE 与BF 相交于G 点.若AB →=a ,AD →=b ,则 AG →=( )A .27a +17bB .27a +37bC .37a +17bD .47a +27b【答案】C8 .(广东省汕头市第四中学2013届高三阶段性联合考试数学(理)试题)已知平面向量a ,b 的夹角为60°,=a ,||1=b ,则|2|+=a b( )A .2B C .D .【答案】C9 .(广东省汕头市2013届高三上学期期末统一质量检测数学(理)试题)若向量)1,1(),0,2(==b a ,则下列结论正确的是( )A .1=⋅B .||||b a =C .⊥-)(D .//【答案】C10.(广东省广州市2013届高三3月毕业班综合测试试题(一)数学(理)试题)如图2,一条河的两岸平行,河的宽度600d =m,一艘客船从码头A 出发匀速驶往河对岸的码头B .已知AB =1km,水流速度为2km/h, 若客船行驶完航程所用最短时间为6分钟,则客船在静水中 的速度大小为( )A .8 km/hB .C .km/hD.10km/h二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. 【答案】B11.(广东省潮州市2013届高三上学期期末教学质量检测数学(理)试题)平面四边形ABCD 中0AB CD += ,()0AB AD AC -=⋅,则四边形ABCD 是( )A .矩形B .菱形C .正方形D .梯形【答案】B 由0AB CD += ,得AB CD DC =-=,故平面四边形ABCD 是平行四边形,又()0AB AD AC -=⋅ ,故0DB AC =⋅,所以DB AC ⊥,即对角线互相垂直.12.(2013年广东省佛山市普通高中高三教学质量检测(一)数学(理)试题)已知(1,2)=a ,(0,1)=b ,(,2)k =-c ,若(2)+⊥a b c ,则k =( )A .2B .8C .2-D .8-【答案】B13.(广东省肇庆市2013届高三4月第二次模拟数学(理)试题)在ABC ∆中,已知||||||2AB BC CA ===,则向量AB BC =( )A .2B .2-C .D .-【答案】B 解析:1cos 22232AB BC AB BC ππ⎛⎫⎛⎫=⋅-=⨯⨯-=- ⎪ ⎪⎝⎭⎝⎭14.(广东省茂名市2013届高三4月第二次高考模拟数学理试题(WORD 版))向量(2,0),(,)a b x y == ,若b 与b a - 的夹角等于6π,则|b |的最大值为( )A .4B .C .2 D【答案】A15.(广东省揭阳市2013年高中毕业班第二次高考模拟考试理科数学试题)已知点A (1,5)-和向量a =(2,3),若3AB a =,则点B 的坐标为( )A .(7,4)B .(7,14)C .(5,4)D .(5,14) 【答案】设(,)B x y ,由3AB a = 得1659x y +=⎧⎨-=⎩,所以选D .16.(广东省惠州市2013届高三4月模拟考试数学理试题(WORD 版))已知向量(1,1)a =- ,(3,)b m = ,//()a a b +,则m =( )A .2B .2-C .3-D .3【答案】【解析】向量(1,1)a =- ,(3,)b m = ,()(2,1)a b m +=+,因为//()a a b +∴(1)2m -+=,3m =-故选C .17.(广东省广州市2013届高三4月综合测试(二)数学理试题(WORD 版))对于任意向量a 、b 、c ,下列命题中正确的是 ( )A .=a b a b B .+=+a b a b C.()()= a b c a b cD .2= a a a【答案】D18.(广东省潮州市2013届高三第二次模拟考试数学(理)试题)设向量12(,)a a a = ,12(,)b b b = ,定义一运算:12121122(,)(,)(,)a b a a b b a b a b ⊗=⊗=,已知1(,2)2m = ,11(,sin )n x x = .点Q 在()y f x =的图像上运动,且满足OQ m n =⊗(其中O 为坐标原点),则()y f x =的最大值及最小正周期分别是 ( )A .1,2π B .1,42π C .2,π D .2,4π(一)必做题:第9至13题为必做题,每道试题考生都必须作答. 【答案】C二、填空题19.(广东省汕头市东厦中学2013届高三第三次质量检测数学(理)试题 )已知向量,的夹角为60,12==,_________=+;向量与向量2+的夹角的大小为_________.【答案】632π20.(广东省珠海一中等六校2013届高三第二次联考数学(理)试题)如图,在边长为2的菱形ABCD 中,60BAD ∠=,E 为CD 的中点,则___________.AE BD ⋅=BAEDC【答案】121.(广东省湛江一中等“十校”2013届高三下学期联考数学(理)试题)在ABC ∆中90C ∠=o ,BC =2 则=⋅BC AB ________ .【答案】-422.(广东省汕头市东山中学2013届高三下学期入学摸底考试数学(理)试题)若向量a 、b 满足2||||==,与b 的夹角为︒60,则=+||_______【答案】32;23.(广东省汕头市2013届高三3月教学质量测评数学(理)试题)已知在三角形ABC中,AB=2,AC=3,∠BAC=θ,若D 为BC 的三等分点〔靠近点B 一侧).则的取值范围为____.【答案】⎪⎭⎫⎝⎛-37,3524.(广东省华附、省实、深中、广雅四校2013届高三上学期期末联考数学(理)试题)已知e 1、e 2、e 3为不共面向量,若a =e 1+e 2+e 3,b =e 1-e 2+e 3,c =e 1+e 2-e 3,d =e 1+2e 2+3e 3,且d =xa +yb +zc ,则x 、y 、z 分别为_*****_.【答案】答案:52 ,-12,-1解:由d =xa +yb +zc 得e 1+2e 2+3e 3=(x +y +z )e 1+(x -y +z )e 2+ (x +y -z )e 3,∴⎩⎪⎨⎪⎧x +y +z =1,x -y +z =2,x +y -z =3,解得:⎩⎪⎨⎪⎧x =52,y =-12,z =-1.故x 、y 、z 分别为52,-12,-1.25.(广东省韶关市2013届高三4月第二次调研测试数学理试题)已知平面向量a2,)(b a a -⊥;则><b a ,cos 的值是_______.【答案】21; 26.(广东省汕头市2013年普通高中高三教学质量测试试题(二)理科数学试卷)已知正方形ABCD 的边长为1,点E 是AB 边上的点,则DE CB ⋅的值为____________.【答案】127.(广东省江门佛山两市2013届高三4月教学质量检测(佛山二模)数学理试题)已知向量,a b, ()-⊥a b a , 向量a 与b 的夹角为________.【答案】4π三、解答题28.(广东省珠海一中等六校2013届高三第二次联考数学(理)试题)已知(s i n ,c o sa θθ= 、b =(1)若//a b,求tan θ的值;(2)若()f a b θ=+, ABC ∆的三个内角,,A B C 对应的三条边分别为a 、b 、c ,且(0)a f =,()6b f π=-,()3c f π=,求AB AC ⋅.【答案】解:(1)//,sin 0a b θθ∴=sin tan θθθ∴⇒(2)(sin 1)a b θθ+=+a b ∴+===(0)a f ∴===()6b f π∴=-==()33c f π∴===由余弦定理可知:222cos 230b c a A bc +-==7cos cos 2AB AC AB AC A bc A ∴⋅=== (其它方法酌情给分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
茂名市2013年第二次高考模拟考试
数学试卷(文科)
本试卷共4页,21小题, 满分150分。
考试用时120分钟。
参考公式: 锥体的体积公式是1
3
V Sh =
,其中S 是锥体的底面积,h 是锥体的高. 一、选择题。
(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1,已知集合22{1},{log 0}A x x B x x =>=>,则A B = ( ) A .{1}x x <- B .{0}x x >
C .{1}x x >
D .{}
1x 1>-<
x x 2, 已知,x y R ∈,i 是虚数单位,且1xi y i -=-+则(1)
x y
i ++的值是( )
A .2
B .2i -
C .4-
D .2i
3.函数1
()3
f x x =
-的定义域是 A .[2,)+∞ B .[2,3) C .(,3)(3,)-∞⋃+∞ D .()[2,3)3,⋃+∞
4,设双曲线22
221x y a b
-=(0,0a b >>)的虚轴长为2 ,焦距为, 则双曲线的渐近线方
程为
A 、1
2
y x =±
,B 、y x =, C 、y =, D 、2y x =± 5,将函数sin(6)4
y x π
=+的图像上各点向右平移
8
π
个单位,则得到新函数的解析式为
A,sin(6)2
y x π
=-
, B
sin(6)4
y x π
=+ C,
5sin(6)8
y x π
=+
D, sin(6)8
y x π
=+
6,若向量a b c →→→
,,满足a //b ,且b c →→⋅=0,则a b c →→→
⎛⎫+⋅= ⎪⎝⎭
2
A .4
B .3
C .2
D .0
7,已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为 A,3242π-
, B, 243π- C, 24π- D, 242
π
-
8,为了在一条河上建一座桥,施工前在河两岸打上两个桥位桩A,B(如图),要测量A ,B 两点的距离,测量人员在岸边定出基线BC ,测得BC=50m ,105ABC ∠= ,45BCA ∠= 就可以计算出A,B 两点的距离为
A
, B
, C
, D
9, 已知椭圆22
1169
x y +=及以下3个函数:①()f x x =②
()sin f x x =③()cos f x x =;
其中函数图像能等分该椭圆面积的函数个数有( )
A, 1个 B ,2个 C, 3个 D,0个
10,设函数()f x 的定义域均为D ,若存在非零实数使得对于任意x M ∈(M D ⊆),有
x l D +∈,且()()f x l f x +≥,则称()f x 为M 上的高调函数。
现给出下列命题:①函数12
()log f x x =为(0,)+∞上的高调函数;②函数()sin f x x =为R 上的2π高调函数;③如
果定义域为[1,)-+∞的函数2
()f x x =为[1,)-+∞上m 高调函数,那么实数m 的取值范围是[2,)+∞;其中正确的命题的个数是( )
A,0个 B, 1个 C ,2个 D, 3个 二、填空题。
(本大题共5小题,考生作答4小题,每小题5分,满分20分)
(一)必做题(11~13题)
11,若在区域34000x y y x +-≤⎧⎪
≥⎨⎪≥⎩
内任取一点P ,则点P
落在单位圆
221x y +=内的概率是_______
12,某篮球队6名主力队员在最近三场比赛中投进的三 分球个数如下表所示:
右图是统计该6名队员在最近三场比赛中投进的 三分球总数s 的程序框图,则图中判断框应填
13,已知(2)y f x =+为定义在R 上的偶函数,且当2x ≥时,2
()810f x x x =-+,则当
2x <时,
()f x 的解析式为______________________________
(二)选做题(14~15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在极坐标系(,)ρθ (02)θπ≤<中,曲线
(cos sin )1ρθθ+=与(cos sin )1ρθθ-=-的交点的极坐标
为 .
15.(几何证明选做题)如图所示,AB 是半径等 于3的圆O 的直径,C D 是圆O 的弦,BA,DC 的延长线交于点P 若PA=4,PC=5,则DBC ∠=
三、解答题。
(本大题共6小题,满分80分.解答须写出 文字说明、证明过程和演算步骤) 16.(本小题满分12分)
如图,A 是单位圆与x 轴正半轴的交点,点B,P 在
单位圆上,且B(34(,)55
-,AOB α∠=,
AOP θ∠=(0θπ<<),OQ OA OP =+
.
设四边形OAQP 的面积为S , (1) 求tan 4πα⎛⎫
-
⎪⎝
⎭
; (2) 求OQ OA S ∙+
的最大值及此时θ的值。
17.(本小题满分12分)
某校高一级数学必修一模块考试的成绩分为四个等级,85分-100
分为A 等,70分-84分为B 等,55分-69分为C 等,54分以下为D 等.右边的茎叶图 (十位为茎,个位为叶)记录了某班某小组6名学生的数学必修一模块考试成绩。
(1) 求出茎叶图中这6个数据的中位数和平均数;
(2) 若从这6名学生中随机抽出2名,分别求恰好有一名学生的
成绩达到A 等的概率和至多有一名学生的成绩达到A 等的概率,
18.(本小题满分14分)如图,在边长为4的菱形ABCD 中,60DAB ∠= ,点E,F 分别在边CD,CB 上,点E 与点C,点D 不重合,EF AC ⊥, EF AC O ⋂= ,沿EF 将CEF ∆折起到PEF ∆的位置,使得平面PEF ⊥ 平面ABFED (1)求证:BD ⊥平面POA
(2)当点O 在何位置时,PB 取得最小值?
(3)当PB 取得最小值时,求四棱锥P-BDEF 的体积
19.(本小题满分14分)数列{}n a 的前n 项和n S ,1a t =,点(n S ,1n a +)在直线y=2x+1上,( ,2,1=n )
(1) 若数列{}n a 是等比数列,求实数t 的值; (2) 设n b =31(1)log n n a ++ ,数列{
1
}n
b 前n 项和n T 。
在(1)的条件下,证明不等式n T <1; (3) 设各项均不为0的数列{}n
c 中,所有满足10i i c c +< 的整数i 的个数称为这个数列{}
n c 的“积异号数”, 在(1)的条件下,令n c =4
n n
na na -( ,2,1=n ),求数列{}n c 的“积异号数”
20.(本小题满分14分)已知椭圆C :22
221x y a b
+=(a>b>0),一条直线20()x y R λλλ--=∈。
所经过的定点恰好是椭圆的一个定点,且椭圆的离心率为1
2
(1) 求椭圆C 的标准方程;
(2) 已知圆O :2
2
2
x y r +=(b<r<a ),若另一条直线与椭圆C 只有一个公共点M , 且直线与圆O 相切于点N,求MN 的最大值。
21.(本小题满分14分)已知函数3
2
(),()ln ,(0)f x x x bx g x a x a =-++=>。
(1)当a=x 时,求函数()g x 的单调区间; (2)若()f x 存在极值点,求实数b 的取值范围;
(3)当b=0时,令(),1
()(),1f x x F x g x x <⎧=⎨
≥⎩。
P(11,()x F x ),Q(22,()x F x )为曲线y=()F x 上
的两动点,O 为坐标原点,能否使得POQ 是以O 为直角顶点的直角三角形,且斜边中点在y 轴上?请说明理由。
