第五章 三维图形
三维形的基本概念和分类
三维形的基本概念和分类三维形是指具有三个维度的几何形状，也被称为立体形。
它在我们的日常生活中无处不在，从自然界的山川河流到人类建造的建筑物和艺术品，都离不开三维形。
本文将介绍三维形的基本概念和分类。
一、基本概念1. 三维空间：三维形是在三维空间中存在的。
三维空间由三个相互垂直的坐标轴组成，通常被表示为x、y和z。
这三个轴使我们能够在空间中确定一个点的位置。
2. 顶点、边和面：三维形由顶点、边和面组成。
顶点是三维形的角点，边是连接两个顶点的线段，面是由三个或更多个边围成的平面区域。
3. 多面体：多面体是一种特殊的三维形，它的面都是平面多边形。
常见的多面体有正方体、长方体、正六面体等。
4. 曲面：曲面是在三维空间中弯曲或扭曲的面。
曲面可以是无限接近于平面的曲面，也可以是复杂的曲线堆积而成的曲面。
二、分类根据三维形的形状和特点，可以将其分类为以下几种类型。
1. 棱柱：棱柱是由两个平行的、相等的多边形组成的三维形。
它的侧面是矩形，在顶部和底部有两个相等的多边形。
2. 棱锥：棱锥是由一个多边形底部和一个顶点连接线段组成的三维形。
它的侧面是三角形，底部是一个多边形。
3. 球体：球体是由无数个半径相等的圆所组成的三维形。
它的每一个点到球心的距离都相等，因此球体具有无限数量的对称轴。
4. 圆柱体：圆柱体是由一个圆形底部和一个平行于底部的圆形顶部连接线段组成的三维形。
它的侧面是一个矩形，底部和顶部都是圆形。
5. 圆锥体：圆锥体是由一个圆形底部和一个顶点连接线段组成的三维形。
它的侧面是一个三角形，底部是一个圆形。
6. 环体：环体是由两个同心圆和圆环之间的曲面组成的三维形。
它的形状类似于一个圆环的截面。
总结：三维形具有三个维度，是在我们的日常生活中广泛存在的几何形状。
通过了解三维形的基本概念和分类，我们能够更好地理解和描述这些形状。
无论是在建筑、艺术还是科学领域，对三维形的认识都是不可或缺的。
通过不断学习和探索三维形的特点和性质，我们可以更好地应用它们，并在实际生活中创造出更加丰富多样的立体作品。
有限元分析及工程应用-2016第五章
5.1 轴对称问题有限单元法
机械学院
（1）三角形截面环形单元 1）位移模式
qe ui wi u j wj uk wk T
与平面三角形单元相似，仍选取线 性位移模式，即：
u w
a1 a4
a2r a5r
aa36zz
u Niui N ju j Nkuk
,
A2
1 2 2(1 )
单元中除了剪应力外其 它应力分量也不是常量
在轴对称情况下，由虚功原理可推导出单元刚度矩阵
K e VBT DBddrdz 2 BT DBrdrdz
5.1 轴对称问题有限单元法
机械学院
（1）三角形截面环形单元
2）单元刚度矩阵
K e VBT DBddrdz
Loads>Apply>Structural>Displacement>Symmetry B.C.>On Lines，用鼠标在图形窗口上拾取编号为“1”和“3”的线段 ，单击[OK]，就会在这两条线上显示一个“S”的标记，即 为对称约束条件。
(7)施加面力：Main Menu>Solution>Define Loads>Apply>Structural>Pressure>On Lines，用鼠标在图形 窗口上拾取编号为“4”，单击[OK] 在“VALUE Load PRES value”后面的输入框中输入“10”，然后单击[OK]即可
5.1 轴对称问题有限单元法
机械学院
（3）应用实例 (3)建立几何模型：
MainMenu>Preprocessor>Modeling>Create>Areas>Rectangle>By Dimension，在出现的对话框中分别输入：X1=5，X2=10，Y1=0， Y2=20，单击[OK]。
幼儿园数学教案：认识三维图形的基本形状
幼儿园数学教案：认识三维图形的基本形状认识三维图形的基本形状一、引言数学对于幼儿的学习发展起着至关重要的作用。
在数学教育中，幼儿园是一个关键的阶段，因为在这个阶段，幼儿开始接触各种基本概念，其中包括认识三维图形的基本形状。
本篇文章将针对幼儿园数学教案，详细介绍如何教导幼儿认识三维图形的基本形状，并提供一些对应的教学活动和资源。
二、认识三维图形的基本形状1. 什么是三维图形的基本形状？三维图形是空间中的图形，拥有三个维度：长、宽和高。
认识三维图形的基本形状是学习几何概念的基础，其中包括立方体、球体、圆柱体、圆锥体和棱柱体。
让幼儿了解这些形状是教育他们观察、描述和比较物体的重要一步。
2. 如何教导幼儿认识三维图形的基本形状？一个有效的幼儿园数学教案应该从幼儿已有的知识出发，通过互动和实际操作的方式帮助他们建立起对于三维图形基本形状的理解和认识。
以下是一些教学活动的建议：（1）观察和描述物体给幼儿提供一些维度明确的物体，如一个立方体、一个球体和一个圆柱体。
引导幼儿观察这些物体的外形和特征，并鼓励他们用自己的话语描述。
老师可以提出一些问题，如“这个物体有几个面？它们是什么形状？”激发幼儿的思考和表达能力。
（2）通过感官体验认识形状通过触摸、观看和感受不同形状的物体，帮助幼儿区分不同的三维图形。
例如，给幼儿提供一些球体、圆柱体和圆锥体模型，让他们自由地感受这些形状的特点，并进行比较。
（3）综合游戏和艺术创作设计一些游戏和艺术活动，让幼儿以互动和创造的方式来加深对于三维图形基本形状的认识。
例如，游戏中可以要求幼儿用积木搭建不同形状的建筑物，艺术活动中可以要求幼儿用纸板和彩纸制作三维图形的模型。
三、教学资源在幼儿园数学教案中，教学资源的选择和使用对于幼儿的学习非常重要。
以下是一些适合的教学资源：1. 物体模型为幼儿提供不同的三维图形物体模型，如立方体、球体、圆柱体、圆锥体和棱柱体的模型。
这样可以让幼儿通过触摸和观察来认识不同形状的物体。
第5章matlab绘制二维图形及三维图形的方法
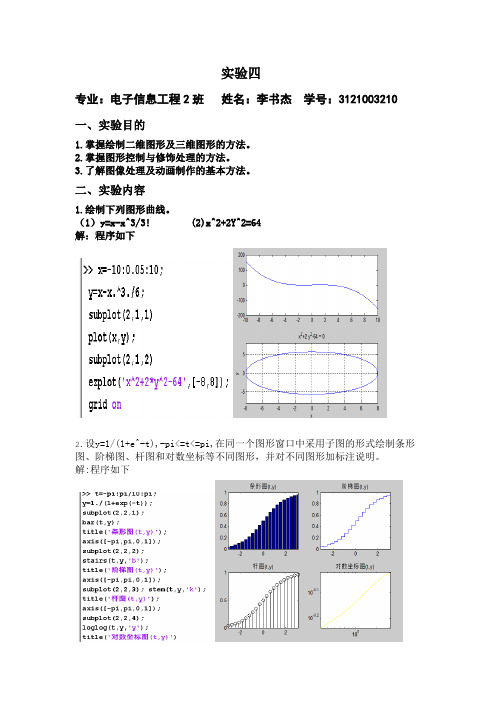
实验四
专业：电子信息工程2班姓名：李书杰学号：3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。
2.掌握图形控制与修饰处理的方法。
3.了解图像处理及动画制作的基本方法。
二、实验内容
1.绘制下列图形曲线。
（1）y=x-x^3/3! (2)x^2+2Y^2=64
解：程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形，并对不同图形加标注说明。
解:程序如下
3.绘制下列极坐标图。
（1）ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解：程序如下
思考练习：
2.绘制下列曲线
（1）y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解：程序如下
（1）
结果如下：
（2）
结果如下：
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。
（1）y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解：程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线，分析两曲线的差别。
解：程序如下
结果如下：
5.绘制下列极坐标图：
(1）p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解：程序如下
结果如下：。
初中数学知识归纳三视的绘制与分析
初中数学知识归纳三视的绘制与分析在初中数学中，我们经常会遇到需要进行三维图形的绘制和分析的问题。
三维图形是由长度、宽度和高度组成的物体，它与我们日常生活息息相关。
掌握绘制和分析三维图形的方法，对于我们理解数学概念、解决实际问题具有重要的意义。
本文将介绍初中数学中常见的三维图形，以及绘制和分析三维图形的方法。
一、三维图形的种类在初中数学中，我们接触到的常见三维图形包括长方体、正方体、棱柱、棱锥、球等。
这些图形具有不同的特征和性质，需要采用不同的方法进行绘制和分析。
1. 长方体和正方体：长方体和正方体都是由六个矩形面构成的，其中长方体的长度、宽度和高度可以不相等，而正方体的长度、宽度和高度相等。
绘制这两种图形时，可以先根据给定的长度、宽度和高度画出底面，然后根据底面的形状和大小绘制出侧面。
2. 棱柱和棱锥：棱柱和棱锥都是由多边形底面和垂直于底面的棱或者边构成的。
在绘制棱柱时，先根据给定的底面形状和大小画出底面，然后根据底面的形状和大小以及给定的高度绘制出侧面。
绘制棱锥时可以按照类似的方法进行，只不过需要注意棱锥的顶点位置。
3. 球：球是由所有离球心的点到球心的距离都相等的点构成的。
要绘制一个球，可以先根据给定的半径画出球心，然后以球心为中心画出若干个同心圆，最后再绘制出连接同心圆上对应点的曲线，即可得到一个球。
二、绘制三维图形的步骤绘制三维图形的步骤可以总结为以下几点：1. 确定基本形状：根据给定的信息，确定图形的基本形状和大小。
2. 绘制底面：根据基本形状和大小，绘制出图形的底面。
对于长方体、正方体、棱柱和棱锥，底面通常是一个多边形；对于球，底面是一个圆。
3. 绘制侧面：根据底面的形状和大小以及给定的高度，绘制出图形的侧面。
对于长方体和正方体，侧面是矩形；对于棱柱和棱锥，侧面是多边形；对于球，侧面是一个曲线。
4. 绘制顶面（可选）：对于某些三维图形，如棱柱和棱锥，可以绘制出图形的顶面。
顶面通常与底面相同。
掌握3D图形的基础知识与应用
掌握3D图形的基础知识与应用3D图形是指用三维坐标系来描述物体或场景的图像。
3D图形的应用广泛，包括电影、游戏、设计、工程等领域。
本文将介绍3D图形的基础知识与应用。
一、基础知识1.1三维坐标系三维坐标系由三个轴构成，分别是x轴、y轴、z轴。
x轴向右，y 轴向上，z轴向前。
这就形成了一个三维空间。
在三维空间中，每一个点都可以用一个三元组(x,y,z)表示。
1.2三维图形的表示方式三维图形可以用多种方式来表示。
其中最常用的是顶点表示法。
顶点表示法是指将物体表示为由一系列顶点组成的集合。
每个顶点都有其在3D空间中的坐标。
这样，三维物体就可以通过连接顶点以及填充三角形、四边形等形状来表示。
1.3三维图形的变换三维图形也可以通过变换来改变其位置、大小和姿态。
常见的变换包括平移、缩放、旋转和投影等。
平移是指将物体沿着坐标轴移动。
缩放是指改变物体的大小。
旋转是指围绕某个轴旋转物体。
投影是指将三维物体映射到二维平面上。
二、应用2.1游戏开发游戏开发是3D图形应用最广泛的领域之一。
3D游戏需要用到大量的3D模型来表示游戏场景和人物角色。
游戏中，通过对3D模型进行变换，使其在屏幕上呈现出绚丽的画面效果。
2.2工程设计工程设计领域也广泛应用3D图形技术。
例如，建筑设计中需要用到三维建模来模拟建筑物的外观和结构。
汽车工程中，也需要用到3D建模来设计汽车的外观和内饰。
2.3电影制作电影制作也是3D图形应用的重要领域。
电影制作中需要用到3D 建模、动画和特效等技术。
3D技术可以帮助电影制作人员创造出逼真的场景和特效，使观众沉浸在电影的世界中。
2.4艺术设计艺术设计也可以借助3D技术来创作出各种有趣的作品。
例如，艺术家可以用3D建模来制作立体雕塑，还可以用3D打印技术将雕塑变成实体。
此外，3D技术还可以用来制作游戏和动漫中的角色和场景。
三、结论随着科技的进步，3D图形技术发展得越来越成熟。
3D技术的广泛应用为很多领域带来了便利和创新。
三维图形的创建.ppt
Segments(段数)设置球体表面的划分复杂度,值越大 三角面越多,球体越光滑.
Geodesic base type (基点面类型)确定由哪种规则的 多面体组成球体.包括以下三cosa(二十面体)
Smooth(光滑)是否进行表面光滑处理. Hemisphere(半球)是否制作半球体. Base to pviot (中心点在底部)设置球体的中心点位
Standard Primitives(标准几何体)
Box:(长方体) 作用是建立正六面体和矩形. 配合Ctrl键可建立正方形底面的长方体。 Cube (立方体)直接建立正方立体模型. Box (长方体)确定长宽高建立长方体模型. Length/width/height(长/宽/高)确定三边的长度. parameters:(参数控制区)建立各种物体的具体参数. Segs(段数)控制长、宽、高，三个方向上的段数的多少. Generate mapping goods(贴图坐标)自动按照三维对象的表
面结构来生成贴图纹理.
cone(锥体) 主要是用来制作圆锥,圆台,棱台,棱锥以及它们的局
部。 Radius1和radius2分别设置锥体两个端面(底面和顶
面)的半径,如果两个值不为0,则产生圆台或棱台体, 如果有一个值为0,则产生锥体,如果两值相等则产 生柱体。 Height(高度)设置锥体的高度. Height segments(高度的段数)设置锥体的高度上的 片断划分数。 Cap segments(端面的段数)设置锥体两端平面沿半 径辐射的段数。 Sides(边数)设置端面圆周上的段数,值越高,锥体就 越光滑。
Slice on(切片)设置是否开启切片设置,打开它,可以在 下面的设置中调节柱体局部切片的大小.
Slice from /slice to (切片开始/切片结束)控制沿柱体 自身Z轴切片开始或结束的度数.
第五章 二维样条线转换三维模型
侧面斜切物体的光滑量由以下2个内容控制： 1、原始截面创建参数中的Steps(步幅数)设置。 2、原始侧面线条创建参数中的Steps(步幅数)设置。
举例：
酒瓶
像框
吊顶的制作
最终效果
屋顶
会议桌Βιβλιοθήκη 桌子腿： 1、画四个圆角矩形L：90 W：17 CR：5 L：120 W：30 CR：5 2、添加Extrude命令，Amount值：80
窗户的制作:
1、在Front视窗内创建一矩形 L:150 W:200 2、添加Edit Spline命令,选择样条线编辑命 令在Outline中
输入值:5。对内样条线进行复制，作为内框使用，用 Detach分离 3、添加Extrude命令，在Amount中输入：20 4、在复制的内框内再画两矩形，分别为：L：40 W：85 L：80 W：85 5、选择内框，添加Edit Spline命令，选择编辑样条线，单 击Attach命令，在内框中单击四个矩形，使其成为一个 整体。调整它们的位置。 6、按内框的大小，用Plane命令在窗体内画一平面作为窗 户的玻璃。
二维样条线转换三维模型
在现实生活中，很多漂亮的场景都有适合 的模型，但3ds max中创建三维模型的方法 有两种：一种是简单的三维模型创建、另 一种是扩展三维模型的创建，这两种方法 创建的模型是简单，而现实场景中的模 型大都是复杂的，而且还不能分解成简单 的三维模型。我们学习将二维图形转为三 维图是创建复杂图形的前奏，也是为以后 学习室内外设计的基础。
Segments(线段数)设置。 3、斜切参数面板中的“Smooth Across levels(平滑层
级的边界)”选项。
举例：
斜切文字
苏科版数学七年级上册第五章 走进图形世界—立体图形、图形的变化教教学设计
苏科版数学七年级上册第五章走进图形世界—立体图形、图形的变化教教学设计一. 教材分析《苏科版数学七年级上册》第五章“走进图形世界”主要介绍了立体图形和图形的变化。
这一章的内容是学生从二维图形向三维图形过渡的关键章节，对于培养学生的空间想象能力和抽象思维能力具有重要意义。
本章内容主要包括立体图形的概念、特征和分类，以及图形的变化，如平移、旋转等。
通过本章的学习，学生能够掌握立体图形的的基本知识，了解图形的变化规律，提高空间想象能力。
二. 学情分析学生在学习本章内容前，已经掌握了基本的二维图形知识，如三角形、四边形等。
但立体图形对学生来说是一个新的概念，需要通过实例和模型来帮助学生理解和掌握。
另外，图形的变化对学生来说也是一个新的知识点，需要通过大量的练习来熟练掌握。
三. 教学目标1.知识与技能：学生能够理解立体图形的概念，掌握立体图形的基本特征和分类；学生能够理解图形的变化规律，学会用平移和旋转的方法来变换图形。
2.过程与方法：通过观察、操作、思考，培养学生的空间想象能力和抽象思维能力；通过小组合作，培养学生的团队协作能力和沟通能力。
3.情感态度价值观：培养学生对数学的兴趣，使学生感受到数学的美妙；培养学生勇于探索、积极思考的科学精神。
四. 教学重难点1.立体图形的概念和分类2.图形的变化规律五. 教学方法采用“问题驱动”的教学方法，通过提出问题，引导学生思考和探索，从而达到理解知识的目的。
同时，结合“实例教学”和“小组合作”的方法，让学生在实际操作中学习，在团队协作中成长。
六. 教学准备1.准备立体图形模型和图片，用于展示和讲解。
2.准备相关的练习题，用于巩固和拓展学生的知识。
七. 教学过程1.导入（5分钟）通过提出问题：“你们在生活中见过哪些立体图形？”引发学生的思考，激发学生的学习兴趣。
2.呈现（10分钟）展示立体图形模型和图片，引导学生直观地理解立体图形的概念和特征。
同时，讲解立体图形的分类，如柱体、锥体、球体等。
教案：认识三维图形
教案：认识三维图形一、教学目标：1.了解三维图形的概念和特点。
2.掌握三维图形的绘制及变换方法。
3.学习应用数学知识分析和解决相关问题。
4.提高学生的空间想象力和创造力。
二、教学重点：1.掌握三维图形的概念和特点。
2.学习三维图形的绘制及变换方法。
三、教学难点：1.理解三维图形的空间特性。
2.掌握三维图形的变换方法。
四、教学准备：计算机、教学软件及教学课件。
五、教学过程：一、引入：通过一个简单的例子引入本节课的内容。
举个例子，当我们看到一个正方体的平面图形时，我们可以轻松地理解它的形状和特征。
然而，当我们看到这个正方体的实物时，它的形状和特征就很难理解了。
为什么呢？因为它有高度、厚度，而不是表面积。
这样我们就可以进入到三维图形的学习。
二、三维图形的概念和特点：1.三维图形的概念：三维图形是指具有高度、宽度、厚度三个维度的图形。
2.三维图形的特点：(1)有可分辨的内部和外部区别。
(2)表面不再是平面而是光滑曲面，有崎岖不平的感觉。
(3)需要使用更多高级几何概念来解决问题。
三、三维图形的绘制及变换方法：1.三维图形的绘制方法：(1)线框图法：将三维图形的表面及边缘用线条勾画出来，以便考察和分析三维图形的内部和外部结构。
(2)透视法：用透视规律表现三维图形的远近、大小和比例关系。
(3)投影法：通过不同的投影方向对三维图形进行投影，获得一个或多个平面图像，以便于分析和处理。
2.三维图形的变换方法：(1)平移：指在三维坐标系中，将物体沿着任意方向移动一定的距离。
(2)旋转：指物体围绕某个中心点旋转一定角度。
(3)缩放：指通过改变三维图形的大小和形状来对三维图形进行变换。
四、应用数学知识分析和解决相关问题：学生应用数学中的几何知识、向量知识、线性代数知识等，对三维图形的表面积、体积、重心等进行计算，并解决一些相关问题。
五、提高学生的空间想象力和创造力：三维图形的学习不仅能够提高学生的空间想象力，而且可以培养学生的创造力。
三维立体图
三维立体图简介在计算机图形学中，三维立体图是一种将三维物体或场景以平面方式展示的图形形式。
它是通过透视投影的方式，将三维物体转换为二维平面上的图像。
三维立体图可以用于可视化和交互式应用，在各种领域中都有广泛的应用，如游戏开发、工程建模、虚拟现实等。
透视投影三维立体图的核心技术是透视投影。
透视投影是一种模拟人眼看到物体的方式，使得近处的物体看起来更大，远处的物体看起来更小。
在三维立体图中，透视投影使得物体在远处逐渐消失，从而产生真实感和深度感。
透视投影的原理是通过将三维物体的坐标变换到一个投影平面上。
这个投影平面通常是一个视口，模拟人眼所看到的视角。
在进行投影前，需要先设定相机的位置和视角，通过相机位置和物体的坐标，可以计算出物体在投影平面上的位置。
然后，将物体的坐标投影到投影平面上，得到二维平面上的坐标。
尽管透视投影能够在二维平面上模拟三维感，但它也有一些局限性。
例如，由于透视投影是线性的，物体越远离相机，投影的误差也越大。
另外，透视投影只能显示物体的一个面，而不能显示物体的背面。
三维立体图的应用游戏开发三维立体图在游戏开发中有着广泛的应用。
它能够实现逼真的游戏场景和角色模型，给玩家带来沉浸式的游戏体验。
通过三维立体图，游戏开发人员可以创建出逼真的山脉、建筑物、车辆等物体，并对其进行动画、碰撞检测等操作。
同时，通过透视投影，游戏开发人员可以为玩家呈现出不同的视角，增加游戏的可玩性。
工程建模在工程领域，三维立体图被广泛应用于建筑、机械等领域的建模和设计中。
通过三维立体图，工程师可以更直观地了解建筑物或机械设备的结构和外观。
工程师可以将设计好的三维模型进行渲染，从不同的角度观察和分析模型，以便作出优化和改进。
虚拟现实三维立体图在虚拟现实中的应用也越来越广泛。
虚拟现实是一种模拟真实世界的技术，通过特殊的设备和软件，使用户感觉像身临其境一样。
三维立体图在虚拟现实中可以构建出虚拟的场景和环境，让用户感受到身处其中的感觉。
三维立体图
立体图（也称为“三维立体图”或“三维立体画”）是一类能够让人从中感觉到立体效果的平面图像。
观察这类图像通常需要采用特殊的方法或借助器材。
立体图最初用来表示需要通过立体镜观察的一对图像，所说的立体图还包括anaglyph和autostereogram等。
机械制图中的轴测图，因它能在一个投影图上把物体的三个方向（如前面、上面、侧面）的形状表示出来，图形具有较好的立体感，故称之为立体图。
立体图是表现物体三维模型最直观形象的图形，它可以生动逼真地描述制图对象在平面和空间上分布的形态特征和构造关系。
立体图最早被Charles Wheatstone于1838年发现，他同时对双目视觉给出了一种解释，这引导他构建了一种由棱镜和镜子组成的器材，从而使人可以从一对二维图像中观察到三维效果。
随着在计算机上制作autostereogram的技术的发展，立体图得以重新流行。
在autostereogram中，三维效果隐藏于一幅单独的二维图像中，观察者只有在正确地将目光聚焦之后才能观察到立体影像。
Magic Eye系列就是一个流行的实例。
Magic Eye将autostereogram称作立体图，这使得许多人认为立体图就是autostereogram的同义词。
Stereoscopic imaging 通常是一对特制的图像，观察者需要通过使用立体镜使双眼分别看到对应的图像才能产生立体感。
如果一对图像比较窄而且被并排放置在一起，也可以直接用裸眼观察，方法类似于观察autostereogram。
Anaglyph images 也称为“红/绿”图，是由一对特制的单色图像通过不同的颜色通道（通常是红和青或品红和绿）混合而成。
观察者通常需要佩戴立体眼镜。
这种立体眼镜的镜片是两块滤光片，滤光片的类型由图像决定。
比如观察一幅通过红色和青色通道混合的图像，观察者需要佩戴带有红色滤光片和青色滤光片的立体眼镜，红色滤光片使一只眼睛只能看到图像上的红色部分，而青色滤光片则使另一只眼睛只能看到图像上的青色部分，从而模拟了观察立体景物的情况。
机械制图电子教案投影法
机械制图电子教案投影法第一章：投影法基础1.1 投影法定义解释投影法的概念和作用。
强调投影法在机械制图中的重要性。
1.2 投影法的分类介绍正投影法和斜投影法的区别和应用。
解释单面投影和双面投影的概念。
1.3 投影法的原理详细解释投影法的基本原理。
探讨投影法如何将三维物体转化为二维图形。
第二章：基本投影变换2.1 投影变换的概念解释投影变换的含义和作用。
强调投影变换在机械制图中的重要性。
2.2 投影变换的类型介绍平移、旋转和缩放等基本投影变换。
解释这些变换对投影图形的影响。
2.3 投影变换的应用探讨如何使用投影变换来解决实际问题。
给出一些示例，展示投影变换在机械制图中的应用。
第三章：直线和角的投影3.1 直线的投影解释直线在投影中的表现形式。
探讨如何通过投影来确定直线的方向和位置。
3.2 角的投影解释角在投影中的表现形式。
探讨如何通过投影来确定角的大小和位置。
3.3 直线和角的投影应用给出一些示例，展示直线和角的投影在机械制图中的应用。
强调这些投影在实际工程中的重要性。
第四章：平面图形的投影4.1 平面图形的投影概念解释平面图形在投影中的表现形式。
强调平面图形的投影在机械制图中的重要性。
4.2 常见平面图形的投影介绍圆形、方形、三角形等常见平面图形的投影。
解释这些图形在投影中的特点和规律。
4.3 平面图形的投影应用给出一些示例，展示平面图形的投影在机械制图中的应用。
强调这些投影在实际工程中的重要性。
第五章：三维图形的投影5.1 三维图形的投影概念解释三维图形在投影中的表现形式。
强调三维图形的投影在机械制图中的重要性。
5.2 常见三维图形的投影介绍长方体、圆柱体、球体等常见三维图形的投影。
解释这些图形在投影中的特点和规律。
5.3 三维图形的投影应用给出一些示例，展示三维图形的投影在机械制图中的应用。
强调这些投影在实际工程中的重要性。
第六章：投影法在机械制图中的应用6.1 零件图的投影解释零件图的概念和作用。
三维几何形状的绘图教学笔记
三维几何形状的绘图教学笔记介绍这份教学笔记旨在帮助学生了解和绘制三维几何形状的图形。
在这些笔记中，我们将介绍一些基本的三维几何形状，包括球体、立方体和圆柱体，并学习如何用几何图形的标准符号来表示它们。
球体球体是一个具有无限个相同半径的点，这些点与球心的距离均相等。
绘制一个球体时，我们需要知道球心的坐标和半径的大小。
我们可以使用圆来表示球面，其中圆心是球心，半径等于球的半径。
绘制球体的步骤如下：1.在纸上选择一个点作为球心，记作O。
2.确定球心到球面上任意一点的半径长度，记作r。
3.以O为圆心，r为半径，绘制一个圆。
立方体立方体是一个具有六个相等面积的正方形的多面体。
每个面都是一个矩形，并且相邻面共享边。
绘制一个立方体时，我们需要知道一个顶点的坐标和两条相邻边的长度。
绘制立方体的步骤如下：1.在纸上选择一个点作为立方体的一个顶点，记作A。
2.确定立方体的其他顶点的坐标。
根据立方体的形状，我们可以计算出其他顶点的坐标。
3.绘制立方体的六个面。
圆柱体圆柱体是一个具有两个平行且相等半径的圆组成的立体。
圆柱体的侧面是一个矩形，并且两个底面共享边。
绘制一个圆柱体时，我们需要知道圆心的坐标、半径的大小和高度。
绘制圆柱体的步骤如下：1.在纸上选择一个点作为圆柱体的一个圆心，记作O。
2.确定圆柱体的底面圆的半径和高度。
3.以O为圆心，绘制一个底面圆。
4.在底面圆上方和下方的相应位置绘制平行于底面圆的圆。
5.连接底面圆和上下两个圆的对应点，形成圆柱体的侧面矩形。
总结通过这份教学笔记，我们学习了如何绘制三维几何形状中的球体、立方体和圆柱体。
掌握这些基本的绘图技巧将帮助我们更好地理解和应用三维几何形状的概念。
以上就是三维几何形状的绘图教学笔记的内容。
希望这份笔记能够对学生们学习三维几何图形有所帮助。
三维图形的名词解释是什么
三维图形的名词解释是什么三维图形是指在三维欧几里得空间中表示的图形。
与二维图形相比，三维图形具有更多的信息和维度，能够更真实地呈现物体的形状和空间关系。
在计算机图形学、建筑设计、工程制图等领域中，三维图形的应用已经变得越来越广泛。
一、三维图形的基本概念在三维图形中，我们首先要了解一些基本概念：1. 顶点：顶点是构成三维图形的基本元素，它们是图形中的一个具体位置，通常以坐标的形式来表示。
顶点是连接线、面和体的基础。
2. 线：线由两个顶点连接而成，它是连接两个点之间最短的路径。
在三维图形中，线可以用来表示物体的边缘、轮廓等。
3. 面：面是由三个或更多个顶点构成的平面图形。
在三维图形中，面可以用来表示物体的表面，如立方体的六个面。
4. 体：体是由多个面构成的三维图形，它可以是实心的，也可以是空心的。
在三维图形中，体可以用来表示实际物体的形状，如球体、圆柱体等。
二、三维图形的表示方法为了将三维图形准确地表示出来，我们需要使用特定的方法。
常见的三维图形表示方法包括：1. 顶点表示法：顶点表示法是最基本的表示方法之一，它通过坐标来表示每个顶点的位置。
通过连接顶点，我们可以得到线、面和体等。
2. 多边形网格表示法：多边形网格是将面划分成许多小的三角形或四边形网格，每个小网格由多个顶点和边构成。
通过连接相邻的顶点和边，我们可以得到更加真实和精确的图形。
3. 参数曲线和曲面表示法：参数曲线和曲面表示法是一种通过参数方程来表示曲线和曲面的方法。
通过调整参数的值，我们可以得到不同形状的曲线和曲面。
4. 体素表示法：体素表示法是一种将三维空间划分成小的立方体网格，并用颜色或纹理来表示每个立方体的属性和形状的方法。
通过组合不同的立方体，我们可以得到更加复杂的三维图形。
三、三维图形的应用领域三维图形在许多领域中都有广泛的应用，下面列举几个主要的应用领域：1. 计算机图形学：三维图形在计算机图形学中扮演着重要的角色，它被广泛应用于电子游戏、动画片、虚拟现实等领域。
三维图形的绘制3篇
三维图形的绘制第一篇：三维图形绘制的基础知识三维图形的绘制是计算机图形学的一个重要分支。
它主要涉及从二维的平面上，通过透视、平移、旋转等变换操作，生成具有三维空间感的图像。
这些图像可以在计算机科学、工程、建筑、影视等领域中得到广泛应用。
三维图形的绘制通常需要借助于专业的三维建模软件或计算机编程语言来实现。
这些软件或语言提供了一套规范和标准的图形库，可以帮助程序员或设计师更加方便快捷地生成所需的三维图形。
在进行三维图形的绘制之前，需要掌握一些基础的知识。
首先，要了解三维坐标系。
三维坐标系一般由X、Y、Z三个轴和一个原点组成，其中X轴表示水平方向、Y轴表示垂直方向，Z轴表示深度方向。
可视化的时候，X、Y、Z三个轴通常用红、绿、蓝三种颜色表示，这就是RGB颜色模式。
其次，要了解三维图形的基本构成单位——三角形。
一个由多个三角形组成的面称为多边形，而一个由多个多边形组成的物体称为模型。
三角形在三维图形中起着至关重要的作用，它们不仅可以构成各种形状的物体，还可以用来做光照处理。
最后，还需要对各种变换操作有一定的了解。
其中比较基础的变换包括平移、旋转、缩放等。
这些变换操作可以将三维图形上的物体，按一定角度或距离进行移动、变形，从而得到不同的视角和效果。
综上所述，三维图形的绘制需要掌握三维坐标系、三角形、变换等基础知识，并借助于专业的建模软件或开发语言进行实现。
对于初学者来说，可以通过学习三维图形的基础知识，逐步掌握绘制技巧，从而进一步提高自己的三维图形绘制能力。
第二篇：三维图形绘制的建模方法三维图形绘制的建模方法有多种，各有其特点和适用范围。
下面介绍其中比较常见的三种建模方法。
第一种是多边形网格建模（Polygon Mesh Modeling）。
这种建模方法是最基础也是最常见的一种，主要通过组合不同数量、不同形状的三角形、四边形面片来构建三维模型。
这种方法的优点是灵活、实时交互性强，适用于低多边形模型的构建，如游戏或一些快速原型设计等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Plot3D命令的选项
例4 Plot3D[1-y^2,{x,-5,5},{y,-5,5},BoxRatios->{1,1,2}, Boxed->False,Axes->False]; Plot3D[1-y^2,{x,-5,5},{y,-5,5},BoxRatios->{1,1,2}, Boxed->False,Axes->False,Shading->False]; Plot3D[1-y^2,{x,-5,5},{y,-5,5},BoxRatios->{1,1,2}, Boxed->False,Axes->False,HiddenSurface->False];
5.1 绘制二元函数的图形
PlotPoints->n：指定在每个方向上取n个点 PlotPoints->{nx,xy}：指定在x轴和y轴的采样点个 数 例2 f[x_,y_]=x^2 y^2 Exp[-(x^2+y^2)]; Plot3D[f[x,y],{x,-2,2},{y,-2,2}]; Plot3D[f[x,y],{x,-2,2},{y,-2,2},PlotPoints->25]; Plot3D[f[x,y],{x,-2,2},{y,-2,2},PlotPoints->40];
5.2 其它的绘图命令
ContourPlot[f[x,y],{x,xmin,max},{y,ymin,ymax}]： 绘制函数f[x,y]在给定矩形上的等高线 Mathematica中绘制的等高线采用了与地图中等高 线绘制的类似处理，采用颜色的深浅来表示值的大 小：值越大的区域，颜色越浅，反之亦反。 Contours->n：确定要绘制的轮廓数，缺省为10 Contours->{k1,k2,...}：指定等高线的值 ContourShading->False：不显示阴影 ContourLines->False：去掉轮廓段
ListContourPlot[array]：生成二维数组的轮廓图 ListDensityPlot[array]：生成二维数组的密度图 例11 lst=Table[Random[],{x,1,10},{y,1,10}]; ListContourPlot[lst,MeshRange->{{-5,5},{3,7}}]; ListDensityPlot[lst,MeshRange->{{-5,5},{3,7}}];
Plot3D命令的选项
AxesEdge->Automatic 由系统确定显示哪个边界轴 BoxStyle：指定包围盒的绘制方式，如Dashing, Thickness,GrayLevel或RGBColor Mesh：确定在曲面上是否显示格线 Shading：确定是否给曲面加阴影效果。默认值为 Shading->True 下面以几种不同方式绘制抛物柱面z=x^2
5.1 绘制二元函数的图形
例3 Plot3D[x^2,{x,-2,2},{y,-2,2}] Plot3D[x^2,{x,-2,2},{y,-2,2},Mesh->False] Plot3D[x^2,{x,-2,2},{y,-2,2},Shading->False] Plot3D[x^2,{x,-2,2},{y,-2,2},BoxRatios->{1,1,1}] Plot3D[x^2,{x,-2,2},{y,-2,2},FaceGrids->{{1,0,0}, {0,1,0}}] Plot3D[x^2,{x,-2,2},{y,-2,2},AxesEdge->{{-1,1},{1,1}, {1,-1}}]
柱形图
例15 <<Graphics`Graphics3D` lst={{1,2,3,4},{5,6,7,8},{9,10,11,12}}; BarChart3D[lst,AxesLabel->{"x","y","z"}]; BarChart3D[lst,XSpacing->.5,YSpacing>.5,AxesLabel->{"x","y","z"}];
例12 <<Graphics`ContourPlot3D` ContourPlot3D[z-x^2-y^2,{x,-5,5},{y,-5,5},{z,0,10}, Contours->{0.,5.}, BoxRatios->{1,1,1}, PlotPoints->5];
Байду номын сангаас
ListContourPlot3D是ContourPlot3D的离散形式， 包含在软件包Graphics`ContourPlot3D`中 ListContourPlot3D[array]：绘制由三维数组f中的 数确定的轮廓图
科学计算软件
三维图形
第五章
5.1 绘制二元函数的图形
具有两个变量的函数可以看作是三维空间中的曲面。 绘制曲面的最简单命令是Plot3D Plot3D[f[x,y],{x,xmin,xmax},{y,ymin,ymax}] 绘制函数f[x,y]在矩形xmin<=x<=xmax，ymin <=y<=ymax上定义的三维曲面 例1 Plot3D[Sin[x-y],{x,-Pi,Pi},{y,-Pi,Pi}]
等高线图
例9 给出抛物面z=x^2+y^2的等高线图。 ContourPlot[x^2+y^2,{x,-10,10},{y,-10,10}] ContourPlot[x^2+y^2,{x,-10,10},{y,-10,10}, ContourLines->False] ContourPlot[x^2+y^2,{x,-10,10},{y,-10,10}, ContourShading->False] ContourPlot[x^2+y^2,{x,-10,10},{y,-10,10}, ContourShading->False, ContourLines->False]
密度图
与等高线图不同，密度图将定义域分成规则的网格， 在每个网格上由一个采样值的大小确定颜色的深浅。 越淡的区域表示的值越高 DensityPlot[f[x,y],{x,xmin,xmax},{y,ymin,ymax}]
例10 DensityPlot[x^2+y^2,{x,-10,10},{y,-10,10}]; DensityPlot[x^2+y^2,{x,-10,10},{y,-10,10},Mesh>False];
5.3 特殊的三维图形
在软件包Graphics`Graphics3D`中包含大量实用的 绘图命令 BarChart3D[array]：利用array确定高度，构造三 维的柱形图。array={{z11,z12,...}, {z21,z22,...},...} zij表示柱(i，j)的高度 XSpacing与YSpacing：确定在x方向与y方向上柱之 间的距离，取值在[0，1]之间 SolidBarEdge->False：去掉柱之间的边界
5.1 绘制二元函数的图形
f[x,y]在给定的矩形内有无数个值，使用计算机绘 图只能计算出其中有限个点处的值，绘制出的曲面 实际上是由有限块简单曲面构成的(类似的一维函 数的图形是由若干段直线段构成的) PlotPoints选项指定生成图形式在每个方向(x、y)上 所用的点数(采样点)，默认值为15。 也就是说将给定的矩形(xmin,xmax)*(ymin,ymax) 分成14*14的网格，先计算出每个网格点上的函数 值(共有15*15个)，再由相邻的4个点确定一个曲面
空间参数曲线的绘制
ParametricPlot3D[{x[t],y[t],z[t]},{t,tmin,tmax}]： 绘制以t为参数的三维曲线 ParametricPlot3D[{x[s,t],y[s,t],z[s,t]},{s,smin,smax}, {t,tmin,tmax}]]绘制由s,t为参数的三维曲面
透视效果：观察的角度
例5 Plot3D[x^2-y^2,{x,-5,5},{y,-5,5},BoxRatios->{1,1,1}]; Plot3D[x^2-y^2,{x,-5,5},{y,-5,5},BoxRatios->{1,1,1}, ViewPoint->{2,2,2}]; Plot3D[x^2-y^2,{x,-5,5},{y,-5,5},BoxRatios>{1,1,1},ViewPoint->{1.5,-2.6,-1.5}];
Plot3D命令的选项
Axes->False：不显示坐标轴 Axes->{True|False,True|False,True|False}：分别控 制三个坐标轴是否显示 Boxed->False：不显示包围图形的盒子 BoxRations->{sx,sy,sz}：指定三维图形包围盒各边 长度的比率 Ticks->False：不显示所有坐标轴上的刻度以及相 应的标签
透视效果：观察的角度
三维图形的透视图的效果与观察点的位置密切相关 ViewPoint->{x,y,z}：给出相当于要绘制曲面的包围 盒中心的视点位置 对于视点坐标而言，包围盒的最长边被缩放为1， 视点必须在包围盒的外部 ViewPoint参数的默认值为{1.3，-2.4，2.0} Input->3D ViesPoint Selector:图形界面交互观察不 同视点的透视效果
空间参数曲线的绘制