2014-2015学年江苏省泰州市泰兴三中高一(下)期初数学试卷
《解析》江苏省泰州市泰兴一中2014-2015学年高一下学期期末数学补考试卷Word版含解析

江苏省泰州市泰兴一中2014-2015学年高一下学期期末数学补考试卷一、填空题(每题5分)1.已知集合A=[1,4),B=(﹣∞,a),若A⊆B,则实数a的取值范围为.2.设函数f(x)=则的值为.3.函数的定义域是.4.若点A(x,y)是300°角终边上异于原点的一点,则的值为.5.求值:=.6.已知向量=(﹣1,1),=(1,2),且(2+)∥(﹣λ),则λ=.7.已知向量与的夹角为θ,且||=3,||=4,|+|=5,则θ=.8.△ABC中,已知AB=2,BC=5,S△ABC=4,∠ABC=θ,则cosθ=.9.已知0<<β<π,且cos,sin(α+β)=,则sinα=.二、解答题10.已知函数f(x)=2sin2x.(Ⅰ)求函数f(x)最小正周期;(Ⅱ)若f(x)=2,求x的值;(Ⅲ)写出函数f(x)的单调递减区间.11.已知向量||=1,||=.(Ⅰ)若向量的夹角为60°,求的值;(Ⅱ)若,求的值;(Ⅲ)若,求的夹角.12.已知向量=(1,cosx),=(,sinx),x∈(0,π).(Ⅰ)若∥,分别求tanx和的值;(Ⅱ)若⊥,求sinx﹣cosx的值.江苏省泰州市泰兴一中2014-2015学年高一下学期期末数学补考试卷一、填空题(每题5分)1.已知集合A=[1,4),B=(﹣∞,a),若A⊆B,则实数a的取值范围为a≥4.考点:集合的包含关系判断及应用.专题:计算题.分析:集合A=[1,4),B=(﹣∞,a),A⊆B,根据子集的定义可求.解答:解:由题意,集合A=[1,4)表示大于等于1而小于4的数,B=(﹣∞,a)表示小于a的数,∵A⊆B,∴a≥4故答案为a≥4点评:本题的考点是集合关系中的参数取值问题,主要考查集合中的子集关系,关键是理解集合表达的数的范围..2.设函数f(x)=则的值为.考点:函数的值;分段函数的解析式求法及其图象的作法.专题:计算题.分析:本题是分段函数求值,规律是先内而外逐层求值,先求f(2)值,再根据的取值范围判断应该用那一段上的函数解析式,代入求值即为的值.解答:解:由于2>1,故f(2)=22+2﹣2=4故=≤1故=1﹣=故答案为.点评:本题考点是求函数的值,本题是一个分段复合型函数,此类题易出错,错因在解析式选用不当.3.函数的定义域是[1,2).考点:函数的定义域及其求法;对数函数的定义域.专题:计算题.分析:根据对数函数的真数一定要大于0,可以得2﹣x>0;又有偶次开方的被开方数非负,得到:x﹣1≥0,进而求出x的取值范围.解答:解:∵2﹣x>0,且x﹣1≥0,解得1≤x<2,∴函数的定义域为[1,2)故答案为:[1,2).点评:本题考查对数函数求定义域问题,注意对数函数的真数一定大于0,偶次开方的被开方数一定非负,属基础题.4.若点A(x,y)是300°角终边上异于原点的一点,则的值为.考点:任意角的三角函数的定义.专题:计算题.分析:根据三角函数的定义,是300°角的正切值,求解即可.解答:解:点A(x,y)是300°角终边上异于原点的一点,则的值就是:tan300°= 所以=tan300°=﹣tan60°=故答案为:﹣点评:本题是基础题,考查任意角的三角函数的定义,诱导公式的应用,考查计算能力.5.求值:=.考点:诱导公式的作用.专题:计算题.分析:直接利用诱导公式,化简表达式为特殊角以及锐角的三角函数,然后求出值即可.解答:解:===.故答案为:.点评:本题是基础题,考查诱导公式的应用,注意特殊角的三角函数值,考查计算能力.6.已知向量=(﹣1,1),=(1,2),且(2+)∥(﹣λ),则λ=.考点:平行向量与共线向量.专题:平面向量及应用.分析:利用向量坐标运算、向量共线定理即可得出.解答:解:2+=2(﹣1,1)+(1,2)=(﹣1,4),=(﹣1,1)﹣λ(1,2)=(﹣1﹣λ,1﹣2λ),∵(2+)∥(﹣λ),∴﹣(1﹣2λ)﹣4(﹣1﹣λ)=0,化为6λ=﹣3,解得λ=﹣.故答案为:﹣.点评:本题考查了向量坐标运算、向量共线定理,属于基础题.7.已知向量与的夹角为θ,且||=3,||=4,|+|=5,则θ=90°.考点:数量积表示两个向量的夹角.专题:计算题.分析:由题意可得=,再利用两个向量的数量积的定义解得cosθ=0,根据θ的范围求出θ的值.解答:解:由题意可得==9+16+2=25+2×3×4cosθ=25,解得cosθ=0.再由0°≤θ≤180°可得θ=90°,故答案为90°.点评:本题主要考查两个向量的数量积的定义,两个向量数量积的运算,根据三角函数的值求角,属于中档题.8.△ABC中,已知AB=2,BC=5,S△ABC=4,∠ABC=θ,则cosθ=.考点:三角形中的几何计算.专题:解三角形.分析:根据三角形的面积公式进行求解即可.解答:解:∵AB=2,BC=5,S△ABC=4,∴S△ABC=AB•BCsinθ=4,即sinθ=4,则sinθ=,则cosθ==,故答案为:点评:本题主要考查三角形面积的计算以及同角的三角函数的基本关系,比较基础.9.已知0<<β<π,且cos,sin(α+β)=,则sinα=.考点:两角和与差的正弦函数.专题:计算题;三角函数的求值.分析:运用同角的平方关系,分别求得sinβ,cos(α+β),再由sinα=sin(α+β﹣β)运用两角差的正弦公式,计算即可得到.解答:解:由于0<<β<π,cos,则sinβ==.由于,则cos(α+β)=﹣=﹣,则有sinα=sin(α+β﹣β)=sin(α+β)cosβ﹣cos(α+β)sinβ=×(﹣)﹣(﹣)×=.故答案为:.点评:本题考查同角的基本关系式,考查两角的正弦公式,考查角的变换的方法,考察运算能力,属于中档题和易错题.二、解答题10.已知函数f(x)=2sin2x.(Ⅰ)求函数f(x)最小正周期;(Ⅱ)若f(x)=2,求x的值;(Ⅲ)写出函数f(x)的单调递减区间.考点:三角函数的周期性及其求法;正弦函数的单调性.专题:三角函数的图像与性质.分析:(1)按三角函数周期公式直接求解;(2)把f(x)=2带入,解三角函数2=2sin2x;(3)根据正弦函数的单调性进行分析;解答:解:(1)T==π…4分(2)∵f(x)=2∴2=2sin2x即sin2x=1∴2x=x=…9分(3)函数f(x)=2sin2x的单调递减区间为2x即x…14分点评:考查了三角函数的基本性质,属于基础题.11.已知向量||=1,||=.(Ⅰ)若向量的夹角为60°,求的值;(Ⅱ)若,求的值;(Ⅲ)若,求的夹角.考点:数量积表示两个向量的夹角;平面向量数量积的运算.专题:计算题;平面向量及应用.分析:(I)根据向量数量积的定义,结合题中数据直接计算,可得的值;(II)将平方,结合题中数据可得=5,代入数据得=1;(III)由已知等式算出==1,再根据平面向量的夹角公式算出夹角的余弦值,即可得到夹角的大小.解答:解:(I)当向量的夹角为60°时,求==;(II)∵||=1,||=.∴由,得()2=1+2+2=5解之得=1;(III)∵∴==1,设的夹角为α则cosα==,可得α=.点评:本题给出向量满足的条件,求的数量积和夹角大小.着重考查了平面向量数量积的定义及其运算性质等知识,属于基础题.12.已知向量=(1,cosx),=(,sinx),x∈(0,π).(Ⅰ)若∥,分别求tanx和的值;(Ⅱ)若⊥,求sinx﹣cosx的值.考点:平面向量共线(平行)的坐标表示;平面向量数量积的运算;同角三角函数基本关系的运用.专题:三角函数的求值;平面向量及应用.分析:(I)利用向量共线定理、同角三角函数基本关系式即可得出;(II)利用向量垂直与数量积的关系、同角三角函数基本关系式即可得出.解答:解:(Ⅰ)∵,∴(Ⅱ)∵,∴,又∵.∴.点评:本题考查了向量共线定理、向量垂直与数量积的关系、同角三角函数基本关系式,考查了推理能力和计算能力,属于中档题.。
江苏省泰州市泰兴中学2015-2016学年高一下学期5月段考数学试卷Word版含解析

2015-2016学年江苏省泰州市泰兴中学高一(下)5月段考数学试卷一、填空题(共14小题,每小题5分,满70分)1.不等式x2<1的解集为.2.在△ABC中,已知b=4,c=2,A=120°,则a等于.3.等差数列{a n}中,a1+a5=10,a4=7,则数列{a n}的公差为.4.若a,b 是异面直线,直线c与a相交,则c与b的位置关系是.5.若直线l1:ax+2y+6=0与直线l2:x+(a﹣1)y+(a2﹣1)=0平行则实数a=.6.已知数列{a n}的前n项和为S n=5n2+kn,且a2=18,则k=.7.设z=x+y,其中x,y满足,若z的最大值为12,则z的最小值为.8.以直线3x﹣4y+12=0夹在两坐标轴间的线段为直径的圆的方程为.9.设关于x的不等式:x2﹣x<2nx(n∈N*)的解集中整数的个数为a n,数列{a n}的前n项的和为S n,则S100=.10.在△ABC中,已知acosA=bcosB,则△ABC的形状是.11.已知圆O:x2+y2=1,由直线l:x+y+k=0上一点P作圆O的两条切线,切点为A,B,若在直线l上至少存在一点P,使∠APB=60°,则k的取值范围是.12.已知tan(α+β)=﹣3,tan(α﹣β)=2,则的值为.13.已知数列{a n}为正项等差数列,满足+≤1(其中k∈N*,且k≥2),则a k 的最小值为.14.在平面直角坐标系xOy中,若与点A(2,2)的距离为1且与点B(m,0)的距离为3的直线恰有两条,则实数m的取值范围为.二、解答题:(共70分)15.如图,A﹣BCD是一个不透明的三棱锥木块,点E,F,G分别在AB,BC,CD上,且F,G是BC,CD的中点,BE:EA=1:2,(1)求证:FG∥平面BAD;(2)设过点E,F,G的平面交平面ABD于直线l.请作出直线l,写出作法,并说明理由.16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知acos2+ccos2=b.(1)求证:a,b,c成等差数列;(2)若b=2,B=,求△ABC的面积.17.已知f(x)=ax2+x﹣a,a∈R.(1)若a=1,解不等式f(x)≥1;(2)若不等式f(x)>﹣2x2﹣3x+1﹣2a对一切实数x恒成立,求实数a的取值范围;(3)若a<0,解不等式f(x)>1.18.扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为平方米,且高度不低于米.记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).(1)求y关于x的函数关系式,并指出其定义域;(2)要使防洪堤横断面的外周长不超过10.5米,则其腰长x应在什么范围内?(3)当防洪堤的腰长x为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.19.已知圆O的方程为x2+y2=13,直线l:x0x+y0y=13,设点A(x0,y0).(1)若点A在圆O外,试判断直线l与圆O的位置关系;(2)若点A在圆O上,且x0=2,y0>0,过点A作直线AM,AN分别交圆O于M,N两点,且直线AM和AN的斜率互为相反数.①若直线AM过点O,求tan∠MAN的值;②试问:不论直线AM的斜率怎么变化,直线MN的斜率是否为定值?若是,求出该定值;若不是,说明理由.20.已知a n=2n+3n,b n=a n+ka n,+1(1)若{b n}是等比数列,求k的值;(2)若C n=log3(a n﹣2n),且数列{C n}的前和为S n,证明:<2;(=+++…+)(3)若k=﹣2,集合A={n∈N*|>},求集合A中所有元素之和.2015-2016学年江苏省泰州市泰兴中学高一(下)5月段考数学试卷参考答案与试题解析一、填空题(共14小题,每小题5分,满70分)1.不等式x2<1的解集为{x|﹣1<x<1} .【考点】一元二次不等式的解法.【分析】由不等式x2<1,通过因式分解可得(x+1)(x﹣1)<0,即可求得解集.【解答】解:由不等式x2<1,化为(x+1)(x﹣1)<0,解得﹣1<x<1.∴不等式x2<1的解集为{x|﹣1<x<1}.故答案为:{x|﹣1<x<1}.【点评】本题考查了一元二次不等式的解法,属于基础题.2.在△ABC中,已知b=4,c=2,A=120°,则a等于2.【考点】余弦定理.【分析】由b,c以及cosA的值,利用余弦定理即可求出a的值.【解答】解:∵在△ABC中,b=4,c=2,A=120°,∴由余弦定理得:a2=b2+c2﹣2bccosA=16+4+8=28,则a=2.故答案为:2【点评】此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.3.等差数列{a n}中,a1+a5=10,a4=7,则数列{a n}的公差为2.【考点】等差数列的性质.【分析】由等差数列的性质,结合a1+a5=10求出a3,由等差数列的定义求得公差.【解答】解:在等差数列{a n}中,由a1+a5=10,得2a3=10,∴a3=5.又a4=7,∴数列{a n}的公差d为a4﹣a3=7﹣5=2.故答案为:2.【点评】本题考查了等差数列的性质,考查了等差中项的概念,是基础题.4.若a,b 是异面直线,直线c与a相交,则c与b的位置关系是平行、相交、异面.【考点】空间中直线与直线之间的位置关系.【分析】若a,b是异面直线,直线c与a相交,所以c与b可能平行、相交、异面.【解答】解:由a、b是异面直线,直线c与a相交,知c与b的位置关系是平行、相交、异面,故答案为:平行、相交、异面.【点评】此题考查学生的空间想象能力,考查对异面直线的理解和掌握.5.若直线l1:ax+2y+6=0与直线l2:x+(a﹣1)y+(a2﹣1)=0平行则实数a=﹣1.【考点】直线的一般式方程与直线的平行关系.【分析】由直线的平行关系可得a的方程,解方程验证可得.【解答】解:∵直线l1:ax+2y+6=0与直线l2:x+(a﹣1)y+(a2﹣1)=0平行,∴a(a﹣1)﹣2×1=0,解得a=﹣1或a=2,经验证当a=2时,直线重合,a=﹣1符合题意,故答案为:﹣1【点评】本题考查直线的一般式方程和直线的平行关系,属基础题.6.已知数列{a n}的前n项和为S n=5n2+kn,且a2=18,则k=3.【考点】等差数列的前n项和.【分析】由数列{a n}的前n项和求出a1和S2,然后利用a2=S2﹣a1列式计算k的值.【解答】解:∵数列{a n}的前n项和为,∴a1=S1=5+k,.由a2=S2﹣a1,得18=20+2k﹣(5+k)=15+k,∴k=3.故答案为:3.【点评】本题考查了等差数列的前n项和,考查了数列的前n项和与项之间的关系,是基础的计算题.7.设z=x+y,其中x,y满足,若z的最大值为12,则z的最小值为﹣6.【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,先求出最优解,利用数形结合即可得到结论.【解答】解:作出不等式组对应的平面区域如图:由z=x+y得y=﹣x+z,则直线截距最大时,z也最大.平移直线y=﹣x+z由图象可知当直线y=﹣x+z经过点B时,直线y=﹣x+z的截距最大,此时z最大为12,即x+y=12,由,得,即B(6,6),此时B也在直线y=k上,∴k=6,当直线y=﹣x+z经过点A时,直线y=﹣x+z的截距最小,此时z最小,由,即,即A(﹣12,6),此时z=x+y=﹣12+6=﹣6,故答案为:﹣6【点评】本题主要考查线性规划的应用,利用z的几何意义,结合数形结合是解决本题的关键.8.以直线3x﹣4y+12=0夹在两坐标轴间的线段为直径的圆的方程为(x+2)2+(﹣)2=.【考点】圆的标准方程.【分析】根据直线3x﹣4y+12=0方程求出它与x轴、y轴交点A、B的坐标,从而得到AB中点为C(﹣2,),即为所求圆的圆心.再用两点的距离公式,算出半径r=|AB|=,最后根据圆的标准方程列式即可得到所求圆的方程.【解答】解:∵对直线3x﹣4y+12=0令x=0,得y=3;令y=0,得x=﹣4∴直线3x﹣4y+12=0交x轴于A(﹣4,0),交y轴于B(0,3)∵所求的圆以AB为直径∴该圆以AB中点C为圆心,半径长为|AB|∵AB中点C坐标为(,),即C(﹣2,)|AB |==∴圆C 的方程为(x +2)2+(y ﹣)2=,即(x +2)2+(y ﹣)2=故答案为:(x +2)2+(y ﹣)2=【点评】本题给出已知直线,求以直线被两坐标轴截得线段为直径的圆方程,着重考查了中点坐标公式、圆的标准方程和两点间的距离公式等知识,属于基础题.9.设关于x 的不等式:x 2﹣x <2nx (n ∈N *)的解集中整数的个数为a n ,数列{a n }的前n 项的和为S n ,则S 100= 10100 .【考点】数列的求和;一元二次不等式的解法.【分析】先整理条件中的不等式,表示出x 的解集,进而得出数列{a n }通项公式和求和公式.代入100即可求得S 100.【解答】解:∵x 2﹣x <2nx 整理得x (x ﹣2n ﹣1)<0,解得0<x <2n +1 则a n =2n ∴S n =n (n +1) ∴S 100=10100 故答案为10100【点评】本题主要考查了数列的求和问题.属基础题.10.在△ABC 中,已知acosA=bcosB ,则△ABC 的形状是 △ABC 为等腰或直角三角形 . 【考点】正弦定理的应用;两角和与差的余弦函数.【分析】根据正弦定理把等式acosA=bcosB 的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B ,进而推断A=B ,或A +B=90°答案可得. 【解答】解:根据正弦定理可知∵acosA=bcosB , ∴sinAcosA=sinBcosB ∴sin2A=sin2B∴A=B ,或2A +2B=180°即A +B=90°, 所以△ABC 为等腰或直角三角形 故答案为△ABC 为等腰或直角三角形.【点评】本题主要考查了正弦定理的应用,属基础题.11.已知圆O:x2+y2=1,由直线l:x+y+k=0上一点P作圆O的两条切线,切点为A,B,若在直线l上至少存在一点P,使∠APB=60°,则k的取值范围是[﹣2,2] .【考点】圆的切线方程.【分析】由题意,∠APB=60°,OP=2,可得P的轨迹方程为x2+y2=4,在直线l上至少存在一点P,使∠APB=60°,可以转化为直线l:x+y+k=0与x2+y2=4至少存在一个交点,利用圆心到直线的距离d=≤2,即可确定k的取值范围.【解答】解:由题意,∠APB=60°,OP=2,∴P的轨迹方程为x2+y2=4,∵在直线l上至少存在一点P,使∠APB=60°,∴直线l:x+y+k=0与x2+y2=4至少存在一个交点,∴圆心到直线的距离d=≤2,∴﹣2≤k≤2,∴k的取值范围是[﹣2,2].故答案为:[﹣2,2].【点评】本题考查直线与圆的位置关系,考查圆的方程,在直线l上至少存在一点P,使∠APB=60°,可以转化为直线l:x+y+k=0与x2+y2=4至少存在一个交点,是解题的关键.12.已知tan(α+β)=﹣3,tan(α﹣β)=2,则的值为.【考点】两角和与差的正切函数.【分析】利用同角三角函数的基本关系,两角差的三角公式,求得要求式子的值.【解答】解:tan(α+β)=﹣3,tan(α﹣β)=2,则=====,故答案为:.【点评】本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于基础题.13.已知数列{a n}为正项等差数列,满足+≤1(其中k∈N*,且k≥2),则a k的最小值为.【考点】数列递推式.【分析】由等差数列的性质得,结合+≤1利用基本不等式求得a k的最小值.【解答】解:∵数列{a n}为正项等差数列,且+≤1,∴≥(+)=≥=.=6时上式等号成立.当且仅当+=1,且,即a1=3,a2k﹣1∴a k的最小值为.故答案为:.【点评】本题考查数列递推式,考查了等差数列的性质,训练了利用基本不等式求最值,是中档题.14.在平面直角坐标系xOy中,若与点A(2,2)的距离为1且与点B(m,0)的距离为3的直线恰有两条,则实数m的取值范围为.【考点】点到直线的距离公式.【分析】根据题意可把点到线的距离转化为圆,进而利用两个圆的位置关系解决问题.【解答】解:由题意可得:与点A(2,2)的距离为1的点确定了一个圆O1,与点B(m,0)的距离为3的点确定了一个圆O2,所以根据题意可得:题中所要求的直线也就是两个圆的公切线,并且这样的公切线只有两条,所以根据两圆位置关系可得:这两个圆必然相交,即有|r1﹣r2|<|O1O2|<r1+r2,即:2<<4,解得:.故答案为.【点评】解决此类问题的关键是熟练掌握两个圆的位置关系,以及进行正确的计算.二、解答题:(共70分)15.如图,A﹣BCD是一个不透明的三棱锥木块,点E,F,G分别在AB,BC,CD上,且F,G是BC,CD的中点,BE:EA=1:2,(1)求证:FG∥平面BAD;(2)设过点E,F,G的平面交平面ABD于直线l.请作出直线l,写出作法,并说明理由.【考点】直线与平面平行的判定.【分析】(1)由中位线定理可知FG∥BD,故而FG∥平面BAD;(2)取线段AD靠近D的三等分点P,则PE为所求直线l.【解答】解:(1)∵F,G是BC,CD的中点,∴FG∥BD,又FG⊄平面BAD,BD⊂平面BAD,∴FG∥平面BAD.(2)在AD上取一点P,使得DP:PA=1:2,连接EP,则直线PE为平面EFG与平面ABD 的交线l.理由如下:∵,∴EP∥BD,又FG∥BD,∴PE∥FG.∴P∈平面EFG,又P∈平面ABD,∴P为平面EFG和平面ABD的公共点,又E为平面EFG和平面ABD的公共点,∴平面EFG∩平面ABD=PE,即PE为所求的交线l.【点评】本题考查了线面平行的判定,平面的基本性质,属于基础题.16.在△ABC中,角A,B,C所对的边分别为a,b,c,已知acos2+ccos2=b.(1)求证:a,b,c成等差数列;(2)若b=2,B=,求△ABC的面积.【考点】正弦定理.【分析】(1)已知等式利用正弦定理化简,再利用二倍角的余弦函数公式及两角和与差的正弦函数公式变形,整理后再利用正弦定理化简,利用等差数列的性质判断即可得证;(2)利用三角形面积公式进行解答.【解答】(1)证明:∵,∴由正弦定理得,…化简得,sinA+sinC+sinAcosC+sinCcosA=3sinB,∴sinA+sinC+sin(A+C)=3sinB,∵sin(A+C)=sinB,∴sinA+sinC=2sinB,由正弦定理化简得:a+c=2b,∴a,b,c成等差数列;(2)由(1)得:a+c=2b,∵b=2,B=,a+c=2b,∴b2=a2+c2﹣2accosB=a2+c2﹣ac=(2b)2﹣3ac,∴ac=b2=8,∴S=acsinB=×8×sin=4×=2.即△ABC的面积是2.【点评】此题考查了正弦、余弦定理,二倍角的余弦函数公式,两角和与差的正弦函数公式,诱导公式,等差数列的性质,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.17.已知f(x)=ax2+x﹣a,a∈R.(1)若a=1,解不等式f(x)≥1;(2)若不等式f(x)>﹣2x2﹣3x+1﹣2a对一切实数x恒成立,求实数a的取值范围;(3)若a<0,解不等式f(x)>1.【考点】其他不等式的解法;函数恒成立问题;一元二次不等式的解法.【分析】(1)当a=1,不等式即(x+2)(x﹣1)≥0,解此一元二次不等式求得它的解集.(2)由题意可得(a+2)x2+4x+a﹣1>0恒成立,当a=﹣2 时,显然不满足条件,故有,由此求得a的范围.(3)若a<0,不等式为ax2+x﹣a﹣1>0,即(x﹣1)(x+)<0.再根据1和﹣的大小关系,求得此不等式的解集.【解答】解:(1)当a=1,不等式f(x)≥1即x2+x﹣1≥1,即(x+2)(x﹣1)≥0,解得x≤﹣2,或x≥1,故不等式的解集为{x|x≤﹣2,或x≥1}.(2)由题意可得(a+2)x2+4x+a﹣1>0恒成立,当a=﹣2 时,显然不满足条件,∴.解得a>2,故a的范围为(2,+∞).(3)若a<0,不等式为ax2+x﹣a﹣1>0,即(x﹣1)(x+)<0.∵1﹣(﹣)=,∴当﹣<a<0时,1<﹣,不等式的解集为{x|1<x<﹣};当a=﹣时,1=﹣,不等式即(x﹣1)2<0,它的解集为∅;当a<﹣时,1>﹣,不等式的解集为{x|﹣<x<1}.【点评】本题主要考查一元二次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.18.扬州某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边成角为60°(如图),考虑到防洪堤坚固性及石块用料等因素,设计其横断面要求面积为平方米,且高度不低于米.记防洪堤横断面的腰长为x(米),外周长(梯形的上底线段BC与两腰长的和)为y(米).(1)求y关于x的函数关系式,并指出其定义域;(2)要使防洪堤横断面的外周长不超过10.5米,则其腰长x应在什么范围内?(3)当防洪堤的腰长x为多少米时,堤的上面与两侧面的水泥用料最省(即断面的外周长最小)?求此时外周长的值.【考点】函数模型的选择与应用;基本不等式在最值问题中的应用.【分析】(1)先由横断面积用x表示BC,从建立y关于x的函数关系式,定义域由线段必须大于零和高度不低于米求解;(2)解y≤10.5分式不等式;(3)求函数y的最小值,根据函数特点及条件可选用不等式解决.【解答】解:(1),其中,,∴,得,由,得2≤x<6∴;(2)得3≤x≤4∵[3,4]⊂[2,6)∴腰长x的范围是[3,4](3),当并且仅当,即时等号成立.∴外周长的最小值为米,此时腰长为米.【点评】本题主要考查利用平面图形建立函数模型以及解模的能力,属于中档题.19.已知圆O的方程为x2+y2=13,直线l:x0x+y0y=13,设点A(x0,y0).(1)若点A在圆O外,试判断直线l与圆O的位置关系;(2)若点A在圆O上,且x0=2,y0>0,过点A作直线AM,AN分别交圆O于M,N两点,且直线AM和AN的斜率互为相反数.①若直线AM过点O,求tan∠MAN的值;②试问:不论直线AM的斜率怎么变化,直线MN的斜率是否为定值?若是,求出该定值;若不是,说明理由.【考点】直线与圆的位置关系;直线的斜率.【分析】(1)由点A在圆O外,可得x02+y02 >13,求得圆心到直线的距离d小于半径,可得直线和圆相交.(2)由条件求得点A(2,3).①若直线AM过点O,求得AM的斜率,可得AN的斜率K AN=﹣,再利用两条直线的夹角公式求得tan∠MAN=||的值.②记直线AM的斜率为k,把直线AM的方程为:y=kx+3﹣2k代入圆O的方程化简,由2是方程的一个根,利用韦达定理求得M的横坐标x M的值,同理可得,x N的值,再根据MN的斜率为,计算结果为,可得结论.【解答】解:(1)∵点A在圆O外,∴x02+y02 >13,由于圆心(0,0)到直线l:x0x+y0y=13的距离d=<=r,故直线和圆相交.(2)∵点A在圆O上,且x0=2,y0>0,可得y0=3,∴点A(2,3).①若直线AM过点O,则AM的斜率为K AM=,∴K AN=﹣,tan∠MAN=||=||=.②记直线AM的斜率为k,则直线AM的方程为:y=kx+3﹣2k.将y=kx+3﹣2k代入圆O的方程得:x2+(kx+3﹣2k)2=13,化简得:(k2+1)x2+2k(3﹣2k)x+(3﹣2k)2﹣13=0,∵2是方程的一个根,∴2x M=,∴x M=,由题意知:k AN=﹣k,同理可得,x N=,∴kMN==k=k=,∴不论直线AM的斜率怎样变化,直线MN的斜率总为定值.【点评】本题主要考查点和圆的位置关系,直线和圆的位置关系,直线的倾斜角和斜率,两条直线的夹角公式的应用,属于中档题.20.已知a n=2n+3n,b n=a n+1+ka n,(1)若{b n}是等比数列,求k的值;(2)若C n=log3(a n﹣2n),且数列{C n}的前和为S n,证明:<2;(=+++…+)(3)若k=﹣2,集合A={n∈N*|>},求集合A中所有元素之和.【考点】数列的求和;等比数列的通项公式.【分析】(1)运用等比数列的性质,可得b22=b1b3,解k的方程可得k的值;(2)求得C n=n,S n=,可得==2(﹣),运用裂项相消求和,即可得证;(3)求得b n=3n,令d n=,作差,判断单调性,可得集合A中的元素,求和可得.【解答】解:(1)由a1=5,a2=13,a3=35,a4=97,又{b n}是等比数列,可得b22=b1b3,则(35+13k)2=(13+5k)(97+35k),解得k=﹣2或k=﹣3,经检验均符合;(2)证明:由题可得C n=log3(a n﹣2n)=n,则S n=,可得==2(﹣),则=2(1﹣+﹣+…+﹣)=2(1﹣)<2;(3)由题可得b n=3n,令d n=,﹣d n=﹣=,则d n+1当n=1时,d1=d2=,当n≥2时,d n<d n,+1又d3=,d4=,则A={1,2,3},所以A中所有元素之和为6.【点评】本题考查等比数列的通项公式和求和公式的运用,考查数列的求和方法:裂项相消求和,以及数列的单调性和运用,属于中档题.。
【数学】江苏省泰州三中2014-2015学年高一11月阶段测试数学试题

泰州三中2014年秋学期高一数学11月段测试一、填空题(本大题共14个小题,每小题5分,共70分)1.若角α与角β的终边关于y 轴对称,则α与β的关系是___________. 2.在函数y = 2sin(4x +32π)图象的对称中心中,离原点最近的点的坐标是___________. 3.已知函数y=cos x 与y=sin (2x +φ)(0≤φ<π),它们的图象有一个横坐标为的交点,则φ的值是________.4.函数=)(x f ⎩⎨⎧<+-≥0,1)3(0,x x a x a x 为R 上的单调增函数,则实数a 的取值范围为 ____.5.函数f (x )=236)21lg(cos x x -+-的定义域是________________________.6.将函数y =sin2x 的图象向左平移6π个单位, 再向上平移1个单位,所得图象的函数解析式是___________.7.已知函数f (x )=2sin(2x +α) (|α|≤2π) 的图象关于直线x =3π对称,则α= . 8.函数)23sin(xy -=π的单调递增区间是____________. 9.设f (x )是R 上的奇函数,当0≥x 时,f (x )=a x x+-22(a 为常数),则当0<x 时f (x )= _______.10.已知函数)tan(x y ω=在)2,2(ππ-内是减函数,则ω的取值范围是__________. 11.设函数2)(-+=x e x f x ,3ln )(2-+=x x x g ,若实数b a ,满足0)(=a f ,0)(=b g 请将0,)(),(a g b f 按从小到大的顺序排列 (用“<”连接). 12.函数11-=+x xy 与x y πsin 2=(42≤≤-x )的图象所有交点横坐标之和是 . 13.已知函数f (x )是定义在R 上的奇函数,且当x ≥0时,f (x )=2x ,若对任意的[]2,+∈t t x 不等式f (x +t )≥2f (x )恒成立,则实数t 的取值范围是 .14.关于f (x )=4sin ⎝⎛⎭⎫2x +π3(x ∈R ),有下列命题: (1)由f (x 1)=f (x 2)=0可得x 1-x 2是π的整数倍;(2)y =f (x )的表达式可改写成y =4cos ⎝⎛⎭⎫2x -π6; (3)y =f (x )图象关于⎝⎛⎭⎫-π6,0对称;(4)y =f (x )图象关于x =-π6对称.其中正确命题的序号为___________________.将填空题答案填在下列区域内:1.____________________ 2.______________________ 3._________________________ 4.____________________ 5.______________________ 6._________________________ 7.____________________ 8.______________________ 9._________________________ 10.___________________11._____________________ 12._________________________ 13.____________________ 14.______________________二、解答题(本大题共6个小题,共90分,解答应写出文字说明、证明过程或演算步骤) 15.(本题14分)已知函数f (x )=a sin ⎝⎛⎭⎫2x +π3+1(a >0)的定义域为R ,若当-7π12≤x ≤-π12时,f (x )的最大值为2,(1)求a 的值;(2)用五点法作出函数在一个周期闭区间上的图象.(3)写出该函数的对称中心的坐标.16.(本题15分)下图为函数)20,0,0()sin()(πϕωϕω<<>>++=A c x A x f 图像的一部分.(1)求函数f (x )的解析式,并写出f (x )的振幅、周期、初相; (2)求使得f (x )>25的x 的集合 ; (3)函数f (x )的图像可由函数y =sin x 的图像经过怎样的变换而得到?17.(本题14分)已知函数cos 2(0)6y a b x b π=-+>⎛⎫⎪⎝⎭的最大值为23,最小值为21-. (1)求b a ,的值;(2)求函数)3sin(4)(π--=bx a x g 的最小值并求出对应x 的集合.18.(本题15分)已知函数]2,0[],21,23[,1sin 2)(2παx αx x x f ∈-∈-+=. (1)当6πα=时,求f (x )的最大值和最小值,并求使函数取得最值的x 的值;(2) 求α的取值范围,使得f (x )在区间]21,23[-上是单调函数.19.(本题16分)设函数xxa ka x f --=)((a >0且1≠a ,R k ∈),f (x )是定义域为R 的奇函数.(1)求k 的值,判断并证明当a >1时,函数f (x )在R 上的单调性; (2)已知f (1)=,函数g (x )=a 2x+a﹣2x﹣2f (x ),]1,1[-∈x ,求g (x )的值域;(3)已知a =3,若f (3x )≥λ•f (x )对于]2,1[∈x 时恒成立.请求出最大的整数λ.20(本题16分)函数f (x )=A sin(ωx +ϕ)(A >0,ω>0,|ϕ|<π2)的一段图象(如下图所示)(1) 求其解析式.(2)令g (x )=1)(2)(2)(2-+-x f x f x f ,当]4,0[π∈x 时,求g (x )的最大值.泰州三中2014年秋学期高一数学11月段测试答案1.)(2Z k k ∈+=+ππβα2. )0,12(π3.6π4. (1,3)5. ]6,35()3,3()35,6[ππππ --- 6. 1)32sin(++=πx y7. 6π-8. ]4311,435[ππππk k ++,(Z k ∈) 9. 122+---x x10. )0,1[-11.g (a )<0<f (b ) 12. 413.),2[+∞ 14. (2)(3) 15.解:(1)当,则∴当,f (x )有最大值为.又∵f(x)的最大值为2,∴=2,解得:a=2.(2)由(1)知令分别取0,,π,,2π,则对应的x与y的值如下表﹣画出函数在区间[﹣,]的图象如下图(3)令Z,解得x=k∈Z,∴函数的对称中心的横坐标为,k∈Z,又∵函数的图象是函数的图象向上平移一个单位长度得到的,∴函数的对称中心的纵坐标为1.∴对称中心坐标为(,1)k∈Z16. 解:(1)由函数图象可知函数的最大值为A+c=4,最小值为﹣A+c=﹣2,∴c=1,A=3,∵,∴函数的周期T=.由=得,ω=,∴y=3sin(x+ϕ)+1∵(12,4)在函数图象上∴4=3sin(•12+ϕ)+1,即sin(+ϕ)=1∴+ϕ=+2kπ,k∈Z,得ϕ=﹣+2kπ,k∈Z∵0<ϕ<2π ∴ϕ=∴函数解析式为y=3sin (•x +)+1.(2))332928,33294(k k ++-,(z k ∈) (3)略17. 解:(1)∵b >0∴﹣b <0,;∴(2)由(1)知:∴∴g (x )∈[﹣2,2]∴g (x )的最小值为﹣2对应x 的集合为18.解:(1) 当6πα=时,116sin2)(22-+=-+=x x πx x x f =45)21(2-+x ∵]21,23[-∈x ∴当x =21-时,f (x )取到最小值45- 当x =21时,f (x )取到最大值41-(2)函数1sin 2)(2-+=αx x x f 图象的对称轴为直线x =αsin -当αsin -≤23-,即αsin ≥23,即323παπ≤≤时,函数f (x )在区间]21,23[-上是增函数; 当23-αsin -<<21,即23sin 21<<-α,即0≤α<3π或32π<α<67π或απ<611≤π2时,f (x )在区间]sin ,23[π--上为减函数,在]21,sin [π-上为增函数; 当αsin -≥21,即αsin ≤21-,即67π≤α≤611π时,函数f (x )在区间]21,23[-上是减函数。
(数学)江苏省泰州中学2015-2016学年高一下学期第一次月考数学试卷-Word版含解析

(数学)江苏省泰州中学2015-2016学年高一下学期第一次月考数学试卷-Word版含解析2015-2016学年江苏省泰州中学高一(下)第一次月考数学试卷一、填空题(本大题共14小题,每小题5分,共70分)1.求:sin15°sin30°sin75°=.2.在△ABC中,若A=,a=,则=.3.在△ABC中,已知(a+b+c)(a+b﹣c)=ab,则∠C的大小为.4.数列{a n}是等差数列,a1与a2的等差中项为1,a2与a3的等差中项为2,则公差d=.5.设S n是等差数列{a n}的前n项和,已知a2=3,a6=11,则S7=.6.在等比数列{a n}中,a1<0,a2a4+2a3a5+a4a6=36,则a3+a5=.7.在△ABC中,已知a=4,b=4,B=45°,则∠A=.8.已知θ为锐角,sin(θ+15°)=,则cos (2θ﹣15°)=.9.把一根长为30cm的木条锯成两段,分别做钝角三角形ABC的两边AB和BC,且∠ABC=120°,当第三边AC最短时,边AB的长为.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.已知{a n}是等差数列,其中a1=25,a4=16 (1)求{a n}的通项;(2)数列{a n}从哪一项开始小于0;(3)求a1+a3+a5+…+a19值.16.在△ABC中,已知,,B=45°,求b及A.17.已知α,β∈(0,),且sin(α+2β)=sinα.(1)求tan(α+β)﹣6tanβ的值;(2)若tanα=3tanβ,求α的值.18.已知函数f(x)=sin2ωx﹣2sin 2ωx的最小正周期为3π.(1)求函数f(x)的解析式;(2)在△ABC中,若f(C)=1,AB=2,2sin2B=cosB+cos(A﹣C),求BC的长.19.在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层,(Ⅰ)共有几种不同的方案?(Ⅱ)已知每根圆钢的直径为10cm,为考虑安全隐患,堆放高度不得高于4m,则选择哪个方案,最能节省堆放场地?20.已知数列{a n}中,a2=1,前n项和为S n,且S n=.(1)求a1;(2)证明数列{a n}为等差数列,并写出其通项公式;(3)设lgb n=,试问是否存在正整数p,q(其中1<p<q),使b1,b p,b q成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.2015-2016学年江苏省泰州中学高一(下)第一次月考数学试卷参考答案与试题解析一、填空题(本大题共14小题,每小题5分,共70分)1.求:sin15°sin30°sin75°=.【考点】同角三角函数基本关系的运用.【分析】注意到题中角15°、75°的互余关系,利用同角公式化成同一个角的三角函数,再反用二倍角公式求解即可.【解答】解:sin15°sin30°sin75°=sin15°××cos15°=××2sin15°cos15°=sin30°=.故填:.2.在△ABC中,若A=,a=,则=2.【考点】三角函数的周期性及其求法.【分析】由条件利用正弦定理求得=的值.【解答】解:△ABC中,若A=,a=,则由正弦定理可得===2,故答案为:2.3.在△ABC中,已知(a+b+c)(a+b﹣c)=ab,则∠C的大小为.【考点】余弦定理.【分析】由题中等式,化简出a2+b2﹣c2=ab,再根据余弦定理算出cosC=的值,结合三角形内角的范围即可算出角C的大小.【解答】解:∵在△ABC中,(a+b+c)(a+b﹣c)=ab,∴(a+b)2﹣c2=ab,整理得a2+b2﹣c2=﹣ab由余弦定理,得cosC==﹣,结合C∈(0,π),可得C=;故答案为:.4.数列{a n}是等差数列,a1与a2的等差中项为1,a2与a3的等差中项为2,则公差d=1.【考点】等差数列的通项公式.【分析】由题意和等差中项可得a1+a2=2,a2+a3=4,两式相减可得答案.【解答】解:∵{a n}是等差数列,a1与a2的等差中项为1,a2与a3的等差中项为2,∴a1+a2=2,a2+a3=4,两式相减可得a3﹣a1=2d=4﹣2,解得d=1,故答案为:1.5.设S n是等差数列{a n}的前n项和,已知a2=3,a6=11,则S7=49.【考点】等差数列的前n项和;等差数列的性质.【分析】由等差数列的性质求得a1+a7,再用前n 项和公式求得.【解答】解:∵a2+a6=a1+a7∴故答案是496.在等比数列{a n}中,a1<0,a2a4+2a3a5+a4a6=36,则a3+a5=﹣6..【考点】等比数列的性质.【分析】根据等比数列的性质进行配方即可.【解答】解:在等比数列{a n}中,a2a4+2a3a5+a4a6=36,∴(a3)2+2a3a5+(a5)2=36,即(a3+a5)2=36,∵a1<0,∴a3=a1q2<0,a5=a1q4<0,即a3+a5<0,则a3+a5=﹣6,故答案为:﹣67.在△ABC中,已知a=4,b=4,B=45°,则∠A=30°.【考点】正弦定理.【分析】由正弦定理,解得sinB.再由b<a,可得B<A=45°,由此可得B的值.【解答】解:在△ABC中,∠A=45°,a=4,b=4,则由正弦定理可得,解得sinA=.再由b>a,可得B>A,故A为锐角,故A=30°,故答案为:30°.8.已知θ为锐角,sin(θ+15°)=,则cos (2θ﹣15°)=.【考点】两角和与差的正弦函数;两角和与差的余弦函数.【分析】由二倍角公式可得cos(2θ+30°)的值,由sin(θ+15°)=<,进一步缩小角的范围,由平方关系可得sin(2θ+30°)的值,可得cos(2θ﹣15°)=cos(2θ+30°﹣45°),由两角差的余弦公式展开,代入数据解得可得.【解答】解:由二倍角公式可得cos(2θ+30°)=1﹣2sin2(θ+15°)=1﹣2×=,又∵θ为锐角,sin(θ+15°)=<,∴θ+15°<60°,即θ<45°,∴2θ+30°<120°,∴sin(2θ+30°)==,由两角差的余弦公式可得cos(2θ﹣15°)=cos(2θ+30°﹣45°)==故答案为:9.把一根长为30cm的木条锯成两段,分别做钝角三角形ABC的两边AB和BC,且∠ABC=120°,当第三边AC最短时,边AB的长为15cm.【考点】三角形中的几何计算.【分析】根据题意设AB=xcm,利用余弦定理列出关系式,利用二次函数性质即可得到AC取得最小值时x的值,从而得出结论.【解答】解:如图所示,设AB=xcm,则BC=(30﹣x)cm,由余弦定理得:AC2=AB2+BC2﹣2AB•BC•cos∠ABC=x2+(30﹣x)2+x(30﹣x)=(x﹣15)2+675,∴当x=15cm时,AC取得最小值为=15cm,即当AB=BC=15cm时,第三边AC的长最短为15cm.故答案为:15cm.10.在等比数列{a n}中,a5•a11=4,a3+a13=5,则= 4或.【考点】等比数列的性质.【分析】先用a1,q表示出a5、a11、a3、a13,然后代入关系式a5•a11=4,a3+a13=5可得a5•a11=a12q14=4、a3+a13=a1(q2+q12)=5,然后对a1(q2+q12)=5两边平方后与a12q14相比即可得到答案.【解答】解:∵=q10a5•a11=a12q14=4 ①a3+a13=a1(q2+q12)=5然后两边平方:a12(q4+q24+2q14)=25 ②===所以或4故答案为:4或11.在△ABC中,已知b=1,c=2,AD是∠A 的平分线,AD=,则∠C=90°.【考点】余弦定理的应用.【分析】根据角平线的性质,可设BD=2x,CD=x,然后结合余弦定理列方程解x,然后利用余弦定理求解C即可.【解答】解:因为AD是∠A的平分线,所以=,不妨设BD=2x,CD=x,结合已知得cos∠BAD=cos∠CAD,在△ABD中由余弦定理得BD2=AB2+AD2﹣2AB•ADcos∠BAD,即:4x2=4+﹣2×cos∠BAD,…①在△ACD中,由余弦定理可得CD2=AC2+AD2﹣2AC•ADcos∠CAD,即:x2=1+﹣2×cos∠BAD…②,①﹣②×2,可得:2x2=2﹣=,解得:x2=.在△ADC则,cosC===0.∠C=90°.故答案为:90°.12.S n是等差数列{a n}的前n项和,若,则=.【考点】等差数列的前n项和.【分析】利用等差数列的通项公式及前n项和公式推导出a1=d,由此能求出的值.【解答】解:∵S n是等差数列{a n}的前n项和,,∴===,∴3a1=2a1+d,∴a1=d,∴===.故答案为:.13.在锐角△ABC中,已知∠A,∠B,∠C成等差数列,设y=sinA﹣cos(A﹣C+2B),则y 的取值范围是(﹣1,2).【考点】任意角的三角函数的定义.【分析】由题意可得2∠B=∠A+∠C,再化简y=sinA﹣cos2A=2﹣,根据sinA∈(0,1),利用二次函数的性质求得y的取值范围.【解答】解:锐角△ABC中,∵∠A,∠B,∠C成等差数列,∴2∠B=∠A+∠C,∴∠B=.设y=sinA﹣cos(A﹣C+2B)=sinA﹣cos2A=sinA ﹣1+2sin2A=2﹣,∵sinA∈(0,1),∴y∈(﹣1,2),故答案为:(﹣1,2).14.已知a n=2n,把数列{a n}的各项排成如图三角形状,记A(i,j)表示第i行中第j个数,则结论①A(2,3)=16;②A(i,3)=2A(i,2)(i≥2);③[A(i,i)]2=A(i,1)•A(i,2i﹣1),(i≥1);④A(i+1,1)=A(i,1)•22i﹣1,(i≥1);其中正确的是①②③④(写出所有正确结论的序号).【考点】数列的应用.【分析】观察三角形中第i行最后一个数的下脚标,得知下脚标值是该行的行数的平方,从而得到A(i,j)的表达式,再依次分析①②③④,可判断其正确性.【解答】解:依题意知,①A(2,3)=a4=24=16;即①正确;由图可知,第i行最后一个数是,∴②A(i,3)==,A(i,2)==∴A(i,3)=2A(i,2)(i≥2);即②正确;③[A(i,i)]2==A(i,1)•A(i,2i﹣1)=•===[A(i,i)]2,即③正确;④A(i+1,1)==,A(i,1)•22i﹣1=•22i ﹣1=∴A(i+1,1)=A(i,1)•22i﹣1,即④正确;故答案为:①②③④.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)15.已知{a n}是等差数列,其中a1=25,a4=16 (1)求{a n}的通项;(2)数列{a n}从哪一项开始小于0;(3)求a1+a3+a5+…+a19值.【考点】等差数列的前n项和;等差数列的性质.【分析】(1)由{a n}是等差数列,其中a1=25,a4=16,利用等差数列通项公式能求出公差d,由此能求出a n=28﹣3n.(2)由a n=28﹣3n<0,得到n>,由此能求出数列{a n}从第几项开始小于0.(3)a1+a3+a5+…+a19是首项为25,公差为﹣6的等差数列,共有10项,由等差数列的前n项和公式能求出其结果.【解答】解:(1)∵a4=a1+3d=25+3d=16,∴d=﹣3,∴a n=28﹣3n…(2)∵∴数列{a n}从第10项开始小于0 …(3)a1+a3+a5+…+a19是首项为25,公差为﹣6的等差数列,共有10项其和…16.在△ABC中,已知,,B=45°,求b及A.【考点】余弦定理;正弦定理.【分析】(1)直接利用余弦定理,由b2=a2+c2﹣2accosB 求得结果.(2)由余弦定理可得cos,求得角A 的值.【解答】解(1)∵b2=a2+c2﹣2accosB=cos45°==8,∴.(2)∵cos,∴A=60°.17.已知α,β∈(0,),且sin(α+2β)=sinα.(1)求tan(α+β)﹣6tanβ的值;(2)若tanα=3tanβ,求α的值.【考点】两角和与差的正切函数;三角函数的化简求值.【分析】(1)把已知等式变形,展开两角和与差的正弦,在转化为正切求得tan(α+β)﹣6tanβ的值;(2)由(1)求出的tan(α+β)﹣6tanβ的值,展开两角和的正切,结合tanα=3tanβ求α的值.【解答】解:(1)由sin(α+2β)=sinα,得sin[(α+β)+β]=sin[(α+β)﹣β],∴5sin(α+β)cosβ+5cos(α+β)sinβ=7sin (α+β)cosβ﹣7cos(α+β)sinβ,得2sin(α+β)cosβ﹣12cos(α+β)sinβ=0,即tan(α+β)﹣6tanβ=0;(2)由tan(α+β)﹣6tanβ=0,得,又tanα=3tanβ,∴tan,代入上式得:,解得:tanα=1,∵α∈(0,),∴.18.已知函数f(x)=sin2ωx﹣2sin 2ωx的最小正周期为3π.(1)求函数f(x)的解析式;(2)在△ABC中,若f(C)=1,AB=2,2sin2B=cosB+cos(A﹣C),求BC的长.【考点】三角函数的周期性及其求法;三角函数中的恒等变换应用.【分析】(1)由三角函数中的恒等变换得f(x)=2sin(2ωx+)﹣1,根据周期公式即可解得ω,可求当解析式;(2)根据(1)的表达式,解关于C的方程f(C)=1,结合C为三角形的内角算出C=,因此将等式2sin2B=cosB+cos(A﹣C)化成关于A的方程,整理得sin2A+sinA﹣1=0,解之即得sinA的值,利用正弦定理即可得解BC 的长.【解答】(本题满分为14分)解:∵f(x)=sin2ωx﹣2sin 2ωx=sin2ωx﹣(1﹣cos2ωx)=2sin(2ωx+)﹣1,…∴依题意函数f(x)的最小正周期为3π,即=3π,解得ω=,所以f(x)=2sin(x+)﹣1.…(2)∵f(C)=2sin(+)﹣1=1,∴sin(+)=1,∵C∈(0,π),可得+∈(,),∴+=,可得C=.…∵在Rt△ABC中,A+B=,有2sin2B=cosB+cos (A﹣C),∴2cos2A﹣sinA﹣sinA=0,即sin2A+sinA﹣1=0,解之得sinA=.…∵0<sinA<1,∴sinA=.…∵AB=2,∴由正弦定理可得:BC===﹣1.…19.在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起.(1)若堆放成纵断面为正三角形(每一层的根数比上一层根数多1根),并使剩余的圆钢尽可能地少,则剩余了多少根圆钢?(2)若堆成纵断面为等腰梯形(每一层的根数比上一层根数多1根),且不少于七层,(Ⅰ)共有几种不同的方案?(Ⅱ)已知每根圆钢的直径为10cm,为考虑安全隐患,堆放高度不得高于4m,则选择哪个方案,最能节省堆放场地?【考点】数列的应用.【分析】(1)根据题意列出前n层可以堆积的圆钢的总数,列出不等式解不等式可得出答案;(2)(Ⅰ)根据题中要求的堆积方式写出堆积的总圆钢数关于层数n的关系式,再根据n与2x+n ﹣1的奇偶性不同讨论可能的堆积方案;(Ⅱ)根据(Ⅰ)中求得的四种堆积方案以及题中圆钢的直径和堆积要求分别讨论符合条件的堆积方案,便可求出选择堆放41层这个方案,最能节省堆放场地【解答】解:(1)由题意可知:第一层放1根,第二层放2根,第三层放3根,…第n层放n 根,∴n层一共放了S n=根圆钢,由题意可知S n=≤2000,解不等式得当n=62时,使剩余的圆钢尽可能地少,此时剩余了56根圆钢;(2)当纵断面为等腰梯形时,设共堆放n层,则从上到下每层圆钢根数是以x为首项、1为公差的等差数列,从而nx+n(n﹣1)=2009,即n(2x+n﹣1)=2×2009=2×7×7×41,因n﹣1与n的奇偶性不同,所以2x+n﹣1与n的奇偶性也不同,且n<2x+n﹣1,从而由上述等式得:或或或,所以共有4种方案可供选择.(3)因层数越多,最下层堆放得越少,占用面积也越少,所以由(2)可知:若n=41,则x=29,说明最上层有29根圆钢,最下层有69根圆钢,此时,两腰之长为400cm,上下底之长为280cm和680cm,从而梯形之高为200cm,而200+10+10<400,所以符合条件;若n=49,则x=17,说明最上层有17根圆钢,最下层有65根圆钢,此时,两腰之长为480cm,上下底之长为160cm和640cm,从而梯形之高为240cm,显然大于4m,不合条件,舍去;综上所述,选择堆放41层这个方案,最能节省堆放场地.20.已知数列{a n}中,a2=1,前n项和为S n,且S n=.(1)求a1;(2)证明数列{a n}为等差数列,并写出其通项公式;(3)设lgb n=,试问是否存在正整数p,q(其中1<p<q),使b1,b p,b q成等比数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.【考点】数列的求和.【分析】(1)令n=1,即可求a1;(2)根据等差数列的定义即可证明数列{a n}为等差数列,并写出其通项公式;(3)根据等比数列的定义和通项公式,建立方程组进行求解即可得到结论.【解答】解:(1)令n=1,则a1=S1==0 (2)由,即,①得.②②﹣①,得(n﹣1)a n+1=na n.③于是,na n+2=(n+1)a n+1.④③+④,得na n+2+na n=2na n+1,即a n+2+a n=2a n+1又a1=0,a2=1,a2﹣a1=1,所以,数列{a n}是以0为首项,1为公差的等差数列.所以,a n=n﹣1(3)假设存在正整数数组(p,q),使b1,b p,b q成等比数列,则lgb1,lgb p,lgb q成等差数列,于是,所以,(☆).易知(p,q)=(2,3)为方程(☆)的一组解当p≥3,且p∈N*时,<0,故数列{}(p≥3)为递减数列,于是≤<0,所以此时方程(☆)无正整数解.综上,存在唯一正整数数对(p,q)=(2,3),使b1,b p,b q成等比数列。
2014-2015学年高一下学期期中考试数学试卷-Word版含答案

2014-2015学年高一下学期期中考试数学试卷-Word版含答案2014——2015学年下学期高一年级期中考数学学科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 不等式0121≤+-x x 的解集为( )A.⎝ ⎛⎭⎪⎫-∞,-12∪[1,+∞) B.⎣⎢⎡⎦⎥⎤-12,1C.⎝ ⎛⎦⎥⎤-∞,-12∪[1,+∞) D. ⎝ ⎛⎦⎥⎤-12,12. 若0<<b a ,则下列不等式不能成立的是 ( ) A.ba11> B .b a 22> C .b a > D .b a )21()21(> 3. 不等式16)21(1281≤<x 的整数解的个数为 ( )A .10B .11C .12D .134. 等差数列{}n a 中,如果39741=++a a a ,27963=++a a a ,则数列{}n a 前9项的和为( )A .297B .144C .99D .665. 已知直线1l :01)4()3(=+-+-y k x k 与2l :032)3(2=+--y x k 平行,则k 的值是( )A .1或3B .1或5C .3或5D .1或26. 在△ABC 中,80=a ,70=b ,45=A ,则此三角形解的情况是 ( ) A 、一解 B 、两解 C 、一解或两解 D 、无解7. 如果0<⋅C A ,且0<⋅C B ,那么直线0=++C By Ax 不通过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限8.已知点()5,x 关于点),1(y 的对称点为()3,2--,则点()y x p ,到原点的距离为( )A .4B .13C .15D .179. 计算机是将信息转换成二进制进行处理的,二进制即“逢二进一”,如(1 101)2表示二进制数,将它转换成十进制数是1×23+1×22+0×21+1×20=13,那么将二进制数(11…114个01)2转换成十进制数是( )A .216-1B .216-2C .216-3D .216-4 10. 数列{}n a 满足21=a ,1111+-=++n n n a a a ,其前n 项积为n T ,则=2014T ( ) A.61B .61- C .6 D .6- 11. 已知0,0>>y x ,且112=+yx,若m m y x 222+>+恒成立,则实数m 的取值范围是( )A .(-∞,-2]∪[4,+∞)B .(-2,4)C .(-∞,-4]∪[2,+∞)D .(-4,2) 12. 设数列{}n a 的前n 项和为n S ,令nS S S T nn +++=21,称n T 为数列n a a a ,,,21 的“理想数”,已知数列50021,,,a a a 的“理想数”为2004,那么数列12,50021,,,a a a 的“理想数”为( ) A .2012 B .2013 C .2014 D .2015第Ⅱ卷(非选择题 共90分)19.(12分) 已知直线l 过点)2,3(P ,且与x 轴、y 轴的正半轴分别交于A ,B 两点,如图所示,求OAB ∆的面积的最小值及此时直线l 的方程.20. (12分) 某观测站C 在城A 的南偏西20˚的方向上,由A 城出发有一条公路,走向是南偏东40˚,在C 处测得距C 为31千米的公路上B 处有一人正沿公路向A 城走去,走了20千米后,到达D 处,此时C 、D 间距离为21千米,问还需走多少千米到达A 城?21. (12分) 在各项均为正数的等差数列{}n a 中,对任意的*N n ∈都有12121+=+++n n n a a a a a . (1)求数列{}n a 的通项公式n a ;(2)设数列{}n b 满足11=b ,na n nb b 21=-+,求证:对任意的*N n ∈都有212++<n n n b b b .22. (12分)设函数())0(132>+=x xx f ,数列{}n a 满足11=a ,)1(1-=n n a f a ,*N n ∈,且2≥n .(1)求数列{}n a 的通项公式; (2)对*N n ∈,设13221111++++=n n n a a a a a a S ,若ntS n 43≥恒成立,求实数t 的取值范围.答案一、选择题:(每题5分,共60分)13、 3 14、349π15、 2 16、 ①②⑤三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17. 解:(1)由题意,得⎩⎪⎨⎪⎧a 3a 6=55,a 3+a 6=a 2+a 7=16.∵公差d>0,∴⎩⎪⎨⎪⎧a 3=5,a 6=11,∴d =2,a n =2n -1.(2)∵b n =a n +b n -1(n≥2,n ∈N *), ∴b n -b n -1=2n -1(n≥2,n ∈N *).∵b n =(b n -b n -1)+(b n -1-b n -2)+…+(b 2-b 1)+b 1(n≥2,n ∈N *),且b 1=a 1=1,∴b n =2n -1+2n -3+…+3+1=n 2(n≥2,n ∈N *). ∴b n =n 2(n ∈N *).题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D BBCCACDCDDA18. 解析 27(1)4sin cos 2180,:22B C A A B C +-=++=︒由及得 22272[1cos()]2cos 1,4(1cos )4cos 5214cos 4cos 10,cos ,20180,60B C A A A A A A A A -+-+=+-=-+=∴=︒<<︒∴=︒即 22222222(2):cos 211cos ()3.2223123,3: 2 :.221b c a A bcb c a A b c a bc bc b c b b a b c bc bc c c +-=+-=∴=∴+-=+===⎧⎧⎧=+==⎨⎨⎨===⎩⎩⎩由余弦定理得代入上式得由得或 19. 解:由题意设直线方程为x a +y b =1(a >0,b >0),∴3a +2b =1.由基本不等式知3a +2b ≥26ab,即ab≥24(当且仅当3a =2b,即a =6,b =4时等号成立).又S =12a ·b ≥12×24=12,此时直线方程为x 6+y4=1,即2x +3y -12=0.∴△ABO 面积的最小值为12,此时直线方程为2x +3y -12=0. 20. 解 据题意得图02,其中BC=31千米,BD=20千米,CD=21千米,∠CAB=60˚.设∠ACD = α ,∠CDB = β . 在△CDB 中,由余弦定理得:71202123120212cos 222222-=⨯⨯-+=⋅⋅-+=BD CD BC BD CD β,734cos 1sin 2=-=ββ.()CDA CAD ∠-∠-︒=180sin sin α ()β+︒-︒-︒=18060180sin()143523712173460sin cos 60cos sin 60sin =⨯+⨯=︒-︒=︒-=βββ在△ACD 中得1514352321143560sin 21sin sin =⨯=⋅︒=⋅=αA CD AD . 所以还得走15千米到达A 城. 21. 解:(1)设等差数列{a n }的公差为d.令n =1,得a 1=12a 1a 2.由a 1>0,得a 2=2.令n =2,得a 1+a 2=12a 2a 3,即a 1+2=a 1+2d ,得d =1.从而a 1=a 2-d =1.故a n =1+(n -1)·1=n. (2)证明:因为a n =n ,所以b n +1-b n =2n ,所以b n =(b n -b n -1)+(b n -1-b n -2)+…+(b 2-b 1)+b 1 =2n -1+2n -2+…+2+1 =2n -1.又b n b n +2-b 2n +1=(2n -1)(2n +2-1)-(2n +1-1)2=-2n <0, 所以b n b n +2<b 2n +1.22. 解:(1)由a n =f ⎝⎛⎭⎪⎫1a n -1,可得a n -a n -1=23,n ∈N *,n≥2.所以{a n }是等差数列.又因为a 1=1,所以a n =1+(n -1)×23=2n +13,n ∈N *.(2)因为a n =2n +13,所以a n +1=2n +33,所以1a n a n +1=92n +12n +3=92⎝⎛⎭⎪⎫12n +1-12n +3.所以S n =92⎝ ⎛⎭⎪⎫13-12n +3=3n 2n +3,n ∈N *. S n ≥3t 4n ,即3n 2n +3≥3t 4n ,得t≤4n 22n +3(n ∈N *)恒成立.令g(n)=4n 22n +3(n ∈N *),则g(n)=4n 22n +3=4n 2-9+92n +3=2n +3+92n +3-6(n ∈N *).令p =2n +3,则p≥5,p ∈N *.g(n)=p +9p -6(n ∈N *),易知p =5时,g(n)min =45.所以t≤45,即实数t 的取值范围是⎝⎛⎦⎥⎤-∞,45.。
2014-2015学年江苏省泰州市姜堰区高一下学期期中考试数学试题(word版)

2014~2015学年度第二学期期中考试高一数学试题(考试时间: 120分钟)注意事项:所有试题的答案均填写在答题纸上,答案写在卷上的无效.......................... 一、填空题:(本大题共14小题,每小题5分,共70分.) 1.直线210x y ++=的斜率为 ▲ 2.圆22260x y x y +++=的半径为 ▲3.若正四棱锥的底面边长为,体积为34cm ,则它的高为 ▲ cm4.已知圆柱的轴截面是边长为2cm 的正方形,则圆柱的表面积为 ▲ 2cm5.已知点(4,1),(3,1)A B --,若直线2y kx =+与线段AB 恒有公共点,则实数k 的取值范围是 ▲ 6.过三点(6,0),(0,2)A B -和原点(0,0)O 的圆的标准方程为 ▲ 7.过原点且与圆()()22121x y -+-=相切的直线的方程 ▲8.已知圆M 过两点C ()1,1-,D ()1,1-且圆心M 在20x y +-=上,则圆M 的方程为 ▲ 9.给出下列命题:(1)若两个平面平行,那么其中一个平面内的直线一定平行于另一个平面; (2)若两个平面平行,那么垂直于其中一个平面的直线一定垂直于另一个平面; (3)若两个平面垂直,那么垂直于其中一个平面的直线一定平行于另一个平面; (4)若两个平面垂直,那么其中一个平面内的直线一定垂直于另一个平面。
其中正确命题的序号是 ▲10.已知圆22x y m +=与圆2268110x y x y ++--=相交,则实数m 的取值范围为 ▲ 11.设点M 在直线y=1上,若在圆O:221x y +=上存在点N ,使得∠OMN=45°,则点M 的横坐标的取值范围是 ▲12.若圆()()22235x y r -++=上有且只有两个点到直线4320x y --=的距离等于1,则半径r 的取值范围是 ▲13.关于x的方程3x m +=有且只有一个实根,则实数m 的取值范围是 ▲14.在平面直角坐标系xOy 中,已知⊙C:22(1)5x y +-=,A为⊙C与x 负半轴的交点,过A 作⊙C的弦AB ,记线段AB 的中点为M.若OA=OM,则直线AB 的斜率为 ▲ 二、解答题(本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.) 15.(本小题14分)如图,在直三棱柱111ABC A B C -中,1111AB AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点. 求证:(1)面ADE ⊥平面11BCC B ; (2)直线1//A F 平面ADE .16.(本小题14分)已知两条直线110l x y +-=:,240l x y -+=:2的交点为P ,动直线210l ax y a --+=:.(1)若直线l 过点P ,求实数a 的值。
2014年中学考试数学精彩试题及问题详解-江苏泰州
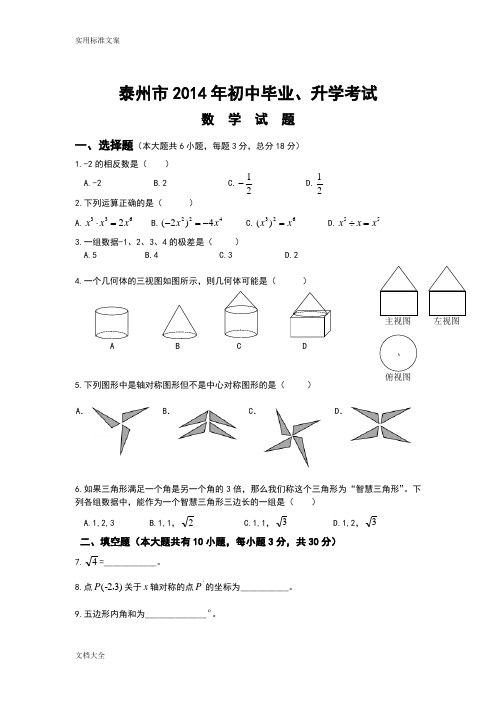
泰州市2014年初中毕业、升学考试数 学 试 题一、选择题(本大题共6小题,每题3分,总分18分)1.-2的相反数是( )A.-2B.2C.21-D.21 2.下列运算正确的是( )A.6332x x x =⋅B.4224)2(x x -=- C.623)(x x = D.55x x x =÷3.一组数据-1、2、3、4的极差是( )A.5B.4C.3D.24.一个几何体的三视图如图所示,则几何体可能是( )A B C D5.下列图形中是轴对称图形但不是中心对称图形的是( )A .B .C .D .6.如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”。
下列各组数据中,能作为一个智慧三角形三边长的一组是( )A.1,2,3B.1,1,2C.1,1,3D.1,2,3二、填空题(本大题共有10小题,每小题3分,共30分)7.4=____________。
8.点)32(-,P 关于x 轴对称的点’P 的坐标为___________。
9.五边形内角和为______________。
俯视图主视图 左视图10.将一次函数13-=x y 的图像沿y 轴向上平移3个单位后,得到的图像对应函数关系式为___________。
11.如图,直线b a ,与直线c 相交,且 a ∥b ,55=∠α,则=∠β________。
12.任意抛掷一枚均匀的骰子一次,朝上的点大于4的概率等于________。
13.圆锥的底面半径为cm 6母线长为10cm ,泽圆锥的侧面积为_______2cm 。
14.已知)0,0(0322≠≠=++b a b ab a ,则代数式baa b +的值为________________。
15.如图,A,B,C,D 依次为一直线上4个点,2=BC ,BCE ∆为等边三角形,圆O 过A,D,E三点,且120=∠AOD ,设x AB =,y CD =,则y 与x 的函数关系式__________。
江苏省泰州市泰兴中学2015-2016学年高一下学期3月段考数学试卷 含解析

2015—2016学年江苏省泰州市泰兴中学高一(下)3月段考数学试卷一、填空题(共14小题,每小题5分,满分70分)1.等差数列{a n }中,若a 1+a 2=5,a 3+a 4=7,则a 5+a 6= . 2.sin15°•cos15°= .3.三个数1,a ,2成等比数列,则实数a= .4.在△ABC 中,若sinA :sinB :sinC=2:3:4,则最大角的余弦值= . 5.在等差数列{a n }中,前15项的和S 15=90,则a 8= . 6.已知,,则= .7.在△ABC 中,已知a 2tanB=b 2tanA ,则此三角形的形状为 三角形. 8.已知数列{a n }的前n 项和S n =3+2n ,则a n = .9.在△ABC 中,内角A ,B,C 的对边分别是a,b ,c ,若a 2﹣b 2=bc ,sinC=2sinB ,则A= .10.设等比数列a n 中,每项均是正数,且a 5a 6=81,则log 3a 1+log 3a 2+…+log 3a 10= . 11.已知cos α=,cos(α+β)=,α,β均为锐角,则cos β= .12.设公比为q 的等比数列{a n }的前n 项和为S n ,若S n +1、S n 、S n +2成等差数列,则q= . 13.已知S n ,T n 分别是等差数列{a n },{b n }的前n 项和,且=,(n ∈N +)则+= .14.在锐角△ABC 中,b=2,B=,sin2A +sin (A ﹣C )﹣sinB=0,则△ABC 的面积为 .二、解答题:15.已知数列{a n }为等差数列,且a 3=5,a 6=11. (1)求数列{a n }的通项公式;(2)若等比数列{b n }满足b 1=3,b 2=a 1+a 2+a 3,求数列{b n }的前n 项和S n . 16.在△ABC 中,角A ,B ,C 所对的边分别为a,b ,c ,a 2+b 2+ab=c 2. (1)求角C 的大小;(2)若c=2acosB ,b=2,求△ABC 的面积.17.在等差数列{a n }中,已知a 1=20,前n 项和为S n ,且S 6=S 15, (1)求{a n }的通项公式;(2)求当n 取何值时,S n 取得最大值,并求出它的最大值; (3)求数列{|a n |}的前n 项和T n .18.在△ABC 中,角A ,B ,C 的对边分别为a,b ,c,且acosC,bcosB ,ccosA 成等差数列, (Ⅰ)求B 的值;(Ⅱ)求2sin 2A +cos(A ﹣C )的范围.19.某地区森林原有木材存量为a ,且每年增长率为25%,因生产建设的需要每年年底要砍伐的木材量为b,设a n 为n 年后该地区森林木材的存量, (1)写出a 1,a 2,a 3; (2)求a n 的表达式;(3)为保护生态环境,防止水土流失,该地区每年的森林木材存量不少于a,如果b=,那么该地区今后会发生水土流失吗?若会,需要经过几年?(参考数据:lg2=0.3)20.已知数列{a n }中,a 1=2,a 2=3,其前n 项和S n 满足S n +1+S n ﹣1=2S n +1,其中n ≥2,n ∈N *.(1)求证:数列{a n }为等差数列,并求其通项公式; (2)设b n =,T n 为数列{b n }的前n 项和,求T n 的取值范围;(3)设c n =4n +(﹣1)n ﹣1λ•2an (λ为非零整数,n ∈N *),试确定λ的值,使得对任意n ∈N *,都有c n +1>c n 成立.2015-2016学年江苏省泰州市泰兴中学高一(下)3月段考数学试卷参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.等差数列{a n}中,若a1+a2=5,a3+a4=7,则a5+a6=9.【考点】等差数列的通项公式.【分析】由等差数列的性质可得:a1+a2,a3+a4,a5+a6成等差数列,即可得出.【解答】解:由等差数列的性质可得:a1+a2,a3+a4,a5+a6成等差数列,∴a1+a2+a5+a6=2(a3+a4),∴5+a5+a6=2×7,解得a5+a6=9,故答案为:9.2.sin15°•cos15°=.【考点】二倍角的正弦.【分析】给原式乘以2后,利用二倍角的正弦函数公式及特殊角的三角函数值化简后,即可求出原式的值.【解答】解:sin15°•cos15°=×2sin15°•cos15°=sin30°=×=.故答案为:3.三个数1,a,2成等比数列,则实数a=±.【考点】等比数列的通项公式.【分析】直接利用等比中项的概念列式得答案.【解答】解:∵三个数1,a,2成等比数列,∴a2=1×2=2,则a=.故答案为:.4.在△ABC中,若sinA:sinB:sinC=2:3:4,则最大角的余弦值=﹣.【考点】余弦定理.【分析】根据题意结合正弦定理得a:b:c=2:3:4.设a=2k,b=3k,c=3k,利用余弦定理求出cosC之值,即得最大角的余弦值【解答】解:∵△ABC中,sinA:sinB:sinC=2:3:4,∴根据正弦定理,得a:b:c=2:3:4,可得c为最大边,角C是最大角设a=2k,b=3k,c=4k(k>0)∴cosC===﹣即最大角的余弦值为﹣故答案为:﹣5.在等差数列{a n}中,前15项的和S15=90,则a8=6.【考点】等差数列的前n项和;等差数列的性质.【分析】由等差数列的前n和可得,由等差数列的性质可得a1+a15=2a8,代入可求a8【解答】解:由等差数列的前n和可得∴a8=6故答案为:66.已知,,则=﹣.【考点】两角和与差的正切函数.【分析】所求式子利用诱导公式化简,将sinα算出并求出tanα带入可求出值.【解答】∵∴sinα==﹣即tanα=∴tan()==﹣故答案为:﹣7.在△ABC中,已知a2tanB=b2tanA,则此三角形的形状为等腰或直角三角形.【考点】三角形的形状判断.【分析】根据同角三角函数的基本关系与正弦定理化简题中的等式,可得sinAcosA=sinBcosB,由二倍角的正弦公式算出sin2A=sin2B,再利用诱导公式得出A=B或A+B=,从而可得△ABC是等腰三角形或直角三角形.【解答】解:∵a2tanB=b2tanA,∴a2•=b2•.根据正弦定理,可得sin2A•=sin2B•,化简整理,得sinAcosA=sinBcosB,∴2sinAcosA=2sinBcosB,即sin2A=sin2B,又∵A、B∈(0,π),∴2A=2B或2A=π﹣2B,解得A=B或A+B=,因此可得△ABC是等腰三角形或直角三角形.故答案为:等腰或直角8.已知数列{a n}的前n项和S n=3+2n,则a n=.【考点】数列的函数特性.【分析】这是数列中的知S n求a n型题目,解决的办法是对n分n=1与n≥2两类讨论解决.【解答】解:∵S n=3+2n,∴当n=1时,S1=a1=3+2=5,=2n﹣1,当n≥2时,a n=S n﹣S n﹣1当n=1时,不符合n≥2时的表达式.∴a n=.故答案为:a n=.9.在△ABC中,内角A,B,C的对边分别是a,b,c,若a2﹣b2=bc,sinC=2sinB,则A=30°.【考点】正弦定理.【分析】已知sinC=2sinB利用正弦定理化简,代入第一个等式用b表示出a,再利用余弦定理列出关系式,将表示出的c与a代入求出cosA的值,即可确定出A的度数.【解答】解:将sinC=2sinB利用正弦定理化简得:c=2b,代入得a2﹣b2=bc=6b2,即a2=7b2,∴由余弦定理得:cosA===,∵A为三角形的内角,∴A=30°.故答案为:30°10.设等比数列a n 中,每项均是正数,且a 5a 6=81,则log 3a 1+log 3a 2+…+log 3a 10= 20 . 【考点】等比数列的性质.【分析】利用等比数列和对数的性质,结合题设条件导出log 3a 1+log 3a 2+…+log 3a 10=log 3(a 1•a 2•a 3…a 10)=log 3(a 5a 6)5,由此能够求出其结果.【解答】解:∵等比数列{a n }中,每项均是正数,且a 5a 6=81, ∴log 3a 1+log 3a 2+…+log 3a 10=log 3(a 1•a 2•a 3…a 10) =log 3(a 5a 6)5 =log 3320 =20.故答案:20.11.已知cos α=,cos(α+β)=,α,β均为锐角,则cos β=.【考点】两角和与差的余弦函数.【分析】由已知利用同角三角函数基本关系式可求sin(α+β),sin α的值,利用两角差的余弦函数公式即可计算求值得解. 【解答】解:∵α、β为锐角, ∴α+β∈(0,π), ∵cos (α+β)=>0,cos α=,∴sin(α+β)==,sin α==, ∴cos β=cos [(α+β)﹣α]=cos(α+β)cos α+sin (α+β)sin α=×+×=.故答案为:.12.设公比为q 的等比数列{a n }的前n 项和为S n ,若S n +1、S n 、S n +2成等差数列,则q= ﹣2 .【考点】等比数列的通项公式.【分析】通过记等比数列{a n }的通项为a n ,利用S n ﹣S n +1=S n +2﹣S n 即﹣a n •q=a n •q +a n •q 2,计算即得结论.【解答】解:记等比数列{a n }的通项为a n , 则a n +1=a n •q ,a n +2=a n •q 2,又∵S n +1、S n 、S n +2成等差数列, ∴S n ﹣S n +1=S n +2﹣S n , 即﹣a n •q=a n •q +a n •q 2, ∴q 2+2q=0, ∴q=﹣2,故答案为:﹣2.13.已知S n,T n分别是等差数列{a n},{b n}的前n项和,且=,(n∈N)则+ +=.【考点】数列的求和.【分析】由等差数列的性质,知+==,由此能够求出结果.【解答】解:∵S n,T n分别是等差数列{a n},{b n}的前n项和,且=,(n∈N),+∴+====.故答案为:.14.在锐角△ABC中,b=2,B=,sin2A+sin(A﹣C)﹣sinB=0,则△ABC的面积为.【考点】解三角形.【分析】根据三角形的内角和定理得到三个角之和为π,表示出B,代入已知的等式中,利用诱导公式化简,再利用二倍角的正弦函数公式及和差化积公式变形,提取2cosA,等式左边变为积的形式,根据两数之积为0,至少有一个为0,可得cosA=0或sinA=sinC,由cosA=0,根据A为三角形的内角,可得A为直角,但三角形为锐角三角形,矛盾,故舍去;由sinA=sinC,根据A和C都为锐角,可得A=C,又B为,可得三角形为等边三角形,且边长为2,进而求出等边三角形的面积即可.【解答】解:∵A+B+C=π,∴B=π﹣(A+C),∴sinB=sin[π﹣(A+C)]=sin(A+C),代入sin2A+sin(A﹣C)﹣sinB=0得:sin2A﹣[sin(A+C)﹣sin(A﹣C)]=0,变形得:2sinAcosA﹣2cosAsinC=0,即2cosA(sinA﹣sinC)=0,所以cosA=0或sinA=sinC,解得A=(又锐角△ABC,此情况不满足,舍去)或A=C,所以A=C,又B=,b=2,所以△ABC为边长为2的等边三角形,则△ABC的面积S=×22=.故答案为:二、解答题:15.已知数列{a n}为等差数列,且a3=5,a6=11.(1)求数列{a n}的通项公式;(2)若等比数列{b n}满足b1=3,b2=a1+a2+a3,求数列{b n}的前n项和S n.【考点】数列的求和;数列递推式.【分析】(1)利用等差数列的通项公式即可得出.(2)利用等比数列的通项公式、求和公式即可得出.【解答】解:(1)设等差数列{a n}的公差d,∵a3=5,a6=11,∴,解得a1=1,d=2,a n=1+(n﹣1)•2=2n﹣1.(2)设等比数列{b n}的公比为q,∵b2=a1+a2+a3=9,b1=3,∴q=3,∴{b n}的前n项和为.16.在△ABC中,角A,B,C所对的边分别为a,b,c,a2+b2+ab=c2.(1)求角C的大小;(2)若c=2acosB,b=2,求△ABC的面积.【考点】余弦定理;正弦定理.【分析】(1)利用余弦定理即可得出.(2)利用余弦定理可得a=b,再利用三角形面积计算公式即可得出.【解答】解:(1)∵a2+b2+ab=c2.∴cosC===﹣.∵C∈(0,π),∴C=.(2)∵c=2acosB,b=2,∴c=2a×,∴a2=b2,即a=b=2,∴△ABC的面积S=absinC=×=.17.在等差数列{a n}中,已知a1=20,前n项和为S n,且S6=S15,(1)求{a n}的通项公式;(2)求当n取何值时,S n取得最大值,并求出它的最大值;(3)求数列{|a n|}的前n项和T n.【考点】数列的求和;数列递推式.【分析】(1)根据等差数列前n项和公式=,将a1=20,即可求得公差d,根据等差数列通项公式即可求得{a n}的通项公式;(2)根据二次函数图象对称确定,当n=11,a11=0,可知n=10或11时,S10=S11,S n取得最大值,根据等差数列前n项和公式,即可求得S n取得最大值;(3)由题意可知当n≤11时,a n≥0,求得T n,当n≥12时,a n<0根据数列的性质,可知T n=2S11﹣(21n﹣n2)=n2﹣21n+220,即可求得数列{|a n|}的前n项和T n.【解答】解:(1)由题意可知:S6=S15,即=,∴2a6=3a1+5a15,∴2(a1+5d)=3a1+5(a1+14d),解得:d=﹣2,∴a n=20+(﹣2)(n﹣1)=22﹣2n,∴{a n}的通项公式a n=22﹣2n;(2)由题意可知,S6=S15,∴S n=f(n)的对称轴方程为:n==10.5,10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年江苏省泰州市泰兴三中高一(下)期初数学试卷
一、填空题:(本大题共14小题,每小题5分,共70分.请将答案填入答题纸填空题的相应答题线上.)
1.(★★★★)已知集合A={x|x 2-2≥0} B={x|x 2-4x+3≤0}则A∪B= {x|x≤- 或
x≥1} .
2.(★★★★)函数的递减区间是(1,3).
3.(★★★★)已知,,若与平行,则λ=
±1 .
4.(★★★★)已知等差数列{a n}中,a 7+a 9=16,a 4=1,则a 12的值是 15 .
5.(★★★★)已知三角形的三个角A,B,C成等差数列,则sinB= .
6.(★★★★)首项为-24的等差数列,从第10项开始为正,则公差d的取值范围是.
7.(★★★)若,则= 5 .
8.(★★★★)等差数列{a n}中,a 5=8,那么S 9= 72 .
9.(★★★)在△ABC中,若∠A=60o,边AB=2,S △ABC= ,则BC边的长为. 10.(★★★★)设S n是等差数列{a n}的前n项和,若= ,则= 2 .
11.(★★★★)一个凸n边形,各内角的度数成等差数列,公差为10o,最小内角为100o,则边数n= 8 .
12.(★★)已知函数f(x)=2sinωx(ω>0)在区间上的最小值是-2,则ω的最小值是.
13.(★★★)已知方程(x 2-2x+m)(x 2-2x+n)=0的四个根组成一个首项为的等差数列,则|m-n|= .
14.(★★)已知数列{a n}、{b n}都是公差为1的等差数列,其首项分别为a 1、b 1,且a
1+b 1=5,a 1、b 1∈N *,设c
n= (n∈N
*),则数列{c
n}的前n项和等于.
二.解答题:(本大题共6小题,共90分.请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤).
15.(★★★)设等差数列{a n}的前n项和为S n,已知S 7=7,S 15=75,
(1)求数列{a n}的通项公式;
(2)设b n= ,求证数列{b n}是等差数列,并求其前n项和T n.
16.(★★★)已知函数.
(1)判断函数f(x)的奇偶性并证明;
(2)当x∈(1,+∞)时,求函数f(x)的值域.
17.(★★★)设等差数列{a n}的前n项和为S n,已知a 3=12,S 12>0,S 13<0.
(1)求数列{a n}的公差d的取值范围;
(2)求数列{a n}的前n项和为S n取得最大值时n的值.
18.(★★★)某单位计划征用一块土地盖一幢每层建筑面积均为30000m 2的宿舍楼,已知土地的征用费是2250元/m 2,土地的征用面积为45000m 2.经核算:第一层的建筑费是400元/m 2,以后每增加一层,建筑费增加30元/m 2.请设计宿舍楼的层数,使得平均每层的总费用最低.(总费用包括建筑费和征地费)
19.(★★)已知:等差数列{a n}中,a 3+a 4=15,a 2a 5=54,公差d<0,前n项和为S n.(1)求数列{a n}的通项公式a n;
(2)求的最大值及相应的n的值;
(3)求数列{|a n|}的前n项和为T n.
20.(★★)设无穷等差数列{a n}的前n项和为S n
(1)a 1=-4,公差d=2,求满足的正整数k;
(2)求满足:对于一切正整数k,都有成立的所有的无穷等差数列{a n}.。
