间接平差习题课
Chapter5-间接平差

ˆ X0 x ˆ2 X 2 2
V1 1 V2 1 V 0 3 V4 0 V 5 0
0 1 1 1 0
0 0 ˆ1 23 0 x ˆ2 0 (m m) 0 x ˆ3 14 1 x 误差方程: V B x l 1 0 B和l分别是???
vi 1 l1 v 1 l 2 x ˆ 2 v 1 n ln 设Li的权为Pi , 权阵P为 : P 1 P P2 Pn
X 2 X n] d2 dn ] b1 t1 b2 t 2 bn t n
T
T
令X X x
0
V B( X x ) d L
0
B x ( L BX 0 d )
令l L ( BX 0 d )
x ( B PB) B Pl
T T
1
ˆ L V ˆ l ,求观测值的平差值 L V Bx
5.1 间接平差原理
例题:如图所示的水准网中,已知水准点A的高程是HA=237.483m,为求B、 C、D三点高程,进行了水准测量,测得高差和水准路线长度见下表。试按 照间接平差方法求B、C和D的高程平差值 。 水准 路线
观测高差
路线长度
1
3 A
B 2 C 4 D
(m)
1 2 3 4 5 5.835 3.782 9.640 7.384 2.270
(km)
3.5 2.7 4.0 3.0 2.5
第四章 间接平差课件ppt课件

返回目录
jk
ˆj, y ˆ j 和x ˆk , y ˆk 设这两点的近似坐标的改正数为 x 即 0 ˆ X ˆ0 x ˆ ˆ ˆ X ˆ X X j j j k k xk , . 0 0 ˆ Y ˆ Y ˆ ˆ Y ˆ Y ˆ Y Y j j j k k k
0 0 0 ˆ x L f X , X , , X i i 1 2 t t 0
f i f i bi1 X , bi 2 X 1 0 2
0 li Li f i X 10 , X 2 ,, X t0 Li L0 i
ˆ i b12 x ˆ 2 b1t x ˆ t d1 L1 V1 b11 x ˆ i b22 x ˆ 2 b2t x ˆt d 2 L2 V2 b21 x ˆ i bn 2 x ˆ t bmt x ˆt d n L1 Vn bn1 x
0 K 0 K
ˆ k Y j0 y ˆi y
k 0 j
ˆ X x
ˆ x
i
将上式右端按台劳公式展开,得
ˆ jk a ˆ jk arctg 0 a 0 XK X j X j ˆ jk a x ˆ Y 0 j ˆ jk a y ˆ X k 0 ˆ jk a ˆk x Y 0 K ˆk , y 0
返回目录
需要指出,线性化的误差方程是个近似式,因为它略 去了的、二次上的各项。当很小时,略去高次项是不会影 响计算精度的。如果由于某种原因不能求得较为准确的参 数近似值,即都很大,这样,平差值之间仍然会存在不符 值。此时,就要把第一次平差结果作为参数的近似值再进 行一次平差。 下面结合测角和测边两种情况,来讲相应误差方程的 线性化问题。
间接平差专题教育课件

第二节 误差方程
要拟定平差问题中未知数旳个数; 选择哪些量作为未知数; 要考虑怎样列出平差值方程; 怎样选用未知救旳近似值; 怎样写出误差方程。
一、拟定未知数旳个数 未知数旳个数等于必要观察数 二、参数旳选择
参数选择旳原则:足数 独立 最简
采用间接平差,应该选定刚好足数而又独立旳一组量 作为未知数。至于应选择其中哪些量为未知数,则可根据 实际需要或是否便于计算而定。
试按间接平差法列出误差方程。 A L1L2LL34 L5
C
解:必要观察为3,设
L6
D
Lˆ1 Xˆ1, Lˆ4 Xˆ 2 , Lˆ6 Xˆ 3
E
Xˆ
0 1
L1
48 1701,
Xˆ
0 2
L4
48
3512,
Xˆ
0 3
L6
56
0149
L1 v1 Xˆ1 L2 v2 Xˆ1 Xˆ 2
v1 xˆ1 0
V T PV V T P V V T PB 0
xˆ
xˆ
BT PV 0
V B xˆ l l L (BX 0 d )
n1 nt t1 n1
以上两式称为间接平差旳基础方程,根据基础方程可得:
BT PB xˆ BT P l 0
令 N BB
tt
BT PB,W t1
BT Pl
则: NBB xˆ W 0
v2 xˆ1 xˆ2 6
L3
v3 Xˆ1 L4 v4
Xˆ 2 Xˆ 2
Xˆ
3
v3
xˆ1 xˆ2 xˆ3 8
v4 xˆ2 0
L5 v5 Xˆ 2 Xˆ 3 L6 v6 Xˆ 3
B
v5 xˆ2 xˆ3 6
测量平差习题3

第五章 间接平差第一节 间接平差原理1在图5-1的水准网中,P 1,P 2及P 3点为待定点,测得各段水准路线高差为:h 1=+1.335m ,S 1=2kmh 2=+0.055m ,S 2=2kmh 3=-1.396m ,S 3=3km若令2km 路线上的观测高差为位权观测,试用间接平差法求高差的平差值。
2在三角形ABC 中(如图5-2),测得不等精度观测值如下:试按间接平差计算各角的平差值。
图5-1 图5-23在图5-3的单一符合水准路线中,A ,B 点为已知点,P 1,P 2点为待定点,观测高差为h 1,h 2,h 3,路线长度为S 1,S 2,S 3,设观测高差的权为P i =1/S i ,并令P 1,P 2点高程为未知参数,试按间接平差原理求待定点高程平差值。
4在图5-4,A ,B ,C ,D 点在同直线上为确定其间的三段距离,测出了距离AB ,BC ,CD ,AC 和BD ,相应的观测值为:l 1=200.000m ,l 2=200.000m ,l 3=200.080m ,l 4=400.040m ,l 5=400.000m , 设它们不相关且等精度。
若分别选取取AB ,BC 及CD 三段距离为未知参数X 1,X 2和X 3,试按间接平差法求A ,D 两点间的距离平差值。
图5-3 图5-41,3.110251101='''=P β2,4.2813402,9.218088303202='''=='''=P P ββ AP P2 A AB1 12 23 h 15在图5-5的直角三角形ABC 中已知AB=100.000m (无误差),测得边长AC 和角A ,得观测值为l 1=115.470m ,l 2=29059’55”,其中误差设为m l 1=±5mm ,m l 2=±4”,试按间接平差法求三角形高BC 的平差值。
《测量平差》实习三例题知识讲解

《测量平差》实习三
例题
实习三:间接平差方法应用
(一)、有关距离的平差:
1、在下图中,A、B、C三点在一直线上,测出了AB、BC及AC的距离,得4个独立观测值:L1=200.010m,L2=300.050m,L3=300.070m,L
4
=500.090m。
若令100m量距的权为单位权,试按条件平差法确定A、C之间各段距离的平差值。
(二)、有关水准的平差
2、水准网图(1)的观测高差及水准路线长度见下表:按条件平差求:(1)高
差平差值ˆ
i
h;
(2)A点至E点平差后高差的中
误差ˆAE h
σ;(3)E点至C点平差后
高差的中误差ˆEC h
σ。
3、在下图的水准网中,观测高差及路线长度见下表:已知A,B点的高程
差法求:(1)各观测高差平差值;(2)平差后P1
到P2点间高差的中误差。
(三)、有关角度的平差
4、在下图左中,观测了测站O上的4个角度,得同精度观测值:
L1=30˚00΄20˝、L2=50˚00΄00˝、L3=20˚00΄00˝、L4=40˚00΄20˝,试按条件平差求:
(1)各角度的平差值及平差值协因数阵;(2)平差后∠AOC的权倒数。
5、在上图右的测角网中,A、B、C、D均为待定点,观测5个角度,得观测值:β1=40˚00΄20˝、β2=100˚00΄30˝、β3=50˚00΄20˝、β4=120˚00΄00˝、
β5=50˚00΄20˝,其中,A角为固定值90˚00΄00˝,按条件平差求各角平差值及其协
因数阵。
平差大全---指导与习题
2.某单位购买了一台新水准仪,经过检测其精度知道,用该仪器单程测量1km 的高差中误 1. 间接平差公式汇编,设观测值的协因数阵为LL Q ,求未知参数平差值的协因数阵。
3.差是5mm 。
该单位接到一个工程任务,其中之一是需要在指定位置建立一个水准点,要求该水准点的高程中误差不大于10mm 。
经过勘查,距该水准点附近有两个高级已知水准点,一个相距约10km ,另外一个相距约20km ,现在两已知水准点之间经过新建的水准点布设一条附合路线,问用新购的水准仪进行单程测量是否满足精度要求。
(使用间接平差解答)。
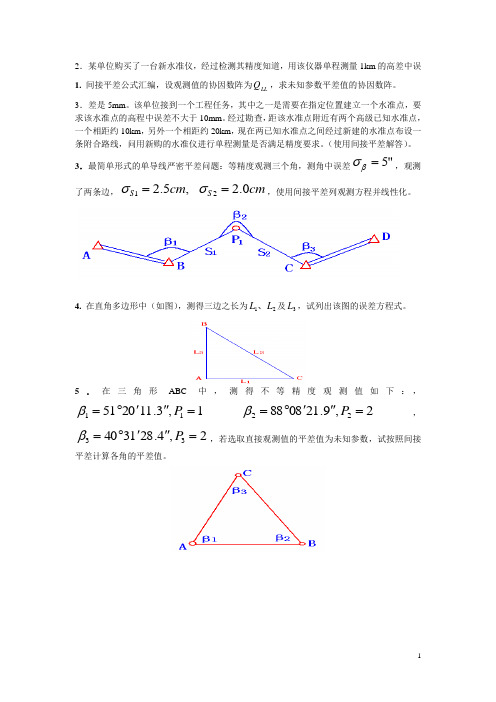
3.最简单形式的单导线严密平差问题:等精度观测三个角,测角中误差"5=βσ,观测了两条边,cm cm S S 0.2,5.221==σσ,使用间接平差列观测方程并线性化。
4. 在直角多边形中(如图),测得三边之长为21L L 、及3L ,试列出该图的误差方程式。
5.在三角形ABC中,测得不等精度观测值如下:,1,3.11205111="'︒=P β2,9.21088822="'︒=P β,2,4.28314033="'︒=P β,若选取直接观测值的平差值为未知参数,试按照间接平差计算各角的平差值。
6.如图所示的直角三角形ABC 中,已知AB=100.00m (无误差),测得边长AC 和角度A ,得观测值为ml 470.1151=,,5559292"'︒=l 其中误差分别为,51mm l ±=σ,42"±=l σ试按间接平差法求三角形ABC中的平差值。
7. 图4.3中,C B A 、、是已知点, 21P P 、为待定点,网中观测了12个角度和6条边长。
已知测角中误差为5.1''±,边长测量中误差为0.2±cm ,起算数据及观测值分别列表于表4.1和表4.2。
8附有限制条件的间接平差

aik xˆ i + bik ˆyi aik xˆ k bik ˆyk w2 0
w1
X
0 k
X
0 i
2
+
Yk0 Yi0
2
Sik
w2
arctan
Yk0
X
0 k
Yi0
X
0 i
aik
§8-1 附有限制条件的间接平差原理
二、基础方程
已知附有限制条件的间接平差法的函数模型
K
s ,1
k1
k2
ks T
称为联系数向量。组成极值函数
V T PV
2K
T s
Cxˆ Wx
将对 求xˆ 一阶导数,并令其为零,得:
xˆ
2V T P V xˆ
2
K
T s
C
2V
T
PB
2
K
T s
CLeabharlann 0转置得 BT PV C T K s 0
§8-1 附有限制条件的间接平差原理
§8-2 精度评定
三、平差值的精度评定
DLˆ Lˆ
ˆ
Q 2
0 Lˆ Lˆ
DXˆ Xˆ
ˆ
Q 2
0 Xˆ Xˆ
§8-2 精度评定
四、参数平差值函数的精度评定
设参数平差值函数为:
ˆ
G(
Xˆ )
G(
Xˆ
1,Xˆ
,
2
Xˆ
)
u
线性化得权函数式为:
dˆ
G Xˆ 1
X0
平差理论及平差基习题集

平差理论及平差基习题集1、在间接平差中,参数X 与平差值L 是否相关?试证明。
答:-111^^2^^^1()(()0T B T T T T T N B PlV B BNbb B Pl L BNbb B E lL L v x xQ x L Q x v Nbb B PQu BNbb P E σ-1-------===-=-=+=+∴==-=σ 2、已知独立观测值L 1、L 2的方差M 1和M 2,求函数211212Y L L L =+的方差。
答:211212112221211212()()Y Y Y L L L L L dL L dL M L L M L M σ=+=++=++3、在相同观测条件下观测A 、B 两个角度,设∠A 观测4测回的权为1,则对∠B 观测9个回合的权是多少? 答:2021==114A P σσ20σ221941149LB P σ=== 4、已知观测值向量L21的协方差阵为DLL=3112⎡⎤⎢⎥⎣⎦,又知协因数Q12=1-5,试求观测值。
答:111222200211221202011111220122-1===-13=-1-1=529315513125532LL L L L QL L QL L D Q QL L QL L QL L QL l DL PLL QLL P P σσσσσ---⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦=⎡⎤⎢⎥⎛⎫⎡⎤====⎢⎥ ⎪⎢⎥-⎣⎦⎢⎥⎝⎭⎢⎥⎣⎦==5 、已求得控制网中P 点误差椭圆参数υE=157°30′、E=1.57dm 和F=1.02dm,已知PB 边坐标方位角αPB=217°30′,SPB=5KM,B 为已知点,求方位角中误差^PA σα和边长相对误差^PAPA S S σ。
6、设某平差问题是按条件平差方法进行的,其法方程为:1210-260-246K K -⎡⎤⎡⎤⎡⎤-=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,求联系数12K K ;求单位权方差20σ。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方程个数 函数模型
条件平差
间接平差
rnt
n
AVW0 VBxˆl
附有参数的条件平 差
cur
AV B xW 0
随机模型
D02Q02P1 D02Q02P1
D
02Q
P 2 1
0
条件/误差方 程
AVW0 VBxˆl AV B xW 0
法方程 法方程解 改正数方程
NaaKW0 KNaa1W V QAT K
h1
P
A
S1
h2 B
S2
测量20平20差/4/11
3、在如图三角形中,以不等精度测得
7 8 o 2 3 1 2 , P 1; 8 5 o 3 0 0 6 , P 2 ; 1 6 o 0 6 3 2 , P 1; 3 4 3 o 5 3 2 4 , P 1;
试用条件或间接平差法求各内角的平差值。
间接平差
测量20平20差/4/11
介绍间接平差基本原理,求 平差值的方法、步骤, 各 类测量控制网观测方程和误 差方程的列立,以及精度评 定的方法。
第七章 间接平差
• 授课目的要求: 熟记间接平差的基础方程和法方程形式; 掌握按间接平差法求平差值的方法、步骤。
• 重 点、难 点: 间接平差法求平差值的方法、步骤 。
测量20平20差/4/11
h2
S2
h3
h4
S3
S4
S1
h1
解题过程区别:
1、所列方程个数不同; 2、方程形式不同。条件平差法为条件方程,不含参数
;间接平差法为观测值方程,即将每个观测值表示 为参数的函数。
测量20平20差/4/11
2、设在单一附合水准路线,已知A、B(如图)两点高程 为HA、HB,路线长为S1、S2,观测高差为h1、h2,试用 条件或间接平差法写出P点高程平差值的公式。
h2
h 4 1 .6 1 3 m , S 4 2 ;
P1
h3
h 5 1 .2 7 0 m , S 5 1;
h 6 2 .9 3 1 m , S 6 2 ;
h 7 0 .7 8 2 m , S 7 2 ;
若设P2点平差值为参数,试求
h7
(1)列出条件方程;
(2)求出法方程; P2
(3)求出观测值的改正数及平差值。
NBB xˆW0 AQTAKBxW0
BTK0
xˆ NB1BW
K
N
1 aa
(W
B
x)
x
N
1 bb
B
T
N
W 1
aa
VBxˆl
V QAT K
平差值
Lˆ LV
Lˆ L V Xˆ X 0 xˆ
Lˆ L V Xˆ X 0 xˆ
习题课
1、如图所示的水准网中,A、B、C为已知点 ,HA=12.000m,HB=12.500m,HC=14.000m; 高h件4差=、1观间.8测5接1值平mh;差1=S法21.=求510高k0mm差,,的sh2平2==1差2k.m0值0,。0ms3,=2hk3=m1.s345=21mkm,,试按条
测量20平20差/4/11
附有参数的条件平差法
4、在下图所示的水准网中,点A有高程HA=10.000m,P1—P4 为待定点,观测高差及路线长度为:
A
h1 1 .2 7 0 m , S 1 2 ;
h 2 3 .3 8 0 m , S 2 2 ;
h1
h 3 2 .1 1 4 m , S 3 1;
测量20平20差/4/11
h5 1
2020/4/11
