必修四综合
高中数学必修一、必修四、必修二综合练习(含答案)

高中数学必修一、必修四、必修二综合练习一. 选择题:1.函数()12x f x =-的定义域是 ( )A .(,0]-∞B .[0,)+∞C .(,0)-∞D .(,)-∞+∞2.下列四个命题中正确的是( )A .lg 2lg3lg5⋅=B .mn n m a a a =⋅C .a a n n =D .yxy x aa a log log log =- 3. cos300︒= ( )(A)32-(B)-12 (C)12(D) 32 4.正三角形ABC 的边长为1,设=u u u rAB c ,=u u u r BC a ,=u u u r CA b ,那么a b b c c a ++g g g 的值是( ) A .32 B .12 C .32- D .12- 5.在正项等比数列{}n a 中,若232a a +=,458a a +=,则56a a += ( )A.16B. 32C. 36D. 646. 程序框图如下:如果上述程序运行的结果为S =40,那么判断框中应填入 A .6k ≤ B .5k ≤ C .6k ≥ D .5k ≥ 7.已知1x > ,则11y x x =+-的最小值为 ( ) A.1 B. 2 C. 22 D. 38.已知图1是函数()y f x =的图象,则图2中的图象对应的函数可能是 ( )A .(||)y f x =B .|()|y f x =C .(||)y f x =-D .(||)y f x =--9.已知全集{}0,1,2U =,且{}2U C A =,则集合A 的子集共有( ) A .2个B .3个C .4个D .5个10.为了得到函数cos(2)3y x π=-的图象,可以将函数sin 2y x =的图象( )A .向右平移6π个单位长度 B .向右平移12π个单位长度 C .向左平移6π个单位长度D .向左平移12π个单位长度二、填空题(每小题5分,共20分)11.已知向量(3,1)a =r ,(1,3)b =r ,(,7)c k =r ,若()a c -r r∥b r ,则k = .12. 满足约束条件|x |+2|y |≤2的目标函数z =y -x 的最小值是________. 13.已知3cos()25πα-=,则cos2α= 14.对定义域是f D 、g D 的函数)(x f y =、)(x g y =,规定:函数⎪⎩⎪⎨⎧∈∉∉∈∈∈=g f gf g f Dx D x x g D x D x x f D x D x x g x f x h 且当且当且当),(),(),()()(,若函数11)(-=x x f ,2)(x x g =,则=+)2()1(h h 。
人教版高中英语必修四Unit4单元综合技能训练

Unit 4单元综合技能训练时间:120分钟,满分:150分第一部分:听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你将有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What probably is the woman?A.A teacher. B.A doctor.C. A shop assistant.2. How did the man think of the movie?A. Uninteresting. B.Very interesting.C. Nothing special.3. Who held a birthday party?A. Jane. B.The man.C. The woman.4. When do the speakers plan to meet?A. This afternoon. B.Tomorrow morning.C. Tomorrow afternoon.5. What does the man mean?A. There's something wrong with the machine.B.There probably is a power failure.C. The woman's unable to work the machine.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
高一数学必修四综合练习题

高一数学必修四综合练习题一、选择题(本大题共12小题,每小题5分,共60分。
) 1、 210sin 的值是 ( ) A. 21- B. 21 C. 23-D. 23 2、函数1)4(cos 22--=πx y 是( )A. 最小正周期为π的奇函数B. 最小正周期为π的偶函数C. 最小正周期为2π的奇函数 D . 最小正周期为2π的偶函数3、设角α是第二象限角,且2cos2cosαα-=,则2α角的终边在( )A 第一象限B 第二象限C 第三象限D 第四象限 4、函数xxx x x x y tan tan cos cos sin sin ++=的值的集合是 ( ) A {}3,1,0,1- B {}3,0,1- C {}3,1- D {}1,1-5、已知平面向量)1,1(=→a ,)1,1(-=→b ,则向量→→-b a 2321的坐标是( )A.(21)--, B .(21)-, C.(10)-, D.6、在锐角△ABC 中,设.cos cos ,sin sin B A y B A x ⋅=⋅=则x,y 的大小关系为( )A.y x ≤B.y x >C.y x <D.y x ≥ 7、将函数sin()3y x π=-图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的函数图象向左平移3π个单位,最后所得到的图象对应的解析式是 ( )A 1sin 2y x = B 1sin()22y x π=-C 1sin()26y x π=- D sin(2)6y x π=-8、已知向量()1,3=→a ,()3,-=→x b ,且→→⊥b a ,则实数x 的值为( )A. 3-B. 3C. 1-D. 1 9、如图,四边形ABCD 是梯形,AD ∥BC ,则OA BC AB ++等于( )A .−→−CDB .−→−OC C .−→−DAD .−→−CO10已知113a (,2sin ),b (cos ,),a 322=α=α且∥b ,则锐角α的值为( ) A 、4π B 、2π C 、8π D 、6π11、设),6,2(),3,4(21--P P 且P 在21P P 的延长线上,使212PP P P =,则点P 的坐标是 ( )A 、)15,8(- B 、 (0,3) C 、)415,21(- D 、)23,1( 12、已知图1是函数π2sin()2y x ωϕϕ⎛⎫=+<⎪⎝⎭的图象上的一段,则( )A.10π116ωϕ==, B.10π116ωϕ==-,C.π26ωϕ==, D.π26ωϕ==-,13.设集合M={x ︱x=9045k ︒︒•+,k ∈Z }N={x ︱x=4590k ︒︒•+,k ∈Z },A M=NB M ⊆NC M ⊇ND M ∩N= ∅ 14.已知22sin cos 11cot 1tan αααα-=++ ,则α是( )A 第一象限角B 第二象限角C 第三象限角D 第四象限角ABODC15.求00080sin 40sin 20sin -+的值( )A 1B 1-C 3D 016. P=sin14cos14︒︒+ , Q=214︒-,R =2, 比较P 、Q 、R 的大小关系( )A P>R>QB Q>R>PC R>Q>PD R>P>Q 17. 求函数sin 2cos 2y x x =的最小正周期是( ) A 2π B π C2πD 32π18.已知函数()f x 为奇函数,当x>0时,函数f(x)=sin2x+sinx,则当x<0时,()f x 的解析式是( )A ()sin 2sin f x x x =+B ()sin 2sin f x x x =-+C ()sin 2sin f x x x =--D ()sin 2sin f x x x =-19. 下列条件中,不能确定三点A 、B 、P 共线的是( ) A .MB MA MP ︒︒+=10cos 10sin 22 B MB MA MP ︒︒+=70sin 20sin 22 C .MB MA MP ︒︒+=80cos 10sin 22 D MB MA MP ︒︒+=200cos 20sin 22 20.在ABC ∆中,若C B A B A 22222sin sin cos cos sin =-,则ABC ∆是( )A 锐角三角形 B 直角三角形 C 等腰或直角三角形D钝角三角形 21. 已知平面向量a ,b ,c 满足|a |=1,|b |=2,|c |=3,且a 、b 、c ,两两所成的角相等,则 |a +b +c |等于( ) A 3 B 6或2 C 6 D 6或322.在三角形ABC 中,向量a OA =, b OB =,OD 是AB 边上的高,若AB AD λ=,则实数λ等于( ) A2||(b a a b a - B||b a - C ||(b a a b a --⋅ D 2||(b a b a a --⋅23.在三角形ABC 中,tanA,tanB 是方程01832=-+x x 的两个根,则cosC 等于( )A -2B 2C 55-D 5524.若方程0sin cos 22=+-a x x 在20π≤<x 内有实根,则a 的取值范围是A 11≤≤-aB 11≤<-aC 01<≤-aD 45-≤a二、填空题(本大题共5小题,每小题4分,共20分) 13. 设向量1e 和2e 不共线,若21e e k +与214e e -共线,则实数k 的值等于_________.14.在直角坐标系XOY 中,已知A (4,-3)和B (-6,8),若C 在角AOB 的平分线上,且|OC,则向量OC =_____________. 15. 求值()()()()1tan11tan 21tan 441tan 45︒︒︒︒++⋅⋅⋅⋅++=___________. 16.下列命题正确的序号有 ________________①已知点O 、N 、P 在ABC ∆所在平面内,且|OA |=|OB |=|OC |,0=++NC NB NA ,且PA PC PC PB PB PA ⋅=⋅=⋅,则点O 、N 、P依次是ABC ∆的外心、重心、垂心②若向量a =)2,(x ,b =)5,3(-,且a 与b 的夹角是锐角,则∈x )310,(-∞ ③0)2()(=--⋅-OA OC OB OC OB ,则三角形ABC 为等腰三角形④在ABC ∆中,a AB =,b BC =且0>⋅b a ,则ABC ∆是钝角三角形。
高中语文人教版必修4单元综合一 课件PPT

作为必修模块的戏剧教学应该完成的任务 学生应了解戏剧发展史的基本知识
1.中国话剧和中国戏曲的不同特点 2.中国话剧和西方戏剧的渊源关系 3.西方戏剧发展的基本脉络 4.中国话剧发展的基本脉络
作为必修模块的戏剧教学应该完成的任务
学生应获得欣赏话剧的基本知识和方法 1.通过演出或观看演出体会剧本 2.不依靠演出,单纯从剧本要素鉴赏(与其
Andbyopposingendthem.Todie,tosleep—— Nomore——andbyasleeptosayweend Theheartacheandthethousandnaturalshocks Thatfleshisheirto.“Tisaconsummation Devoutlytobewished.Todie,tosleep; Tosleep,perchancetodream.Ay,there’stherub,……”
他文学体裁的文本鉴赏关注点不同)
通过演出或观看演出体会或鉴赏话剧
戏剧的舞台设计(人物活动的时代和空间背景) 人物表演的核心——戏剧的动作(形体动作、语
言动作、静止动作) 动作受制于人内心,动作是能够最深刻地表现人的
精神世界的直观表现。美国戏剧教育家贝克认为 ,最能直接表现一个人性格的不是他自己怎样在 思想,而是遇到危机之时,他怎样本能地、自发 地、作出行动。在现实生活中,存在着人与人、 人与自然、人与社会的矛盾,这些矛盾在不同的 人的心里有着不同的感受,由此而产生不同的人 物个性。在戏剧中,那些表现人物内心世界的直 观动作,成为表现人的个性最有力手段,动作体 现了人的内心,也即展示了生活中的矛盾冲突, 又促进了戏剧情节的进一步发展。
教学设计参考(汪文龙老师的课例)
高中政治新教材 必修四 模块综合试卷(二)

模块综合试卷(二)(时间:90分钟满分:100分)一、选择题(每小题2分,共40分)1.生活中,很多老年人以“万一将来用到了呢?”的观念而将许多旧物进行保存,同时不少的年轻人则以“旧的不去新的不来”的心态迅速将不用的东西丢弃。
其原因在于() A.有什么样的世界观,就有什么样的方法论B.方法论决定世界观,世界观体现方法论C.世界观不同,做事的具体方法就必然不同D.哲学为生活和实践提供积极有益的指导答案 A解析题目中,一些老人因旧物件以后可能会用到而进行了保存,一些年轻人则以“旧的不去新的不来”的心态迅速将不用的东西丢弃,从哲学角度来看,体现了世界观决定方法论,A正确。
2.中医学以阴阳五行作为理论基础,将人体看成是气、形、神的统一体,通过“望闻问切”四诊合参的方法探求病因,分析人体内五脏六腑、经络关节等的变化,使用中药、针灸、推拿、拔罐、食疗等多种治疗手段,使人体达到阴阳调和而康复。
从哲学角度看,中医药文化()①具有古代朴素唯物主义哲学思想②博大精深、源远流长③是系统化理论化的世界观④蕴含着自发的辩证法思想A.①②B.①④C.②③D.②④答案 B解析中医学的阴阳五行学说“将人体看成是气、形、神的统一体”,属于古代朴素唯物主义思想,①正确。
中医学“分析人体内五脏六腑、经络关节等的变化”,使用多种治疗手段治病,蕴含着联系、变化、发展等自发的辩证法思想,④正确。
3.英国华威大学的科学家们发现了一种新的囊泡。
它是人类细胞中一种前所未知的成分,能像骑自行车的快递员一样穿梭于繁忙的交通中运送蛋白质。
这项发现或许可以解释细胞在疾病(比如癌症)中扩散的机制。
这一发现佐证了()①世界的真正统一性就在于它的物质性②思维和存在具有同一性③唯物主义是现时代的思想智慧④具体科学的进步推动哲学的发展A.①②B.③④C.①③D.②④答案 A解析材料中这一发现佐证了世界的真正统一性就在于它的物质性,世界是可知的,①②正确。
辩证唯物主义和历史唯物主义是现时代的思想智慧,③错误。
必修3-4综合测试题1
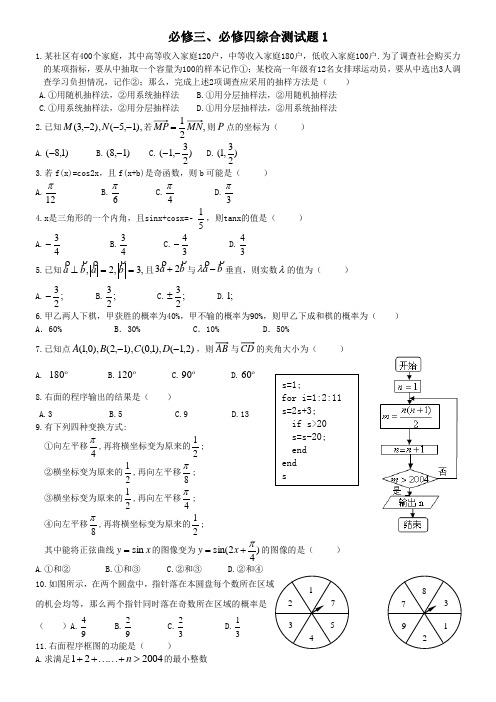
必修三、必修四综合测试题11.某社区有400个家庭,其中高等收入家庭120户,中等收入家庭180户,低收入家庭100户.为了调查社会购买力的某项指标,要从中抽取一个容量为100的样本记作①;某校高一年级有12名女排球运动员,要从中选出3人调查学习负担情况,记作②;那么,完成上述2项调查应采用的抽样方法是( ) A.①用随机抽样法,②用系统抽样法 B.①用分层抽样法,②用随机抽样法 C.①用系统抽样法,②用分层抽样法 D.①用分层抽样法,②用系统抽样法2.已知),1,5(),2,3(---N M 若,21MN MP =则P 点的坐标为( )A.)1,8(-B.)1,8(-C.)23,1(-- D.)23,1( 3.若f(x)=cos2x ,且f(x+b)是奇函数,则b 可能是( )A.12π B.6π C.4π D.3π4.x 是三角形的一个内角,且sinx+cosx=15-,则tanx 的值是( )A.43-B.43C.34-D.345.已知,3,2,==⊥b a b a且b a 23+与b a -λ垂直,则实数λ的值为( )A.;23-B.;23 C.;23±D.;16.甲乙两人下棋,甲获胜的概率为40%,甲不输的概率为90%,则甲乙下成和棋的概率为( ) A .60% B .30% C .10% D .50%7.已知点)2,1(),1,0(),1,2(),0,1(--D C B A ,则AB 与CD 的夹角大小为( ) A. 180 B. 120 C. 90 D. 608.右面的程序输出的结果是( )A.3B.5C.9D.13 9.有下列四种变换方式:①向左平移4π,再将横坐标变为原来的21;②横坐标变为原来的21,再向左平移8π; ③横坐标变为原来的21,再向左平移4π;④向左平移8π,再将横坐标变为原来的21;其中能将正弦曲线x y sin =的图像变为)42sin(π+=x y 的图像的是( )A.①和②B.①和③C.②和③D.②和④ 10.的机会均等,那么两个指针同时落在奇数所在区域的概率是( )A.49B.29C.23D.1311.右面程序框图的功能是( ) A.求满足200421>+⋯⋯++n 的最小整数B.求满足2004121>-+⋯⋯++n 的最小整数C.求满足200421<+⋯⋯++n 的最大整数D.求满足2004121<-+⋯⋯++n 的最大整数 ★12.若对任意实数a ,函数⎪⎭⎫⎝⎛-+=6312sin 5ππx k y (k ∈N)在区间[a ,a +3]上的值45出现不少于4次且不多于8次,则k 的值是( ) A.2 B.4 C.3或4 D.2或3二、填空题:13.为了了解参加运动会的2000名运动员的年龄情况,从中抽取100名运动员;就这个问题,下列说法中正确的有 .①2000名运动员是总体;②每个运动员是个体;③所抽取的100名运动员是一个样本;④样本容量为100;⑤这个抽样方法可采用按年龄进行分层抽样;⑥每个运动员被抽到的概率相等.14.取一个边长为2a 的正方形及其内切圆,若随机地向正方形内丢一粒豆子,则豆子落入圆内的概率为 ★15.函数x y 22sinlog =的单调减区间是____________________16.已知正方形ABCD 的边长为1,设,,,c AC b BC a AB===则c b a +-的模为 .三、解答题: 17. 已知),0(,,55cos ,31tan πβαβα∈=-=(1)求βsin 的值; (2)求)tan(βα+的值.18.从4名男生和2名女生中任选3人参加演讲比赛, ⑴求所选3人都是男生的概率; ⑵求所选3人恰有1名女生的概率;⑶求所选3人中至少有1名女生的概率。
必修四生活与哲学综合测试及其答案

必修四生活与哲学综合测试及其答案IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】高三必修四模块测试1、每年11月的第三个星期四是“世界哲学日”。
世界哲学日是联合国教科文组织在2002年发起的,目的是鼓励世界各国与其他民族分享他们的哲学传统,提高青少年对哲学的兴趣,激发人们对现代社会面临的问题进行思考。
下列关于哲学的表述,正确的是()①哲学是关于世界观的学说②哲学是世界观与方法论的统一③哲学是自然、社会和思维知识的概括总结④哲学是科学的世界观和方法论A.①②④B.①③④C.②③④D.①②③2、世界观和方法论的关系是()A.世界观和方法论相互决定B.方法论决定世界观,世界观体现方法论C.世界观决定方法论,方法论体现世界观D.世界观和方法论相互影响,相互促进3、哲学与世界观既有区别又有联系。
下列关于二者关系的说法中,正确揭示出二者区别的是()①世界观人人都有,但不是人人都是哲学家②一般人的世界观是自发的、零散的,而哲学则是系统化的理论体系③世界观就是哲学,哲学是理论化、系统化的世界观④世界观和哲学的研究对象都是整个世界A.①②B.①③C.②④D.③④4、甲乙两人高考均失利而落榜。
甲认为,高考落榜是天命所致,我应顺应天命,另谋其他出路;乙认为,事在人为,没有过不去的坎,重新选择复读。
由此可见()①世界观决定方法论②哲学源于对实践问题的思考③生活需要科学世界观的指导④学习哲学是走向成功的关键A.①②B.③④C.①③D.②④5、每年9月18日,全国各地都会举行各种形式的纪念活动,让每一个中国人都牢记国耻,发奋图强,为中华民族的伟大复兴而生命不息,奋斗不止。
这表明() A.世界观和方法论的统一,就构成了马克思主义哲学B.世界观对人们认识和改造世界有重要的指导意义C.世界观决定方法论并决定一个人作出贡献的大小D.世界观决定方法论,方法论反映世界观6、“治自然科学者,局守一门,而不肯稍涉哲学,而不知哲学之归宿,其中如自然哲学一部,尤为科学家所需要。
必修四综合练习题

必修四综合练习题1.若角0600的终边上有一点()a ,4-,则a 的值是( )A .34B .34-C .34±D .32.函数xx xx xx y tan tan cos cos sin sin ++=的值域是( )A .{}3,1,0,1-B .{}3,0,1-C .{}3,1-D .{}1,1-3.若α为第二象限角,那么α2sin ,2cosα,α2cos 1,2cos1α中,其值必为正的有( )A .0个B .1个C .2个D .3个4.已知)1(,sin <=m m α,παπ<<2,那么=αtan ( ).A .21mm-B .21mm--C .21mm-±D . mm 21-±5.若角α的终边落在直线0=+y x 上,则ααααcos cos 1sin 1sin 22-+-的值等于( ).A .2B .2-C .2-或2D .06.已知sin sin αβ>,那么下列命题成立的是( )A .若,αβ是第一象限角,则cos cos αβ>B .若,αβ是第二象限角,则tan tan αβ>C .若,αβ是第三象限角,则cos cos αβ>D .若,αβ是第四象限角,则tan tan αβ>7.若θ为锐角且2coscos 1-=--θθ,则θθ1coscos -+的值为( )A .22B .6C .6D .48.若点(sin cos ,tan )P ααα-在第一象限,则在[0,2)π内α的取值范围是( ) A .35(,)(,)244ππππ B .5(,)(,)424ππππ C .353(,)(,)2442ππππ D .33(,)(,)244ππππ9.在函数x y sin =、x y sin =、)322sin(π+=x y 、)322cos(π+=x y 中,最小正周期为π的函数的个数为( ) A .1个 B .2个 C .3个 D .4个 10.已知函数()2sin()f x x ωϕ=+对任意x 都有()(),66f x f x ππ+=-则()6f π等于( )A . 2或0B . 2-或2C . 0D . 2-或0 11.函数2cos 3cos 2++=x x y 的最小值为( )A .2B .0C .1D .612.曲线sin (0,0)y A x a A ωω=+>>在区间2[0,]πω上截直线2y =及1y =-所得的弦长相等且不为0,则下列对,A a 的描述正确的是( )A .13,22a A =>B .13,22a A =≤C .1,1a A =≥D .1,1a A =≤13.已知下列命题中:(1)若k R ∈,且0k b = ,则0k =或0b = ,(2)若0a b ⋅= ,则0a =或0b =(3)若不平行的两个非零向量b a ,,满足||||b a =,则0)()(=-⋅+b a b a(4)若a 与b 平行,则||||a b a b =⋅其中真命题的个数是( )A .0B .1C .2D .3 14.下列命题中正确的是( )A .若a ⋅b =0,则a =0或b =0B .若a ⋅b =0,则a ∥bC .若a ∥b ,则a 在b 上的投影为|a|D .若a ⊥b ,则a ⋅b =(a ⋅b)215.已知平面向量(3,1)a = ,(,3)b x =- ,且a b ⊥,则x =( )A .3-B .1-C .1D .316.已知向量)sin ,(cos θθ=a ,向量)1,3(-=b 则|2|b a -的最大值,最小值分别是( )A .0,24B .24,4C .16,0D .4,017.设点(2,0)A ,(4,2)B ,若点P 在直线A B 上,且AB = 2A P,则点P 的坐标为( ) A .(3,1) B .(1,1)- C .(3,1)或(1,1)- D .无数多个18.若平面向量b 与向量)2,1(-=a 的夹角是o180,且53||=b ,则=b ( )A .)6,3(-B .)6,3(-C .)3,6(-D .)3,6(-19.向量(2,3)a = ,(1,2)b =-,若m a b + 与2a b - 平行,则m 等于A .2-B .2C .21 D .12-20.若,a b 是非零向量且满足(2)a b a -⊥,(2)b a b -⊥ ,则a 与b 的夹角是( )A .6πB .3πC .32π D .65π21.设3(,sin )2a α=,1(cos ,)3b α= ,且//a b ,则锐角α为( )A .030B .060C .075D .04522.设212tan 13cos 6sin 6,,221tan 13a b c =-==+则有( )23.在△ABC 中,cos cos sin sin A B A B >,则△ABC 为( )A .锐角三角形B .直角三角形C .钝角三角形D .无法判定24.设00sin 14cos14a =+,00sin 16cos16b =+,2c =,,a b c 大小关系( )A .a b c <<B .b a c <<C .c b a <<D .a c b <<25.函数)cos[2()]y x x ππ=-+是( )A .周期为4π的奇函数 B .周期为4π的偶函数C .周期为2π的奇函数D .周期为2π的偶函数26.已知cos 23θ=,则44sin cos θθ+的值为( )A .1813 B .1811 C .97 D .1-A .a b c >>B .a b c <<C .a c b <<D .b c a << 27.sin 163sin 223sin 253sin 313+=( )A .12-B .12C .2-D .228.已知3sin(),45x π-=则sin 2x 的值为( )A .1925B .1625C .1425D .72529.函数2sin cos y x x x =+-)A .2(,32π- B .5(,62π-C .2(,32π-D .(,3π30.△ABC 中,090C ∠=,则函数2sin 2sin y A B =+的值的情况( ) A .有最大值,无最小值 B .无最大值,有最小值C .有最大值且有最小值D .无最大值且无最小值31.0000(1tan 21)(1tan 22)(1tan 23)(1tan 24)++++ 的值是( )A . 16B . 8C . 4D . 2 32.当04x π<<时,函数22cos ()cos sin sin x f x x x x=-的最小值是( )A .4B .12C .2D .1433.函数y=Asin(ωx+φ)(A >0,ω>0)的部分图象如图2所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( ) A.2B.2+2C.2+22D.-2-22图2二、填空题1.给出下列命题:①存在实数x ,使3sin cos 2x x +=;②若,αβ是第一象限角,且αβ>,则cos cos αβ<;③函数2sin()32y x π=+是偶函数;④函数sin 2y x =的图象向左平移4π个单位,得到函数sin(2)4y x π=+的图象.其中正确命题的序号是____________.2.计算:oooooo80cos 15cos 25sin 10sin 15sin 65sin -+的值为_______.3.已知sin cos αβ+13=,sin cos βα-12=,则sin()αβ-=__________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修四综合一、选择题1.化简sin()2απ+等于( ). A.cos α B.sin α C.cos α- D.sin α-2.已知M 是ABC ∆的BC 边上的一个三等分点,且BM MC <,若AB = a ,AC =b ,则AM 等于( ).A.1()3-a bB.1()3+a bC.1(2)3+b aD.1(2)3+a b3.已知3tan =α,则αααα22cos 9cos sin 4sin 2-+的值为( ).A.3B.1021 C.31 D.3014.化简=--+( ).A. B.0 C.BC D. 5.函数x x y 2cos 2sin =是( ). A.周期为4π的奇函数 B.周期为2π的奇函数 C.周期为2π的偶函数 D.周期为4π的偶函数 6.已知)7,2(-M ,)2,10(-N ,点P 是线段MN 上的点,且−→−PN −→−-=PM 2,则P 点的坐标为( ). A.)16,14(- B.)11,22(- C.)1,6( D.)4,2( 7.已知函数sin()y A x B ωφ=++(0,0,||2A ωφπ>><)的周期为T 正确的结论是( ). A.3,2A T ==π B.2,1=-=ωB C.4,6T φπ=π=-D.3,6A φπ==8.将函数sin()3y x =-π的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移3个单位,则所得函数图像对应的解析式为( ).A.1sin()26y x =-πB.1sin(23y x =-πC.1sin 2y x = D.sin(2)6y x =-π9.若平面四边形ABCD 满足0,()0AB CD AB AD AC +=-⋅=,则该四边形一定是( ).A.直角梯形B.矩形C.菱形D.正方形10.函数()sin 2cos2f x x x =-的最小正周期是( ). A.π2B.πC.2πD.4π11.设单位向量1e ,2e 的夹角为︒60,则向量1234e e +与向量1e 的夹角的余弦值是( ). A.43 B.375 C.3725D.375二、填空题13.︒75sin 的值为 .14.已知向量(2,4)=a ,(1,1)=b ,若向量()⊥+λb a b ,则实数λ的值是.15.︒︒︒80cos 40cos 20cos 的值为_____________________________. 16.在下列四个命题中:①函数tan()4y x π=+的定义域是{,}4x x k k π≠+π∈Z ; ②已知1sin 2α=,且[0,2]α∈π,则α的取值集合是{}6π;③函数x a x x f 2cos 2sin )(+=的图象关于直线8x π=-对称,则a 的值等于1-;④函数2cos sin y x x =+的最小值为1-.把你认为正确的命题的序号都填在横线上____________________. 三、解答题17.已知4cos()45x π+=,(,)24x ππ∈--,求x x x tan 1sin 22sin 2+-的值.18.已知函数()sin sin()2f x x x π=++,x ∈R . (1)求)(x f 的最小正周期;(2)求)(x f 的的最大值和最小值;(3)若43)(=αf ,求α2sin 的值. 19.(1)已知函数1()sin()24f x x π=+,求函数在区间[2,2]-ππ上的单调增区间; (2)计算:)120tan 3(10cos 70tan -︒︒︒.20.已知函数()sin()f x x ωφ=+(0>ω,0φ≤≤π)为偶函数,其图象上相邻的两个最高点之间的距离为2π.(1)求)(x f 的解析式;(2)若(,)32αππ∈-,1()33f απ+=,求5sin(2)3απ+的值. 21.已知a ,b ,c 是同一平面内的三个向量,其中)2,1(=a .(1)若||=c ,且//c a ,求c 的坐标;(2)若||=b ,且2+a b 与2-a b 垂直,求a 与b 的夹角θ. 22.已知向量33(cos ,sin )22x x =a ,(cos ,sin )22x x =-b ,且[0,]2x π∈,()2||f x =⋅-λ+a b a b (λ为常数),求:(1)⋅a b 及||+a b ; (2)若)(x f 的最小值是23-,求实数λ的值.必修四综合训练题(六)参考答案一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的.)1.A 由诱导公式易得A 正确.2.C BC =- b a ,11()33BM BC ==- b a ,11()(2)33AM AB BM =+=+-=+ a b a b a .3.B αααααααααα222222cos sin cos 9cos sin 4sin 2cos 9cos sin 4sin 2+-+=-+10211tan 9tan 4tan 222=+-+=ααα. 4.B 0)()(=-=+-+=--+AD AD CD AC BD AB CD AC BD AB . 5.B x x x y 4sin 212cos 2sin ==,故是周期为2π的奇函数. 6.D 设),(y x P ,则)2,10(y x PN ---=,)7,2(y x PM ---=, −→−PN ⎩⎨⎧==⇒⎩⎨⎧--=-----=-⇒-=−→−.4,2),7(22),2(2102y x y y x x PM7.C ⎩⎨⎧-==⇒⎩⎨⎧-=+-=+,1,3,4,2B A B A B A ππππ42)32(342=⇒=--=T T ,21422===πππωT ,623421πϕπϕπ-=⇒=+⨯. 8.A sin()sin()sin[(]sin(3336111))2232y x y y x x x πππππ=-→=→==-+--.9.C 0AB CD AB CD +=⇒=-⇒四边形ABCD 为平行四边形,()0AB AD AC DB AC DB AC -⋅=⋅=⇒⊥,对角线互相垂直的平行四边形为菱形.10.B ()sin 2cos 2)4f x x x x π=-=-,ππ==22T .11.D 1||1=e ,1||2=e ,2160cos ||||2121=︒⋅=⋅e e e e ,543)43(2121121=⋅+=⋅+e e e e e e ,37|43|21===+e e ,375cos 121121==θ.12.A ⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡-+=⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡⋅⎥⎦⎤⎢⎣⎡002cos sin )cos()sin(sin sin cos cos sin cos cos sin sin cos sin cos cos sin ππβαβαβαβαβαβαββαααα.二、填空题(本大题共4小题,每小题4分,共16分. 把答案填在题中的横线上.) 13.426+ ︒︒+︒︒=︒+︒=︒30sin 45cos 30cos 45sin )3045sin(75sin 42621222322+=⨯+⨯=. 14.3- 30)4(2)4,2()1,1()()(-=⇒=+++=++⋅=+⋅⇒+⊥λλλλλλλb a b b a b . 15.818120sin 8160sin 20sin 880cos 40cos 20cos 20sin 880cos 40cos 20cos =︒︒=︒︒︒︒︒=︒︒︒. 16.①③④ )(424Z k k x k x ∈+≠⇒+≠+πππππ,故①正确;1sin 2α=,且[0,2]6παπα∈⇒=或65πα=,故②不正确;函数)(x f 的图象关于直线8π-=x 对称1)4()0(-=⇒-=⇒a f f π,故③正确;22215cos sin 1sin sin (sin )24y x x x x x =+=-+=--+,451≤≤-y ,故④正确.三、解答题(本大题共6小题,共74分,解答应写出必要的文字说明、证明过程及演算步骤.) 17.解:∵)4,2(ππ--∈x , ∴)0,4(4ππ-∈+x ,∵54)4cos(=+x π, ∴53)4sin(-=+x π,4sin )4cos(4cos )4sin(]4)4sin[(sin ππππππx x x x +-+=-+=102722542253-=⋅-⋅-=, ∴102cos =x , ∴7528sin cos )sin (cos cos sin 2cos sin 1sin 2cos sin 2tan 1sin 22sin 22=+-=+-=+-x x x x x x xx x x x x x x .18.解:)4sin(2cos sin )2sin(sin )(ππ+=+=++=x x x x x x f ,(1))(x f 的最小正周期为ππ212==T ;(2))(x f 的最大值为2和最小值2-; (3)因为43)(=αf ,即167cos sin 2169)cos (sin 43cos sin 2-=⇒=+⇒=+αααααα,即1672sin -=α. 19.解:(1)由πππππk x k 2242122+≤+≤+-(Z k ∈)得ππππk x k 42423+≤≤+-(Z k ∈), 当0=k 时,得223ππ≤≤-x ,]2,2[]2,23[ππππ-⊂-,且仅当0=k 时符合题意,∴函数)421sin()(π+=x x f 在区间]2,2[ππ-上的单调增区间是]2,23[ππ-.(2)︒︒-︒⋅︒⋅︒︒=-︒︒︒20cos 20cos 20sin 310cos 70cos 70sin )120tan 3(10cos 70tan︒︒⋅︒︒-=︒︒-⋅︒⋅︒︒=20cos 20sin 70cos 70sin 20cos 10sin 210cos 70cos 70sin 120cos 20sin 20sin 20cos -=︒︒⋅︒︒-=.20.解:(1)∵图象上相邻的两个最高点之间的距离为π2,∴π2=T , 则12==Tπω,∴)sin()(ϕ+=x x f ,∵)(x f 是偶函数, ∴)(2Z k k ∈+=ππϕ,又πϕ≤≤0, ∴2πϕ=, 则x x f cos )(=.(2)由已知得31)3cos(=+πα, ∵)2,3(ππα-∈, ∴)65,0(3ππα∈+, 则322)3sin(=+πα, ∴924)3cos()3sin(2)322sin()352sin(-=++-=+-=+παπαπαπα. 21.解:(1)设),(y x =, ∵//,)2,1(=, ∴02=-y x , ∴x y 2=,∵52||=c , ∴5222=+y x , ∴2022=+y x , 即20422=+x x ,∴⎩⎨⎧==,4,2y x 或⎩⎨⎧-=-=,4,2y x ∴)4,2(=c 或)4,2(--=c(2)∵⊥+b a 2b a -2, ∴)2(b a +0)2(=-⋅b a , ∴023222=-⋅+, 即0||23||222=-⋅+,又∵5||2=,45)25(||22==, ∴0452352=⨯-⋅+⨯b a , ∴25-=⋅b a , ∵5||=,25||=, ∴125525cos -=⋅-==θ,∵],0[πθ∈, ∴πθ=. 22.解:(1)x xx x x 2cos 2sin 23sin 2cos 23cos=-=⋅, x x xx x x 222cos 22cos 22)2sin 23(sin )2cos 23(cos||=+=-++=+, ∵]2,0[π∈x , ∴0cos ≥x , x cos 2||=+.(2)2221)(cos 2cos 42cos )(λλλ---=-=x x x x f ,∵]2,0[π∈x , ∴1cos 0≤≤x ,①当0<λ时,当且仅当0cos =x 时,)(x f 取得最小值1-,这与已知矛盾; ②当10≤≤λ,当且仅当λ=x cos 时,)(x f 取得最小值221λ--, 由已知得23212-=--λ,解得21=λ; ③当1>λ时,当且仅当1cos =x 时,)(x f 取得最小值λ41-, 由已知得2341-=-λ,解得85=λ,这与1>λ相矛盾. 综上所述,21=λ为所求.。
