自控系统方框图极性表示及动态波形图
自动控制原理课件

2.根轨迹法
在系统中加入校正装置,相当于增加 了新的开环零极点,这些零极点将使 校正后的闭环根轨迹,向有利于改善 系统性能的方向改变,系统闭环零极 点重新布置,从而满足闭环系统性能 要求。
§6.2 线性系统的基本控制规律
校正装置 Gc(s)
R(s)
+
+
+
原有部分 C(s)
Go(s)
-
(d)前馈补偿
对扰动
信号直
接或间
测 量 , R(s) +
+
形成附 加扰动
+ -
补偿通
道
校正装置 Gc(s)
原有部分 + Go2(s)
N(s)
+ 原有部分 C(s) Go2(s)
(e)扰动补偿
•串联校正和反馈校正属于主反馈回路之内的校正。
根据校正装置加入系统的方式和所起的作用不同, 可将其作如下分类:
+
+
-
-
原有部分 Go(s)
校正装置 Gc(s)
(b)反馈校正
C(s)
R(s) +
校正装置 +
Gc1(s)
-
-
原有部分 C(s) Go(s)
校正装置 Gc2(s)
(c)串联反馈校正
相当于 对给定 值信号 进行整 形和滤 波后再 送入反 馈系统
•知 识 要 点
线性系统的基本控制规律比例(P)、积 分(I)、比例-微分(PD)、比例-积分(PI) 和比例-积分-微分(PID)控制规律。超前校 正,滞后校正,滞后-超前校正,用校正装置 的不同特性改善系统的动态特性和稳态特性。 串联校正,反馈校正和复合校正。
第四节自动控制系统方块图
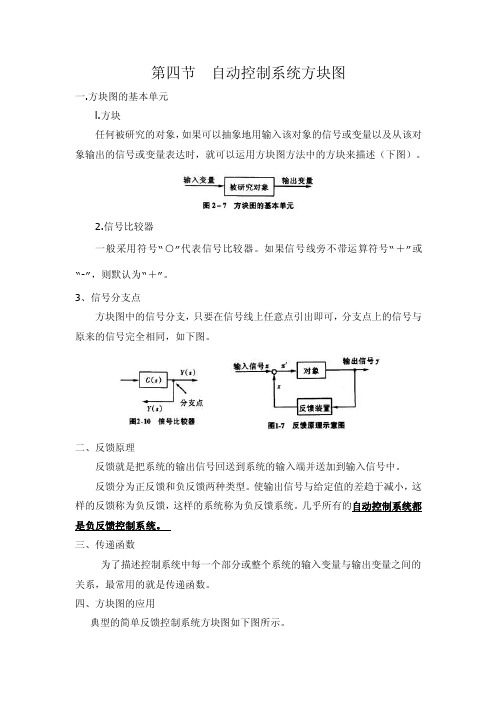
第四节自动控制系统方块图一.方块图的基本单元l.方块任何被研究的对象,如果可以抽象地用输入该对象的信号或变量以及从该对象输出的信号或变量表达时,就可以运用方块图方法中的方块来描述(下图)。
2.信号比较器一般采用符号“○”代表信号比较器。
如果信号线旁不带运算符号“+”或“-”,则默认为“+”。
3、信号分支点方块图中的信号分支,只要在信号线上任意点引出即可,分支点上的信号与原来的信号完全相同,如下图。
二、反馈原理反馈就是把系统的输出信号回送到系统的输入端并送加到输入信号中。
反馈分为正反馈和负反馈两种类型。
使输出信号与给定值的差趋于减小,这样的反馈称为负反馈,这样的系统称为负反馈系统。
几乎所有的自动控制系统都是负反馈控制系统。
三、传递函数为了描述控制系统中每一个部分或整个系统的输入变量与输出变量之间的关系,最常用的就是传递函数。
四、方块图的应用典型的简单反馈控制系统方块图如下图所示。
第五节控制系统分类一、各种分类的方法(l)如果按被控变量可划分为:温度、压力、液位、流量和成分等控制系统。
这是一种常见的分类。
(2)如果按被控系统中控制仪表及装置所用的动力和传递信号的介质可划分为:气动、电动、液动、机械式等控制系统。
(3)如果按被控制对象可划分为:流体输送设备、传热设备、精馏塔和化学反应器控制系统等。
(4)按调节器的控制规律可划分为:比例控制、积分控制、微分控制、比例积分控制、比例微分控制、比例积分微分控制等。
(5)按系统功能与结构可划分为:单回路简单控制系统;串级、比值、选择性、分程、前馈和均匀等常规复杂控制系统。
(6)按给定值的变化情况可划分为:定值控制系统、随动控制系统和程序控制系统。
第六节自动控制系统的过渡过程及品质指标一、瞬态响应分析方法瞬态响应分析方法的基本做法是:给系统输入各种不同的典型信号,观察并分析系统的响应曲线。
1、静态与动态静态是指该变量不随时间而变化的某个平衡状态;动态是指该变量随时间而变化的不平衡状态。
自动控制原理方框图

[注意]:
相临的信号相加点位置可以互换;见下例
X1(s)
X2(s)
X3(s)
Y (s)
X1(s)
X3(s)
X 2 (s)
Y (s)
同一信号的分支点位置可以互换:见下例
X1(s)
X (s) G(s) Y (s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下,不能互换。
§2-3 控制系统的结构图与信号流图
一、结构图的组成和绘制
1、结构图的组成 由四种基本图形符号组成
(1)函数方块
R(s) r(t) G(s)
C(s) c(t)
(2)信号线
R(s) r(t)
(3)分支点(引出点)
R(s) r(t)
R(s) r(t) R(s) r(t)
(4)综合点(比较点或相加点)
R(s)
R
R1Cs
2I
2
(s)
UI (cs)(s)
R2
R1
Uc (s)
U c (s)
I1 (s)
Uc (s)
几点说明:
(1)在结构图中,每一个方框中的传递函数都应是考虑了负 载效应后的传递函数。
(2)描述一个系统的结构图不是唯一的,选择不同的中间变 量得到不同的结构图;
(3)结构图中的方框与实际系统的元部件并非一定是一一对 应的;
X1(s) G(s) X2(s) N(s)
Y (s)
N(s) ? Y (s) [X1(s) X 2 (s)]G(s), 又 : Y (s) X (s)1G(s) X 2 (s)N(s), N(s) G(s)
把相加点从环节的输出端移到输入端:
自动控制原理方框图

自动控制原理方框图自动控制原理方框图是指在自动控制原理的基础上,通过方框图的形式来描述和分析控制系统的结构和动态特性。
方框图是一种直观、简洁的表示方法,能够清晰地展现控制系统的各个组成部分之间的关系,有利于工程师们对控制系统进行分析、设计和调试。
在自动控制系统中,方框图是一种非常重要的工具,它能够帮助工程师们更好地理解系统的结构和工作原理,从而更好地进行系统的设计和优化。
方框图可以将控制系统的各个组成部分以及它们之间的相互作用清晰地表示出来,有利于工程师们对系统进行全面的分析和评估。
自动控制原理方框图主要包括系统的输入、输出、控制器、执行器和被控对象等几个基本组成部分。
通过方框图,我们可以清晰地看到这些组成部分之间的关系,以及它们是如何相互作用的。
这有助于工程师们更好地理解系统的工作原理,从而更好地进行系统的设计和调试。
在实际工程中,方框图常常被用于描述和分析各种类型的控制系统,比如PID控制系统、模糊控制系统、神经网络控制系统等。
通过方框图,工程师们可以清晰地看到系统的结构和动态特性,有助于他们更好地理解系统的工作原理,从而更好地进行系统的设计和调试。
除此之外,方框图还可以用于系统的故障诊断和故障排除。
通过对系统的方框图进行分析,工程师们可以清晰地看到系统中存在的问题,并且能够有针对性地进行故障排除。
这对于提高系统的可靠性和稳定性非常重要。
总的来说,自动控制原理方框图是一种非常重要的工具,它能够帮助工程师们更好地理解和分析控制系统,有助于他们更好地进行系统的设计和调试。
因此,掌握方框图的绘制和分析方法对于自动控制工程师来说是非常重要的。
希望通过本文的介绍,能够对方框图有一个更加清晰的认识。
自控系统方框图极性表示及动态波形图

直流可逆调速系统方框图及各种状态下对应各点极性表示
3.2.1简要分析说明正向起动运行时系统工作过程。
并在逻辑选触无环流可逆直流调速系统原理图中标出正向运行时系统工作状态(各物理量的极性)。
=f(t)的波形试画出电动机从正向(900转/分)运行到反向(900转/分)运行时的n=f(t)和I
d
图并加以简单说明。
标出反向运行时系统工作状态(各物理量的极性)。
=f(t)的波形试画出电动机从正向(800转/分)运行到反向(800转/分)运行时的n=f(t)和I
d
图并加以简单说明。
正向制动时(它组逆变子阶段)系统工作状态(各物理量的极性)。
=f(t)的波形图并加以简单说明。
试画出电动机从正向1000 r/nim制动停车时的n=f(t)和I
d
标出反向制动停车(本组逆变阶段)时系统工作状态(各物理量的极性)。
=f(t)的波形图并加以简单说明。
试画出电动机从正向1200 r/nim制动停车时的n=f(t)和I
d
原理图中标出反向运行时系统工作状态(各物理量的极性)。
=f(t)的波形图并加以简单说试画出电动机从正向起动至1050 r/min稳定运行时的n=f(t)和I
d
明。
控制系统的方块图及其基本组成

Υ Υ
1
3
-
Υ 1-Υ 2+Υ 3
-
Υ2
R2 (s)
图2-15比较点示意图
Υ2
注意:进行相加减的量,必须具有相同的量刚。 (3)分支点(引出点、测量点)Branch Point 表示信号测量或引出的位置 C(s) 注意:同一位置引出的信号 R(s) P(s) G1 (s) G2 (s) 大小和性质完全一样。
注意:由于N(s)极性的随机性,因而在求E(s)时,不能认
为利用N(s)产生的误差可抵消R(s)产生的误差。 2.4.3 方块图的绘制 (1)考虑负载效应分别列写系统各元部件的微分方程或传递 函数,并将它们用方框(块)表示。 (2)根据各元部件的信号流向,用信号线依次将各方块连接 起来,便可得到系统的方块图。 系统方块图-也是系统数学模型的一种。
**
R(s)
+ -
E(s)
G1 (s)
+
+
G2 (s)
C(s)
B(s)
H(s)
打开反馈
N(s)
G1 (s)
G2 (s)
C(s)
H(s)
图2-18 输出对扰动的结构图 利用公式**,直接可得:
M N ( s) G2 ( s ) C ( s) N ( s) 1 G( s) H ( s)
(7)误差对扰动的传递函数 假设R(s)=0
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
G1 ( s)G2 ( s) C ( s) G( s) R( s) 1 H ( s)G( s) 1 H ( s)G( s)
自动控制原理第二章方框图

R1C2s
(R1C1s 1)(R2C2s 1) R1C2s
(R1C1s 1)(R2C2s 1)
解法二:
ui (s)
-
1 I1(s) - 1 u(s)
R1
I (s) C1s
-
1
1 uo (s)
R2 I2(s) C2s
ui (s) 1
R1
ui (s) 1
R1
-
1
-
C1s
1 R1
-
1
-
C1s
1 R1
1
自动控制原理第二章方框图自动控制方框图闭环控制系统方框图串级控制系统方框图前馈控制系统方框图控制系统方框图单回路控制系统方框图过程控制系统的方框图自动调节系统方框图控制方框图
传递函数的表达形式
有理分式形式:G(s)
b0 s m a0 s n
b1s m1 a1s n1
bm1s an1s
bm an
H3
相加点移动 G3 G1
G3 G1
向同无类用移功动
G2
错!
G2
H1
G(s) G1G2 G2G3 1 G1G2 H1
G2
G1 H1
总的结构图如下:
ui (s)
-
1 I1(s) - 1 u(s)
R1
I (s) C1s
-
1
1 uo (s)
R2 I2(s) C2s
ui (s)
-
C2s
1 I1(s) - 1 u(s)
X 2 (s)
X (s) G(s) Y (s)
X 2 (s)
X1(s)
相加点和分支点在一般情况下,不能互换。
X 3 (s)
X (s)
第4讲控制系统的方块图及其基本组成

例2-8 画出下列RC电路的方块图. 解:由图2-20,利用基尔霍夫电压定律 及电容元件特性可得: ui uo i = R idt u = ∫ ui o c 对其进行拉氏变换得:
R i C (a) uo
U i (s) U o (s) I ( s) = R I (s) U o ( s ) = sC
由传递函数定义
m ( s) K1 G( s) = = U a ( s) Tm S + 1
m ( s) K2 = M c ( s) Tm S + 1
b令
U a (t ) = 0
Gm ( s) =
K2 Tm s + 1
Tm S m ( s) + m ( s) = K 2 M c ( s)
M c (s)
线性系统满足叠加原理,当控制输入R(s)与扰动N(s) 同时作用于系统时,系统的输出及误差可表示为:
C (s) = G2 (s) G (s) R( s) + N (s) 1 + G ( s) H (s) 1 + G (s) H (s)
G2 (s) H (s) 1 E (s) = R( s) N (s) 1 + G ( s) H ( s) 1 + G (s) H (s)
(1) (2)
图2-20一阶RC网络
Ui (s)
I (s )
I( s ) (c)
Uo (s)
U o (s) (b)
U i (s) - Uo (s)
I(sபைடு நூலகம்)
U o (s)
(d)
将图(b)和(c)组合起来即得到图(d), 图(d)为该一阶RC网络的方块图.
例2-9 画出下列R-C网络的方块图 由图清楚地看到,后一级 R2-C2网络作为前级R1-C1网 络的负载,对前级R1-C1网 络的输出电压 u c1 产生影响,这就是负 载效应. 解:(1)根据电路定理 列出方程,写出对应的拉 氏变换,也可直接画出该 电路的运算电路图如图 (b);(2)根据列出的4 个式子作出对应的框图; (3)根据信号的流向将 各方框依次连接起来.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直流可逆调速系统方框图及各种状态下对应各点极性表示
3.2.1简要分析说明正向起动运行时系统工作过程。
并在逻辑选触无环流可逆直流调速系统原理图中标出正向运行时系统工作状态(各物理量的极性)。
=f(t)的波形试画出电动机从正向(900转/分)运行到反向(900转/分)运行时的n=f(t)和I
d
图并加以简单说明。
标出反向运行时系统工作状态(各物理量的极性)。
=f(t)的波形试画出电动机从正向(800转/分)运行到反向(800转/分)运行时的n=f(t)和I
d
图并加以简单说明。
正向制动时(它组逆变子阶段)系统工作状态(各物理量的极性)。
=f(t)的波形图并加以简单说明。
试画出电动机从正向1000 r/nim制动停车时的n=f(t)和I
d
标出反向制动停车(本组逆变阶段)时系统工作状态(各物理量的极性)。
=f(t)的波形图并加以简单说明。
试画出电动机从正向1200 r/nim制动停车时的n=f(t)和I
d
原理图中标出反向运行时系统工作状态(各物理量的极性)。
=f(t)的波形图并加以简单说试画出电动机从正向起动至1050 r/min稳定运行时的n=f(t)和I
d
明。
