第六章 电容元件与电感元件
电路讲义第六章_new

f (t ) f (0 ) e
t
2)一阶电路的零输入响应和初始值成正比,称为零输入线性。 3) 零输入响应的衰减快慢取决于时间常数τ,其中RC 电路τ=RC , RL 电 路τ=L/R ,R 为与动态元件相连的一端口电路的等效电阻。 4) 同一电路中所有响应具有相同的时间常数。
【例6-5】 电路中开关SW闭合已久, t=0时SW断开,试求电流 iL(t),t0。
diL (t ) d u L (t ) L dt dt
C R ) (1) i 的大小取决于 u 的变化率, 与 u 的大
1 1 t uc (t ) ic d uc (t 0 ) ic d C C t0
1 t 1 t iL (t ) u L d iL (t 0 ) u L d L L t0
§6-1 动态电路的方程及其初始条件
跳变(跃变):
换路定则:
当 i C 和 u L 为有限值时,状态变量电容电压 u C 和电感电流 i L 无跳变, 即有 u C ( 0 )
u C ( 0 ) ; i L (0 ) i L (0 ) ;
过渡过程:动态电路的特点是,当电路状态发生改变后(换 路后)需要经历一个变化过程才能达到新的稳定状态,这个 变化过程称为电路的过渡过程。
§6-1 动态电路的方程及其初始条件
基本概念:
动态电路:含有动态元件电容和电感的电路称动态电路。 一阶电路:用一阶微分方程描述的电路(或只含一个独立 的动态元件的电路)
换路:电路结构、状态发生变化,即支路接入或断开或电 路参数变化; 若换路在t=0时刻进行,则换路前的最终时刻记为t=0- ;换 路后最初时刻记为t=0+ ;换路经历的时间为0-~0+ ;
电路原理第6章

储能元件
6.1 电容元件
6.2 电感元件
电容、 6.3 电容、电感元件的串并联
6.1 电容元件
如果一个二端元件在任一时刻, 如果一个二端元件在任一时刻,其电荷与电压之间 的关系由uq平面上一条曲线所确定 平面上一条曲线所确定, 的关系由 平面上一条曲线所确定 , 则称此二端元件 为电容元件。 为电容元件。 q q 电容器 _
结 论
(1) 元件方程的形式是相似的; 元件方程的形式是相似的; (2) 若把 u-i,q-ψ ,C-L, i-u互换 可由电容元件 互换,可由电容元件 , , 互换 的方程得到电感元件的方程; 的方程得到电感元件的方程;
(3) C 和 L称为对偶元件 Ψ 、q等称为对偶元素。 称为对偶元件, 等称为对偶元素。 称为对偶元件 等称为对偶元素 * 显然,R、G也是一对对偶元素 显然, 、 也是一对对偶元素 也是一对对偶元素: U=RI ⇔ I=GU I=U/R ⇔ U=I/G
电感器
把金属导线绕在一骨架上构 成一实际电感器, 成一实际电感器,当电流通过 线圈时,将产生磁通, 线圈时,将产生磁通,是一种 储存磁能的部件
i (t)
+
u (t)
-
1)线性电感
韦安特性曲线是通过坐标原点 一条的直线的电感元件称为线性 一条的 直线的电感元件称为线性 电感元件, 电感元件 , 否则称为非线性电感 元件。 元件。 线性时不变电感元件的特性曲线是一条通过原点不随时 间变化的直线, 间变化的直线,其数学表达式为
3)电感的储能 ) 在电压电流采用关联参考方向的情况下, 在电压电流采用关联参考方向的情况下,电感 的吸收功率为 di p (t ) = u (t )i(t ) = i(t ) L dt 当p>0时,电感吸收功率;当p<0时,电感发出功率。 时 电感吸收功率; 时 电感发出功率。 电感在从初始时刻t 到任意时刻t时间内得到的 电感在从初始时刻 0到任意时刻 时间内得到的 能量为
电路第5版 第六章

返 回
上 页
下 页
为有限值, ③实际电路中通过电容的电流 i 为有限值, 必定是时间的连续函数。 则电容电压 u 必定是时间的连续函数。 u
du →∞ i →∞ dt
0
0
t
0
t 1 t i(ξ)dξ = 1 ∫−∞i(ξ)dξ + 1 ∫tt i(ξ)dξ u(t)= ∫−∞ C C C =u(t )+ 1 ∫tt idξ C
实际电容器的模型 C i + u C + G u - + -
q +
i
q _
ε
C G u -
返 回
上 页
下 页
实际电容器
返 回 上 页 下 页
电力电容
返 回 上 页 下 页
冲击电压发生器
返 回
上 页
下 页
6.2 电感元件
电感线圈 把金属导线绕在一骨架上构成一实际 电感线圈,当电流通过线圈时,将产生磁通, 电感线圈,当电流通过线圈时,将产生磁通,是 一种抵抗电流变化、储存磁能的部件。 一种抵抗电流变化、储存磁能的部件。
1H=103 mH 1 mH =103 µ H
返 回 上 页 下 页
3.线性电感的电压、 3.线性电感的电压、电流关系 线性电感的电压
i + L u (t) u、i 取关联 参考方向
根据电磁感应定律与楞次定律
dψ di(t) u(t) = =L dt dt
电感元件VCR 电感元件 的微分关系
返 回
实际电感线圈的模型 i L u (t) L u - - + C u - L G
+
G +
返 回
上 页
下 页
贴片型功率电感
贴片电感
大学物理电路分析基础第6章一阶电路分析.ppt

t
iC d 1(V)
1
其波形如图6-5(c)所示。
第6章 一阶电路分析
6.1.2
通常把由导线绕成的线圈称为电感器或电感线圈。 当 线圈通过电流时, 即在线圈内外建立磁场并产生磁通Φ, 如 图6-6所示。 各线匝磁通的总和称为磁链φ(若线圈匝数为N, 则φ=NΦ )。 可见, 电感器是一种能建立磁场、 储存磁场 能量的器件。
从本例可以看出: (1) 电容电流是可以跳变的。 (2) 电容的功率也是可以跳变的,这是由于电容电流跳 变的原因。 功率值可正可负: 功率为正值, 表示电容从电 源us(t)吸收功率; 功率为负值, 表示电容释放功率且交还 电源。 (3) wC(t)总是大于或等于零,储能值可升可降, 但为连 续函数。
第6章 一阶电路分析
图6-4 例6-1波形图
第6章 一阶电路分析
例 6-2 在图6-5(a)所示电路中, is(t)的波形如图6-5(b)所 示, 已知电容C=2 F, 初始电压uC(0)=0.5 V, 试求t≥0时的 电容电压, 并画出其波形。
第6章 一阶电路分析
图6-5 例6-2题图
第6章 一阶电路分析
dq dt
和电容的定义q(t)=Cu(t),
可得
i C du
(6-2)
dt
第6章 一阶电路分析
这就是电容元件微分形式的VCR。 若电容端电压u与电流i 参考方向不关联, 则上式右边应加负号, 即
du i C
(6-3)
dt
式(6-2)表明, 任一时刻通过电容的电流i取决于该时刻电容
两端的电压的变化率 du 。若电压恒定不变, 则虽有电压 dt
与电阻元件相类似, 若约束电容元件的q—u平面上的 曲线为通过原点的直线, 则称它为线性电容; 否则, 称为 非线性电容。 若曲线不随时间而变化, 则称为非时变电容; 否则, 称为时变电容。
电路第五版储能元件1
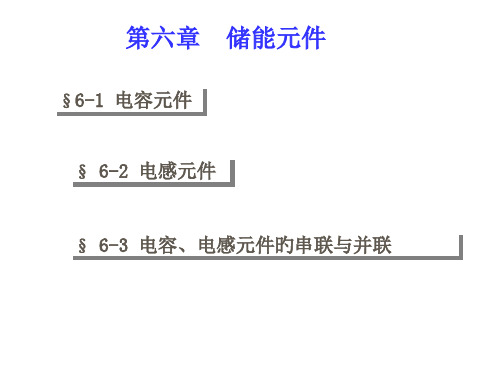
i1
C1
du dt
, i2
C2
du dt
,..., in
Cn
du dt
由KVL,端口电流
i
i1
i2
... in
(C1
C2
...
C
n
)
du dt
Ceq
du dt
n
式中 Ceq C1 C2 ... Cn Ck
k 1
Ceq为n个电容并联旳等效电容。
例: 如图所示电路,各个电容器旳初始电压均为零,
(3)实际电路中电感旳电压 u为有限值,则电感电流i
不能跃变,肯定是时间旳连续函数.
i(t)
1 L
t
ud ξ
1 L
0
udξ
1 L
t
0
udξ
i(0)
1 L
t
0
udξ
电感元件VCR
表白:
旳积分关系
电感元件有记忆电压旳作用,故称电感为记忆元件
注意:(1)当 u,i为非关联方向时,上述微分和积分体现
式前要冠以负号 ; (2)上式中i(0)称为电感电流旳初始值,它反应电 感初始时刻旳储能情况,也称为初始状态。
2、电容旳储能
W
(c)
t
-
p(
)d
t u(
)C
du
d
d
WC
t du Cu dξ dξ
1 Cu2 (ξ ) t 1 Cu2 (t ) 1 Cu2 ()
2
2
2
若u(
)
0
1
Cu
2
(
t
)
1
q2(t) 0
2
2C
电容元件与电感元件

电容元件与电感元件
1.1 电容元件 1.2 电容的串、并联 1.3 电感元件
1.1 电 容 元 件
1.1.1 电容
1、电容器
任何两个彼此靠近而且又相互绝缘的导体都可以构成 电容器。这两个导体叫做电容器的极板,它们之间的绝缘物 质叫做介质。
2、电容器符号
+q和-q为该元件正、负极板上的电荷量
1.3 电感元件
1.1.2 电感元件的电压电流关系
电感元件的电流变化时,其自感磁链也随之变化,由电 磁感应定律可知,在元件两端会产生自感电压。 关联参考方向下电感元件的电流、电压关系:
u L di dt
结论: 1、任何时刻,线性电感元件上的电压与其电流的变化率成正比。 2、只有当通过元件的电流变化时,其两端才会有电压。 3、电流变化越快,自感电压越大。当电流不随时间变化时,则 自感电压为零。这时电感元件相当于短路
求(1)开关S打开时,(2) 开关S关
a
闭时,ab间的等效电容Cab。
S b
C3 C4
, 解:(1)当S打开时,C1与 C2串联,C3与C4串联,两串联 支路再并联,所以
(2)当S闭合时,C1与C3并 联,C2与C4并联,并联之后再串
联,所以
Cab
C1C2 C1 C2
C3C4 C3 C4
10 10 20 20 10 10 20 20
1.2 电容的串、并联
1.2.1 电容器的并联
图1.2(a)所示为三个电容器并联的电路
u
+q1 C1 +q2 C2 +q3 C3
-q1
q2
-q 3
+q
u
C
-q
(a)
(b)
电容元件与电感元件

第六章 电容元件与电感元件电路在任一时刻t 的相应与激励的全部过去历史有关,因此动态电路是有记忆的。
由于动态元件的V AR 是对时间变量t 的微分或积分关系,所以动态电路需要用微分方程或积分方程来描述。
动态元件:电容元件、电感元件动态电路:至少包含一个动态元件的电路。
6-1 电容元件1、定义:一个二端元件,如果在任一时刻t ,它所存储的电荷和它的端电压 之间的关系可以用平面上的一条曲线来确定,则该二端元件称为电容元件。
线性时不变电容:平面上通过原点的一条直线,且不随时间变化。
电容元件的符号及线性电容的u-q 曲线对于线性电容有6-2 电容的伏安关系(V AR 关系)若采用关联方向,V AR 关系为讨论: 1、任何时刻i 与 成正比,即与电容电压的变化率成正比。
2、若电容电压为直流电压,则 =0,i =0。
所以电容具有隔直作用。
3、在某一时刻t 时,电容电压的数值并不取决于该时刻的电流值,而是取决于从-∞到t 所有时刻的电流值,也就是说与电流全部过去历史有关。
)()(t Cu t qdt du dt du为电容电压的初始值,它反映了电容初始时刻的储能状况。
电容是一个记忆电流的记忆元件。
4、由于实际电路中,电流i 为有限值,即 为有限值,所以u 必为连续函数,电压值在某一时刻不能跃变,即6-3 电容电压的连续性质和记忆性质1、电容电压的连续性质: 若电容电流i(t)在闭区间〔ta 、tb 〕内为有界的,则电容电压uc(t)在开区间(ta 、tb )内为连续的。
特别是,对任何时间t ,且ta <t <tb ,2、电容电压的记忆性质:电容是一种记忆元件。
通常只知道在某一时刻t0后作用于电容的电流情况,而对在此之前电容电流的情况并不了解。
在求解具体电路时,给出或求解初始电压是必不可少的。
例:p15页,当u 为9.9V 时,作用过的脉冲数目是多少?解:电容电压为对节点a 由KCL 得:)(0t u )0()0(+-=u u )()(+-=t u t u CC ⎰=tt id C t u 199.01)(ξ0)(,311==t u s t 且设其中μ5099.0su i +=5001.0su i =即su i 2=即u 由0线性增长至0.099V 。
电路分析课件第6章

实际电容器类型,在工作电压低的情况下, 实际电容器类型,在工作电压低的情况下,电 容器的漏电很小, );当漏电不能忽略时 容器的漏电很小,图(a);当漏电不能忽略时,图 );当漏电不能忽略时, );在工作频率很高的情况下 (b);在工作频率很高的情况下,图(c); );在工作频率很高的情况下, );t0 −1123
4
t(s)
1 2 = t − 4t +8 2
u(4) = 0
以上分析看出电容具有 两个基本的性质: 两个基本的性质: (1)电容电压的连续性; 电容电压的连续性; 电容电压的连续性
1 2 3 4
u(V)
1 0.5 0
t(s)
(2)电容电压的记忆性。 电容电压的记忆性。 电容电压的记忆性
§6 − 3
电容电压的连续性质和记忆性质
电容元件特点: 电容元件特点: 1、电容电压的连续性质 电流为有限值时, 电流为有限值时,电压是时间的连续 函数, 函数,即: uc (t − ) = uc (t + ) 也叫做电容电压不能跃变; 也叫做电容电压不能跃变;
证明如下:
1 要证明 uc (t ) = uc (t0 ) + ∫ i (ξ )dξ C t0
第二部分
动态电路分析
第六章 电容元件与电感元件 动态电路:含有电容、电感元件的电路。 动态电路:含有电容、电感元件的电路。 本章主要内容: 本章主要内容: 电容、 1、电容、电感元件定义及伏安关系 2、电容、电感元件性质 电容、 3、电容、电感元件的储能 电容、 4、电路的对偶性
§6 − 1
电容元件
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在已知电容电压u(t)的条件下,用式(7-12)容易求出其电流 的条件下,用式 - 容易求出其电流 在已知电容电压 的条件下 i(t)。例如已知C=1µF电容上的电压为 。例如已知 电容上的电压为u(t)=10sin(5t)V,其波形 µ 电容上的电压为 , 如图7-7(a)所示,与电压参考方向关联的电流为 如图 - 所示, 所示
5.当5s≤t时,iC(t)=0,根据式 -13可以得到 . ≤时 ,根据式7- 可以得到
t 1 t 6 uC (t ) = ∫ iC (ξ )dξ = uC (5) + 2 × 10 ∫ 0dξ =6V + 0 = 6V 5 C −∞
根据以上计算结果, 根据以上计算结果,可 以画出电容电压的波形如图(c) 以画出电容电压的波形如图 所示, 所示,由此可见任意时刻电 容电压的数值与此时刻以前 的全部电容电流均有关系。 的全部电容电流均有关系。 例如, 例如,当1s<t<3s时,电 时 容电流i 容电流 C(t)=0,但是电容电压 , 并不等于零,电容上的 电 并不等于零,电容上的2V电 压是0<t<1s时间内电流作用的 时间内电流作用的 压是 结果。 结果。
的电容电流波形如图7-9(b)所示,试求电容 所示, 例7-2 C=0.5µF的电容电流波形如图 µ 的电容电流波形如图 所示 电压u 。 电压 C(t)。
图7-9
波形的情况, 解:根据图(b)波形的情况,按照时间分段来进行计算 根据图 波形的情况 1.当t≤0时,iC(t)=0,根据式 . ≤ 时 ,根据式7-13可以得到 可以得到
(7 −13)
从上式可以看出电容具有两个基本的性质 (1)电容电压的记忆性。 电容电压的记忆性。 电容电压的记忆性 从式( - )可见,任意时刻T电容电压的数值 电容电压的数值u 从式(7-13)可见,任意时刻 电容电压的数值 C(T), , 要由从-∞到时刻T之间的全部电流 之间的全部电流i 来确定 也就是说, 来确定。 要由从 ∞到时刻 之间的全部电流 C(t)来确定。也就是说, 此时刻以前流过电容的任何电流对时刻T 此时刻以前流过电容的任何电流对时刻 的电压都有一定 的贡献。 的贡献。这与电阻元件的电压或电流仅仅取决于此时刻的 电流或电压完全不同,我们说电容是一种记忆元件。 电流或电压完全不同,我们说电容是一种记忆元件。
图7-8 例7-1 - -
图7-8 例7-1 - -
3.当3s≤t≤5s时,uC(t)=-8+2t,根据式 -12可以得到 当 ≤≤ 时 ,根据式7- 可以得到
du C −6 d(8 + 2t ) iC (t ) = C = 0.5 × 10 = 1 × 10 −6 A = 1µA dt dt
4.当5s≤t时,uC(t)=12-2t,根据式 -12可以得到 当 ≤时 ,根据式7- 可以得到
其中
1 0 u C (0) = ∫ iC (ξ )dξ C −∞
(7 −13)
称为电容电压的初始值。 称为电容电压的初始值。
1 t uC (t) = ∫ iC (ξ )dξ C −∞ 1 0 1 t 1 t = ∫ iC (ξ )dξ + ∫ iC (ξ )dξ = uC (0) + ∫ iC (ξ )dξ C −∞ C 0 C 0
1 T +dt ∆u = uC (T + dt ) − uC (T ) = ∫ iC (ξ )dξ T C
dt →0
→0
当i(ξ )有界时
当电容电流有界时,电容电压不能突变的性质, 当电容电流有界时,电容电压不能突变的性质,常用 下式表示
u C ( t + ) = u C (t − )
对于初始时刻t=0来说, 对于初始时刻 来说,上式表示为 来说
4.当3s≤t<5s时,iC(t)=1µA,根据式 -13可以得到 . ≤ 时 µ ,根据式7- 可以得到
t 1 t 6 u C (t ) = ∫ iC (ξ )dξ = u C (3) + 2 × 10 ∫ 10 −6 dξ = 2 + 2(t − 3) 3 C −∞ 当t = 5s 时 u C (5s) = 2V + 4V = 6V
du C −6 d (12 − 2t ) iC (t ) = C = 0.5 × 10 = −1 × 10 −6 A = −1µA dt dt
在已知电容电流i 的条件下 其电压u 为 的条件下, 在已知电容电流 C(t)的条件下,其电压 C(t)为
1 t uC (t) = ∫ iC (ξ )dξ C −∞ 1 0 1 t = ∫ iC (ξ )dξ + ∫ iC (ξ )dξ C −∞ C 0 1 t = uC (0) + ∫ iC (ξ )dξ C 0
图7-5
电容元件的符号和特性曲线如图7-5(a)和(b)所示。 和 所示 所示。 电容元件的符号和特性曲线如图
图7-5 a) 电容元件的符号 b) 电容元件的特性曲线 (c) 线性时不变电容元件的符号 (d) 线性时不变电容元件的特性曲线
其特性曲线是通过坐标原点一条直线的电容元件称为 线性电容元件,否则称为非线性电容元件。 线性电容元件,否则称为非线性电容元件。
(7 − 11)
式中的系数C为常量,与直线的斜率成正比,称为电 式中的系数 为常量,与直线的斜率成正比, 为常量
实际电路中使用的电容器类型很多, 实际电路中使用的电容器类型很多,电容的范围变化 很大,大多数电容器的漏电很小,在工作电压低的情况下, 很大,大多数电容器的漏电很小,在工作电压低的情况下, 可以用一个电容作为它的电路模型。当其漏电不能忽略时, 可以用一个电容作为它的电路模型。当其漏电不能忽略时, 则需要用一个电阻与电容的并联作为它的电路模型。 则需要用一个电阻与电容的并联作为它的电路模型。 在工作频率很高的情况下, 在工作频率很高的情况下,还需要增加一个电感来构 如图7-6所示 所示。 成电容器的电路模型,如图 成电容器的电路模型,如图7-6所示。
第六章 电容元件与电感元件
• 6-1 电容元件 - • 6-2 电容的 - 电容的VCR • 6-3 电容电压的连续性质和记忆性质 - • 6-4 电容的储能 6- • 6-5 电感元件 - • 6-6 电感的 - 电感的VCR • 6 – 7 电容与电感的对偶性 • 6 – 8 电容、电感的串、并联 电容、电感的串、 状态变量
图7-5
线性时不变电容元件的符号与特性曲线如图(c)和 所 线性时不变电容元件的符号与特性曲线如图 和(d)所 示,它的特性曲线是一条通过原点不随时间变化的直线, 它的特性曲线是一条通过原点不随时间变化的直线, 其数学表达式为
q = Cu
表示。 容,单位是法[拉],用F表示。 单位是法 拉 用 表示
图7-9
所示的峰值检波器电路, 图7-10(a)所示的峰值检波器电路,就是利用电容的 - 所示的峰值检波器电路 记忆性,使输出电压波形[如图 中实线所示]保持输入电 记忆性,使输出电压波形 如图(b)中实线所示 保持输入电 如图 中实线所示 波形[如图 中虚线所示]中的峰值 压uin(t)波形 如图 中虚线所示 中的峰值。 波形 如图(b)中虚线所示 中的峰值。
du i (t ) = C dt d[10 sin(5t )] = 10 × dt −6 = 50 × 10 cos(5t )A = 50 cos(5t )µ A
−6
图7-7 -
已知C=0.5µF电容上的电压波形如图 -8(a)所示, 电容上的电压波形如图7- 所示, 例7-1 已知 电容上的电压波形如图 所示 试求电压电流采用关联参考方向时的电流i 试求电压电流采用关联参考方向时的电流 C(t),并画 并画 出波形图。 出波形图。
§6-1 -
电容元件
电容元件的定义是:如果一个二端元件在任一时刻, 电容元件的定义是:如果一个二端元件在任一时刻 , 平面上一条曲线所确定, 其电荷与电压之间的关系由u 其电荷与电压之间的关系由 -q平面上一条曲线所确定, 平面上一条曲线所确定 则称此二端元件为电容元件。 则称此二端元件为电容元件。
图7-10 峰值检波器电路的输入输出波形 -
(2)电容电压的连续性 电容电压的连续性 从例7- 的计算结果可以看出 的计算结果可以看出, 从例 -2的计算结果可以看出, 电容电流的波形是不 连续的矩形波,而电容电压的波形是连续的。 连续的矩形波,而电容电压的波形是连续的。 从这个平滑 的电容电压波形可以看出电容电压是连续的一般性质。 的电容电压波形可以看出电容电压是连续的一般性质。 即 电容电流在闭区间[t 有界时, 电容电流在闭区间 1,t2]有界时,电容电压在开区间 1,t2)内 有界时 电容电压在开区间(t 内 是连续的。这可以从电容电压、电流的积分关系式中得到 是连续的。这可以从电容电压、 证明。 证明。 将 t=T 和 t=T+dt 代 入 式 (7 - 13) 中 , 其 中 t1<T<t2 和 t1<T+dt<t2得到
图7-11
解:开关闭合已久,各电压电流均为不随时间变化的恒定 开关闭合已久, 值,造成电容电流等于零,即 造成电容电流等于零,
du C iC (t ) = C =0 dt
电路如图7- 所示 所示。 例7-4 电路如图 -12所示。已知两个电容在开关闭合前一 瞬间的电压分别为u 瞬间的电压分别为 C1(0-)=0V, uC2(0-)=6V,试求在开 , 关闭合后一瞬间,电容电压 关闭合后一瞬间,电容电压uC1(0+), uC2(0+)。 。
t 1 t 6 u C (t ) = ∫ iC (ξ )dξ = 2 × 10 ∫ 0dξ = 0 −∞ C −∞
2.当0≤t<1s时,iC(t)=1µA,根据式 . ≤ 时 µ ,根据式7-13可以得到 可以得到
t 1 t 6 u C (t ) = ∫ iC (ξ )dξ = u C (0) + 2 × 10 ∫ 10 −6 dξ = 0 + 2t = 2t 0 C −∞ 当 t = 1s 时 u C (1s) = 2V
