2009-2010学年九年级下同步测试期中测试(26～27章)

合集下载

九年级(下)期中数学试卷附答案

九年级（下）期中数学试卷一、选择题（本大题共6小题，每小题3分，共18分）1．﹣1+2的值是（）A．﹣1 B．1 C．﹣3 D．32．下列单项式中，与a2b是同类项的是（）A．2a2b B．a2b2 C．ab2D．3ab3．如图，AB∥CD，FE⊥DB，垂足为E，∠1=50°，则∠2的度数是（）A．60°B．50°C．40°D．30°4．如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（）A．B．C．D．5．菱形ABCD的一条对角线长为6，边AB的长为方程y2﹣7y+10=0的一个根，则菱形ABCD的周长为（）A．8 B．20 C．8或20 D．106．如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位；天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列结论错误的是（）A．第24天的销售量为200件B．第10天销售一件产品的利润是15元C．第12天与第30天这两天的日销售利润相等D．第30天的日销售利润是750元二、填空题（本大题共6小题，每小题3分，共18分）7．计算：20=．8．如图，在△ABC中，D、E为边AB、AC的中点，已知△ADE的面积为4，那么△ABC的面积是．9．如图，已知AB=CB，要使四边形ABCD成为一个轴对称图形，还需添加一个条件，你添加的条件是．（只需写一个，不添加辅助线）10．关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，则实数k的取值范围是．11．如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，边B1C1与CD交于点O，则四边形AB1OD的面积是．12．平面内有四个点A、O、B、C，其中∠AOB=120°，∠ACB=60°，AO=BO=2，则满足题意的OC长度为整数的值可以是．三、解答题（本大题共5小题，每小题6分，共30分）13．（1）计算：﹣3tan30°+（2）在平行四边形ABCD中，对角线AC于BD交于点O，∠DAC=42°，∠CBD=23°，求∠COD的度数．14．解不等式组：．15．先化简，再求值：（1﹣），其中x=3．16．如图，在正方形ABCD中，点M是BC边上任意一点，请你仅用无刻度直尺、用连线的方法，分别在图（1）、图（2）中按要求作图（保留作图痕迹，不写作法）．（1）在图（1）中，在AB边上求作一点N，连接CN，使CN=AM；（2）在图（2）中，在AD边上求作一点Q，连接CQ，使CQ∥AM．17．A、B、C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B、C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．（1）画树状图，求两次传球后，球恰在B手中的概率；（2）画树状图，求三次传球后，球恰在A手中的概率．四、解答题（本大题共3小题，每小题8分，共24分）18．雾霾天气严重影响市民的生活质量．在今年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．（1）本次被调查的市民共有多少人？（2）分别补全条形统计图和扇形统计图，并计算图2中区域B所对应的扇形圆心角的度数；（3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？组雾霾天气的主要成因百分比别A工业污染45%B汽车尾气排放mC炉烟气排放15%D其他（滥砍滥伐等）n19．如图是一座人行天桥的示意图，天桥的高度是10米，CB⊥DB，坡面AC的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC 的坡度为i=：3．若新坡角外需留3米宽的人行道，问离原坡角（A点处）10米的建筑物是否需要拆除？（参考数据：≈1.414，≈1.732）20．如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．（1）求BC的长；（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．五、解答题（本大题共2小题，每小题9分，共18分）21．如图，▱ABCD放置在平面直角坐标系中，已知点A（2，0），B（6，0），D （0，3），反比例函数的图象经过点C．（1）求反比例函数的解析式；（2）将▱ABCD向上平移，使点B恰好落在双曲线上，此时A，B，C，D的对应点分别为A′，B′，C′，D′，且C′D′与双曲线交于点E，求线段AA′的长及点E的坐标．22．小明在课外学习时遇到这样一个问题：定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．求函数y=﹣x2+3x﹣2的“旋转函数”．小明是这样思考的：由y=﹣x2+3x﹣2函数可知a1=﹣1，b1=3，c1=﹣3，根据a1+a2=0，b1=b2，c1+c2=0求出a2，b2，c2，就能确定这个函数的“旋转函数”．请参考小明的方法解决下面的问题：（1）写出函数y=﹣x2+3x﹣2的“旋转函数”；（2）若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2017的值；（3）已知函数y=﹣（x+1）（x﹣4）的图象与x轴交于A，B两点，与y轴交于点C，点A，B，C关于原点的对称点分别是A1，B1，C1，试证明经过点A1，B1，C1的二次函数与函数y=﹣（x+1）（x﹣4）互为“旋转函数”．六、解答题（本大题共1小题，共12分）23．（1）问题如图1，在四边形ABCD中，点P为AB 上一点，当∠DPC=∠A=∠B=90°时，求证：AD•BC=AP•BP．（2）探究如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=α时，上述结论是否依然成立？说明理由．（3）应用请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．参考答案与试题解析一、选择题（本大题共6小题，每小题3分，共18分）1．﹣1+2的值是（）A．﹣1 B．1 C．﹣3 D．3【考点】19：有理数的加法．【分析】依据有理数的加法法则计算即可．【解答】解：﹣1+2=2﹣1=1．故选：B．2．下列单项式中，与a2b是同类项的是（）A．2a2b B．a2b2 C．ab2D．3ab【考点】34：同类项．【分析】根据同类项的概念：所含字母相同，并且相同字母的指数也相同，结合选项解答即可．【解答】解：A、2a2b与a2b所含字母相同，且相同字母的指数也相同，是同类项，故本选项正确；B、a2b2与a2b所含字母相同，但相同字母b的指数不相同，不是同类项，故本选项错误；C、ab2与a2b所含字母相同，但相同字母a的指数不相同，不是同类项，本选项错误；D、3ab与a2b所含字母相同，但相同字母a的指数不相同，不是同类项，本选项错误．故选A．3．如图，AB∥CD，FE⊥DB，垂足为E，∠1=50°，则∠2的度数是（）A．60°B．50°C．40°D．30°【考点】JA：平行线的性质；J3：垂线．【分析】根据直角三角形的两锐角互余，求出∠D=40°，再根据平行线的性质即可解答．【解答】解：如图所示，∵FE⊥BD，∴∠FED=90°，∴∠1+∠D=90°，∵∠1=50°，∴∠D=40°，∵AB∥CD，∴∠2=∠D=40°．故选C．4．如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是（）A．B．C．D．【考点】X4：概率公式；P3：轴对称图形．【分析】由随机选择标有序号①②③④⑤中的一个小正方形涂黑，共有5种等可能的结果，使与图中阴影部分构成轴对称图形的有3种情况，直接利用概率公式求解即可求得答案．【解答】解：∵在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，共有5种等可能的结果，使与图中阴影部分构成轴对称图形的有②④⑤，3种情况，∴使与图中阴影部分构成轴对称图形的概率是：3÷5=．故选C．5．菱形ABCD的一条对角线长为6，边AB的长为方程y2﹣7y+10=0的一个根，则菱形ABCD的周长为（）A．8 B．20 C．8或20 D．10【考点】L8：菱形的性质；A8：解一元二次方程﹣因式分解法．【分析】边AB的长是方程y2﹣7y+10=0的一个根，解方程求得y的值，根据菱形ABCD的一条对角线长为6，根据三角形的三边关系可得出菱形的边长，即可求得菱形ABCD的周长．【解答】解：∵解方程y2﹣7y+10=0得：y=2或5∵对角线长为6，2+2＜6，不能构成三角形；∴菱形的边长为5．∴菱形ABCD的周长为4×5=20．故选B．6．如图是本地区一种产品30天的销售图象，图①是产品日销售量y（单位：件）与时间t（单位；天）的函数关系，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列结论错误的是（）A．第24天的销售量为200件B．第10天销售一件产品的利润是15元C．第12天与第30天这两天的日销售利润相等D．第30天的日销售利润是750元【考点】FH：一次函数的应用．【分析】根据函数图象分别求出设当0≤t≤20，一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系为z=﹣x+25，当0≤t≤24时，设产品日销售量y（单位：件）与时间t（单位；天）的函数关系为y=，根据日销售利润=日销售量×一件产品的销售利润，即可进行判断．【解答】解：A、根据图①可得第24天的销售量为200件，故正确；B、设当0≤t≤20，一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系为z=kx+b，把（0，25），（20，5）代入得：，解得：，∴z=﹣x+25，当x=10时，y=﹣10+25=15，故正确；C、当0≤t≤24时，设产品日销售量y（单位：件）与时间t（单位；天）的函数关系为y=k1t+b1，把（0，100），（24，200）代入得：，解得：，∴y=，当t=12时，y=150，z=﹣12+25=13，∴第12天的日销售利润为；150×13=1950（元），第30天的日销售利润为；150×5=750（元），750≠1950，故C错误；D、第30天的日销售利润为；150×5=750（元），故正确．故选：C二、填空题（本大题共6小题，每小题3分，共18分）7．计算：20=1．【考点】6E：零指数幂．【分析】直接根据非0数的0次幂等于1进行解答．【解答】解：∵2≠0，∴20=1．故答案为：1．8．如图，在△ABC中，D、E为边AB、AC的中点，已知△ADE的面积为4，那么△ABC的面积是16．【考点】S9：相似三角形的判定与性质；KX：三角形中位线定理．【分析】根据三角形的中位线定理求出DE=BC，DE∥BC，求出△ADE∽△ABC，根据相似三角形的性质得出比例式，代入求出即可．【解答】解：∵D、E为边AB、AC的中点，∴DE=BC，DE∥BC，∴△ADE∽△ABC，∴=（）2=，∵△ADE的面积为4，∴△ABC的面积是16，故答案为：16．9．如图，已知AB=CB，要使四边形ABCD成为一个轴对称图形，还需添加一个条件，你添加的条件是AD=CD．（只需写一个，不添加辅助线）【考点】P3：轴对称图形．【分析】轴对称图形的定义即可得到结论．【解答】解：AD=CD，理由：在△ABD与△CBD中，，∴△ABD≌△CBD，∴四边形ABCD是一个轴对称图形，故答案为：AD=CD．10．关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，则实数k的取值范围是k＜2且k≠1．【考点】AA：根的判别式；A1：一元二次方程的定义．【分析】根据一元二次方程的定义和判别式的意义得到k﹣1≠0且△=（﹣2）2﹣4（k﹣1）＞0，然后求出两个不等式的公共部分即可．【解答】解：∵关于x的一元二次方程（k﹣1）x2﹣2x+1=0有两个不相等的实数根，∴k﹣1≠0且△=（﹣2）2﹣4（k﹣1）＞0，解得：k＜2且k≠1．故答案为：k＜2且k≠1．11．如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1，边B1C1与CD交于点O，则四边形AB1OD的面积是﹣1．【考点】R2：旋转的性质；LE：正方形的性质．【分析】先根据正方形的边长，求得CB1=OB1=AC﹣AB1=﹣1，进而得到S△OB1C==，即可得出四边形AB1OD的面积．（﹣1）2，再根据S△ADC【解答】解：∵四边形ABCD是正方形，∴AC=，∠OCB1=45°，∴CB1=OB1∵AB1=1，∴CB1=OB1=AC﹣AB1=﹣1，=•OB1•CB1=（﹣1）2，∴S△OB1C=AD•AC=×1×1=，∵S△ADC=S△ADC﹣S△OB1C=﹣（﹣1）2=﹣1，∴S四边形AB1OD故答案为：﹣1．12．平面内有四个点A、O、B、C，其中∠AOB=120°，∠ACB=60°，AO=BO=2，则满足题意的OC长度为整数的值可以是2，3，4．【考点】M2：垂径定理；KM：等边三角形的判定与性质．【分析】分类讨论：如图1，根据圆周角定理可以推出点C在以点O为圆心的圆上；如图2，根据已知条件可知对角∠AOB+∠ACB=180°，则四个点A、O、B、C共圆．分类讨论：如图1，如图2，在不同的四边形中，利用垂径定理、等边△MAO的性质来求OC的长度．【解答】解：如图1，∵∠AOB=120°，∠ACB=60°，∴∠ACB=∠AOB=60°，∴点C在以点O为圆心的圆上，且在优弧AB上．∴OC=AO=BO=2；如图2，∵∠AOB=120°，∠ACB=60°，∴∠AOB+∠ACB=180°，∴四个点A、O、B、C共圆．设这四点都在⊙M上．点C在优弧AB上运动．连接OM、AM、AB、MB．∵∠ACB=60°，∴∠AMB=2∠ACB=120°．∵AO=BO=2，∴∠AMO=∠BMO=60°．又∵MA=MO，∴△AMO是等边三角形，∴MA=AO=2，∴MA＜OC≤2MA，即2＜OC≤4，∴OC可以取整数3和4．综上所述，OC可以取整数2，3，4．故答案是：2，3，4．三、解答题（本大题共5小题，每小题6分，共30分）13．（1）计算：﹣3tan30°+（2）在平行四边形ABCD中，对角线AC于BD交于点O，∠DAC=42°，∠CBD=23°，求∠COD的度数．【考点】L5：平行四边形的性质；2C：实数的运算；T5：特殊角的三角函数值．【分析】（1）首先代入30°角的正切值、化简二次根式，即可得出答案；（2）由平行四边形的性质得出∠BCA=∠DAC=42°，再由三角形的外角性质得出∠COD=∠CBD+∠BCA，即可得出结果．【解答】解：（1）﹣3tan30°+=﹣3×+2=﹣+2=（2）解：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠BCA=∠DAC=42°，∴∠COD=∠CBD+∠BCA=42°+23°=65°．14．解不等式组：．【考点】CB：解一元一次不等式组．【分析】先求出两个不等式的解集，再求其公共解．【解答】解：，由①得，x＞﹣1，由②得，x＞﹣3，所以，不等式组的解集为x＞﹣1．15．先化简，再求值：（1﹣），其中x=3．【考点】6D：分式的化简求值．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．【解答】解：原式=•=•=，当x=3时，原式=2．16．如图，在正方形ABCD中，点M是BC边上任意一点，请你仅用无刻度直尺、用连线的方法，分别在图（1）、图（2）中按要求作图（保留作图痕迹，不写作法）．（1）在图（1）中，在AB边上求作一点N，连接CN，使CN=AM；（2）在图（2）中，在AD边上求作一点Q，连接CQ，使CQ∥AM．【考点】N3：作图—复杂作图．【分析】（1）连接BD，BD与AM交于点O，连接CO并延长交于AB，则CO与AB的交点为点N．可先证明△AOD≌△COD，再证明△MOB≌NOB，从而可得NB=MB；（2）连接AC，BD交于点O，连接MO并延长与AE交于点Q，连接QC，则CQ ∥AM．理由如下：由正方形的性质以及对顶角相等可证△BMO≌DQO，所以QO=MO，由于∠QOC=∠MOA，CO=AO，所以△COQ≌AOM，则∠QCO=∠MAO，从而可得CQ∥AM．【解答】解：（1）在BA上截取BN=BM，连结CN，则CN为所作，如图1（2）在DA上截取DQ=BM，连结CQ，则CQ为所作，如图2．17．A、B、C三人玩篮球传球游戏，游戏规则是：第一次传球由A将球随机地传给B、C两人中的某一人，以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人．（1）画树状图，求两次传球后，球恰在B手中的概率；（2）画树状图，求三次传球后，球恰在A手中的概率．【考点】X6：列表法与树状图法．【分析】（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两次传球后，球恰在B手中的情况，再利用概率公式即可求得答案；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与三次传球后，球恰在A手中的情况，再利用概率公式即可求得答案．【解答】解：（1）画树状图得：∵共有4种等可能的结果，两次传球后，球恰在B手中的只有1种情况，∴两次传球后，球恰在B手中的概率为：；（2）画树状图得：∵共有8种等可能的结果，三次传球后，球恰在A手中的有2种情况，∴三次传球后，球恰在A手中的概率为：=．四、解答题（本大题共3小题，每小题8分，共24分）18．雾霾天气严重影响市民的生活质量．在今年寒假期间，某校八年级一班的综合实践小组同学对“雾霾天气的主要成因”随机调查了所在城市部分市民．并对调查结果进行了整理．绘制了如图不完整的统计图表．观察分析并回答下列问题．（1）本次被调查的市民共有多少人？（2）分别补全条形统计图和扇形统计图，并计算图2中区域B所对应的扇形圆心角的度数；（3）若该市有100万人口，请估计持有A、B两组主要成因的市民有多少人？组雾霾天气的主要成因百分比别A工业污染45%B汽车尾气排放mC炉烟气排放15%D其他（滥砍滥伐等）n【考点】VC：条形统计图；V5：用样本估计总体；VB：扇形统计图．【分析】（1）根据条形图和扇形图信息，得到A组人数和所占百分比，求出调查的市民的人数；（2）根据B组人数求出B组百分比，得到D组百分比，根据扇形圆心角的度数=百分比×360°求出扇形圆心角的度数，根据所求信息补全条形统计图和扇形统计图；（3）根据持有A、B两组主要成因的市民百分比之和求出答案．【解答】解：（1）从条形图和扇形图可知，A组人数为90人，占45%，∴本次被调查的市民共有：90÷45%=200人；（2）60÷200=30%，30%×360°=108°，区域B所对应的扇形圆心角的度数为：108°，1﹣45%﹣30%﹣15%=10%，D组人数为：200×10%=20人，（3）100万×（45%+30%）=75万，∴若该市有100万人口，持有A、B两组主要成因的市民有75万人．19．如图是一座人行天桥的示意图，天桥的高度是10米，CB⊥DB，坡面AC的倾斜角为45°．为了方便行人推车过天桥，市政部门决定降低坡度，使新坡面DC 的坡度为i=：3．若新坡角外需留3米宽的人行道，问离原坡角（A点处）10米的建筑物是否需要拆除？（参考数据：≈1.414，≈1.732）【考点】T9：解直角三角形的应用﹣坡度坡角问题．【分析】需要拆除，理由为：根据题意得到三角形ABC为等腰直角三角形，求出AB的长，在直角三角形BCD中，根据新坡面的坡度求出∠BDC的度数为30，利用30度所对的直角边等于斜边的一半求出DC的长，再利用勾股定理求出DB 的长，由DB﹣AB求出AD的长，由AD+3与10比较即可得到结果．【解答】解：需要拆除，理由为：∵CB⊥AB，∠CAB=45°，∴△ABC为等腰直角三角形，∴AB=BC=10米，在Rt△BCD中，新坡面DC的坡度为i=：3，即∠CDB=30°，∴DC=2BC=20米，BD==10米，∴AD=BD﹣AB=（10﹣10）米≈7.32米，∵3+7.32=10.32＞10，∴需要拆除．20．如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．（1）求BC的长；（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．【考点】MD：切线的判定；KO：含30度角的直角三角形；M5：圆周角定理．【分析】（1）根据圆周角定理求得∠ADB=90°，然后解直角三角形即可求得BD，进而求得BC即可；（2）要证明直线DE是⊙O的切线只要证明∠EDO=90°即可．【解答】证明：（1）解：连接AD，∵AB是⊙O的直径，∴∠ADB=90°，又∵∠ABC=30°，AB=4，∴BD=2，∵D是BC的中点，∴BC=2BD=4；（2）证明：连接OD．∵D是BC的中点，O是AB的中点，∴DO是△ABC的中位线，∴OD∥AC，则∠EDO=∠CED又∵DE⊥AC，∴∠CED=90°，∠EDO=∠CED=90°∴DE是⊙O的切线．五、解答题（本大题共2小题，每小题9分，共18分）21．如图，▱ABCD放置在平面直角坐标系中，已知点A（2，0），B（6，0），D （0，3），反比例函数的图象经过点C．（1）求反比例函数的解析式；（2）将▱ABCD向上平移，使点B恰好落在双曲线上，此时A，B，C，D的对应点分别为A′，B′，C′，D′，且C′D′与双曲线交于点E，求线段AA′的长及点E的坐【考点】L5：平行四边形的性质；G6：反比例函数图象上点的坐标特征；G7：待定系数法求反比例函数解析式．【分析】（1）由A与B的坐标求出AB的长，根据四边形ABCD为平行四边形，求出DC的长，进而确定出C坐标，设反比例解析式为y=，把C坐标代入求出k的值，即可确定出反比例解析式；（2）根据平移的性质得到B与B′横坐标相同，代入反比例解析式求出B′纵坐标得到平移的距离，即为AA′的长，求出D′纵坐标，即为E纵坐标，代入反比例解析式求出E横坐标，即可确定出E坐标．【解答】解：（1）∵▱ABCD中，A（2，0），B（6，0），D（0，3），∴AB=CD=4，DC∥AB，∴C（4，3），设反比例解析式为y=，把C坐标代入得：k=12，则反比例解析式为y=；（2）∵B（6，0），∴把x=6代入反比例解析式得：y=2，即B′（6，2），∴平行四边形ABCD向上平移2个单位，即AA′=2，∴D′（0，5），把y=5代入反比例解析式得：x=，即E（，5）．22．小明在课外学习时遇到这样一个问题：定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．求函数y=﹣x2+3x﹣2的“旋转函数”．小明是这样思考的：由y=﹣x2+3x﹣2函数可知a1=﹣1，b1=3，c1=﹣3，根据a1+a2=0，b1=b2，c1+c2=0求出a2，b2，c2，就能确定这个函数的“旋转函数”．请参考小明的方法解决下面的问题：（1）写出函数y=﹣x2+3x﹣2的“旋转函数”；（2）若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2017的值；（3）已知函数y=﹣（x+1）（x﹣4）的图象与x轴交于A，B两点，与y轴交于点C，点A，B，C关于原点的对称点分别是A1，B1，C1，试证明经过点A1，B1，C1的二次函数与函数y=﹣（x+1）（x﹣4）互为“旋转函数”．【考点】HF：二次函数综合题．【分析】（1）由函数函数y=﹣x2+3x﹣2的解析式可知a1=﹣1，b1=3，c1=﹣2，然后依据旋转函数的定义得到﹣1+a2=0，b2=3，﹣2+c2=0，然后求得a2，b2，c2的值即可；（2）依据旋转函数的定义列出关于m、n的方程，从而可求得m、n的值，然后代入计算即可；（3）先求得A，B，C三点的坐标，然后再求得A1，B1，C1的坐标，然后可求得经过点A1，B1，C1的二次函数的解析式，最后依据旋转函数的定义进行判断即可．【解答】解：（1）∵a1=﹣1，b1=3，c1=﹣2，∴﹣1+a2=0，b2=3，﹣2+c2=0，∴a2=1，b2=3，c2=2，∴函数y=﹣x2+3x﹣2的“旋转函数”为y=x2+3x+2；（2）解：根据题意得m=﹣2n，﹣2+n=0，解得m=﹣3，n=2，∴（m+n）2017=（﹣3+2）2017=﹣1；（3）证明：当x=0时，y=﹣（x+1）（x﹣4）=2，则C（0，2），当y=0时，﹣（x+1）（x﹣4）=0，解得x1=﹣1，x2=4，则A（﹣1，0），B（4，0），∵点A、B、C关于原点的对称点分别是A1，B1，C1，∴A1（1，0），B1（﹣4，0），C1（0，﹣2），…设经过点A1，B1，C1的二次函数解析式为y=a2（x﹣1）（x+4），把C1（0，﹣2）代入得a2•（﹣1）•4=﹣2，解得a2=，∴经过点A1，B1，C1的二次函数解析式为y=（x﹣1）（x+4）=x2+x﹣2，∵y=﹣（x+1）（x﹣4）=﹣x2+x+2，∴a1+a2=﹣+=0，b1=b2=，c1+c2=2﹣2=0，∴经过点A1，B1，C1的二次函数与函数y=﹣（x+1）（x﹣4）互为“旋转函数．六、解答题（本大题共1小题，共12分）23．（1）问题如图1，在四边形ABCD中，点P为AB 上一点，当∠DPC=∠A=∠B=90°时，求证：AD•BC=AP•BP．（2）探究如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=α时，上述结论是否依然成立？说明理由．（3）应用请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=6，AD=BD=5．点P以每秒1个单位长度的速度，由点A出发，沿边AB向点B运动，且满足∠DPC=∠A．设点P的运动时间为t（秒），当以D为圆心，以DC为半径的圆与AB相切，求t的值．【考点】MR：圆的综合题．【分析】（1）由∠DPC=∠A=∠B=90°可得∠ADP=∠BPC，即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；（2）由∠DPC=∠A=∠B=α可得∠ADP=∠BPC，即可证到△ADP∽△BPC，然后运用相似三角形的性质即可解决问题；（3）过点D作DE⊥AB于点E，根据等腰三角形的性质可得AE=BE=3，根据勾股定理可得DE=4，由题可得DC=DE=4，则有BC=5﹣4=1．易证∠DPC=∠A=∠B．根据AD•BC=AP•BP，就可求出t的值．【解答】（1）证明：如图1，∵∠DPC=∠A=∠B=90°，∴∠ADP+∠APD=90°，∠BPC+∠APD=90°，∴∠APD=∠BPC，∴△ADP∽△BPC，∴=，∴AD•BC=AP•BP；（2）结论AD•BC=AP•BP仍成立；理由：如图2，∵∠BPD=∠DPC+∠BPC，又∵∠BPD=∠A+∠APD，∴∠DPC+∠BPC=∠A+∠APD，∵∠DPC=∠A=α，∴∠BPC=∠APD，又∵∠A=∠B=α，∴△ADP∽△BPC，∴=，∴AD•BC=AP•BP；（3）解：如图3，过点D作DE⊥AB于点E，∵AD=BD=5，AB=6，∴AE=BE=3∴DE==4，∵以D为圆心，以DC为半径的圆与AB相切，∴DC=DE=4，∴BC=5﹣4=1，∵AD=BD，∴∠A=∠B，又∵∠DPC=∠A，∴∠DPC=∠A=∠B，由（1）（2）的经验得AD•BC=AP•BP，又∵AP=t，BP=6﹣t，∴t（6﹣t）=5×1，∴解得：t1=1，t2=5，∴t的值为1秒或5秒．。

2023-2024学年人教版英语九年级全册期中测试卷(含答案)

Chinese buyers think China is good and ‘Made in China’ is not bad at all,” Charlie Chen,head of China buyer
research at Credit Suisse, told South China Morning Post in March.
market by 3.3% over the last ten years to nearly 70%.
“Chinese buyers, especially the younger ones, don't just believe that foreign brands are better.Right now,
B. CCTV 9.
C. South China Morning Post.
D. Business Insider.
( ) 7. Which fact best explains “home brand bias”?
A. Apple had a market share of 54% in 2015.
increasingly showing a “home brand bias”.
More than 90% of young Chinese buyers would prefer to buy home appliance brands, according to the study.
Meanwhile, home companies producing food, drinks, or personal care products have increased their share of the

(完整版)人教九年级数学下册同步练习题及答案

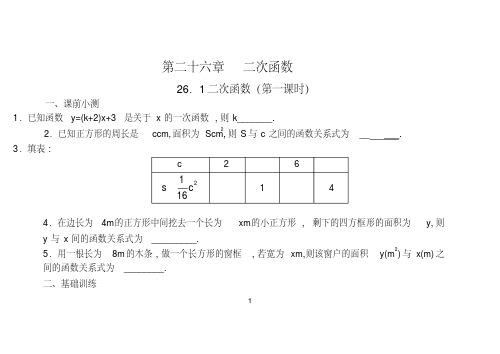
2. 已知函数 y=(m+2) xm2 m 4 是关于 x 的二次函数 . 求 : (1) 满足条件的 m的值 ; (2)m 为何值时 ,
抛物线有最低点 ?求出这个最低点 , 这时当 x 为何值时 ,y 随 x 的增大而增大 ?(3)m 为何值时 , 函数有最大值 ?最大值是多少 ?这时当 x 为何值时 ,y 随 x 的增大而减小 ?
．
4．抛物线 y=3x 2＋ 5x 与两坐标轴交点的个数为（
）
11
A． 3 个 B ． 2 个
C． 1 个
D． 0 个
5．二次函数 y=x2－ 4x+3 的图象交 x 轴于 A、 B 两点，交 y 轴于点 C，△ ABC的面积为
A.1
B.3
C.4 D.6
三、综合训练
1．抛物线与 x 轴的公共点是 (-1,0),(3,0), 这条抛物线的对称轴是
2．二次函数 y=(x-1)(x+2) 的图象顶点为 ____, 对称轴为 _____。 3．若二次函数 y=2x2+4x+c 图象的顶点在 x 轴上，则 c 等于 ( )A. － 1 B.1
1
C.
D.2
2
4．如果关于 x 的一元二次方程 x2 kx 4 0 有两个相等根，则 k
5．一元二次方程 x2 2 x 3 0 的根的情况是（
求此二次函数的解析式。
6
一、课前小测
26．1 二次函数（第四课时）
1．已知抛物线 y x2 ( m 2) x 2m ，当 m=______时，抛物线经过原点。
2．抛物线 y=2x 2-3 的开口向 _____ ___ ，对称轴是 _______，顶点坐标是 ________，顶点是最 _____点，所以函数有最 ________值是 ____ 。

2024年全新九年级语文下册期中试卷及答案(人教版)

2024年全新九年级语文下册期中试卷及答案(人教版)一、选择题1. 下列词语中，加点字的读音完全相同的一项是( )A. 琴弦/弦外之音B. 强迫/强词夺理C. 沉溺/溺爱D. 拒绝/狙击2. 下列各句中，没有语病的一句是( )A. 这几天我接到了一些亲戚和朋友的来信。

B. 学校运动会将于下月中旬前后举行。

C. 老师多次强调，要认真完成作业，否则，一旦考试不及格，就会前功尽弃。

D. 爱国主义教育使同学们认识到中华民族有着悠久的文明史。

3. 下列词语解释有误的一项是( )A. 轻歌曼舞：形容轻松愉快的音乐和柔和优美的舞蹈。

B. 孜孜不倦：指工作或学习勤奋不知疲倦。

C. 满腔热血：形容非常热情，充满激情。

D. 指手画脚：形容说话时放肆或得意忘形。

4. 下列各句中，标点符号使用正确的一项是( )A. “我们一定要保持清醒的头脑，防止类似的事件再次发生。

”他严肃地说。

B. “这里的风景真美啊!”他情不自禁地赞叹道。

C. “一定要记住：”老师语重心长地说，“做事要持之以恒，不能半途而废。

”D. “你难道不知道我正在工作吗?”他生气地问道。

5. 下列句子中，没有使用比喻修辞的一项是( )A. 那女孩的脸红得像苹果一样。

B. 他像一只受伤的鸟儿，默默地承受着痛苦。

C. 他的笑容像阳光一样温暖。

D. 他的歌声像清泉一样悦耳动听。

二、填空题6. 请根据拼音写出相应的汉字。

(1) fù( ) (2) shū( ) (3) huì( ) (4) yù( )7. 请将下列词语补充完整。

(1) 不求( ) (2) 专心( ) (3) 自( )其( ) (4) 自( )其( )8. 请将下列词语补充完整。

(1) ( ) (2) ( ) (3) ( ) (4) ( )9. 请将下列词语补充完整。

(1) ( ) (2) ( ) (3) ( ) (4) ( )10. 请将下列词语补充完整。

(1) ( ) (2) ( ) (3) ( ) (4) ( )三、简答题11. 请简述《沁园春·雪》这首诗的写作背景和主题。

2024-2025学年第一学期九年级数学期中测评卷(21-23章)

2024-2025学年第一学期期中测评卷九年级数学（卷面分值：100分考试时间：100分钟）一、选择题(每题3分，共27分，请将选择题的答案写在下面的表格中) 题号 1 2 3 4 5 6 7 8 9答案 D B A C A D B D C1.下列是一元二次方程的是（ D ）0.2=++c bx ax A 0.23=−x x B 052.=−y x C 01.2=−x D2.函数32+=x y 的图像经过点（-2，m ）,则m 的值为（ B ）1.A 7.B 5.C 4.D3.下列图形中，是中心对称图形但不是轴对称图形的是( A )4.若抛物线142−+=x ax y 与x 轴有两个交点，则a 的取值范围是（C ）4.＞a A 4.−＞a B 04.≠−a a C 且＞ 4.−＜a D5.如果将方程0262=+−x x 配方成b a x =+2)(的形式，则a-b 的值为（ A ）10.−A 10.B 5.C 9.D6.关于函数342++=x x y 的图像和性质，下列说法错误的是（D ）A.函数图像开口向上B.当x ＞-2时，y 随x 的增大而增大C.函数图像的顶点坐标是（-2，-1）D.函数图像与x 轴没有交点7.三角形的两边长分别是3和6，第三边长是方程0862=+−x x 的根，则该三角形的周长等于（B ）11.A 13.B 1311.或C 12.D8.已知方程0252=+−x x 的两根分别是21x x ，，则2221x x +的值为（ D ）18.A 19.B 20.C 21.D9.如图所示为长20米、宽 15米的矩形空地，现计划要在中间修建三条等宽的小道，其余面积种植绿植，种植面积为 400平方米，若设小道的宽为 xx 米，则根据题意，列方程为（ C ）40021520.2=−×+x x A 40021520.=−×x B400)15)(220.(=−−x x C 400)215)(20.(=−−x x D二.填空题（每空3分，共18分）10.将方程1322+=−x x x 化为一般式，其结果是__0122=−−x x ___.11.若m 是方程0752=−−x x 的根，则152+−m m 的值等于___8_____.12.已知关于x 的方程0142=−+x kx 没有实数根，则k 的取值范围是___k ＜-4_____.13.将二次函数2)1(3+−=x y 的图像先向右平移2个单位长度，再向下平移4个单位长度，所得到的函数解析式为__4)1(32−−−=x y ___.14.已知抛物线c ax y +=2与22x y =的形状相同，开口方向相反，且经过点(-1,5),则其解析式为__722+−=x y ____.15.超市搞促销活动，将某商品经过两次降价，售价由86元降至52元，若两次降价的百分率相同均为x,可列方程为__52)1(862=−x ___.三.解答题（共6小题，共,55分）16.（10分）解方程091012=+−x x ）（ 1,921==x x6)6()2(+=+x x x 6,121−==x x17.（8分）已知关于x 的一元二次方程024)12(2=−++−m x m x .求证：无论 m 取何值，这个方程总有实数根．解：222)3-m 2()24(4)12(4=−−+=−m m ac b 证明：无论 m 取何值，042≥−ac b18.（10分）已知抛物线的顶点坐标为（-1,3），且经过点（2,12）.（1）求函数解析式.（2）当21≤≤−x 时，求函数的最大值.解：3)1(12++=x y ）（（2）当21≤≤−x 时，函数的最大值为12.19. （8分）冬季易引发流感，刚开始有2人患流感，经过两轮传染共有288人患病，求每轮传染中平均一个人传染几个人？解：设每轮传染中平均一个人传染x 个人.288)122=+x （)(13,1121舍去−==x x答：每轮传染中平均一个人传染11个人.20.（9分）某商品售价为每件60元，每周可卖出300件，为提高利润，商家决定涨价销售，经过一段时间发现，每涨价5元，每周少卖50件，已知商品的进价为每件40元，当售价定为多少时利润最大？求最大利润. 解：售价应定为65元时，利润最大为6250元21.（10分）如图为抛物线c x y +−=2，图像经过点（-1,8）.直线3+=ax y 与抛物线交于B,C 两点.点A,B 在x 轴上.（1）求抛物线与直线的函数解析式.（2）求△ABC 的面积.解：（1）将点(-1,8)代入中c x y +−=2，得c=9 92+−=x y 即令y=0,得A(-3,0),B(3,0）13)0,3(−=+=a ax y B ，得代入将3+−=x y 即（2）联立函数解析式，得C(-2,5)△ABC 的面积为15.。

九年级下学期期中质量检测(二模)英语试题附答案

九年级下学期期中质量检测（二模）英语试题B. Listen to the dialogue and choose the best answer to the question you hear（根据你听到的对话和问题，选出最恰当的答案）：洪8分）7: A) Her can. B) Her cake. C) Her key to her bookcase. D) Her key to her bike8. A) On Tuesday. B) On Wednesday. C) On Thursday. D) On Friday.9. A) 6:10. B) 6:20. C) 5:45. D) 6:15.10. A) Mother and son. B) Customer and shop assistant.C) Conductor and passenger. D) Teacher arid student.11．A) In Miss Green's class: B) After class.C) In a drawing class. D) After school.12. A) To go back home. B) To do shopping.C) To have supper. D) To have lunch.13. A) They are traveling by plane. B) The woman enjoys the trip.C) The man likes his job. D) The woman likes his job.14. A) She'll fail in the exam. B) She'll go to see the doctor.C) She'll go over the lessons. D) She'll take her holidays.C. Listen to the passage and tell whether the following statements are true or false（判断下列句子是否符合你听到的内容，符合的用“T，，表示，不符合的用+F;表示）：（共6分）15．The passage tells us five students' special homework for the winter holiday.16. Liu Tongtong couldn't play on his phones for at least a week this winter holiday.17. Yang Qiushi learned how to recognize crops like wheat, peanuts, potatoes from the leaves. 18．Li Jie's teacher asked them to learn a skill from their grandparents as their homework.19. Taking exercise every week and taking photos of it was Zhou Zirun's homework from hisclass teacher.20. From the passage, we know that the special homework brings students a lot of fun.Part 2 Phonetics, Vocabulary and Grammar(第二部分语音、词汇和语法)II. Choose the best answer (选择最恰当的答案): (共20分)26. Which of the following word matches the sound /waɪn/ ?A) win B) wine C)when D) widen27. Which of the following underlined parts is different in pronunciation from others?A) My office is on the ground floor.B) It was cloudy yesterday afternoon.C) I’d like to buy this pair of tr ousers.D) I’ve been here for a c ouple of days.28. A: Do you know _______ lady with long black hair?B: Yes. She is my daughter’s maths teacher.A) the B) / C) a D) an29. The opening ceremony of Wulong International Kite Flying Festival was held _______ the morning ofApril 4, 2015 in Chongqing.A) at B) in C) on D) by30. Mrs. Smith wants to buy an Apple Watch for ________ husband as a birthday present.A) hers B) her C) she D) herself31. Do n’t be angry with your deskmate when he makes a mistake again because ________ of us areperfect after all.A) all B) none C) each D) neither32. The cake you made tastes so _________. Would you please tell me how you made it?A) nicer B) very nice C) nice D) nicely33. My daughter has _________life goals and one of them is to be a volunteer to help the poor children.A) a few B) few C) a little D) little34. Our monitor didn’t feel well last week, but she didn’t give up ______ the writing contest.A) attend B) attends C) attending D) to attend35. My uncle ________ as a manager since he came back from the USA five years ago.A) worked B) has worked C) works D) had worked36. The road ________ be dry, because it has just rained heavily.A) can’t B) mustn’t C) must D) can37. When I got to the booking office, they ________ all the tickets.A) were selling B) had sold C) would sell D) have sold38. ________ pleasant weather it is! Let’s go out and enjoy the sunshine!A) How B) What C) What a D) What an39. Tom ’s mother has to work very late even at weekends, ________?A) has she B) hasn’t she C) does she D) doesn’t she40. ________ he is only 8 years old, he knows more about science than his mother.A) Because B) But C) Although D) So41. Our English teacher always encourages us________ English as much as possible.A) speak B) speaking C) speaks D) to speak42. We’re proud of the great changes in our school . We’re sure it will develop even ________ tomorrow.A) quickly B) less quickly C) more quickly D) the most quickly43. Hi, could you please tell me ________ your father has gone to Sydney?A) when B) how often C) how long D) if44. A: I’m too busy to go to the cinema with you.B: ________ The film is said to be a very good one.A) That’s all right. B) Don ’t worry.C) What a pity! D) It doesn’t matter.45. A: Thank you very much for helping me to solve the problem.B: ________A) You’re welcome. B) Of course not.C) Yes, please. D) That’s right.III. Complete the following passage with the words or phrases in the box. Each can only be used once （将下列单词或词组填入空格。

【初中数学】2009-2010学年人教七年级下册数学期末复习分章同步测试卷(含期末测试共37套) 人教版34

2009－2010学年七年级下册期末复习第十章《数据的收集、整理与描述》水平测试B一、慧眼识金（每小题3分，共24分）1. 下列调查，适合用全面调查方式的是（）.A.了解武汉市居民年人均收入B.了解北京市初中生体育中考的成绩C.了解南京市中小学生的近视率D.了解某一天某小区经过小区大门的人口流量2. 某商店一周中每天卖出的衬衣分别是：15件、17件、18件、14件、21件、30件、28件，为了反映这一周销售衬衣的变化情况，应该制作的统计图是（）.A．条形图B．折线图C．扇形图D．非上述统计图3. 在2008年的世界无烟日（5月31日），小华学习小组为了解本地区大约有多少成年人吸烟，随机调查了100个成年人，结果其中有15个成年人吸烟．对于这个关于数据收集与处理的问题，下列说法正确的是（）．A．调查的方式是普查B．本地区只有85个成年人不吸烟C．样本是15个吸烟的成年人D．本地区约有15%的成年人吸烟4.某校在“创新素质实践行”活动中，组织学生进行社会调查，并对学生的调查报告进行了评比，如图是将某年级60篇学生调查报告的成绩进行整理，•分成5组画出的频率分布直方图，已知从左至右4个小组的频率分别是0.05，0.15，0.35，•0.30，那么在这次评比中被评为优秀的调查报告有（分数大于或等于80分为优秀，且分数为整数）（）.A．18篇B．24篇C．25篇D．27篇5. 张颖同学把自己一周的支出情况，用如图1所示的统计图来表示．则从图中可以看出( ).A．一周支出的总金额B．一周各项支出的金额C．一周内各项支出金额占总支出的百分比D．各项支出金额在一周中的变化情况6. 有50个数据，其中最大值为86，最小值为57，若取组距为6，则应该分的组数是（）．A．4 B．5 C．6 D．77. 如图2所示是某班60名学生一分钟跳绳测试成绩的频数分布直方图，从左起第一、二、三、四个小长方形的高的比是1∶4∶3∶2 ，那么一分钟跳绳次数在100 次以上的学生有（）．A．12 人B．20人C．25人D．30 人8. 为了估计湖里有多少条鱼,先捕上100条做上标记,然后放回到湖里,过一段时间,待带标记的鱼完成混合群后,再捕上200条,发现其中带标记的鱼有20条, 湖里大约有多少条鱼( ). 图2 图1A.400条B.600条C.800条D.1000条二、画龙点睛（每小题3分，共24分）1. 某校初三年级在期中考试后，从全年级200名学生中抽取20名学生的考试成绩作为一个样本，用来分析全年级的考试情况，这个问题中的样本容量是．2. 一组数据的最大值为169，最小值为143，在绘制频数直方图时要求组距为3，则组数为 .3. 在对一个含有80个数据的样本绘制统计表时，•发现其中一个小组的数据的个数占80的20%，那么这个小组含有________个数据．4. 已知七年级一班共有60人，分成四个组，•各组人数在频数分布直方图中的小长方形高的比依次为1：2：5：4，则人数最多的一组有_______人．5. 为了了解某所初级中学学生对2008年6月1日起实施的“限塑令”是否知道，从该校全体学生1200名中，随机抽查了80名学生，结果显示有2名学生“不知道”．由此，估计该校全体学生中对“限塑令”约有名学生“不知道”．6. 2008年春运期间，由于受冰雪天气影响，广州站滞留旅客近千万人，政府出于安全考虑，发出了“在当地过年的倡导”，2月1号车站广场上仍有滞留旅客近100万人，某工作小组在车站广场随机采访了100名滞留旅客，将数据经过整理后绘成如图4所示的统计图，请你根据统计图3中的信息估计出100万名旅客中决定回老家过节的有人.7. 九年级三班共有学生54人，学习委员调查了班级学生参加课外活动情况（每人只参加一项活动），其中：参加读书活动的18人，参加科技活动的占全班总人数的16，参加艺术活动的比参加科技活动的多3人，其他同学参加体育活动．则在扇形图中（如图4所示）表示参加体育活动人数的扇形的圆心角是度．8. 图5是根据某初中为地震灾区捐款的情况而制作的统计图，已知该校在校学生有2000人，请根据统计图计算该校共捐款元．三、考考你的基本功（本大题共28分）1.（本题8分）在数学、外部、语言3门学科中，某校一年级开展了同学们最喜欢学习哪门学科的调查（一年级共有200人）．（1）调查的问题是什么？（2）调查的对象是谁？（3）在被调查的200名学生中，有40人最喜欢学语文，60人最喜欢学数学，80•人最喜欢初三初二初一 32% 33%35%人数统计图3再决定图5读书体育科技艺术图4学外部，其余的人选择其他，求最喜欢学数学这门学科的学生占学生总数的比例；（4）根据调查情况，把一年级的学生最喜欢学习某学科的人数及其占学生总数的百分比填入下表：2.（本题10分）在城关中学开展的“我为四川地震灾区献爱心”捐书活动中，校团委为了了解九年级同学的捐书情况，用简单的随机抽样方法从九年级的10个班中抽取50名同学，对这50名同学所捐的书进行分类统计后，绘制了如下统计表：捐书情况统计表（1）在图（2）若九年级共有475名同学，请你估计九年级同学的捐书总册数及学辅类书的册数3.（本题10分）李明对某校九年级（2）班进行了一次社会实践活动调查，从调查的内容中抽出两项．调查一：对小聪、小亮两位同学的毕业成绩进行调查，其中毕业成绩按综合素质、考试成绩、体育测试三项进行计算，计算的方法按4:4:2进行，毕业成绩达80分以上（含80分）为“优图7优秀3人学类图6 捐书情况频数分布直方图普类辅类育类它种类调查二：对九年级（2）班50名同学某项跑步成绩进行调查，并绘制了一个不完整的扇形统计图，如图7所示．请你根据以上提供的信息，解答下列问题：（1）小聪和小亮谁能达到“优秀毕业生”水平？哪位同学的毕业成绩更好些？（2）升入高中后，请你对他俩今后的发展给每人提一条建议．（3）扇形统计图中“优秀率”是多少？（4）“不及格”在扇形统计图中所占的圆心角是多少度？四、同步大闯关（本大题共24分）1.（本题12分）今年6月奥运圣火将在历史名城遵义传递．为迎接奥运圣火的到来，我市某中学积极组织学生开展体育活动，为此，该校抽取若干名学生对“你最喜欢的球类运动项目是什么？”进行问卷调查．整理收集到的数据绘制成如下统计图（图8，图9）．根据统计图8，图9提供的信息，解答下列问题：（1）参加问卷调查的学生有名；（2）将统计图8中“足球”部分补充完整；（3）在统计图9中，“乒乓球”部分扇形所对应的圆心角是度；（4）若全校共有2000名学生，估计全校喜欢“篮球”的学生有名．图8 15% 图92.（本题12分）某中学团委举行了一次以“弘扬民族精神，做社会有用人才”为主题的演讲比赛，分段统计参赛同学的成绩，结果如下表：（分数均为整数，满分为100分）请根据表中提供的信息，解答下列各题：（1）参加这次演讲比赛的同学有人；（2）已知成绩在91～100分的同学为优胜者，那么优胜率为；（3）将图10的成绩频数分布直方图补充完整；（4）画出频数折线图，分析数据分布情况．下列各题供各地根据实际情况选用1. 2007年4月，国民体质监测中心等机构开展了青少年形体测评.专家组随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对专家的测评数据做了适当处理(如果一个学生有一种以上不良姿势，我们以他最突出的一种作记录)，并将统计结果绘制了如下两幅不完整的统计图如图11所示，请你根据图中所给信息解答下列问题：（1）请将两幅统计图补充完整；（2）在这次形体测评中，一共抽查了名学生，如果全市有10万名初中生，那么全市初中生中，三姿良好的学生约有人；（3）根据统计结果，请你简单谈谈自己的看法.25 50 75 100125150175200图11成绩（分）图102.小明调查了他们班50名同学各自家庭的人均日用水量（单位：升），结果如下：55 42 50 48 42 35 38 39 40 51 47 52 50 42 43 47 52 •48 54 52 38 42 60 52 41 46 35 47 53 48 52 47 50 49 57 •43 40 44 52 50 49 37 46 42 62 58 46 48 39 60请根据以上数据绘制频数分布表和频数分布直方图，并回答下列问题：（1）家庭人均日用水量在哪个范围的家庭最多？•这个范围的家庭占全班家庭的百分之几？（2）家庭人均日用水量最少和最多的家庭各占全班家庭的百分几之？（3）如果每人每天节约用水8升，按全班50人计算，一年（按365•天计算）可节约用水多少吨？按生活基本日均需水量50升的标准计算，这些水可供1•个人多长时间的生活用水？参考答案一、慧眼识金1.A.2.C.3. D.4. C.5. B.6.A.7.C.8.B.二、画龙点睛1.20 .2. 9 .3.16.4.25.5.30 .6.50万.7.100 . 8. 25180．三、考考你的基本功1. （1）在数学、外部、语文3门学科中，你最喜欢学习哪一门学科？（2）某校一年级的全体同学．（3）30%．（4）如下表．2. （1）如图：（2）50名同学捐书平均数为5605011.2÷=，47511.25320∴⨯=，14053201330560⨯=，即可估计九年级同学的捐书为5320册，学辅类书1330册．3. （1）小聪成绩是：7240%9840%6020%80⨯+⨯+⨯=（分）小亮成绩是：9040%7540%9520%85⨯+⨯+⨯=（分）∴小聪、小亮成绩都达到了“优秀毕业生”水平．小亮毕业生成绩好些．（2）小聪要加强体育锻炼，注意培养综合素质．小亮在学习文化知识方面还要努力，成绩有待进一步提高．（3）优秀率是：3100%6%50⨯=．（4）“不及格”在扇形统计图中所占的圆心角是：360(16%18%36%)144⨯---=．四、同步大闯关1. （1）30÷15%×100%＝200（人）（2）足球人数为200－80－30－50＝40（人），补充完整即可（3）80÷200×360＝1440(4) 2000×（50÷200）＝500（人） 2. ⑴ 20 ；⑵ 4÷20＝20％；文学类捐书情况频数分布直方图科普类学辅类体育类其它种类⑶图略；⑷折线图如图所示；从图表中可看出71～80分的最多，占40%；81～90分次之，占30%．选用题目参考答案1. （1）补充图略；（2）500，12000；（3）答案不唯一，要点：中学生应该坚持锻炼身体，努力纠正坐姿、站姿、走姿中的不良习惯，促进身心健康发育.2. 这组数据中最大值是62，最小值是35，它们的差是27．若取组距为4，由于27÷4≈7，因此要将整个数据分为7组，用x（升）表示人均日用水量，则所分的组为35≤x<39，39≤x<43，43≤x<47，…，59≤x<63．整理可得下列频数分布表：用横轴表示人均日用水量，等距离标出各组的端点35、39、43、……、63，用纵轴表示频数，等距离标出3、6、9、12、15等，•以各组的频数为高画出与这一组对应的长方形，得到频数分布直方图（如图）根据频数分布表和频数分布直方图可以得到：（1）家庭人均日用水量在不小于47升而小于51升的范围内的家庭最多，•这个范围内的家庭共有14家，占全班家庭的20%．（2）家庭人均日用水量最少和最多的家庭分别占全班家庭的10%和6%．（3）一天可节约用水：8×50×365÷1000=146（吨）按生活基本日均需水量50升的标准计算，这些水可供1个人生活：146×1000÷50÷365=8（年）．备用试题1.某中学为了解毕业年级800名学生每学期参加社会实践活动的时间，随机对该年级60名学生每学期参加社会实践活动的时间（单位：天）进行了统计（统计数据取整数），整理后分成5组，绘制成频数分布表和频数分布直方图（部分）如图3．（1）补全频数分布表和频数分布直方图；（2）请你估算这所学校该年级的学生中，每学期参加社会实践活动的时间大于7天的约有多少人？（1）频数分布表中自上而下应填20，16；（2）800×4360≈573. 答：这所学校该年级的学生中，每学期参加社会实践活动的时间大于7天的约有573人. 2.一游泳馆对一年的门票收入进行统计，结果如下表.请根据上表，回答下列问题：（1）计算一年中各个季度的收入情况，并用适当的统计图表示；（2）计算一年中各个季度的收入在全年收入中所占的百分比，并用适当的统计图表示；（3）一年中各季度收入的变化情况如何？并用适当的统计图表示；（4）如果你是管理员，你能从以上的统计图表中获得哪些信息？•它对你的决策有何影响？（1）一年中各个季度的收入如下：第一季度：1000+1200+1600=3800（元）；第二季度：3000+4200+6000=13200（元）；第三季度：27000+30000+20000=77000（元）；第四季度：9000+2000+1000=12000（元）．用条形图表示如图所示．图3（2）一年中各季度在全年收入的百分比计算如下：全年收入是3800+13200+77000+12000=106000（元）．第一季度占：3800÷106000≈3.6%；第二季度占：13200÷106000≈12.．5%；第三季度占：77000÷106000≈72.6%；第四季度占：12000÷106000≈11.3%．用扇形图表示如图所示．（3）一年中各季度收入的变化情况如图所示．从图中可知，第一.二季度逐月上升，第三季度收入最高，且8月收入最高，•第四季度则逐月降低．（4）从图上可以看出，第三季度收入最多，第一季度收入最少，在安排工作时要注意季节性安排．。

沪科版初中九年级下册数学第26章概率初步 26.3 用频率估计概率 2

26.3 用频率估计概率练习沪科版数学九年级下册一、单选题1．王师傅对某批零件的质量进行了随机抽查，并将抽查结果绘制成如下表格，请你根据表格估计，若从该批零件中任取一个，为合格零件的概率为（）A．0.9 B．0.8 C．0.5 D．0.1 2．某人在做抛掷硬币试验中，抛掷n次，正面朝上有m次，若正面朝上的频率是P m，则下列说法正确的是( )nA．P一定等于0.5 B．多投一次，P更接近0.5 C．P一定不等于0.5 D．投掷次数逐渐增加，P稳定在0.5附近3．不透明的袋子中装有10个黑球和若干个白球，这些球除颜色外无其他差别．从袋子中随机摸出一球记下其颜色，再把它放回袋子中摇匀，重复上述过程，共试验400次，其中有300次摸到白球，由此估计袋子中的白球大约有( )A．6个B．10个C．15个D．30个4．数学社团的同学做了估算π的实验．方法如下：第一步：请全校同学随意写出两个实数x、y（x、y可以相等），且它们满足：0＜x ＜1，0＜y ＜1；第二步：统计收集上来的有效数据，设“以x ，y ，1为三条边长能构成锐角三角形”为事件A ；第三步：计算事件A 发生的概率，及收集的本校有效数据中事件A 出现的频率；第四步：估算出π的值．为了计算事件A 的概率，同学们通过查阅资料得到以下两条信息： ①如果一次试验中，结果落在区域D 中每一个点都是等可能的，用A 表示“试验结果落在区域D 中一个小区域M 中”这个事件，那么事件A 发生的概率为P(A)＝MD ；②若x ，y ，1三个数据能构成锐角三角形，则需满足份数据中能和“1”成锐角三角形的数据有n 份，则可以估计π的值为（）A ．42n m m +B ．2n mC ．4nmD ．44m nm- 5．在不透明的袋子中有黑棋子10枚和白棋子若干（它们除颜色外都相同），现随机从中摸出10枚记下颜色后放回，这样连续做了10次，记录了如下的数据：根据以上数据，估算袋中的白棋子数量为（）A．60枚B．50枚C．40枚D．30枚6．在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外其他完全相同，小明通过多次摸球试验后发现其中摸到红色球、黑色球的频率稳定在0.15和0.45，则布袋中白色球的个数可能是（）A．24 B．18 C．16 D．67．小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表，若抛掷硬币的次数为1000，则“正面朝上”的频数最接近（）A．200 B．300 C．500 D．800 8．“十一”长假期间，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动，顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据：下列说法错误的是（）A．转动转盘20次，一定有6次获得“文具盒”铅笔文具盒B．转动转盘一次，获得“铅笔”的概率大约是0.70C．再转动转盘100次，指针落在“铅笔”区域的次数不一定是68次D．如果转动转盘3000次，指针落在“文具盒”区域的次数大约有900次9．一个不透明的袋子中装有除颜色外均相同的4个白球和若干个绿球，每次摇均匀后随机摸出一个球，记下颜色后再放回袋中，经大量试验，发现摸到绿球的频率稳定在0.2，则摸到绿球的概率约为（）A．0.2 B．0.5 C．0.6 D．0.8 10．在一个不透明的袋子里装有红球、黄球共40个，这些球除颜色外都相同，小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中黄球的个数最有可能是（）A．10 B．15 C．20 D．30二、填空题11．某射手在相同条件下进行射击训练，当射击次数很大时，该射手击中靶心的频率在常数0.9附近摆动，则在这种条件下，该射手射击一次击中靶心的概率的估计值是________．12．某林业部门统计某种幼树在一定条件下的移植成活率，结果如下表所示：根据表中数据，估计这种幼树移植成活率的概率为___（精确到0.1）．13．社团课上，同学们进行了“摸球游戏”：在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球，将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程．整理数据后，制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示，经分析可以推断盒子里个数比较多的是___________（填“黑球”或“白球”）．14．如图是康康的健康绿码示意图，用黑白打印机打印于边长为10cm的正方形区域内，为了估计图中黑色部分的总面积，在正方形区域内随机掷点，经过大量重复试验，发现点落入黑色部分的频率稳定在0.65左右，据此可以估计黑色部分的总面积约为___cm2．三、解答题15．某水果公司新进一批柑橘，销售人员首先从所有的柑橘中随机抽取若干柑橘，进行“柑橘损坏率”统计，并把获得的数据记录在下表中．(1)柑橘损坏的概率约为______（精确到0.1）；(2)当抽取柑橘的总质量n＝kg时，损坏柑橘质量m最有可能是______．A．99.32kg B．203.45kg C．486.76kg D．894.82kg(3)若水果公司新进柑橘的总质量为10000kg，成本价是1.8元/kg，公司希望这些柑橘能够获得利润5400元，那么在出售柑橘（去掉损坏的柑橘）时，每千克大约定价为多少元比较合适？16．某种油菜籽在相同条件下的发芽试验的结果如下：(1)上表中a＝，b＝；(2)请估计，当n很大时，频率将会接近；(3)这种油菜籽发芽的概率的估计值是多少？请简要说明理由；(4)如果该种油菜籽发芽后的成秧率为90%，则在相同条件下用10000粒该种油菜籽估计可得到油菜秧苗多少棵？17．在一个不透明的袋子中装有红、黄两种颜色的球共20个，每个球除颜色外完全相同．某学习兴趣小组做摸球试验，将球搅匀后从中随机摸出1个球，记下颜色后再放回袋中，不断重复．下表是活动进行中的部分统计数据．(1)完成上表；(2)“摸到红球”的概率的估计值．（精确到0.1）(3)试估算袋子中红球的个数．18．对某篮球运动员进行3分球投篮测试的结果如下表：(1)将表格补充完整；(2)这个运动员投篮命中的概率约是______；(3)估计这个运动员3分球投篮15次能得多少分．参考答案：1．A2．D3．D4．D5．C6．A7．C8．A9．A10．D11．0.912．0.913．白球14．6515．(1)0.1(2)B(3)2.6元16．(1)0.70；0.70(2)0.70(3)0.70，在相同条件下，当实验次数很大时，事件发生的频率可作为概率的近似值(4)630017．(1)0.64，0.58(2)0.6(3)1218．(1)0.6，0.6；(2)0.6(3)27分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2009-2010学年九年级下同步测试期中测试(26～27章)
（时间90分钟满分100分）
班级学号姓名得分
一、选择题（共8小题，每题3分，共24分）
1．在相同时刻的物高与影长成比例，如果高为1.5米的测竿的影长为2.5米，
那么影长为30米的旗杆的高是（）
A ．20米 .
B ．18米
C ．16米
D ．15米
2．如图，AB ∥CD ，AC 、BD 交于O ，BO =7，DO =3，AC =25，则AO 长为（）
A ．10
B ．12．5
C ．15
D ．17．5
3．顺次连接三角形三边的中点，所构成的三角形与原三角形对应高的比是（）
A ．1:4
B ．1:3
C ．1:2
D ．1:2
4．如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是（）
5．已知抛物线21y x x =--与x 轴的一个交点为(0)m ，，则代数式22009m m -+的
值为（） A ．2007
B ．2008
C ．2009
D ．2010
6．根据下列表格中的二次函数y =ax 2+bx +c (a ≠0，a 、b 、c 为常数)的自变量x 与函数y 的对
应值，判断ax 2+bx +c =0的一个解x 的取值范围。

A ．1.40＜x ＜1.43
B ．1.43＜
x ＜1.44 C ．1.44
＜
x ＜1.45 D ．1.45＜x ＜1.46
7．如图，□ABCD 中，E 为AD 的中点．已知△DEF 的面积为
第2题
A ．S
B ．2S
C ．3S
D ．4S
8．如图，在△ABC 中，m 是AC 边中点，E 是AB 上一点，且AE ＝4
1AB ，
连结Em 并延长，交BC 的延长线于D ，此时BC ︰CD 为（） A ．2︰1 B ．3︰2 C ．3︰1 D ．5︰2 二、填空题（共10小题，每题2分，共20分）
9．已知二次函数的图象开口向上，且顶点在y 轴的负半轴上，请你写
出一个满足条件的二次函数表达式：。

10．函数=y =
2
1(x -1)2
+3，当x 时，函数值y 随x 的增大而增大。

11．抛物线y =ax 2+x +2经过点（-1，0），则a = 。

12．如图，△AED ∽△ABC ，其中∠1＝∠B ，则AD ∶______＝______∶BC ＝_____∶AB ．
13．如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则图中与△ABC 相似的三角
形共有________个，它们是_______________．
14．二次函数y =x 2+x -6的图象与y 轴的交点坐标是，与x 轴交点的坐标
是。

15．抛物线y =9x 2-Px +4与x 轴只有一个公共点，则P 的值是。

16．在直角坐标系中，已知A （－3，0）、B （0，－4）、C （0，1），过C 点作直线l 交x 轴
于D ，使得以点D 、C 、O 为顶点的三角形与△A O B 相似，这样的直线有条。

17．如图，在△ABC 中，∠C ＝900
，AC ＝8，CB ＝6，在斜边AB 上取一点m ，使mB ＝CB ，
过m 作mn ⊥AB 交AC 于n ，则mn ＝。

第12题第13题
第8题
18．如图，在锐角△ABC 中，BD ⊥AC ，DE ⊥BC ，AB ＝14，AD ＝4，BE ∶EC ＝5∶1，则CD
＝。

三、解答题（共10题，共56分）
19．（4分）已知二次函数的图象经过点A （0，-3），且顶点P 的坐标为（1，-4），
（1）求这个函数的关系式；
（2）在平面直角坐标系中，画出它的图象。

20．（4分）用配方法把函数y =-3x 2-6x +10化成y =a (x -h)2+k 的形式，然后指出它的图象开口
方向，对称轴，顶点坐标和最值。

第17题
N
M
C
B
A
第5题图 E
D
C
B
A
第18题
21．（4分）已知线段DE 分别交△ABC 的边AB 、AC 于D 、E ，且
2
3===DE
BC AE
AC AD
AB ，
△ABC 的周长是6cm ，面积是22cm ，求△ADE 的周长和面积。

22．（6分）如图，在平行四边形ABCD 中，E 是DC 上的一点，AE 的延长线交BC 于F ，
求证：ED AF AE AB ∙=∙ A
B
C
D
E A
B
C
D
E
F
23．（6分）如图，矩形的长是4cm，宽是3cm，如果将长和宽都增加xcm，那么面积增加ycm2，
（2）求当边长增加多少时，面积增加8cm2。

24．（6分）已知点A（－2，－c）向右平移8个单位得到点A'，A与A'两点均在抛物线
2
=++上，且这条抛物线与y轴的交点的纵坐标为－6，求这条抛物线的顶点坐y ax bx c
标．
25．（6分）如图，AC ⊥BC ，CD ⊥AB ，BC ⊥DE ，若AC =6cm ，DE = 4cm ，求CD 之长；
26．（6分）E 为正方形 ABCD 的边上的中点，AB = 1 ，mn ⊥DE 交 AB 于 m ，交 DC 的
延长线于 n ，求证：⑴ EC 2= DC ·Cn ； ⑵ Cn = 4
1； ⑶ nE =
4
5；
A B
C
D
E A
B
C
D
E
M
N
27．（6分）枇杷是莆田名果之一，某果园有100棵枇杷树．每棵平均产量为40千克，现准备多种一些枇杷树以提高产量，但是如果多种树，那么树与树之间的距离和每一棵数接受的阳光就会减少，根据实践经验，每多种一棵树，投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克，问：增种多少棵枇杷树，投产后可以使果园枇杷的总产量最多？最多总产量是多少千克？
注：抛物线2
y ax bx c
=++的顶点坐标是
2
4
(,) 24
b a
c b
a a
-
-
28．（8分）已知：如图，Rt△A O B的两直角边O A、O B分别在x轴的正半轴和y轴的负半轴上，C为O A上一点且O C＝O B，抛物线y=(x－2)(x－m)－(P-2)(P-m)（m、P为常数且m+2≥2P>0）经过A、C两点．
（1）用m、P分别表示O A、O C的长；
（2）当m、P满足什么关系时，△A O B的面积最大．
期中测试
一、选择题
1．B 2．D 3．C 4．A5．D 6．C 7．B 8．A
二、填空题
9．如y=x2-2 10．＞1 11．-1 12．AC，ED，AE 13．4，△ADF、△DBE、△FEC、△EFD14．(0, -6)；(-3, 0)，(2, 0) 15．±12 16．4条27．3，5 18．6
三、解答题
19．（1）y=x2-2x-3；（2）图略20．y=-3(x+1)2+13，开口向下，对称轴x=-1，顶点坐标（-1，
13），最大值13 21．8
cm
3
，2
8
cm
9
22．略23．（1）y=x2+7x；（2）1cm 24．（2，－
10）25．26．略27．30，4225 28．（1）2,
OA m p OC p
=+-=；（2）1
(2) 2
p m =+。