1.5《三角函数的应用》同步练习(含答案)
北师大版九年级数学下册 1.5 三角函数的应用 同步测试题(有答案)

故答案为.
14.
【答案】
【解答】
解:∵,,米,
∴,
∴,,
∴,
∴,
∴米∴学校要购买米的草皮才能正好铺满空地.
故答案为:.
15.
【答案】
【解答】
解:由于山路的坡角为度,则坡角的正弦值,
∴他在竖直方向上上升的高度(米).
16.
【答案】
【解答】
解:在中,(米).
17.
【答案】
【解答】
解:由已知得,
则斜坡的坡度.
故选.
10.
【答案】
A
【解答】
故选:.
二、
11.
【答案】
【解答】
解:在中
,
∴.
故答案为:.
12.
【答案】
海里/分
【解答】
解:作,
∵,,
∴海里,则海里,
在中,,
则,
解得,
在中,海里,
海里/分.
故答案为:海里/分.
13.
【答案】
【解答】
解:如图,在直角中,,,,
∴,.
在直角中,,,,
∴,
∴,
(参考数据:,,,.)
26.某区域平面示意图如图,点在河的一侧,和表示两条互相垂直的公路.甲勘测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,.请求出点到的距离.
参考数据:,,
参考答案
一、
1.
【答案】
B
【解答】
解:如图,
由已知得:,,米.
∵,
∴ (米).
故选.
2.
【答案】
D
【解答】
解:根据题意得:,
25.某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端、间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点的一点,并测得=米,点位于点的北偏西方向,点位于点的北偏东方向.
专题1-5三角函数的应用-方向角问题-(解析版)
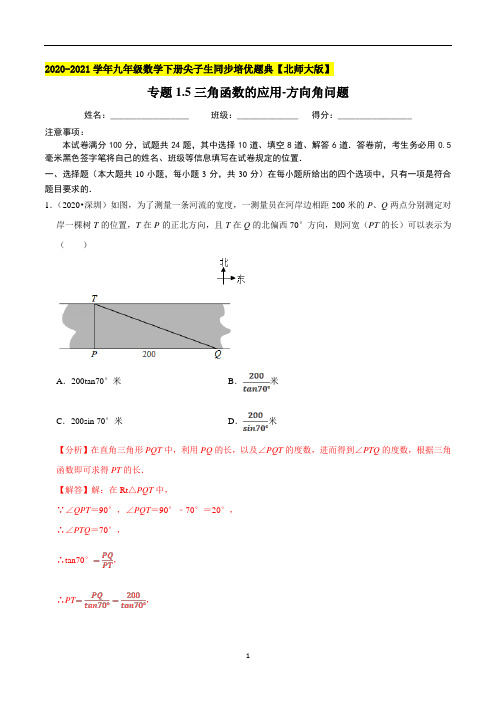
2020-2021学年九年级数学下册尖子生同步培优题典【北师大版】专题1.5三角函数的应用-方向角问题姓名:__________________ 班级:______________ 得分:_________________注意事项:本试卷满分100分,试题共24题,其中选择10道、填空8道、解答6道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2020•深圳)如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为()A.200tan70°米B.米C.200sin 70°米D.米【分析】在直角三角形PQT中,利用PQ的长,以及∠PQT的度数,进而得到∠PTQ的度数,根据三角函数即可求得PT的长.【解答】解:在Rt△PQT中,∵∠QPT=90°,∠PQT=90°﹣70°=20°,∴∠PTQ=70°,∴tan70°,∴PT,即河宽米,故选:B.2.(2020•济宁)一条船从海岛A出发,以15海里/时的速度向正北航行,2小时后到达海岛B处.灯塔C 在海岛A的北偏西42°方向上,在海岛B的北偏西84°方向上.则海岛B到灯塔C的距离是()A.15海里B.20海里C.30海里D.60海里【分析】根据题意画出图形,根据三角形外角性质求出∠C=∠CAB=42°,根据等角对等边得出BC=AB,求出AB即可.【解答】解:如图.根据题意得:∠CBD=84°,∠CAB=42°,∴∠C=∠CBD﹣∠CAB=42°=∠CAB,∴BC=AB,∵AB=15×2=30(海里),∴BC=30(海里),即海岛B到灯塔C的距离是30海里.故选:C.3.(2019•济南)某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为()(参考数据:tan37°,tan53°)A.225m B.275m C.300m D.315m【分析】如图,作CE⊥BA于E.设EC=xm,BE=ym.构建方程组求出x,y即可解决问题.【解答】解:如图,作CE⊥BA于E.设EC=xm,BE=ym.在Rt△ECB中,tan53°,即,在Rt△AEC中,tan37°,即,解得x=180,y=135,∴AC300(m),故选:C.4.(2020•岱岳区一模)如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间时轮船离灯塔最近?()A.1小时B.小时C.2小时D.小时【分析】过B作AC的垂线,设垂足为D.由题易知:∠DAB=30°,∠DCB=60°,则∠CBD=∠CBA =30°,得AC=BC.由此可在Rt△CBD中,根据BC(即AC)的长求出CD的长,进而可求出该船需要继续航行的时间.【解答】解:作BD⊥AC于D,如下图所示:易知:∠DAB=30°,∠DCB=60°,则∠CBD=∠CBA=30°.∴AC=BC,∵轮船以40海里/时的速度在海面上航行,∴AC=BC=2×40=80海里,∴CD BC=40海里.故该船需要继续航行的时间为40÷40=1小时.故选:A.5.(2020•开平区一模)如图,甲、乙两船同时从港口O出发,其中甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,已知两船的航行速度相同,如果1小时后甲、乙两船分别到达点A、B处,那么点B位于点A的()A.南偏西40°B.南偏西30°C.南偏西20°D.南偏西10°【分析】由甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,得出∠BOA的度数,由两船的航行速度相同,得出AO=BO,得出∠BAO=50°,以及求出∠BAD的度数,得出点B位于点A的方向.【解答】解:∵甲船沿北偏西30°方向航行,乙船沿南偏西70°方向航行,两船的航行速度相同,∴AO=BO,∠BOA=80°,∠OAD=30°∴∠BAO=∠ABO=50°,∴∠BAD=∠BAO﹣∠OAD=50°﹣30°=20°,∴点B位于点A的南偏西20°的方向上,故选:C.6.(2019•泰安)如图,一艘船由A港沿北偏东65°方向航行30km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为()km.A.30+30B.30+10C.10+30D.30【分析】根据题意得,∠CAB=65°﹣20°,∠ACB=40°+20°=60°,AB=30,过B作BE⊥AC 于E,解直角三角形即可得到结论.【解答】解:根据题意得,∠CAB=65°﹣20°=45°,∠ACB=40°+20°=60°,AB=30,过B作BE⊥AC于E,∴∠AEB=∠CEB=90°,在Rt△ABE中,∵∠ABE=45°,AB=30,∴AE=BE AB=30km,在Rt△CBE中,∵∠ACB=60°,∴CE BE=10km,∴AC=AE+CE=30+10,∴A,C两港之间的距离为(30+10)km,故选:B.7.(2019秋•乐亭县期中)如图,一艘油轮在海中航行,在A点看到小岛B在A的北偏东25°方向距离60海里处,油轮沿北偏东70°方向航行到C处,看到小岛B在C的北偏西50°方向,则油轮从A航行到C处的距离是()海里.(结果保留整数)(参考数据: 1.41, 1.74, 2.45)A.66.8 B.67 C.115.8 D.116【分析】过B作BD⊥AC于D,求出∠BAC和∠BCA,解直角三角形求出AD、BD、CD,即可求出答案.【解答】解:过B作BD⊥AC于D,则∠BDA=∠BDC=90°,由题意知:∠BAC=70°﹣25°=45°,∵AM∥CN,∴∠MAC+∠NCA=180°,∴∠NCA=180°﹣70°=110°,∴∠BCA=110°﹣50°=60°,∵AB=60海里,∠BAD=45°,∴AD=AB×cos45°=30海里,BD=AD=30海里,CD10海里,301030×1.41+10×2.45≈67∴AC=AD+CD=67海里,故选:B.8.(2019•咸安区一模)如图,某轮船在点O处测得一个小岛上的电视塔A在北偏西60°的方向,船向西航行20海里到达B处,测得电视塔A在船的西北方向,若要轮船离电视塔最近,则还需向西航行()A.海里B.海里C.海里D.海里【分析】作AC⊥OB于C点,根据题目提供的方向角,并从图中整理出直角三角形的模型,利用解直角三角形的知识求得BC的长即可.【解答】解:作AC⊥OB于C点,只要到C处,轮船离电视塔最近,求出BC长即可,由已知得:∠AOB=30°,∠ABC=45°、OB=20海里,∴BC=AC,CO=AC÷tan∠AOB=AC÷tan30°,∵CO﹣CB AC=20,解得:AC海里,∴BC=AC=10(1)海里,故选:A.9.(2019•张家口二模)如图,小明为了测量河宽AB,先在BA延长线上取一点D,再在同岸取一点C,测得∠CAD=60°,∠BCA=30°,AC=15m,那么河AB宽为()A.15m B.m C.m D.m【分析】先过C作CE⊥AB,在Rt△ACE中,根据∠CAD=60°,AC=15m可得出∠ACE的度数及AE、CE的长,再根据∠BCA=30°可求出∠BCE的度数,由锐角三角函数的定义即可得出BE的长,进而可求出AB的长.【解答】解:过C作CE⊥AB,Rt△ACE中,∵∠CAD=60°,AC=15m,∴∠ACE=30°,AE AC15=7.5m,CE=AC•cos30°=15,∵∠BAC=30°,∠ACE=30°,∴∠BCE=60°,∴BE=CE•tan60°22.5m,∴AB=BE﹣AE=22.5﹣7.5=15m.补充方法:∵∠CAD=60°,∠BCA=30°,∴∠CBA=∠CAD﹣∠BCA=30°,∴AB=AC=15m.故选:A.10.(2018•苏州)如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为()A.40海里B.60海里C.20海里D.40海里【分析】首先证明PB=BC,推出∠C=30°,可得PC=2P A,求出P A即可解决问题;【解答】解:在Rt△P AB中,∵∠APB=30°,∴PB=2AB,由题意BC=2AB,∴PB=BC,∴∠C=∠CPB,∵∠ABP=∠C+∠CPB=60°,∴∠C=30°,∴PC=2P A,∵P A=AB•tan60°,∴PC=2×2040(海里),故选:D.二、填空题(本大题共8小题,每小题3分,共24分)请把答案直接填写在横线上11.(2020•邹城市一模)如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我航海区域的C处截获可疑渔船,问我渔政船的航行路程是18海里(结果保留根号).【分析】作CD⊥AB于点D,垂足为D,首先在Rt△BCD中求得CD的长,然后在Rt△ACD中求得AC 的长即可.【解答】解:作CD⊥AB于点D,垂足为D,在Rt△BCD中,∵BC=12×1.5=18(海里),∠CBD=45°,∴CD=BC•sin45°=189(海里),则在Rt△ACD中,AC92=18(海里).故我渔政船航行了18海里.故答案为:18.12.(2019•荆州)如图,灯塔A在测绘船的正北方向,灯塔B在测绘船的东北方向,测绘船向正东方向航行20海里后,恰好在灯塔B的正南方向,此时测得灯塔A在测绘船北偏西63.5°的方向上,则灯塔A,B间的距离为22海里(结果保留整数).(参考数据sin26.5°≈0.45,cos26.5°≈0.90,tan26.5°≈0.50,2.24)【分析】根据题意得MN=20,∠ANB=63.5°,∠BMN=45°,∠AMN=∠BNM=90°,于是得到BN =MN=20,如图,过A作AE⊥BN于E,得到四边形AMNE是矩形,根据矩形的性质得到AE=MN=20,EN=AM,解直角三角形即可得到结论.【解答】解:由题意得,MN=20,∠ANB=63.5°,∠BMN=45°,∠AMN=∠BNM=90°,∴BN=MN=20,如图,过A作AE⊥BN于E,则四边形AMNE是矩形,∴AE=MN=20,EN=AM,∵AM=MN•tan26.5°=20×0.50=10,∴BE=20﹣10=10,∴AB1022海里.故答案为:22.13.(2019•宁波)如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为566米.(精确到1米,参考数据: 1.414, 1.732)【分析】通过解直角△OAC求得OC的长度,然后通过解直角△OBC求得OB的长度即可.【解答】解:如图,设线段AB交y轴于C,在直角△OAC中,∠ACO=∠CAO=45°,则AC=OC.∵OA=400米,∴OC=OA•cos45°=400200(米).∵在直角△OBC中,∠COB=60°,OC=200米,∴OB400566(米)故答案是:566.14.(2019•新宾县四模)如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2)km.【分析】根据题意在CD上取一点E,使BD=DE,进而得出EC=BE=2km,再利用勾股定理得出DE 的长,即可得出答案.【解答】解:在CD上取一点E,使BD=DE,∵CD⊥AB,∴∠EBD=45°,AD=DC,∵AB=AD﹣BD,CE=CD﹣DE,∴CE=AB=2km,∵从B测得船C在北偏东22.5°的方向,∴∠BCE=∠CBE=22.5°,∴BE=EC=2km,∴BD=ED km,∴CD=2(km).故答案为:(2)km.15.(2019秋•德州期中)某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=7海里.【分析】过P作AB的垂线PD,在直角△BPD中可以求的∠P AD的度数是30度,即可证明△APB是等腰三角形,即可求解.【解答】解:过P作PD⊥AB于点D.∵∠PBD=90°﹣60°=30°且∠PBD=∠P AB+∠APB,∠P AB=90﹣75=15°∴∠P AB=∠APB∴BP=AB=7(海里)故答案是:7.16.(2018•辽阳)如图,一艘轮船自西向东航行,航行到A处测得小岛C位于北偏东60°方向上,继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上,此时轮船与小岛C的距离为5海里.(结果保留根号)【分析】如图,作BH⊥AC于H.在Rt△ABH中,求出BH,再在Rt△BCH中,利用等腰直角三角形的性质求出BC即可.【解答】解:如图,作BH⊥AC于H.在Rt△ABH中,∵AB=10海里,∠BAH=30°,∴∠ABH=60°,BH AB=5(海里),在Rt△BCH中,∵∠CBH=∠C=45°,BH=5(海里),∴BH=CH=5海里,∴CB=5(海里).故答案为5.17.(2018•潍坊)如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行小时即可到达.(结果保留根号)【分析】如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,通过解直角△AQP、直角△BPQ求得PQ的长度,即MN的长度,然后通过解直角△BMN求得BM的长度,则易得所需时间.【解答】解:如图,过点P作PQ⊥AB交AB延长线于点Q,过点M作MN⊥AB交AB延长线于点N,在直角△AQP中,∠P AQ=45°,则AQ=PQ=60×1.5+BQ=90+BQ(海里),所以BQ=PQ﹣90.在直角△BPQ中,∠BPQ=30°,则BQ=PQ•tan30°PQ(海里),所以PQ﹣90PQ,所以PQ=45(3)(海里)所以MN=PQ=45(3)(海里)在直角△BMN中,∠MBN=30°,所以BM=2MN=90(3)(海里)所以(小时)故答案是:.18.(2018秋•顺义区期末)轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在观测灯塔A北偏东60°方向上,则C处与灯塔A的距离是25海里.【分析】根据题中所给信息,求出∠BCA=90°,再求出∠CBA=45°,从而得到△ABC为等腰直角三角形,然后根据解直角三角形的知识解答.【解答】解:根据题意,得∠1=∠2=30°,∵∠ACD=60°,∴∠ACB=30°+60°=90°,∴∠CBA=75°﹣30°=45°,∴△ABC为等腰直角三角形,∵BC=50×0.5=25,∴AC=BC=25(海里).故答案为:25.三、解答题(本大题共6小题,共46分.解答时应写出文字说明、证明过程或演算步骤)19.(2020•湘阴县一模)如图,台风中心位于点P,并沿东北方向PQ移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B市位于点P的北偏东75°方向上,距离点P点320千米处.(1)说明本次台风会影响B市;(2)求这次台风影响B市的时间.【分析】(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与200千米相比较即可.(2)以B为圆心,以200为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.【解答】(1)如图所示:∵台风中心位于点P,并沿东北方向PQ移动,B市位于点P的北偏东75°方向上,∴∠QPG=45°,∠NPB=75°,∠BPG=15°,∴∠BPQ=30°作BH⊥PQ于点H,在Rt△BHP中,由条件知,PB=320,得BH=320sin30°=160<200,∴本次台风会影响B市.(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.由(1)得BH=160,由条件得BP1=BP2=200,∴P1P2=2240,∴台风影响的时间t8(小时).20.(2020•枣阳市校级模拟)已知:如图,一艘渔船正在港口A的正东方向40海里的B处进行捕鱼作业,突然接到通知,要该船前往C岛运送一批物资到A港,已知C岛在A港的北偏东60°方向,且在B的北偏西45°方向.问该船从B处出发,以平均每小时20海里的速度行驶,需要多少时间才能把这批物资送到A港(精确到1小时)(该船在C岛停留半个小时)?.【分析】作CD⊥AB于D点.设CD=x海里,在直角△ACD中,利用x表示出AC,AD,同理表示出BD,BC,根据AB=40即可列出方程求得CD的长,则AC+CB即可求得,然后除以速度即可得到时间.【解答】解:作CD⊥AB于D点.设CD=x海里,在直角△ACD中,∠CAD=90°﹣60°=30°,则AC=2x,AD x,在直角△BCD中,∠CBD=45°,则BD=CD=x,BC CD x,∵AB=40,即AD+BD=40,∴x+x=40,解得:x=20(1),∴BC=20(1)=2020,AC=2x=40(1),则总路程是:202040(1)海里,则时间是:22≈2.45﹣1.41+2×1.73﹣2≈2.5(小时).∵该船在C岛停留半个小时,∴需要3小时能把这批物资送到A港.21.(2020•铁西区模拟)如图,海中有一小岛P,在距小岛P的海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?【分析】过P作PB⊥AM于B,则PC的长是A沿AM方向距离P点的最短距离,求出PC长和16比较即可,第二问设出航行方向,利用特殊角的三角函数值确定答案.【解答】解:过P作PB⊥AM于B,在Rt△APB中,∵∠P AB=30°,∴PB AP32=16海里,∵16<16,故轮船有触礁危险.为了安全,应改变航行方向,并且保证点P到航线的距离不小于暗礁的半径16海里,即这个距离至少为16海里,设安全航向为AC,作PD⊥AC于点D,由题意得,AP=32海里,PD=16海里,∵sin∠P AC,∴在Rt△P AD中,∠P AC=45°,∴∠BAC=∠P AC﹣∠P AB=45°﹣30°=15°.答:若轮船继续向正东方向航行,轮船有触礁危险.轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.22.(2020•潮南区模拟)如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.【分析】作CD⊥AB于点D,求出C到航线的最近的距离CD的长,与6海里比较大小即可.【解答】解:作CD⊥AB于点D,由题意可知,∠CAB=30°,∠CBD=60°,∴∠ACB=30°,在Rt△BCD中,∵∠BDC=90°,∠CBD=60°,∴∠BCD=30°,∴∠ACB=∠BCD.∴△CDB∽△ADC.∴∵AB=CB=8∴BD=4,AD=12.∴∴CD=4≈6.928>6.∴船继续向东航行无触礁危险.23.(2020春•呼兰区期中)如图,一艘轮船位于灯塔B的正西方向A处,且A处与灯塔B相距60海里,轮船沿东北方向匀速前行,到达位于灯塔B的北偏东15°方向上的C处.(1)求∠ACB的度数;(2)求灯塔B到C处的距离.(结果保留根号)【分析】(1)利用三角形内角和定理进行计算;(2)过点B作AC的垂线,垂足为D.在△BDC中利用三角函数即可求解.【解答】解:(1)在△ABC中,∠CAB=45°,∠CBA=90°+15°=105°.则∠ACB=180°﹣45°﹣105°=30°,即∠ACB=30°;(2)过点B作AC的垂线,垂足为D,依题意可得∠DAB=45°,∠DBA=45°,AB=60海里.在△BDC中,∠DBC=45°+15°=60°,∠BDC=90°,cos∠DBC cos60°.∴BC=60(海里).答:灯塔B到C处的距离是60海里.24.(2020•滨州模拟)在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN 的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5千米的C处.(1)该飞机航行的速度是多少千米/小时?(结果保留根号)(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.【分析】(1)先求出∠BAC=90°,然后利用勾股定理列式求解即可得到BC,再求解即可;(2)作CE⊥l于E,设直线BC交l于F,然后求出CE、AE,然后求出AF的长,再进行判断即可.【解答】解:(1)由题意,得∠BAC=90°,∴BC10,∴飞机航行的速度为:1060=600(km/h);(2)能;作CE⊥l于点E,设直线BC交l于点F.在Rt△ABC中,AC=5,BC=10,∴∠ABC=30°,即∠BCA=60°,又∵∠CAE=30°,∠ACE=∠FCE=60°,∴CE=AC•sin∠CAE,AE=AC•cos∠CAE.则AF=2AE=15(km),∴AN=AM+MN=14.5+1=15.5km,∵AM<AF<AN,∴飞机不改变航向继续航行,可以落在跑道MN之间.。
2022-2023学年北师大版九年级数学下册《1-5三角函数的应用》题型分类练习题(附答案)

2022-2023学年北师大版九年级数学下册《1.5三角函数的应用》题型分类练习题(附答案)一.测量计算物体高度问题1.如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上.(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.(2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:≈1.41,≈1.73)2.两栋居民楼之间的距离CD=30米,楼AC和BD均为10层,每层楼高3米.(1)上午某时刻,太阳光线GB与水平面的夹角为30°,此刻B楼的影子落在A楼的第几层?(2)当太阳光线与水平面的夹角为多少度时,B楼的影子刚好落在A楼的底部?3.如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).(1)求灯杆CD的高度;(2)求AB的长度(结果精确到0.1米).(参考数据:=1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)4.某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)5.一种可折叠的医疗器械放置在水平地面上,这种医疗器械的侧面结构如图实线所示,底座为△ABC,点B、C、D在同一条直线上,测得∠ACB=90°,∠ABC=60°,AB=32cm,∠BDE=75°,其中一段支撑杆CD=84cm,另一段支撑杆DE=70cm.求支撑杆上的点E到水平地面的距离EF是多少?(用四舍五入法对结果取整数,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,≈1.732)6.“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)7.第24届冬季奥林匹克运动会于今年2月4日至20日在北京举行,我国冬奥选手取得了9块金牌、4块银牌、2块铜牌,为祖国赢得了荣誉,激起了国人对冰雪运动的热情.某地模仿北京首钢大跳台建了一个滑雪大跳台(如图1),它由助滑坡道、弧形跳台、着陆坡、终点区四部分组成.图2是其示意图,已知:助滑坡道AF=50米,弧形跳台的跨度FG=7米,顶端E到BD的距离为40米,HG∥BC,∠AFH=40°,∠EFG=25°,∠ECB=36°.求此大跳台最高点A距地面BD的距离是多少米(结果保留整数).(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)8.如图,信号塔PQ座落在坡度i=1:2的山坡上,其正前方直立着一警示牌.当太阳光线与水平线成60°角时,测得信号塔PQ落在斜坡上的影子QN长为2米,落在警示牌上的影子MN长为3米,求信号塔PQ的高.(结果不取近似值)9.太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D、F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号).10.图1是太阳能热水器装置的示意图.利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角(θ)确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:如图2,AB⊥BC,垂足为点B,EA⊥AB,垂足为点A,CD∥AB,CD=10cm,DE=120cm,FG⊥DE,垂足为点G.(1)若∠θ=37°50′,则AB的长约为cm;(参考数据:sin37°50′≈0.61,cos37°50′≈0.79,tan37°50′≈0.78)(2)若FG=30cm,∠θ=60°,求CF的长.11.汛期即将来临,为保证市民的生命和财产安全,市政府决定对一段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡坡面从A至B共有30级阶梯,平均每级阶梯高30cm,斜坡AB的坡度i=1:1;加固后,坝顶宽度增加2米,斜坡EF的坡度i=1:,问工程完工后,共需土石多少立方米?(计算土石方时忽略阶梯,结果保留根号)12.如图1,水坝的横截面是梯形ABCD,∠ABC=37°,坝顶DC=3m,背水坡AD的坡度i(即tan∠DAB)为1:0.5,坝底AB=14m.(1)求坝高;(2)如图2,为了提高堤坝的防洪抗洪能力,防汛指挥部决定在背水坡将坝顶和坝底同时拓宽加固,使得AE=2DF,EF⊥BF,求DF的长.(参考数据:sin37°≈,cos37°≈,tan37°≈)二.实际问题数学抽象13.如图,有一个三角形的钢架ABC,∠A=30°,∠C=45°,AC=2(+1)m.请计算说明,工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门?14.日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.(1)求山坡EF的水平宽度FH;(2)欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C 处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?15.图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.(1)求点M到地面的距离;(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:≈1.73,结果精确到0.01米)16.如图是把一个装有货物的长方体形状的木箱沿着坡面装进汽车货厢的示意图.已知汽车货厢高度BG=2米,货厢底面距地面的高度BH=0.6米,坡面与地面的夹角∠BAH=α,木箱的长(FC)为2米,高(EF)和宽都是1.6米.通过计算判断:当sinα=,木箱底部顶点C与坡面底部点A重合时,木箱上部顶点E会不会触碰到汽车货厢顶部.三.三角函数的应用17.如图1是某中学教学楼的推拉门,已知门的宽度AD=2米,且两扇门的大小相同(即AB=CD),将左边的门ABB1A1绕门轴AA1向里面旋转35°,将右边的门CDD1C1绕门轴DD1向外面旋转45°,其示意图如图2,求此时B与C之间的距离(结果保留一位小数).(参考数据:sin35°≈0.6,cos35°≈0.8,≈1.4)18.2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,OA是垂直于工作台的移动基座,AB、BC为机械臂,OA=1m,AB=5m,BC=2m,∠ABC=143°.机械臂端点C到工作台的距离CD=6m.(1)求A、C两点之间的距离;(2)求OD长.(结果精确到0.1m,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈2.24)19.随着我国科学技术的不断发展,科学幻想变为现实.如图1是我国自主研发的某型号隐形战斗机模型,全动型后掠翼垂尾是这款战斗机亮点之一.图2是垂尾模型的轴切面,并通过垂尾模型的外围测得如下数据,BC=8,CD=2,∠D=135°,∠C=60°,且AB∥CD,求出垂尾模型ABCD的面积.(结果保留整数,参考数据:≈1.414,≈1.732)20.如图1为搭建在地面上的遮阳棚,图2、图3是遮阳棚支架的示意图.遮阳棚支架由相同的菱形和相同的等腰三角形构成,滑块E,H可分别沿等长的立柱AB,DC上下移动,AF=EF=FG=1m.(1)若移动滑块使AE=EF,求∠AFE的度数和棚宽BC的长.(2)当∠AFE由60°变为74°时,问棚宽BC是增加还是减少?增加或减少了多少?(结果精确到0.1m,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)21.小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2,已知AD=BE=10cm,CD=CE=5cm,AD⊥CD,BE⊥CE,∠DCE=40°.(1)连结DE,求线段DE的长.(2)求点A,B之间的距离.(结果精确到0.1cm.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)参考答案一.测量计算物体高度问题1.解:(1)如图2中,作BO⊥DE于O.∵∠OEA=∠BOE=∠BAE=90°,∴四边形ABOE是矩形,∴∠OBA=90°,∴∠DBO=150°﹣90°=60°,∴OD=BD•sin60°=20(cm),∴DE=OD+OE=OD+AB=20+5≈39.6(cm).(2)作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形,∵∠CBH=60°,∠CHB=90°,∴∠BCH=30°,∵∠BCD=165°,∴∠DCP=45°,∴CH=BC sin60°=10(cm),DP=CD sin45°=10(cm),∴DF=DP+PG+GF=DP+CH+AB=(10+10+5)(cm),∴下降高度:DE﹣DF=20+5﹣10﹣10﹣5=10﹣10≈3.2(cm).2.解:(1)延长BG,交AC于点F,过F作FH⊥BD于H,由图可知,FH=CD=30m,∵∠BFH=∠α=30°,在Rt△BFH中,BH=,FC=30﹣17.32=12.68,再用12.68÷3≈4.23,所以在四层的上面,即第五层,答:此刻B楼的影子落在A楼的第5层;(2)连接BC,∵BD=3×10=30=CD,∴∠BCD=45°,答:当太阳光线与水平面的夹角为45度时,B楼的影子刚好落在A楼的底部.3.解:(1)延长DC交AN于H.∵∠DBH=60°,∠DHB=90°,∴∠BDH=30°,∵∠CBH=30°,∴∠CBD=∠BDC=30°,∴BC=CD=10(米).(2)在Rt△BCH中,CH=BC=5米,BH=5≈8.65(米),∴DH=15(米),在Rt△ADH中,AH=≈=20(米),∴AB=AH﹣BH=20﹣8.65≈11.4(米).答:AB的长度约为11.4米.4.解:如图作CM∥AB交AD于M,MN⊥AB于N.由题意=,即=,CM=(米),在Rt△AMN中,∵∠ANM=90°,MN=BC=4,∠AMN=72°,∴tan72°=,∴AN≈12.32(米),∵MN∥BC,AB∥CM,∴四边形MNBC是平行四边形,∴BN=CM=(米),∴AB=AN+BN=12.32+1.5≈13.8(米).5.解:方法一:如图1,过点D作DM⊥EF于M,过点D作DN⊥BA交BA延长线于N,在Rt△ABC中,∠ABC=60°,AB=32(cm),∴BC=AB•cos60°=32×=16(cm),∵DC=84(cm),∴BD=DC+BC=84+16=100(cm),∵∠F=90°,∠DMF=90°,∴DM∥FN,∴∠MDB=∠ABC=60°,在Rt△BDN中,sin∠DBN=sin60°=,∴DN=×100=50(cm),∵∠F=90°,∠N=90°,∠DMF=90°,∴四边形MFND是矩形,∴DN=MF=50,∵∠BDE=75°,∠MDB=60°,∴∠EDM=∠BDE﹣∠MDB=75°﹣60°=15°,∵DE=70(cm),∴ME=DE•sin∠EDM=70×sin15°≈18.2(cm),∴EF=ME+MF=50+18.2≈104.8≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.方法二:如图2,过点D作DH⊥BA交BA延长线于H,过点E作EG⊥HD延长线于G,在Rt△ABC中,∠ABC=60°,AB=32(cm),∴BC=AB•cos60°=32×=16(cm),∵DC=84(cm),∴BD=DC+BC=84+16=100(cm),同方法一得,DH=BD•sin60°=50(cm),∵在Rt△BDH中,∠DBH=60°,∴∠BDH=30°,∵∠BDE=75°,∴∠EDG=180°﹣∠BDH﹣∠BDE=180°﹣75°﹣30°=75°,∴∠DEG=90°﹣75°=15°,∴DG=DE•sin15°≈18.2(cm),∴GH=DG+DH=18.2+50≈104.8≈105(cm),∵∠F=90°,∠H=90°,∠G=90°,∴EF=GH≈105(cm),答:支撑杆上的点E到水平地面的距离EF大约是105cm.6.解:∵BN∥ED,∴∠NBD=∠BDE=37°,∵AE⊥DE,∴∠E=90°,∴BE=DE•tan∠BDE≈18.75(cm),如图,过C作AE的垂线,垂足为F,∵∠FCA=∠CAM=45°,∴AF=FC=25cm,∵CD∥AE,∴四边形CDEF为矩形,∴CD=EF,∵AE=AB+EB=35.75(cm),∴CD=EF=AE﹣AF≈10.8(cm),答:线段BE的长约等于18.8cm,线段CD的长约等于10.8cm.7.解:如图,过点E作EN⊥BC于点N,交HG于点M,则AB=AH﹣EM+EN.根据题意可知,∠AHF=∠EMF=∠EMG=90°,EN=40(米),∵HG∥BC,∴∠EGM=∠ECB=36°,在Rt△AHF中,∠AFH=40°,AF=50,∴AH=AF•sin∠AFH≈50×0.64=32(米),在Rt△FEM和Rt△EMG中,设MG=m米,则FM=(7﹣m)米,∴EM=MG•tan∠EGM=MG•tan36°≈0.73m,EM=FM•tan∠EFM=FM•tan25°≈0.47(7﹣m),∴0.73m=0.47(7﹣m),解得m≈2.7(米),∴EM≈0.47(7﹣m)=2.021(米),∴AB=AH﹣EM+EN≈32﹣2.021+40≈70(米).∴此大跳台最高点A距地面BD的距离约是70米.8.解:如图作MF⊥PQ于F,QE⊥MN于E,则四边形EMFQ是矩形.在Rt△QEN中,设EN=x米,则EQ=2x米,∵QN2=EN2+QE2,∴20=5x2,∵x>0,∴x=2,∴EN=2(米),EQ=MF=4(米),∵MN=3米,∴FQ=EM=1(米),在Rt△PFM中,PF=FM•tan60°=4(米),∴PQ=PF+FQ=(4+1)米.9.解:过A作AG⊥CD于G,则∠CAG=30°,在Rt△ACG中,CG=AC sin30°=50×=25(cm),∵GD=50﹣30=20(cm),∴CD=CG+GD=25+20=45(cm),连接FD并延长与BA的延长线交于H,则∠H=30°,在Rt△CDH中,CH==2CD=90(cm),∴EH=EC+CH=AB﹣BE﹣AC+CH=300﹣50﹣50+90=290(cm),在Rt△EFH中,EF=EH•tan30°=290×=(cm),答:支撑角钢CD和EF的长度各是45cm,cm.10.解:(1)如图,作EP⊥BC于点P,作DQ⊥EP于点Q,则CD=PQ=10,∠2+∠3=90°,∵∠1+∠θ=90°,且∠1=∠2,∴∠3=∠θ=37°50′,则EQ=DE sin∠3=120×sin37°50′,∴AB=EP=EQ+PQ=120sin37°50′+10=83.2(cm),故答案为:83.2;(2)如图,延长ED、BC交于点K,由(1)知∠θ=∠3=∠K=60°,在Rt△CDK中,CK==(cm),在Rt△KGF中,KF===(cm),则CF=KF﹣KC=﹣==(cm).11.解:过A作AH⊥BC于H,过E作EG⊥BC于G,则四边形EGHA是矩形,∴EG=AH=30×30=900,GH=AE=2,∵斜坡AB的坡度i=1:1,∴AH=BH=9米,∴AB=9,∴BG=BH﹣HG=7米,∵斜坡EF的坡度i=1:,∴FG=9米,∴BF=FG﹣BG=9﹣7,∴S梯形ABFE=(2+9﹣7)×9=,∴共需土石为×200=100(81﹣45)立方米.12.解:(1)作DM⊥AB于M,CN⊥AN于N.由题意:tan∠DAB==2,设AM=x,则DM=2x,∵四边形DMNC是矩形,∴DM=CN=2x,在Rt△NBC中,tan37°===,∴BN=x,∵x+3+x=14,∴x=3,∴DM=6,答:坝高为6m.(2)作FH⊥AB于H.设DF=y,则AE=2y,EH=3+2y﹣y=3+y,BH=14+2y﹣(3+y)=11+y,由△EFH∽△FBH,可得=,即=,解得y=﹣7+2或﹣7﹣2(舍弃),∴DF=2﹣7,答:DF的长为(2﹣7)m.二.实际问题数学抽象13.解:工人师傅搬运此钢架能通过一个直径为2.1m的圆形门,理由是:过B作BD⊥AC于D,∵AB>BD,BC>BD,AC>AB,∴求出DB长和2.1m比较即可,设BD=xm,∵∠A=30°,∠C=45°,∴DC=BD=xm,AD=BD=xm,∵AC=2(+1)m,∴x+x=2(+1),∴x=2,即BD=2m<2.1m,∴工人师傅搬运此钢架能通过一个直径为2.1m的圆形门.14.解:(1)在Rt△EFH中,∵∠H=90°,∴tan∠EFH=i=1:0.75==,设EH=4xm,则FH=3xm,∴EF==5xm,∵EF=15m,∴5x=15m,x=3,∴FH=3x=9m.即山坡EF的水平宽度FH为9m;(2)∵L=CF+FH+EA=CF+9+4=CF+13,H=AB+EH=22.5+12=34.5,H1=0.9,∴日照间距系数=L:(H﹣H1)==,∵该楼的日照间距系数不低于1.25,∴≥1.25,∴CF≥29.答:要使该楼的日照间距系数不低于1.25,底部C距F处29m远.15.解:(1)如图,过M作MN⊥AB于N,交BA的延长线于N,Rt△OMN中,∠NOM=60°,OM=1.2,∴∠M=30°,∴ON=OM=0.6,∴NB=ON+OB=3.3+0.6=3.9;即点M到地面的距离是3.9米;(2)取CE=0.65,EH=2.55,∴HB=3.9﹣2.55﹣0.65=0.7,过H作GH⊥BC,交OM于G,过O作OP⊥GH于P,∵∠GOP=30°,∴tan30°==,∴GP=OP=≈0.404,∴GH=3.3+0.404=3.704≈3.70>3.5,∴货车能安全通过.16.解:∵BH=0.6米,sinα=,∴AB==1米,∴AH=0.8米,∵AF=FC=2米,∴BF=1米,作FJ⊥BG于点J,作EK⊥FJ于点K,∠EKF=∠FJB=∠AHB=90°,∠EFK=∠FBJ=∠ABH,BF=AB,∴△EFK∽△FBJ∽△ABH,△FBJ≌△ABH,∴,BJ=BH=0.6米,即,解得,EK=1.28,∴BJ+EK=0.6+1.28=1.88<2,∴木箱上部顶点E不会触碰到汽车货厢顶部.三.三角函数的应用17.解:作BE⊥AD于点E,作CF⊥AD于点F,延长FC到点M,使得BE=CM,∵AB=CD,AB+CD=AD=2,∴AB=CD=1,在Rt△ABE中,∠A=35°,AB=1,∴BE=AB•sin A=1×sin35°≈0.6,∴AE=AB•cos A=1×cos35°≈0.8,在Rt△CDF中,∠D=45°,CD=1,∴CF=CD•sin D=1×sin45°≈0.7,∴DF=CD•cos D=1×cos45°≈0.7,∵BE⊥AD,CF⊥AD,∴BE∥CM,又∵BE=CM,∴四边形BEMC是平行四边形,∴BC=EM,在Rt△MEF中,FM=CF+CM=1.3,EF=AD﹣AE﹣FD=0.5,∴EM==≈1.4,答:B与C之间的距离约为1.4米.18.解:(1)如图,过点A作AE⊥CB,垂足为E,在Rt△ABE中,AB=5m,∠ABE=37°,∵sin∠ABE=,cos∠ABE=,∴=0.60,=0.80,∴AE=3m,BE=4m,∴CE=6m,在Rt△ACE中,由勾股定理AC==3≈6.7m.(2)过点A作AF⊥CD,垂足为F,∴FD=AO=1m,∴CF=5m,在Rt△ACF中,由勾股定理AF==2m.∴OD=2≈4.5m.19.解:如图,过点A作CD的垂线,交CD的延长线于F,过点C作AB的垂线,交AB 的延长线于E,∵AB∥CD,∴四边形AECF是矩形,∵∠BCD=60°,∴∠BCE=90°﹣60°=30°,在Rt△BCE中,∠BCE=30°,BC=8,∴BE=BC=4,CE=BC=4,∵∠ADC=135°,∴∠ADF=180°﹣135°=45°,∴△ADF是等腰直角三角形,∴DF=AF=CE=4,由于FC=AE,即4+2=AB+4,∴AB=4﹣2,∴S梯形ABCD=(2+4﹣2)×4=24,答:垂尾模型ABCD的面积为24.20.解:(1)∵AE=EF=AF=1m,∴△AEF是等边三角形,∴∠AFE=60°,连接MF并延长交AE于K,则FM=2FK,∵△AEF是等边三角形,∴AK=(m),∴FK==(m),∴FM=2FK=(m),∴BC=4FM=4≈6.92≈6.9(m),答:∠AFE的度数为60°,棚宽BC的长约为6.9m;(2)∵∠AFE=74°,∴∠AFK=37°,∴KF=AF•cos37°≈0.80(m),∴FM=2FK=1.60(m),∴BC=4FM=6.40(m)<6.92(m),6.92﹣6.40=0.52≈0.5(m),答:当∠AFE由60°变为74°时,棚宽BC是减少了,减少了0.5m.21.解:(1)如图,过点C作CF⊥DE于点F,∵CD=CE=5cm,∠DCE=40°.∴∠DCF=20°,∴DF=CD•sin20°≈5×0.34≈1.7(cm),∴DE=2DF≈3.4cm,∴线段DE的长约为3.4cm;(2)∵横截面是一个轴对称图形,∴延长CF交AD、BE延长线于点G,连接AB,∴DE∥AB,∴∠A=∠GDE,∵AD⊥CD,BE⊥CE,∴∠GDF+∠FDC=90°,∵∠DCF+∠FDC=90°,∴∠GDF=∠DCF=20°,∴∠A=20°,∴DG=≈≈1.8(cm),∴AG=AD+DG=10+1.8=11.8(cm),∴AB=2AG•cos20°≈2×11.8×0.94≈22.2(cm).∴点A,B之间的距离22.2cm.。
九年级数学下册1_5三角函数的应用专项练习2解答新版北师大版

∵ ∠PBC是△APB的一个外角,∴∠APB=∠PBC-∠PAB=30°. …………………3分
∴∠PAB=∠APB. …………………4分
故AB=PB=400米. …………………………6分
在Rt△PBC中,∠PCB=90°,∠PBC=60°,PB=400,
解:(1)电线杆落在广告牌上的影长为3+1.5=4.5(米)…………(2分)
(2)作GH⊥AB于H,依题意得:HG=BC+0.5CD=5+1.5=6.5…………(3分)
因为: ,DF=3,DE=4.…………(4分)
因此:AH= =4.875…………(5分)
因此:电线杆的高度为:
AB=AH+BH=AH+DF=3+4.875=7.875≈7.9.…………(6分)
在Rt 中,∵ ∴ = 米 ……4分
那么DA=DB-AB= ≈10×1.732 =7.32米. ……5分
∵3 + DA ,因此离原坡角10米的建筑物应拆除. ……6分
答:离原坡角10米的建筑物应拆除. ……7分
5.某风光治理区,为提高游客到某景点的平安性,决定将抵达该景点的步行台阶进行改善,把倾角由45°减至30°,已知原台阶坡面AB的长为 m(BC所在地面为水平面).
答:(1)广告牌上的影长为4.5米;(2)电线杆的高度为7.9米.…………(7分)
范围内形成气旋风暴,有极强的破坏力.如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动,且台风中心风力不变.假设城市所受风力达到或超过四级,那么称为受台风阻碍.
北师大版初三数学9年级下册 第1章 1.5 三角函数的应用 同步练习卷(含答案)

北师大版数学九年级下册1.5《三角函数的应用》同步练习卷一、选择题1.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)()A.7sinαB.7cosαC.7tanαD.2.如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是()A.sinA的值越大,梯子越陡B.cosA的值越大,梯子越陡C.tanA的值越小,梯子越陡D.陡缓程度与∠A的函数值无关3.一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为()A.10海里/小时B.30海里/小时C.20海里/小时D.30海里/小时4.如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )A.10海里B.(10-10)海里C.10海里D.(10-10)海里5.如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二踩档与第三踩档的正中间处有一条60 cm长的绑绳EF,tanα=2.5,则“人字梯”的顶端离地面的高度AD是( )A.144 cm B.180 cm C.240 cm D.360 cm6.一座楼梯的示意图如图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要()A.米2B.米2C.(4+)米2D.(4+4tanθ)米27.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )A.100sin 35°米B.100sin 55°米C.100tan 35°米D.100tan 55°米8.如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是()A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米9.如图,将一个 Rt△ABC 形状的楔子从木桩的底端点 P 沿水平方向打入木桩底下,使木桩向上运动.已知楔子斜面的倾斜角为 15°,若楔子沿水平方向前进 6cm(如箭头所示),则木桩上升了()A.6sin15°cmB.6cos15°cmC.6tan15°cmD.cm10.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,则旗杆PA的高度为()A. B. C. D.二、填空题11.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为米(结果保留整数,测角仪忽略不计)12.如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为__________米.13.如图,河坝横断面迎水坡AB的坡比是1:,堤高BC=5米,则坝底AC的长度是米.14.如图,一艘船向正北航行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S的最近距离是海里(结果保留根号).15.如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,则求该塔的高度为米.(参考数据:≈1.41,≈1.73)16.如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,则cos∠BAC的值为 .三、解答题17.如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据≈1.414,≈1.732)18.如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°,使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?19.鲁南高铁临沂段修建过程中需要经过一座小山.如图,施工方计划沿AC方向开挖隧道,为了加快施工速度,要在小山的另一侧D(A、C、D共线)处同时施工.测得∠CAB=30°,AB=4km,∠ABD=105°,求BD的长.20.为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423)参考答案1.C2.A3.D4.D5.B6.D7.C;8.C;9.C;10.A11.答案为:137.12.答案为:160.13.答案为:.14.答案为:。
高一数学必修《三角函数的应用》课时同步练习(有答案)

高一数学必修一5.7《三角函数的应用》课时同步练习一、选择题:1、一种波的波形为函数y =-sin π2x 的图象,若其在区间[0,t ]上至少有2个波峰(图象的最高点),则正整数t 的最小值是( )A .5B .6C .7D .82、如图,单摆从某点开始来回摆动,离开平衡位置O 的距离()cm s 和时间()t s 的函数关系式为:π6sin 2π6s t ⎛⎫=+⎪⎝⎭,那么单摆来回摆动一次所需的时间为( )A .2πsB .πsC .0.5sD .1s3、已知某人的血压满足函数解析式f (t )=24sin 160πt +110.其中f (t )为血压,t 为时间,则此人每分钟心跳的次数为( )A .60B .70C .80D .904、电流强度I (A)随时间t (s)变化的函数I =A sin(ωt+φ)(A >0,ω>0,0<φ<π2)的图象如图所示,则当t =1100s 时,电流强度是( )A .−5 AB .5 AC .D .10 A5、某简谐运动的图象满足函数y =2sin(ωx +φ)(φ>0),其初相和频率分别为-π和32,则它的相位是( )A. 3πx-πB. 3πxC. 3πx+πD. πx+π6、据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=A sin(ωx+φ)+b(b>0,ω>0,|φ|<π2)的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)的解析式为( )A.f(x)=2sin(π4x–π4)+7(1≤x≤12,x∈N+)B.f(x)=9sin(π4x–π4)+7(1≤x≤12,x∈N+)C.f(x)π4x+7(1≤x≤12,x∈N+)D.f(x)=2sin(π4x+π4)+7(1≤x≤12,x∈N+)二、填空题:7、中国最高的摩天轮是“南昌之星”,它的最高点离地面160米,直径为156米,并以每30分钟一周的速度匀速旋转,若摩天轮某座舱A经过最低点开始计时,则10分钟后A离地面的高度为米。
三角函数的应用同步练习(含答案)

三角函数的应用同步练习(含答案)1、三角函数可以作为描述现实世界中__周期_______现象的一种数学模型.2、|sin |y x =是以____π________为周期的波浪型曲线.3、设()y f t =是某港口水的深度关于时间t (时)的函数,其中024t ≤≤,下表是该港口某一经长期观察,函数()y f t =的图象可以近似地看成函数sin()y k A t ωϕ=++的图象. 根据上述数据,函数()y f t =的解析式为( A ) A .123sin,[0,24]6ty t π=+∈ B .123sin(),[0,24]6ty t ππ=++∈C .123sin ,[0,24]12t y t π=+∈D .123sin(),[0,24]122t y t ππ=++∈4、从高出海面hm 的小岛A 处看正东方向有一只船B ,俯角为30看正南方向的一船C 的俯角为45,则此时两船间的距离为( A ).A .2hmBCD .5、受日月引力,海水会发生涨落,这种现象叫做潮汐。
在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋,某港口水的深度y (米)是时间,240(≤≤t t 单位:时)的函数,记作)(t f y =,下面是该港口在某季节每天水深的数据:⑴根据以上数据,求出函数)(t f y =近似表达式。
⑵一般情况下,船舶航行时,船底离海底的距离为5m 或5m 以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(航底离水面的距离)为6.5米,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需的时间)?解析:⑴由表中数据知:12)39(2=-⨯=T ∴6122ππω==,即k t A x f +=6sin )(π又∵当t=0时,0)(=x f 及t=3时,13)(max =x f∴⎩⎨⎧=+=1310k A k ,∴⎩⎨⎧==310A k 。
1.5《三角函数的应用》同步练习(含答案)

5 三角函数的应用知识点 1 解决与方向角有关的问题1.如图1-5-1,小雅家(图中点O 处)门前有一条东西走向的公路,经测得有一水塔(图中点A 处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB 是( )A .250米B .250 3米 C.50033米 D .500 2米1-5-1 1-5-22.如图1-5-2,一艘海轮位于灯塔P 的东北方向,距离灯塔40 2海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东30°方向上的B 处,则海轮行驶的路程AB 为( )A .(40+40 3)海里B .80 3海里C .(40+20 3)海里D .80海里3.2017·十堰如图1-5-3,海中有一小岛A ,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B 点测得小岛A 在北偏东60°方向上,航行12海里到达D 点,这时测得小岛A 在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?图1-5-3知识点 2 解决与仰角、俯角有关的问题4.如图1-5-4所示,某地修建高速公路,要从B 地向C 地修一条隧道(B ,C 在同一水平面上),为了测量B ,C 两地之间的距离,某工程师乘坐热气球从C 地出发,垂直上升100 m 到达A 处,在A 处观察B 地的俯角为30°,则B ,C 两地之间的距离为( )A .100 3 mB .50 2 mC .50 3 m D.100 33m1-5-4 1-5-55.如图1-5-5所示,在天水至宝鸡(天宝)高速公路建设中需要确定某条隧道AB 的长度.已知在离地面2700米高度(C 处)的飞机上,测量人员测得正前方A ,B 两点处的俯角分别是60°和30°,则隧道AB 的长为__________米.(结果保留根号)6.[2016·成都] 在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图1-5-6,在测点A 处安置测倾器,量出高度AB =1.5 m ,测得旗杆顶端D 的仰角∠DBE =32°,量出测点A 到旗杆底部C 的水平距离AC =20 m ,根据测量数据,求旗杆CD 的高度.(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)图1-5-6知识点 3 解决与坡度、坡角有关的问题7.一个台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图1-5-7所示,则下列关系或说法正确的是( )A .斜坡AB 的坡度是10° B .斜坡AB 的坡度是tan 10°C .AC =1.2tan 10°米D .AB = 1.2cos 10°米1-5-7 1-5-88.[2017·四川] 如图1-5-8所示,某拦水大坝的横断面为梯形ABCD ,AE ,DF 为梯形的高,其中迎水坡AB 的坡角α=45°,坡长AB =6 2米,背水坡CD 的坡度i =1∶3(i 为DF 与FC 的比值),则背水坡的坡长为__________米.9.小明发现在教学楼走廊上有一拖把以15°的倾斜角斜靠在栏杆上,严重影响了同学们的行走安全.他自觉地将拖把挪动位置,使其倾斜角变为75°,如果拖把的总长为1.80 m,则小明拓宽了行路通道________m.(结果精确到0.01 m,参考数据:sin15°≈0.26,cos15°≈0.97)10.如图1-5-9,小华站在贵阳花溪水库的堤坝上的G点,看见水库里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角∠FDC=30°,若小华的眼睛与地面的距离DG=1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4∶3,坡长AB=8米,点A,B,C,D,F,G在同一平面内,则此时小船C到岸边的距离CA的长为________米.(结果保留根号)图1-5-911.[2017·德州] 如图1-5-10所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10 m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒.已知∠B=30°,∠C=45°.(1)求B,C之间的距离;(结果保留根号)(2)如果此地限速80 km/h,那么这辆汽车是否超速?请说明理由.(参考数据:3≈1.7,2≈1.4)图1-5-1012.2017·遵义模拟在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图1-5-11),在跑道MN的正西端14.5 km处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15 km的B处;经过1 min,又测得该飞机位于点A的北偏东60°,且与点A相距5 3 km的C处.(1)该飞机航行的速度是多少km/h?(结果保留根号)(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.图1-5-11答案详解1.A2.A [解析] 根据题意得P A =40 2海里,∠A =45°,∠B =30°. 在Rt △P AC 中,AC =PC =P A ·cos 45°=40 2×22=40(海里), 在Rt △PBC 中,BC =PC tan B =4033=40 3(海里),∴AB =AC +BC =(40+40 3)海里. 故选A.3.解:过点A 作AC ⊥BD 于点C ,则AC 的长是点A 到BD 的最短距离. 依题意知∠CAD =30°,∠CAB =60°,∴∠BAD =60°-30°=30°,∠ABD =90°-60°=30°, ∴∠ABD =∠BAD ,∴AD =BD =12海里. ∵∠CAD =30°,∠ACD =90°, ∴CD =12AD =6海里,由勾股定理得AC =122-62=6 3(海里)>8海里, 故渔船没有触礁的危险. 4.A [解析] 因为tanB =tan 30°=AC BC =100BC =33,解得BC =100 3,即B ,C 两地之间的距离为100 3 m .故选A.5.1800 3 [解析] 由题意得∠CAO =60°,∠CBO =30°. ∵OA =2700tan60°=2700×33=900 3,OB =2700tan30°=2700 3,∴AB =2700 3-900 3=1800 3(米).故填1800 3.6.解:由题意得AC =20 m ,AB =1.5 m . ∵在Rt △DBE 中,∠DBE =32°, BE =AC =20 m ,∴DE =BEtan 32°≈20×0.62=12.4(m ),∴CD =DE +CE =DE +AB ≈12.4+1.5=13.9(m ). 答:旗杆CD 的高度约为13.9 m . 7.B8.12 [解析] 锐角三角函数的简单实际应用.在等腰直角三角形ABE 中,AB =6 2米,AE =DF =6米,由坡度知∠DCF =30°,则CD =2DF =12米.9.1.28[解析] 如图,在Rt △DCE 中, ∵cos ∠EDC =DC DE,∴DC =DE ·cos ∠EDC =1.8×cos 15°≈1.746(m ). 在Rt △ABC 中,∠BAC =90°-75°=15°. ∵sin ∠BAC =BC AB,∴BC =AB ·sin ∠BAC =1.8×sin 15°≈0.468(m ). ∴BD =DC -BC ≈1.28 m .10.(8 3-5.5) [解析] 如图,过点B 作BE ⊥AC 于点E ,延长DG 交CA 于点H ,得Rt △ABE 和矩形BEHG .∵i =BE AE =43,AB =8,∴BE =325,AE =245.∵DG =1.6,BG =0.7, ∴DH =DG +GH =1.6+325=8,AH =AE +EH =245+0.7=5.5.在Rt △CDH 中,∵∠C =∠FDC =30°,DH =8,tan 30°=DH CH =33, ∴CH =8 3. 又∵CH =CA +5.5, 即8 3=CA +5.5, ∴CA =8 3-5.5.即CA 的长是(8 3-5.5)米.11.解:(1)如图,过点A 作AD ⊥BC 于点D ,则AD =10 m .∵在Rt △ACD 中,∠C =45°, ∴Rt △ACD 是等腰直角三角形. ∴CD =AD =10 m .在Rt △ABD 中,tanB =AD BD,∵∠B =30°,∴33=10BD,∴BD =10 3 m . ∴BC =BD +CD =(10 3+10)m . 答:B ,C 之间的距离是(10 3+10)m . (2)这辆汽车超速.理由如下:由(1)知BC =(10 3+10)m ,又3≈1.7, ∴BC ≈27 m . ∴汽车速度v =270.9=30(m /s ). 又30 m /s =108 km /h ,此地限速80 km /h , ∵108>80,∴这辆汽车超速. 答:这辆汽车超速.12.解: (1)由题意,得∠BAC =90°,AB =15 km ,AC =5 3 km , ∴BC =152+(5 3)2=10 3(km ), ∴飞机航行的速度为10 3÷160=600 3(km /h ).(2)能.理由如下:如图,过点C 作CE ⊥l 于点E ,设直线BC 交l 于点F .在Rt △ABC 中,AC =5 3 km ,BC =10 3 km , ∴∠ABC =30°,即∠BCA =60°.又∵∠CAE =30°,∴∠ACE =∠FCE =60°, ∴CE =AC ·sin ∠CAE =523 km ,AE =AC ·cos ∠CAE =152 km .则AF =2AE =15 km .∵AN =AM +MN =14.5+1=15.5(km ), ∴AM <AF <AN ,∴飞机不改变航向继续航行,可以降落在跑道MN 之间.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 三角函数的应用知识点 1 解决与方向角有关的问题1.如图1-5-1,小雅家(图中点O 处)门前有一条东西走向的公路,经测得有一水塔(图中点A 处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB 是( )A .250米B .250 3米 C.50033米 D .500 2米1-5-1 1-5-22.如图1-5-2,一艘海轮位于灯塔P 的东北方向,距离灯塔40 2海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东30°方向上的B 处,则海轮行驶的路程AB 为( )A .(40+40 3)海里B .80 3海里C .(40+20 3)海里D .80海里3.2017·十堰如图1-5-3,海中有一小岛A ,它周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在B 点测得小岛A 在北偏东60°方向上,航行12海里到达D 点,这时测得小岛A 在北偏东30°方向上.如果渔船不改变航线继续向东航行,有没有触礁的危险?图1-5-3知识点 2 解决与仰角、俯角有关的问题4.如图1-5-4所示,某地修建高速公路,要从B 地向C 地修一条隧道(B ,C 在同一水平面上),为了测量B ,C 两地之间的距离,某工程师乘坐热气球从C 地出发,垂直上升100 m 到达A 处,在A 处观察B 地的俯角为30°,则B ,C 两地之间的距离为( )A .100 3 mB .50 2 mC .50 3 m D.100 33m1-5-4 1-5-55.如图1-5-5所示,在天水至宝鸡(天宝)高速公路建设中需要确定某条隧道AB 的长度.已知在离地面2700米高度(C 处)的飞机上,测量人员测得正前方A ,B 两点处的俯角分别是60°和30°,则隧道AB 的长为__________米.(结果保留根号)6.[2016·成都] 在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图1-5-6,在测点A 处安置测倾器,量出高度AB =1.5 m ,测得旗杆顶端D 的仰角∠DBE =32°,量出测点A 到旗杆底部C 的水平距离AC =20 m ,根据测量数据,求旗杆CD 的高度.(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)图1-5-6知识点 3 解决与坡度、坡角有关的问题7.一个台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图1-5-7所示,则下列关系或说法正确的是( )A .斜坡AB 的坡度是10° B .斜坡AB 的坡度是tan 10°C .AC =1.2tan 10°米D .AB = 1.2cos 10°米1-5-7 1-5-88.[2017·四川] 如图1-5-8所示,某拦水大坝的横断面为梯形ABCD ,AE ,DF 为梯形的高,其中迎水坡AB 的坡角α=45°,坡长AB =6 2米,背水坡CD 的坡度i =1∶3(i 为DF 与FC 的比值),则背水坡的坡长为__________米.9.小明发现在教学楼走廊上有一拖把以15°的倾斜角斜靠在栏杆上,严重影响了同学们的行走安全.他自觉地将拖把挪动位置,使其倾斜角变为75°,如果拖把的总长为1.80 m,则小明拓宽了行路通道________m.(结果精确到0.01 m,参考数据:sin15°≈0.26,cos15°≈0.97)10.如图1-5-9,小华站在贵阳花溪水库的堤坝上的G点,看见水库里有一小船沿垂直于岸边的方向划过来.此时,测得小船C的俯角∠FDC=30°,若小华的眼睛与地面的距离DG=1.6米,BG=0.7米,BG平行于AC所在的直线,迎水坡i=4∶3,坡长AB=8米,点A,B,C,D,F,G在同一平面内,则此时小船C到岸边的距离CA的长为________米.(结果保留根号)图1-5-911.[2017·德州] 如图1-5-10所示,某公路检测中心在一事故多发地段安装了一个测速仪器,检测点设在距离公路10 m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒.已知∠B=30°,∠C=45°.(1)求B,C之间的距离;(结果保留根号)(2)如果此地限速80 km/h,那么这辆汽车是否超速?请说明理由.(参考数据:3≈1.7,2≈1.4)图1-5-1012.2017·遵义模拟在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图1-5-11),在跑道MN的正西端14.5 km处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15 km的B处;经过1 min,又测得该飞机位于点A的北偏东60°,且与点A相距5 3 km的C处.(1)该飞机航行的速度是多少km/h?(结果保留根号)(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.图1-5-11答案详解1.A2.A [解析] 根据题意得P A =40 2海里,∠A =45°,∠B =30°. 在Rt △P AC 中,AC =PC =P A ·cos 45°=40 2×22=40(海里), 在Rt △PBC 中,BC =PC tan B =4033=40 3(海里),∴AB =AC +BC =(40+40 3)海里. 故选A.3.解:过点A 作AC ⊥BD 于点C ,则AC 的长是点A 到BD 的最短距离. 依题意知∠CAD =30°,∠CAB =60°,∴∠BAD =60°-30°=30°,∠ABD =90°-60°=30°, ∴∠ABD =∠BAD ,∴AD =BD =12海里. ∵∠CAD =30°,∠ACD =90°, ∴CD =12AD =6海里,由勾股定理得AC =122-62=6 3(海里)>8海里, 故渔船没有触礁的危险. 4.A [解析] 因为tanB =tan 30°=AC BC =100BC =33,解得BC =100 3,即B ,C 两地之间的距离为100 3 m .故选A.5.1800 3 [解析] 由题意得∠CAO =60°,∠CBO =30°. ∵OA =2700tan60°=2700×33=900 3,OB =2700tan30°=2700 3,∴AB =2700 3-900 3=1800 3(米).故填1800 3.6.解:由题意得AC =20 m ,AB =1.5 m . ∵在Rt △DBE 中,∠DBE =32°, BE =AC =20 m ,∴DE =BEtan 32°≈20×0.62=12.4(m ),∴CD =DE +CE =DE +AB ≈12.4+1.5=13.9(m ). 答:旗杆CD 的高度约为13.9 m . 7.B8.12 [解析] 锐角三角函数的简单实际应用.在等腰直角三角形ABE 中,AB =6 2米,AE =DF =6米,由坡度知∠DCF =30°,则CD =2DF =12米.9.1.28[解析] 如图,在Rt △DCE 中, ∵cos ∠EDC =DC DE,∴DC =DE ·cos ∠EDC =1.8×cos 15°≈1.746(m ). 在Rt △ABC 中,∠BAC =90°-75°=15°. ∵sin ∠BAC =BC AB,∴BC =AB ·sin ∠BAC =1.8×sin 15°≈0.468(m ). ∴BD =DC -BC ≈1.28 m .10.(8 3-5.5) [解析] 如图,过点B 作BE ⊥AC 于点E ,延长DG 交CA 于点H ,得Rt △ABE 和矩形BEHG .∵i =BE AE =43,AB =8,∴BE =325,AE =245.∵DG =1.6,BG =0.7, ∴DH =DG +GH =1.6+325=8,AH =AE +EH =245+0.7=5.5.在Rt △CDH 中,∵∠C =∠FDC =30°,DH =8,tan 30°=DH CH =33, ∴CH =8 3. 又∵CH =CA +5.5, 即8 3=CA +5.5, ∴CA =8 3-5.5.即CA 的长是(8 3-5.5)米.11.解:(1)如图,过点A 作AD ⊥BC 于点D ,则AD =10 m .∵在Rt △ACD 中,∠C =45°, ∴Rt △ACD 是等腰直角三角形. ∴CD =AD =10 m .在Rt △ABD 中,tanB =AD BD,∵∠B =30°,∴33=10BD,∴BD =10 3 m . ∴BC =BD +CD =(10 3+10)m . 答:B ,C 之间的距离是(10 3+10)m . (2)这辆汽车超速.理由如下:由(1)知BC =(10 3+10)m ,又3≈1.7, ∴BC ≈27 m . ∴汽车速度v =270.9=30(m /s ). 又30 m /s =108 km /h ,此地限速80 km /h , ∵108>80,∴这辆汽车超速. 答:这辆汽车超速.12.解: (1)由题意,得∠BAC =90°,AB =15 km ,AC =5 3 km , ∴BC =152+(5 3)2=10 3(km ), ∴飞机航行的速度为10 3÷160=600 3(km /h ).(2)能.理由如下:如图,过点C 作CE ⊥l 于点E ,设直线BC 交l 于点F .在Rt △ABC 中,AC =5 3 km ,BC =10 3 km , ∴∠ABC =30°,即∠BCA =60°.又∵∠CAE =30°,∴∠ACE =∠FCE =60°, ∴CE =AC ·sin ∠CAE =523 km ,AE =AC ·cos ∠CAE =152 km .则AF =2AE =15 km .∵AN =AM +MN =14.5+1=15.5(km ), ∴AM <AF <AN ,∴飞机不改变航向继续航行,可以降落在跑道MN 之间.。
