《电工学》第四章课件
合集下载
电工学第四章

+
ɺ UA
N C –
ɺ IN
ɺ UB
– +
RA N′ ′ RC RB
B
– ɺ UC +
ɺ IB ɺ I
C
A +
ɺ IA
ɺ UA
N C
–
ɺ IN
ɺ UB
– +
RA N′ ′ RC RB
B
– ɺ UC +
ɺ IB ɺ I
C
解: 已知: 已知: ɺAB = 380 30° V U (1) 线电流 三相对称
A、B、C三端称为始端, 、 、 三端称为始端 三端称为始端, X、Y、Z三端称为末端。 、 、 三端称为末端 三端称为末端。 uC
O
ωt
3. 相量表示
•
ɺ UC
U
•
A
= U∠0
U
B
= U ∠ − 120
• C
120° ° 120° ° 120° °
ɺ UB
UA
•
U
= U ∠ 120
4. 对称三相电源的特点 uA + uB + uC = 0 UA + UB + UC = 0
C
相电压:端线与中性线间(发电机每相绕组) 相电压:端线与中性线间(发电机每相绕组)的电压 ɺ ɺ ɺ UA、UB、UC 、Up
ɺ ɺ ɺ 线电压: 线电压:端线与端线间的电压 UAB、UBC、UCA、Ul
(2) 线电压与相电压的关系 + + – + A
eA
– Z X –Y –
ɺ UA
eB
– – – +
2009 年 11月
第四章 三相电路
ɺ UA
N C –
ɺ IN
ɺ UB
– +
RA N′ ′ RC RB
B
– ɺ UC +
ɺ IB ɺ I
C
A +
ɺ IA
ɺ UA
N C
–
ɺ IN
ɺ UB
– +
RA N′ ′ RC RB
B
– ɺ UC +
ɺ IB ɺ I
C
解: 已知: 已知: ɺAB = 380 30° V U (1) 线电流 三相对称
A、B、C三端称为始端, 、 、 三端称为始端 三端称为始端, X、Y、Z三端称为末端。 、 、 三端称为末端 三端称为末端。 uC
O
ωt
3. 相量表示
•
ɺ UC
U
•
A
= U∠0
U
B
= U ∠ − 120
• C
120° ° 120° ° 120° °
ɺ UB
UA
•
U
= U ∠ 120
4. 对称三相电源的特点 uA + uB + uC = 0 UA + UB + UC = 0
C
相电压:端线与中性线间(发电机每相绕组) 相电压:端线与中性线间(发电机每相绕组)的电压 ɺ ɺ ɺ UA、UB、UC 、Up
ɺ ɺ ɺ 线电压: 线电压:端线与端线间的电压 UAB、UBC、UCA、Ul
(2) 线电压与相电压的关系 + + – + A
eA
– Z X –Y –
ɺ UA
eB
– – – +
2009 年 11月
第四章 三相电路
电工学(第七版)上册秦曾煌第四章_图文

相位差
定义:
XL
感抗:
()
则:
O
f
XL与 f 的关系
直流:f = 0, XL =0,电感L视为短路
交流:f
XL
超前
电感L具有通直阻交的作用
相量式:
电感电路相量形式的欧姆定律
相量图
2. 功率关系 (1) 瞬时功率
(2) 平均功率
L是非耗 能元件
(3)无功功率Q 用以衡量电感电路中能量交换的规模。
阻抗模:
阻抗角:
由电路参数决定。
电路参数与电路性质的关系:
当 XL >XC 时, > 0 ,u 超前 i 呈感性 当 XL < XC 时 , < 0 , u 滞后 i 呈容性 当 XL = XC 时 , = 0 , u. i 同相 呈电阻性
2) 相量图
参考相量
XL > XC
XL < XC
用相量表示后,即可用直流电路的分析方法。
4.1 正弦电压与电流
I, U
o
t
直流电流和电压
正弦电流和电压
正弦交流电的优越性: 便于传输;易于变换 便于运算; 有利于电器设备的运行;
.....
_
正半周
_
负半周
4.1 正弦电压与电流
设正弦交流电流:
i
Im
O
T
初相角:决定正弦量起始位置 角频率:决定正弦量变化快慢 幅值:决定正弦量的大小 幅值、角频率、初相角成为正弦量的三要素。
2.4 电阻、电感与电容元件串联的交流电路
1. 电流、电压的关系 (1) 相量式
设
(参考相量)
则
如用相量表示电压与 电流关系,可把电路模型 改画为相量模型。 总电压与总电流
电工学第四章课件

B a
B¬ £
b
B BJ B0
B
0
磁化曲线
O
B和与H的关系
H
注
当有磁性物质存在时 B与H不成比例,与I也不成比例。
三、磁滞性
当铁心线圈中通有交变电流(大小和方向都变化) 时,铁心就受到交变磁化,电流变化时,B随H而变化, 当H已减到零值时,但B未回到零,这种磁感应强度滞 后于磁场强度变化的性质称磁性物质的磁滞性。
I N
磁路与电路对照 I
+
磁路
E
_
U
R 电路
磁通势F 磁通 磁感应强度B 磁阻Rm
电动势E 电流I 电流密度J 电阻R
l Rm Sl R S源自磁路的计算在计算电机、电器等的磁路时,要预先给定铁心 中的磁通(或磁感应强度),而后按照所给的 磁通及磁路各段的尺寸和材料去求产生预定磁通所 需的磁通势F=NI。 计算均匀磁路要用磁场强度H,即NI=Hl, 如磁路由不同的材料、长度和截面积的几段组 成,则磁路由磁阻不同的几段串联而成。 NI=H1 l1+H2 l2+=(H l)
0
如:由三段串联而成的
继电器磁路
2
1 l2
I
1
l1 S1
S2
S 1 S 2 S 0
B 1 B 2 B 0
= ( ) B f H H 1 = ( ) B f H = ( ) B f H H 2 H 0
l1
2
H 1l 1 H 2 l2
l) ( H H 0/ = N I
例题4.1 有一环形铁心线圈,其内径为10cm,外径为15cm,铁 心材料为铸钢。磁路中含有一空气气隙,其长度等于 0.2cm。设线圈中通有1A电流,如要得到0.9T的磁感应 强度,试求线圈匝数。
电工学第4章

例题3:试判断下列电路中引入的反馈是电 例题 试判断下列电路中引入的反馈是电 压反馈还是电流反馈. 压反馈还是电流反馈.
+VCC Cb2 T
+
Rb1 Cb1
+
Rc
+VCC Rb C1
+
RL
ui +
Rb2
uf -
+
ic Re
uo -
RS uS +
+
T C2 uf +
ui -
+
Re
RL
uo -
+V cc
R1
-
id
+ ui -
ii
+
Rf
A
∞
+
io + uo RL -
if
R
分立电路组成的电流并联负反馈
引入电流负反馈的目的——稳定输出电流 稳定输出电流 引入电流负反馈的目的 稳定过程: 稳定过程: RL ↑ io(ic2) ↓ io(ic2) ↑ 负载变化时,输出电流稳定 输出电阻↑ 负载变化时,输出电流稳定——输出电阻 输出电阻
R1
uf ↑
ud ↓
+ ui + -
+ + ∞ ud - - A +
uf Rf
Rb1
io RL
Rc T u be + uf ic Re
+VCC Cb2
+ uo -
Cb1
+
+
+
RL
+
ui +
Rb2
uo -
五.反馈类型及判别方法总结
电工学课件第四章

对称而又没有中线时,负载上可能得 A
会不会出 现问题?
到大小不等的电压,有的超过用电设
一层楼 ...
备的额定电压,有的达不到额定电压 N
,都不能正常工作。比如,照明电路 中各相负载不能保证完全对称,所以 绝对不能采用三相三相制供电,而且 必须保证零线可靠。
二层 楼 B C
三层楼
28
第二十八页,共48页
Em sin( t + 120 °)
6
第六页,共48页
4.1.2 三相电源的表示法
1.瞬时值表达式
2.波形图
Em
eA = Em sin wt
eB = Em sin (wt - 120 °) eC = Em sin (wt - 240 °)
= Em sin(w t + 120 °)
eA eB eC
星形连接(Y接) 三角形连接(接)
相电流(IP): 流过每一相负载的电流 线电流(IL) : 流过每一根火线的电流
15
第十五页,共48页
4.2.1 负载星形连接的三相电路
1. 连接
三相四线制
A iA
三相四线
ZX Y
uA
i ZA
AN
N
iCN
i uB B i i uC C
B ZB
ZC
BN
C
相电流IP(负载上的电流):
三表法适用于三相四线制接法的不对称负载。
38
第三十八页,共48页
3. 两表法:(用两个功率表测量)
* P1
线电压
A
*W 1
*P2
电压
B
*W 2
线圈
第十九页,共48页
例1 已知: 三相负载 R、L、C
会不会出 现问题?
到大小不等的电压,有的超过用电设
一层楼 ...
备的额定电压,有的达不到额定电压 N
,都不能正常工作。比如,照明电路 中各相负载不能保证完全对称,所以 绝对不能采用三相三相制供电,而且 必须保证零线可靠。
二层 楼 B C
三层楼
28
第二十八页,共48页
Em sin( t + 120 °)
6
第六页,共48页
4.1.2 三相电源的表示法
1.瞬时值表达式
2.波形图
Em
eA = Em sin wt
eB = Em sin (wt - 120 °) eC = Em sin (wt - 240 °)
= Em sin(w t + 120 °)
eA eB eC
星形连接(Y接) 三角形连接(接)
相电流(IP): 流过每一相负载的电流 线电流(IL) : 流过每一根火线的电流
15
第十五页,共48页
4.2.1 负载星形连接的三相电路
1. 连接
三相四线制
A iA
三相四线
ZX Y
uA
i ZA
AN
N
iCN
i uB B i i uC C
B ZB
ZC
BN
C
相电流IP(负载上的电流):
三表法适用于三相四线制接法的不对称负载。
38
第三十八页,共48页
3. 两表法:(用两个功率表测量)
* P1
线电压
A
*W 1
*P2
电压
B
*W 2
线圈
第十九页,共48页
例1 已知: 三相负载 R、L、C
电工学第四章 变压器

END
I →S
节省金属材料(经济)
电力工业中常采用高压输电低压配电,实现节能 并保证用电安全。具体如下:
发电厂 10.5kV
输电线 220kV
升压
…
实验室
380 / 220V
降压
变电站 10kV
降压
降压
仪器 36V 降压
变压器的结构
铁心
+ i1
Φ
u1
i2
+
u2 ZL
–
一次
N1
–
N2 二次
绕组
绕组
单相变压器
阻抗变化后,扬声器得到更大功率
思考
变压器能用于直流变压吗?
与普通变压器相比
自耦变压器
普通变压器:原副边之间仅有磁联系
自耦变压器:原副边之间有磁、电联系
+
原副边电压电流的关系
U1 = N1 = K
+
U2 N2
_
_
I1 = N2 = 1 I2 N1 K
注意:一次、二次侧千万不能对调使用,以防变压器损坏。 因为N变小时,磁通增大,电流会迅速增加。
一次绕组 绕组: 二次绕组 铁心
变压器的电路
由高导磁硅钢片叠成
厚0.35mm 或 0.5mm 变压器的磁路
变压器的结构
变压器的分类
按用途分
电力变压器 (输配电用)
仪用变压器 电压互感器 电流互感器
整流变压器
三相变压器 按相数分
单相变压器 按制造方式 壳式
心=K
举例
收音机的扬声器可近似认为是纯电阻负载,设其值为8Ω
1)若直接连在内阻RS为800 Ω,电动势ES为10V的交流放大 器起上,求放大器输送给扬声器的功率。
电工学第四章
ห้องสมุดไป่ตู้为1/亨(H-1)。
§4-2 单相变压器和三相变压器
高压包
电力变压器
电视机中的高压包
变压器
电动车充电器
变压器的主要功能是改变交流电压的大小 ,此外还有改 变电流、变换阻抗等作用。
一、变压器的基本结构
变压器基本结构
变压器符号
变压器的主要组成部分是铁心和绕组。
工作时和电源相连的绕组称为一次绕组(原线圈、初 级绕组),与负载相连的线圈称为二次绕组(副线圈、
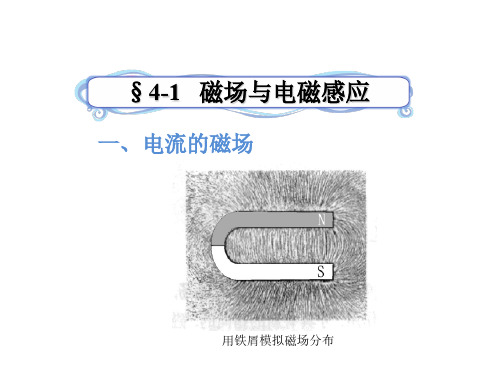
这种利用磁场产生电流的现象称为电磁感应 现象,产生的电流称为感应电流,产生感应电流 的电动势称为感应电动势。
2. 电磁感应定律
(1)楞次定律 在线圈回路中产生感应电动势和感应电流的
原因是由于磁铁的插入和拔出导致线圈中的磁通 发生了变化。
楞次定律指出了磁通的变化与感应电动势在 方向上的关系,即:感应电流产生的磁通总是阻
如果导体运动方向与磁感线方向有一夹角α,则 导体中的感应电动势为
e = Blvsinα
发电机就是应用导线切割磁感线产生感应电动 势的原理发电的,实际应用中,将导线做成线圈, 使其在磁场中转动,从而得到连续的电流。
在磁感应强度为B的匀强磁场中,有一长度 为l 的直导体AB,可沿平行导电轨道滑动。当导体以速 度v向左匀速运动时,试确定导体中感应电动势的方向
次级绕组)。
根据绕组和铁心的安装位置不同,可分为心式和壳式两种 。
心式
壳式
二、单相变压器的工作原理
忽略绕组电阻和各种电磁能量损耗的变压器称为理想变压器。
三、单相变压器的运行特性
1.变压器的空载运行
变压器的控制运行就是变压器一次绕组加额定电压 、二次绕组开路的工作状态,此时,二次绕组没有
§4-2 单相变压器和三相变压器
高压包
电力变压器
电视机中的高压包
变压器
电动车充电器
变压器的主要功能是改变交流电压的大小 ,此外还有改 变电流、变换阻抗等作用。
一、变压器的基本结构
变压器基本结构
变压器符号
变压器的主要组成部分是铁心和绕组。
工作时和电源相连的绕组称为一次绕组(原线圈、初 级绕组),与负载相连的线圈称为二次绕组(副线圈、
这种利用磁场产生电流的现象称为电磁感应 现象,产生的电流称为感应电流,产生感应电流 的电动势称为感应电动势。
2. 电磁感应定律
(1)楞次定律 在线圈回路中产生感应电动势和感应电流的
原因是由于磁铁的插入和拔出导致线圈中的磁通 发生了变化。
楞次定律指出了磁通的变化与感应电动势在 方向上的关系,即:感应电流产生的磁通总是阻
如果导体运动方向与磁感线方向有一夹角α,则 导体中的感应电动势为
e = Blvsinα
发电机就是应用导线切割磁感线产生感应电动 势的原理发电的,实际应用中,将导线做成线圈, 使其在磁场中转动,从而得到连续的电流。
在磁感应强度为B的匀强磁场中,有一长度 为l 的直导体AB,可沿平行导电轨道滑动。当导体以速 度v向左匀速运动时,试确定导体中感应电动势的方向
次级绕组)。
根据绕组和铁心的安装位置不同,可分为心式和壳式两种 。
心式
壳式
二、单相变压器的工作原理
忽略绕组电阻和各种电磁能量损耗的变压器称为理想变压器。
三、单相变压器的运行特性
1.变压器的空载运行
变压器的控制运行就是变压器一次绕组加额定电压 、二次绕组开路的工作状态,此时,二次绕组没有
电工学-第四章 正弦波振荡电路

R
1 jL jC j(L 1
C
)
( R L)
.
I
L/C
R j(L 1 )
C
+ L
•
U
C
_
R
2020/4/18
24
LC并联谐振回路的选频特性
•
Z
U
•
I
L/C
R j(L
1)
C
.
I
+ L
•
U
C
_
R
•
当LC并联回路发生谐振时,端电压 U 与总电
流
•
I
同相,即阻抗Z表现为纯电阻性。
谐振频率
o
Uf
•
F
Uo
•
•
由以上知,放大电路产生自激振荡的条件是 U f U i
••
•
则
AuF
Uo
•
U
•
f
U
•
f
1
Ui Uo Ui
2020/4/18
7
自激振荡
总结出自激振荡的条件:
(1)相位平衡条件
反馈电压
•
U
f
与输入电压
•
U
i
同相位,形成正反馈
(2)幅值平衡条件
反馈电压与输入电压大小相等: U f U i
C2
uf
首先判断相位平衡条件,见瞬时极性
2020/4/18
35
RB1
RC
+
RB2
uf
+
ube
RE
UCC
+
C1
L
+
C2
CE
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§4.2 正弦量的相量表示法
1.复数
A a jb
r A a 2 b2
+j b P
r
b arct an ( 2 ) a
O a +1
a r cos b r sin
2. 复数的四种形式
(1)复数的代数形式
A a jb
(2) 复数的三角形式 A r cos jr sin
时值与电流的瞬时值的乘积叫做该元件的瞬时
功率, 用小写字母p表示, 即
p ui pR uRiR U Rm sin t I Rm sin t U Rm I Rm U Rm I Rm sin t (1 cos2t ) 2 U R I R (1 cos2t )
2
5)平均功率 工程上都是计算瞬时功率的平均值, 即平 均功率, 用大写字母P表示。 周期性交流电路 中的平均功率就是其瞬时功率在一个周期内的 1 T 1 T 平均值, 即 P pdt U R I R (1 cos 2t )dt
1、测量交流电压,交流电流的仪表所指示的数字,电气 设备铭牌上的额定值都指的有效值。 2、定义交流电流I通过电阻R在一个周期内所产生的热量
和直流I通过同一电阻R在相同时间内所产生的热量相等, 则这个直流电流I的数值叫做交流I的有效值
一个周期内直流电通过电阻R所产生的热量为:
Q I RT
2
交流电通过同样的电阻R,在一个周期内所产生
(3) 0 , 称这两个正弦量同相; 12 1 2
(4) 12 1 2 , 称这两个正弦量反相; (5) 12 1 2
2
, 称这两个正弦量正交。
u u2
u u1 u2
u u1 u2
u u1 u2
u1
Байду номын сангаас
0
t 0
t
0
所以
u1 2U1 sin(t 1 ) 20sin(100t 60)V u2 2U 2 sin(t 2 ) 40sin(100t 30)V
§4.3
单一参数的交流电路
4.3.1 电阻元件的交流电路 1) 电阻元件上电流和电压之间的大小关系 若 uR U Rm sin(t )
A2的模
辐角
r2 ( 3) 4 5
2 2
4 2 arctan 126 .9 3
(在第二象限)
则A2的极坐标形式为 A2 5126.9
例8:写出复数A=100 30°的三角形式和代数形式。 解 : 三角形式A=100(cos30°+jsin30°)
代数形式A=100(cos30°+jsin30°)=86.6+j50
设两正弦量:
u1 U m1 sin(t 1 ) u2 U m 2 sin(t 2 )
12 (t 1 ) (t 2 ) 1 2
(1) 12 1 2 0 且 12 弧度U1达到振幅值 后,U2需经过一段时间才能到达,U1越前于U2; (2) 12 1 2 0 且 12 弧度,U1滞后U2;
t
0
2
3 2
2
t
=
(a)
(b)
i i1 i2
i
i1
i2
2
3 2 2
t
2
3 2
2
t
3 4
(c)
(d)
解:(a) 由图知θ1=0, θ2=90°,
φ12=θ1-θ2=-90°, 表明i1滞后于i2 90°。
(b) 由图知θ1=θ2, φ12=θ1-θ2=0, 表明二者
A B r1 1 r2 2 r1 r2 1 2 A r1 1 r1 1 2 B r2 2 r2
例9:求复数A=8+j6 , B=6-j8之和A+B及积A· B
解:
A+B=(8+j6)+(6-j8)=14-j2
A· B=(8+j6)(6-j8)
+j · I 30° O 45° +1
· U
例11:已知工频条件下, 两正弦量的有效值相量 分别为
U 1 10 2 60V ,U 2 20 2 30V
试求两正弦电压的解析式。
解:由于 2f 2 50 100rad / s
U1 10 2V , 1 60 U 2 20 2V , 2 30
2 m
I I ( dt cos2tdt) (T 0) 0 2T 0 2T
Im I 0.707I m 2 Um U 0.707 m U 2 U m 220 2 311 V
例1:电容器的耐压值为 250V, 问能否用在 220V的单相交流电源上? 解:因为 220V的单相交流电源为正弦电压, 其振幅值为311V, 大于其耐压值250V,电容可 能被击穿, 所以不能接在220V的单相电源上。 各种电器件和电气设备的绝缘水平(耐压 值), 要按最大值考虑。
例10:已知同频率的正弦量的解析式分别为
u 220 2 sin(t 45) i 10 sin(t 30 )
0
写出电流和电压的有效值相量 I 、 ,并绘出 U
相量图。
解:由解析式可得
10 I 30 5 2 30 A 2 220 2 U 45V 2
0
例4:已知选定参考方向下正弦量的波形图如图
所示, 试写出正弦量的解析式。
解:
u /V 250 200 u2 u1
u1 200sin(t u2 250sin(t
6 2
3 6
)V )V
0 3
t
两个同频率正弦量的相位之差, 称为相
位差, 用字母“φ”表示。
初 相 u 160 。
0
(2)
i 5 sin(314t 30 ) A
0
5 sin(314t 30 180 )
0 0
5 sin(314t 150 ) A
0
所以电流的振幅值 I m 5 A , 角频率 314rad / s , 初 相 i 150。
相位:
ωt+θ
初相θ: t=0时的相位 正弦量零值:负值向正值变化之间的零点。 若零点在坐标原点左侧, θ>0 若零点在坐标原点右侧, θ<0
i i1=Imsint
i
i2=Imsin( t+ 2)
i
i3=Imsin( t+ 6 )
i
i4=Imsin( t- 6)
0
t
t
0
t
(a)
(b)
(c)
(d)
同频率正弦量的几种相位关系
例5:已知
u 220 2 sin(t 235)V , i 10 2 sin(t 45) A
求u和i的初相及两者间的相位关系。
解:
u 220 2 sin(t 235)V 220 2 sin(t 125)V
正弦量瞬时值中的最大值, 叫振幅值, 也叫峰值。
用大写字母带下标“m”表示, 如Um、Im等。
交流电的有效值是根据它的热效应确定的。交流
电流I通过电阻R在一个周期内所产生的热量和直流电
流I通过同一电阻R在相同时间内所产生的热量相等,
则这个直流电流I的数值叫做交流电流i的有效值, 用
大写字母表示, 如I、U等。
第四章
正弦交流电路
所谓正弦交流电路,是指含有正弦电源
(激励)而且电路各部分所产生的电压和电流
(响应)均按正弦规律变化的电路。
§4.1
正弦交流电:
正弦电压与电流
电压、电流均随时间按正弦函数规律变化。
u
Um 0 (T ) 2 T
t
正弦量的三要素:频率、幅值、相位。
1. 振幅值(最大值)、有效值
2
0
t
6
0
t
0 6
t
(a)
(b)
(c)
(d)
几种不同计时起点的正弦电流波形
例2:一正弦电压的初相为60°, 有效值为100V,
试求它的解析式。
解:因为 U 100V , 所以其最大值为 100 2V
则电压的解析式为
u 100 2 sin(t 60)V
例3:在参考方向下, 已知两正弦量的解析式
(3) 复数的指数形式
A re
j
(4) 复数的极坐标形式 A r
例7:写出复数A1=4-j3, A2=-3+j4的极坐标形式。
解:A1的模 r1 42 ( 3)2 5
3 辐角 1 arctan 4 36.9 (在第四象限)
则A1的极坐标形式为 A1=5 -36.9°
所以电压u的初相角为-125°, 电流i的初 相角为45°。 ui u i 125 45 170 0
表明电压u 滞后于电流I 170°。
例6:分别写出图中各电流i1、i2的相位差, 并
说明i1 与i2的相位关系。
i i1 2 0 i i2 3 2 i2 i1 2
热量:
Q i Rdt
2 0
T
根据定义,这两个电流所产生的热量应相等,即
I RT i 2 R dt
2 0
T
1 T 2 I 0 i dt T 1 T 2 U 0 u dt T
1 I T
2 m
T
0 T
I sin tdt
2 m 2 T
