2020初中七年级数学下册新教材期中复习课件人教版
2020-2021学年七年级数学人教版下册 第七章 7.1.1 有序数对 课件(共59张PPT)

11.(2020·泰州)以水平数轴的原点 O 为圆心,过正半轴 Ox 上的 每一刻度点画同心圆,将 Ox 逆时针依次旋转 30°,60°,90°,…, 330°得到 11 条射线,构成如图所示的“圆”坐标系,点 A、B 的坐标分别表示为(5,0°),(4,300°),则点 C 的坐标表示为
合作探究
例2 如图是某教室学生座位的平面图.
(1)请说出王明和陈帅的座位位置; (2)若用(3,2)表示第3排第2列的位置,那么(5,5)
表示什么位置?王明和陈帅的座位位置可以怎 样表示?
(3)请说出(3,3)和(4,8)分别表示哪两位同学的座位 位置;
(4)(2,3)和(3,2)表示的位置相同吗?一般地,若 a≠b,(a,b)与(b,a)表示的位置相同吗?
4.用 7 和 8 组成一个有序数对,可以写成( D )
A.(7,8)
B.(8,7)
C.7,8 或 8,7 D.(7,8)或(8,7)
5.下列关于有序数对的说法正确的是( C ) A.(3,2)与(2,3)表示相同的位置 B.(a,b)与(b,a)表示的位置一定不同 C.(3,-2)与(-2,3)是表示不同的位置的两个有序数对 D.(4,4)与(4,4)表示两个不同的位置
3 小明坐在第5行第6列,简记为(5,6),小刚
坐在第7行第4列,应记为( A )
A.(7,4)
B.(4,7)
C.(7,5)
D.(7,6)
4 如图所示,小亮从学校到家所走最短路线是( B ) (3,2)→(3,1)→(0,1) B.(2,2)→(2,1)→(1,1)→(0,1) C.(2,2)→(2,3)→(0,3)→(0,1) D.(2,2)→(2,0)→(0,0)→(0,1)
2020春七年级数学下册 5.1.3 同位角、内错角、同旁内角课件 (新版)新人教版

有几对同旁内角,几对内错角,几对同位角?
共有18对同旁内角, 18对内错角,36对同位角.
提升拓展·考向导练
由于两条直线被第三条直线所截会出现2对同旁内角, 2对内错角,4对同位角,因此,我们主要判断出现多 少次两条直线被第三条直线所截的情况.取a、b两条 直线,截线可以分别是直线d,e,取b,c或a,c两条 直线,截线同样是直线d,e,这样共有6种情况.取 直线d,e时,截线可以分别是直线a,b,c,这时有3 种情况,因此,共有9种情况.
解此题可以运用分离图形法,将图形分离出三种情况 讨论:AB、AC被DE所截,AC、DE被AB所截,AB、 DE被AC所截.
提升拓展·考向导练
3
利用邻补角的性质说明“三线八角”的数量关系 14.如图,
(1)∠2与∠B是什么角?若∠1=∠B,则∠2与 ∠B有何数量关系?请说明理由;
(2)∠3与∠C是什么角?若∠4+∠C=180°,则∠3与 ∠C有何数量关系?请说明理由.
提升拓展·考向导练
(1)同旁内角.∠2+∠B=180°. 理由:因为∠1+∠2=180°,∠1=∠B, 所以∠2+∠B=180°.
2020-2021学年七年级数学下册教材配套教学课件之邻补角、对顶角的定义及性质

1 2
6.如图,直线AB,CD相交于点O, ∠EOC=70°, OA平分∠EOC,求 ∠BOD的度数.
解:∵OA平分∠EOC,
∴∠AOC=
1 2
∠EOC=35°,
∴∠BOD=∠AOC=35°.
E
D
A
B
O
C
拓展题:观察下列各图,寻找对顶角(不含平角)
思考 :剪刀剪东西的过程中,你能说说∠AOC与∠AOD,∠AOC与∠BOD这两 对角的位置保持怎样的关系吗?
A
C
O
∠AOC和∠AOD有一条公共边AO,且∠AOC的
另一边是∠AOD另一边的反向延长线.
∠AOC和∠BOD有公共顶点,且∠AOC的两边 分别是∠BOD两边的反向延长线.
DB
一、邻补角的概念 邻补角:如果两个角有一条公共边,它们的另一边互为__反__向__延__长__线__,那 么这两个角互为邻补角.图中∠1的邻补角有__∠__2_,_∠__3___.
解:(1)∠AOC的邻补角是∠AOD和 ∠COB;∠BOE的邻补角是 ∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB; ∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°; ∠COB=180°-∠AOC=130°.
D E
A
O
B
F
C
5. 在下图中,花坛转角(红色标注的角)按图纸要求为135°;施工结束 后,要求你检测它是否合格?请你设计检测的方法.
不是
12
是
1( )2
不是
12
不是
3.找出图中∠AOE的邻补角及对顶角,若没有请画出.
人教版七年级下册数学作业课件 第五章 第1课时 平行线的性质 (2)

14.(2020·张家界中考)如图,∠AOB 的一边 OA 为平 面镜,∠AOB=38°,一束光线(与水平线 OB 平行)从 点 C 射入经平面镜反射后,反射光线落在 OB 上的点 E 处,其中∠1=∠2,则∠DEB 的度数是 76° .
15.如图,已知 AB∥CD,直线 EF 分别交直线 AB、 CD 于点 E、F,∠EFB=∠B,FH⊥FB. (1)若∠B=20°,求∠DFH 的度数; 解:∵AB∥CD,∠B=20°, ∴∠B=∠BFD=20°. ∵FH⊥FB, ∴∠BFH=90°. ∴∠DFH=∠BFH-∠BFD=70°.
10.如图①是大众汽车的图标,图②反映的是其中直 线间的关系,并且 AC∥BD,AE∥BF.试问:∠A 与 ∠B 的大小关系如何?为什么? 解:∠A=∠B.理由如下: 因为 AC∥BD, 所以∠A=∠DOE. 又因为 AE∥BF, 所以∠DOE=∠B.所以∠A=∠B.
11.(2020·枣庄中考)一副直角三角板如图放置,点 C 在 FD 的延长线上,AB∥CF,∠F=∠ACB=90°,则 ∠DBC 的度数为( B ) A.10° B.15° C.18° D.30°
6.如图,直线 AB∥CD,BC 平分∠ABD,∠1=54°, 求∠2 的度数. 解:如图,∵直线 AB∥CD, ∴∠3=∠1=54°. ∵BC 平分∠ABD,∴∠4=∠3=54°. 又∵CD∥AB, ∴∠2=∠CDB =180°-∠3 -∠4=180°- 54°- 54°=72°.
7.如图,点 A、B、C、D 在一条直线上,CE 与 BF 交于点 G,∠A=∠1,CE∥DF.试说明:∠E=∠F. 解:∵CE∥DF, ∴∠2=∠F. ∵∠A=∠1,∴AE∥BF. ∴∠2=∠E.∴∠E=∠F.
(2) 如图②,∠DCE 的平分线 CG 的反向延 长线交 ∠ABE 的平分线 BF 于 F.若 BF∥CE,∠BEC=26°, 求∠BFC 的度数. 解:∵FB∥CE, ∴∠FBE=∠BEC=26°. ∵BF 平分∠ABE, ∴∠ABE=2∠FBE=52°. 由(1)得∠DCE=180°-∠ABE+∠BEC =180°-52° +26°=154°.
七年级数学下册期中复习课件

第五章过关测试 ┃ 知识归纳
4.平行线的判定
同位角 定理 1: 相等,两直线平行. _____________________
定理 2: 定理 3:
内错角 相等,两直线平行. _____________________ 同旁内角 互补,两直线平行. _____________________
七年级数学下册期中复习课件
数学·新课标(RJ)
第五章过关测试 ┃ 知识归纳
┃知识归纳┃
1.相交线 邻补角:若两角有一条公共边,它们的另一边互为反向延 长线,具有这种关系的两个角,互为邻补角. 对顶角:若两个角有一个公共顶点,且两角的两边互为反 向延长线,具有这种位置关系的两个角,互为对顶角. 对顶角的性质:对顶角____相____等_________.
数学·新课标(RJ)
第五章过关测试 ┃ 考点攻略
► 考例点六6 如平图移5-7 所示,一块矩形 ABCD 场地的长 AB
为 102 米,宽 AD 为 51 米,从 A、B 两处入口的小路宽 都
为 1 米,两小路汇合处路口宽为 2 米,除小路外,其余部
分植草坪,则草坪的面积为
(C )
图 5-7 A.5050 平方米 B.4900 平方米 C.5000 平方米 D.4998 平方米
因为 AB∥CD,所以 EF∥CD,
所以∠C+∠FEC=180°.所以∠FEC=180°-52°=128°,
所以∠FEA=∠FEC-∠AEC
图5-6
=128°-28°=100°;因为 EF∥AB,
所以∠EAB=180°-∠FEA=180°-100°=80°.
数学·新课标(RJ)
第五章过关测试 ┃ 考点攻略
人教版2020七年级数学下册期中综合复习培优训练题1(附答案详解)

人教版2020七年级数学下册期中综合复习培优训练题1(附答案详解)1.和数轴上的点一一对应的是( )A .整数B .实数C .有理数D .无理数2.如图,已知直线AB ∥CD ,直线l 与直线AB 、CD 相交于点,E 、F ,将l 绕点E 逆时针旋转40°后,与直线AB 相交于点G ,若∠GEC=80°,那么∠GFE=( )A .60°B .50°C .40°D .30°3.如图,在平面直角坐标系上有个点()1,0P ,点P 第1次向上跳运1个单位至点()11,1P 紧接着第2次向左跳动2个单位至点()21,1P-,第3次向上跳动1个单位,第4次向右跳运3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位, ⋯,依此规律跳动下去,点P 第2016次跳动至点2016P 的坐标是( )A .()505,1008B .()505,1008-C .()504,1007D .()504.1007- 4.下列命题正确的个数是( )①等腰三角形的腰长大于底边长;②三条线段a 、b 、c ,如果a b c +>,那么这三条线段一定可以组成三角形;③等腰三角形是轴对称图形,它的对称轴是底边上的高;④面积相等的两个三角形全等.A .0个B .1个C .2个D .3个5.下列各数是无理数的是( )A .4B .2.2020020002C .39D .﹣16.一个运算程序输入后,得到的结果是221x -,则这个运算程序是( )A.先乘2,然后平方,再减去1 B.先平方,然后减去1,再乘2C.先平方,然后乘2,再减去1 D.先减去1,然后平方,再乘27.如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2017的横坐标为()A.1010B.2C.1D.﹣10068.下列计算结果正确的是:( )A.B.C.D.9.我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形的边在轴上,的中点是坐标原点固定点,,把正方形沿箭头方向推,使点落在轴正半轴上点处,则点的对应点的坐标为()A.B.C.D.10.若点A到直线l的距离为7cm,点B到直线l的距离为3cm,则线段AB的长度为()A.10cm B.4cm C.10cm或4cm D.至少4cm11.关于x轴、y轴或远点对称的点的坐标的特征点P与点p′关于x轴对称⇔_____坐标相等,_____坐标互为相反数点P与点p′关于y轴对称⇔______坐标相等,_____坐标互为相反数点P与点p′关于原点对称⇔___________坐标均互为相反数12.在平面直角坐标系中,点P(﹣2,6)在第____象限.13.已知点A(-2,0),B(3,0),则S∆ABC=_______.14.如图,在一次军棋比赛中,如果团长所在的位置的坐标为(2,-5),司令所在的位置的坐标为(4,-2),那么工兵所在的位置的坐标为_________.15.若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为______. 16.已知31x 0216+=,则x=_______ 17.借助于计算器计算,可求2243+;224433+;22444333+…… 仔细观察上面几题的计算结果,试猜想2220092009444333⋅⋅⋅+⋅⋅⋅n n 的结果为_________. 18.已知|x ﹣y+2|+2x y +-=0,则x 2﹣y 2的值为______.19.在平面坐标系中,正方形ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0,2),延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ,延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1,…按这样的规律进行下去,第2017个正方形的面积为__________。
人教版七年级数学下册精品课件 第八章 8.3 第1课时 利用二元一次方程组解决实际问题

40 y
370
解得
x 25,
y15.
答:甲种票25张,乙种票15张.
2020/6/11
3.课本中介绍我国古代数学名著《孙子算经》上有这 样的一道题:今有鸡兔同笼,上有三十五头,下有 九十四足,问鸡兔各多少只?
解:设鸡有x只,兔有y只. 则2x xy4y3594
解得
x 23,
y12.
答:鸡有23只,兔有12只.
2020/6/11
剧情发展:随着养牛场规模逐渐扩大,李大叔需聘 请饲养员协助管理现有的42头大牛和20头小牛,已 知甲种饲养员每人可负责8头大牛和4头小牛,乙种 饲养员每人可负责5头大牛和2头小牛,请问李大叔 应聘请甲乙两种饲养员各多少人?
解:设李大叔应聘请甲种饲养员x人,乙种饲养员 y人,则:
根据题意,可列方程组:
x 60
y 80
10
x
y
15.
60 40
解方程组,得
x 300
y400
所以,小明家到学校的距离为700m.
2020/6/11
方法二(间接设元法) 解:设小华下坡路所花时间为xmin,
上坡路所花时间为ymin.
平路 坡路 距离 距离
上学 60(10 x) 80x
放学 60(15 y) 40 y
2020/6/11
02 横着画,把宽分成两段,则长不变
D
200m
C 解:过点E作EF⊥AD,交
BC于点F.
x
甲种作物 200x 100m
设DE=xm,AE=ym.
E y
F
乙种作物 200y
根据题意列方程组为
x+y=100
A
Hale Waihona Puke B200x:400y=3:4
2020人教版七年级下册数学《期中考试试题》附答案
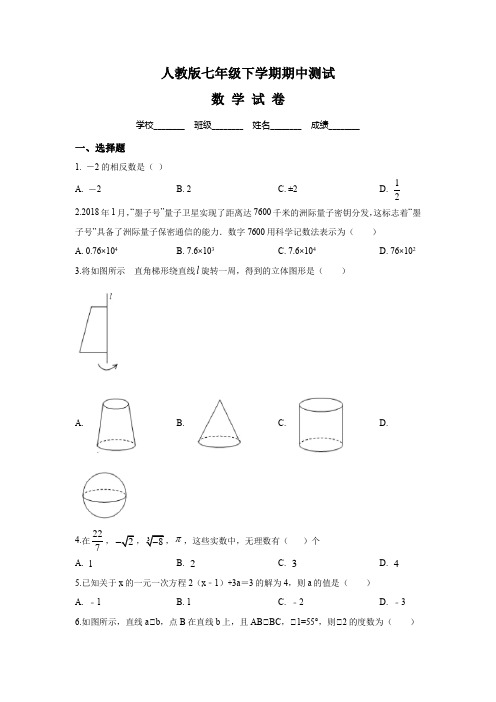
人教版七年级下学期期中测试数 学 试 卷学校________ 班级________ 姓名________ 成绩________一、选择题1. -2的相反数是( )A. -2B. 2C. ±2D. 122.2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为( )A. 0.76×104B. 7.6×103C. 7.6×104D. 76×102 3.将如图所示直角梯形绕直线l 旋转一周,得到的立体图形是( )A.B. C.D.4.在227,π,这些实数中,无理数有( )个 A. 1 B. 2 C. 3 D. 4 5.已知关于x 的一元一次方程2(x ﹣1)+3a =3的解为4,则a 的值是( ) A. ﹣1 B. 1 C. ﹣2 D. ﹣36.如图所示,直线a∥b ,点B 在直线b 上,且AB∥BC ,∥1=55°,则∥2的度数为( )A. 55°B. 45°C. 35°D. 25° 7.半面直角坐标系中,点A (-2,1)到y 轴的距离为( )A. -2B. 1C. 2D. 8.下列计算正确的是( )A.B. C. ∥2 D. ∥±29.把不等式x+2>4的解集表示在数轴上,正确的是 ( )A. B. C. D.10.下列命题中是假命题的是( )A. 若a >b ,则a+3>b+3B. 若a >b ,则-a <-bC. 若a >b ,则a 2>b 2D. 若a >b ,则33a b > 11.《九章算术》是中国传统数学名著,其中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛,5只羊,值金8两.问每头牛、每只羊各值金多少两?”若设每头牛、每只羊分别值金x 两、y 两,则可列方程组为( )A. 5210258x y x y +=⎧⎨+=⎩B. 5210258x y x y -=⎧⎨-=⎩C. 5210258x y x y +=⎧⎨-=⎩D.5282510x y x y +=⎧⎨+=⎩ 12.已知方程ax+by=10的两个解是10x y =-⎧⎨=⎩,15x y =⎧⎨=⎩,求a+b 的值( ) A. 6 B. -6 C. 1 D. -1二、填空题13.比较实数的大小:3.14.在平面直角坐标系中,已知,点A(m-2,3+m)x轴上,则m=______.15.如图:已知:a∥b,∥1=80°,则∥2=______.16.如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,则线段AD的长为______cm.17.不等式8x2>1的解集是______.18.如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标.如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2),那么,2019的对应点的坐标是______.三、解答题19.求值:(-1)2018-|1|20.如图,在平面直角坐标系中,∥ABC的三个顶点的坐标分别为:A(-1,2),B(-2,-1),C(2,0).(1)作图:将∥ABC先向右平移4个单位,再向上平移3个单位,则得到∥A1B1C1,作出∥A1B1C1;(不要求写作法)(2)写出下列点的坐标:A1______;B1______;C1______.(3)求∥ABC面积.21.已知关于x,y方程组4x y53x y9-=⎧⎨+=⎩和13418ax byx by+=-⎧⎨+=⎩有相同的解.(1)求出它们相同的解;(2)求(2a+3b)2019的值.22.某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:(1)该商场购进甲、乙两种矿泉水各多少箱?(2)全部售完500箱矿泉水,该商场共获得利润多少元?23.如图,在∥ABC中,CD∥AB,垂足为D,点E在BC上,EF∥AB,垂足为F.(1)CD 与EF 平行吗?为什么?(2)如果∥1=∥2,CD 平分∥ACB ,且∥3=120°,求∥ACB 与∥1的度数.24.阅读材料:我们把多元方程(组)的正整数解叫做这个方程(组)的“好解”例如:18x y =⎧⎨=⎩就是方程3x+y=11的一组“好解”;123x y z =⎧⎪=⎨⎪=⎩是方程组3206x y z x y z ++=⎧⎨++=⎩的一组“好解”. (1)请直接写出方程x+2y=7所有“好解”;(2)关于x ,y ,k 的方程组1551070x y k x y k ++=⎧⎨++=⎩有“好解“吗?若有,请求出对应的“好解”;若没有,请说明理由;(3)已知x ,y 为方程33x+23y=2019的“好解”,且x+y=m ,求所有m 的值.25.如图,以直角三角形AOC 的直角顶点O 为原点,以OC ∥OA 所在直线为x 轴和y 轴建立平面直角坐标系,点()0,A a ∥(),0C b 20b -=∥()1则C 点的坐标为______∥A 点的坐标为______∥()2已知坐标轴上有两动点P ∥Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.AC 的中点D 的坐标是()1,2,设运动时间为(0)t t >秒.问:是否存在这样的t ,使ODP ODQ S S =V V ?若存在,请求出t 的值;若不存在,请说明理由. ()3点F 是线段AC 上一点,满足FOC FCO ∠=∠,点G 是第二象限中一点,连OG ,使得.AOG AOF ∠=∠点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACE OEC∠+∠∠的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.的26.已知a+1是4的算术平方根,b-1是27的立方根,化简求值:2(2a-b2)-(4a-a2).答案与解析一、选择题1. -2的相反数是()A. -2B. 2C. ±2D. 1 2【答案】B【解析】【分析】直接利用相反数的定义进而分析得出答案.【详解】解:-2的相反数是:2.故选:B.【点睛】此题主要考查了相反数,正确把握相反数的定义是解题关键.2.2018年1月,“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发,这标志着“墨子号”具备了洲际量子保密通信的能力.数字7600用科学记数法表示为()A. 0.76×104B. 7.6×103C. 7.6×104D. 76×102【答案】B【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.【详解】解:7600=7.6×103,故选B.【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是()A. B. C. D.【答案】A【解析】【分析】根据直角梯形上下底不同得到旋转一周后上下底面圆的大小也不同,进而得到旋转一周后得到的几何体的形状.【详解】题中的图是一个直角梯形,上底短,下底长,绕对称轴旋转后上底形成的圆小于下底形成的圆,因此得到的立体图形应该是一个圆台.故选:A .【点睛】本题主要考查学生是否具有基本的识图能力,以及对点、线、面、体之间关系的理解.4.在227,π,这些实数中,无理数有( )个 A. 1B. 2C. 3D. 4 【答案】B【解析】【分析】根据无限不循环小数是无理数的定义进行判断选择即可.2=-,所以在227,π,这些实数中,无理数有,π共两个,故答案选B.【点睛】本题考查的是无理数的概念,能够准确区别无限不循环小数是解题的关键. 5.已知关于x 一元一次方程2(x ﹣1)+3a =3的解为4,则a 的值是( )A. ﹣1B. 1C. ﹣2D. ﹣3【答案】A【解析】【分析】把x=1代入方程,即可得到一个关于a 的方程,即可求解.【详解】把x =4代入方程得()24133,a -+=解得: 1.a =-故选∥A.【点睛】考查方程解的概念,使方程左右两边相等的未知数的值就是方程的解. 6.如图所示,直线a∥b ,点B 在直线b 上,且AB∥BC ,∥1=55°,则∥2的度数为()A. 55°B. 45°C. 35°D. 25°【答案】C【解析】【分析】先根据余角的定义求出∠3的度数,再由平行线的性质即可得出结论.【详解】解:∵∥1=55°,∥ABC=90°,∴∥3=90°-55°=35°.∵a ∥b ,∴∥2=∥3=35°. 的故选:C.【点睛】本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.7.半面直角坐标系中,点A(-2,1)到y轴的距离为()A. -2B. 1C. 2【答案】C【解析】【分析】根据点到y轴的距离等于横坐标的绝对值解答.【详解】解:∵点A(-2,1),∴点A(-2,1)到y轴的距离=|-2|=2,故选:C.【点睛】本题考查了点的坐标,熟记点到y轴的距离等于横坐标的绝对值是解题的关键.8.下列计算正确的是()∥2∥±2【答案】A【解析】【分析】根据算数平方根的定义可判断:若一个正数的平方等于a,则这个正数就是a的算数平方根【详解】A=2故B是错误C=4故C、D都是错误所以本题答案应为:A【点睛】算术平方根的定义是本题的考点,注意区别算数平方根和平方根.9.把不等式x+2>4的解集表示在数轴上,正确的是( )A. B.C.D.【答案】B【解析】 试题分析:移项得,x >4-2,合并同类项得,x >2,把解集画在数轴上,故选B .考点: 在数轴上表示不等式的解集.10.下列命题中是假命题的是( )A. 若a >b ,则a+3>b+3B. 若a >b ,则-a <-bC. 若a >b ,则a 2>b 2D. 若a >b ,则33a b > 【答案】C【解析】【分析】利用不等式的性质分别判断后即可确定正确的选项.【详解】解:A.若a >b ,则a+3>b+3,正确,是真命题;B.若a >b ,则-a <-b ,正确,是真命题;C.若a >b ,则a 2>b 2不一定成立,错误,是假命题;D.若a >b ,则33a b >,正确,是真命题; 故选:C.【点睛】本题考查了命题与定理的知识,解题的关键是了解不等式的性质,难度不大. 11.《九章算术》是中国传统数学名著,其中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛,5只羊,值金8两.问每头牛、每只羊各值金多少两?”若设每头牛、每只羊分别值金x 两、y 两,则可列方程组为( )A. 5210258x y x y +=⎧⎨+=⎩B. 5210258x y x y -=⎧⎨-=⎩C. 5210258x y x y +=⎧⎨-=⎩D.5282510x y x y +=⎧⎨+=⎩ 【答案】A【解析】 【分析】每头牛、每只羊分别值金x 两、y 两,根据“5头牛,2只羊,值金10两;2头牛,5只羊,值金8两”列出方程组即可得答案.【详解】由题意可得,5210258x y x y +=⎧⎨+=⎩∥ 故选A∥【点睛】本题考查由实际问题抽象出二元一次方程组,解答本题的关键是明确题意,找准等量关系列出相应的方程组.12.已知方程ax+by=10的两个解是10x y =-⎧⎨=⎩,15x y =⎧⎨=⎩,求a+b 的值( ) A. 6B. -6C. 1D. -1【答案】B【解析】【分析】把方程的两个解代入,则可得到一个关于a 和b 的二元一次方程组,解答即可. 【详解】解:把两个解10x y =-⎧⎨=⎩,15x y =⎧⎨=⎩分别代入方程ax+by=10中, 得:10510a a b -=⎧⎨+=⎩, 解得:104a b =-⎧⎨=⎩, ∴a+b=-10+4=-6,故选:B.【点睛】本题考查了二元一次方程的解,解题关键把方程的两个解代入原方程,得到关于a和b的二元一次方程组,再求解.二、填空题13.比较实数的大小:.【答案】>【解析】【分析】此题涉及的知识点是二次根式的性质,根据二次根式的性质,将3化成根号的形式即可比较出两实数的大小.【详解】将39>5,所以3【点睛】此题重点考察学生对二次根式的理解,熟练掌握二次根式的性质是本题解题的关键.14.在平面直角坐标系中,已知,点A(m-2,3+m)x轴上,则m=______.【答案】-3【解析】【分析】根据x轴上点的纵坐标为0列式计算即可得解.【详解】解:∵点A(m-2,3+m)在x轴上,∴3+m=0,解得:m=-3.故答案为:-3.【点睛】本题考查了点的坐标,熟记x轴上点的纵坐标为0是解题的关键.15.如图:已知:a∥b,∥1=80°,则∥2=______.【答案】100°【解析】【分析】利用两直线平行,同位角相等和邻补角的定义求∠2的度数.【详解】解:∵a∥b,∴∥3=∥1=80°.∥∥2=180°-∥3=100°.故答案为:100°.【点睛】本题比较简单,考查的是平行线的性质和邻补角的定义.16.如图,已知C点为线段AB的中点,D点为BC的中点,AB=10cm,则线段AD的长为______cm.【答案】7.5【解析】【分析】根据C点为线段AB的中点,D点为BC的中点,可知AC=CB=12AB,CD=12CB,AD=AC+CD,又AB=10cm,继而即可求出答案.【详解】解:∵C点为线段AB的中点,D点为BC的中点,AB=10cm,∴AC=CB=12AB=5cm,CD=12BC=2.5cm,∴AD=AC+CD=5+2.5=7.5cm.故答案为:7.5.【点睛】本题考查了比较线段的长短的知识,注意理解线段的中点的概念.利用中点性质转化线段之间的倍分关系是解题的关键.17.不等式8x2->1的解集是______.【答案】x<6【解析】【分析】先去分母,去括号,然后移项,合并同类项,系数化成1即可.【详解】解:8x1 2->,82x ->,28x->-,x->-,6x<,6x<.故答案为:6【点睛】本题考查了解一元一次不等式,能正确根据不等式的性质进行变形是解此题的关键.18.如图,把自然数按图的次序排在直角坐标系中,每个自然数都对应着一个坐标.如1的对应点是原点(0,0),3的对应点是(1,1),16的对应点是(-1,2),那么,2019的对应点的坐标是______.【答案】(16,-22)【解析】【分析】观察图的结构,发现所有奇数的平方数都在第四象限的角平分线上.依此先确定2025的坐标为(22,-22),再根据图的结构求得2019的坐标.【详解】解:观察图的结构,发现所有奇数的平方数都在第四象限的角平分线上.452=2025,由2n+1=45得n=22,∴2025的坐标为(22,-22),由9的对应点是(1,1),在同一直线上且在第四象限,9的前面有0个点,25的对应点是(2,2),在同一直线上且在第四象限,10的前面有1个点,∴2019在同一直线上且在第四象限,2019的前面有21个点,2019=2025-6,22-6=16,∴2019坐标是(16,-22).故答案为:(16,-22).【点睛】本题考查了点的坐标,找到所有奇数的平方数所在位置是解题的关键.三、解答题19.求值:(-1)2018-|1|【答案】2【解析】【分析】直接利用绝对值的性质以及二次根式的性质分别化简得出答案.【详解】解:原式=1--1)-2+2=1+1-2+2=2【点睛】此题主要考查了实数运算,正确化简各数是解题关键.20.如图,在平面直角坐标系中,∥ABC的三个顶点的坐标分别为:A(-1,2),B(-2,-1),C(2,0).(1)作图:将∥ABC先向右平移4个单位,再向上平移3个单位,则得到∥A1B1C1,作出∥A1B1C1;(不要求写作法)(2)写出下列点的坐标:A1______;B1______;C1______.(3)求∥ABC的面积.【答案】(1)详见解析;(2)(3,5),(2,2),(6,3);(3)5.5【解析】【分析】(1)、(2)利用点平移的坐标变换规律,然后写出A1、B1、C1的坐标,然后描点、连线即可;(3)用一个矩形的面积分别减去三个直角三角形的面积可计算出△ABC的面积.【详解】解:(1)如图,∥A1B1C1为所作.(2)写出下列点的坐标:A1坐标为(3,5);B1坐标为(2,2);C1坐标为(6,3).故答案为:(3,5),(2,2),(6,3);(3)∥ABC 的面积=4×3-12×1×3-12×4×1-12×3×2=5.5. 【点睛】本题考查了作图-平移变换:确定平移后图形基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.21.已知关于x ,y 的方程组4x y 53x y 9-=⎧⎨+=⎩和13418ax by x by +=-⎧⎨+=⎩有相同的解. (1)求出它们相同的解;(2)求(2a+3b )2019的值.【答案】(1)x 2y 3=⎧⎨=⎩;(2)-1 【解析】【分析】(1)求出第一个方程组的解即可;(2)求出a 、b 的值,再代入求出即可.【详解】解:(1)∵解方程组4x y 5{3x y 9-=+=得:x 2{y 3==, ∴它们的相同的解是x 2{y 3==; (2)把x 2{y 3==代入方程组ax by 1{3a 4by 18+=-+=, 得:2a 3b 1{612b 18+=-+=, 解得:a 2{b 1=-=, ∴(2a+3b )2019=[2×(-2)+3×1]2019=-1.【点睛】本题考查了二元一次方程组的解,解二元一次方程组和求代数式的值等知识点,能求出两方程组的相同的解是解此题的关键.22.某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如的的(1)该商场购进甲、乙两种矿泉水各多少箱?(2)全部售完500箱矿泉水,该商场共获得利润多少元?【答案】(1)商场购进甲种矿泉水300箱,购进乙种矿泉水200箱(2)该商场共获得利润6600元【解析】【详解】(1)设商场购进甲种矿泉水x箱,购进乙种矿泉水y箱,由题意得:500{243313800 x yx y+=+=,解得:300 {200 xy==,答:商场购进甲种矿泉水300箱,购进乙种矿泉水200箱;(2)300×(36−24)+200×(48−33)=3600+3000=6600(元),答:该商场共获得利润6600元.23.如图,在∥ABC中,CD∥AB,垂足为D,点E在BC上,EF∥AB,垂足为F.(1)CD与EF平行吗?为什么?(2)如果∥1=∥2,CD平分∥ACB,且∥3=120°,求∥ACB与∥1的度数.【答案】(1)详见解析;(2)∥ACB=120°,∥1=60°【解析】(1)根据垂直于同一直线的两直线平行判定;(2)根据平行线的性质和已知求出∠1=∠2=∠DCB,推出DG∥BC,根据平行线的性质得出∠ACB的度数即可;再由∠ACB的度数和已知得∠DCG的度数,利用三角形的外角的性质即可求出∠1的度数.【详解】解:(1)CD∥EF,理由是:∵CD⊥AB,EF⊥AB,∴CD∥EF;(2)∵CD∥EF,∴∥2=∥DCB,∵∥1=∥2,∴∥1=∥DCB,∴DG∥BC,∴∥ACB=∥3,∵∥3=120°,∴∥ACB=120°.∵CD平分∥ACB,∴∥DCG=12∥ACB=60°,∵∥3=∥1+∥DCG,∴∥1=120°-60°=60°.∴∥ACB=120°,∥1=60°.【点睛】本题考查了对平行线的性质和判定的应用,三角形的内角和定理以及三角形外角的性质,角平分线的定义.熟练掌握平行线的判定与性质是解决本题的关键.24.阅读材料:我们把多元方程(组)的正整数解叫做这个方程(组)的“好解”例如:18 xy=⎧⎨=⎩就是方程3x+y=11的一组“好解”;123xyz=⎧⎪=⎨⎪=⎩是方程组3206x y zx y z++=⎧⎨++=⎩的一组“好解”.(1)请直接写出方程x+2y=7的所有“好解”;(2)关于x,y,k的方程组1551070x y kx y k++=⎧⎨++=⎩有“好解“吗?若有,请求出对应的“好解”;若没有,请说明理由;(3)已知x,y为方程33x+23y=2019的“好解”,且x+y=m,求所有m的值.【答案】(1)x1y3=⎧⎨=⎩,x3y2=⎧⎨=⎩,x5y1=⎧⎨=⎩;(2)x3y7=⎧⎨=⎩;(3)63,73,83【解析】【分析】(1)根据“好解”的定义,求方程的正整数解,先把方程做适当的变形,再列举正整数代入求解;(2)解方程组求得554{5594kxky+=-=,,根据“好解”的定义得5519k-<<,在范围内列举正整数代入求解;(3)根据题意,联立方程组,求出方程组的解,根据“好解”的定义得到k的取值范围,在范围内列举正整数代入求解.【详解】解:(1)由x+2y=7,得y=7x2-(x.y为正整数).∵x0 {7x2->>,即0<x<7,∴当x=1时,y=3;当x=3时,y=2;当x=5时,y=1;∴方程x+2y=7的“好解”有x1{y3==,x3{y2==,x5{y1==;(2)由x y k15{x5y10k70++=++=,解得554{5594kxky+=-=,∵55k 04{559k 04+->>,即-1<k <559, ∴当k=3时,x=5,y=7,∴方程组x y k 15{x 5y 10k 70++=++=有“好解“, ∴“好解”为x 3{y 7==;(3)由33x 23y 2019{x y m +=+=,解得201923m x 10{33m 2019y 10-=-=, ∵201923m 010{33m 2019010-->>,即201933<m <201923, ∴当m=63时,x=57,y=6;m=73时,x=38,y=39;m=83时,x=11,y=72;∴所有m 的值为63,73,83.【点睛】本题考查了三元一次方程组的应用,解题关键是要理解方程(组)的“好解”条件,根据条件求解.25.如图,以直角三角形AOC 的直角顶点O 为原点,以OC ∥OA 所在直线为x 轴和y 轴建立平面直角坐标系,点()0,A a ∥(),0C b20b -=∥()1则C 点的坐标为______∥A 点的坐标为______∥()2已知坐标轴上有两动点P ∥Q 同时出发,P 点从C 点出发沿x 轴负方向以1个单位长度每秒的速度匀速移动,Q 点从O 点出发以2个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束.AC 的中点D 的坐标是()1,2,设运动时间为(0)t t >秒.问:是否存在这样的t ,使ODP ODQ S S =V V ?若存在,请求出t 的值;若不存在,请说明理由.()3点F 是线段AC 上一点,满足FOC FCO ∠=∠,点G 是第二象限中一点,连OG ,使得.AOG AOF ∠=∠点E 是线段OA 上一动点,连CE 交OF 于点H ,当点E 在线段OA 上运动的过程中,OHC ACE OEC∠+∠∠的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.【答案】(1)()2,0;()0,4 ;(2)1;(3)2.【解析】分析:(1)根据绝对值和算术平方根的非负性,求得a ,b 的值即可;(2)先得出CP =t ,OP =2﹣t ,OQ =2t ,AQ =4﹣2t ,再根据S △ODP =S △ODQ ,列出关于t 的方程,求得t 的值即可;(3)过H 点作AC 的平行线,交x 轴于P ,先判定OG ∥AC ,再根据角的和差关系以及平行线的性质,得出∠PHO =∠GOF =∠1+∠2,∠OHC =∠OHP +∠PHC =∠GOF +∠4=∠1+∠2+∠4,最后代入OHC ACE OEC ∠∠∠+进行计算即可.详解:(1+|b ﹣2|=0,∴a ﹣2b =0,b ﹣2=0,解得:a =4,b =2,∴A (0,4),C (2,0);(2)由条件可知:P 点从C 点运动到O 点时间为2秒,Q 点从O 点运动到A 点时间为2秒,∴0<t ≤2时,点Q 在线段AO 上,即 CP =t ,OP =2﹣t ,OQ =2t ,AQ =4﹣2t ,∴1111222212222DOP D DOQ D S OP y t t S OQ x t t =⋅=-⨯=-=⋅=⨯⨯=V V (),. ∵S △ODP =S △ODQ ,∴2﹣t =t ,∴t =1;(3)OHC ACE OEC∠∠∠+的值不变,其值为2. ∵∠2+∠3=90°.又∵∠1=∠2,∠3=∠FCO ,∴∠GOC +∠ACO =180°,∴OG ∥AC ,∴∠1=∠CAO ,∴∠OEC =∠CAO +∠4=∠1+∠4,如图,过H 点作AC 的平行线,交x 轴于P ,则∠4=∠PHC ,PH ∥OG ,∴∠PHO =∠GOF =∠1+∠2,∴∠OHC =∠OHP +∠PHC =∠GOF +∠4=∠1+∠2+∠4,∴124421421414OHC ACE OEC ∠∠∠∠∠∠∠∠∠∠∠∠∠+++++===++().点睛:本题主要考查了坐标与图形性质,解决问题的关键值作辅助线构造平行线.解题时注意:任意一个数的绝对值都是非负数,算术平方根具有非负性,非负数之和等于0时,各项都等于0.26.已知a+1是4的算术平方根,b -1是27的立方根,化简求值:2(2a -b 2)-(4a -a 2).【答案】-31【解析】【分析】先根据算术平方根和立方根的定义得出a 、b 的值,再去括号、合并同类项化简原式,继而代入计算可得.【详解】解:∵a+1是4的算术平方根,b -1是27的立方根,∴a+1=2,b -1=3,解得a=1,b=4,原式=4a -2b 2-4a+a 2=a 2-2b 2,当a=1,b=4时,原式=1-2×16=1-32=-31.【点睛】本题主要考查整式的化简求值,熟练掌握整式的混合运算顺序和法则是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E
D
解:因为直线AB与EF相交与点O 所以∠AOE+∠BOE=180°
A
O
B 因为∠AOE=36°
所以∠BOE=180°-∠AOE
C
F
=180°-36°=144°
因为∠DOE=90°
所以∠AOD=∠AOE+∠DOE=126°
例3:如图,要把水渠中的水引到水池C中,在渠岸的什么地
方开沟,水沟的长度才能最短?请画出图来,并说明理由.
理由:垂线段最短
C
例4:你能量出C到AB的距离,B到AC的距离,A到BC的距离 吗?
F
E
C
A
D
B
例5:你能画出ABC三点到对边的垂线吗?
思考:三角形的三条垂线有什么特点? 三角形的三条垂线都交于一点; 锐角三角形的三条垂线交点在三角形的内部; 直角三角形的三条垂线交点在直角顶点; 钝角三角形的三条垂线交点在三角形的外部;
例 2 . 已 知 O A O C , O B O D , A O B : B O C 3 2 :1 3 ,
求 C O D 的 度 数 。解 .由 O A O C 知 : A O C 9 0 0
CB
即 AO B BO C 900 由 A O B : B O C 3 2 :1 3,
D O
设 A O B 3 2 x, 则 B O C = 1 3 x
A
列 方 程 :32x+13x=900
x 20
由垂直先找到90° 的角,再根据角之 间的关系求解.
BO C 13 20 260 又 Q OB OD BO D 900
C O D 900 260 640
2. 对顶角: (1)两条直线相交所构成的四个角中,
有公共顶点但没有公共边的两个角是对顶角.
如图(2). 1 与 2 , 3 与 4 是 对 顶 角 。 2 1
(2)一个角的两边分别是另一个角的两边的
(1)
反向延长线,这两个角是对顶角.
3. 邻补角的性质: 同角的补角相等. 1与 3互 补 , 2与 3互 补
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
垂线
1.垂线的定义: 两条直线相交,所构成的四个角中,有一 个角是90°时,就说这两条直线互相垂直.其中一条直线 叫做另一条直线的垂线.它们的交点叫垂足.
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线 垂直.(2): 直线外一点与直线上各点连结的所有线段中, 垂线段最短.简称:垂线段最短.
求 B O D 的 度 数 D 。 解:设∠AOC=2x°,则∠AOD=3x°
A
因为∠AOC+∠AOD=180°
所以2x°+3x°=180°
O
解得x=36°
B 所以∠AOC=2x=72°
C
∠BOD=∠AOC=72°
答: ∠BOD的度数是72°
在解决与角的计算有关的问题时,经常用到代数 方法.
例2.已知直线AB、CD、EF相交于点O,
第五章 相交线与平行线
相 交
知线 识 构 图
平 行 线
两条 直线 相交
一般情况 特殊
两条直线被 第三条所截
邻补角
邻补角互补
对顶角 垂直
对顶角相等
存在性和唯一性
点到直
垂线段最短 线的距
离
同位角、内错角、同旁内角
平行线的判定
平行公理及其推论
平行线的性质 两条平行线的距离
命题、定理
平移
平移的特征
1共.互边为的邻两补个角角:是两邻条补直角线.相如交图所(1)构成的四个角中, 有1 公与 共 顶2 点是 且邻 有补 一角 条公。
平行
1. 平行线的概念:在同一平面内,不相交的两条直线叫做平行线. 2. 两直线的位置关系: 在同一平面内,两直线的位置关系只 有两种:(1)相交; (2)平行.
3. 平行线的基本性质: (1) 平行公理(平行线的存在性和唯一性)
经过直线外一点,有且只有一条直线与已知直线平行.
(2) 推论(平行线的传递性) 如果两条直线都和第三条直线 平行,那么这两条直线也互相平行.
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角,指的是一条直线分别与两条 直线相交构成的八个角中,不共顶点的角之间的特殊位置 关系.它们与对顶角、邻补角一样,总是成对存在着的.
1、同位角的位置特征是: (1)在截线的同旁, (2)在被截两直线的同方向.
2、内错角的位置特征是:
(1)在截线的两旁, (2)在被截两直线之间. 3、同旁内角的位置特征是:
3.点到直线的距离: 从直线外一点到这条直线的垂线段的 长度,叫做点到直线的距离.
4.如遇到线段与线段,线段与射线,射线与射线,线段 或射线与直线垂直时,特指它们所在的直线互相垂直.
5.垂线是直线,垂线段特指一条线段是图形,点到直线距 离是指垂线段的长度,是指一个数量,是有单位的.
例 1 .直 线 A B 、 C D 相 交 于 点 O , O E A B , 垂 足 为 O ,
3
1
2
4
12(同 角 的 补 角 相 等 )
(2)
4. 对顶角性质:对顶角相等.
两个特征:(1) 具有公共顶点; 5. n条直线相交于一点,
(2) 角的两边互为反向延长线. 就有n(n-1)对对顶角.
例 1 .直 线 A B 与 C D 相 交 于 O , A O C : A O D 2 :3
(1)在截线的同旁,
三线八角
(2)在被截两直线之间.
C
3E1Fra bibliotek7542
A 86
F
截线
D B
被截线
判定两直线平行的方法有三种:
(1)定义法;在同一平面内不相交的两条直线是平行线.
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行.
(3)因为a⊥c, a⊥b; 所以b//c
且 D O E 5 C O E 。 求 A O D 的 度 数 。
CE
┓
AO
B
D
此题需要正确地 应用、对顶角、 邻补角、垂直的 概念和性质.
解 :由 邻 补 角 的 定 义 知 : C O E + D O E = 1 8 0 0, 又 由 D O E 5 C O E C O E 5 C O E 1800 CO E 300 又 Q OE AB BO E 900 BO C BO E CO E 1200 由对顶角相等得: AOD= BOC=1200
