2021年高三数学一轮复习 3.5两角和与差的正弦、余弦和正切公式精品试题
高考论坛新课标数学理一轮教师备课练习3.5两角和与差的正弦、余弦和正切公式(含答案详析)

第五节两角和与差的正弦、余弦和正切公式[考情展望] 1.利用两角和与差的正弦、余弦和正切公式进行三角函数式的化简与求值.2.利用二倍角公式进行三角函数式的化简与求值.3.与三角函数y=A sin(ωx+φ)的图象和性质相结合,考查学生的综合能力.一、两角和与差的正弦、余弦、正切公式1.六个公式:①sin(α±β)=sin_αcos_β±cos_αsin_β;②cos(α±β)=cos_αcos_β∓sin_αsin_β;③tan(α±β)=tan α±tan β1∓tan αtan β.2.公式T(α±β)的变形:①tan α+tan β=tan(α+β)(1-tan_αtan_β);②tan α-tan β=tan(α-β)(1+tan_αtan_β).二、二倍角的正弦、余弦、正切公式1.三个公式:①sin 2α=2sin_αcos_α;②cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;③tan 2α=2tan α1-tan2α.2.公式S2α、C2α的变形:①sin αcos α=12sin 2α;②sin2α=12(1-cos 2α);③cos2α=12(1+cos 2α).1.sin 34°sin 26°-cos 34°cos 26°的值是( ) A.12B.32C .-12D .-32【解析】 sin 34°sin 26°-cos 34°cos 26°=-(cos 34°cos 26°-sin 34°sin 26°)=-cos 60°=-12. 【答案】 C2.下列各式中,值为32的是( ) A .2sin 15°cos 15° B .cos 215°-sin 215° C .2sin 215°-1D .sin 215°+cos 215°【解析】 2sin 15°cos 15°=sin 30°=12,cos 215°-sin 215°=cos 30°=32,2sin 215°-1=-cos 30°=-32,sin 215°+cos 215°=1.故选B. 【答案】 B3.已知tan(α+β)=3,tan(α-β)=5,则tan 2α=( ) A.18 B .-18 C.47D .-47【解析】 tan 2α=tan[(α+β)+(α-β)] =tan (α+β)+tan (α-β)1-tan (α+β)·tan (α-β)=3+51-3×5=-47.【答案】 D4.若cos α=-45,α是第三象限角,则sin ⎝ ⎛⎭⎪⎫α+π4=( )A .-7210 B.7210 C .-210D.210【解析】 由题意知sin α=-35,∴sin ⎝ ⎛⎭⎪⎫α+π4=sin αcos π4+cos αsin π4=-35×22+⎝ ⎛⎭⎪⎫-45×22=-7210.【答案】 A5.(2013·江西高考)若sin α2=33,则cos α=( ) A .-23 B .-13 C.13D.23【解析】 cos α=1-2sin 2α2=1-2×⎝ ⎛⎭⎪⎫332=1-23=13.【答案】 C6.(2013·四川高考)设sin 2α=-sin α,α∈⎝ ⎛⎭⎪⎫π2,π,则tan 2α的值是________.【解析】 由sin 2α=2sin αcos α及sin 2α=-sin α,α∈⎝ ⎛⎭⎪⎫π2,π解出α,进而求得tan 2α的值.∵sin 2α=-sin α,∴2sin αcos α=-sin α. ∵α∈⎝ ⎛⎭⎪⎫π2,π,sin α≠0,∴cos α=-12.又∵α∈⎝ ⎛⎭⎪⎫π2,π,∴α=23π,∴tan 2α=tan 43π=tan ⎝ ⎛⎭⎪⎫π+π3=tan π3= 3. 【答案】3考向一 [060] 三角函数的给值求值(1)(2014·郑州模拟)若0<α<π2,-π2<β<0,cos ⎝ ⎛⎭⎪⎫π4+α=13,cos ⎝ ⎛⎭⎪⎫π4-β2=33,则cos ⎝ ⎛⎭⎪⎫α+β2=( )A.33 B .-33 C.539 D .-69 (2)(2013·广东高考)已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫x -π12,x ∈R. ①求f ⎝ ⎛⎭⎪⎫-π6的值;②若cos θ=35,θ∈⎝ ⎛⎭⎪⎫3π2,2π,求f ⎝ ⎛⎭⎪⎫2θ+π3.【思路点拨】(2)①把x =-π6代入函数解析式,借助特殊角的三角函数值和诱导公式求f ⎝ ⎛⎭⎪⎫-π6. ②由cos θ求出sin θ,利用两角和的余弦公式和二倍角公式求f ⎝ ⎛⎭⎪⎫2θ+π3.【尝试解答】 (1)∵0<α<π2,∴π4<π4+α<34π, 所以由cos ⎝ ⎛⎭⎪⎫π4+α=13,得sin ⎝ ⎛⎭⎪⎫π4+α=223,又-π2<β<0,且cos ⎝ ⎛⎭⎪⎫π4-β2=33,则π4<π4-β2<π2,∴sin ⎝ ⎛⎭⎪⎫π4-β2=63,故cos ⎝ ⎛⎭⎪⎫α+β2=cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫π4+α-⎝ ⎛⎭⎪⎫π4-β2=cos ⎝ ⎛⎭⎪⎫π4+αcos ⎝ ⎛⎭⎪⎫π4-β2+sin ⎝ ⎛⎭⎪⎫π4+αsin ⎝ ⎛⎭⎪⎫π4-β2=593. 【答案】 C(2)①因为f (x )=2cos ⎝ ⎛⎭⎪⎫x -π12,所以f ⎝ ⎛⎭⎪⎫-π6=2cos ⎝ ⎛⎭⎪⎫-π6-π12=2cos ⎝ ⎛⎭⎪⎫-π4=2cos π4=2×22=1.②因为θ∈⎝ ⎛⎭⎪⎫3π2,2π,cos θ=35,所以sin θ=-1-cos 2θ=-1-⎝ ⎛⎭⎪⎫352=-45, cos 2θ=2cos 2θ-1=2×⎝ ⎛⎭⎪⎫352-1=-725, sin 2θ=2sin θcos θ=2×35×⎝ ⎛⎭⎪⎫-45=-2425.所以f ⎝ ⎛⎭⎪⎫2θ+π3=2cos ⎝ ⎛⎭⎪⎫2θ+π3-π12=2cos ⎝ ⎛⎭⎪⎫2θ+π4=2×⎝ ⎛⎭⎪⎫22cos 2θ-22sin 2θ=cos 2θ-sin 2θ=-725-⎝ ⎛⎭⎪⎫-2425=1725.规律方法1 给值求值问题,解决的关键是把所求角用已知角表示.,(1)当已知角有两个时,所求角一般表示为两个已知角的和或差的形式.(2)当已知角有一个时,此时应着眼于所求角与已知角的和或差的关系,然后应用诱导公式把所求角变成已知角.(3)注意根据角的象限确定三角函数值的符号.对点训练 (1)(2012·江苏高考)设α为锐角,若cos ⎝ ⎛⎭⎪⎫α+π6=45,则sin ⎝ ⎛⎭⎪⎫2α+π12的值为________.(2)已知cos ⎝ ⎛⎭⎪⎫α-π6+sin α=435,则sin ⎝ ⎛⎭⎪⎫α+7π6=________.【解析】 (1)∵α为锐角且cos ⎝ ⎛⎭⎪⎫α+π6=45,∴sin ⎝ ⎛⎭⎪⎫α+π6=35.∴sin ⎝ ⎛⎭⎪⎫2α+π12=sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫α+π6-π4 =sin 2⎝ ⎛⎭⎪⎫α+π6cos π4-cos 2⎝ ⎛⎭⎪⎫α+π6sin π4 =2sin ⎝ ⎛⎭⎪⎫α+π6cos ⎝ ⎛⎭⎪⎫α+π6-22⎣⎢⎡⎦⎥⎤2cos 2⎝ ⎛⎭⎪⎫α+π6-1=2×35×45-22⎣⎢⎡⎦⎥⎤2×⎝ ⎛⎭⎪⎫452-1 =12225-7250=17250.(2)cos ⎝ ⎛⎭⎪⎫α-π6+sin α=cos αcos π6+sin αsin π6+sin α=32cos α+32sin α=3sin ⎝ ⎛⎭⎪⎫α+π6=45 3.∴sin ⎝ ⎛⎭⎪⎫α+π6=45,∴sin ⎝ ⎛⎭⎪⎫α+76π=sin ⎝ ⎛⎭⎪⎫π+α+π6=-sin ⎝ ⎛⎭⎪⎫α+π6=-45.【答案】 (1)17250 (2)-45考向二 [061] 三角函数的给值求角已知0<α<π2<β<π,tan α2=12,cos(β-α)=210. (1)求sin α的值;(2)求β的值.【思路点拨】 (1)tan α2――→二倍角公式tan α――→同角三角函数的关系sin α. (2)cos(β-α)――→同角三角函数的关系sin(β-α)――→拆角变换sin β――→结合β的范围β 【尝试解答】 (1)由tan α2=12,得tan α=2tan α21-tan 2α2=43, ∴cos α=34sin α,①又sin 2α+cos 2α=1,②由①、②联立,得25sin 2α=16,∵0<α<π2,∴sin α=45. (2)由(1)知,cos α=35,sin α=45, 又0<α<π2<β<π,∴0<β-α<π. 由cos(β-α)=210,得0<β-α<π2. ∴sin(β-α)=9810=7210,∴sin β=sin[(β-α)+α]=sin(β-α)cos α+cos(β-α)·sin α=7210×35+210×45=25250=22.由π2<β<π得β=34π.规律方法2 1.第(2)问中,由sin β=22 易错误得出β=π4,这些错误的原因都是忽视了角的范围.2.“给值求角”的求解思路:(1)求角的某一三角函数值,(2)讨论角的范围,确定角的大小.其中求角的某一三角函数值时,应选择在该范围内是单调函数,若角的范围是(0,π),选余弦较好;若角的范围为(-π2,π2) ,选正弦较好.对点训练 已知cos α=17,cos(α-β)=1314,且0<β<α<π2,试求角β的值. 【解】 由cos α=17,0<α<π2,得sin α=1-cos 2α=1-(17)2=437.由0<β<α<π2,得0<α-β<π2. 又∵cos(α-β)=1314, ∴sin(α-β)=1-cos 2(α-β)=3314,由β=α-(α-β),得cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β) =17×1314+437×3314=12. 又0<β<π2,所以β=π3.考向三 [062] 三角函数式的化简化简:(1)sin 50°(1+3tan 10°); (2)()1+sin θ+cos θ⎝ ⎛⎭⎪⎫sin θ2-cos θ22+2cos θ(0<θ<π).【思路点拨】 (1)切化弦,逆用两角和的正弦公式; (2)统一为θ2的三角函数,变形化简. 【尝试解答】 (1)sin 50°()1+3tan 10° =sin 50°⎝ ⎛⎭⎪⎫cos 10°+3sin 10°cos 10°=2sin 50°⎝ ⎛⎭⎪⎫12cos 10°+32sin 10°cos 10°=2sin 50°sin (30°+10°)cos 10°=2sin 50°cos 50°cos 10°=sin 100°cos 10°=cos 10°cos 10°=1.(2)由θ∈(0,π),得0<θ2<π2,∴cos θ2>0. 因此2+2cos θ=4cos 2θ2=2cos θ2.又(1+sin θ+cos θ)⎝ ⎛⎭⎪⎫sin θ2-cos θ2=⎝ ⎛⎭⎪⎫2sin θ2cos θ2+2cos 2θ2⎝ ⎛⎭⎪⎫sin θ2-cos θ2 =2cos θ2⎝ ⎛⎭⎪⎫sin 2θ2-cos 2θ2=-2cos θ2cos θ.故原式=-2cos θ2cos θ2cos θ2=-cos θ.规律方法3 1.本例(2)中有开方运算,联想二倍角公式的特征进行升幂,化为完全平方式.2.三角函数式的化简要遵循“三看”原则,(1)一看“角”,这是最重要的一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式;(2)二看“函数名称”,看函数名称之间的差异,从而确定使用的公式,常见的有“切化弦”;(3)三看“结构特征”,帮助我们找到变形的方向. 对点训练 化简:2cos 4x -2cos 2x +122tan ⎝ ⎛⎭⎪⎫π4-x sin 2⎝ ⎛⎭⎪⎫x +π4.【解】 原式=2cos 2x (cos 2x -1)+122tan ⎝ ⎛⎭⎪⎫π4-x ·cos 2⎝ ⎛⎭⎪⎫π4-x=-4cos 2x sin 2x +14cos ⎝ ⎛⎭⎪⎫π4-x sin ⎝ ⎛⎭⎪⎫π4-x =1-sin 22x 2sin ⎝ ⎛⎭⎪⎫π2-2x=cos 22x 2cos 2x =12cos 2x .规范解答之五 三角函数中给值求值问题的解题策略 ——— [1个示范例] ———[1个规范练] ———(12分)(2012·广东高考)已知函数f (x )=A cos ⎝ ⎛⎭⎪⎫x 4+π6,x ∈R ,且f ⎝ ⎛⎭⎪⎫π3= 2.(1)求A 的值;(2)设α,β∈⎣⎢⎡⎦⎥⎤0,π2,f ⎝ ⎛⎭⎪⎫4α+43π=-3017,f ⎝ ⎛⎭⎪⎫4β-23π=85,求cos(α+β)的值.【规范解答】 (1)由f ⎝ ⎛⎭⎪⎫π3=2得A cos ⎝ ⎛⎭⎪⎫π12+π6=2,2分即A ·cos π4=2,∴A =2.4分 (2)由(1)知f (x )=2cos ⎝ ⎛⎭⎪⎫x 4+π6.由⎩⎪⎨⎪⎧f ⎝ ⎛⎭⎪⎫4α+43π=-3017,f ⎝ ⎛⎭⎪⎫4β-23π=85,得⎩⎪⎨⎪⎧2cos ⎝ ⎛⎭⎪⎫α+π3+π6=-3017,2cos ⎝ ⎛⎭⎪⎫β-π6+π6=85,6分解得⎩⎪⎨⎪⎧ sin α=1517,cos β=45.8分∵α,β∈⎣⎢⎡⎦⎥⎤0,π2,∴cos α=1-sin 2α=817, sin β=1-cos 2β=35.10分∴cos(α+β)=cos αcos β-sin αsin β=817×45-1517×35=-1385.12分 【名师寄语】 (1)在利用诱导公式时,先判断角的范围,确定三角函数值的符号,再写出结果.(2)对于两角和与差的余弦公式,应特别注意符号的差别,防止出错.(2014·三明模拟)已知0<α<π4,β为f (x )=cos ⎝ ⎛⎭⎪⎫2x +π8的最小正周期,a =⎝ ⎛⎭⎪⎫tan ⎝ ⎛⎭⎪⎫α+14β,-1,b =(cos α,2),且a·b =m ,求2cos 2α+sin 2(α+β)cos α-sin α的值. 【解】 因为β为f (x )=cos ⎝ ⎛⎭⎪⎫2x +π8的最小正周期,所以β=2π2=π. 又a·b =cos αtan ⎝ ⎛⎭⎪⎫α+14β-2=m , 故cos αtan ⎝ ⎛⎭⎪⎫α+π4=m +2. 由于0<α<π4,所以2cos 2α+sin 2(α+β)cos α-sin α=2cos 2α+sin (2α+2π)cos α-sin α=2cos 2α+sin 2αcos α-sin α=2cos α(cos α+sin α)cos α-sin α=2cos α·1+tan α1-tan α=2cos αtan ⎝ ⎛⎭⎪⎫α+π4=2(2+m ).。
高考数学一轮复习 第三章 三角函数、解三角形 3-5 两角和与差的正弦、余弦与正切公式练习 文-人教

3-5 两角和与差的正弦、余弦与正切公式练习 文[A 组·基础达标练]1.化简cos15°cos45°-cos75°sin45°的值为( ) A.12B.32 C .-12D .-32答案 A解析 cos15°cos45°-cos75°sin45°=cos15°cos45°-sin15°·sin45°=cos(15°+45°)=cos60°=12.2.[2015·某某中学二调]3cos10°-1sin170°=( )A .4B .2C .-2D .-4 答案 D 解析3cos10°-1sin170°=3cos10°-1sin10°=3sin10°-cos10°sin10°cos10°=2sin 10°-30°12sin20°=-2sin20°12sin20°=-4,故选D.3.[2016·某某四校联考]已知sin ⎝ ⎛⎭⎪⎫π2+α=12,-π2<α<0,则cos ⎝ ⎛⎭⎪⎫α-π3的值是( )A.12B.23 C .-12D .1答案 C解析 由已知得cos α=12,sin α=-32,cos ⎝ ⎛⎭⎪⎫α-π3=12cos α+32sin α=-12. 4.[2016·某某期末]tan π12-1tan π12等于( )A .4B .-4C .23D .-2 3 答案 D解析 ∵tan π12=tan ⎝ ⎛⎭⎪⎫π3-π4=tan π3-tanπ41+tan π3·ta nπ4=3-11+3=2-3,∴tan π12-1tan π12=2-3-12-3=-2 3.5.[2015·某某监测]已知sin ⎝ ⎛⎭⎪⎫π3+α+sin α=435,则sin ⎝ ⎛⎭⎪⎫α+7π6的值是( ) A .-235 B.235C.45D .-45 答案 D解析 sin ⎝ ⎛⎭⎪⎫π3+α+sin α=435⇒sin π3cos α+cos π3sin α+sin α=435⇒32sin α+32cos α=435⇒32sin α+12cos α=45,故sin ⎝ ⎛⎭⎪⎫α+7π6=sin αcos 7π6+cos αsin 7π6=-⎝ ⎛⎭⎪⎫32sin α+12cos α=-45.6.[2015·某某一模]已知cos α=13,cos(α+β)=-13,且α,β∈⎝ ⎛⎭⎪⎫0,π2,则cos(α-β)的值等于( )A .-12B.12C .-13D.2327答案 D解析 ∵α∈⎝⎛⎭⎪⎫0,π2,∴2α∈(0,π).∵cos α=13,∴cos2α=2cos 2α-1=-79,∴sin2α=1-cos 22α=429,而α,β∈⎝⎛⎭⎪⎫0,π2,∴α+β∈(0,π),∴sin(α+β)=1-cos2α+β=223, ∴cos(α-β)=cos[2α-(α+β)] =cos2αcos(α+β)+sin2αsin(α+β)=⎝ ⎛⎭⎪⎫-79×⎝ ⎛⎭⎪⎫-13+429×223=2327. 7.[2016·某某检测]在斜三角形ABC 中,sin A =-2cos B ·cos C ,且tan B ·tan C =1-2,则角A 的值为( )A.π4B.π3C.π2D.3π4 答案 A解析 由题意知,sin A =-2cos B ·cos C =sin(B +C )=sin B ·cos C +cos B ·sin C ,在等式-2cos B ·cos C =sin B ·cos C +cos B ·sin C ,两边同除以cos B ·cos C 得tan B +tan C =-2,又tan(B +C )=tan B +tan C 1-tan B tan C =-1=-tan A ,即tan A =1,所以A =π4.8.[2016·日照一模]函数y =sin ⎝ ⎛⎭⎪⎫3x +π3·cos ⎝ ⎛⎭⎪⎫x -π6-cos ⎝ ⎛⎭⎪⎫3x +π3cos ⎝ ⎛⎭⎪⎫x +π3的图象的一条对称轴方程是( )A .x =π12B .x =π6C .x =-π12D .x =-π24答案 A解析 对函数进行化简可得y =sin ⎝⎛⎭⎪⎫3x +π3cos ⎝⎛⎭⎪⎫x -π6-cos ⎝⎛⎭⎪⎫3x +π3cos ⎝⎛x +π2⎭⎪⎫-π6=sin ⎝ ⎛⎭⎪⎫3x +π3cos ⎝ ⎛⎭⎪⎫x -π6+cos ⎝⎛⎭⎪⎫3x +π3· sin ⎝ ⎛⎭⎪⎫x -π6=sin ⎝ ⎛⎭⎪⎫3x +π3+x -π6=sin ⎝ ⎛⎭⎪⎫4x +π6, 则由4x +π6=k π+π2,k ∈Z ,得x =k π4+π12,k ∈Z . 当k =0时,x =π12.故选A.9.化简:sin50°(1+3tan10°)=________. 答案 1 解析sin50°(1+3tan10°)=sin50°⎝ ⎛⎭⎪⎫1+3·sin10°cos10°=sin50°×cos10°+3sin10°cos10°=sin50°×2⎝ ⎛⎭⎪⎫12cos10°+32sin10°cos10°=2sin50°·cos50°cos10°=sin100°cos10°=cos10°cos10°=1.10.[2015·某某摸底]已知tan(3π-α)=-12,tan(β-α)=-13,则tan β=________.答案 17解析 依题意得tan α=12,又tan(β-α)=-13,∴tan β=tan[(β-α)+α]=tan β-α+tan α1-tan β-α·tan α=17.11.[2014·某某高考]已知α∈⎝ ⎛⎭⎪⎫π2,π,sin α=55. (1)求sin ⎝ ⎛⎭⎪⎫π4+α的值;(2)求cos ⎝⎛⎭⎪⎫5π6-2α的值.解 (1)因为α∈⎝ ⎛⎭⎪⎫π2,π,sin α=55,所以cos α=-1-sin 2α=-255.故sin ⎝ ⎛⎭⎪⎫π4+α=sin π4cos α+cos π4sin α=22×⎝ ⎛⎭⎪⎫-255+22×55=-1010. (2)由(1)知sin2α=2sin αcos α=2×55×⎝ ⎛⎭⎪⎫-255=-45,cos2α=1-2sin 2α=1-2×⎝⎛⎭⎪⎫552=35,所以cos ⎝ ⎛⎭⎪⎫5π6-2α=cos 5π6cos2α+sin 5π6sin2α=⎝ ⎛⎭⎪⎫-32×35+12×⎝ ⎛⎭⎪⎫-45=-4+3310.12.[2015·某某模拟]已知函数f (x )=2sin ωx +m cos ωx (ω>0,m >0)的最小值为-2,且图象上相邻两个最高点的距离为π.(1)求ω和m 的值;(2)若f ⎝ ⎛⎭⎪⎫θ2=65,θ∈⎝ ⎛⎭⎪⎫π4,3π4,求f ⎝ ⎛⎭⎪⎫θ+π8的值.解 (1)易知f (x )=2+m 2sin(ωx +φ)(φ为辅助角), ∴f (x )min =-2+m 2=-2,∴m = 2. 由题意知函数f (x )的最小正周期为π, ∴2πω=π,∴ω=2.(2)由(1)得f (x )=2sin2x +2cos2x =2sin ⎝⎛⎭⎪⎫2x +π4,∴f ⎝ ⎛⎭⎪⎫θ2=2sin ⎝ ⎛⎭⎪⎫θ+π4=65, ∴sin ⎝ ⎛⎭⎪⎫θ+π4=35,∵θ∈⎝ ⎛⎭⎪⎫π4,3π4,∴θ+π4∈⎝ ⎛⎭⎪⎫π2,π, ∴cos ⎝⎛⎭⎪⎫θ+π4=-1-sin 2⎝⎛⎭⎪⎫θ+π4=-45,∴sin θ=sin ⎝ ⎛⎭⎪⎫θ+π4-π4=sin ⎝ ⎛⎭⎪⎫θ+π4cos π4-cos ( θ+π4 )sin π4=7210,∴f ⎝ ⎛⎭⎪⎫θ+π8=2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫θ+π8+π4=2sin ⎝ ⎛⎭⎪⎫2θ+π2=2cos2θ=2(1-2sin 2θ)=2⎣⎢⎡⎦⎥⎤1-2×⎝⎛⎭⎪⎫72102=-4825. [B 组·能力提升练]1.设a =12cos6°-32sin6°,b =2tan13°1+tan 213°,c =1-cos50°2,则有() A .a >b >c B .a <b <c C .b <c <a D .a <c <b 答案 D 解析 a =12cos6°-32sin6°=sin24°,b =2tan13°1+tan 213°=sin26°,c =1-cos50°2=sin25°,所以b >c >a ,故选D. 2.设α为锐角,若cos ⎝ ⎛⎭⎪⎫α+π6=45,则sin ⎝ ⎛⎭⎪⎫2α+π12的值为________. 答案17250解析 因为α为锐角,cos ⎝ ⎛⎭⎪⎫α+π6=45,所以sin ⎝ ⎛⎭⎪⎫α+π6=35,sin2⎝ ⎛⎭⎪⎫α+π6=2425,cos2⎝⎛⎭⎪⎫α+π6=725, 所以sin ⎝ ⎛⎭⎪⎫2α+π12=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫α+π6-π4=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫α+π6cos π4-cos ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫α+π6sin π4=2425×22-725×22=17250. 3.[2016·某某八校联考]如图,圆O 与x 轴的正半轴的交点为A ,点C ,B 在圆O 上,且点C 位于第一象限,点B 的坐标为⎝ ⎛⎭⎪⎫1213,-513,∠AOC =α.若|BC |=1,则3cos 2α2-sin α2·cos α2-32的值为________.答案513解析 由题意得|OB |=|BC |=1,从而△OBC 为等边三角形,∴sin ∠AOB =sin ⎝ ⎛⎭⎪⎫π3-α=513,3cos 2α2-sin α2cos α2-32=3·1+cos α2-sin α2-32=-12sin α+32cos α=sin ⎝ ⎛⎭⎪⎫α+2π3=sin ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫α+2π3=sin ⎝ ⎛⎭⎪⎫π3-α=513.4.[2015·某某二模]已知向量m =⎝ ⎛⎭⎪⎫3sin x 4,1,n =⎝ ⎛⎭⎪⎫cos x 4,cos 2x4,函数f (x )=m ·n .(1)若f (x )=1,求cos ⎝⎛⎭⎪⎫2π3-x 的值;(2)在锐角△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,且满足a cos C +12c =b ,求f (2B )的取值X 围.解 f (x )=3sin x 4cos x 4+cos 2x 4=32sin x 2+12cos x 2+12=sin ⎝ ⎛⎭⎪⎫x 2+π6+12. (1)由f (x )=1,可得sin ⎝ ⎛⎭⎪⎫x 2+π6=12,则cos ⎝⎛⎭⎪⎫2π3-x =-cos ⎝ ⎛⎭⎪⎫x +π3=2sin 2⎝ ⎛⎭⎪⎫x 2+π6-1=-12.(2)由余弦定理及a cos C +c2=b ,可得b 2+c 2-a 2=bc , ∴cos A =b 2+c 2-a 22bc =12,∴A =π3,∴B +C =2π3.又∵△ABC 是锐角三角形,∴B ∈⎝ ⎛⎭⎪⎫π6,π2, ∴π3<B +π6<2π3,又f (2B )=sin ⎝ ⎛⎭⎪⎫B +π6+12,∴1+32<f (2B )≤32.∴f (2B )的取值X 围是⎝ ⎛⎦⎥⎤1+32,32.。
2021年高考数学一轮复习 3.5 两角和与差的正弦、余弦、正切公式课时作业 理(含解析)新人教A版

2021年高考数学一轮复习 3.5 两角和与差的正弦、余弦、正切公式课时作业 理(含解析)新人教A 版一、选择题1.若sin α=-35,α∈⎝ ⎛⎭⎪⎫-π2,0,则cos ⎝ ⎛⎭⎪⎫α+54π=( )A .-210 B.210 C .-7210 D.7210解析:由sin α=-35,α∈⎝⎛⎭⎪⎫-π2,0得cos α=45, 所以cos ⎝⎛⎭⎪⎫α+5π4=cos 5π4cos α-sin 5π4sin α=-22⎝ ⎛⎭⎪⎫45+35=-7210. 答案:C2.(xx·山东卷)若θ∈⎣⎢⎡⎦⎥⎤π4,π2,sin 2θ=378,则sin θ=( )A.35B.45C.74D.34解析:由θ∈⎣⎢⎡⎦⎥⎤π4,π2,得2θ∈⎣⎢⎡⎦⎥⎤π2,π.又sin 2θ=378,故cos 2θ=-18.故sinθ=1-cos 2θ2=34. 答案:D3.已知tan ⎝ ⎛⎭⎪⎫α-π6=37,tan ⎝ ⎛⎭⎪⎫π6+β=25,则tan(α+β)的值为( )A.2941 B.129 C.141D .1 解析:tan(α+β)=tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π6+⎝ ⎛⎭⎪⎫π6+β=tan ⎝⎛⎭⎪⎫α-π6+tan ⎝ ⎛⎭⎪⎫π6+β1-tan ⎝ ⎛⎭⎪⎫α-π6·ta n ⎝ ⎛⎭⎪⎫π6+β=37+251-37×25=1,故选D.答案:D4.(xx·辽宁五校第二次模拟) 1-2sinπ+θsin ⎝⎛⎭⎪⎫3π2-θ=( )其中θ∈⎝ ⎛⎭⎪⎫π2,π( )A .sin θ-cos θB .cos θ-sin θC .±(sin θ-cos θ)D .sin θ+cos θ解析:1-2sinπ+θsin ⎝ ⎛⎭⎪⎫3π2-θ=1-2sin θcos θ=|sin θ-cos θ|,又因为θ∈⎝ ⎛⎭⎪⎫π2,π,所以sin θ>cos θ,故选A. 答案:A5.(xx·云南昆明高三调研)已知sin ⎝⎛⎭⎪⎫x -π4=35,则sin 2x 的值为( )A .-725 B.725 C.925 D.1625解析:依题意得22(sin x -cos x )=35,12(sin x -cos x )2=925,1-sin 2x =1825,sin 2x =725,选B. 答案:B6.(xx·潍坊市模拟)已知α,β∈⎝⎛⎭⎪⎫0,π2,满足tan(α+β)=4tan β,则tan α的最大值是( )A.14B.34C.34 2D.32解析:tan α=tan(α+β-β)=tan α+β-tan β1+tan α+βtan β=3tan β1+4tan 2β=31tan β+4tan ββ∈⎝⎛⎭⎪⎫0,π2,tan β>0,1tan β+4tan β≥24=4,当且仅当tan β=12时分母取最小值,tan α取最大值34.答案:B 二、填空题7.(xx·浙江五校第二次联考)已知α∈⎣⎢⎡⎦⎥⎤π2,π,sinα=33,则sin 2α=________.解析:α∈⎣⎢⎡⎦⎥⎤π2,π,sin α=33,cos α=-63,sin 2α=2sin α·cos α=-223. 答案:-2238.tan 15°+tan 30°+tan 15°·tan 30°的值是________. 解析:由tan(15°+30°)=tan 15°+tan 30°1-tan 15°tan 30°可得结果.答案:19.(xx·湖北七市联考)若tan θ=12,θ∈⎝ ⎛⎭⎪⎫0,14π,则sin ⎝ ⎛⎭⎪⎫2θ+14π=________. 解析:由θ∈⎝⎛⎭⎪⎫0,π4及tan θ=12可求得sin θ=55,cos θ=255.sin ⎝⎛⎭⎪⎫2θ+π4=22(sin 2θ+cos 2θ)=7210. 答案:7210三、解答题10.(xx·江西南昌调研)已知α∈(0,π)且cos ⎝ ⎛⎭⎪⎫α-π6=35.求cos α. 解:因为α∈(0,π),所以α-π6∈⎝ ⎛⎭⎪⎫-π6,5π6,又0<cos ⎝⎛⎭⎪⎫α-π6=35<cos ⎝ ⎛⎭⎪⎫-π6,所以α-π6∈⎝ ⎛⎭⎪⎫0,π2,sin ⎝⎛⎭⎪⎫α-π6=45, cos α=cos ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α-π6+π6=cos ⎝⎛⎭⎪⎫α-π6cosπ6-sin ⎝⎛⎭⎪⎫α-π6sin π6=35×32-45×12=33-410. 11.已知α为第二象限的角,sin α=35,β为第三象限的角,tan β=43.(1)求tan(α+β)的值; (2)求cos(2α-β)的值. 解:(1)因为α为第二象限的角, sin α=35,所以cos α=-1-sin 2α=-45,tan α=sin αcos α=-34.又tan β=43, 所以tan(α+β)=tan α+tan β1-tan α·tan β=724.(2)因为β为第三象限的角,tan β=43,所以sin β=-45,cos β=-35.又sin 2α=2sin αcos α=-2425,cos 2α=1-2sin 2α=725, 所以cos(2α-β)=cos 2αcos β+sin 2αsin β=35.12.已知sin α+cos α=355,α∈⎝ ⎛⎭⎪⎫0,π4,sin ⎝ ⎛⎭⎪⎫β-π4=35,β∈⎝ ⎛⎭⎪⎫π4,π2.(1)求sin 2α和tan 2α的值; (2)求cos(α+2β)的值.解:(1)由题意得(sin α+cos α)2=95,即1+sin 2α=95,∴sin 2α=45.又2α∈⎝ ⎛⎭⎪⎫0,π2,∴cos 2α=1-sin 22α=35,∴tan 2α=sin 2αcos 2α=43.(2)∵β∈⎝ ⎛⎭⎪⎫π4,π2,β-π4∈⎝ ⎛⎭⎪⎫0,π4,∴cos(β-π4)=45,于是sin 2⎝⎛⎭⎪⎫β-π4 =2sin ⎝ ⎛⎭⎪⎫β-π4cos ⎝⎛⎭⎪⎫β-π4=2425. 又sin 2⎝⎛⎭⎪⎫β-π4=-cos 2β,∴cos 2β=-2425. 又2β∈⎝ ⎛⎭⎪⎫π2,π,∴sin 2β=725.又cos 2α=1+cos 2α2=45,∴cos α=25,sin α=15⎣⎢⎡⎦⎥⎤α∈⎝ ⎛⎭⎪⎫0,π4. ∴cos(α+2β)=cos αcos 2β-sin αsin 2β =255×⎝ ⎛⎭⎪⎫-2425-55×725=-11525. [热点预测] 13.如图,圆O 的内接“五角星”与原O 交于A i (i =1,2,3,4,5)点,记弧A i A i +1在圆O 中所对的圆心角为αi (i =1,2,3,4),弧A 5A 1所对的圆心角为α5,则cos 3α1cos(α3+α5)-sin 3α2sin 2α4等于( )A .-12B .-32C .1D .0(2)(xx·成都市高中毕业班第一次诊断性检测)已知角α,β,γ构成公差为π3的等差数列.若cos β=-23,则cos α+cos γ=________.解析:(1)如图可知五边形A 1A 2A 3A 4A 5是一个正五边形,所以可知α1=α2=…=α5=72°,故cos 3α1cos(α3+α5)-sin 3α2sin 2α4=cos(5×72°)=cos 360°=1(2)α=β-π3,γ=β+π3,∴cos α+cos γ=cos ⎝ ⎛⎭⎪⎫β-π3+cos ⎝⎛⎭⎪⎫β+π3=2cosβcos π3=-23.答案:(1)C (2)-2325088 6200 戀 20623 508F 傏33934 848E 蒎 \225004 61AC 憬35804 8BDC 诜35358 8A1E 訞31339 7A6B 穫k33487 82CF 苏.36697 8F59 轙。
一轮复习课时训练§3.5:两角和与差的正弦、余弦和正切公式

第三章§5:两角和与差的正弦、余弦和正切公式(与一轮复习课件对应的课时训练)满分100,训练时间45钟一、选择题:本大题共5小题,每小题8分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.3-sin70°2-cos 210°等于 A .12 B .22 C .2 D .322.已知tan(α+β)=25,tan(β-π4)=14,那么tan(α+π4)等于 A .1318 B .1322 C .322 D .163.在△ABC 中,若sinA·sinB <cosA·cosB ,则△ABC 一定为A .等边三角形B .直角三角形C .锐角三角形D .钝角三角形 4.若f(x)=sin(x +α)-2cos(x -α)是偶函数,则cos2α等于A .35B .25C .15D .45或15.如图,角α的顶点在坐标原点O ,始边在y 轴的正半轴上,终边经过点P(-3,-4).角β的顶点在原点O ,始边在x 轴的正半轴上,终边OQ落在第二象限,且tanβ=-2,则cos ∠POQ 的值为A .-55B .-11525C .11525D .55二、填空题:本大题共3小题,每小题8分,共24分.6.3tan12°-3(4cos 212°-2)sin12°=________. 7.如图,图中的实线是由三段圆弧连结而成的一条封闭曲线C ,各段弧所在的圆经过同一点P(点P 不在C 上)且半径相等,设第i 段弧所对的圆心角为αi (i =1,2,3),则cos α13cos α2+α33-sin α13sin α2+α33=________. 8.若cos2θ+cosθ=0,则sin2θ+sinθ的值等于________.三、解答题:本大题共2小题,共36分.解答应写出文字说明、证明过程或演算步骤.9.(本小题满分18分)已知cos(π4+x)=35,求sin2x -2sin 2x 1-tanx的值.10.(本小题满分18分,(1)小问8分,(2)小问10分)已知α,β为锐角,向量a =(cosα,si nα),b =(cosβ,sinβ),c =(12,-12). (1)若a·b =22, a·c =3-14,求角2β-α的值; (2)若a =b +c ,求tanα的值.参考答案及其解析一、选择题:本大题共5小题,每小题8分,共40分.1.解析:原式=3-sin70°2-1+cos20°2=6-2sin70°3-sin70°=2.故选C 项. 答案:C2.解析:tan(α+π4)=tan[(α+β)-(β-π4)]=tan (α+β)-tan (β-π4)1+tan (α+β)tan (β-π4)=322. 答案:C3.解析:由已知cosAcosB -sinAsinB >0,∴cos(A +B)>0,又∵在△ABC 中,0<A +B <π,∴0<A +B <π2, ∴C >π2,∴△ABC 为钝角三角形. 答案:D4.解析:∵f(x)是偶函数,∴f(-x)=f(x),∴sin(-x +α)-2cos(-x -α)=sin(x +α)-2cos(x -α), ∴sinαcosx -cosαsinx -sinxcosα-cosxsinα=2cosxcosα-2sinxsinα-2cosxcosα-2sinxsinα.∴cosαsinx =2sinxsinα对x ∈R 成立,∴cosα=2sinα,由sin 2α+cos 2α=1,∴sin 2α=15. ∴cos2α=1-2sin 2α=35. 答案:A5.解析:由三角函数的定义得sin(π2+α)=-45, cos(π2+α)=-35. ∴cosα=-45,sinα=35. 又∵β在第二象限,tanβ=-2,∴sinβ=255,cosβ=-55∴cos ∠POQ =cos [(π2+α)-β]=-sin(α-β)=-sin αcosβ+cosαsinβ =-35×(-55)+(-45)×(255)=-55. 答案:A二、填空题:本大题共3小题,每小题8分,共24分.6.3tan12°-3(4cos 212°-2)sin12°=________. 解析:原式=3×sin12°-3cos12°cos12°2cos24°sin12°=23(12sin12°-32cos12°)2cos24°sin12°cos12°=23sin (-48°)cos24°sin24° =-23sin48°12sin48°=-4 3. 答案:-437.解析:设三个圆的圆心分别为C 1,C 2,C 3,连结C 1C 2,C 2C 3,C 1C 3,则∠C 2C 1C 3=12(2π-α1),∠C 1C 2C 3=12(2π-α2),∠C 1C 3C 2=12(2π-α3), 又∠C 2C 1C 3+∠C 1C 2C 3+∠C 1C 3C 2=π,所以α1+α2+α3=4π.所以cos α13cos α2+α33-sin α13sin α2+α33=cos α1+α2+α33=-12. 答案:-128.解析:∵cos2θ+co sθ=0,∴2cos 2θ+cosθ-1=0,∴cosθ=12或cosθ=-1. 当cosθ=12时,sinθ=±32. 则cosθ=12,sinθ=32时, sin2θ+sinθ=2sinθcosθ+sinθ=2×12×32+32=3, cosθ=12,si nθ=-32时,sin2θ+sinθ=2sinθcosθ+sinθ=2×(-32)×12-32=-3; 当cosθ=-1时,sinθ=0,∴sin2θ+sinθ=2sinθcosθ+sinθ=0.综上所述sin2θ+sinθ=0或±3.答案:0或±3三、解答题:本大题共2小题,共36分.9.(本小题满分18分)解:sin2x -2sin 2x 1-tanx=cosx·2sinx (cosx -sinx )cosx -sinx=sin2x =-cos(2x +π2) =-2cos 2(x +π4)+1 =-2×925+1=725. 10.(本小题满分18分,(1)小问8分,(2)小问10分)解:(1)∵a·b =(cosα,sinα)·(cosβ,sinβ)=cosαcosβ+sinαsinβ=cos(α-β)=22,① a·c =(cos α,sin α)·(12,-12) =12cos α-12sin α=3-14,② 又∵0<α<π2,0<β<π2, ∴-π2<α-β<π2. 由①得α-β=±π4, 由②得α=π6. 由α,β为锐角,∴β=5π12. 从而2β-α=23π. (2)由a =b +c 可得⎩⎨⎧ cosβ=cosα-12 ③sinβ=sinα+12④ ③2+④2得cosα-sinα=12, ∴sin2α=34. 又∵sin2α=2sinαcosα=2sinαcosαsin 2α+cos 2α=2tanαtan 2α+1=34, ∴3tan 2α-8tanα+3=0. 又∵α为锐角,∴tanα>0,∴tanα=8±82-4×3×36=8±286=4±73.。
2021年高考数学一轮总复习 3.5两角和与差的正弦、余弦和正切公式 课时作业 文(含解析)新人

2021年高考数学一轮总复习 3.5两角和与差的正弦、余弦和正切公式课时作业 文(含解析)新人教版一、选择题1.(xx·郑州模拟)计算cos42°cos18°-cos48sin18°的结果等于( ) A.12 B.33 C.22D.32解析:原式=sin48°cos18°-cos48°sin18°=sin(48°-18°)=sin30°=12.答案:A2.(xx·湖州模拟)已知sin ⎝ ⎛⎭⎪⎫π2+α=13,则cos(π+2α)的值为( )A .-79B.79C.29D .-23解析:由题意,得sin ⎝⎛⎭⎪⎫π2+α=cos α=13. 所以co s(π+2α)=-cos2α=-(2cos 2α-1)=1-2cos 2α=79.答案:B3.(xx·山东实验中学诊断)已知cos ⎝ ⎛⎭⎪⎫π4-x =35,则sin2x =( )A.1825B.725C .-725D .-1625解析:因为sin2x =cos ⎝ ⎛⎭⎪⎫π2-2x =cos2⎝ ⎛⎭⎪⎫π4-x =2cos 2⎝ ⎛⎭⎪⎫π4-x -1,所以sin2x=2×⎝ ⎛⎭⎪⎫352-1=1825-1=-725.答案:C4.(xx·成都模拟)已知α∈⎝ ⎛⎭⎪⎫π,32π,且cos α=-45,则tan ⎝ ⎛⎭⎪⎫π4-α等于( )A .7B.17C .-17D .-7解析:因为α∈⎝⎛⎭⎪⎫π,32π,且cos α=-45, 所以sin α<0,得sin α=-35,所以tan α=34.所以tan ⎝ ⎛⎭⎪⎫π4-α=1-tan α1+tan α=1-341+34=17.答案:B5.(xx·金华十校模拟)已知tan ⎝ ⎛⎭⎪⎫α+π4=-12,且π2<α<π,则sin2α-2cos 2αsin ⎝⎛⎭⎪⎫α-π4等于( ) A.255B .-3510 C .-255D .-31010解析:sin2α-2cos 2αsin ⎝ ⎛⎭⎪⎫α-π4=2sin αcos α-2cos 2α22sin α-cos α=22cos α,由tan ⎝ ⎛⎭⎪⎫α+π4=-12,得tan α+11-tan α=-12,解得tan α=-3,因为π2<α<π,所以解得cos α=-1tan 2α+1=-1010所以原式=22cos α=22×⎝ ⎛⎭⎪⎫-1010=-255. 答案:C6.(xx·娄底模拟)已知tan α,tan β是方程x 2+33x +4=0的两根,若α,β∈⎝ ⎛⎭⎪⎫-π2,π2,则α+β=( )A.π3B.π3或-23π C .-π3或23πD .-23π解析:由题意得tan α+tan β=-33, tan αtan β=4,所以tan α<0,tan β<0,又α,β∈⎝ ⎛⎭⎪⎫-π2,π2,故α,β∈⎝ ⎛⎭⎪⎫-π2,0,所以-π<α+β<0.又tan(α+β)=tan α+tan β1-tan αtan β=-331-4= 3.所以α+β=-2π3.答案:D 二、填空题7.计算:3-tan15°1+3tan15°=________.解析:3-tan15°1+3tan15°=tan60°-tan15°1+tan60°tan15°=tan45°=1.答案:18.(xx·宜昌模拟) 计算: sin50°1+3tan10°-cos20°cos80°1-cos20°=__________.解析:因为sin50°(1+3tan10°)=sin50°·cos10°+3sin10°cos10°=sin50°·2sin40°cos10°=1,cos80°1-cos20°=sin10°2sin 210°=2sin 210°. 所以sin50°1+3tan10°-cos20°cos80°1-cos20°=1-cos20°2sin 210°= 2.答案:29.(xx·南京模拟)已知sin ⎝ ⎛⎭⎪⎫π4-x =513,0<x <π4,则cos2xcos ⎝ ⎛⎭⎪⎫π4+x =__________.解析:因为x ∈⎝ ⎛⎭⎪⎫0,π4,所以π4-x ∈⎝ ⎛⎭⎪⎫0,π4.又因为sin ⎝ ⎛⎭⎪⎫π4-x =513,所以cos ⎝ ⎛⎭⎪⎫π4-x =1213.又cos2x =cos ⎣⎢⎡⎦⎥⎤π2-2⎝ ⎛⎭⎪⎫π4-x =sin2⎝ ⎛⎭⎪⎫π4-x=2sin ⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x=2×513×1213=120169.cos ⎝ ⎛⎭⎪⎫π4+x =cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4-x=sin ⎝ ⎛⎭⎪⎫π4-x=513. 所以原式=120169513=2413.答案:2413三、解答题10.(xx·江苏卷)已知α∈⎝ ⎛⎭⎪⎫π2,π,sin α=55.(1)求sin ⎝ ⎛⎭⎪⎫π4+α的值;(2)求cos ⎝ ⎛⎭⎪⎫5π6-2α的值. 解析:(1)因为α∈⎝ ⎛⎭⎪⎫π2,π,sin α=55,故sin ⎝ ⎛⎭⎪⎫π4+α=sin π4cos α+cos π4sin α=22×⎝ ⎛⎭⎪⎫-255+22×55=-1010. (2)由(1)知sin2α=2sin αcos α=2×55×⎝ ⎛⎭⎪⎫-255=-45, cos2α=1-2sin 2α=1-2×⎝ ⎛⎭⎪⎫552=35,所以cos ⎝ ⎛⎭⎪⎫5π6-2α=cos 5π6cos2α+sin 5π6sin2α=⎝ ⎛⎭⎪⎫-32×35+12×⎝ ⎛⎭⎪⎫-45=-4+3310.11.(xx·济南模拟)已知0<α<π2<β<π,tan α2=12,cos(β-α)=210. (1)求sin α的值. (2)求β的值.解析:(1)因为tanα2=12,所以sin α=sin ⎝⎛⎭⎪⎫2·α2=2sin α2cos α2=2sin α2cosα2sin2α2+cos2α2=2tan α21+tan2α2=2×121+⎝ ⎛⎭⎪⎫122=45. (2)因为0<α<π2,sin α=45, 所以cos α=35.又0<α<π2<β<π, 所以0<β-α<π.由cos(β-α)=210,得0<β-α<π2. 所以sin(β-α)=9810=7210,所以sin β=sin[(β-α)+α]=sin(β-α)cos α+cos(β-α)sin α =7210×35+210×45=25250=22. 由π2<β<π,得β=34π. ⎝⎛⎭⎪⎫或求cos β=-22,得β=34π.12.(xx·浙大附中模拟)已知函数f (x )=cos ⎝ ⎛⎭⎪⎫x -π3-sin ⎝ ⎛⎭⎪⎫π2-x .(1)求函数f (x )的最小正周期;(2)若α∈⎝ ⎛⎭⎪⎫0,π2,且f ⎝ ⎛⎭⎪⎫α+π6=35,求f (2α)的值.解析:(1)f (x )=12cos x +32sin x -cos x=32sin x -12cos x =sin ⎝⎛⎭⎪⎫x -π6.∴f (x )的最小正周期为2π. (2)由(1)知f (x )=sin ⎝⎛⎭⎪⎫x -π6.所以f ⎝ ⎛⎭⎪⎫α+π6=sin ⎝ ⎛⎭⎪⎫α+π6-π6=sin α=35,∵α∈⎝⎛⎭⎪⎫0,π2,∴cos α=1-sin 2α=1-⎝ ⎛⎭⎪⎫352=45.∴sin2α=2sin αcos α=2×35×45=2425,cos2α=2cos 2α-1=2×⎝ ⎛⎭⎪⎫452-1=725,∴f (2α)=sin ⎝⎛⎭⎪⎫2α-π6=32×2425-12×725=243-750.36200 8D68 赨22528 5800 堀"J28332 6EAC 溬26824 68C8 棈(k26015 659F 斟rul23698 5C92 岒3。
【创新方案】2021届高考数学一轮复习 3.5两角和与差的正弦、余弦、正切公式讲解与练习 理 新人教

第五节 两角和与差的正弦、余弦、正切公式[备考方向要明了]考 什 么怎 么 考1.会用向量的数量积推导出两角差的余弦公式.2.能利用两角差的余弦公式推导出两角差的正弦、正切公式.3.能利用两角差的余弦公式推导出两角和的正弦、余弦、正切公式,推导出二倍角的正弦、余弦、正切公式,了解它们的内在联系. 1.主要考查利用两角和与差的正弦、余弦、正切公式及二倍角公式进行化简、求值,如2012年江苏T11,广东T16等.2.考查形式既有选择题、填空题,也有解答题,且常与三角函数的性质、向量、解三角形的知识相结合命题,如2012年安徽T16,山东T17等.[归纳·知识整合]1.两角和与差的正弦、余弦、正切公式 sin(α±β)=sin_αcos_β±cos _αsin_β cos(α±β)=cos_αcos_β∓sin_αsin_β tan(α±β)=tan α±tan β1∓tan αtan β[探究] 1.两角和与差的正切公式对任意角都适用吗?若出现不适用的情况如何化简?提示:在T(α+β)与T(α-β)中,α,β,α±β都不等于k π+π2(k ∈Z ),即保证tan α,tan β,tan(α+β)都有意义;若α,β中有一角是k π+π2(k ∈Z ),可利用诱导公式化简.2.二倍角余弦公式的常用变形是什么?它有何重要应用?提示:二倍角余弦公式的常用变形是:cos 2α=1+cos 2α2,sin 2α=1-cos 2α2,这就是使用极其广泛的降幂扩角公式.在三角恒等变换中,这两个公式可以实现三角式的“次数”降低,利于问题的研究.2.二倍角的正弦、余弦、正切公式 sin 2α=2sin_αcos_αcos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α tan 2α=2tan α1-tan 2α[自测·牛刀小试]1.计算cos 28°cos 17°-sin 28°sin 17°的结果等于( ) A.12 B.22 C.32D.33解析:选B 原式=cos(28°+17°)=cos 45°=22. 2.已知tan ⎝ ⎛⎭⎪⎫α-π6=37,tan ⎝ ⎛⎭⎪⎫π6+β=25,则tan(α+β)的值为( )A.2941 B.129C.141D .1解析:选D tan(α+β)=tan ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-π6+⎝ ⎛⎭⎪⎫π6+β =tan ⎝ ⎛⎭⎪⎫α-π6+tan ⎝ ⎛⎭⎪⎫π6+β1-tan ⎝ ⎛⎭⎪⎫α-π6·ta n ⎝ ⎛⎭⎪⎫π6+β=37+251-37×25=1.3.(教材习题改编)下列各式中,值为12的是( )A .2sin 15°cos 15°B .cos 215°-sin 215° C .2sin 215°-1D .sin 215°+cos 215°解析:选A 2sin15°cos 15°=sin 30°=12;cos 215°-sin 215°=cos 30°=32; 2sin 215°-1=-cos 30°=-32;sin 215°+cos 215°=1. 4.(教材习题改编)已知cos α=35,0<α<π,则cos ⎝⎛⎭⎪⎫α-π6=________.解析:∵cos α=35,0<α<π,∴sin α=45,∴cos ⎝ ⎛⎭⎪⎫α-π6=cos αcos π6+sin αsin π6 =32cos α+12sin α=32×35+12×45 =4+3310. 答案:4+33105.(教材习题改编)在△ABC 中,cos A =45,tan B =2,则tan(2A +2B )=________.解析:在△ABC 中,∵cos A =45,0<A <π,得sin A =35.∴tan A =sin A cos A =34.∴tan 2A =2tan A 1-tan 2A =247, tan 2B =2tan B 1-tan 2B =-43,∴tan(2A +2B )=tan 2A +tan 2B 1-tan 2A ·tan 2B =44117.答案:44117三角函数式的化简[例1] (1)化简:1+sin θ+cos θ⎝⎛⎭⎪⎫sin θ2-cos θ22+2cos θ(0<θ<π);(2)求值:1+cos 20°2sin 20°-sin 10°⎝ ⎛⎭⎪⎫1tan 5°-tan 5°.[自主解答] (1)原式=⎝⎛⎭⎪⎫2sin θ2cos θ2+2cos 2θ2⎝ ⎛⎭⎪⎫sin θ2-cos θ24cos2θ2=cos θ2⎝ ⎛⎭⎪⎫sin 2θ2-cos 2θ2⎪⎪⎪⎪⎪⎪cos θ2=-cos θ2·cos θ⎪⎪⎪⎪⎪⎪cos θ2.因为0<θ<π,所以0<θ2<π2,所以cos θ2>0,所以原式=-cos θ.(2)原式=2cos 210°2×2sin 10°cos 10°-sin 10°⎝ ⎛⎭⎪⎫cos 5°sin 5°-sin 5°cos 5°=cos 10°2sin 10°-sin 10°·cos 25°-sin 25°sin 5°cos 5° =cos 10°2sin 10°-sin 10°·cos 10°12sin 10°=cos 10°2sin 10°-2cos 10°=cos 10°-2s in 20°2sin 10°=cos 10°-2sin 30°-10°2sin 10°=cos 10°-2⎝ ⎛⎭⎪⎫12cos 10°-32sin 10°2sin 10°=3sin 10°2sin 10°=32.———————————————————1.三角函数式化简的原则三角函数式的化简要遵循“三看”原则,即一看角,二看名,三看式子结构与特征. 2.解决给角求值问题的基本思路对于给角求值问题,往往所给角都是非特殊角,解决这类问题的基本思路有: 1化为特殊角的三角函数值; 2化为正、负相消的项,消去求值;3化分子、分母出现公约数进行约分求值.1.化简下列各式: (1)sin α+cos α-1sin α-cos α+1sin 2α;(2)sin 50°1+3tan 10°-cos 20°cos 80°1-cos 20°.解:(1)原式=⎝ ⎛⎭⎪⎫2sin α2cos α2-2sin 2α2⎝ ⎛⎭⎪⎫2sin α2cos α2+2sin 2α24sinα2cos α2cos α=⎝ ⎛⎭⎪⎫cos α2-sin α2⎝ ⎛⎭⎪⎫cos α2+sin α2sin α2cos α2cos α=⎝ ⎛⎭⎪⎫cos 2α2-sin 2α2sin α2cos α2cos α=cos αsin α2cos α2cos α=tan α2.(2)∵s in 50°(1+3tan 10°) =sin 50°·cos 10°+3sin 10°cos 10°=sin 50°·2sin 40°cos 10°=1,cos 80°1-cos 20°=sin 10°2sin 210°=2sin 210°. ∴sin 50°1+3tan 10°-cos 20°cos 80°1-cos 20°=1-cos 20°2sin 210°= 2.三角函数的求值问题[例2] (2012·广东高考)已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫ωx +π6(其中ω>0,x ∈R )的最小正周期为10π.(1)求ω的值;(2)设α,β∈⎣⎢⎡⎦⎥⎤0,π2,f ⎝ ⎛⎭⎪⎫5α+53π=-65,f ⎝ ⎛⎭⎪⎫5β-56π=1617,求cos(α+β)的值.[自主解答] (1)∵f (x )=2cos ⎝⎛⎭⎪⎫ωx +π6,ω>0的最小正周期T =10π=2πω,∴ω=15. (2)由(1)知f (x )=2cos ⎝ ⎛⎭⎪⎫15x +π6,而α,β∈⎣⎢⎡⎦⎥⎤0,π2,f ⎝⎛⎭⎪⎫5α+5π3=-65,f ⎝⎛⎭⎪⎫5β-5π6=1617, 即2cos ⎣⎢⎡⎦⎥⎤15⎝ ⎛⎭⎪⎫5α+5π3+π6=-65, 2cos ⎣⎢⎡⎦⎥⎤15⎝ ⎛⎭⎪⎫5β-5π6+π6=1617, 即cos ⎝ ⎛⎭⎪⎫α+π2=-35,cos β=817, 于是sin α=35,cos α=45,sin β=1517,故cos(α+β)=cos αcos β-sin αsin β=45×817-35×1517=-1385.———————————————————解决给值求值问题的方法三角函数的给值求值,关键是把待求角用已知角表示:(1)已知角为两个时,待求角一般表示为已知角的和或差.(2)已知角为一个时,待求角一般与已知角成“倍的关系”或“互余互补”的关系.2.已知0<β<π2<α<π,且cos ⎝ ⎛⎭⎪⎫α-β2=-19,sin ⎝ ⎛⎭⎪⎫α2-β=23,求cos(α+β)的值.解:∵0<β<π2<α<π,∴-π4<α2-β<π2,π4<α-β2<π,∴cos ⎝ ⎛⎭⎪⎫α2-β= 1-sin 2⎝⎛⎭⎪⎫α2-β=53,sin ⎝ ⎛⎭⎪⎫α-β2=1-cos 2⎝⎛⎭⎪⎫α-β2=459,∴cosα+β2=cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫α-β2-⎝ ⎛⎭⎪⎫α2-β=cos ⎝ ⎛⎭⎪⎫α-β2cos ⎝ ⎛⎭⎪⎫α2-β+sin ⎝ ⎛⎭⎪⎫α-β2sin ⎝ ⎛⎭⎪⎫α2-β=⎝ ⎛⎭⎪⎫-19×53+459×23=7527,∴cos(α+β)=2cos 2α+β2-1=2×49×5729-1=-239729.三角函数的求角问题[例3] 若sin A =55,sin B =1010,且A ,B 均为钝角,求A +B 的值. [自主解答] ∵A 、B 均为钝角且sin A =55,sin B =1010,∴cos A =-1-sin 2A =-25=-255,cos B =-1-sin 2B =-310=-31010,∴cos(A +B )=cos A cos B -sin A sin B =-255×⎝ ⎛⎭⎪⎫-31010-55×1010=22,① 又∵π2<A <π,π2<B <π,∴π<A +B <2π,② 由①②知,A +B =7π4.若将“A ,B 均为钝角”改为“A ,B 均为锐角”,如何求解? 解:∵A ,B 均为锐角,且sin A =55,sin B =1010, ∴cos A =1-sin 2A =255,cos B =1-sin 2B =31010,∴cos A +B =cos A cos B -sin A sin B =255×31010-55×1010=22.又∵A ,B ∈(0, π2),∴A +B ∈0,π, ∴A +B =π4.———————————————————1.解决给值求角问题的一般步骤 (1)求角的某一个三角函数值; (2)确定角的范围;(3)根据角的范围写出要求的角.2.在求角的某个三角函数值时,应注意根据条件选择恰当的函数 (1)已知正切函数值,选正切函数;(2)已知正、余弦函数值,选正弦或余弦函数;若角的范围是⎝ ⎛⎭⎪⎫0,π2,选正、余弦皆可;若角的范围是(0,π),选余弦较好;若角的范围为⎝ ⎛⎭⎪⎫-π2,π2,选正弦较好.3.已知cos α=17,cos(α-β)=1314,且0<β<α<π2.(1)求tan 2α的值;(2)求β. 解:(1)由cos α=17,0<α<π2,得sin α=1-cos 2α=1-⎝ ⎛⎭⎪⎫172=437.故tan α=sin αcos α=437×71=4 3.于是tan 2α=2tan α1-tan 2α=2×431-432=-8347. (2)由0<β<α<π2,得0<α-β<π2.又∵cos(α-β)=1314,∴sin(α-β)=1-cos2α-β=1-⎝ ⎛⎭⎪⎫13142=3314. 由β=α-(α-β),得cos β=cos[α-(α-β)] =cos αcos(α-β)+sin αsin(α-β)=17×1314+437×3314=12. ∴β=π3.1组关系——两角和与差的正弦、余弦、正切公式与倍角公式的关系2个技巧——拼角、凑角的技巧 (1)用已知角表示未知角2α=(α+β)+(α-β);2β=(α+β)-(α-β);α=(α+β)-β=(α-β)+β;α=α+β2+α-β2,β=α+β2-α-β2;α-β2=⎝ ⎛⎭⎪⎫α+β2-⎝ ⎛⎭⎪⎫α2+β等.(2)互余与互补关系⎝ ⎛⎭⎪⎫π4+α+⎝ ⎛⎭⎪⎫π4-α=π2;⎝ ⎛⎭⎪⎫π3+α+⎝ ⎛⎭⎪⎫π6-α=π2; ⎝ ⎛⎭⎪⎫3π4-α+⎝ ⎛⎭⎪⎫π4+α=π;⎝ ⎛⎭⎪⎫π6+α+⎝ ⎛⎭⎪⎫5π6-α=π; …3个变化——应用公式解决问题的三个变化角度(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”. (2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等.(3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等.易误警示——三角函数求角中的易误点[典例] (2011·天津高考)已知函数f (x )=tan ⎝ ⎛⎭⎪⎫2x +π4. (1)求f (x )的定义域与最小正周期;(2)设α∈⎝ ⎛⎭⎪⎫0,π4,若f ⎝ ⎛⎭⎪⎫α2=2cos 2α,求α的大小.[解] (1)由2x +π4≠π2+k π,k ∈Z ,得x ≠π8+k π2,k ∈Z ,所以f (x )的定义域为⎩⎨⎧⎭⎬⎫x ∈R |x ≠π8+k π2,k ∈Z .f (x )的最小正周期为π2.(2)法一:由f ⎝ ⎛⎭⎪⎫α2=2cos 2α,得tan ⎝ ⎛⎭⎪⎫α+π4=2cos 2α,sin ⎝ ⎛⎭⎪⎫α+π4cos ⎝ ⎛⎭⎪⎫α+π4=2(cos 2α-sin 2α),整理得sin α+cos αcos α-sin α=2(cos α+sin α)(cos α-sin α).∵α∈⎝⎛⎭⎪⎫0,π4,所以sin α+cos α≠0.∴(cos α-sin α)2=12,即sin 2α=12.由α∈⎝ ⎛⎭⎪⎫0,π4,得2α∈⎝⎛⎭⎪⎫0,π2,∴2α=π6,即α=π12.法二:∵由f ⎝ ⎛⎭⎪⎫α2=2cos 2α,得tan ⎝ ⎛⎭⎪⎫α+π4=2cos 2α,即tan ⎝ ⎛⎭⎪⎫α+π4=2sin ⎝ ⎛⎭⎪⎫π2+2α=2sin2⎝ ⎛⎭⎪⎫π4+α,∴sin ⎝ ⎛⎭⎪⎫α+π4cos ⎝ ⎛⎭⎪⎫α+π4=4sin ⎝ ⎛⎭⎪⎫π4+αcos ⎝ ⎛⎭⎪⎫π4+α. 又∵α∈⎝ ⎛⎭⎪⎫0,π4,∴sin ⎝⎛⎭⎪⎫α+π4≠0.∴1cos ⎝⎛⎭⎪⎫α+π4=4cos ⎝⎛⎭⎪⎫π4+α.∴cos 2⎝⎛⎭⎪⎫π4+α=14.∵α∈⎝ ⎛⎭⎪⎫0,π4,∴π4+α∈⎝ ⎛⎭⎪⎫π4,π2.∴cos ⎝ ⎛⎭⎪⎫π4+α=12,π4+α=π3.即α=π3-π4=π12.[易误辨析]1.解决本题易忽视“α∈⎝ ⎛⎭⎪⎫0,π4”,由sin 2α=12得出2α=π6或2α=56π,即α=π12或α=512π的错误结论或由cos 2⎝ ⎛⎭⎪⎫π4+α=14得出cos ⎝ ⎛⎭⎪⎫π4+α=12或cos ⎝ ⎛⎭⎪⎫π4+α=-12,从而造成结论错误. 2.在解决三角函数中的问题时,要牢记:当求出某角的三角函数值,如果要求这角的取值时,一定要考虑角的范围,只有同时满足三角函数值及角的范围的角才是正确的.[变式训练]1.已知tan α,tan β是方程x 2+33x +4=0的两根,若α、β∈⎝ ⎛⎭⎪⎫-π2,π2,则α+β=( )A.π3B.π3或-23π C .-π3或23πD .-23π解析:选D 由题意得tan α+tan β=-33,tan αtan β=4.所以tan α<0,tan β<0.又α,β∈⎝ ⎛⎭⎪⎫-π2,π2, 故α,β∈⎝ ⎛⎭⎪⎫-π2,0,所以-π<α+β<0. 又tan(α+β)=tan α+tan β1-tan αtan β=-331-4= 3.故α+β=-2π3.2.如图所示,点B 在以PA 为直径的圆周上,点C 在线段AB 上,已知PA =5,PB =3,PC =1527,设∠APB =α,∠APC =β,α,β均为锐角,则角β的值为________.解析:因为点B 在以PA 为直径的圆周上,所以∠ABP =90°,所以cos α=PB PA =35,sinα=45,所以tan α=43.因为cos ∠CPB =cos(α-β)=PB PC =31527=7210,所以sin(α-β)=210,所以tan(α-β)=17,tan β=tan[α-(α-β)]=tan α-tan α-β1+tan αtan α-β=1.又β∈⎝⎛⎭⎪⎫0,π2,所以β=π4.答案:π4一、选择题(本大题共6小题,每小题5分,共30分)1.(2012·辽宁高考)已知sin α-cos α=2,α∈(0,π),则tan α=( ) A .-1 B .-22C.22D .1解析:选A 由sin α-cos α=2sin ⎝ ⎛⎭⎪⎫α-π4=2,α∈(0,π),解得α=3π4,所以tan α=tan 3π4=-1.2.(2012·江西高考)若tan θ+1tan θ=4,则sin 2θ=( )A.15B.14C.13D.12解析:选D 法一:∵tan θ+1tan θ=1+tan 2θtan θ=4,∴4tan θ=1+tan 2θ, ∴sin 2θ=2sin θcos θ=2sin θcos θsin 2 θ+cos 2 θ=2tan θ1+tan 2θ=2tan θ4tan θ=12.法二:∵tan θ+1tan θ=sin θcos θ+cos θsin θ=1cos θsin θ=2sin 2θ,∴4=2sin 2θ,故sin 2θ=12.3.已知α为第二象限角,sin α+cos α=33,则cos 2α=( ) A .-53B .-59C.59D.53解析:选A 将sin α+cos α=33两边平方,可得1+sin 2α=13,sin 2α=-23,所以(-sin α+cos α)2=1-sin 2α=53.因为α是第二象限角,所以sin α>0,cos α<0,所以-sin α+cos α=-153,所以cos 2α=(-sin α+cos α)·(cos α+sin α)=-53. 4.在△ABC 中,tan B =-2,tan C =13,则A 等于( )A.π4B.3π4C.π3D.π6解析:选A tan A =tan[π-(B +C )]=-tan(B +C )=-tan B +tan C1-tan B tan C =--2+131--2×13=1.故A =π4.5.已知α+β=π4,则(1+tan α)(1+tan β)的值是( )A .-1B .1C .2D .4 解析:选C ∵α+β=π4,tan(α+β)=tan α+tan β1-tan αtan β=1,∴tan α+tan β=1-tan αtan β.∴(1+tan α)(1+tan β)=1+tan α+tan β+tan αtan β =1+1-tan αtan β+tan αtan β=2.6.(2013·合肥模拟)已知cos ⎝ ⎛⎭⎪⎫π6-α+sin α=453,则sin ⎝ ⎛⎭⎪⎫α+7π6的值是( ) A .-235B.235C.45D .-45解析:选D 由条件知cos ⎝ ⎛⎭⎪⎫π6-α+sin α=⎝ ⎛⎭⎪⎫32cos α+12sin α+sin α=3⎝ ⎛⎭⎪⎫32sin α+12cos α=3sin ⎝⎛⎭⎪⎫α+π6=435, 即sin ⎝⎛⎭⎪⎫α+π6=45. 故sin ⎝⎛⎭⎪⎫α+7π6=-32sin α-12cos α =-⎝ ⎛⎭⎪⎫32sin α+12cos α=-sin ⎝ ⎛⎭⎪⎫α+π6=-45. 二、填空题(本大题共3小题,每小题5分,共15分) 7.3-sin 70°2-cos 210°=________. 解析:3-sin 70°2-cos 210°=3-cos 20°2-cos 210°=3-2cos 210°-12-cos 210°=2. 答案:28.已知cos(α+β)=16,cos(α-β)=13,则tan αtan β的值为________.解析:因为cos(α+β)=16,所以cos αcos β-sin αsin β=16.①因为cos(α-β)=13,所以cos αcos β+sin αsin β=13.②①+②得cos αcos β=14.②-①得sin αsin β=112.所以tan αtan β=sin αsin βcos αcos β=13.答案:139.(2013·南通模拟)设f (x )=1+cos 2x 2sin ⎝ ⎛⎭⎪⎫π2-x +sin x +a 2sin ⎝ ⎛⎭⎪⎫x +π4的最大值为2+3,则常数a =________.解析:f (x )=1+2cos 2x -12cos x +sin x +a 2sin ⎝⎛⎭⎪⎫x +π4=cos x +sin x +a 2sin ⎝ ⎛⎭⎪⎫x +π4=2sin ⎝ ⎛⎭⎪⎫x +π4+a 2sin ⎝ ⎛⎭⎪⎫x +π4=(2+a 2)sin ⎝⎛⎭⎪⎫x +π4.依题意有2+a 2=2+3,故a =± 3. 答案:± 3三、解答题(本大题共3小题,每小题12分,共36分) 10.已知函数f (x )=2cos 2x2-3sin x .(1)求函数f (x )的最小正周期和值域.(2)若α为第二象限角,且f ⎝⎛⎭⎪⎫α-π3=13,求cos 2α1+cos 2α-sin 2α的值. 解:(1)因为f (x )=1+cos x -3sin x =1+2cos ⎝⎛⎭⎪⎫x +π3,所以函数f (x )的最小正周期为2π,值域为[-1,3]. (2)因为f ⎝⎛⎭⎪⎫α-π3=13,所以1+2cos α=13,即cos α=-13.又因为α为第二象限角, 所以sin α=223.因为cos 2α1+cos 2α-sin 2α=cos 2α-sin 2α2cos 2α-2sin αcos α =cos α+sin αcos α-sin α2cos αcos α-sin α=cos α+sin α2cos α,所以原式=cos α+sin α2cos α=-13+223-23=1-222.11.已知sin α+cos α=355,α∈⎝ ⎛⎭⎪⎫0,π4,sin ⎝ ⎛⎭⎪⎫β-π4=35,β∈⎝ ⎛⎭⎪⎫π4,π2.(1)求sin 2α和tan 2α的值; (2)求cos(α+2β)的值.解:(1)∵由题意得(sin α+cos α)2=95,即1+sin 2α=95,∴sin 2α=45.又2α∈⎝ ⎛⎭⎪⎫0,π2,∴cos 2α=1-sin 22α=35,∴tan 2α=sin 2αcos 2α=43.(2)∵β∈⎝ ⎛⎭⎪⎫π4,π2,β-π4∈⎝ ⎛⎭⎪⎫0,π4,sin ⎝ ⎛⎭⎪⎫β-π4=35,∴cos ⎝⎛⎭⎪⎫β-π4=45,于是sin 2⎝ ⎛⎭⎪⎫β-π4=2sin ⎝ ⎛⎭⎪⎫β-π4cos ⎝ ⎛⎭⎪⎫β-π4=2425.又sin 2⎝ ⎛⎭⎪⎫β-π4=-cos 2β,∴cos 2β=-2425. 又2β∈⎝ ⎛⎭⎪⎫π2,π,∴sin 2β=725.又cos 2α=1+cos 2α2=45⎝ ⎛⎭⎪⎫α∈⎝ ⎛⎭⎪⎫0,π4,∴cos α=255,sin α=55.∴cos(α+2β)=cos αcos 2β-sin αsin 2β =255×⎝ ⎛⎭⎪⎫-2425-55×725=-11525. 12.(2013·岳阳模拟)已知向量a =(sin ωx ,cos ωx ),b =(cos φ,sin φ),函数f (x )=a·b ⎝ ⎛⎭⎪⎫ω>0,π3<φ<π的最小正周期为2π,其图象经过点M ⎝ ⎛⎭⎪⎫π6,32.(1)求函数f (x )的解析式;(2)已知α,β∈⎝ ⎛⎭⎪⎫0,π2,且f (α)=35,f (β)=1213,求f (2α-β)的值.解:(1)依题意有f (x )=a·b =sin ωx cos φ+cos ωx sin φ=sin(ωx +φ). ∵函数f (x )的最小正周期为2π,∴2π=T =2πω,解得ω=1. 将点M ⎝ ⎛⎭⎪⎫π6,32代入函数f (x )的解析式, 得sin ⎝⎛⎭⎪⎫π6+φ=32.∵π3<φ<π,∴π6+φ=2π3,∴φ=π2. 故f (x )=sin ⎝⎛⎭⎪⎫x +π2=cos x .(2)依题意有cos α=35,cos β=1213,而α,β∈⎝ ⎛⎭⎪⎫0,π2,∴sin α=1-⎝ ⎛⎭⎪⎫352=45,sin β= 1-⎝ ⎛⎭⎪⎫12132=513,∴sin 2α=2425,cos 2α=cos 2α-sin 2α=925-1625=-725,∴f (2α-β)=cos(2α-β)=cos 2αcos β+sin 2αsin β =-725×1213+2425×513=36325.1.化简2cos 4x -2cos 2x +122tan ⎝ ⎛⎭⎪⎫π4-x sin 2⎝ ⎛⎭⎪⎫π4+x .解:原式=-2sin 2x cos 2x +122sin ⎝ ⎛⎭⎪⎫π4-x cos 2⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x=121-sin 22x 2sin ⎝ ⎛⎭⎪⎫π4-x cos π4-x =12cos 22x sin ⎝ ⎛⎭⎪⎫π2-2x =12cos 2x .2.已知sin ⎝ ⎛⎭⎪⎫α-π4=7210,cos 2α=725,求sin α及tan ⎝ ⎛⎭⎪⎫α+π3的值. 解:由题设条件,应用两角差的正弦公式, 得sin ⎝⎛⎭⎪⎫α-π4=22(sin α-cos α). 又sin ⎝ ⎛⎭⎪⎫α-π4=7210,所以sin α-cos α=75.① 由题设条件,应用二倍角的余弦公式,得cos 2α=cos 2α-sin 2α=(cos α-sin α)(cos α+sin α) =-75(cos α+sin α).又cos 2α=725,故cos α+sin α=-15.②联立①②,解得sin α=35,cos α=-45,因此tan α=-34.由两角和的正切公式,得tan ⎝⎛⎭⎪⎫α+π3=tan α+31-3tan α=48-25311. 3.已知向量a =(sin θ,-2)与b =(1,cos θ)互相垂直,其中θ∈⎝⎛⎭⎪⎫0,π2.(1)求sin θ和cos θ的值; (2)若sin(θ-φ)=1010,0<φ<π2,求cos φ的值. 解:(1)∵a⊥b ,∴sin θ-2cos θ=0, 又∵θ∈⎝ ⎛⎭⎪⎫0,π2,∴sin θ=255,cos θ=55.(2)∵sin(θ-φ)=1010, ∴cos(θ-φ)=31010或-31010.当cos(θ-φ)=31010时,cos φ=cos[θ-(θ-φ)]=cos θ·cos(θ-φ)+sin θ·sin(θ-φ)=55×31010+255×1010=22.当cos(θ-φ)=-31010时,cos φ=cos[θ-(θ-φ)]=cos θ·cos(θ-φ)+sinθ·sin(θ-φ)=-55×31010+255×1010=-210<0. ∵φ∈⎝⎛⎭⎪⎫0,π2,∴cos φ<0不合题意,舍去. ∴cos φ的值等于22. 4.已知α,β∈(0,π),且tan(α-β)=12,tan β=-17,求2α-β的值.解:∵tan α=tan[(α-β)+β]=tan α-β+tan β1-tan α-βtan β=12-171+12×17=13>0,∴0<α<π2.又tan 2α=2tan α1-tan 2α=2×131-19=34>0, ∴0<2α<π2.此时tan(2α-β)=tan 2α-tan β1+tan 2αtan β=34+171-34×17=1.∵tan β=-17<0,∴π2<β<π.则-π<2α-β<0.∴2α-β=-3π4.附:什么样的考试心态最好大部分学生都不敢掉以轻心,因此会出现很多过度焦虑。
高考数学一轮复习 3.5两角和与差的正弦、 余弦和正切公式 文 湘教版
整理ppt
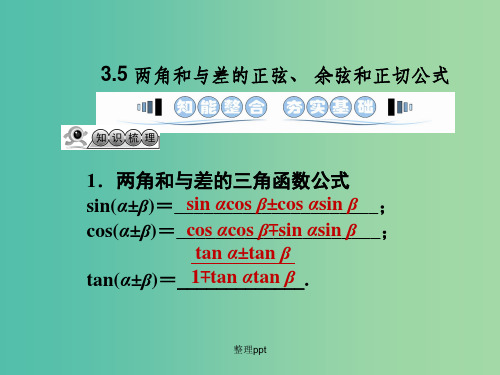
2.二倍角公式 sin 2α=__2_s_i_n_α_c_o_s_α___; cos 2α=_c_o_s_2_α_-__s_in_2_α__=__2_c_o_s2_α_-__1__= __1_-__2_s_in_2_α___;
cos 2 cos 2 1 2 49 5 1 239
2
729
729
整理ppt
3 sin sin 4 3
3
5
所以 sin cos cos sin sin 4 3
3
3
5
化简得 3 sin 3 cos 4 3
2
2
5
3 sin 1 cos 4 , 即 sin 4
(2。 )∵2012<βssi<i1nn22 。 2。 4<-cα2o3<π2cs,。 4o1∴s。 2-4 。2<s122is-n1i2<n462。 8,。 04<4 -源自2<π
∵sin - 2 >0,∴
2 3
- 0,
2 2
又∵cos
- - 1
2 9
<0,∴ - ,
C. 3
D.- 3
2
2
2
2
【解析】cos2si1n151。 5。 s0siin2n210。5。 5sicn7o0。 3ssi1n。 200。coc2so0。 5ssi0。 n20。
12ssiin4n4。 00。12
【答案】B
整理ppt
2.(2014·长春二模)在△ABC中,若tan A·tan B=tan A +tan B+1,则cos C的值是( )
2021年高考数学 3.5 两角和与差的正弦、余弦和正切公式练习

2021年高考数学 3.5 两角和与差的正弦、余弦和正切公式练习 (25分钟50分)一、选择题(每小题5分,共35分)1.(xx·重庆模拟)计算sin 20°cos 110°+cos 160°sin 70°=( )A.0B.1C.-1D.【解析】选C.原式=sin 20°cos(180°-70°)+cos(180°-20°)sin 70°=-sin 20°cos 70°-cos 20°sin 70°=-(sin 20°cos 70°+cos 20°sin 70°)=-sin 90°=-1.【一题多解】本题还可如下解答:原式=sin 20°cos(90°+20°)+cos(180°-20°)sin(90°-20°)=-sin220°-cos220°=-1.【加固训练】(xx·成都模拟)cos 38°sin 98°-cos 52°sin 188°的值为.【解析】cos 38°sin 98°-cos 52°sin 188°=cos 38°cos 8°+sin 38°sin 8°=cos 30°=.答案:2.计算: =()【解析】选D.原式3.(xx·张家口模拟)计算:tan 15°+=()A. B.2 C.4 D.2【解析】选C.tan 15°+4.(xx·成都模拟)已知锐角α满足cos 2α=cos(-α),则sin 2α等于()【解析】选A.由cos 2α=cos(-α),得(cosα-sinα)(cosα+sinα)=(cosα+sinα),由α为锐角知cosα+sinα≠0.所以cosα-sinα=,平方得1-sin 2α=.所以sin 2α=.【一题多解】本题还可如下解答:因为α是锐角,所以0<2α<π,-<-α<.又因为cos 2α=cos(-α),所以2α=-α,即α=.故sin 2α=sin.5.已知角θ的顶点在坐标原点,始边与x轴的正半轴重合,终边上有一点A(3,-4),则sin(2θ+)的值为()A. B.- C.-1 D.1【解题提示】根据题意求得sinθ和cosθ的值,进而利用诱导公式和二倍角公式求得答案.【解析】选B.依题意知sinθ=-,cosθ=,所以sin(2θ+)=cos 2θ=cos2θ-sin2θ=,故选B.6.(xx·济南模拟)若θ∈[, ],sin 2θ=,则sinθ=()【解题提示】根据θ的取值范围,先求cos 2θ,再求sinθ.【解析】选D.由于θ∈[, ],则2θ∈[,π],所以cos 2θ<0,sinθ>0.因为sin 2θ=,所以cos 2θ=又cos 2θ=1-2sin2θ,所以sinθ=【加固训练】(xx·汕头模拟)若,则tan 2α等于()【解析】选D.所以tanα=2,所以7.(xx·呼和浩特模拟)已知cos(α+)-sinα=,则sin(α+)的值是()【解题提示】利用两角和的三角函数化简已知条件,展开所求表达式,即可得到结果.【解析】选B.cos(α+)-sinα=,所以cosα-sinα=,cosα-sinα=,所以sin(α+)=sinαcos +cosαsin=sinα-cosα=-.故选B.二、填空题(每小题5分,共15分)8.(xx·兰州模拟)计算: =.【解题提示】拆角,50°=30°+20°,利用两角和的正弦公式展开合并计算.【解析】原式==1.答案:1【加固训练】(xx·武汉模拟)计算: =.【解析】原式=答案:9.(xx·汉中模拟)设θ为第二象限角,若tan(θ+)=,则sinθ+cosθ=.【解题提示】先由tan(θ+)=,求tanθ的值,再利用同角的三角函数关系式及θ的范围分别求sinθ,cosθ的值.【解析】因为tan(θ+)=,所以tanθ=tan[(θ+)-]即sinθ=-cosθ,又因为sin2θ+cos2θ=1,所以cos2θ+cos2θ=1,cos2θ=,因为θ为第二象限角,所以cosθ=,sinθ=-cosθ=,sinθ+cosθ=+=-.答案:-【加固训练】已知tan(α+)=2,则sin 2α+tan 2α=.【解析】因为tan(α+)=2,所以tanα=tan[(α+)-]所以sin 2α=故sin 2α+tan 2α=答案:10.若=2 015,则+tan 2α=.【解析】因为=2 015,所以答案:2 015(20分钟40分)1.(5分)(xx·新课标全国卷Ⅱ)已知sin 2α=,则cos2(α+)=()【解题提示】利用“降幂公式”将cos2(α+)化简,建立与sin 2α的关系,可得结果. 【解析】选A.因为2.(5分)(xx·宝鸡模拟)已知cos(+θ)cos(-θ)= ,则sin4θ+cos4θ的值等于()【解题提示】先化简已知条件,再把要求的式子变形,代入求值.【解析】选C.因为cos(+θ)cos(-θ)=(cosθ-sinθ)( cosθ+sinθ)=(cos2θ-sin2θ)= cos 2θ=.所以cos 2θ=,sin4θ+cos4θ=221cos 21cos 2195 ()().2216168 -θ+θ+=+=3.(5分)(xx·兰州模拟)设α为锐角,若cos(α+)=,则sin(2α+)的值为.【解题提示】解答本题的关键是角的变化,即把角2α+转化为(2α+)-.【解析】因为cos(α+)=,所以α+∈(0,),所以sin(α+)=,所以sin(2α+)=2sin(α+)cos(α+)=2××=,cos(2α+)=2cos2(α+)-1=,所以sin(2α+)=sin[(2α+)-]=sin(2α+)cos-cos(2α+)sin=.答案:4.(12分)(xx·江西高考改编)已知函数f(x)=-(-1+2cos2x)sin 2x,若,α∈(,π),求sin(α+)的值. 【解析】f(x)=-(-1+2cos2x)sin 2x=-cos 2xsin 2x=-sin 4x,因为,所以=-sinα=-,故sinα=,又α∈(,π),所以cosα=-,sin(α+)=×+(-×)=.5.(13分)(能力挑战题)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.①sin213°+cos217°-sin 13°cos 17°;②sin215°+cos215°-sin 15°cos 15°;③sin218°+cos212°-sin 18°cos 12°;④sin2(-18°)+cos248°-sin(-18°)cos 48°;⑤sin2(-25°)+cos255°-sin(-25°)cos 55°.(1)试从上述五个式子中选择一个,求出这个常数.(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.【解析】(1)选择②式,计算如下:sin215°+cos215°-sin 15°cos 15°=1-sin 30°=1-.(2)三角恒等式sin2α+cos2(30°-α)-sinαcos(30°-α)=.证明如下:sin2α+cos2(30°-α)-sinαcos(30°-α)=sin2α+(cos 30°cosα+sin 30°sinα)2-sinα(cos 30°cosα+sin 30°sinα)=sin2α+cos2α+sinαcosα+sin2α-sinαcosα-sin2α=sin2α+cos2α=. 【一题多解】本题第(2)问还可用以下方法解答:三角恒等式为sin2α+cos2(30°-α)-sinαcos(30°-α)= .证明如下:sin2α+cos2(30°-α)-sinαcos(30°-α)=-sinα(cos 30°cosα+sin 30°sinα)=-cos 2α++ (cos 60°cos 2α+sin 60°sin 2α)- sinαcosα-sin2α=-cos 2α++cos 2α+sin 2α-sin 2α- (1-cos 2α)=1-cos 2α-+cos 2α=.25901 652D 攭F)c 36170 8D4A 赊X35277 89CD 觍22329 5739 圹20096 4E80 亀36255 8D9F 趟26878 68FE 棾w 26794 68AA 梪。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年高三数学一轮复习 3.5两角和与差的正弦、余弦和正切公式精品试题
一、选择题(每小题5分,共40分)
1.(xx·绍兴模拟)已知cos2θ=,则sin4θ-cos4θ的值为( )
A. B.- C. D.-
【解析】选B.sin4θ-cos4θ=(sin2θ+cos2θ)·(sin2θ-cos2θ)=-cos2θ=-.
2.计算:tan15°+=( )
A. B.2 C.4 D.2
【解析】选C.tan15°+
=+
===4.
3.(xx·杭州模拟)在△ABC中,若cos2B+3cos(A+C)+2=0,则sinB的值是( )
A. B. C. D.1
【解析】选A.由cos2B+3cos(A+C)+2=0,得2cos2B-3cosB+1=0,所以cosB=或cosB=1(舍去).
4.(xx·温州模拟)已知α∈,cosα=-,则tan等于( )
A.7
B.
C.-
D.-7
【解析】选B.因为α∈,cosα=-,
所以sinα<0,即sinα=-,tanα=,
所以tan===.
5.(xx·汕头模拟)若=,则tan2α等于( )
A. B.- C. D.-
【解析】选D.===,
所以tanα=2,
所以tan2α===-.
6.(xx·新课标全国卷Ⅱ)已知sin2α=,则cos2=( )
A. B. C. D.
【思路点拨】利用“降幂公式”将cos2化简,建立与sin2α的关系,可得结果.
【解析】选A.因为cos2=
==,
所以cos2===.
7.(xx·金华模拟)已知cos+sinα=,则sin的值是( )
A.-
B.
C.-
D.
【解析】选C.cos+sinα
=⇒sinα+cosα
=⇒sin=,
所以sin=-sin=-.
8.若tanα=lg(10a),tanβ=lg,且α+β=,则实数a的值为( )
A.1
B.
C.1或
D.1或10
【思路点拨】利用α+β=得tan(α+β)=1,由此构造含有a的方程求解. 【解析】选C.α+β=⇒tan(α+β)=1⇒
==1⇒lg2a+lga=0,
所以lga=0或lga=-1,即a=1或a=.
【加固训练】若a,b是非零实数,且=tan,则= .
【解析】由=,
及tan=tan=,
得=tan=.
答案:
二、填空题(每小题5分,共20分)
9.已知cos(α+β)=,cos(α-β)=,则tanαtanβ的值为. 【解析】因为cos(α+β)=,
所以cosαcosβ-sinαsinβ=.①
因为cos(α-β)=,
所以cosαcosβ+sinαsinβ=.②
①+②得cosαcosβ=.
②-①得sinαsinβ=.
所以tanαtanβ==.
答案:
10.计算:= .
【解析】
==
==.
答案:
11.(xx·台州模拟)设sin=,sin2θ= .
【解析】因为sin=,
即sinθ+cosθ=,
所以sinθ+cosθ=,
两边平方,得:1+2sinθcosθ=,
所以sin2θ=-.
答案:-
12.函数y=sin(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB= .
【解析】过点P作PD⊥AB,垂足为D,则∠APB=∠APD+∠BPD.函数的最大值是1,周期T==4,
则AD==1,BD=3,PD=1,
则tan∠APD==1,tan∠BPD==3,
所以tan∠APB=tan(∠APD+∠BPD)
===-2.
答案:-2
三、解答题(13题12分,14~15题各14分)
13.若sin=,cos=,且0<α<<β<π,求cos(α+β)的值.
【解析】因为0<α<<β<π,
所以π<π+α<π,-<-β<0.
又sin=,cos=,
所以cos=-,sin=-,
所以cos(α+β)=sin
=sin
=sincos-
cossin
=-.
【方法技巧】
1.给值求值问题的关键
解决三角函数的给值求值问题的关键是寻求“已知角”与“所求角”之间的关系,用“已知角”表示“所求角”.
(1)已知角为两个时,待求角一般表示为已知角的和与差.
(2)已知角为一个时,待求角一般与已知角成“倍”的关系或“互余互补”关系.
2.拼角、凑角的技巧
(1)用已知角表示未知角:
2α=(α+β)+(α-β);2β=(α+β)-(α-β);
α=(α+β)-β=(α-β)+β;
α=+,β=-;
=-等.
(2)互余与互补关系:
+=;
+=;
+=π;
+=π;
…
14.(xx·宁波模拟)已知cosα=,cos(α-β)=,且0<β<α<.
(1)求tan2α的值.
(2)求β.
【解析】(1)由cosα=,0<α<,得sinα===,
所以tanα==×=4,
于是tan2α===-.
(2)由0<β<α<,得0<α-β<.
又因为cos(α-β)=,
所以sin(α-β)===.
由β=α-(α-β)得:
cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)
=×+×=,
所以β=.
15.(能力挑战题)某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos55°.
(1)试从上述五个式子中选择一个,求出这个常数.
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
【解析】(1)选择②式,计算如下:
sin215°+cos215°-sin15°cos15°
=1-sin30°=1-=.
(2)三角恒等式
sin2α+cos2(30°-α)-sinαcos(30°-α)=.
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=sin2α+(cos30°cosα+sin30°sinα)2-sinα(cos30°cosα+sin30°sinα)
=sin2α+cos2α+sinαcosα+sin2α-sinαcosα-sin2α
=sin2α+cos2α=.
【一题多解】本题第(2)问还可用以下方法解答:
三角恒等式为
sin2α+cos2(30°-α)-sinαcos(30°-α)=.
证明如下:
sin2α+cos2(30°-α)-sinαcos(30°-α)
=+-sinα(cos30°cosα+sin30°sinα)
=-cos2α++(cos60°cos2α+
sin60°sin2α)-sinαcosα-sin2α
=-cos2α++cos2α+sin2α-sin2α-(1-cos2α)
=1-cos2α-+cos2α=.35192 8978 襸22243 56E3 団20011 4E2B 丫36170 8D4A 赊26793 68A9 梩D 26709 6855 桕39295 997F 饿 )32598 7F56 罖S32236 7DEC 緬28941 710D 焍。
