3.1.1数系的扩充和复数的概念(公开课)

5m
6
0 , 解的m
3
m2 3m 0
例2: 已知 (x y) y 1i 2x 3y (2y 1)i 其中
x, y R, 求 x与y.
解：根据复数相等的定义，得方程组
x y 2x 3y
y 1 2 y 1
得 x 4, y 2
2020/4/25
变式2：
已知x是实数，y是纯虚数，满足 x y 3 xi,求x与y
2020/4/25
练习:完成下列表格（分类一栏填实数、虚数
或纯虚数）
2-3i
0 14i 23
6i
实部 2
0
1 2
0
虚部 -3 0
4 3
6
分类
虚数 实数
虚数
纯虚 数
i2
-1 0
实数
2020/4/25
问 题 5：
若复数a + bi = c + di(a, b,c,d R) a,b,c,d应满足什么条件呢？
数 z 是纯虚数．
2020/4/25
变式1：实数m取什么值时，复数 m2 5m 6 m2 3m i是
（1）实数 （2）虚数 （3）纯虚数 （4）零
解： 1m2 3m 0,解的m 0或3
2m2 3m 0,解的m 0且m 3
3m2
5m
6
0 ,
解的m
2
m2 3m 0
4m2
复数的有关概念及应用
1545年意大利有名的数学 “怪杰” 卡尔丹 第一次开始讨论负数开平方的问题，当时
这种数被他称作“诡辩量”.几乎过了100年， 法国数学家笛卡尔才给这种“虚幻之数”取 了一个名字——虚数．1777年 瑞士数学家 欧拉还是说这种数只是存在于“幻想之中”， 并用i（imaginary，即虚幻的缩写）来表 示它的单位.直到1801年，德国数学家高斯
2020/4/25
问 题 3：
复数z=a+bi(a ∈ R、b ∈ R)能表示实数和
虚数
如何对复数a+bi(a,b∈R)进行分类?
复数z
实数b纯虚数
2020/4/25
问 题 4：
你们可以用韦恩图把复数集与实数集、虚 数集、纯虚数集之间的关系表示出来吗？
虚 数 集 复数集C 纯 虚 数 集 实数集R
3.若4+bi=a-2i，求实数a,b的值。
2020/4/25
预习自测答案：
1. 实部分别是：0， 2 ， 2，2，0,0；
2
虚部分别是：0,0，1 ,1， 3,1. 3
2. 2 7,0.618,0,i2是实数；
2 i,i,i 1 3 ,5i 8,3 9 2i, 2 2i是虚数；
7
2 i,i,i 1 3 是纯虚数.
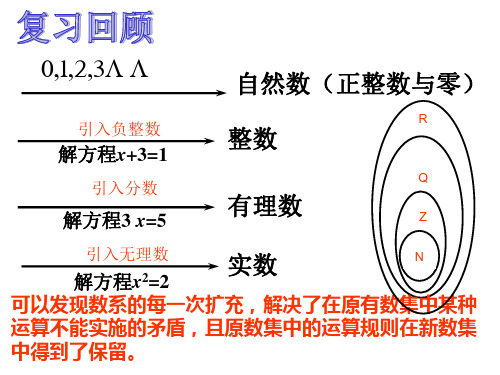
0,1,2,3
自然数（正整数与零）
引入负整数
整数
R
解方程x+3=1
引入分数
Q
解方程3 x=5
有理数
Z
引入无理数
实数
N
解方程x2=2
可以发现数系的每一次扩充，解决了在原有数集中某种
运算不能实施的矛盾，且原数集中的运算规则在新数集
中得到了保留。
问 题1：
一元二次方程 x2 1 0 ，有没有实数根？
2020/4/25
新知
复数的概念
形如a+bi(a,b∈R)的数叫做复数 通常用字 ,母z表示.全体复数所成的集合叫做复数集，
一般用字母C表示.
复数的代数形式：
z a bi (a R,b R)
实虚 部部
2020/4/25
小试牛刀
说出下列复数的实部和虚部？
实数
- 2 1 i， 3- 9 2i. - 3i, 2 .
解： 设y bib R,且b 0
x y 3 xi x bi 3 xi
x 0 b 3 x x 0,b 3
x 0, y 3i
数系的扩充
复数
z = a + bi (a,b∈R)
复数的分类
当b=0时z为实数; 当b0时z为虚数
(此时,当a =0时z为纯虚数).
复数的相等
你得到什么样的数？ 把实数a与新引入的数i相加，结果记作a+i；把 实数b与i相乘，结果记作bi；把实数a与bi相加， 结果记作a+bi,等等.
由于加法和乘法的运算律仍然成立，从而这些运
算的结果都可以写成 a bia,b R 的形式，
所以实数系经过扩充后得到的新数集应该是
C a bi a,b R
7
3. x 1, y 7
例1：
实数m取什么值时，复数 z m 1 (m 1)i是
（1）实数？
（2）虚数？ （3）纯虚数？
解：（1）当 m 1 0 ，即m 1 时，复数z 是实数．
（2）当m 1 0 ，即m 1 时，复数z 是虚数．
（3）当m 1 0 ，且 m 1 0，m即m1 m1010时0，复
2020/4/25
问题解决:
新知
▲ 如果两个复数的实部和虚部分别相等，那
么我们就说这两个复数相等.即
a bi c di
思考 (a, b, c, d R)
a c b d
若a
bi
0(a、b
R)
ba
0 0
2020/4/25
口答
1.若2-3i=a-3i，求实数a的值； 2.若8+5i=8+bi，求实数b的值；
3
2
虚数
复数z=a+bi(a ∈ R、b ∈ R)能表示实数和虚数
2020/4/25
自主学习
• 对于复数a+bi(a,b∈R), • 当且仅当＿＿＿b=＿0 ＿时,它是实数; • 当且仅当＿a=＿0且＿b＿=0＿时,它是实数0; • 当＿＿＿＿b≠0＿＿＿时, 叫做虚数; • 当＿＿a=＿0且＿b＿≠0＿＿时, 叫做纯虚数;
类比每一次数系的扩充过程，我们能否引 进一个新数，将实数集进行扩充，使得在 新的数集中，该问题能得到解决呢？
2020/4/25
学习目标：
1.了解数系的扩充过程； 2.理解复数的有关概念以及符号表示； 3.掌握复数的代数表示形式及其有关概念
学习重点：
理解虚数单位i引进的必要性及复数的 有关概念
学习难点：
a+bi=c+di
a=c
(a, b,c,dR) b=d
2020/4/25
一、教材第106页，A组1、2
系统地使用了i这个符号，于是使之通行于 世。
2020/4/25
问题解决:
为了解决负数开平方问题，数学家引
入一个新数 i ，把 i 叫做虚数单位，并且 满足：
(1) i21 ；
(2)实数可以与i 进行四则运算,在进行四 则运算时,原有的加法与乘法的运算律仍 然成立.
2020/4/25
问 题 2：
把实数和新引进的数i 像实数那样进行运算，