黑龙江省哈尔滨市第六中学2012-2013学年度上学期期中考试(高一数学)

合集下载

2013-2014学年度上学期期中考试(高一数学)附答案

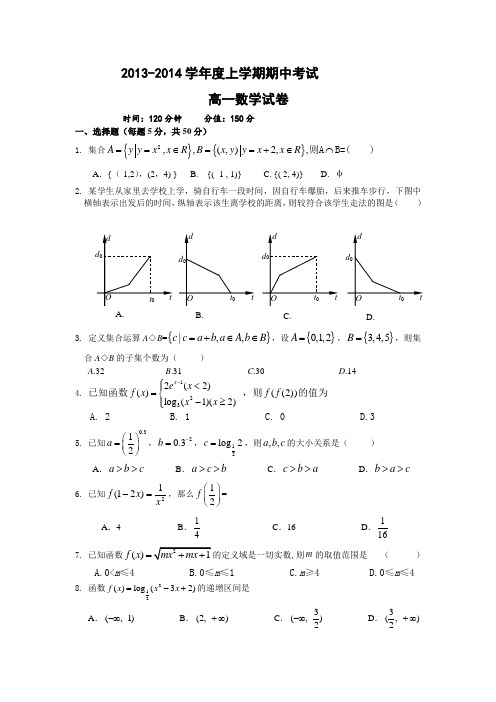
2013-2014学年度上学期期中考试高一数学试卷时间：120分钟分值：150分一、选择题（每题5分，共50分）1. 集合{}{}2,,(,)2,,A y y x x R B x y y x x R ==∈==+∈⋂则A B=( )A ．{（-1,2），(2，4) } B. {( -1 , 1)} C. {( 2, 4)} D. φ2. 某学生从家里去学校上学，骑自行车一段时间，因自行车爆胎，后来推车步行，下图中横轴表示出发后的时间，纵轴表示该生离学校的距离，则较符合该学生走法的图是（）3. 定义集合运算A ◇B =|,,c c a b a A b B =+∈∈，设0,1,2A =，3,4,5B =，则集合A ◇B 的子集个数为（）A .32B .31C .30D .144. 已知函数1232(2)()log (1)(2)x e x f x x x -⎧<⎪=⎨-≥⎪⎩ ，则))2((f f 的值为 A. 2 B. 1 C. 0 D.35. 已知0.312a ⎛⎫= ⎪⎝⎭，20.3b -=，12log 2c =，则,,a b c 的大小关系是（）A ．a b c >>B ．a c b >>C ．c b a >>D ．b a c >> 6. 已知21)21(x x f =-，那么12f ⎛⎫⎪⎝⎭= A ．4 B ．41 C ．16 D ．1617. 已知函数()=f x 的定义域是一切实数,则m 的取值范围是（）A.0<m ≤4B.0≤m ≤1C.m ≥4D.0≤m ≤48. 函数212()log (32)f x x x =-+的递增区间是A ． (,1)-∞B ． (2,)+∞C ． 3(,)2-∞ D ．3(,)2+∞　9. 已知函数()f x 是定义在R 上的偶函数，在(),0-∞上单调递减，且有()3=0f ，则使得()0<f x 的x 的范围为（）A.(),3-∞B. ()3,+∞C.()(),33,-∞+∞D.()3,3-10.对实数a 和b 定义运算“⊗”：,1,,1a ab a b b a b -≤⎧⊗=⎨->⎩．设函数22()(2)()f x x x x =-⊗-，x ∈R ，若函数()y f x c =-的图像与x 轴恰有两个公共点，则实数c 的取值范围是（）A ．3(,2](1,)2-∞--B ．3(,2](1,)4-∞---C ．11(1,)(,)44-+∞D ．31(1,)[,)44--+∞二、填空题（每题5分，共25分） 11．函数)12(log 741)(2++-=x x x f 的定义域为 .12．幂函数()22211m m y m m x--=--在()0,x ∈+∞时为减函数，则m= ．13. 已知2510m n==，则11m n+= ． 14. 如果函数()f x 满足：对任意实数,a b 都有()()()f a b f a f b +=,且()11f =，则()()()()()()()()()()2342011201212320102011f f f f f f f f f f +++++= _________．15. 给出下列命题：①()f x 既是奇函数，又是偶函数；②()f x x =和2()x f x x=为同一函数；③已知()f x 为定义在R 上的奇函数，且()f x 在(0,)+∞上单调递增，则()f x 在(,)-∞+∞上为增函数；④函数y =[0,4) 其中正确命题的序号是 .三、解答题（共75分）16.（本小题满分12分）⑴计算：0.25-2-25.0log 10log 2)161(85575.032----⑵已知函数)(x f 是定义域为R 的奇函数，当x ≤0时，)(x f =x(1+x).求函数)(x f 的解析式并画出函数)(x f 的图象.17.（本小题满分12分）已知集合{}|5239A x x =-≤+≤，{}|131B x m x m =+≤≤- （1）求集合A ；（2）若B A ⊆，求实数m 的取值范围.18．（本小题满分12分）某商品在近30天内每件的销售价格p （元）与时间t （天）的函数关20,025,,100,2530,.t t t N p t t t N +<<∈⎧=⎨-+≤≤∈⎩该商品的日销售量Q （件）与时间t （天）的函数关系是40+-=t Q ),300(N t t ∈≤<，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？19．（本小题满分12分）定义运算：a bad bc c d=- （1）若已知1k =,求解关于x 的不等式101x x k< -（2）若已知1()1x f x k x=- -，求函数()f x 在[1,1]-上的最大值。

黑龙江省哈尔滨市第六中学2012届高三第二次模拟考试数学文

HLLYBQ 整理供“高中试卷网（）”哈尔滨市第六中学2012届高三第二次模拟考试数学（文史类）本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，试卷满分150分，答题时间为120分钟．考试结束后，将试卷和答题卡一并交回．注意事项：1．答题前，考生必须将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内．2．选择题必须用2B 铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚．3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．4．保持卡面清洁，不要折叠、不要弄破、不准使用涂改液、刮纸刀．第I 卷(选择题，共60分)一、选择题(本大题共12小题，每小题5分,共60分.在每小题的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡上) 1.已知i 为虚数单位,则1i i+的实部与虚部的乘积等于( )A.14B. 14- C.14i D. 14i -2．在下列结论中，正确的结论为（）（1）“q p ∧”为真是“q p ∨”为真的充分不必要条件（2）“q p ∧”为假是“q p ∨”为真的充分不必要条件（3）“q p ∨”为真是“p ⌝”为假的必要不充分条件（4）“p ⌝”为真是“q p ∧”为假的必要不充分条件A.（1）（2）B.（1）（3）C.（2）（4）D.（3）（4） 3.设非零向量b a ,满足+==，则a 与b a -的夹角为（） A. 60 B. 30 C. 120 D. 1504.︒-︒20sin 2135sin2的值为（）7．要得到函数sin y x =的图象，只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象( ) A ．向右平移π6个单位 B ．向左平移π6个单位 C ．向左平移π3个单位 D ．向右平移π3个单位8.已知直线a 和平面,αβ,,,l a a αβαβ⋂=⊄⊄,且a 在,αβ内的射影分别为直线b 和c ,则b 和c 的位置关系是( )A.相交或平行B.相交或异面C.平行或异面D.相交﹑平行或异面 9.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( ) A.()334π+ B.()34π+ C.()638π+ D.()238π+10．若A 为不等式组0,0,2x y y x ≤⎧⎪≥⎨⎪-≤⎩表示的平面区域，则当a 从－2连续变化到1时，动直线x y a += 扫过A 中的那部分区域的面积为 ( ) A ．1B ．32C ．34D ．7411.已知函数()⎩⎨⎧>≤+=0,log 0,12x x x x x f ，则函数()[]1+=x f f y 的零点个数（）A.4B.3C. 2D. 1 12.已知点P 是椭圆)0,0(181622≠≠=+y x y x 上的动点，12,F F 为椭圆的两个焦点，O 是坐标原点，若M 是12F PF ∠的角平分线上一点，且10F M M P ⋅= ，则O M的取值范围是（）A ．(0,3)B ．(0,C ．3)D ．(0,4)D CBA 'D CBA第Ⅱ卷(非选择题，共90分)二、填空题(本大题共4小题，每小题5分，共20分．把正确答案填在答题卡中的横线上) 13.以抛物线24y x =的焦点为圆心，且与直线y x =相切的圆的标准方程为____ ． 14．一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）。

黑龙江省哈六中2014-2015学年高一上学期期末考试数学 Word版含答案

哈尔滨市第六中学2014—2015学年度上学期期末考试高一数学试题考试时间：120分钟满分：150分一、选择题：（本大题共12小题，每小题5分，共60分）1.已知集合}1,)21(|{},1,log |{2>==>==x y y B x x y y A x，则A =B ( )A ． ⎭⎬⎫⎩⎨⎧<<210|y y B. {}10|<<y y C. ⎭⎬⎫⎩⎨⎧<<121|y y D. Φ 2.设()2log log ,2log ,3log 3232===c b a ,则（） A.a b c << B. b c a << C. a c b << D.b a c <<3.在ABC ∆中，60C =，AB =BC ，则A 等于（） A.135 B.105 C. 45 D.754．化简22cos 5sin 5sin 40cos 40-=（） A. 1 B.2 C.12D.1- 5.定义在R 上的函数()f x 满足()()0f x f x +-=，当0m >时，()()f x m f x ->，则不等式2(2)()0f x f x -++<的解集为（）A. (2,1)-B. (,2)(1,)-∞-⋃+∞C. (1,2)-D.(,1)(2,)-∞-⋃+∞6．将函数)42sin(3π-=x y 的图象经过（）变换，可以得到函数x y 2sin 3=的图象A. 沿x 轴向右平移8π个单位 B. 沿x 轴向左平移8π个单位 C. 沿x 轴向右平移4π个单位 D. 沿x 轴向左平移4π个单位7.已知tan 2α=-，且满足42ππα<<，则⎪⎭⎫ ⎝⎛+--απαα4sin 21sin 2cos 22值( )A ．2B ．－2C ．223+-D ．223- 8．已知函数()()⎪⎭⎫ ⎝⎛<>>∈+=200sin πϕωϕω，，，A R x x A x f 的图象（部分）如图所示，则()x f 的解析式是 ( ) A ．()2sin()()6f x x x R ππ=+∈ Ｂ．()2sin(2)()6f x x x R ππ=+∈Ｃ.()2sin()()3f x x x R ππ=+∈ Ｄ．()2sin(2)()3f x x x R ππ=+∈9．)(x f 是R 上的偶函数，当0≥x 时，有(2)()f x f x +=-,且当[0,2)x ∈时，2()log (1)f x x =+，则)()2012()2011(=+-f f A. 21log 3+ B. 21log 3-+ C.-1 D.110．函数)0(cos sin 3)(>+=ωωωx x x f 与直线2=y 的两个相邻的交点距离等于π，则)(x f 的单调递增区间是（）（A ）Z k k k ∈+-],125,12[ππππ （B ）Z k k k ∈+-],12,125[ππππ（C ）Z k k k ∈+-],6,3[ππππ （D ）Z k k k ∈++],32,6[ππππ 11．已知函数()sin()(,0)4f x x x R πωω=+∈>的最小正周期为π，将()y f x =的图象向左平移ϕ个单位长度，所得图象关于y 轴对称，则ϕ的一个值是（）A.2π B. 38π C.4π D.8π12．设()f x 是定义在R 上的偶函数，且(2)(2)f x f x +=-，当[2,0)x ∈-时，()()12xf x =-，若函数()()log (2)a g x f x x =-+(0a >且1a ≠）在区间(2,6)-内恰有4个零点，则实数a 的取值范围是（）A.1(,1)4 B. (1,4) C.(1,8) D. (8,)+∞二、填空题：（本大题共4小题，每小题5分，共20分）13．关于x 的方程2cos sin 0x x a +-=有实数解，则实数a 的取值范围是__________ 14．已知方程220x ax a -+=的两个根均大于1，则实数a 的取值范围为_____________ 15．已知函数()2sin(2)6f x x π=+，在ABC ∆中，,,a b c 分别是角,,A B C 的对边，若()1a f A ==，则b c +的最大值为____________16.关于函数()4sin(2)()3f x x x R π=-∈，有以下命题：（1）4()3y f x π=+是偶函数；（2）要得到()4sin 2g x x =-的图象，只需将()f x 的图象向右平移3π个单位；（3）()y f x =的图象关于直线12x π=-对称；（4）()y f x =在[0,]π内的增区间为511[0,],[,]1212πππ，其中正确命题的序号为______________三、解答题（本大题共6小题，共70分，解答时写出必要的文字说明，证明过程或解题步骤）17．（本题满分10分）设函数2()log ()x x f x a b =-，且(1)1f =，2(2)log 12f =．（1）求a b ，的值；（2）当[12]x ∈，时，求()f x 的最大值．18．（本题满分12分）已知2sin ()cos(2)tan()(),sin()tan(3)f παπαπααπααπ-⋅-⋅-+=+⋅-+(1)化简()f α；(2)若1(),8f α=且,42ππα<<求cos sin αα-的值；(3)求满足1()4f α≥的α的取值集合.19．（本题满分12分）已知βαt an ,t an 是一元二次方程02532=-+x x 的两根，且),2(),2,0(ππβπα∈∈，（1）求)cos(βα-的值；（2）求βα+的值．20．（本题满分12分）已知函数()4cos sin()16f x x x π=+-（1）求()f x 在区间[,]64ππ-上的最大值和最小值及此时的x 值；（2）求()f x 的单调增区间；（3）若1()2f α=，求sin(4)6πα-21．（本题满分12分）已知在ABC ∆中，,,a b c 分别是角,,A B C 的对边，，且满足1cos cos )2A A A ⋅-=（1）求角A 的大小；（2）若ABC a S ∆==，求,b c 的长。

黑龙江省哈六中12—13学年上学期高二数学(理科)期中考试试卷

哈尔滨市第六中学2012—2013学年度上学期期中考试高二理科数学考试时间：120分钟满分：150分一、选择题(本大题共12个小题，每个小题5分，共60分) 1．下列命题中，正确的个数有 ( ) (1)抛物线22x y =的准线方程为81-=y ； (2)双曲线1422=-y x 的渐近线方程为x y 2±=； (3)椭圆1422=+y x 的长轴长为2； (4)双曲线17922=-y x 的离心率与椭圆171622=+y x 的离心率之积为1. A ．1B ．2C ．3D ．42．若双曲线以x y 2±=为渐近线，且)0,1(A 为一个顶点，则双曲线的方程为 ( )A ．1422=-y x B ．1422=-x y C ．1422=-y x D ．1422=-x y 3．设n m l ,,表示三条不同的直线，γβα,,表示三个不同的平面，给出下列四个命题中真命题的个数为 ( )①若βα⊥m l m l ,//,//，则βα⊥； ②若,α⊥m n m ⊥，则α//n ；③若n m ,为异面直线，αα//,//n m ，ββ//,//n m ，则βα//； ④若γαβα⊥⊥,，则βγ⊥. A ．1B ．2C ．3D ．44．已知21,A A 分别是双曲线1:2222=-by a x E 的左、右顶点， P 为直线c x 23=(c 为半焦距)上的一点，12PA A ∆是底角为︒30的等腰三角形，则双曲线E 的离心率为 ( ) A ．45B ．34 C ．23 D ．25．直三棱柱111C B A ABC -的底面是边长为3的正三角形，且侧棱长为2，则这个三棱柱的外接球的体积为 ( )A ．3π4 B ．π4C ．3π32 D ．π16 6．如图，三棱锥ABC P -中，⊥PA 平面ABC ，ABC ∆是等边三角形，E 是BC 中点，若AB PA =，则异面直线PE 与AB 所成角的余弦值 ( ) A ．1473 B ．621 C ．105 D ．32 7．已知抛物线)0(2:2>=p px y C 的焦点为F ，过F 且斜率为1的直线l 与抛物线C 相交于B A ,两点，若线段AB 的中点到抛物线C 准线的距离为4，则p 的值为 ( ) A ．1 B ．2 C ．3 D ．48．一个几何体的正视图和俯视图如图所示，其中俯视图为边长为32的正三角形，且圆与三角形内切，则该几何体侧视图的面积为 ( ) A ．π4+ B ．π34+ C ．π36+ D ．π6+9．已知F 是双曲线1822=-y x 的右焦点，)3,2(-A ，P是双曲线右支上的动点，则||||PF PA -的最小值为 ( )A ．2B ．4C ．6D ．810．已知M 是正四面体ABCD 棱AB 的中点，N 是棱CD 的中点，则下列结论中，正确的个数有 ( )(1)AB MN ⊥；(2)MCD B MCD A V V --=； (3)平面⊥CDM 平面ABN ；(4)CM 与AN 是相交直线. A ．1个 B ．2个C ．3个D ．4个11．已知,A B 是椭圆22221(0)x y a b a b+=>>长轴的两个端点，,M N 是椭圆上关于x 轴对称的两点，直线,AM BN 的斜率分别为12,k k )0(21≠k k ，若椭圆的离心率为23，则||||21k k +的最小值为 ( ) A ．1B ．2C ．3D ．212．设点P 是椭圆)0(12222>>=+b a by a x 与圆2223b y x =+的一个交点，21,F F 分别是椭圆的左、右焦点，且||3||21PF PF =，则椭圆的离心率为 ( )A ．410 B ．53 C ．47 D ．414 二、填空题：(本大题共4小题，每小题5分，共20分．将答案填在机读卡上相应的位置) 13．在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点12,F F 在x 轴上，且椭圆C 与椭圆184:221=+y x C 的离心率相同，过1F 的直线交椭圆C 于,A B 两点，且2ABF ∆的周长为24，那么椭圆C 的方程为________.14．如图所示几何体的三视图，则该几何体的体积为________.15．抛物线)0(2:2>=p px y C 的焦点为F ，准线为l ，M 是抛物线C 上一动点，)3,0(A ，过M 作MN 垂直准线l ，垂足为N ，若||||MA MN +的最小值为2，则抛物线C 的方程为________.16．已知点D C B A P ,,,,都是直径为3的球O 表面上的点，⊥PA 平面ABCD ，四边形ABCD 是正方形，若1=PA ，则几何体ABCD P -的体积为________.三、解答题(本大题共6个小题，共70分,解答时写出必要的文字说明和演算步骤)17．(本小题满分10分)如图，四棱锥ABCD P -的底面ABCD 为直角梯形，⊥PA 底面A B C D 其中AD CD AD AB ⊥⊥,，AB PA AD CD 2===，E 是PC 中点.(1)求证：//BE 平面PAD ；(2)求异面直线PD 与BC 所成角的余弦值.18．(本小题满分12分)如图，三棱柱111C B A ABC -中，AC AA CAA 2,6011=︒=∠，⊥BC 平面C C AA 11.(1)证明：AB C A ⊥1；(2)设2==AC BC ，求三棱锥11BC A C -的体积.19．(本小题满分12分)已知抛物线)0(22>=p px y 的焦点为F ，过F 且斜率为3直线与抛物线在x 轴上方的交点为M ，过M 作y 轴的垂线，垂足为N ，O 为坐标原点，若四边形OFMN 的面积为34. (1)求抛物线的方程；(2)若Q P ,是抛物线上异于原点O 的两动点，且以线段PQ 为直径的圆恒过原点O ，求证：直线PQ 过定点，并指出定点坐标.20．(本小题满分12分)如图，直四棱柱1111D C B A ABCD -中，平面⊥BC A 1平面11ABB A ，2==BC AB ，221=AA .(1)求证：⊥BC 平面11ABB A ；(2)求直线B A 1与平面AC A 1成角的正弦值.21．(本小题满分12分)设过点(,)P x y 的直线分别与x 轴和y 轴交于,A B 两点，点Q 与点P 关于y 轴对称，O 为坐标原点，若3=且4=⋅. (1)求点P 的轨迹M 的方程；(2)过)0,2(F 的直线与轨迹M 交于B A ,两点，求⋅的取值范围.22．(本小题满分12分)已知椭圆)0(1:2222>>=+b a by a x E 的左、右焦点为21,F F ，且离心率为23. (1)若过1F 的直线交椭圆E 于Q P ,两点，且F PF 113=，求直线PQ 的斜率； (2)若椭圆E 过点)1,0(，且过1F 作两条互相垂直的直线，它们分别交椭圆E 于C A ,和D B ,，求四边形ABCD 面积的最大值和最小值.高二理科数学参考答案1－5BCBDC 6－10ABDAC 11－12AD13．1222=+y x ；14．4；15．x y 42=；16．34； 17．解：(1)取PD 中点F ，连接AF EF ,，证明ABEF 为平行四边形即可；(2)取CD 中点H ，连接PH AH ,，PHA ∠为所求，余弦值为51018．(1)证明略；(2)体积为334； 19．(1)x y 42=；(2)恒过(4,0)20．(1)略；(2)66 21．(1)1322=+y x ；(2)]1,21( 22．(1)2±；(2)最大值为2，最小值为2532；。

黑龙江省哈六中2012-2013学年高一数学下学期期中试题新人教A版

黑龙江省哈六中2012-2013学年高一数学下学期期中试题考试时间：120分钟满分：150分一、选择题：本大题共12个小题，每小题5分，共60分，每小题只有一个正确选项．1. 已知向量,a b 满足1,4,a b ==且2a b ⋅=,则a 与b 的夹角为( ) A.6πB.4πC.3πD.2π2.已知等比数列{}n a 的前n 项和为13n n S a +=+，N *n ∈，则实数a 的值是( ) A ． 1- B ． 3 C ．3- D ．1 3.与向量a →=的夹角为30︒的单位向量是（）A ．1(2或 B ． ()0,1或1)2 C ．()0,1D ．1)24.在ABC ∆中23BC B π,=,=,若ABC ∆则tan C为( )B.15.已知平面向量),2(),2,1(m b a -==，且a ∥b ，则b a 32+=（） A ．(2,4)-- B. (3,6)-- C. (5,10)-- D. (4,8)--6.设n S 是等差数列{}n a 的前n 项和，若4813S S =，则816S S 等于( )A.310 B. 13 C. 19 D. 187.已知向量等于则垂直与若a b a n b n a,),,1(),,1(-==（） A ．1B ．2C ．2D ．48.已知数列121,,,4a a --成等差数列，1231,,,4b b b --成等比数列，则212a ab -的值为( ) A.14 B.12- C.12或12- D. 129.ABC ∆中，下列判断正确的是（）A.︒===30,18,7A b a 有两解B.︒===150,24,28A b a 有一解C.︒===45,9,6B c b 有两解D.︒===60,10,9A c a 无解10.等比数列{}n a 中，已知对任意自然数n ，12321-=+⋅⋅⋅+++n n a a a a ，则2232221n a a a a +⋅⋅⋅+++等于 ( )A.314-n B.2)12(-nC.14-nD.12-n11．如图，非零向量OA =a →，OB b →=且BC OA ⊥， C 为垂足，设向量OC aλ→=，则λ的值为（） A. ||||⋅⋅a b a b B.||||⋅⋅a b a b C.2||⋅a b b D. 2||⋅a b a 12．在ABC ∆中，P 是BC 边中点，角A ，B ，C 的对边分别是a ，b ，c ，若0cAC aPA bPB ++=，则ABC ∆的形状为A. 等边三角形B.钝角三角形C.直角三角形D.等腰三角形但不是等边三角形. 二、填空题：本大题共4个小题，每小题5分，共20分．13．数列{}n a 的通项公式449n a n =-，则{}n a 的前n 项和取得最小值时，n 等于 14．在,,ABC A B C ∆中，的对边分别为,,a b c ，若cos ,cos ,cos a C b B c A 成等差数列,则B =______15．“嫦娥奔月,举国欢庆”,据科学计算,运载“神八”的“长征”系列火箭,在点火第一秒钟通过的路程为2 km,以后每秒钟通过的路程都增加2 km,在到达离地面240 km 的高度时,火箭与飞船分离,则这一过程需要的时间大约是秒钟。

黑龙江省哈尔滨市第六中学2012-2013学年高一下学期期末考试语文试题 Word版含答案

高一下学期期末考试语文试题（满分：150分时间：120分钟命题：高一语文备课组）一、基础知识检测（每题2分，共6分）1、下列加点成语使用不恰当的一项是（）A．三军在江、淮、河、汉之间布成“品”字形阵势，互为觭角，逐鹿中原．．．．，机动歼敌。

B．王熙凤是一个精明能干、八面玲珑．．．．的人，她为人刁钻狡黠，明是一盆火，暗是一把刀。

C．马克思在当时极其艰难的条件下从事《资本论》的写作，其坚苦卓绝．．．．的精神令人惊叹！D．那股偷袭的匪徒，看到这支厉兵秣马．．．．的队伍，犹豫了一阵之后，别转马头跑了。

2、下列各句没有语病的一项是（）A．交通运输部在对革命老区农村公路建设已给予支持的基础上，将加大对中西部“少边穷”地区农村公路建设的支持力度，提高对这些地区公路建设的补助标准。

B．理科综合、文科综合的考试形式，对许多习惯了单科考试的高三学生，最初的确会感到不适应。

C．认识沙尘暴，了解沙尘暴，是为了从科学的角度达到对沙尘暴进行预防，减少沙尘暴造成的损失。

D．许多网友认为，标榜“大众”和“草根”的山寨文化之所以能大行其道的原因，是由于它在一定程度上反映出普通人的文化需求、适应了大众文化的消费需求所致。

3、依次填入下面句子中横线处的语句，与上下文衔接最恰当的一项是（）（1）向西越过桐庐县城，，这就是富春山的山子山孙了。

东北面山下，有一条长蛇似的官道，隐而复现，。

绕过一支小岭，便是富阳县的境界。

（2）鸟儿鸣叫着，一批又一批飞过旷野。

它们时而飞过碧绿的田野，看到小河在太阳照耀下流淌；时而飞过丛林，窥见。

①遥遥对着一排高低不定的青峦②一排高低不定的青峦遥遥地对着③出没盘曲在桃花杨柳洋槐榆树的中间④在桃花杨柳洋槐榆树的中间盘曲出没⑤在枝头闪烁的鲜红的果实⑥鲜红的果实在枝头闪烁A．②③⑥B．①③⑥C．②④⑤D．①③⑤寡人闻命矣。

”乃令出裘发粟以与饥寒者。

孔子闻之曰：“晏子能明．其所欲，景公能行其所善．也。

”【注】①景公：齐国国君。

黑龙江省哈尔滨市第六中学校2022-2023学年高三上学期10月月考数学试题

黑龙江省哈尔滨市第六中学校2022-2023学年高三上学期10月月考数学试题一、单选题1．已知集合(){}2=log 1<0A x x -，4=0+1x B xx -≥⎧⎫⎨⎬⎩⎭，则()A B ⋂=R ð（） A ．()1,1-B ．()2,4C ．(][]1,12,4-⋃D ．[][]1,12,4-⋃ 2．在等比数列{}n a 中，1a ，13a 是方程213160x x -+=的两根，则2127a a a 的值为（） AB．C ．4D ．4±3．某学习小组的学习实践活动是测量图示塔AB 的高度．他们选取与塔底在同一水平面内的两个测量基点C ，D ，测得3BCD π∠=，4BDC π∠=，且基点C ，D间的距离为(30m CD =+，同时在点C 处测得塔顶A 的仰角为6π，则塔高AB 为（）A ．20mB．C ．40mD．4．下列说法正确的是（）A ．命题“2x ∀>，ln 1x x ≤-”的否定是“02x ∃≤，00ln 1x x >-”B ．命题p ：0x ∃∈R ，02010ax ax ++≤，若命题p 是假命题，则04a <<C ．“0a b ⋅<”是“a ，b 的夹角为钝角”的充分不必要条件D ．ABC 中，A B >是sin sin A B >的充要条件5．向量OA ，OB 满足0OA OB ⋅=，点C 在以点O 为圆心的劣弧AB 上，OC xOA yOB =+uu u r uu r uu u r，则2x y +的最大值为（）6．已知函数()f x 定义域为R ，()1f x -为奇函数，()1f x +为偶函数，当[]1,3x ∈时，()f x kx m =+，若()()031f f -=-，则()2022f =（）A ．1-B ．1C ．2-D ．27．已知函数()()π=sin 2+>0,0<<2f x x ωϕωϕ⎛⎫ ⎪⎝⎭的部分图象如图所示，则下列结论正确的是（）A ．()f x 的图象关于点,03π⎛⎫- ⎪⎝⎭对称B ．()f x 在区间π0,2⎡⎤⎢⎥⎣⎦的最小值为C ．()f x 在[]0,π上的单调递增区间为π0,6⎡⎤⎢⎥⎣⎦D ．将()f x 图象的横坐标变为原来的()1>0t t 倍，纵坐标不变得到函数()g x ，若()12g x =在[]0,π上有且只有三个不等实根，则41<3t ≤8．若关于x 的不等式ln x a e x a -≥+对一切正实数x 恒成立，则实数a 的取值范围是（）A ．1,e ⎛⎫-∞ ⎪⎝⎭B ．(],e -∞C ．(],1-∞D ．(],2∞-二、多选题9．下列关于复数的四个命题正确的是（） A ．若2z =，则4z z ⋅= B ．若()72i3i z +=+，则z 的共轭复数的虚部为1C ．若1i 1z +-=，则1i z --的最大值为3D ．若复数1z ，2z 满足12z =，22z =，121z z +=，则12z z -=10．已知等差数列{}n a 的前n 项和为n S ，若23a =，77S =，则（） A ．5n a n =- B ．若210m n a a a a +=+，则116m n+的最小值为2512C ．n S 取到最大值时，5n =D ．设2nn n a b =，则数列{}n b 的最小项为164- 11．设锐角三角形ABC 的对边分别为a ，b ，c ，若cos cos a a B b A +=，则（） A ．22b a ac -= B ．2B A = C ．04A π<<D．)2b ca+∈12．平面向量a ，b ，c ，满足1a =，2b =且()a ab ⊥-，2,30c a c b <-->=︒r r r r，则下列说法正确的是（）A．2a b +=r r B ．a 在b 方向上的投影向量为12bC ．c的最大值是2 D ．若向量m 满足2m a ⋅=u r r，则()m m b⋅-u r u r r 的最小值为54三、填空题13．记n S 为等差数列{}n a 的前n 项和．若32236S S =+，则公差d =_______．14．通过研究正五边形和正十边形的作图，古希腊数学家毕达哥拉斯发现了黄金分割率，黄金分割率的值也可以用2sin18︒2sin18=︒．记2sin18m =︒，则=______．15．已知O 是ABC 的外心，若22AC AB AB AO AC AO mAO AB AC⋅+⋅=uuu r uu u r uu u r uuu r uuu r uuu r uuu r uu u r uuu r，且sin sin B C +=m 的最大值为______．16．已知函数()()()222e 1e x x f x a a x x =+-++有三个不同的零点1x ，2x ，3x ，且123x x x <<，则3122312111e e e x x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值为______．四、解答题17．已知函数()2sin cos 3f x x x π⎛⎫=- ⎪⎝⎭．(1)求函数()f x 的最小正周期及单调递增区间； (2)在锐角ABC 中，若()f AACBC =ABC 的面积． 18．设n S 是正项等比数列{}n a 的前n 项和，且26S =，430S =． (1)求数列{}n a 的通项公式； (2)设()121n n n b n n a ++=+，求数列{}n b 的前n 项和n T ．19．在ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，ABC 的面积214S a =． (1)cos B b =-，求sin sin CB的值； (2)求c bb c+的最大值．20．已知等差数列{}n b 满足32b =，251681b b b b =++，数列{}n a 的前n 项和2124n n S b +=⋅-，*n ∈N(1)求数列{}n a ，{}n b 的通项公式；(2)记数列{}n n a b 的前n 项和为n T ，若226825n n kT n a n n >-+对一切*n ∈N 恒成立，求正整数k 的最小值．21．已知函数()2x x f x e ae -=+-，()2g x x =(1)讨论()f x 的单调性；(2)设()()()h x f x g x =-．若函数()h x 有相同零点和极值点0x ，求()h x 的最小值．22．已知函数()21e xf x x =+-．(1)求曲线()=y f x 在点()()0,0P f 处的切线方程；(2)设函数()()()ln 1g x f x a x =-+有三个零点，求实数a 的取值范围．参考答案：1．C【分析】根据对数函数的单调性化简集合A ，根据分式不等式的解法化简集合B ，结合集合的补集和交集的定义进行求解即可.【详解】不等式()2log 1<0x -可化为()22log 1<log 1x -，所以011x <-<，所以12x <<，所以()1,2A =，不等式40+1xx -≥可化为()()4+10x x ->或=4x ，所以14x -<?，所以(]=1,4B -，所以(][)R 12A ，，=-∞+∞ð，所以()A B ⋂=R ð(][]1,12,4-⋃，故选：C. 2．C【分析】由已知条件结合一元二次方程根与系数的关系，利用等比数列的性质求解．【详解】113,a a 是方程213160x x -+=的两根，11311313,16a a a a ∴+=⋅=，21131132127>0,>0,===16a a a a a a a ∴⋅⋅，又等比数列{}n a 中奇数项符号相同，可得74a =21271644a a a ⋅∴==. 故选：C ． 3．A【分析】设,AB x =则BC =，利用正弦定理即得解. 【详解】解：设,AB x =则BC . 由题得53412CBD ππππ∠=--=. 51sinsin()12642πππ=+==在△BCD20x ∴=. 所以塔高20m. 故选：A4．D【分析】对于A ，利用含量词的命题的否定即可判断；对于B ，由p 是假命题可得p ⌝：x ∀∈R ，210ax ax ++>为真命题，分=0a 和0a ≠进行讨论即可；对于C ，利用“,a b 的夹角为钝角”的充要条件即可判断；对于D ，利用正弦定理和三角形性质即可求解.【详解】对于A ，由含量词的命题的否定知，命题“2x ∀>，ln 1x x ≤-”的否定是“02x ∃>，00ln 1x x >-”，故不正确；对于B ，因为命题p 是假命题，所以p ⌝：x ∀∈R ，210ax ax ++>为真命题，当=0a 时，不等式为10>恒成立；当0a ≠时，需满足2>0Δ=4<0a a a -⎧⎨⎩，解得04a <<，综上所述，a 的取值范围为{}0<4a a ≤，故不正确；对于C ，“,a b 的夹角为钝角”的充要条件是“0a b ⋅<且a 不平行于b ”，所以“0a b ⋅<”是“a ，b 的夹角为钝角”的必要不充分条件，故不正确；对于D ，若A B >，由三角形中“大边对大角”可知，a b >，由正弦定理可知，sin sin A B >；若sin sin A B >，由正弦定理可知，a b >，从而A B >，故“A B >”是“sin sin A B >”的充要条件，故正确，故选：D 5．D【分析】由OC xOA yOB =+uu u r uu r uu u r两边平方可得,x y 的关系，设(),m x y =，()2,1n =由数量积的性质求2x y +的最大值.【详解】因为OC xOA yOB =+uu u r uu r uu u r，两边平方可得()()()222222OC x OA xyOA OB y OB =+⋅+uuu r uu r uu r uu u r uu u r ，因为0OA OB ⋅=，所以()()()22222OC x OA y OB =+uu u r uu r uu u r ，因为点C 在以点O 为圆心的劣弧AB 上，所以OC OA OB ==uuu r uu r uu u r，且0x ≥，0y ≥，所以221x y +=，设(),m x y =，()2,1n =，则2m n x y ?+，又=cos ,m n m n m n m n ⋅⋅⋅≤⋅，当且仅当m ，n 同向时等号成立，所以2x y +?x y ==故选：D. 6．B【分析】由题意表示出()1(1)--=--f x f x 与()1(1)f x f x -+=+，令=1x ，=0x ，=2x ，结合题目所给条件列式求解,k m ，再由两式化简可推导出()f x 的周期为8T =，从而代入计算. 【详解】因为()1f x -为奇函数，所以()1(1)--=--f x f x ①；又()1f x +为偶函数，所以()1(1)f x f x -+=+②；令=1x ，由②得：()(2)20==+f f k m ，又()33=+f k m ，所以()()032(3)1f f k m k m k -=+-+=-=-，得=1k ，令=0x ，由①得：()()1(1)10-=--⇒-=f f f ；令=2x ，由②得：()1(3)0-==f f ，所以()3330f k m m =+=⇒=-. 得[]1,3x ∈时，()3f x x =-，结合①②得，()2()(2)(4)()(8)(4)()f x f x f x f x f x f x f x f x +=-=--⇒+=-⇒+=-+=，所以函数()f x 的周期为8T =，所以()()()()()20222528662231f f f f =⨯+==-=--=. 故选：B 7．D【分析】由图象求出()f x 的解析式，再结合三角函数的性质与图像逐项分析即得. 【详解】由图可知，1(0)sin 2f ϕ==，又π02ϕ<<，所以π6ϕ=，所以由五点作图法可知4ππ3π362ω⋅+=，得1ω=，所以()πsin 26f x x ⎛⎫=+ ⎪⎝⎭，对于A ，由π2ππ133sin 6f ⎛⎫-⎛⎫+ ⎪⎝⎭=-=- ⎪⎝⎭，所以A 错误；对于B ，当π0,2x ⎡⎤∈⎢⎥⎣⎦时，ππ7π2,666x ⎡⎤+∈⎢⎥⎣⎦，所以1πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭，所以()f x 在区间π0,2⎡⎤⎢⎥⎣⎦的最小值为12-，所以B 错误；对于C ，当[]0,πx ∈，则ππ13π2,666x ⎡⎤⎢⎥⎣∈⎦+，由πππ2,662x ⎡+∈⎤⎢⎥⎣⎦，可得π0,6x ⎡⎤∈⎢⎥⎣⎦，由π13π22π,66x +∈⎡⎤⎢⎥⎣⎦，可得11π,π12x ⎡⎤∈⎢⎥⎣⎦，所以()f x 在[]0,π上的单调递增区间为π0,6⎡⎤⎢⎥⎣⎦，11π,π12⎡⎤⎢⎥⎣⎦，故C 错误；对于D ，由题可得()πsin 26g x tx ⎛⎫+ ⎝=⎪⎭，因为()12g x =在[]0,π上有且只有三个不等实根，所以π1sin 262tx ⎛⎫+= ⎪⎝⎭在[]0,π上有且只有三个不等实根，由[]0,πx ∈，可得πππ2,2π666tx t ⎡⎤+∈+⎢⎥⎣⎦，作出正弦函数的图象，由图象可知ππ5π2π2π2π666t +≤+<+，即413t ≤<，故D 正确. 故选：D. 8．C【分析】构造函数()(0)x a f x e lnx a x -=-->，将原不等式转化为求解函数()f x 的最小值，通过导数判断函数的单调性研究函数的最值，得到000x a e lnx a ---…，再利用基本不等式进行求解即可．【详解】解：设()(0)x a f x e lnx a x -=-->，则()0f x …对一切正实数x 恒成立，即()0min f x …，由1()x a f x e x -'=-，令1()x a h x e x -=-，则21()0x ah x e x -'=+>恒成立，所以()h x 在(0,)+∞上为增函数，当0x →时，()h x →-∞，当x →+∞时，()h x →+∞，则在(0,)+∞上，存在0x 使得0()0h x =，当00x x <<时，()0h x <，当0x x >时，()0h x >，故函数()f x 在0(0,)x 上单调递减，在0(x ，)∞+上单调递增，所以函数()f x 在0x x =处取得最小值为000()0x a f x e lnx a -=--…，因为001x aex -=，即00x a lnx -=-，所以0010x a a x +--…恒成立，即0012a x x+…，又0012x x +=…，当且仅当001x x =，即01x =时取等号，故22a …，所以1a …．故选：C ．【点睛】方法点睛：不等式恒成立问题常见方法：① 分离参数()a f x ≤恒成立(min ()a f x ≤即可)或()a f x ≥恒成立（max ()a f x ≥即可）；② 数形结合(()y f x = 图象在()y g x = 上方即可)；③ 讨论最值min ()0f x ≥或max ()0f x ≤恒成立；④ 讨论参数. 9．ACD【分析】根据复数模、共轭复数的积运算即可判断A ，由复数除法的运算及共轭复数、虚部的概念判断B ，根据复数模的几何意义及圆的性质判断C ，利用复数的加减运算、模的运算求解可判断D.【详解】设i,(,R)z a b a b =+∈，对A ，2224z a b =⇒+=，22i)(i (4)z a b a b a z b +-=+⋅==，故正确；对B ，()72i3i z(2i)3i z +=+⇒-=+，所以3i (3i)(2i)55iz 1i 2i (2i)(2i)5++++====+--+， z 1i =-，其虚部为1-，故错误；对C ，由1i 1z +-=的几何意义，知复数z 对应的动点Z 到定点(1,1)-的距离为1，即动点Z 的轨迹为以(1,1)-为圆心，1为半径的圆，1i z --表示动点Z 到定点(1,1)的距离，由圆的性质知，max 1i 13z --==，故正确；对D ，设12=+i,=+i,(,,,R)z m n z c d m n c d ∈，因为12z =，22z =，所以22224+=4m n c d +=，，又121z z +=，所以+=1,+m c n d 所以+=2mc nd -，所以12=|()+(z z m c n d ---.故选：ACD 10．AD【分析】求得等差数列{}n a 的通项公式判断选项A ；求得116m n+的最小值判断选项B ；求得n S 取到最大值时n 的值判断选项C ；求得数列{}n b 的最小项判断选项D.【详解】由11+=37?67+=72a d a d ⎧⎪⎨⎪⎩，可得1=4=1a d -⎧⎨⎩，则等差数列{}n a 的通项公式为5n a n =-，则选项A 判断正确；若210m n a a a a +=+，则21012m n +=+= 则116116116125(17)(178)12121212m n n m m n m n m n +⎛⎫+=+⨯=++≥+= ⎪⎝⎭ （当且仅当1248,55m n ==时等号成立）又,m n ∈Z ，则116m n +的最小值为不为2512.则选项B 判断错误；等差数列{}n a 中，123456432101a a a a a a =>=>=>=>=>=->则等差数列{}n a 的前n 项和n S 取到最大值时，=4n 或5n =.则选项C 判断错误；设2n n n a b =，则52n n n b -=，则111546222n n n n n n n n b b +++----=-= 则12345678b b b b b b b b >>>>>=<<则数列{}n b 的最小项为766561264b b -===-.则选项D 判断正确故选：AD 11．ABD【分析】利用余弦定理可判断A ，利用正弦定理结合三角恒等变换可判断B ，结合条件可得角A 的范围可判断C ，利用正弦定理及三角函数的性质可判断D. 【详解】因为cos cos a a B b A +=，所以22222222a c b b c a a a b ac bc +-+-+⋅=⋅，整理可得22=b a ac -，故A 正确；由cos cos a a B b A +=，可得sin sin cos sin cos A A B B A +=，所以()sin sin cos sin cos sin A B A A B B A =-=-，所以A B A =-或πA B A +-=(舍去)，即2B A =，故B 正确；因为ABC △为锐角三角形，所以π0<<2π0<=2<2π0<=π3<2A B A C A -⎧⎪⎪⎪⎨⎪⎪⎪⎩，解得ππ<<64A ，故C 错误；由题可得()sin 2sin 3sin sin sin sin A A b c B C a A Aπ+-++==， sin 2sin 2cos cos 2sin sin A A A A A A++=22cos 2cos cos2A A A =++ 24cos 2cos 1A A =+-，又ππ<<64AA所以)+b ca∈，故D 正确. 故选：ABD 12．ACD【分析】利用向量的数量积运算律和模的运算求解2a b +r r，根据投影向量定义求解a 在b 方向上的投影向量，构造如图所示的几何图形集合几何意义求c 的最小值，作出满足题意的几何图形求解()m m b ⋅-的最小值.【详解】因为1a =，2b =且()a ab ⊥-，所以()20a a b a a b ⋅-=-⋅=，所以1a b ⋅=，1cos ,2a b a ba b⋅=，所以a ，b 的夹角为60，因为()222224423a b a ba b a b +=+=++⋅=，所以A 正确;a 在b 方向上的投影向量为1cos ,4ba ab b b ⋅=,所以B 错误;如图，作半径都等于2且公共弦长等于2的两个圆中， 2,,,OA a OB b OC c ===则2,AC c a BC c b =-=-，因为30ACB ∠=，所以2,30c a c b --=︒,符合题意，由图可知，当OC 同过两圆的圆心时c 最大，此时c 的最大值等于圆心距加半径为2，所以C 正确;作,,OA a OB b ==如图，222222()23AB b a b a b a OB OA =-=+-⋅==-, 所以90OAB ∠=,令OM m =，由2m a ⋅=得cos 2OM AOM ∠=, 在射线OA 上取点E ，使得2OE =,过E 作直线l OA ⊥,则有点M 在直线l 上，取OB 中点C ,过C 作CD l ⊥，垂足为D , 连接,,BM CM OM ,()()()()()m m b OM BM OC CM BC CM OC CM OC CM ⋅-=⋅=+⋅+=+⋅-+2222151124CM OC CD OA AE ⎛⎫=-≥-=+-= ⎪⎝⎭，当且仅当,M D 重合时取得等号，所以()m m b ⋅-的最小值为54. 所以D 正确. 故选:ACD.【点睛】结合向量间的关系作出满足题意的几何图形，利用几何意义求解相关最值问题是向量最值问题有效的手段. 13．2【分析】转化条件为()112+226a d a d =++，即可得解.【详解】由32236S S =+可得()()123122+36a a a a a +=++，化简得31226a a a =++，即()112+226a d a d =++，解得2d =. 故答案为：2.14．【分析】将2sin18m =︒代入，根据恒等变换公式化简，即可求得结果【详解】2sin18m =︒Q ，2sin144m -⋅︒4sin 182sin 36︒-︒===故答案为：15．32##1.5【分析】设三角形ABC 的外接圆的半径为r ，根据向量数量积的几何定义可得22211222b c c b mr c b ⋅+⋅=，从而可得22bc mr =，从而可得222m b br r =⋅，又sin sin B C +=正弦定理可得sin 2b B r =，sin 2cC r =，从而可得22b c r r+ 【详解】设三角形ABC 的外接圆的半径为r ，2||||2()||||AC AB AB AO AC AO m AO AB AC ⋅+⋅=， ∴根据向量数量积的几何定义可得：22211222b c c b mr c b ⋅+⋅=，即22bc mr =，∴=222m b c r r⋅，又sin sin B C +=sin 2b B r =，sin 2cC r =，∴22b c r r+ ∴2322()22224b cm b b r r r r +=⋅≤=，当且仅当22b c r r =时，即ABC △为等边三角形时取等号，∴324m ≤，32m ∴≤，∴实数m 的最大值为32．故答案为：3216．4【分析】先将题给条件转化为()()2+1++2=0e e x x x x a a -⎛⎫⎪⎝⎭有三个不同的零点1x ，2x ，3x ，且123<<x x x ，再转化为()()2+1++2=0t a t a -有二根12,t t ，且121<0,0<<et t ，进而利用根与系数关系求得3122312111e e e x x x x x x ⎛⎫⎛⎫⎛⎫--- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的值【详解】()()()()()22222e 1e =e 12e e xxxx x x xf x a a x x a a ⎡⎤⎛⎫=+-++-+++⎢⎥ ⎪⎝⎭⎢⎥⎣⎦，又2e >0x ，则()()2+1++2=0e e x x x x a a -⎛⎫⎪⎝⎭有三个不同的零点1x ，2x ，3x ，且123<<x x x ，令()e xx g x =，则1()e x x g x -'=，当>1x 时()<0g x '，()g x 单调递减；当<1x 时()>0g x '，()g x 单调递增则()g x 在=1x 时取得最大值1(1)=eg ，>0x 时()>0g x ，令e xx t =，则1e t ≤ 则()()2+1++2=0t a t a -必有二根12,t t ，且121<0,0<<et t则12121,2t t a t t a +=+=+ 则1e x x t =有一解1<0x ，2ex xt =有二解23,x x 且230<<1<x x 故()()3122223121211111e e ex x x x x x t t ⎛⎫⎛⎫⎛⎫---=-- ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭[][]221212=1(+)+=1(+1)++2=4t t t t a a --故答案为：417．(1)函数()f x 的最小正周期为π，单调递增区间为5,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【分析】（1）由三角恒等变换化简解析式，求出周期，再由正弦函数的单调性求解即可；（2）由()f A sin 23A π⎛⎫=-= ⎪⎝⎭A ，利用余弦定理可求得AB 边的长，再利用三角形的面积公式可求得结果. （1）()22sin cos cos sin sin sin cos 33f x x x x x x x ππ⎛⎫=+= ⎪⎝⎭)1cos211sin2sin2sin 22223x x x x x π-⎛⎫=+==- ⎪⎝⎭ 所以函数()f x 的最小正周期为22T ππ== 由222,232k x k k Z πππππ-+≤-≤+∈得出5,1212k x k k Z ππππ-+≤≤+∈ 故函数()f x 的单调递增区间为5,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦（2）()f A sin 23A π⎛⎫=-=⎪⎝⎭因为02A π<<，则22333A πππ-<-<，所以233A ππ-=，可得3A π=，由余弦定理可得222232cos23BC AB AC AB AC AB π==+-⋅=+，即210AB -=，因为0AB >，解得AB = 此时，AB 为最长边，角C 为最大角，此时222cos 02AC BC AB C AC BC+-=>⋅，则角C 为锐角，所以，11sin 22ABCSAB AC A =⋅=18．(1)2n n a =；(2)1112(1)2n n T n +=-+⋅．【分析】（1）由等比数列前n 项和公式列方程组求得1,a q ，得通项公式；（2）用裂项相消法求和．（1）设{}n a 的公比为q ，显然1q ≠，0q >，由题意1141+=6(1)=301a a q a q q--⎧⎪⎨⎪⎩，解得1=2=2a q ⎧⎨⎩（负数舍去）．所以1222n nn a -=⨯=；（2）由（1）11211(1)22(1)2n n n n n b n n n n +++==-+⋅⋅+⋅，所以2231111111()()[]122222322(1)2n n n T n n+=-+-++-⋅⋅⋅⋅⋅+⋅1112(1)2n n +=-+⋅．19．1； (2)【分析】（1）已知214S a =，由面积公式和余弦定理得π)4c b A b c +=+，由已知及正弦定理和三角恒等变换得π4A =，则有c b b c+=. （2）由π)4c b A b c +=+，结合正弦函数性质求最值..（1）ABC 的面积211sin 42S a bc A ==，有22sin a bc A =，由余弦定理，2222sin 2cos a bc A b c bc A ==+-，得2sin 2cos c bA A bc=+-，即π2sin +2cos)4c bA A A b c +==+， cosB b -cos sin A B CB =-，由[]sin sin()sin()sin coscos sin C A B A B A B A B =π-+=+=+， i n c n n cos sin sin os si A A B C B B A B B =--=sin sin 0A B B -=，ABC 中sin 0B ≠，∴cos A =(0,π)A ∈，则π4A =，∴π)4c b A b c +=+=c t b =，则有1t t+=1t ，由正弦定理，sin 1sin C cB b==. （2）由（1）有：π)4c b A b c +=+，A 为ABC 的内角，当π4A =时，c bb c +有最大值20．(1)12n n a +=，12n n b +=； (2)3【分析】（1）由等差数列的基本量法求得n b ，由1(2)n n n a S S n -=-≥求得n a ；（2）用错位相减法求得和n T ，代入不等式化简后转化为用基本不等式求函数的最值．（1）设数列{}n b 的公差为d ，则225168(22)1222325b d b b b d d d +==++-++++，12d =，所以112(3)22n n b n +=+-⨯=， 1=1b ，224n n S +=-，311244a S ==-=，2n ≥时，211124(24)2n n n n n n a S S +++-=-=---=，1=4a 也适用，所以12n n a +=；（2）由（1）(1)2nn n a b n =+⋅，22232(1)2n n T n =⨯+⨯+++⋅，231222322(1)2n n n T n n +=⨯+⨯++⋅++⋅，两式相减得2314222(1)2n n n T n +-=++++-+⋅1114(12)4(1)2212n n n n n -++-=+-+⋅=-⋅-，所以12n n T n +=⋅．所以不等式226>8+25n n kT n a n n -即为26>8+25nk n n -，又266258258n n n n n =-++-，2510n n +≥=，当且仅当5n =时等号成立，所以26825n n n -+的最大值是63108=-，故3k ≥，所以k 的最小值是3．21．(1)当0a ≤ 时，()f x 在R 上单调递增；当>0a 时，()f x在)∞上单调递增，在(-∞上单调递减. (2)()h x 的最小值为0.【分析】（1）先函数求导，对参数进行分类讨论得出结论（2）构造函数对函数求导，利用已知条件求出参数，分析问题，将参数的值代入表达式中求出函数的最小值. （1）由()e e 2x xf x a -=+-，所以()e e x x f x a -'=-，当0a ≤ 时，()0f x '≥，此时()f x 在R 上单调递增，当0a > 时，由()0f x '>，有x >()f x在)+∞上单调递增，由()0f x '<，有x <()f x在(-∞上单调递减，综上所述：当0a ≤ 时，()f x 在R 上单调递增；当0a > 时，()f x在)+∞上单调递增，在(-∞上单调递减. （2）由()()()2e 2x x e a h x g x xf x ---==+-所以()e e 2x xa x x h --'=-，又函数()h x 有相同零点和极值点0x ，所以有0000200e +e 2=0e e 2=0x x x x a x a x --⎧--⎪⎨--⎪⎩，两式相加得：02002e 22x x x =++，令()22e 22x p x x x =---，则()2e 22xp x x '=--，设()2e 22x s x x =--，则()2e 2xs x '=-，所以()s x 在(),0-∞上单调递减，在()0,+∞上单调递增，所以()()00s x s ≥=，所以()p x 单调递增，由()00p =可得00x =，=1a ，所以()22x x e x e x h -+--=，所以()2x x e x h x e ---'=，设()2x xe e x t x --=-所以()120xxx e t e '+-≥=,当且仅当=0x 时取等号. 所以()h x '在R 单调递增，又()00h '=所以当0x >时，()0'>h x ，所以()h x '在(0,)+∞上单调递增，当0x <时，()0'<h x ，所以()h x '在(,0)-∞上单调递减所以()min 0)0(h x h == 故()h x 的最小值为0. 22．(1)=y x (2)(0,1)【分析】（1）求得(0),(0)f f '，利用导数的几何意义得出切线的方程；（2）求出()g x 的导数，通过分类讨论a 的范围，求出函数的单调区间，结合函数的零点个数确定a 的范围即可．（1）()21e x f x x =+-，()2e x f x '=-∴，则(0)0,(0)1f f '==，因此，曲线()y f x =在点()()0,0P f 处的切线方程为y x =．（2）()21e ln(1),(1)x g x x a x x =+--+>-，则()(1)e 2()2e 11x xa x a g x x x ⎡⎤-++-⎣⎦'=---=++，设h ()()(1)e 2xx a x =++-，则()(2)e 2x h x x '=+-，显然()h x '在(1,)-+∞内递增且(0)0h '=，所以，在(1,0)x ∈-时，()0,()h x h x <'单调递减，在(0,)x ∈+∞时，()0,()h x h x >'单调递增，所以()h x 有极小值(0)1h a =-，又(1)h a -=，①当1a ≥时，()0h x ≥在(1,)x ∈-+∞恒成立，即()0g x '≤，所以()g x 在区间(1,)-+∞内单调递减，最多一个零点，不符合题意； ②当01a <<时，(1)0,(0)0,(2)0h h h -><>，所以存在12(1,0),(0,2)x x ∈-∈使得()()120h x h x ==，则在()11,x -内，()0h x >，()0,()g x g x <'单调递减，在()12,x x 内，()0h x <，()0,()g x g x >'单调递增，在()2,x +∞内，()0h x >，()0,()g x g x <'单调递减，又()()12(0)0g x g g x <=<，则()g x 在()12,x x 上有且只有一个零点0，又2(2)5e ln30g a =--<，则()g x 在()2,x +∞上有且只有一个零点，又4411544442e e e e 12e 11eln e 2e e 2e e 130a a a a a a ag a ----------⎛⎫⎛⎫-=-+-+--=->> ⎪⎝⎝⎭+⎪ ⎭，则()g x 在()11,x -上有且只有一个零点，所以函数()g x 恰有三个零点；③当0a ≤时，在(1,0]-内()(0)0h x h <<，又()2(2)(3)e (3)02ah a a a a a --=+->+->-，结合()h x 的单调性可知，存在0(0,)x ∈+∞，使得()00h x =，在()01,x -内，()0h x <，()0g x '>，()g x 单调递增，在()0,x +∞内，()0h x >，()0g x '<，()g x 单调递减，函数()g x 最多两个零点，不合题意．综上所述，实数a 的取值范围是(0,1)．。

黑龙江省哈尔滨市人教版高一数学上册期中考试卷

哈尔滨市第六中学2016—2017学年度上学期期中考试高一数学试题考试时间：120分钟满分：150分一、选择题：本大题共12小题，每小题5分，共60分．1．设全集，集合，则＝（）2AC5}|x??{x?NA2}?x?N|x{U?U A．? B．{2} C．{2,5} D．5)[2,0x??x,?,若，则实数等于（．设函数2）a?f(x)4?a)f(?20x,x??A．－4或－2 B．－4或2 C．－2或4 D．－2或23．若函数的值域是，则函数的值域是（）[1,3]3)x???f(x)2f(?F(x)1y A．[－5，－1] B．[－2,0] C．[－6，－2] D．[1,3] 4．若函数的最小值为，则实数的取值范围是（）A．(1,3) B．(1,3] C．[3，＋2a]ax)?x?6x?8,x?[1,f()(af∞) D．(3，＋∞)5．下列函数中，满足“任意且，”0)]??f(xx(x?)[f(xf(x)?x,x(0,??))x?x22211112的是（）1 D．C．A．B．x2)?f(xxx)??f(1)??ln(xfxf(x)?|?1|(x)x x14?）的图象（6．函数?x)f(x2A．关于原点对称B．关于直线y＝x 对称C．关于x轴对称D．关于y轴对称1的最大值是（7．函数）?)f(x)x(1?1?x4534A．B．C．D．3445111），则（．设8 0.5c,?ba?0.4,?0.5334 A．B．．CD．babc????abc?c?aa?c?b9．已知函数（且），当时，，则在R上（）x2?a?f(x)2x?a?a?01)xf(x)?1(f :]来源[A．是增函数B．是减函数C．当时是增函数，当时是减函数2xx?2?D．当时是减函数，当时是增函数2xx?2?10．函数的单调递减区间是（）3333????????－∞，，＋∞－1，，2)?xln(4?3xxf()?4A．C．B．D．???????? 2222????????11．若不等式对一切恒成立，则的取值范围是（）2a0x?2)?4(a?2)x??2(aR?xA．(－∞，2] B．[－2,2] C．(－2,2]D．(－∞，－2)12．若函数的图象如图所示，其中a，b为常数，则函数x)blogf(x)?(x??abxg()?a的大致图象是（）分．205分，共4二、填空题：本大题共小题，每小题2x?3, x?0?是奇函数，则＝________. ．如果函数13?x)(f)xg(?g(x), x?0?1的定义域是________．14．函数)??ln(1f(x)x?11 ?，则的取值范围是________．15．已知幂函数，若a x?f(x))af(10?2f(a?1)?2 ________．16．直线与曲线有四个交点，则的取值范围是2aa?xy?x|?|1y? 70分，解答时写出必要的文字说明，证明过程或解题步骤．三、解答题：本大题共6小题，共分）（本小题满分17．1011???．（1）计算100??lg25lg2??4??112?2?a1?a?的值．，且（2）设，求3?a?a0a?22 ?1?1a?a12分）（本小题满分18．:]来源[若集合，且，求实数的取值范围．22A?Ba0}ax6?0},B?{|x??x?|A?{xxx??19．（本小题满分12分）已知二次函数的最小值为2)b?R?1,xR,(a,?f(x)axbx??0??1)f(（1）求的解析式，并写出单调区间；)xf(（2）在区间上恒成立，求的取值范围．k3,1][?k(fx?x?)20．（本小题满分12分）函数在区间上的最大值记为．21x)??x??4f(x)g()?1](t?Rt[t,t（1）求的解析式；)g(t（2）求的最大值．)g(t21．（本小题满分12分）已知函数，且．)(x)??(1?x)ff(?xloglogf(x)?(x?1)?t22（1）求函数的解析式；)xf(a?b，其中2）证明：．（1?b???1?a?1,1)b?f()?f()f(a1?ab22．分）（本小题满分12a，且（）已知．xx?)(fxaa(?)?1??a0a21a?（1）判断的奇偶性并用定义证明；)(xf（2）判断的单调性并有合理说明；)(fx （3）当时，恒成立，求的取值范围．b1,1]?[x?bf()x?高一数学答案1 B2 B3 A4B5 C6 D7 D8 B9A10D11C12 D13、2x＋3 14 、(－∞，1)∪(2，＋∞) 15、(3,5)5 16、1<a< 411111???17（1）＝lg÷＝2÷＝－20 ……5分100lg?lg25?2??10100104??11 ?11－－＝＋a7.）将（2＋2＝9两边平方得a＋a即a3?a?a2222－a＋a＋147＋112222－－－将a＋a＝7两边平方有a＋a＋2＝49，得a＋a＝47，∴＝1－1a＋1＋7a＋＝6. ……5分18解：A＝{－3,2}．……2分2＋x＋a＝0，对于x1①当Δ＝1－4a<0，即a>时，B＝，成立；……3分?AB?411??－，不成立；……3a＝时，B＝分1②当Δ＝－4a＝0，即??AB?24??1③当Δ＝1－4a>0，即a<时，若成立，则B＝{－3,2}，∴a＝－3×2＝－A?B46. ……3分1???6＝－或aa> 分综上，a的取值范围为a……1. ???4???b2x ＝(fx)1，b＝2.∴＝，且－＝由题意有f(－1)a－b＋1＝0＝－1，∴a19解：(1)a2＋2x＋1，……4分单调减区间为(－∞，－1]，单调增区间为[－1，＋∞)． (2)分(2)f(x)>x＋k在区间[－3，1]上恒成立，22＋x＋1，x∈[－＝xg上恒成立．，－在1>x转化为x＋＋k[31]设()x3，1]，……4 分．133分……2∴g(x)＝.∴??)?kg(min442，x＝2的位置关系进行讨论：①当t＋1<2，20解：(1)对区间[tt＋1](t ∈R)与对称轴2 t；＋2t＋2t，＋1]上递增，此时g(t)＝f(t＋1)＝－即t<1时，函数f(x)在区间[t上先增后减，在区间[t，t＋1]1≤≤2≤t＋1，即t≤2时，函数f(x)②当t3；＝f(2)＝此时g(t)＝－t)＝f()在区间[t，t＋1]上递减，此时g(t)时，函数③当t>2f(x21.t－＋4t2，，t<1＋2t＋2－t???，t≤23，1≤分综上，g(t)＝ (7)??2>2.－tt＋4t－1，分……5(t)的最大值是3. (2) 分段求最大值得g，x)x)＝－f(21解：(1)由于f(－，x)]tlog(1－)＋x＝－[log(x＋1)＋即log(－x＋1)＋tlog(122220，＋x)]＝[log(1－x)＋log(1)所以log(1－x)＋log(1＋x＋t22220.(*))]＝log(1＋xt)[log(1－x)＋所以(1＋22 1，，即t＝－(*)在定义域内恒成立，必须有1＋t＝0欲使分……6(1－x)．＋故f(x)＝log(x1)－log22x＋1＋)(a)＝log，所以flog＝(x＋1)－log(1－x＜(2)证明：因为－1＜x1时，f(x)222x1－b1＋1＋a b?ab?a1?为因logf(b)＝＝log＋，又log22ba－1－12b?ab??a1b?a?1b?aba?1?ab?ab1?=，gfo)(?llog22ba?b?a?1?abab1??1ab1?ba＋??分. ……6所以f(a)＋f(b)＝f ??ab＋1??．a x－a(－x)＝解：(1)因为函数的定义域为R，所以关于原点对称．又因为f(2221a－x)＝－f(x)，所以f(x)为奇函数．－a……4分2xxxx－－为增－a为减函数，从而y＝－1>0，y＝aa为增函数，y＝a时，(2)当a>1a函数，所以f(x)为增函数，2xxxx－－为减－y＝＝ay为减函数，＝aaa为增函数，从而当0<a<1时，a －1<0，y函数，所以f(x)为增函数．故当a>0，且a≠1时，f(x)在定义域内单调递增．……4分(3)由(2)知f(x)在R上是增函数，所以在区间[－1,1]上为增函数，所以f(－1)≤f(x)≤f(1)，21－aaa1－－a)＝·＝－1，所以要使f(x(－＝f所以(x)f(1)＝a)≥b在[－1,1]22min a1aa－－1上恒成立，则只需b≤－1，故b的取值范围是(－∞，－1]．……4分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

黑龙江省哈尔滨市第六中学2012-2013学年度上学期期中考试高一数学试题考试时间：120分钟满分：150分一、选择题：本大题共12个小题，每小题5分，共60分，每小题只有一个正确选项． 1.在①{}10,1,2⊆；②{}{}10,1,2∈；③{}{}0,1,20,1,2⊆； ④∅{}0上述四个关系中，错误．．的个数是（） A.1个 B.2个 C.3个 D.4个 2. 函数1()lg(1)1f x x x=++-的定义域是( )A ．(),1-∞-B ．()1,+∞C ．()()1,11,-+∞D ．(),-∞+∞ 3. 若372log πlog 6log 0.8a b c ===，，，则（） A ．a b c >>B ．b a c >>C ．c a b >>D ．b c a >>4．函数212log (231)y x x =-+的递减区间为（）A. ()1,+∞B.3,4⎛⎤-∞ ⎥⎝⎦ C.3,4⎛⎫+∞ ⎪⎝⎭ D.1,2⎛⎫-∞ ⎪⎝⎭5．下列等式中一定正确的是 ( )A．23x y =+ B ．82710log 9log 329⋅=C．= D ．2log log aa x x =6．已知()f x 是定义在R 上的奇函数，当0x >时，()23x f x =-,那么(2)f -的值是( ) A ．1-B ．114C ．1D ．114-7. 在下列区间中，函数()43xf x e x =+-的零点所在的区间为( )A.1,04⎛⎫-⎪⎝⎭ B. 10,4⎛⎫ ⎪⎝⎭ C. 11,42⎛⎫ ⎪⎝⎭ D.13,24⎛⎫⎪⎝⎭8.设函数⎩⎨⎧+∞∈-∞∈=),2(,log ]2,(,2)(2x x x x f x ，则满足4)(=x f 的x 的值是（）A.2B.16C.2或16D.-2或16 9.已知函数()()()f x x a x b =--（其中a b >）的图象如下面右图所示，则函数()xg x a b =+的图象是（）A ．B ．C ．D ．f (x )10.当]2,0[∈x 时，函数3)1(4)(2--+=x a ax x f 在2=x 时取得最大值，则a 的取值范围是（） A.),21[+∞-B.),0[+∞C.),1[+∞D.),32[+∞11.已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()2x x f x g x a a -+=-+(0a >，且1a ≠)．若(2)g a =，则(2)f ＝( )A ．2 B.154C.174D ．2a12.对实数a 和b ，定义运算“⊗”：,1.1a ab a b b a b -≤⎧⊗=⎨->⎩设函数()()22()2,f x x x xx R =-⊗-∈，若函数()y f x c =-的图象与x 轴恰有两个公共点，则实数c 的取值范围是( )A ．(]3,21,2⎛⎫-∞-- ⎪⎝⎭ B ．(]3,21,4⎛⎫-∞--- ⎪⎝⎭ C.111,,44⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭D. 311,,44⎛⎫⎡⎫--+∞ ⎪⎪⎢⎝⎭⎣⎭二、填空题：本大题共4个小题，每小题5分，共20分． 13．已知x x f alog)(3=，且1)8(=f ，则=a ________14.函数232(01)y x x x =-+≤≤的值域为15. 函数 )10(31≠>+=-a a a y x 且的图象必过定点P , P 点的坐标为_________.16. 关于函数22log (23)y x x =-+有以下4个结论:其中正确的有① 定义域为(,3](1,);-∞-⋃+∞ ② 递增区间为[1,);+∞ ③ 最小值为1; ④ 图象恒在x 轴的上方三、解答题：本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤．17.（10分）已知集合}06|{2<--=x x x A ,2{|280}B x x x =+-≥(1)求A B ; (2)求R A C B .18. （满分12分）（1）化简：11lg 9lg 240212361lg 27lg35+-+-+（2）已知：lg(1)lg(2)lg 2x x -+-=，求x 的值19. （12分） 2()1x f x x=+是定义在()1,1-上的函数(1)用定义证明()f x 在()1,1-上是增函数； (2)解不等式(1)()0f t f t -+<.20. （12分）已知110,0x y ≤≤>，且1002=xy ，求22)(lg )(lg y x +的最大值和最小值。

21. （12分）已知22(log )24f x x x =-+，]4,2[∈x（1）求)(x f 的解析式及定义域；（2）若方程a x f =)(有实数根，求实数a 的取值范围22．（12分）已知函数aax f x+-=241)(（0>a 且1≠a ）是定义在),(+∞-∞上的奇函数．（1）求a 的值；（2）当]1,0(∈x 时，22)(-≥⋅x x f t 恒成立，求实数t 的取值范围．黑龙江省哈尔滨市第六中学2012-2013学年度上学期期中考试数学答案13. 2 14.23,412⎡⎤⎢⎥⎣⎦15.()1,4 16.②③④17.（1）由已知得：{}23A x x =-<<，{}24B x x x =≥≤-或┄┄┄┄┄┄2分所以{}23A B x x =≤< ┄┄┄┄┄┄5分（2）因为{}42R C B x x =-<< ┄┄┄┄┄┄7分所以{}43R A C B x x =-<< ┄┄┄┄┄┄10分 18.（1）0 ┄┄┄┄┄┄6分（2）3x = ┄┄┄┄┄12分（不舍0x =扣4分） 19.（1）设12,x x 为(－1,1)内任意两实数，且12x x <，则22121221121212222222121212(1)(1)()(1)()()11(1)(1)(1)(1)x x x x x x x x x x f x f x x x x x x x +-+---=-==++++++又因为1211x x -<<<，所以120x x -<，1210x x -> 所以12()()0f x f x -<，即12()()f x f x <所以函数()f x 在（－1，1）上是增函数；-----------------------------------5分（2）由函数()f x 是定义在(－1,1)上的奇函数且(1)()0f t f t -+<得：(1)()()f t f t f t -<-=-又由（1）可知函数()f x 是定义在(－1,1)的增函数，所以有111111021t t t t t-<-<⎧⎪-<<⇒<<⎨⎪-<-⎩. ---------------------------------12分20.由已知得：y =所以()222225(lg )(lg )(lg )(lglg lg 14t x y x x x =+=+=-+ ---------4分令lg m x =，因为110x ≤≤所以01m ≤≤ --------------------6分既求01m ≤≤时2514t m m =-+的最值所以当25m =，既2510x =时t 有最小值45；当1m =，既10x =时t 有最大值54---------------------------------12分21.（1）令2log t x =则2t x =，因为24x ≤≤则12t ≤≤()221()2224224tt tt f t +=-⋅+=-+所以)(x f 的解析式为21()224x x f x +=-+，定义域为[]1,2 --------------6分（2）因为21()224x x f x +=-+，在[]1,2上的值域为[]4,12所以若方程a x f =)(有实数根，则a 的取值范围为[]4,12。

--------------12分 22.（1）因为函数aax f x+-=241)(（0>a 且1≠a ）是定义在),(+∞-∞上的奇函数，所以4(0)102f a=-=+，解得2a =。

--------------4分（2）由（1）得21()21xxf x -=+，当01x <≤时，()0f x >。

所以当01x <≤时22)(-≥⋅xx f t 恒成立，⇔22(22)(21)()21xxxxt f x --+≥=-当01x <≤时恒成立令21,01xm m =-<≤⇔11t m m≥-+当01m <≤时恒成立既11t y m m≥=-+在(]0,1上的最大值，易知11y m m=-+在(]0,1上单调递增，所以当1m =时11y m m=-+有最大值1，所以1t ≥，所以，若]1,0(∈x 时，22)(-≥⋅xx f t 恒成立，则1t ≥。

-------------------------12分。