LMS算法自适应均衡器实验
自适应均衡算法LMS研究

自适应均衡算法LMS研究一、自适应滤波原理与应用所谓自适应滤波器,就是利用前一时刻已获得的滤波器参数等结果,自动地调节现时刻的滤波器参数,以适应信号和噪声未知的或随时间变化的统计特性,从而实现最优滤波。
根据环境的改变,使用自适应算法来改变滤波器的参数和结构。
1.1均衡器的发展及概况均衡是减少码间串扰的有效措施。
均衡器的发展有史已久,二十世纪60年代前,电话信道均衡器的出现克服了数据传输过程中的码间串扰带来的失真影响。
但是均衡器要么是固定的,要么其参数的调整是手工进行。
1965年,Lucky在均衡问题上提出了迫零准则,自动调整横向滤波器的权系数。
1969年,Gerhso和Porkasi,Milier分别独立的提出采用均方误差准则(MSE)。
1972年,ungeboekc将LMS算法应用于自适应均衡。
1974年,Gedard 在kalmna滤波理论上推导出递推最小均方算法RLS(Recursive least-squares)。
LMS类算法和RLS类算法是自适应滤波算法的两个大类。
自适应滤波在信道均衡、回波抵消、谱线增强、噪声抑制、天线自适应旁瓣抑制、雷达杂波抵消、相参检测、谱估计、窄带干扰抑制、系统辨识、系统建模、语音信号处理、生物医学、电子学等方面获得广泛的应用。
1.2均衡器种类均衡技术可分为两类:线性均衡和非线性均衡。
这两类的差别主要在于自适应均衡器的输出被用于反馈控制的方法。
如果判决输出没有被用于均衡器的反馈逻辑中,那么均衡器是线性的;如果判决输出被用于反馈逻辑中并帮助改变了均衡器的后续输出,那么均衡器是非线性的。
图1.1 均衡器的分类1.3自适应算法LMS 算法LMS 算法是由widrow 和Hoff 于1960年提出来的,是统计梯度算法类的很重 要的成员之一。
它具有运算量小,简单,易于实现等优点。
LMS 算法是建立在Wiener 滤波的基础上发展而来的。
Wiener 解是在最小均方误差(MMSE)意义下使用均方误差作为代价函数而得到的在最小误差准则下的最优解。
基于LMS与RLS算法的自适应均衡器性能研究

滤 波 器 ,由 一 条 带 抽 头 的 延 时 线 构 成 ,抽 头 间 隔 等 于 码 元 周 期 ,
每个抽头的延时信号ห้องสมุดไป่ตู้加权送到一个相加电路汇总后输出。
用
表示自适应滤波器在
时刻 n 的权矢量,则滤波器输出信号为:
(3)
自适应均衡器根据自适应算法估计系统特性,并自动调整
滤波器权矢量 ,以达到最佳滤波效果,对未知的时变信道做
出 补 偿 。 本 文 采 用 最 小 均 方 算 法 (LMS) 和 递 推 最 小 二 乘 算 法
雷利华: 博士研究生
(RLS)自 适 应 地 更 新 均 衡 器 的 抽 头 系 数 来 跟 踪 信 道 的 变 化 。
基金项目: 基金申请人: 施浒立; 项目名称: 基于通信卫星的
卫星导航系统的基础研究和理论探索; 基金颁发部门: 科技
b.对
计算: 滤波:
(4)
误差估计:
(5)
权矢量更新:
(6)
其中, 收敛因子是用来控制稳定性和收敛速度的
步长参数。 一般为了获得较好的收敛速度与稳态性能, 通常取
(7)
其中 为接收信号功率,可在接收端进行估计得到。
3.2 递推最小二乘算法(RLS)
基 于 MMSE 准 则 的 自 适 应 算 法 目 标 在 于 使 滤 波 器 输 出 与
器具有很大的参考价值与指导意义。
参考文献
[1]胡广书.数字信号处理—— —理论、算法与实现[M].北京:清华大
学出版社,1997. [2]孙永梅,李晖.数字通信系统中自适应均衡技术的研究[J].信息
技术, 2006,No.4:53-55.
(下转第 111 页)
- 26 - 360元 /年 邮局订阅号:82-946
基于LMS算法的无线信道自适应均衡器
基于LMS 算法的无线信道自适应均衡器一、 无线衰落信道与码间干扰无线信道容易受到噪声、干扰和其他随时间变化的信道因素的影响。
其中,大尺度传播效应(large-scale propagation effects ),包括路径损耗(path loss )和阴影(shadowing )效应,这类衰落比较容易克服。
而由多径引起的小尺度传播效应(small-scale propagation effects),特别是宽带信道下的频率选择性衰落,将使接收信号产生严重的码间干扰,如果不经处理,将无法得到原始信号的精确还原。
宽带通信系统下,如果信号带宽B 远远大于相干带宽c B ,那么在间隔超过相干带宽的两个频率点上的信道幅度特性近似独立。
根据相干带宽c B 与多径信号时延扩展m T σ 的关系,码元周期1s T B ≈ 远远小于1m T cB σ= 。
因此,信道的频率选择性衰落伴随着接收信号严重的码间干扰。
无线通信系统的设计必须以合适的复杂度解决这一问题。
二、 自适应均衡器大多实用的无线通信系统都采用时域均衡作为对抗ISI 的手段。
由于无线信道是时变的,在设计接收机的时候,通常并不能精确地了解信道的冲激响应,因此,所设计的均衡器应该能根据具体的信道特性进行自适应的调整。
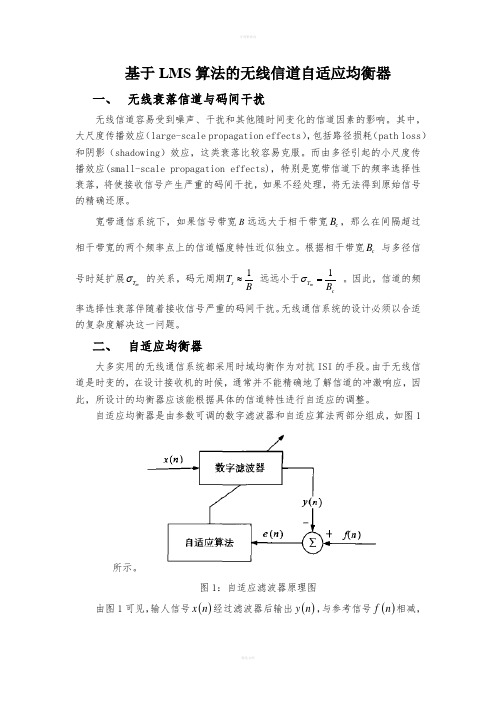
自适应均衡器是由参数可调的数字滤波器和自适应算法两部分组成,如图1所示。
图1:自适应滤波器原理图 由图1可见,输人信号()x n 经过滤波器后输出()y n ,与参考信号()f n 相减,得出误差信号()e n ,然后通过自适应算法调节滤波器系数设置,按照某种算法准则判断误差信号()e n 是否达到最小,重复以上过程,滤波器逐渐掌握了输人信号与噪声规律,通过调节滤波器系数,达到最佳的滤波效果。
参数可调数字滤波器可以是FIR(Finite-duration impulse Response)数字滤波器或IIR(Infinite-duration impulse Response)数字滤波器,也可以是格形数字滤波器。
LMS算法自适应均衡器实验

LMS 算法自适应均衡器实验08S005073 房永奎一、实验目的1、掌握LMS 算法的计算过程,加深对LMS 算法的理解。
2、研究用LMS 算法自适应均衡引起失真的线性色散信道问题。
3、研究特征值扩散度()R χ和步长参数μ对学习曲线的影响。
二、实验原理1、自适应均衡器)n图1 自适应信道均衡试验原理图自适应均衡器用来纠正存在加性白噪声的信道的畸变,信道均衡器的原理框图如1所示。
随机噪声发生器(1)产生用来探测信道的测试信号序列{n x },本实验中由Bernoulli 序列组成,n x =±1,随机变量n x 具有零均值和单位方差。
随机噪声发生器(2)产生干扰信道的白噪声()n ν,具有零均值,方差为2νσ=0.001。
信道的脉冲响应用升余弦表示为:20.51cos (2)1,2,30n n n h W π⎧⎡⎤⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩(1) 其中,参数W 控制均衡器抽头输入相关矩阵的特征值分布()R χ,并且特征值分布随着W 的增大而扩大。
均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于n =2时对称,那么均衡器的最优抽头权值on ω在5n =时对称。
因此,信道的输入n x 被延时了257∆=+=个样值,以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时∆,LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
2、均衡器输入相关矩阵在时刻n ,均衡器第1个抽头的输入为()()()31k k u n h x n k v n ==-+∑ (2)其中所有参数均为实数。
因此,均衡器输入的11个抽头(),(1),,(10)u n u n u n --的自相关矩阵R 为一个对称的1111⨯矩阵。
此外,因为脉冲响应n h 仅在1,2,3n =时为非零,且噪声过程()v n 是零均值、方差为2v σ的白噪声,因此相关矩阵R 是主对角线的,有以下特殊结构所示:()()()()()()()()()()()()()()()012001012021010021000000r r r r r r r r r r r r r r r ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦R (3) 其中()22221230v r h h h σ=+++ (4)()12231r h h h h =+ (5)()132r h h = (6)其中方差20.001v σ=。
毕业论文-基于LMS算法的自适应线性均衡器设计

基于LMS算法的自适应线性均衡器设计摘要:在信息业快速发展的今天,进行快速准确的通信是各个行业的基本要求。
影响移动通信质量和通信速度的一个重要因素是码间干扰,即串扰。
在一个实际的通信系统中,基带传输系统不可能完全满足理想的波形传输无失真条件,因而串扰几乎是不可避免的。
对串扰进行校正的电路称为均衡器,其实质是信道的一个逆滤波器。
信道均衡器是通信系统中一项重要的技术,它能够很好的补偿信道的非理想特性,从而减轻信号的畸变,降低误码率。
在高速通信、无线通信领域,信道对信号的畸变将更加的严重,因此信道均衡技术是不可或缺的。
本文介绍了自适应均衡器的基本理论、最小均方(LMS)算法的原理与设计、自适应的基本原理、线性均衡器的基本理论与设计,并结合归一化(NLMS)算法、递归最小二乘法(RLS)算法对最小均方(LMS)算法作了进一步说明,最终用MATLAB对基于LMS算法的自适应线性均衡器进行了仿真设计。
关键词:LMS算法;自适应;线性均衡器;(NLMS)算法;(RLS)算法LMS Algorithm Based on Adaptive LinearEqualizer DesignAbstract:The rapid development of information industry today, for fast and accurate communication is the basic requirement of various industries. Affect the quality of mobile communications and the communication speed is an important factor in inter-symbol interference, that is, crosstalk. In a practical communication system, base-band transmission system can not fully meet the ideal conditions for wave transmission without distortion, thus crosstalk is almost inevitable. The crosstalk correction circuit called equalizer, and its essence is an inverse channel filter. Channel equalizer is an important communication systems technology, it can be well compensated non-ideal characteristics of the channel, thereby reducing the signal distortion, reduce the error rate. In the high-speed communications, wireless communications, channel distortion of the signal will be more serious, so the channel equalization is indispensable.This article describes the basic theory of adaptive equalizer, the minimum mean square (LMS) algorithm and design principles, basic principles of adaptive linear equalizer of the basic theory and design, combined with normalized (NLMS) algorithm, recursive least squares (RLS) algorithm for least-mean-square (LMS) algorithm was further described, and ultimately using MA TLAB LMS algorithm based adaptive linear equalizer for simulation design.Key words:LMS algorithm; Adaptive; Linear equalizer; (NLMS) Algorithm; (RLS) Algorithm目录第1章绪论 (1)1.1均衡器研究背景及意义 (1)1.2国内外对均衡技术的研究动态 (3)1.3本文研究内容和主要工作 (4)第2章自适应均衡器基本理论 (5)2.1通信系统中的失真分析 (5)2.1.1、数字基带传输系统模型 (5)2.1.2通信系统中的噪声干扰 (5)2.1.3、通信系统的传输特性 (7)2.1.4、均衡技术 (8)2.2自适应滤波原理 (8)2.2.1、自适应滤波器的分类 (8)2.2.2、自适应滤波器的基本构成 (9)2.2.3、与普通滤波器的区别 (9)2.2.4、自适应过程 (10)2.3自适应滤波结构 (10)2.3.1、滤波器的实现结构 (11)第3章基于LMS算法自适应均衡原理 (14)3.1最小均方(LMS)算法基本原理 (14)3.1.1、最佳滤波器准则 (14)3.1.2MMSE准则 (14)3.1.3LMS迭代算法 (16)3.2最小均方(LMS)算法的性能分析 (18)3.2.1LMS算法的稳定性 (18)3.2.2LMS算法的收敛速度 (20)3.2.3LMS算法的性能学习曲线及稳态误差 (21)第4章基于LMS自适应均衡算法仿真 (23)4.1MATLAB简介 (23)4.2LMS算法的自适应均衡的计算机仿真实现 (23)4.2.1信道失真参数W(特征值分散)对系统的收敛性和稳态性的影响 (25)4.2.2迭代步长 对系统的收敛性和稳态性的影响 (27)4.2.3横向自适应滤波器的抽头数M对系统的收敛性和稳态性的影响 (28)第5章归一化LMS算法与RLS算法 (31)5.1基于LMS算法的归一化LMS算法 (31)5.1.1NLMS算法基本理论简介 (31)5.2.2RLS算法与LMS算法仿真比较 (31)5.2RLS算法的自适应均衡的计算机仿真实现 (32)5.2.1RLS算法基本理论简介 (32)5.2.2RLS算法与LMS算法仿真比较 (33)第6章结论 (35)致谢 (37)参考文献 (38)附录1 (39)第1章绪论1.1 均衡器研究背景及意义在信息业快速发展的今天,进行快速准确的通信是各个行业的基本要求。
LMS算法实验报告

LMS算法实验报告LMS(Least Mean Squares)算法是一种基于梯度下降的自适应滤波算法,常用于信号处理、通信系统等领域。
本实验通过实现LMS算法并对其性能进行评估,探究其在自适应滤波中的应用。
1.实验背景自适应滤波在许多领域中被广泛应用,如信号降噪、语音增强、通信频谱感知等。
自适应滤波的核心思想是根据输入信号的特性自动调整滤波器的系数,以实现信号的最佳重构或增强。
2.实验目的本实验旨在通过实现LMS算法并对其性能进行评估,探究其在自适应滤波中的应用。
具体目的如下:1)了解LMS算法的基本原理和实现步骤;2)实现LMS算法,完成自适应滤波任务;3)评估LMS算法的性能,分析其在不同情况下的表现;4)对比LMS算法和其他自适应滤波算法的优缺点。
3.实验步骤本实验的实现步骤如下:1)理解LMS算法的基本原理和数学模型;2)根据LMS算法的更新规则,实现算法的代码;3)根据自适应滤波的具体任务需求,选择合适的输入信号和期望输出;4)根据实验需求,设置合适的参数(如学习率、滤波器长度等);5)使用LMS算法对输入信号进行滤波,并计算输出信号的均方误差;6)根据实验结果,评估LMS算法的性能,并进行分析。
4.实验结果根据以上步骤,完成了LMS算法的实现和性能评估。
实验结果显示,LMS算法能够有效地调整滤波器的权值,实现输入信号的滤波和增强。
随着学习率的增加,LMS算法的收敛速度较快,但容易发生震荡现象。
而学习率过小,则会导致算法收敛速度慢,需要更多的迭代次数才能达到较小的均方误差。
此外,在不同噪声情况下,LMS算法的性能表现也有所差异。
在信噪比较低的情况下,LMS算法的滤波效果明显,能够有效抑制噪声并实现信号增强。
然而,在信噪比较高的情况下,LMS算法的性能受到一定影响,可能会出现性能下降或收敛困难的情况。
5.总结与分析通过本实验,深入了解了LMS算法的原理和实现步骤,并对其性能进行了评估。
哈工大-自适应信号处理_LMS自适应滤波器实验报告

.Harbin Institute of Technology自适应平衡器计算机实验课程名称:自适应信号处理院系:电子与信息工程学院姓名:学号:授课教师:**哈尔滨工业大学一、实验目的:1. 深入掌握自适应平衡器的理论基础和以及它的可能用途。
2. 理解最小均方自适应算法的适用条件,以及最小均方自适应算法的理论推导。
3. 改变特征值扩散度)(R χ与步长参数μ,观察实验结果,深入理解理解这些参数对实验结果的重要性。
4. 探究在线性色散信道中使用最小均方自适应算法引起的失真问题。
二、实验内容:在此次实验中我们研究LMS 算法自适应均衡引起未知失真的线性色散信道问题。
假设数据是实数,图2.1表示用来进行该项研究的系统框图。
自适应均衡器用来纠正存在白噪声的信道的畸变。
通过随机数发生器1产生用来探测信道的测试信号n x ;通过随机数发生器2来产生干扰信道输出的白噪声源()v n 。
这两个发生器是相互独立的。
经过适当延迟,随机数发生器1页提供用作训练序列的自适应均衡器的期望相应。
加到信道输入的随机序列{}n x 由伯努利序列组成,其中1n x =±,随机变量n x 具有零均值和单位方差。
信道的单位脉冲响应应用升余弦表示为20.5[1cos((2))]1,2,30n n n h Wπ⎧+-=⎪=⎨⎪⎩,其他 (2-1)等价地,参数W 控制均衡器抽头输入的相关矩阵的特征值分布()χR ,并且特征值分布随着W 的增大而扩大。
随机数发生器2产生的序列是零均值,方差20.001v σ=。
随机噪声发生器(1)信道随机噪声发生器(2)延迟∑自适应横向滤波器∑nx nv +-ne图2.1 自适应均衡实验框图这里均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于2n =时对称,均衡器的最优抽头权值on w 在5n =时对称。
因此信道的输入n x 被延时了=∆2+5=7个样值,以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时Δ,LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
自适应均衡实验报告
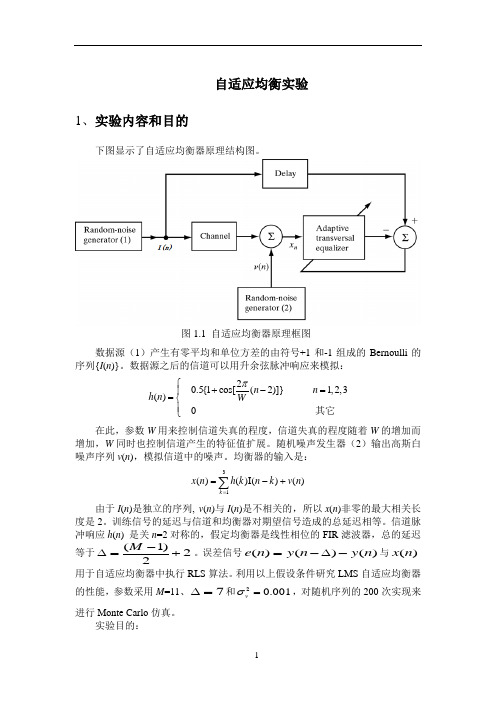
自适应均衡实验1、实验内容和目的下图显示了自适应均衡器原理结构图。
数据源(1)产生有零平均和单位方差的由符号+1和-1组成的Bernoulli 的序列{I (n )}。
数据源之后的信道可以用升余弦脉冲响应来模拟:20.5{1cos[(2)]}1,2,3()0n n h n Wπ⎧+-=⎪=⎨⎪⎩其它在此,参数W 用来控制信道失真的程度,信道失真的程度随着W 的增加而增加,W 同时也控制信道产生的特征值扩展。
随机噪声发生器(2)输出高斯白噪声序列v (n ),模拟信道中的噪声。
均衡器的输入是:31()()I()()k x n h k n k v n ==-+∑由于I (n )是独立的序列, v (n )与I (n )是不相关的,所以x (n )非零的最大相关长度是2。
训练信号的延迟与信道和均衡器对期望信号造成的总延迟相等。
信道脉冲响应h (n ) 是关n =2对称的,假定均衡器是线性相位的FIR 滤波器,总的延迟等于(1)22M -∆=+。
误差信号()()()e n y n y n =-∆-与()x n 用于自适应均衡器中执行RLS 算法。
利用以上假设条件研究LMS 自适应均衡器的性能,参数采用M =11、7∆=和20.001vσ=,对随机序列的200次实现来进行Monte Carlo 仿真。
实验目的:图1.1 自适应均衡器原理框图● 掌握RLS 算法原理及处理流程,分析对比不同信道参数与算法参数对RLS 性能的影响。
● 分析对比RLS 算法与LMS 算法的性能。
2、基本原理分析2.1 最小均方(LMS )算法LMS 算法是一种以期望响应和滤波器输出信号之间误差的均方值最小为准则的,依据输入信号在迭代过程中估计梯度矢量,并更新权系数以达到最优的自适应迭代算法,其显著特点和优点是它的简单性。
这种算法不需要计算相应的相关矩阵,也不需要进行矩阵运算。
LMS 算法是一种线性自适应滤波算法,是最简单的均衡算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LMS 算法自适应均衡器实验
08S005073 房永奎
一、实验目的
1、掌握LMS 算法的计算过程,加深对LMS 算法的理解。
2、研究用LMS 算法自适应均衡引起失真的线性色散信道问题。
3、研究特征值扩散度()R χ和步长参数μ对学习曲线的影响。
二、实验原理
1、自适应均衡器
)
n
图1 自适应信道均衡试验原理图
自适应均衡器用来纠正存在加性白噪声的信道的畸变,信道均衡器的原理框
图如1所示。
随机噪声发生器(1)产生用来探测信道的测试信号序列{n x },本实验中由Bernoulli 序列组成,n x =±1,随机变量n x 具有零均值和单位方差。
随机噪声发生器(2)产生干扰信道的白噪声()n ν,具有零均值,方差为2νσ=0.001。
信道的脉冲响应用升余弦表示为:
20.51cos (2)1,2,30n n n h W π⎧⎡⎤
⎛⎫+-=⎪ ⎪⎢⎥=⎝⎭⎨⎣⎦⎪⎩
(1) 其中,参数W 控制均衡器抽头输入相关矩阵的特征值分布()R χ,并且特征值分布随着W 的增大而扩大。
均衡器具有11M =个抽头。
由于信道的脉冲响应n h 关于n =2时对称,那么
均衡器的最优抽头权值on ω在5n =时对称。
因此,信道的输入n x 被延时了
257∆=+=个样值,以便提供均衡器的期望响应。
通过选择匹配横向均衡器中点的合适延时∆,LMS 算法能够提供信道响应的最小相位分量和非最小相位分量之逆。
2、均衡器输入相关矩阵
在时刻n ,均衡器第1个抽头的输入为
()()()3
1k k u n h x n k v n ==-+∑ (2)
其中所有参数均为实数。
因此,均衡器输入的11个抽头(),(1),,(10)u n u n u n -- 的自相关矩阵R 为一个对称的1111⨯矩阵。
此外,因为脉冲响应n h 仅在1,2,3n =时为非零,且噪声过程()v n 是零均值、方差为2v σ的白噪声,因此相关矩阵R 是主对角线的,有以下特殊结构所示:
()()()
()()()()()()()()()()()()0120010120210100
21000
0000r r r r r r r r r r r r r r r ⎡⎤
⎢
⎥
⎢⎥⎢⎥
=⎢
⎥⎢⎥⎢⎥
⎢
⎥
⎢⎥⎣⎦
R (3)
其中
()222
21230v r h h h σ=+++ (4)
()12231r h h h h =+ (5)
()132r h h = (6)
其中方差20.001v σ=。
123,,h h h 由(1)式中参数W 决定。
附表1中列出:(1)自相关函数(),0,1,2r l l =的值;(2)最小特征值min λ,最大特征值max λ,特征值扩散度()max min /χλλ=R 。
由表可见,这些特征值扩散度范围为6.0782(W=2.9)到46.8216(W=3.5)。
三、程序流程图
程序的主要流程图如图2所示。
实验中在测特征值扩散度和步长参数时,对χ分别赋予不同的值,即可画出学习曲线。
于μ和()R
图2 实验主要程序流程图
四、实验内容及结果分析
χ与步长参数μ,用来估计实验分为两个部分,以便改变特征值扩散度()R
基于LMS算法的自适应均衡器的响应。
实验1:特征值扩散度的影响
设定步长参数μ=0.075,满足max 1μ<,对于每一个特征值扩散度()R χ,经过N=200次独立计算机实验,通过对瞬时均方误差2()e n 与n 的关系曲线平均,可获得自适应滤波器的集平均学习曲线。
050100150
200250300
350400450500
10
10
10
10
10
1
迭代次数
集平均平法误差
图3 自适应均衡LMS 算法学习曲线[0.075μ=,改变特征值扩散度(
)R χ]
从图3中可以看出,当W 值增大时,特征值扩散度的变化范围增大,但自适应均衡器的收敛速率降低。
比如,当()R χ=6.0782(即W=2.9)时,自适应滤波器在均方意义上收敛到稳态大约要80次迭代,500次迭代后平均均方误差值大约等于0.003;当()R χ=46.8216(即W=3.5)时,均衡器大约经过200次迭代才收敛到稳态,500次迭代后平均均方误差值大约为0.04。
024
681012
-101w =2.9
024
681012
-101w =3.1
024
681012
-101w =3.3
024681012
-1
01w =3.5
图4 四个不同特征值扩散度下均衡器集平均脉冲响应[1000次迭代]
图4是经过1000次迭代后自适应均衡器的集平均脉冲响应,这个结果基于200次独立试验。
可以看出,在不同的W 值情况下,自适应均衡器的脉冲响应都关于中心抽头对称。
也就是说,从一个特征值扩散度到另一个特征值扩散度,脉冲响应的变化仅仅反映了信道脉冲响应相应变化的影响。
实验2:步长参数μ的影响
固定W=3.1,即均衡器抽头输入相关矩阵的特征值扩散度为11.1238。
步长参数μ分别取0.075、0.025、0.0075。
每一条学习曲线都是瞬态2()e n 与n 的关系曲线经过200次独立试验后得到的集平均结果。
0500
10001500
10
10
10
10
10
1
迭代次数
集平均平方误差
图5 固定特征值扩散度,改变步长参数μ时自适应均衡器LMS 算法学习曲线
从图5中可以看出,自适应均衡器的收敛速率在很大程度上取决于步长参数
μ。
当步长参数μ较大时(如μ=0.075),均衡器收敛到稳态需要120次迭代;当步长参数μ较小时(μ=0.0075),收敛速率降低超过一个数量级。
同时,平均均方误差的稳态值随着μ的变大而增大。
附表。
