高三文科数学模拟试题含答案
高三文科数学模拟试题含答案

高三文科数学模拟试题含答案高三文科数学模拟试题本试卷共150分,考试时间120分钟。
第Ⅰ卷(选择题,共50分)一、选择题(共10小题,每小题5分,共50分。
在每小题中,只有一项是符合题目要求的)1.复数3+ i的虚部是()。
A。
2.B。
-1.C。
2i。
D。
-i2.已知集合A={-3,-2,0,1,2},集合B={x|x+2<0},则A∩(CRB) =()。
A。
{-3,-2,0}。
B。
{0,1,2}。
C。
{-2,0,1,2}。
D。
{-3,-2,0,1,2}3.已知向量a=(2,1),b=(1,x),若2a-b与a+3b共线,则x=()。
A。
2.B。
11/22.C。
-1.D。
-24.如图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为()。
A。
4π/3.B。
π。
C。
3π/2.D。
2π5.将函数f(x)=sin2x的图像向右平移π/6个单位,得到函数g(x)的图像,则它的一个对称中心是()。
A。
(π/6,0)。
B。
(π/3,0)。
C。
(π/2,0)。
D。
(π,0)6.执行如图所示的程序框图,输出的s值为()。
开始是否输出结束A。
-10.B。
-3.C。
4.D。
57.已知圆C:x^2+2x+y^2=1的一条斜率为1的切线l1,若与l1垂直的直线l2平分该圆,则直线l2的方程为()。
A。
x-y+1=0.B。
x-y-1=0.C。
x+y-1=0.D。
x+y+1=08.在等差数列{an}中,an>0,且a1+a2+⋯+a10=30,则a5⋅a6的最大值是()。
A。
4.B。
6.C。
9.D。
369.已知变量x,y满足约束条件2x-y≤2,x-y+1≥0,设z=x^2+y^2,则z的最小值是()。
A。
1.B。
2.C。
11.D。
3210.定义在R上的奇函数f(x),当x≥0时,f(x)=2,当x<0时,f(x)=1-|x-3|,则函数F(x)=f(x)-a(0<a<1)的所有零点之和为()。
高三文科数学模拟题一

高三数学模拟试题(一)一、选择题(5×10=50分)1. 设集合{}2|230A x x x =--<,{}|14B x x =≤≤,则AB =( )A .{}|13x x ≤<B .{}|13x x ≤≤C .{}|34x x <≤D . {}|34x x ≤≤ 2.若命题:|1|4p x +≤,命题2:56q x x <-,则p q ⌝⌝是的( )A .必要不充分条件B .充分不必要条件C .充要条件D .既不充分也不必要条件 3.已知向量(1,),(1,),a n b n a b b ==--若2与垂直,则||a =( ) A .1B .2C .2D .44.过点)2,1(与圆221x y +=相切的直线方程是( ) A .1x =B .3450x y -+=C .34501x y x -+==或D .54301x y x -+==或5.已知函数⎩⎨⎧=x x x f 3log )(2 00≤>x x ,则))41((f f = ( )A .9B .19C .9-D .91-6.ABC ∆中,三边之比4:3:2::=c b a ,则最大角的余弦值等于( ) A .41 B .87 C .21- D .41-7.已知焦点在x 轴上的椭圆22219x y a +=的离心率是12e =,则a 的值为( ) A .23 B .3 C .32 D .12 8.若不等式4)2(2)2(2<-+-x a x a 的解集为R ,则实数a 的取值范围是( ) A .)2,2(- B .]2,2(- C .),2()2,(+∞--∞ D .)2,(-∞9.函数236()(04)1x x f x x x ++=≤≤+的最小值为( ) A .2 B .1 C .6 D .510. 已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示,则ω等于( )A .13 B .1 C .32D .2二、填空题(5×5=25分)11.若点(),9a 在函数3xy =的图象上,则tan6a π= 12.经过圆2220x x y ++=的圆心C ,且与直线0x y +=垂直的直线方程是13.设y x ,满足约束条件⎪⎩⎪⎨⎧≤-≥-≥+,1,1,1x y x y x 则y x z 2-=的最小值是_______14.已知数列{}n a 为等差数列,且28143,a a a ++=则()2313log a a +=_______ 15.若扇形的面积和弧长都是10,则这个扇形中心角的弧度数是____三、解答题(75分)16.(本题满分13分)已知集合{}|||2A x x a =-<,26|12x B x x +⎧⎫=>⎨⎬+⎩⎭. (1)求集合A 和集合B(2)若A B R =,求a 的取值范围17.(本小题满分13分)等比数列{}n a 中,已知142,16a a == (1)求数列{}n a 的通项公式(2)若35,a a 分别为等差数列{}n b 的第3项和第5项,试求数列{}n b 的通项公式及前n 项和n S18.(本小题满分12分)已知向量a =(sin ,cos())x x π-,b =(2cos ,2cos )x x ,函数()1f x =⋅a b+.(1)求π()4f -的值;(2)求()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值,并求出相应的x 的值.19.(本小题满分13分)如图所示,已知三棱锥BPC A -中,,,AP PC AC BC M ⊥⊥为AB 中点D 为PB 中点,且PMB ∆为正三角形。
江西高三模拟考试(文科)数学试卷附答案解析

江西高三模拟考试(文科)数学试卷附答案解析班级:___________姓名:___________考号:__________一、单选题1.设集合{}2560A x x x =--<和{}4,2,0,2,4B =--,则A B =( )A .{}0,2B .{}2,0-C .2,0,2D .{}0,2,42.复数1z 在复平面内对应的点为()1,3,22z i =-+(i 为虚数单位),则复数12z z 的虚部为( ). A .75B .75-C .7i 5D .7i 5-3.在ABC ∆中AB =AC=1,B=30°,和ABC S ∆=,则C = A .60或120B .30C .60D .454.已知x 与y 的数据如表所示,根据表中数据,利用最小二乘法求得y 关于x 的线性回归方程为0.7 1.05y x =+,则m 的值是( )A .3.8B .3.85C .3.9D .4.05.已知tan 2x =,则sin cos 1x x +=( ) A .25B .75C .2D .36.已知直线:210l x y k +++=被圆22:4C x y +=所截得的弦长为4,则k 为( ) A .1-B .2-C .0D .27.若0a >,0b >且24a b +=,则4ab的最小值为( ) A .2B .12C .4D .148.已知命题:p 已知实数,a b ,则0ab >是0a >且0b >的必要不充分条件,命题:q 在曲线cos y x =上存在 ( ) A .p 是假命题 B .q 是真命题 C .()p q ∧⌝是真命题D .()p q ⌝∧是真命题9.执行如图所示的程序框图,若输出i 的值为7,则框图中①处可以填入( )A .7S >?B .15S >?C .21S >?D .28S >?10.已知椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为1F ,2F 椭圆C 在第一象限存在点M ,使得112=MF F F ,直线1F M 与y 轴交于点A ,且2F A 是21MF F ∠的角平分线,则椭圆C 的离心率为( )A B C .12D 11.已知函数()()22e (e =--x xf x x x a )有三个零点,则实数a 的取值范围是( )A .(0,1e -)B .(0,2e -)C .(0,1)D .(0,e )12.在棱长为2的正方体ABCD —A 1B 1C 1D 1中E 是正方形BB 1C 1C 的中心,M 为C 1D 1的中点,过A 1M 的平面α与直线DE 垂直,则平面α截正方体ABCD —A 1B 1C 1D 1所得的截面面积为( )A .B .CD .3二、填空题13.已知向量(),2AB m =,()1,3AC =和()4,2BD =--,若B ,C ,D 三点共线,则m =______.14.双曲线2219x y -=的渐近线方程为__________.15.已知f (x )=sin 6x πω⎛⎫+ ⎪⎝⎭(ω>0),f (6π)=f (3π),且f (x )在区间63ππ⎛⎫ ⎪⎝⎭,上有最小值,无最大值,则ω=_____.16.已知过点(0,1)M 的直线与抛物线22(0)x py p =>交于不同的A ,B 两点,以A ,B 为切点的两条切线交于点N ,若0NA NB ⋅=,则p 的值为__________.三、解答题17.已知数列{}n a 的前n 项和为n S ,且()21n n S a n *=-∈N .(1)求数列{}n a 的通项公式;(2)设13log n n b a =,n C ={}n C 的前n 项和n T18.如图,三棱柱111ABC A B C 各棱长均为2,且13C CA π∠=.(1)求证1AC BC ⊥;(2)若1BC 与平面ABC 所成的角为6π,求三棱柱111ABC A B C 的体积. 19.某工厂生产的产品是经过三道工序加工而成的,这三道工序互不影响,已知生产该产品三道工序的次品率分别为(1)求该产品的次品率;(2)从该工厂生产的大量产品中随机抽取三件,记次品的件数为X ,求随机变量X 的分布列与期望()E X . 20.已知椭圆()2222:10x y C a b a b +=>>,且过点()3,1A .(1)求椭圆C 的方程;(2)点M ,N 在椭圆C 上,且AM AN ⊥.证明:直线MN 过定点,并求出该定点坐标.21.已知函数()f x 对任意实数x 、y 恒有()()()f x y f x f y +=+,当x>0时f (x )<0,且(1)2f =-. (1)判断()f x 的奇偶性;(2)求()f x 在区间[-3,3]上的最大值;(3)若2()22f x m am <-+对所有的[][]1,1,1,1x a ∈-∈-恒成立,求实数m 的取值范围.22.数学上有很多美丽的曲线令人赏心悦目,例如,极坐标方程()1cos a ρθ=+(0a >)表示的曲线为心形线,它对称优美,形状接近心目中的爱心图形.以极点O 为原点,极轴为x 轴的正半轴建立直角坐标系,直线l的参数方程为1,2x t y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数).(1)求直线l 的极坐标方程和心形线的直角坐标方程;(2)已知点P 的极坐标为()2,0,若P 为心形线上的点,直线l 与心形线交于A ,B 两点(异于O 点),求ABP 的面积.23.已知函数()2|1|||(R)f x x x a a =-+-∈. (1)若()f x 的最小值为1,求a 的值;(2)若()||6f x a x <+恒成立,求a 的取值范围.参考答案与解析1.D【分析】求出集合A 中元素范围,然后求A B ⋂即可.【详解】{}{}256016A x x x x x =--<=-<<,又{}4,2,0,2,4B =--{}0,2,4A B ∴=.故选:D. 2.B【解析】根据题意,先得到113z i =+,再由复数的除法运算求出12z z ,即可得出其虚部. 【详解】因为复数1z 在复平面内对应的点为()1,3,所以113z i =+ 又22z i =-+所以()()()()1213213263171722241555i i z i i i i i z i i i +--+++--+===-=-=--+-+--+因此其虚部为75-.故选:B.【点睛】本题主要考查求复数的虚部,考查复数的除法运算,涉及复数的几何意义,属于基础题型. 3.C【分析】由三角形面积公式可得A ,进而可得解.【详解】在ABC ∆中AB 1AC =与30B =12ABC S AB ACsinA ∆=⋅=,可得1sinA =,所以90A = 所以18060C A B =--=【点睛】本题主要考查了三角形的面积公式,属于基础题. 4.D【分析】计算样本中心,将样本中心 710,24m +⎛⎫⎪⎝⎭代入线性回归方程中即可求解. 【详解】因为()17234542x =⨯+++= ()1102.5 3.0 4.544m y m +=⨯+++=.所以样本中心为710,24m +⎛⎫⎪⎝⎭,将其代入回归方程0.7 1.05y x =+得1070.7 1.0542m +=⨯+,解得4m =. 故选:D . 5.B【分析】利用同角三角函数的平方关系、商数关系,将目标式化为2tan 1tan 1xx ++,结合已知即可求值.【详解】222sin cos tan 27sin cos 1111sin cos tan 155x x x x x x x x +=+=+=+=++. 故选:B . 6.A【分析】利用点线距离公式求弦心距,再由弦长与半径、弦心距的几何关系列方程求参数k . 【详解】设圆心()0,0到直线:210l x y k +++=的距离为d ,则由点到直线的距离公式得|1|d k ==+由题意得:42==1k =-.故选:A 7.A【分析】利用基本不等式可求出2ab ≤,即可得出所求. 【详解】0a > 0b >42a b ∴=+≥2a b =,即1,2a b ==时等号成立所以2ab ≤,则42ab≥,即4ab 的最小值为2.故选:A. 8.C【分析】首先判断命题,p q 的真假,再判断选项.【详解】00ab a >⇒> 且0b >,反过来0a >且00b ab >⇒>,所以0ab >是0a > 且0b >的必要不充分条件,所以命题p 是真命题cos y x =,[]sin 1,1y x '=-∈-根据导数的几何意义可知曲线cos y x =所以命题q是假命题根据复合命题的真假判断可知()p q ∧⌝是真命题. 故选:C 9.C故选:C. 10.B【分析】根据题意和椭圆定义可得到2MF ,AM 和a ,c 的关系式,再根据122MF F MF A ∽△△,可得到关于a ,c 的齐次式,进而可求得椭圆C 的离心率e . 【详解】由题意得1122F M F F c == 又由椭圆定义得222MF a c =- 记12MF F θ∠=则212AF F MF A θ∠=∠= 121222F F M F MF MAF θ∠=∠=∠= 则2122AF AF a c ==- 所以42AM c a =- 故122MF F MF A ∽△△则2122MF AMF F MF = 则2a c c a c a c --=-,即222010c ac a e e e +-=⇔+-=⇒=(负值已舍). 故选:B . 11.A【分析】令()()()22ee 0=--=xxf x x x a ,得到22e 0-=x x或e 0x x a -=,令()22e =-xg x x ,易知有一个零点,转化为则e 0x x a -=有两个根求解.【详解】令()()()22ee 0=--=xxf x x x a所以22e 0-=x x 或e 0x x a -=令()22e =-xg x x ,则()()2e '=-x g x x令()2(e )=-x h x x ,则()2(1)e '=-xh x当(,0)x ∈-∞时()0h x '>,h (x )在(-∞,0)上单调递增; 当,()0x ∈+∞时()0h x '<,h (x )在(0,+∞)上单调递减 所以()(0)20h x h ≤=-<,即()0g x '< 所以g (x )在R 上单调递减,又()2110g e-=->,g (0)=20-< 所以存在0(1,0)x ∈-使得()00g x =所以方程e 0x x a -=有两个异于0x 的实数根,则xxa e = 令()x x k x e =,则()1xx e xk -=' 当(,1)x ∞∈-时()0k x '>,k (x )在(-∞,1)上单调递增;当(1,)x ∈+∞时()0k x '<,k (x )在(1,+∞)上单调递减,且()0k x >.所以()1()1k x k e≤= 所以()xxk x e =与y a =的部分图象大致如图所示由图知10a e<< 故选:A . 12.B【解析】确定平面1A MCN 即为平面α,四边形1A MCN 是菱形,计算面积得到答案.【详解】如图,在正方体1111ABCD A B C D -中记AB 的中点为N ,连接1,,MC CN NA 则平面1A MCN 即为平面α.证明如下: 由正方体的性质可知1A MNC ,则1A ,,,M C N 四点共面记1CC 的中点为F ,连接DF ,易证DF MC ⊥. 连接EF ,则EF MC ⊥EFDF F =,EF DF ⊂,平面DEF所以MC ⊥平面DEF又DE ⊂平面DEF ,则DE MC ⊥.同理可证,DE NC ⊥ NC MC C =则DE ⊥平面1A MCN 所以平面1A MCN 即平面α四边形1A MCN 即平面α截正方体1111ABCD A B C D -所得的截面. 因为正方体的棱长为2,易知四边形1A MCN 是菱形其对角线1AC = MN =所以其面积12S =⨯=故选:B【点睛】本题考查了正方体的截面面积,意在考查学生的空间想象能力和计算能力. 13.1-【分析】根据给定条件,求出向量BC 坐标,再利用共线向量的坐标表示计算作答. 【详解】因为向量(),2AB m =,()1,3AC =则(1,1)BC AC AB m =-=-,而()4,2BD =-- 又B ,C ,D 三点共线,则有//BC BD ,因此2(1)4m --=-,解得1m =- 所以1m =-. 故答案为:-1 14.30x y ±-=【分析】根据焦点在横轴上双曲线的渐近线方程的形式直接求出双曲线2219x y -=的渐近线方程.【详解】通过双曲线方程可知双曲线的焦点在横轴上,3,1a b ==,所以双曲线2219x y -=的渐近线方程为:1303b y x y x x y a =±⇒=±⇒±-=. 故答案为30x y ±-=【点睛】本题考查了求双曲线的渐近线方程,通过双曲线方程判断双曲线的焦点的位置是解题的关键. 15.163【分析】由题意可得函数的图象关于直线4x π=对称,再根据()f x 在区间,63ππ⎛⎫⎪⎝⎭上有最小值,无最大值,可得3462πππω+=,由此求得ω的值. 【详解】对于函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭,由63f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭得函数图象关于6324x πππ+==对称 又()f x 在区间,63ππ⎛⎫⎪⎝⎭有最小值,无最大值可得()32462k k Z πππωπ+=+∈,即()1683k k Z ω=+∈,又342Tππ-≤,即12ω≤ 所以163ω=. 故答案为163. 【点睛】本题主要考查正弦函数的图象的对称性,正弦函数的最值,属于中档题. 16.2【分析】设()()1122,,,A x y B x y ,设直线AB 的方程为1y kx =+,利用“设而不求法”得到122x x p =-.利用导数求出两条切线斜率为1x p 和2x p,得到121x x p p ⋅=-,即可求出p =2.【详解】设()()1122,,,A x y B x y ,且设直线AB 的方程为1y kx =+,代入抛物线的方程得2220x pkx p --=,则122x x p =-.又22x py =,得22x y p=,则x y p '=,所以两条切线斜率分别为1x p 和2x p .由0NA NB ⋅=,知NA NB ⊥,则121x x p p ⋅=-,所以221pp -=-,即p =2. 故答案为:2 17.(1)13n n a =(2)1n T =【分析】(1)由n a 与n S 关系可推导证得数列{}n a 为等比数列,由等比数列通项公式可得n a ; (2)由(1)可推导得到,n n b C ,采用裂项相消法可求得n T . (1)当1n =时111221a S a =-=,解得:113a =;当2n ≥时1122211n n n n n a S S a a --=-=--+,即113n n a a -=∴数列{}n a 是以13为首项,13为公比的等比数列,1133nn n a ⎛⎫∴== ⎪⎝⎭. (2)由(1)得:131log 3n n b n ⎛⎫== ⎪⎝⎭n C ∴==11n T ∴=⋅⋅⋅=18.(1)证明见解析【分析】(1)通过线面垂直的性质定理证明线线垂直;(2)由(1)知AC ⊥平面1BDC ,则进一步知平面1BDC ⊥平面ABC ,故过1C 作平面ABC 的垂线,垂足为E ,则1C E ⊥平面ABC ,求出1C E 的大小即可求解.【详解】(1)证明:取AC 的中点D ,连接BD ,1C D 和1C A ,则BD AC ⊥因为12CC CA ==,13C CA π∠=所以1ACC △为等边三角形又D 为AC 的中点,所以1C D AC ⊥ 因为1C D BD D =,1,C D BD ⊂平面1BDC ,所以AC ⊥平面1BDC ,.又1BC ⊂平面1BDC ,所以1AC BC ⊥.(2)由(1)知AC ⊥平面1BDC ,又AC ⊂平面ABC ,所以平面1BDC ⊥平面ABC平面1BDC 平面ABC BD =,故过1C 作平面ABC 的垂线,垂足为E ,则E 一定在直线BD 上,因为1BC 与平面ABC 所成的角为6π,所以16C BD π∠= 由题意知1C D BD =,所以123C DB π∠=所以13BC == 所以113sin 62C E BC π==.(或:由题意知1C D BD =13C DE π∠=,所以113sin 32C E CD π===)所以11322sin 232ABC V S C E π=⋅=⨯⨯⨯⨯=△19.(1)14(2)分布列见解析,()34E X =【分析】(1)利用相互独立事件的乘法概率计算公式能求出产品为正品的概率,即可由对立事件求次品概率(2)由题意得X 0=,1,2,3,分别求出其相对应的概率,能求出X 的分布列和数学期望.【详解】(1)产品正品的概率为:11131111011124P ⎛⎫⎛⎫⎛⎫=---= ⎪⎪⎪⎝⎭⎝⎭⎝⎭ 所以为次品的概率为31144-= (2)由题意得X 0=,1,2,3,且13,4X B ⎛⎫~ ⎪⎝⎭3327(0)464P X ⎛⎫=== ⎪⎝⎭ 2133127(1)C 4464P X ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ 223319(2)C 4464P X ⎛⎫⎛⎫=== ⎪⎪⎝⎭⎝⎭ 311(3)464P X ⎛⎫=== ⎪⎝⎭ X ∴的分布列如下:∴()27279130123646464644E X =⨯+⨯+⨯+⨯=. 20.(1)221124x y += (2)证明详见解析,定点坐标3122⎛⎫ ⎪⎝⎭,-【分析】(1)根据已知条件列方程组,由此求得222,,a b c ,从而求得椭圆C 的方程.(2)根据直线MN 的斜率进行分类讨论,结合根与系数关系以及·0AM AN =求得定点坐标.【详解】(1)由题意可得:22222911c aab a bc ⎧=⎪⎪⎪+=⎨⎪=+⎪⎪⎩,解得:2221248a b c ===,, 故椭圆方程为221124x y +=. (2)设点()()1122,,,M x y N x y若直线MN 斜率存在时设直线MN 的方程为:y kx m =+代入椭圆方程消去y 并整理得:()2221363120k x kmx m +++-= 可得122613km x x k +=-+ 212231213m x x k -=+ 因为AM AN ⊥,所以·0AM AN =,即()()()()121233110x x y y --+--=根据1122,kx m y kx m y =+=+有()()()()221212121239110x x x x k x x k m x x m -++++-++-=整理可得: ()()()()22121213190k x x km k x x m ++--++-+= 所以()()()222223126131901313m km k km k m k k -⎛⎫++---+-+= ⎪++⎝⎭ 整理化简得2299210k km m m ++--=则有()()321310k m k m +++-=得3210k m ++=或310k m +-=若3210k m ++=,则直线MN 的方程为:3122y k x ⎛⎫=-- ⎪⎝⎭,恒过3122⎛⎫- ⎪⎝⎭, 若310k m +-=,则直线MN 的方程为:()31y k x =-+,过A 点,舍去.所以直线MN 过定点P 3122⎛⎫- ⎪⎝⎭, 当直线MN 的斜率不存在时可得()11,N x y -由·0AM AN =得:()()()()121233110x x y y --+--=得()1221210x y -+-=()2211310x y -+-=,结合22111124x y += 解得:132x = 或23x =(舍去),此时直线MN 方程为32x =,过点P 3122⎛⎫- ⎪⎝⎭,. 综上,直线MN 过定点P 3122⎛⎫- ⎪⎝⎭,. 21.(1)奇函数(2)6(3){2,m m 或者2}m <-【分析】(1)令x =y =0⇒f (0)=0,再令y =﹣x ,⇒f (﹣x )=﹣f (x );(2)设x 1,x 2∈R ,且x 1<x 2,结合条件用单调性的定义证明函数f (x )为R 上的增函数,从而得到()f x 在区间[-3,3]上的最大值;(3)根据函数f (x )≤m 2﹣2am ﹣2对所有的x ∈[﹣1,1],a ∈[﹣1,1]恒成立,说明f (x )的最大值2小于右边,因此先将右边看作a 的函数,m 为参数系数,解不等式组,即可得出m 的取值范围.【详解】(1)取x=y=0,则f (0+0)=f (0)+f (0);则f (0)=0;取y =﹣x ,则f (x ﹣x )=f (x )+f (﹣x )∴f (﹣x )=﹣f (x )对任意x ∈R 恒成立∴f (x )为奇函数;(2)任取x 1,x 2∈(﹣∞,+∞)且x 1<x 2,则x 2﹣x 1>0;∴f (x2)+f (﹣x1)=f (x2﹣x1)<0; ∴f (x2)<﹣f (﹣x1)又∵f (x )为奇函数∴f (x 1)>f (x 2);∴f (x )在(﹣∞,+∞)上是减函数;∴对任意x ∈[﹣3,3],恒有f (x )≤f (﹣3)而f (3)=f (2+1)=f (2)+f (1)=3f (1)=﹣2×3=﹣6; ∴f (﹣3)=﹣f (3)=6;∴f (x )在[﹣3,3]上的最大值为6;(3)由(2)可知函数()f x 在[]1,1-的最大值为()12f -=所以要使()222f x m am <-+对所有的[][]1,1,1,1x a ∈-∈-恒成立只需要()()2max 2212m am f x f -+>=-=即220m am ->对所有[]1,1a ∈-恒成立令()[]22,1,1g a m am a =-∈-,则()()1010g g ⎧->⎪⎨>⎪⎩即222020m m m m ⎧+>⎨->⎩解得22m m ><-,或者 所以实数m 的取值范围是{}2,2m m m <-或者【点睛】本题考查了抽象函数的奇偶性、单调性与函数的值域、不等式恒成立等知识点,属于中档题,解题时应该注意题中的主元与次元的处理.22.(1)极坐标方程为π3θ=或4π3θ=;()()222222x y ax a x y +-=+【分析】(1)先消去参数t 得到直线l 的普通方程,进而得到极坐标方程,由()1cos a ρθ=+,得到2cos a a ρρρθ=+,即22x y ax +=求解.(2)将()2,0代入方程()1cos a ρθ=+得到1a =,进而得到1cos ρθ=+,分别与直线l 的极坐标方程联立,求得A ,B 坐标求解.【详解】(1)解:消去参数t 得到直线l 的普通方程为y = 所以极坐标方程为π3θ=或4π3θ=; (π3θ=(ρ∈R 也正确)由()1cos a ρθ=+,得2cos a a ρρρθ=+,即22x y ax +=化简得心形线的直角坐标方程为()()222222x y ax a x y +-=+. (2)将()2,0代入方程()1cos a ρθ=+,得1a =∴1cos ρθ=+.由π,31cos ,θρθ⎧=⎪⎨⎪=+⎩得3π,23A ⎛⎫ ⎪⎝⎭ 由4π,31cos ,θρθ⎧=⎪⎨⎪=+⎩得14π,23B ⎛⎫ ⎪⎝⎭∴13π112π2sin 2sin 223223ABP AOP BOP S S S =+=⨯⨯+⨯⨯=△△△23.(1)0或2(2)[)3,4【分析】(1)根据1()(1)1x a x x a x a -+-≥---=-结合取等条件即可得解;(2)把()||6f x a x <+恒成立,转化为()2160g x x x a a x =-+---<恒成立,分情况讨论去绝对值符号,从而可得出答案.【详解】(1)因为1()(1)1x a x x a x a -+-≥---=-,当且仅当()(1)0x a x --≤时取等号()2|1||||1||1||1|f x x x a x a a =-+-≥-+-≥-,当且仅当1x =时取等号 所以11a -=,解得0a =或2a =故a 的值为0或2;(2)令g()2|1|||6x x x a a x =-+---,由题意知()0g x <恒成立 当{1x x x ∈≥且}x a ≥时 ()()()g()21638x x x a ax a x a =-+---=---,要使得()0g x <恒成立则30,a -≤可得3,a ≥当3a ≥时()()()()()34,034,0118,138,a x a x a x a x g x a x a x a a x a x a ⎧-+-<⎪-++-≤<⎪=⎨-+-≤<⎪⎪---≥⎩因为()0g x <恒成立, 则max ()0g x <,由图像可知()max ()0g x g = 所以()g()g 040x a ≤=-<,所以4a < 综上可知实数a 的取值范围为[)3,4.。
高三文科数学模拟考试(含答案解析)
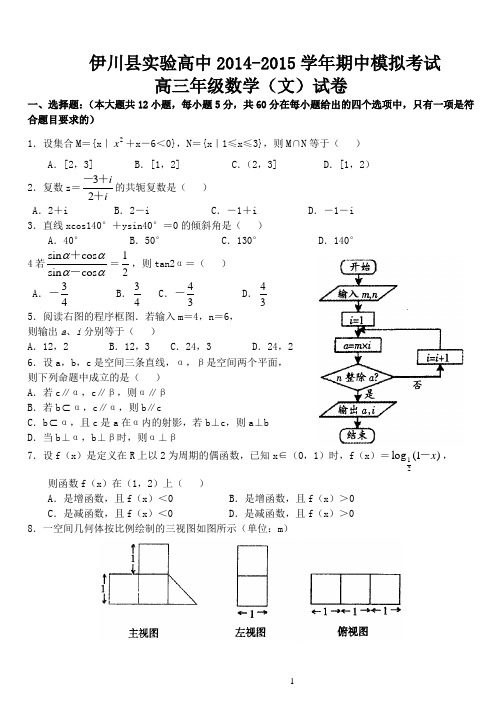
伊川县实验高中2014-2015学年期中模拟考试高三年级数学(文)试卷一、选择题:(本大题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的)1.设集合M ={x |2x +x -6<0},N ={x |1≤x ≤3},则M ∩N 等于( )A .[2,3]B .[1,2]C .(2,3]D .[1,2) 2.复数z =32ii-++的共轭复数是( ) A .2+i B .2-i C .-1+i D .-1-i 3.直线xcos140°+ysin40°=0的倾斜角是( )A .40°B .50°C .130°D .140°4若sin cos sin cos αααα+-=12,则tan2α=( )A .34-B .34C .43-D .435.阅读右图的程序框图.若输入m =4,n =6,则输出a 、i 分别等于( )A .12,2B .12,3C .24,3D .24,2 6.设a ,b ,c 是空间三条直线,α,β是空间两个平面, 则下列命题中成立的是( ) A .若c ∥α,c ∥β,则α∥β B .若b ⊂α,c ∥α,则b ∥cC .b ⊂α,且c 是a 在α内的射影,若b ⊥c ,则a ⊥bD .当b ⊥α,b ⊥β时,则α⊥β7.设f (x )是定义在R 上以2为周期的偶函数,已知x ∈(0,1)时,f (x )=12log (1)x -,则函数f (x )在(1,2)上( )A .是增函数,且f (x )<0B .是增函数,且f (x )>0C .是减函数,且f (x )<0D .是减函数,且f (x )>0 8.一空间几何体按比例绘制的三视图如图所示(单位:m )则该几何体的体积(单位:m 3)为( )A .72 B .92 C .73 D .94 9.向量a =(x ,2),b =(4,y ),若a ⊥b ,则39y x+的最小值为( )A .2 D .210.点P 在曲线y =3x -x +2上移动,在点P 处的切线的倾斜角为α,则α的取值范围是( )A .[0,2π] B .[0,2π)∪[4π3,π) C .[4π3,π) D .(2π,4π3]11.设点P 是双曲线2221x a b2y -=(a >0,b >0)与圆222x a b 2+y =+在第一象限的交点,其中F 1,F 2分别是双曲线的左、右焦点,且|PF 1|=2|PF 2|,则双曲线的离心率为( )A 12.在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边.已知a ,b ,c 成等比数列,且22a c - =ac -bc ,则sin b Bc的值为( )A .2 B .12 C .3 D .3二、填空题(本大题共4小题,每小题5分,共20分)13.在等比数列{n a }中,如果5a 和9a 是一元二次方程2x +7x +9=0的两个根,则4a 7a 10a 的值为_________.14. 在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =2b =,sin cos B B +=则角A的大小为 _ .15、设椭圆的两个焦点分别为12,F F ,过2F 作椭圆长轴的垂线交椭圆于一点P ,若12F PF ∆为等腰三角形,则该椭圆的离心率是________.P16.若点 P (x ,y为坐标原点,则OA OP ⋅的最大值_______三、解答题(本大题共6小题。
高三文科数学模拟试卷含答案

文科数学试卷参考答案及评分标准一、选择题:1. 设全集I 是实数集R , 3{|2}{|0}1x M x x N x x -=>=≤-与都是I 的子集(如图所示), 则阴影部分所表示的集合为A .{}2x x <B .{}21x x -≤<C .{}12x x <≤D .{}22x x -≤≤2.下列函数中既不是奇函数,又不是偶函数的是A .2xy = B . ()2lg 1y x x =++C . 22xxy -=+ D . 1lg1y x =+ 3.若曲线x x x f -=4)(在点P 处的切线平行于直线03=-y x ,则点P 的坐标为A .(1,0)B .(1,5)C .(1,-3)D .(-1,2)4.在ABC ∆中,a b 、分别是角A B 、所对的边,条件“a b <”是使 “cos cos A B >”成立的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5. 若抛物线1262222=+=y x px y 的焦点与椭圆的右焦点重合,则p 的值为 A .-4 B .4 C .-2 D .26. 已知函数),6cos()6sin()(ππ++=x x x f 则下列判断正确的是A .)(x f 的最小正周期为2π,其图象的一条对称轴为12π=xB .)(x f 的最小正周期为2π,其图象的一条对称轴为6π=xC .)(x f 的最小正周期为π,其图象的一条对称轴为12π=xD .)(x f 的最小正周期为π,其图象的一条对称轴为6π=x2 2 222 2 正视图侧视图7. 一空间几何体的三视图如图所示,则该几何体的表面积为A.223π+ B .4232π+- C .627π+ D .6272π+- 8. 若直线:10 l ax by ++=始终平分圆M :224210x y x y ++++=的周长,则()()2222a b -+-的最小值为A .5B .5C .25D .109. 设b c 、表示两条直线,αβ、表示两个平面,下列命题中真命题是A .若c ∥α,c ⊥β,则αβ⊥B .若b α⊂,b ∥c ,则c ∥αC .若b α⊂,c ∥α,则b ∥cD .若c ∥α,αβ⊥,则c β⊥10. 已知数列{}n x 满足3n n x x +=,21||()n n n x x x n N *++=-∈,若11x =,2 (1,0)x a a a =≤≠,则数列{}n x 的前2010项的和2010S 为 A .669B .670C .1338D .134011. 在平面直角坐标系中,O 为坐标原点,设向量).3,1(),1,3(,,====b a b OB a OA 其中若10,≤≤≤+=μλμλ且b a OC ,C 点所有可能的位置区域用阴影表示正确的是12.已知点F 是双曲线)0,0(12222>>=-b a by a x 的左焦点,点E 是该双曲线的右顶点,过F 且垂直于x 轴的直线与双曲线交于A B 、两点,若ABE ∆是锐角三角形,则该双曲线的离心率e 的A .B .C .D .取值范围是A . ()1,+∞B .()1,2C.(1,1D.(2,1+二、填空题:本大题共4小题,每小题4分,共16分. 13. 对任意非零实数a b 、,若a b ⊗的运算原理如图所示,则()221log 82-⎛⎫⊗= ⎪⎝⎭___1___.14.在ABC ∆中,已知41AB AC ==u u u r u u u r,,ABCS AB AC ∆=⋅u u u r u u u r则的值为 ±2 .15. 设n S 表示等差数列{}n a 的前n 项和,且918S =,240n S =,若()4309n a n -=>,则n = 15 .16. 已知两个不相等的实数a b 、满足以下关系式:204a sin a cos πθθ⋅+⋅-=,204b sin b cos πθθ⋅+⋅-=,则连接A ()2a ,a 、 B ()2b ,b 两点的直线与圆心在原点的单位圆的位置关系是 相交 . 三、解答题:本大题共6个小题,共74分. 17.(本小题满分12分)已知函数2()sin cos f x x x x =+.(Ⅰ)求()f x 的最小正周期; (Ⅱ)求()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 解:(Ⅰ)∵2()sin cos f x x x x =+)12sin cos cos 212x x x =⋅++(第13题图)1sin 222x x =++ ……………3分sin 232x π⎛⎫=++ ⎪⎝⎭ ……………5分 ∴ 函数()f x 的最小正周期22T ππ==. ……………6分 (Ⅱ)∵ 62x ππ-≤≤,40233x ππ≤+≤∴sin 213x π⎛⎫≤+≤ ⎪⎝⎭, ……………9分 ∴20sin 213222x π⎛⎫≤++≤+= ⎪⎝⎭, ∴ ()f x 在区间,62ππ⎡⎤-⎢⎥⎣⎦,最小值为0.……………12分18.(本小题满分12分)如图,已知AB ⊥平面ACD ,DE ∥AB ,ACD ∆是正三角形,2AD DE AB ==,且F 是CD 的中点. (Ⅰ)求证:AF ∥平面BCE ; (Ⅱ)求证:平面BCE ⊥平面CDE . 解:(Ⅰ)取CE 中点P ,连结FP 、BP ,∵F 为CD 的中点,∴FP ∥DE ,且FP =.21DE又AB ∥DE ,且AB =.21DE∴AB ∥FP ,且AB =FP ,∴ABPF 为平行四边形,∴AF ∥BP .…………4分 又∵AF ⊄平面BCE ,BP ⊂平面BCE ,ABCD EF(第18题图)ABCDEFP (第18题图)∴AF ∥平面BCE …………6分(Ⅱ)∵△ACD 为正三角形,∴AF ⊥CD∵AB ⊥平面ACD ,DE //AB∴DE ⊥平面ACD 又AF ⊂平面ACD ∴DE ⊥AF又AF ⊥CD ,CD ∩DE=D∴AF ⊥平面CDE …………10分 又BP ∥AF ∴BP ⊥平面CDE 又∵BP ⊂平面BCE∴平面BCE ⊥平面CDE …………12分 19.(本小题满分12分)已知数列{}n a 的首项15a =,前n 项和为n S ,且125n n S S n +=++()n N *∈.(Ⅰ)设1n n b a =+,求数列{}n b 的通项公式; (Ⅱ)求数列{}n a 的前n 项和n S . 解:(Ⅰ)由125n n S S n +=++()n N *∈得 ()1215n n S S n -=+-+(,2)n N n *∈≥两式相减得 121n n a a +=+ ……………………………… 3分 ∴ ()1121n n a a ++=+即 n n b b 21=+(,2)n N n *∈≥ …………………………………… 4分 又1165111122=+=++=-=a S S S a ∴ 12122=+=a b ,6111=+=a b∴ 122b b = …………………………………… 6分∴ 数列{}n b 是首项为6,公比为2的等比数列∴ nn n b 23261⋅=⋅=- ………………………………… 8分(Ⅱ)法一由(Ⅰ)知321nn a =⋅- ……………………………… 9分∴ 12n n S a a a =++⋅⋅⋅+2323232nn =⨯+⨯+⋅⋅⋅+⋅-()221321n n -=⨯--1626326n n n n +=⋅--=⋅--. ……………………… 12分(Ⅱ)法二由已知125n n S S n +=++()n N *∈ ① 设()()112n n S c n d S cn d ++++=++ 整理得 12n n S S cn d c +=++- ②对照① 、②,得 1,6c d == ……………………………………8分 即①等价于 ()()11626n n S n S n ++++=++∴ 数列{}6n S n ++是等比数列,首项为11161612S a ++=++=,公比为2q =∴ 11612232n n n S n -+++=⋅=⋅∴ 1326n n S n +=⋅--. …………………………………… 12分20.(本小题满分12分)如图所示,将一矩形花坛ABCD 扩建成一个更大的矩形花坛AMPN ,要求B 点在AM 上,D 点在AN 上,且对角线MN 过C 点,已知3=AB 米,2=AD 米.(I )要使矩形AMPN 的面积大于32平方米,则DN 的长应在什么范围内? (II )当DN 的长度是多少时,矩形花坛AMPN 的面积最小?并求出最小值. 解:(I )设DN 的长为x (0x >)米,则2AN x =+米∵AMDC ANDN =,∴()32x AM x+=, ……………………2分 ∴ ()232AMPNx S AN AM x +=⋅=由32>AMPN S 得 ()23232x x+> ,又0x >,得 2320120x x -+>,解得:2063x x <<> 或 即DN 长的取值范围是2(0)(6)3∞U ,,+ ……………………7分(II )矩形花坛AMPN 的面积为()22323121212312x x x y x x x x+++===++12231224x x≥⋅= ……………………10分 当且仅当1232x x ,x==即时矩形花坛AMPN 的面积取得最小值24. 故,DN 的长度是2米时,矩形AMPN 的面积最小,最小值为24平方米.…12分(第20题图)21.(本小题满分12分)已知函数22()ln ()f x x a x ax a R =-+∈.(Ⅰ)当1a =时,证明函数()f x 只有一个零点;(Ⅱ)若函数()f x 在区间()1,+∞上是减函数,求实数a 的取值范围. 解:(Ⅰ)当1a =时,2()ln f x x x x =-+,其定义域是(0,)+∞∴ 2121()21x x f x x x x --'∴=-+=- …………2分令()0f x '=,即2210x x x ---=,解得12x =-或1x =. 0x >Q ,∴ 12x ∴=-舍去. 当01x <<时,()0f x '>;当1x >时,()0f x '<.∴ 函数()f x 在区间()01,上单调递增,在区间()1,+∞上单调递减 ∴ 当x =1时,函数()f x 取得最大值,其值为2(1)ln1110f =-+=. 当1x ≠时,()(1)f x f <,即()0f x <.∴ 函数()f x 只有一个零点. ……………………6分(Ⅱ)显然函数22()ln f x x a x ax =-+的定义域为(0,)+∞∴ 222121(21)(1)()2a x ax ax ax f x a x a x x x-++-+-'=-+== ………7分① 当0a =时,1()0,()f x f x x'=>∴在区间()1,+∞上为增函数,不合题意……8分 ② 当0a >时,()()00f x x '≤>等价于()()()21100ax ax x +-≥>,即1x a≥ 此时()f x 的单调递减区间为1,a ⎡⎫+∞⎪⎢⎣⎭.依题意,得11,0.a a ⎧≤⎪⎨⎪>⎩解之得1a ≥.………10分③ 当0a <时,()()00f x x '≤>等价于()()()21100ax ax x +-≥>,即12x a≥- 此时()f x 的单调递减区间为12,a ⎡⎫-+∞⎪⎢⎣⎭, ∴1120a a ⎧-≤⎪⎨⎪<⎩得12a ≤-综上,实数a 的取值范围是1(,][1,)2-∞-+∞U …………12分 法二:①当0a =时,1()0,()f x f x x'=>∴在区间()1,+∞上为增函数,不合题意……8分 ②当0a ≠时,要使函数()f x 在区间()1,+∞上是减函数,只需()0f x '≤在区间()1,+∞上恒成立,0x >Q ∴只要22210a x ax --≥恒成立,2214210aaa a ⎧≤⎪∴⎨⎪--≥⎩解得1a ≥或12a ≤- 综上,实数a 的取值范围是1(,][1,)2-∞-+∞U …………12分 22.(本小题满分14分)已知椭圆C :()222210x y a b a b +=>>过点3(1,)2A ,且离心率12e =.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线l :()0y kx m k =+≠与椭圆交于不同的两点M N 、,且线段MN 的垂直平分线过定点1(,0)8G ,求k 的取值范围.解:(Ⅰ)由题意12e =,即12c e a ==,2a c =, ∴ ()22222223b a c c c c =-=-=∴ 椭圆C 的方程可设为2222143x y c c +=………………………………… 3分代入3(1,)2A ,得222312143c c ⎛⎫ ⎪⎝⎭+= 解得21c =∴ 所求椭圆C 的方程是22143x y +=. ……………………………………… 6分 (Ⅱ)法一由方程组22143x y y kx m⎧⎪+=⎨⎪=+⎩ 消去y ,得()2223484120k x kmx m +++-= ……… 4分 由题意,△()()()22284344120km km=-+->整理得:22340k m +->① …… 7分设()()1122,,M x y N x y 、,MN 的中点为00(,)P x y ,则12024234x x km x k +==-+, 002334my kx m k=+=+ ………………… 8分 由已知,MN GP ⊥ 即1MN GP k k ⋅=-即 223034141348mk k km k -+⋅=---+;整理得:2348km k +=-………… 10分 代入①式,并整理得:2120k >, 即||k >………………………12分∴,1010k ⎛⎛⎫∈-∞-+∞ ⎪ ⎪⎝⎭⎝⎭U ……………… 14分 (Ⅱ)法二,由方程组221,43x y y kx m⎧⎪+=⎨⎪=+⎩ 消去y ,得()2223484120k x kmx m +++-= ……… 4分由题意,△()()()22284344120km km =-+-> 整理得:22340k m +-> ① …… 7分设()()1122,,M x y N x y 、,MN 的中点为00(,)P x y ,则22112222143143x y x y ⎧+=⎪⎨⎪+=⎩ 整理得: 00314y x k =-⋅ ② 又MN GP ⊥ ∴ 00118y k x =-- ③ …………9分 由②、③解得 001238x y k ⎧=⎪⎨⎪=-⎩代入()0y kx m k =+≠,得 2348k m k+=- ……………………… 12分 代入①式,并整理得: 2120k >, 即||10k > ∴,k ⎛⎫∈-∞+∞ ⎪ ⎪⎝⎭⎝⎭U ……………… 14分 法三:由00(,)P x y 在椭圆内部,得:221328143k ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭+< 整理得: 2120k >, 即||k > ∴,k ⎛⎫∈-∞+∞ ⎪ ⎪⎝⎭⎝⎭U ……………… 14分。
四川省绵阳南山中学2024届高三上学期零诊考试(9月)文科数学试题及参考答案

一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.绵阳南山中学2021级高三上期零诊考试试题数学(文科)第Ⅰ卷 (选择题,共60分))1.集合A =-2,-1,0,1,2 ,∁A B =-1,0,2 ,则B =( )A .-2 B .1C .-2,1D .-2,0,22.设z =1-i1+i+2i ,则z 的虚部为( )A .iB .3iC .1D .33.“m >2”是“关于x 的方程2x 2-m x +1=0有两个不等实根”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.已知sin α+π6 =-13,则cos π3-α =( )A .223B .-13C .-223D .135.已知向量a =3,0 ,b =-1,1 ,c =1,k ,若a +b ⎳c ,则实数k 的值为( )A .-2B .-1C .2D .126.折扇在我国已有三千多年的历史,“扇”与“善”谐音,折扇也寓意“善良”“善行”.它常以字画的形式体现我国的传统文化,也是运筹帷幄、决胜千里、大智大勇的象征(如图1),图2为其结构简化图,设扇面A ,B 间的圆弧长为l ,A ,B 间的弦长为d ,圆弧所对的圆心角为θ(θ为弧度角),则l 、d 和θ所满足的恒等关系为( )A .2sin θ2θ=d l B .sin θ2θ=d l C .2cos θ2θ=d l D .cos θ2θ=d l7.将f (x )=cos ωx -π4 (ω>0)的图象向左平移π3个单位长度后与函数g (x )=cos ωx 的图象重合,则ω的最小值为( )A .34B .12C .14D .328.已知函数f (x )在区间[-2,2]上的大致图象如图所示,则f (x )的解析式可以是( )A .f (x )=e x -e -x xB .f (x )=e x -e -x sin xC .f (x )=e x -e -x cos xD .f (x )=e x -e -x x 29.若点P 是曲线y =ln x -x 2上任意一点,则点P 到直线l :x +y -4=0距离的最小值为( )A .22B .2C .2D .2210.一架飞机从保山云瑞机场出发飞往昆明长水机场,两地相距350km ,因雷雨天气影响,飞机起飞后沿与原来飞行方向成15°角的方向飞行,飞行一段时间后,再沿与原来飞行方向成30°角的方向继续飞行至终点,则本架飞机的飞行路程比原来的350km 大约多飞了( )(参考数据:2≈1.41,3≈1.73)A .15kmB .25kmC .30kmD .40km11.下列结论正确的个数为( )①在△ABC 中,若a >b ,则cos A <cos B ;②在△ABC 中,不等式b 2+c 2-a 2>0恒成立,则△ABC 为锐角三角形;③在△ABC 中,若C =π4,a 2-c 2=bc ,则△ABC 为等腰直角三角形;④若△ABC 为锐角三角形,则sin A <B cos .A .1B .2C .3D .412.对于函数y =f x ,若存在非零实数x 0,使得f x 0 =-f -x 0 ,则称点x 0,f x 0 与点-x 0,f -x 0 是函数的一对“隐对称点”.若m >0时,函数f x =ln x ,x >0-mx 2-mx ,x ≤0的图象上恰有2对“隐对称点”,则实数m 的取值范围为( )A .0,1e B .1,+∞C .0,1e ∪1e,+∞ D .0,1 ∪1,+∞第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每题5分,共20分.)13.命题“∃x ∈-1,1 ,x 2-x +3<0”的否定是.14.曲线y =1x在x =3处切线的斜率为.15.函数y =2-sin x -cos 2x 的值域为.16.已知f (x )为奇函数,当x ∈(0,1],f (x )=ln x ,且f (x )关于直线x =1对称.设方程f (x )=x +1的正数解为x 1,x 2,⋯,x n ,⋯,且任意的n ∈N ,总存在实数M ,使得x n +1-x n <M 成立,则实数M 的最小值为.三、解答题(共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)已知向量a ,b 满足a +b ⋅a -2b =-6,且a =1,b =2.(1)求a ⋅b ;(2)若a 与b 的夹角为θ,求θ的值.18.(本小题满分12分)函数f x =cos ωx +φ ω>0,φ <π2的相邻两条对称轴之间的距离为π2,且f π6=1.(1)求f x 的单调递减区间;(2)当x ∈-π6,π3时,方程f x -a =0恰有两个不同解,求实数a 的取值范围.19.(本小题满分12分)已知二次函数f x =x 2-2mx -1,m ∈R .(1)若函数f x +1 是偶函数,求m 的值;(2)是否存在m ,使得函数f x 有两个零点x 1和x 2x 1<x 2 ,且在区间x 1,x 2 内至少存在两个整数点?若存在,求出m 的取值范围;若不存在,请说明理由.20.(本小题满分12分)如图所示:(1)证明余弦定理:a2=b2+c2-2bc⋅cos A;(2)在△ABC边AC上侧有一点D,若A,B,C,D四点共圆,且∠ABC=π3,AB=2,AC= 3,求△ACD周长的取值范围.21.(本小题满分12分)已知函数f x =ln x+a a∈R.(1)若函数g x =f x +12x2+ax,讨论函数g x 的单调性;(2)证明:当a≤12时,f x <e x-sinθ.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.22. [选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy中,曲线C的参数方程为x=3cosαy=sinα(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为ρsinθ+π4=22.(1)求直线l的直角坐标方程和曲线C的普通方程;(2)点P为曲线C上一点,求点P到直线l距离的最小值.23.[选修4-5:不等式选讲](本小题满分10分)已知f x =2x+1+2x-1(1)解不等式f x ≤7;(2)若a+b+c=3,求证:∃x0∈R,使得f x0≤a+12+b2+c-12成立.数学(文科)参考答案一、选择题1.C2.C3.B4.B5.D6.A7.A8.C9.D10.B11.B12.D12.【详解】由题意可得,函数f(x)=-mx2-mx(x≤0)关于原点对称的图象g(x)= mx2-mx与函数f(x)=ln x(x>0)的图象有两个交点,即方程mx2-mx=ln x(x>0)有两个根,即m(x-1)=ln xx,令h(x)=ln xx(x>0),则h (x)=1-ln xx2,当0<x<e时,h (x)>0,当x>e时,h (x)<0,所以h(x)在0,e上递增,在e,+∞上递减,y=m(x-1)的图象恒过点(1,0),h(x)=ln xx(x>0)的图象也过点(1,0),因为h (1)=1,所以h(x)=ln x x(x>0)在x=1处的切线方程为y=x-1,由图可知当0<m<1或m>1时,h(x)=ln x x(x>0)与y=m(x-1)的图象有2个交点,即mx2-mx=ln x(x>0)有两个根,所以实数m的取值范围为0,1∪1,+∞,故选:D二、填空题13.∀x∈-1,1,x2-x+3≥014.-1915.32,316.2【详解】因为f(x)为奇函数,所以f x =-f-x,且f0 =0,又f(x)关于直线x=1对称,所以f1+x=f1-x,所以f2+x=f-x=-f x ,则f4+x=-f2+x=f x ,所以函数f x 是以4为周期的周期函数,作出函数y=f x 和y=x+1的图像如图所示:由f (x )=x +1的正数解依次为x 1、x 2、x 3、⋅⋅⋅、x n 、⋅⋅⋅,则lim n →∞(x n +1-x n )的几何意义为函数f x 两条渐近线之间的距离为2,所以lim n →∞(x n +1-x n )=2.所以得任意的n ∈N ,x n +1-x n <2,已知任意的n ∈N ,总存在实数M ,使得x n +1-x n <M 成立,可得M ≥2,即M 的最小值为2.故答案为:2.三、解答题17.(1)-1;(2)2π3.【详解】(1)解:a +b ⋅a -2b=a 2-a ⋅b -2b 2=-6,又因为a=1,b =2,∴a ⋅b =a2-2b 2+6=1-8+6=-1;(2)解:由题意可得cos θ=a ⋅b |a |⋅|b |=-12=-12,又因为θ∈[0,π],所以θ=2π3.18.(1)k π+π6,k π+2π3,k ∈Z ;(2)12,1 .【详解】(1)由题意可知,函数的周期T =2πω=2×π2,得ω=2,所以f π6 =cos 2×π6+φ =1,φ <π2,得φ=-π3,所以f x =cos 2x -π3,令2k π≤2x -π3≤2k π+π,解得:k π+π6≤x ≤k π+2π3,k ∈Z ;所以函数的单调递减区间是k π+π6,k π+2π3,k ∈Z ,(2)方程f x -a =0有两解,即a =f x ,x ∈-π6,π3,2x -π3∈-2π3,π3 ,所以f x ∈-12,1,又因为有两个不同解,所以由函数图象(略)可知,实数a 的取值范围是12,1 .19.(1)m =1;(2)-∞,0 ∪0,+∞ 【详解】(1)∵函数f x +1 是偶函数,∴f x +1 =f -x +1 对任意的x 恒成立.∴(x +1)2-2m x +1 -1=(-x +1)2-2m -x +1 -1,即4x -4mx =0.∴m =1.(2)∵二次函数f x 的图像开口向上且过点0,-1 ,对称轴为x =m ,∴对任意的实数m ,函数f x 都有两个零点x 1和x 2,且0∈x 1,x 2 .∴①当m =0时,函数f x =x 2-1的两个零点分别为-1,1,在区间-1,1 内只有一个整数点,不满足题目要求;②当m >0时,只需f 1 =-2m <0,即m >0,此时至少有两个整数0和1在区间x 1,x 2 内;③当m <0时,只需f -1 =2m <0,即m <0,此时至少有两个整数0和-1在区间x 1,x 2 内.∴m 的取值范围是-∞,0 ∪0,+∞ .20.(1)证明见解析;(2)(23,2+3].【详解】(1)向量法:因为BC =AC -AB,则BC 2=AC -AB 2=AC 2+AB 2 -2AC ⋅AB =b 2+c 2-2bc cos A ,即a 2=b 2+c 2-2bc cos A .(2)因为A ,B ,C ,D 四点共圆,所以D +B =π,D =π-B =2π3.在△ACD 中,由正弦定理得AD sin ∠ACD =CD sin ∠CAD =ACsin ∠ADC=2,即AD =2sin ∠ACD ,CD =2sin ∠CAD ,所以周长=AD +CD +AC =2(sin ∠ACD +sin ∠CAD )+3=2(sin ∠ACD +sin (π3-∠ACD )+3=sin ∠ACD +3cos ∠ACD +3=2sin (∠ACD +π3)+3,又因为∠ACD ∈(0,π3),所以(∠ACD +π3)∈(π3,2π3),所以sin (∠ACD +π3)∈(32,1],所以周长的取值范围为(23,2+3]21.(1)答案见解析;(2)证明见解析【详解】(1)g x =f x +12x 2+ax =ln x +a +12x 2+ax x >0 ,g x =1x +x +a =x 2+ax +1x,当a ≥0时,在区间0,+∞ 上,g x >0,g x 单调递增,当a <0时,若Δ=a 2-4≤0,即-2≤a <0时,在区间0,+∞ 上,g x >0,g x 单调递增,若Δ=a 2-4>0,即当a <-2时,函数y =x 2+ax +1的开口向上,对称轴x =-a2>1,令gx =0,即x 2+ax +1=0,解得x 1=-a -a 2-42,x 2=-a +a 2-42,而x 1+x 2=-a >0,x 1x 2=1>0,所以x 1,x 2是两个正根,所以在区间0,x 1 ,x 2,+∞ 上,g x >0,g x 单调递增,在区间x 1,x 2 上,g x <0,g x 单调递减.综上所述,当a ≥-2时,g x 在区间0,+∞ 上单调递增;当a <-2时,g x 在区间0,-a -a 2-42 ,-a +a 2-42,+∞上单调递增,在区间-a -a 2-42,-a +a 2-42上单调递减.(2)要证明:当a ≤12时,f x <e x -sin θ,即证明:当a ≤12时,ln x +a <e x -sin θ,即证明:当a ≤12时,ln x +a -e x +sin θ<0,构造函数h x =ln x +a -e x +sin θx >0,a ≤12,h x =1x -e x ,函数h x =1x-e x 在0,+∞ 上为减函数,h 1 =1-e <0,h 12 =2-e >0,所以存在x 0∈12,1 ,使h x =1x 0-e x=0,1x 0=e x,所以h x 在区间0,x 0 上h x >0,h x 单调递增,在区间x 0,+∞ 上,h x <0,h x 单调递减,h x ≤h x 0 =ln x 0-e x 0+a +sin θ=ln e -x 0-1x 0+a +sin θ=-x 0+1x 0+a +sin θ<-2x 0⋅1x 0+a +sin θ=-2+a +sin θ<0,即h x <0,所以当a ≤12时,ln x +a -e x +sin θ<0,所以当a ≤12时,f x <e x -sin θ.22.(1)直线l 的直角坐标方程为x +y -4=0,曲线C 的普通方程为x 23+y 2=1(2)2【详解】(1)由ρsin θ+π4 =22,得ρsin θcos π4+ρcos θsin π4=22,22ρsin θ+22ρcos θ=22,所以ρsin θ+ρcos θ=4,所以直线l 的直角坐标方程为x +y -4=0,由x =3cos αy =sin α (α为参数),得x23+y 2=1,即曲线C 的普通方程为x 23+y 2=1,(2)设点P (3cos α,sin α)(α∈[0,2π)),则点P 到直线l 距离为d =3cos α+sin α-412+12=2sin α+π3 -4 2,所以当sin α+π3 =1时,d 取得最小值22= 2.23.(1)-2,32;(2)证明见解析.【详解】(1)f x ≤7可化为x ≤-1-2x +1 -2x +1≤7 或-1<x <122x +1 -2x +1≤7或x ≥122x +1 +2x -1≤7,解得-2≤x ≤-1或-1<x <12或12≤x ≤32,∴f x ≤7解集为-2,32(2)f x =2x +1 +2x -1 ≥2x +1 -2x -1 =3当x =-1时取“=”,∴f x min =3∵a +b +c =3,∴a +1 +b +c -1 =3,∴12+12+12 a +1 2+b 2+c -1 2 ≥a +1 +b +c -1 2 =32,∴a +1 2+b 2+c -1 2≥3,故∃x 0∈R ,使得f x 0 ≤a +1 2+b 2+c -1 2.。
高三下学期数学(文科)模拟考试卷(带参考答案与解析)

高三下学期数学(文科)模拟考试卷(带参考答案与解析)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.答选择题时,则选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,则将答案写在答题卡上。
写在本试卷上无效。
3.本试卷共22题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中只有一项是符合题目要求的。
1.已知向量(2,1)a =和(3,2)b =,则()a a b ⋅-=( ) A .-5 B .-3C .3D .52.不等式312x >+的解集为( ) A .{1,2}x x x <≠- B .{1}x x >C .{21}x x -<<D .{21}x x x <->或3.直线x +ay -3=0与直线(a +1)x +2y -6=0平行,则a =( )A .-2B .1C .-2或1D .-1或24.古希腊科学家阿基米德发明了享誉世界的汲水器,称为阿基米德螺旋泵,两千多年后的今天,左图所示的螺旋泵,仍在现代工农业生产中使用,其依据是“阿基米德螺线”.在右图所示的平面直角坐标系xOy 中点A 匀速离开坐标系原点O ,同时又以固定的角速度绕坐标系原点O 逆时针转动,产生的轨迹就是“阿基米德螺线”,该阿基米德螺线与坐标轴交点依次为A 1(-1,0),A 2(0,-2),A 3(3,0),A 4(0,4),A 5(-5,0),…按此规律继续,若四边形123n n n n A A A A +++的面积为220,则n =( )A .7B .8C .9D .105.△ABC 中AC =,BC =和60A =︒,则cos B =( )A .2±B .12±C .12D .26.设函数()f x 满足(1)()0f x f x ++=,当0≤x <1时,则1()2xf x -=,则()0.5log 8f =( ) A .-2B .12-C .12D .27.若cos 0,2(sin 2)1cos2αααα≠+=+,则tan2α=( ) A .43-B .34-C .34D .438.设函数()y f x =由关系式||||1x x y y +=确定,函数(),0,()(),0.f x xg x f x x -≥⎧=⎨-<⎩,则( )A .g (x )为增函数B .g (x )为奇函数C .g (x )值域为[1,)-+∞D .函数()()y f x g x =--没有正零点二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分。
高三数学模拟试卷文科答案

一、选择题(本大题共10小题,每小题5分,共50分)1. 若函数f(x) = ax^2 + bx + c在x=1时取得极值,则a、b、c之间的关系为()A. a+b+c=0B. a+b+c=1C. 2a+b=0D. 2a+b=1答案:C解析:因为函数f(x) = ax^2 + bx + c在x=1时取得极值,所以f'(1)=0,即2a+b=0。
2. 已知等差数列{an}的公差为d,首项为a1,第n项为an,则an = ()A. a1 + (n-1)dB. a1 - (n-1)dC. a1 + ndD. a1 - nd答案:A解析:等差数列的通项公式为an = a1 + (n-1)d。
3. 下列各式中,等式成立的是()A. sin(α+β) = sinαcosβ + cosαsinβB. cos(α+β) = cosαcosβ - sinαsinβC. tan(α+β) = tanαtanβD. cot(α+β) = cotαcotβ答案:B解析:根据三角函数的和角公式,cos(α+β) = cosαcosβ - sinαsinβ。
4. 已知复数z = a + bi(a,b∈R),若|z| = 1,则复数z的实部a和虚部b之间的关系为()A. a^2 + b^2 = 1B. a^2 - b^2 = 1C. a^2 + b^2 = 0D. a^2 - b^2 = 0答案:A解析:复数z的模|z| = √(a^2 + b^2),由|z| = 1,得a^2 + b^2 = 1。
5. 已知函数f(x) = x^3 - 3x,则f(x)的图像关于点()A. (0,0)B. (1,0)C. (-1,0)D. (0,1)答案:B解析:由f(1) = 1^3 - 31 = -2,f(0) = 0^3 - 30 = 0,得f(x)的图像关于点(1,0)。
6. 下列各式中,正确的是()A. loga(b^2) = 2logabB. loga(b^3) = 3logabC. loga(ab) = 1D. loga(a^2) = 2答案:B解析:根据对数的运算法则,loga(b^3) = 3logab。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三文科数学模拟试题满分:150分 考试时间:120分钟第Ⅰ卷(选择题 满分50分一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数31ii++(i 是虚数单位)的虚部是( )A .2B .1-C .2iD .i -2.已知集合{3,2,0,1,2}A =--,集合{|20}B x x =+<,则()R A C B ⋂=( ) A .{3,2,0}-- B .{0,1,2} C . {2,0,1,2}- D .{3,2,0,1,2}-- 3.已知向量(2,1),(1,)x ==a b ,若23-+a b a b 与共线,则x =( ) A .2 B .12 C .12- D .2- 4.如图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为( )A .4πB .32π C .3π D .2π 5.将函数()sin 2f x x =的图象向右平移6π个单位,得到函数()y g x =的图象,则它的一个对称中心是( ) A .(,0)2π-B . (,0)6π-C . (,0)6πD . (,0)3π.2:2x x ++正视图 侧视图俯视图A .94B .6C .9D .369.已知变量,x y 满足约束条件102210x y x y x y +-≥⎧⎪-≤⎨⎪-+≥⎩,设22z x y =+,则z 的最小值是( )A.1213 10. 定义在R 上的奇函数()f x ,当0≥x 时,⎪⎩⎪⎨⎧+∞∈--∈+=),1[|,3|1)1,0[),1(log )(21x x x x x f ,则函数)10()()(<<-=a a x f x F 的所有零点之和为( )A .12-aB .12--aC .a --21D .a21-第Ⅱ卷(非选择题 满分100分)二、填空题:(本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置)11. 命题“若12<x ,则11<<-x ”的逆否命题是_______________________.12.函数()f x =的定义域是 . 13.抛物线22y x =-的焦点坐标是__________.14.若23mx m ≥-恒成立,则实数m 的取值范围为__________. 15.某学生对函数()cos f x x x =的性质进行研究,得出如下的结论: ①函数()f x 在[,0]π-上单调递增,在[0,]π上单调递减;②点(,0)2π是函数()y f x =图象的一个对称中心; ③函数()y f x =图象关于直线x π=对称;④存在常数0M >,使|()|||f x M x ≤对一切实数x 均成立;⑤设函数()y f x =在(0,)+∞内的全部极值点按从小到大的顺序排列为12,,x x 则212x x ππ<-<.其中正确的结论是__________.三、解答题:(本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
解答写在答题卡上的指定区域内)16.(本小题满分12分)在ABC ∆中,c ,b ,a 分别是角A 、B 、C 的对边,且满足:AcA b sin 2sin 2=(1)求C ; (2)当]0,3[π-∈x 时,求函数()()x B x A y -++=sin sin 3的值域.17. (本小题满分13分)某中学举行了一次“交通安全知识竞赛”, 全校学生参加了这次竞赛.为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:(1)写出,,,a b x y 的值; (2)若现在需要采用分层抽样的方式从5个小组中抽取25人去参加市里的抽测考试,则第1,2,3组应分别抽取多少人?(3)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加交通安全知识的志愿宣传活动.求所抽取的2名同学中至少有1名同学来自第5组的概率.18. (本小题满分12分)已知函数2()1xe f x ax =+,其中a为正实数,12x =是()f x 的一个极值点 (1)求a 的值; (2)当12b >时,求函数()f x 在[,)b +∞上的最小值.50 60 70 80 90 100 成绩(分)0.040 xy0.008频率组距D 1B19. (本小题满分13分)如图,矩形11A B BA 和矩形11A ADD 所在的平面与梯形ABCD 所在的平面分别相交于直线AB 、CD ,其中AB ∥CD ,1112AB BC BB CD ====,60ABC ∠= (1) 证明:平面1BB C 与平面1DD C 的交线平行于平面11A B BA ; (2) 证明:AD ⊥平面1AAC ; (3) 求几何体111A B D ABCD -的体积.20. (本小题满分12分)设等比数列{}n a 的前n 项和为n S ,已知122()n n a S n N *+=+∈ (1)求数列{}n a 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这2n +个数组成公差为n d 的等差数列,求数列1n d ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T .21.(本小题满分13分)已知椭圆22221(0)x y a ba b +=>>的离心率为3,且过点(0,1)(1)求此椭圆的方程;(2)已知定点)0,1(-E ,直线2y kx =+与此椭圆交于C 、D 两点.是否存在实数k ,使得以线段CD 为直径的圆过E 点.如果存在,求出k 的值;如果不存在,请说明理由.高考模拟数学(文科)试卷参考答案一、选择题:(本大题共10小题,每小题5分,共50分)1. B2. C3. B4. B5. C6. A7. D8. C9. A 10. D 解析: 1. 经计算得321ii i+=-+,故虚部为1-,选B. 2.{|2}R C B x x =≥-,因此(){2,0,1,2}R A C B ⋂=-,选C.3. 2(3,2),3(5,13)x x -=-+=+a b a b ,由向量共线的条件得3(13)5(2)x x +=-,解得12x =,选B. 4. 根据三视图可知这是一个圆柱体,易知选B. 5. 由已知得()sin 2()6g x x π=-,易知(,0)6π为其一个对称中心,选C.6. 经过计算易知选A.7. 由已知得直线2l 的斜率为1-,且直线2l 过圆C 的圆心(1,0)-,根据直线的点斜式可计算得选D. 8. 1101210()10302a a a a a ++++=⨯=,于是1106a a +=,即566a a +=,又0n a >所以25656()92a a a a +⋅≤=,当且仅当563a a ==时等号成立,故选C. 9. 由约束条件可作出可行域可知,z 的最小值就是原点到直线10x y +-=距离的平方,经计算可得选A. 10. 作出()y f x =的图像如下所示,则()()F x f x a =-的零点即为函数()y f x =与y a =图像交点的横坐标,由图可知共有五个零点,不妨设为12345,,,,x x x x x 且12345x x x x x <<<<,从图中可看出1x 与2x 关于直线3x =-对称,4x 与5x 关于直线3x =对称,故12452(3)230x x x x +++=⨯-+⨯=,当(1,0)x ∈-时12()log (1)f x x =--+,因此由12log (1)x a --+=解得312a x =-,故1234512a x x x x x ++++=-二、填空题:(本大题共5小题,每小题5分,共25分)11. 若1x ≥或1x ≤-,则21x ≥ 12. {|221}x x x -≤≤≠且13. 108-(,)14. 5(,]12m ∈-∞解析:由题意得(2)3x m -≥恒成立,又22x -≤≤,当2x =时03≥-恒成立;当22x -≤<时20x -<只需m ≤即可,令k =,则只需min m k ≤.若设y =,则32y k x -=-,其表示两点(,),(2,3)x y 之间连线的斜率,其中点(,)x y 在半圆224(0)x y y +=≥上,则当过点(2,3)的直线与圆相切时斜率k 有最值,易知其中一条切线为:2x =,不妨设另一条切线方程为3(2)y k x -=-,即230kx y k --+=2=得512k =为最小值,故512m ≤. 15. ④⑤ 解析:()cos f x x x =为奇函数,则函数()f x 在[,0]π-和[0,]π上单调性相同,所以①错.由于(0)0f =,()f ππ=-,所以②错.再由(0)f =,(2)2f ππ=,所以③错. |()||cos ||||cos |||f x x x x x x ==≤,令1M =,则||()|||f x M x ≤对一切实数x 均成立,所以④对.由()cos sin 0f x x x x '=-=得cos sin 0x x x -=,显s 0x ≠所以1tan x x =,易知方程1tan x x=的实根就是()f x 的极值点。
在除(,)22ππ-外的正切函数的每一个周期1tan y y x x===与125(,),(,)424x x ππππ∈∈,故212x x ππ<-<,所以⑤对.三、解答题:(本大题共6小题,共75分。
)16. (本小题满分12分) 解:(1)由已知A c A b sin 2sin 2=得sin cos sin b c A A A=根据正弦定理得:sin sin cos B C A =,而sin sin()sin cos cos sin B A C A C A C =+=+ 由此可得 sin cos 0A C =,又因为三角形中sin 0A ≠ 所以cos 0C =,得2C π∠=…………6分(2)由(1)知2A B π+=, 所以sin()sin()sin[()]cos()22B x A x A x A x ππ-=--=-+=+()()()()sin cos 2sin 6y A x B x A x A x A x π=++-=+++⎛⎫=++ ⎪⎝⎭因为]0,3[π-∈x ,[0,]2A π∈,故2(,)663A x πππ++∈- 所以2sin (1,2]6y A x π⎛⎫=++∈- ⎪⎝⎭,即值域为(1,2]-…………12分 17.(本小题满分13分)解:(1)由题意可知,样本总人数为,5016.08=,04.0502==∴b16,0.04,0.032,0.004a b x y ====.…………4分(2)第1,2,3组应分别抽取4,8,10人…………8分(3)由题意可知,第4组共有4人,记为,,,A B C D ,第5组共有2人,记为,X Y .从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有,,,,,,,AB AC AD BC BD CD AX AY ,,,,,,,BX BY CX CY DX DY XY共15种情况. 设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E , 有,AX AY ,,,,,,,BX BY CX CY DX DY XY 共9种情况.所以93()155P E ==. 答:随机抽取的2名同学中至少有1名同学来自第5组的概率35…………13分 18. (本小题满分12分)解:222(-21)()(1)xax ax e f x ax +'=+ (1)因为12x =是函数()y f x =的一个极值点, 所以1()02f '=因此1104a a -+= 解得43a =经检验,当34=a 时,21=x 是)(x f y =的一个极值点,故所求a 的值为34. ………………………5分(2)由(1)可知,22248(1)33()4(1)3xx x e f x x -+'=+ 令()0f x '=,得1213,22x x == ()f x 与'()f x 的变化情况如下:所以,()f x 的单调递增区间是13(,),(,),22-∞+∞ 单调递减区间是13(,)22D 1B 当1322b <<时,()f x 在3[,)2b 上单调递减,在3(,)2+∞上单调递增所以()f x 在[,)b +∞上的最小值为3()2f =当32b ≥时,()f x 在[,)b +∞上单调递增, 所以()f x 在[,)b +∞上的最小值为223()134b be ef b ab b ==++ ………………………………12分19. (本小题满分13分)(1)证明:在矩形11A B BA 和矩形11A ADD 中1AA ∥1BB ,1AA ∥1DD ∴1BB ∥1DD又1BB ⊄平面1DD C ,1DD ⊂平面1DD C∴1BB ∥平面1DD C不妨设平面1BB C 与平面1DD C 的交线为l ,平行的性质定理知1BB ∥l又l ⊄平面11A B BA ,1BB ⊂平面11A B BA ∴l ∥平面11A B BA …………4分(2)在矩形11A B BA 和矩形11A ADD 中11,AA AB AA AD ⊥⊥且AB AD A =∴1AA ⊥平面ABCD在ABC ∆中1AB BC ==,60ABC ∠= ∴ABC ∆为正三角形且1AC =又梯形ABCD 中AB ∥CD∴120BCD ∠=,故60ACD ∠=又∵2CD =,在ACD ∆中由余弦定理可求得AD =∴222AC AD CD +=,故AC AD ⊥又∵1AA ⊥平面ABCD∴1AA AD ⊥,而1AA AC A =∴AD ⊥平面1AAC …………9分 (3)111111111133C AA B B C AA D D V V V --=+=⨯⨯⨯⨯=…………13分 20. (本小题满分12分)解:(1)由122(n n a S n +=+∈Z *)得*122(n n a S n N -=+∈,2n ≥), 两式相减得:12n n n a a a +-=, 即*13(n n a a n N +=∈,2n ≥),∵{}n a 是等比数列,所以213a a =,又2122,a a =+ 则11223a a +=,∴12a =,∴123n n a -=. …………………………………6分(2)由(1)知123n n a +=,123n n a -=∵1(1)n n n a a n d +=++ ,∴1431n n d n -⨯=+,………8分 令123111n T d d d =+++…1n d +, 则012234434343n T =++⨯⨯⨯+…1143n n -++ ① +⋅+⋅=2134334231n T …114343n n n n -+++ ② ①-②得01222113434343n T =+++…1114343n n n -++- 111(1)111525331244388313n n n n n --++=+⨯-=-- 1152516163n n n T -+∴=-. ………………12分21. 解:(1)根据题意,222222331, 1.2c a a b b a b c c ⎧=⎪⎧=⎪⎪⎪==⎨⎨⎪⎪=+=⎩⎪⎪⎩解得, 所以椭圆方程为2213x y +=. ………………………………5分 (2)将2y kx =+代入椭圆方程,得22(13)1290k x kx +++=,由直线与椭圆有两个交点,所以22(12)36(13)0k k ∆=-+>,解得21k >.设),(11y x C 、),(22y x D ,则1221213k x x k +=-+,122913x x k ⋅=+,若以CD 为直径的圆过E 点,则0=⋅,即0)1)(1(2121=+++y y x x ,而1212(2)(2)y y kx kx =++=212122()4k x x k x x +++,所以212121212(1)(1)1)(21)()5x x y y k x x k x x +++=+++++(2229(1)12(21)501313k k k k k ++=-+=++,解得76k =,满足21k >.所以存在7,6k =使得以线段CD 为直径的圆过E 点. ………………………………13分。
