角平分线的判定学案
11.1.2三角形的高、中线、角平分线学案使用

11.1.2三角形的高,中线,角平分线导学案主备人:张伟班级:________ 使用人:________ 时间8月26日【学习目标】1.认识并会画出三角形的高线、三角形的角平分线、三角形的中线、并利用其解决相关问题;2、认识三角形的稳定性,并会用其解决一些实际问题【重点】1、认识三角形的高线、中线与角平分线。
并会画出图形。
2、三角形的稳定性【难点】1、画出三角形的高线、中线与角平分线.2、三角形的稳定性的理解一、【温故而知新】下列长度的三个线段能否组成三角形?(1)3,6,8 (2)1,2,3 (3)6,8,2二、【预习检测】知识点1:认识并会画三角形的高线,利用其解决相关问题自学课本4页三角形的高并完成下列各题:1、作出下列三角形三边上的高:2、上面第1图中,AD是△ABC的边BC上的高,则∠ADC=∠ = °3、由作图可得出如下结论:(1)三角形的三条高线所在的直线相交于点;(2)锐角三角形的三条高相交于三角形的;(3)钝角三角形的三条高所在直线相交于三角形的;(4)直角三角形的三条高相交三角形的;练习一:如图所示,画△ABC的一边上的高,下列画法正确的是().知识点二:认识并会画三角形的中线,利用其解决相关问题自学课本4页下方三角形的中线并完成下列各题:1、作出下列三角形三边上的中线2、AD是△ABC的边BC上的中线,则有BD = =21,3、由作图可得出如下结论:(1)三角形的三条中线相交于点,这个交点叫做三角形的(2)锐角三角形的三条中线相交于三角形的;(3)钝角三角形的三条中线相交于三角形的;(4)直角三角形的三条中线相交于三角形的;练习二:如图,D、E是边AC的三等分点,图中有个三角形,BD是三角形中边上的中线,BE是三角形中________上的中线;知识点三:认识并会画三角形的角平分线,利用其解决相关问题自学课本5页三角形的角平分线并完成下列各题:1、作出下列三角形三角的角平分线:2、AD是△ABC中∠BAC的角平分线,则∠BAD=∠ =3、由作图可得出如下结论:(1)三角形的三条角平分线相交于点;(2)锐角三角形的三条角平分线相交三角形的;(3)钝角三角形的三条角平分线相交三角形的;(4)直角三角形的三条角平分线相交三角形的 .练习三:如图,已知∠1=21∠BAC,∠2 =∠3,则∠BAC的平分线为,∠ABC的平分线为 .总结:三角形的高、中线、角平分线都是一条线段。
专题06 角的平分线的性质(解析版)八年级上册数学精品学案(人教版)

专题06 角的平分线的性质1、如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量内槽宽的卡钳,卡钳的工作原理利用了三角形全等判定定理.【答案】SAS.2.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90∘),点C在DE上,点A和B分别与木墙的顶端重合,求两堵木墙之间的距离.【答案】解:由题意得:AC=BC,∠ACB=90∘,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90∘,∴∠ACD+∠BCE=90∘,∠ACD+∠DAC=90∘,∴∠BCE=∠DAC,在ΔADC和ΔCEB中,{∠ADC=∠CEB ∠DAC=∠BCEAC=BC,∴ΔADC≅ΔCEB(AAS);由题意得:AD=EC=6cm,DC=BE=14cm,∴DE=DC+CE=20(cm),答:两堵木墙之间的距离为20cm.知识梳理知识点一:角的平分线的性质角的平分线的性质:角的平分线上的点到角两边的距离相等.要点诠释:用符号语言表示角的平分线的性质定理:若CD平分∠ADB,点P是CD上一点,且PE⊥AD于点E,PF⊥BD于点F,则PE=PF.例题精讲例1、已知:如图,AD是△ABC的角平分线,且,则△ABD与△ACD的面积之比为()A.3:2 B. C.2:3 D.【答案】B;提示:∵AD是△ABC的角平分线,∴点D到AB的距离等于点D到AC的距离,又∵,则△ABD与△ACD的面积之比为例2、已知:如图,在ABC∆中,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F.求证:AE=AF.:3:2AB AC=3:22:3:3:2AB AC=3:2【答案】 证明:∵AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F.∴DE =DF (角平分线上的点到角两边的距离相等)90AED AFD ∠=∠=︒(垂直定义)在Rt AED ∆和Rt AFD ∆中 DE DF AD AD =⎧⎨=⎩∴Rt AED ∆≌Rt AFD ∆(HL )∴AE AF =巩固练习1、如图,AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE =DG ,△ADG 和△AED 的面积分别为50和39,则△EDF 的面积为:( )A.11B.5.5C.7D.3.5【答案】解: 过D 点作DH ⊥AC 于H ,∵AD 是△ABC 的角平分线,DF ⊥AB ,DH ⊥AC∴DF =DH在Rt △EDF 和Rt △GDH 中DE =DG ,DF =DH∴Rt △EDF ≌Rt △GDH同理可证Rt △ADF 和Rt △ADH∴AED EDF ADG GDH S =S S S +-△△△△∴EDF ADG AED 2=S S S -△△△=50-39=11,∴△EDF 的面积为5.52、如图,AD 是∠BAC 的平分线,DE ⊥AB ,交AB 的延长线于点E ,DF ⊥AC 于点F ,且DB =DC. 求证:BE =CF.【答案】证明:∵DE ⊥AE ,DF ⊥AC ,AD 是∠BAC 的平分线,∴DE =DF ,∠BED =∠DFC =90°在Rt △BDE 与Rt △CDF 中,DB DCDE DF =⎧⎨=⎩,∴Rt △BDE ≌Rt △CDF (HL )∴BE =CF知识点二:角的平分线的判定角平分线的判定:角的内部到角两边距离相等的点在角的平分线上.要点诠释:用符号语言表示角的平分线的判定:若PE ⊥AD 于点E ,PF ⊥BD 于点F ,PE =PF ,则PD 平分∠ADB例题精讲例3、如图,AC=DB ,△PAC 与△PBD 的面积相等.求证:OP 平分∠AOB .【答案】证明:作PM ⊥OA 于M ,PN ⊥OB 于N12PAC S AC PM =△∵,12PBD S BD PN =△,且PAC S =△PBD S △∴ 12AC PM 12BD PN =又∵AC =BD∴PM =PN又∵PM ⊥OA ,PN ⊥OB∴OP 平分∠AOB巩固练习1、已知:如图,CD ⊥AB 于D ,BE ⊥AC 于E ,CD 、BE 交于O ,∠1=∠2.求证:OB =OC.【答案】证明:∵CD ⊥AB ,BE ⊥AC ,∠1=∠2.∴OD =OE在Rt △ADO 与Rt △AEO 中,OD OEAO AO =⎧⎨=⎩∴Rt △ADO ≌Rt △AEO (HL )∴AD =AE在Rt △ADC 与Rt △AEB 中,DAC EABAD AEADC AEB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴Rt △ADC ≌Rt △AEB (ASA )∴CD =BE∴CD -OD =BE -OE ,即OC =OB.知识点三:角的平分线的尺规作图角平分线的尺规作图(1)以O为圆心,适当长为半径画弧,交OA于D,交OB于E.(2)分别以D、E为圆心,大于12DE的长为半径画弧,两弧在∠AOB内部交于点C.(3)画射线OC.射线OC即为所求.例题精讲1、如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC 于点D,若CD=4,AB=15,则△ABD的面积是()A.15 B.30 C.45 D.60【答案】B;【解析】由题意得AP是∠BAC的平分线,过点D作DE⊥AB于E,又∵∠C=90°,∴DE=CD,∴△ABD的面积=AB•DE=×15×4=30.知识点四:三角形角平分线的性质三角形三条角平分线交于三角形内部一点,此点叫做三角形的内心且这一点到三角形三边的距离相等.三角形的一内角平分线和另外两顶点处的外角平分线交于一点.这点叫做三角形的旁心.三角形有三个旁心.所以到三角形三边所在直线距离相等的点共有4个.如图所示:△ABC 的内心为1P ,旁心为234,,P P P ,这四个点到△ABC 三边所在直线距离相等.知识点五:角的平分线的性质综合应用例4、如图,四边形ABDC 中,∠D=∠ABD=90゜,点O 为BD 的中点,且OA 平分∠BAC .(1)求证:OC 平分∠ACD ;(2)求证:OA ⊥OC ;(3)求证:AB+CD=AC .【答案】证明:(1)过点O 作OE ⊥AC 于E ,∵∠ABD=90゜,OA 平分∠BAC ,∴OB=OE ,∵点O 为BD 的中点,∴OB=OD ,∴OE=OD,∴OC平分∠ACD;(2)在Rt△ABO和Rt△AEO中,,∴Rt△ABO≌Rt△AEO(HL),∴∠AOB=∠AOE,同理求出∠COD=∠COE,∴∠AOC=∠AOE+∠COE=×180°=90°,∴OA⊥OC;(3)∵Rt△ABO≌Rt△AEO,∴AB=AE,同理可得CD=CE,∵AC=AE+CE,∴AB+CD=AC.巩固练习已知:如图,在ΔABC中,AD是△ABC的角平分线,E、F分别是AB、AC上一点,并且有∠EDF+∠EAF=180°.试判断DE和DF的大小关系并说明理由.【答案】证明:过点D 作DM ⊥AB 于M ,DN ⊥AC 于N ,∵AD 是△ABC 的角平分线,∴DM =DN∵∠EDF +∠EAF =180°,即∠2+∠3+∠4+∠EAF =180°又∵∠1+∠2+∠3+∠EAF =180°∴∠1=∠4在Rt △DEM 与Rt △DFN 中14DM DNEMD FND ∠=∠⎧⎪=⎨⎪∠=∠⎩∴Rt △DEM ≌Rt △DFN (ASA )∴DE =DF1.如图,已知∠AOB =30∘,P 是∠AOB 平分线上一点,CP//OB ,交OA 于点C ,PD ⊥OB ,垂足为点D ,且PC =4,则PD 等于_______.【解答】解:作PE ⊥OA 于E ,∵CP//OB,∴∠OPC=∠POD,∵P是∠AOB平分线上一点,∴∠POA=∠POD=15∘,∴∠ACP=∠OPC+∠POA=30∘,∴PE=1PC=2,2∵P是∠AOB平分线上一点,PD⊥OB,PE⊥OA,∴PD=PE=2,2.如图,AD是ΔABC的角平分线,∠C=90∘,CD=3cm,点P在AB上,连接DP,则DP的最小值为________cm.【解答】解:作DP′⊥AB于P′,∵AD是ΔABC的角平分线,∠C=90∘,DP′⊥AB∴DP′=DC=3cm,则DP的最小值为3cm,3.如图,ΔABC中,∠C=90∘,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若CD=√3,则DE的长为()A. 2B. 3C. √3D. 2√3【解答】解:∵AD平分∠CAB,DE⊥AB,∠C=90∘,∴CD=DE=√3,4.如图,ΔABC,用尺规作图作角平分线CD.(保留作图痕迹,不要求写作法)【解答】解:如图所示:DC即为所求.5.如图,已知DE∥BC,BE是∠ABC的平分线,∠C=70∘,∠ABC=50∘.求∠DEB和∠BEC的度数.【解答】解:∵BE是∠ABC的平分线,∠ABC=50∘,∴∠1=∠2=25°∵DE∥BC,∴∠DEB=∠2=25∘,在△BEC中,∠C=70∘,∴∠BEC=180∘−∠C−∠2=180∘−70∘−25∘=85∘.6.如图,OC 是∠AOB 的角平分线,点P 、F 在OC 上,PD ⊥AO 于点D ,PE ⊥BO 于点E ,连接DF 、EF .求证:DF =EF .【解答】证明:∵OC 是∠AOB 的平分线,PD ⊥OA ,PE ⊥BO ,∴PD =PE ,在Rt△OPD 和Rt△OPE 中,{OP =OP PD =PE ,∴Rt△OPD ≌Rt△OPE (HL ),∴OD =OE ,∵OC 是∠AOB 的平分线,∴∠DOF =∠EOF ,在△ODF 和△OEF 中,{OD =OE∠DOF =∠EOF OF =OF,△ODF ≌△OEF (SAS ),∴DF =EF .课后巩固1.请将本次课错题组卷,进行二次练习,培养错题管理习惯;2.学霸笔记复习,培养复习习惯。
八年级数学上册111与三角形有关的线段1112三角形的高中线与角平分线3学案新人教

11.1.2 三角形的高、中线与角平分线(3)一、新课导入 请画出∠AOB 的角平分线。
二、学习目标 1、了解三角形的角平分线的概念;2、会用工具准确画出三角形的角平分线。
三 、研读课本 认真阅读课本的内容,完成以下练习。
(一)划出你认为重点的语句。
(二)完成下面练习,并体验知识点的形成过程。
(1)定义:三角形一个内角的 与它的 相交,这个角 与之间的线段,叫做三角形的角平分线。
(2)几何语言(右图):AD 是△ABC 的角平分线 ∴∠ =∠ 逆向: ∠ =∠ ∴AD 是△ABC 的角平分线(3)画出下列三角形的角平分线思考:三角形的角平分线与一个角的角平分线有何异同?AOB(1) (2) (3)图3AB CD 1 2(三)在研读的过程中,你认为有哪些不懂的问题?四、归纳小结(一)这节课我们学到了什么? (二)你认为应该注意什么问题?五、强化训练【A 】组1、三角形的角平分线是( )A .直线B .射线C .线段D .垂线2、如图。
在 △ABC 中, AD 是角平分线,AE 是中线,AF 是高,则(1)BE = = 21 . A(2)∠BAD = = 21(3)∠AFB = = 90° B E D F C(4)△ABC 的面积 = .3、如右图,在ΔABC 中,AD 平分∠BAC 且与BC相交于点D ,∠B=400,∠BAD=300,则∠C 的度数是 ;【B 】组4.以下说法错误的是( )A .三角形的三条高一定在三角形内部交于一点B .三角形的三条中线一定在三角形内部交于一点C .三角形的三条角平分线一定在三角形内部交于一点D .三角形的三条高可能相交于外部一点5.如图,在△ABC 中,AE 是角平分线,且∠B=52°,∠C=78°,求∠AEB 的度数.【C】组6.直角三角形两锐角的平分线所夹的钝角为_______度.7、如图,在ΔABC中,AD是ΔABC的高,AE是ΔABC的角平分线,已知∠BAC=820,∠C=400,求∠DAE的大小。
250.角平分线和线段垂直平分线(二)
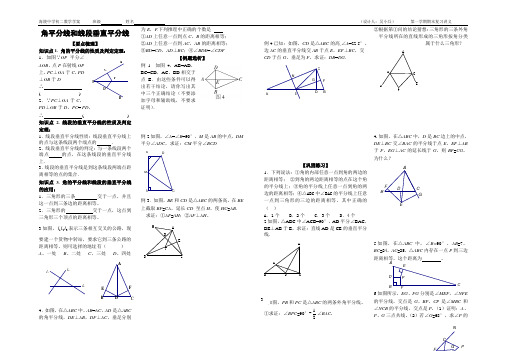
E D C A G NCF B D E A角平分线和线段垂直平分线【要点梳理】知识点1. 角的平分线的性质及判定定理: 1.如图∵OP 平分∠AOB ,点P 在射线OP上,PC ⊥OA 于C ,PD⊥OB 于D ∴ ( )2.∵PC ⊥OA 于C ,PD ⊥OB 于D ,PC = PD ,∴ ( ) 知识点 2. 线段的垂直平分线的性质及判定定理:1.线段垂直平分线性质:线段垂直平分线上的点与这条线段两个端点的 .2.线段垂直平分线的判定:与一条线段两个端点 的点,在这条线段的垂直平分线上. 3.线段的垂直平分线是到这条线段两端点距离相等的点的集合.知识点 3. 角的平分线和线段的垂直平分线的应用:1.三角形的三条 交于一点,并且这一点到三条边的距离相等。
2.三角形的 交于一点,这点到三角形三个顶点的距离相等。
3.如图,321l l l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( ) A 、一处 B 、二处 C 、三处 D 、四处4.如图,在△ABC 中,AB =AC ,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F .下列推理中正确的个数是 . ①AD 上任意一点到点C ,B 的距离相等; ②AD 上任意一点到AC ,AB 的距离相等; ③BD =CD ,AD ⊥BC ;④∠BDE =∠CDF【例题选析】例1 如图4,AB=AD ,BC=CD ,AC 、BD 相交于点E .由这些条件可以得出若干结论,请你写出其中三个正确结论(不要添加字母和辅助线,不要求证明).例2.如图,∠A =∠B =90°,M 是AB 的中点,DM 平分∠ADC ,求证:CM 平分∠BCDMDBCA例3.如图,BE 和CD 是△ABC 的两条高,在BE 上截取BF =CA ,延长CD •至点H ,使HC =AB . 求证:①AF =AH ;②AF ⊥AH 。
八上数学三角形的中线与角平分线学案
A
2 1
1 2
C
从一个角的顶点引出一条射线,把这个角分成两个相等的角,这条射线叫做这 个角的角平分线(bisector of angle). 三角形的角平分线的数学语言: 要点诠释: (1)三角形的角平分线是 ; 部; .
(2)一个三角形有三条角平分线,并且都在三角形的 (3) 三角形三条角平分线交于三角形
A D C
2
吗?说出你是怎样做的.
E
8.如图所示,在△ABC 中,D、E 分别是 BC、AD 的中点,S△ABC=4cm ,求 S△ABE.
B
D
A
9.如图,在 ABC 中,点 D、E、F 分别是 BC、AD、CE 的中点,且 S △ ABC 4cm ,则 S △ BEF
2
的值是多少
A
E F B D C
的连线叫三角形的中线.
; 部; 部一点,这一点叫三角形的 的两个三角形. 的中线,AE 是△ A D 的中线。 .
1 EC,则 AD 是△ 2
B
D
E
C 图1
C 图2
B
例 2.在直角三角形 ABC 中,∠ABC=90 ,AC=3cm,BC=4cm,CD 是 AB 边上的中线,则 AC 边 上的高为 cm,△BCD 的面积= cm 。
1 ∠BAC,则 AD 是△ABC 的角平分线 2
(4)三角形的中线.高.角平分线都是线段 A.1 B.2 C.3 D.4 9.下列把四边形的不稳定性合理地应用到生产实际中的例子有( ) (1)活动挂架 (2)放缩尺 (3)屋顶钢架 (4)能够推拢和拉开的铁拉门 (5)自行车的车架 (6)大桥钢架 A.1 B.2 C.3 D.4 10.根据你画图的实践,用序号字母填写下表(有几种可能情况填写几个字母) : A.在三角形的内部 B.在三角形的边上 C.在三角形的外部 锐角三角形 角平分线 中线 高 11.如图,在△ABC 中,AE 是中线,AD 是角平分线,AF 是高,则根据图形填空: ⑴BE= = 直角三角形 钝角三角形
角平分线(复习)

EDCBAADBC《与角平分线有关的问题》复习学案 学习目标:1、 掌握角平分线的性质与判定定理2、 知道与角平分线有关问题的常见辅助线的作用 专题训练一:1、 如图:AB=AC ,BD 平分∠ ABC ,CD 平分∠ ACB ,EF ∥ BC 交AB 、AC 于E ,F ,且经过点D ,问:线段EF 与线段BE ,CF 有何数量关系?2、 如图,在△ABC 中,BI 、CI 分别平分∠ABC 、∠ACF ,DE 过点I ,且DE ∥ BC .BD=8cm ,CE=5cm ,求DE 的长。
3、已知:如图,)(AC AB ABC ≠∆中,D 、E 在BC 上,且DE=EC ,过D 作DF ∥AB,交AE 于点F ,DF=AC.求证:AE 平分BAC ∠专题训练二:1、如图所示,AB ∥CD ,∠B=90º,E 是BC 的中点,DE 平分∠ADC ,求证:AE 平分∠DAB 。
2、如图在四边形ABCD 中,BC>BA ,AD=DC ,BD 平分∠ABC .求证:︒=∠+∠180C A .3、已知:如图,在 ABC中,∠A=90°,AB=AC,∠1=∠2,求证:BC=AB+AD.专题训练三:B C1、如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,求△EDF的面积。
2、如图,O是三条角平分线的交点,OD⊥BC于D,OD=3,△ABC的周长为15,求S△ABC 。
专题训练四:1、如图,在△ABC中,BE是∠ABC的角平分线,AD⊥BE,垂足为D,求证:∠2=∠1+∠C.2、已知:如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE ,求证:BD=2CE.。
《三角形的高、中线、角平分线》优秀教案

用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商
业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得
侵犯本网站及相关权利人地合法权利 . 除此以外,将本文任何内容或服务用
于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬 . Zzz6ZB2Ltk
Users may use the contents or services of this article for
AB=2 ,BD=,AE=
1
.
2
5.如图 2, AD , BE, CF 是 Δ ABC地三条角平分线,则∠ 1= ,
1
∠ 3=
,
2
∠ ACB=2.
A
F
E
A F 12 E
B
D
C
B
3 D
4
C
图1
图2
6.如图
3,
1
BD=
BC,则
BC边上地中线为
______,△ ABD地面积 =地面积.
2
图 3图 4 7.如图 4,△ ABC中,高 CD、 BE、AF 相交于点 O,则△ BOC?地三条高分别为线段 . 8.如图 5,在△ ABC中, D、 E 分别是 BC、AD地中点, S△ABC =4cm2,则 S△ABE = .
personal study, research or appreciation, and other non-commercial
or non-profit purposes, but at the same time, they shall abide by the
provisions of copyright law and other relevant laws, and shall not
角的平分线的性质教案

《12.3 角的平分线的性质》教案李爽2013-9-24一、内容和内容解析1、内容:角的平分线的性质2、内容解析:角的平分线的性质反映了角的平分线的基本特征,也是证明两条线段相等的常用方法。
角的平分线的性质的研究过程为以后学习线段的垂直平分线的性质提供了思路和方法。
.本节内容是全等三角形知识的运用和延续,用尺规作一个角的平分线,其作法原理是三角形全等的“边边边”判定方法和全等三角形的性质;角的平分线的性质证明,运用了三角形全等的“角角边”判定方法和全等三角形的性质。
角的平分线的性质证明提供了使用角的平分线的一种重要模式------利用角的平分线构造两个全等的直角三角形,进而证明相关元素对应相等。
基于以上分析,确定本节课的教学重点:探索并证明角的平分线的性质。
二、目标和目标解析1、目标(1)会用尺规作一个角的平分线,知道作法的合理性;(2)探索并证明角的平分线的性质;(3)能用角的平分线的性质解决简单问题。
2、目标解析达成目标(1)的标志是:学生明确尺规作图的基本要求,知道用尺规作图作角的平分线的方法与原理,能在教师的引导下用尺规作出一个已知角的平分线。
达成目标(2)的标志是:学生能在教师的引导下通过观察、测量等方法,发现角的平分线的性质,能准确表达性质的内容,能正确地写出已知、求证,能运用三角形全等的“AAS”判定方法和全等三角形的性质证明角的平分线的性质。
达成目标(3)的标志是:学生能利用角的平分线的性质构造全等三角形,证明与线段相等有关的简单问题。
三、教学问题诊断分析本节课的学习中,学生在分清角的平分线的性质的条件和结论,并进行严格的逻辑证明的过程中常常感到困难。
例如,在用符号语言表述性质的条件和结论时,不知“距离”应为“条件”还是“结论”。
其重要原因是角的平分线的性质是以文字命题的形式给出的,其条件和结论具有一定的隐蔽性。
教学时,教师要引导学生分析性质中的条件和结论(必要时可让学生将性质改写成“如果······那么······”的形式),找出结论中的隐含条件(垂直),正确写出已知和求证,并归纳出证明命题的一般步骤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角平分线的判定 1、角平分线的性质定里: 。
2、利用角平分线的性质和全等三角形的相关知识完成下题 已知,如图,四边形ABCD ,E 是AC 上一点,E D ⊥CD 于D ,E B ⊥BC 于B ,CA 平分∠BCD 。
求证:AD=AB (用两种方法证明) 方法1: 方法2:
3、利用角平分线常用的做题思路完成下题:
已知:如图,∠B =∠C=900,DM 平分∠ADC ,AM 平分∠DAB ,求证:MB=MC
M
D C
B
A
新课:
1、完成下面命题的证明:到角的两边距离相等的点在角的平分线上。
已知: 在此画图
求证:
证明:
2、利用角平分线的性质及判定完成下列问题:
问题1:求证:三角形两个内角的平分线的交点到三角形三边的距离相等。
问题2:说明三角形的三个内角的平分线交于一点。
&&了解什么是三角形的内心等&&
D C A
问题3:求证:三角形的两个外角平分线的交点到三角形三边距离相等。
应用:
1、已知C D ⊥AB 于D ,B E ⊥AC 于E ,CD 与BE 相交于点O ,OB=OC ,求证:∠1=∠2.
2、如图,PA=PB ,∠1+∠2=1800,求证:OP 平分∠AOB
3、已知E 是正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE =∠FAE ,
求证:AF=AD+CF
4、如图,已知直线a 、b 、c 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等地,则可选择的地点有几处?
O E 21D C B A O
21P B
A E F D C
A c
b
a。
