材料力学习题答案_刘文鸿_第四版
刘鸿文材料力学

分布力:体积力、表面力; 集中力:火车车轮对钢轨、支座等。
2019/9/20
材料力学 第一章 绪论
§1-3 外力及其分类
外力按随时间变化分:
静载荷:自重,变化相对较慢; 动载荷:交变载荷、冲击;
2019/9/20
材料力学 第一章 绪论
§1-4 内力、截面法和应力的概念
内力:受外力作用引起的相互作用; 材料力学中的内力:物体内部各部分之间因外力而 引起的附加相互作用力,即“附加内力”;
d
m
aa 0.025125106 ab 200
a a’
tgm
aa 0.025100106ra ad 250
d
2019/9/20
材料力学 第一章 绪论
小变形假设
δ远小于构件的最小尺
A
寸,在研究构件的平衡和运动 时按变形前的原始尺寸进行计
算,以保证问题在几何上是线
δ1
2019/9/20
材料力学 第一章 绪论
刚体静力学中关于平衡的理论和方法能否应用于 材料力学?
上述两种情形下对弹性杆的平衡和变形将会产 生什么影响?
2019/9/20
材料力学 第一章 绪论
第一章结束
2019/9/20
2019/9/20
材料力学 第一章 绪论
§1-1 材料力学的任务
强度问题:
美国的Tacoma老桥于 1940年11月7日因风力引 起的振动而产生断裂
2019/9/20
材料力学 第一章 绪论
§1-1 材料力学的任务
强度问题:
垮塌后的彩虹桥
1999年1月4日,我
国重庆市綦江县彩虹桥 发生垮塌,造成:
在满足上述强度、刚度和稳定性要求的同时, 须尽可能合理选用材料和降低材料消耗量,以节约 投资。
刘鸿文材料力学习题册

正确的是(
)
(A) 50 MPa (压应力); (B) 40 MPa (压应力);
m
5 kN
4 kN
13 kN
(C) 90 MPa (压应力); (D) 90 MPa (拉应力)。
m
(2)等截面直杆受轴向拉力 F 作用发生拉伸变形。已知横截面面积为 A,以下给出的横截面上 的正应力和 45 斜截面上的正应力的四种结果,正确的是( )
(4)应力是内力分布集度。( )
(5)材料力学主要研究构件弹性范围内的小变形问题。( )
(6)若物体产生位移,则必定同时产生变形。 ( )
(7)各向同性假设认为,材料沿各个方向具有相同的变形。( )
(8)均匀性假设认为,材料内部各点的力学性质是相同的。
()
(9)根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
(D)若物体产生变形,则必定物体内各点均有位移。
(8)关于确定截面内力的截面法的适用范围,有下列说法正确的是( ) (A)等截面直杆; (B)直杆承受基本变形; (C)不论基本变形还是组合变形,但限于直杆的横截面; (D)不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情
况。
1)同一截面上正应力 与切应力 必相互垂直。
2)同一截面上各点的正应力 必定大小相等,方向相同。
3)同一截面上各点的切应力 必相互平行。
现有四种答案,正确答案是( )
(A)1 对;
(B)1、2 对; (C)1、3 对; (D)2、3 对。
(5)材料力学中的内力是指( ) (A)构件内部的力; (B)构件内部各质点间固有的相互作用力; (C)构件内部一部分与另一部分之间的相互作用力; (D)因外力作用,而引起构件内部一部分对另一部分作用力的改变量
材料力学-刘鸿文-第4版(一)

F1
F2
F3
Fn
内力主矢与主矩
分布内力
F1
FR
F3
M
41
内力分量(Components of the Internal Forces)
FQ
FR
FN MB
Mx M
在确定的坐标系中,轴力、剪力、扭矩、 弯矩及其可能产生的变形效应。
42
内力的正负号规则(Sign Rule of Internal
58
补充: 1.一点的应力状态:过一点有无数的截面,这一点的各个截面
上的应力情况,称为这点的应力状态。
2、单元体:单元体—构件内的点的代表物,是包围被研究点的
无限小的几何体,常用的是正六面体。
单元体的性质—a、平行面上,应力均布;
M P
b、平行面上,应力相等。
3、拉压杆内一点M 的应力单元体:
59
其他塑性材料
对没有明显屈服极限的塑性材料, 可以用产生0.2%塑性变
形时的应力作为屈服指标, 并用 p0.2 来表示.
铸铁和玻璃钢
只有一个强度指标b. 并用割线的斜率作为弹性模量.
卸载定律: 卸载过程中应力和应变按直线变化
弹性阶段: 弹性现象, 弹性极限 e elastic limit
3. 加载-卸载-重新加载实验
冷作硬化现象 Phenomenon of Cold-working :
试件加载超过屈服极限,卸载后重新加载引起比例极限增加和残余变形减少
的现象.
62
2、其他材料的拉伸实验
度
F1
F2
F3
Fn
46
正应力和切应力
垂直于截面的应力称为“正应力”
材料力学第四版版答案7.docx
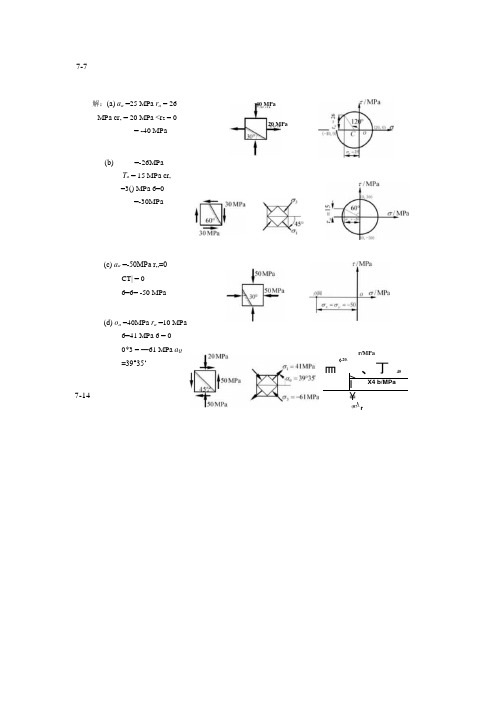
(c) a a =-50MPa r…=0CT| = 0 6=6= -50 MPa(d) o a =40MPa r a =10 MPa6=41 MPa 6 = 0 0*3 = —61 MPa a Q =39°35‘7-7 解:(a) a a =25 MPa r a = 26 MPa cr, = 20 MPa <r 2 = 0= -40 MPa (b) =-26MPa T a = 15 MPa cr, =3() MPa 6=0=-30MPa40 MPa20 MPa7-14(-20.皿、丁40> I X4 b/MPa ¥\ (0?^rr/MPa7-15单元体各面上的应力如图所示。
试用应力圆的儿何关系求主应力及最人切应力。
解:(a)由卩平面内应力值作a, b点,连接"交O•轴得圆心C (5(). 0)应力圆半径心)2+时=44.726 =50+44.7 = 94.7 MPa cr3=50-44.7 = 5.3 MPa (T2 = 50MPa2= 44.7 MPay r/MPa(b)由心平面内应力作g b点,连接血交O•轴丁•(?点,0030.故应力圆半径则: r = >/302 +402 = 506 =30 +50 = 8() MPaa2 =50 MPa a3=-20 MPa= 5() MPa(c)由图7-15 (c)yz平面内应力值作a, b点,圆心为O,半径为50,作应力圆得6 = 5() MPaa2 =-50 MPa6 =-80 MPa50 MPar/MPamax '6 一6 ,二」——=65MPa27-187-19在矩形截面钢拉伸试样的轴向拉力F = 20kN时,测得试样中段B点处与其轴线成30°方向的线应变为a. =3.25x10"。
已知材料的弹性模量£ = 210GPa ,试求泊松比解:F 20X103A " 20x10x10" = 10() MPa CT=a cos2a = —a = 75 MPa4cr|20. = cr cos2a = 25 MPa3.25X10_4 X210X 109 = (75-yx25)x IO6 v = 0.27M c = M n = 690kN- m Fsc 狂=佗 D 右=670 kN7-197-20 D= 120mm,治&hnm 的空心圆轴,两端承受一对扭转力偶矩,如图所示。
材料力学ppt(刘鸿文第四版含课后答案)

应力分布均匀 均匀时 应力分布均匀时
N Al N l U = uV = V = = 2 2E 2EA 2EA
Nl 推广到多杆系统 U = ∑ i=1 2E A i i
1 由能量守恒原理 U =W= P∆l 2 2 n 有 1 Ni li P∆l = ∑ 2 i=1 2E A i i
n 2 i i
关于静不定的基本概念
静定问题
静不定问题 —— 静不定次数 —— 多余约束 ——
求解静不定问题的基本方法
力的平衡关系。 静力平衡方程 -力的平衡关系。 变形与约束的协调关系。 变形协调方程 - 变形与约束的协调关系。 力与变形的关系。 物理关系 - 力与变形的关系。
例 1 (书p.50) 书 已知:1、2杆相同,抗拉 杆相同, 已知: 、 杆相同 刚度为E 刚度为 1A1 , 3杆的抗拉 杆的抗拉 长为l 角 刚度为E 刚度为 3A3 , 长为 , α角。 各杆的内力。 求:各杆的内力。 解: 静不定的次数? 静不定的次数?
(2) 变形协调方程 (3) 物理关系
∆l1 = ∆l2 = ∆l3 cosα (3) N1l N3l ∆l1 = ∆l3 = E1A cosα E3 A 1 3
(4)
物理关系代入变形协调方程
N1l N3l = cosα E A cosα E3 A 1 1 3
与平衡方程联立,可解出 与平衡方程联立,可解出:
D
C
B
2 l N2
3
1
αα
A P y N3
αα
∑X = 0 N1 sin α − N2 sinα = 0 N1 = N2 ∑Y = 0 N3 +2N1 cosα − P = 0
N1
x
P
材料力学-刘鸿文-第四版-第五章

σmax
M
y max max Iz
σ
1.弯矩最大的截面上
2.离中性轴最远处
3.变截面梁要综合考虑 M与 Iz
4.脆性材料抗拉和抗压性能不同,二方面都要考虑
s t,max s t
s c,max s c
2019年9月22日2时45分
材料力学 第五章 弯曲应力
根据强度条件可进行:
s t,max
2.5103 88103 7.64106
28.8106 Pa 28.8MPa s t
2019年9月22日2时45分
材料力学 第五章 弯曲应力
例5-3-5:图a所示为横截面如图b所示的槽形截面铸铁梁,该 截面对于中性轴z 的惯性矩Iz=5493×104 mm4。已知图a中, b=2 m。铸铁的许用拉应力[st]=30 MPa,许用压应力[s c]=90 MPa 。试求梁的许可荷载[F]。
4
Iz
显然,B截面上的最大拉应力控制了梁的强度。
2019年9月22日2时45分
材料力学 第五章 弯曲应力 第四章 弯曲应力
于是由B截面上最大拉应力不得超过铸铁的许用拉应
力[st]的条件来求该梁的许可荷载[F]:
F 2 m 86103 m
2
5493108 m4
l /2
F
AaCB Nhomakorabeal
z
NO.16
2019年9月22日2时45分
材料力学 第五章 弯曲应力
解: 1)s C EC 210 103 400 10 6 84MPa
M
C
s C
FB (l a) 0.25F
刘鸿文《材料力学》复习笔记和课后习题及考研真题详解(10-12章)【圣才出品】

第 10 章 动载荷
10.1 复习笔记
本章节的主要研究内容是构件作匀加速运动时,或受到作匀加速运动的物体作用时,以 及构件受到冲击时的应力和变形计算。
静载荷:载荷由零平缓地增加到最终值,且之后载荷值再也不变化。 动载荷:随时间明显变化的载荷,即具有较大加载速率的载荷。 一、动静法的应用 动静法是将动力学问题转化为静力学问题的方法,来自于达朗贝尔原理:假想地在做加 速运动的质点系上的每一个质点上施加惯性力,使原力系与惯性力系组成平衡力系。质点上 的惯性力等于该质点质量 m 与其加速度 a 的乘积,惯性力方向与加速度反向。 对于匀加速平动杆件或者匀角加速转动杆件,使用动静法作动应力分析的一般步骤: (1)求出动荷系数 Kd; (2)按静载荷求解应力 σst、变形 Δst 等; (3)将所得结果乘以动荷系数 Kd 可得动载荷作用下的动应力和变形分别为 σd=Kdσst Δd=KdΔst
= st
1−
Fd P
2.交变应力 在静平衡位置上下作受迫振动的杆件,其上各点应力作周期性交替变化。交变应力下的 强度条件不可用静载的方法建立。
3.动应力、动荷载与放大因子的关系(
曲线)
①ω/ω0→1:即干扰力频率接近系统固有频率,此时 β 最大,引起共振。通过改变 ω/ω0 或增大阻尼 δ 可降低 β 避免共振。
dmax
= st
1+
Fd st
= st
1+
Fd P
=
Kd st
式中,振动的动荷载因数
Kd
=1+
Fd st
=1+
Fd P
4 / 128
Fd 为干扰力 Fd 按静载荷方式作用在弹性系统上的静位移。
刘鸿文材料力学习题册

材料力学A习题册学院专业学号教师学生姓名练习1 绪论及基本概念1-1 是非题(1)材料力学是研究构件承载能力的一门学科。
()(2)可变形固体的变形必须满足几何相容条件,即变形后的固体既不可以引起“空隙”,也不产生“挤入”现象。
()(3)构件在载荷作用下发生的变形,包括构件尺寸的改变和形状的改变。
()(4)应力是内力分布集度。
()(5)材料力学主要研究构件弹性范围内的小变形问题。
()(6)若物体产生位移,则必定同时产生变形。
()(7)各向同性假设认为,材料沿各个方向具有相同的变形。
()(8)均匀性假设认为,材料内部各点的力学性质是相同的。
()(9)根据连续性假设,杆件截面上的内力是连续分布的,分布内力系的合力必定是一个力。
()(10)因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
()1-2 填空题(1)根据材料的主要性质对材料作如下三个基本假设:、、。
(2)工程中的,是指构件抵抗破坏的能力;,是指构件抵抗变形的能力。
(3)保证构件正常或安全工作的基本要求包括,,和三个方面。
(4)图示构件中,杆1发生变形,杆2发生变形,杆3发生变形。
(5)认为固体在其整个几何空间内无间隙地充满了物质,这样的假设称为。
根据这一假设构件的应力,应变和位移就可以用坐标的函数来表示。
(6)图示结构中,杆1发生变形,构件2发生变形,杆件3发生变形。
(7)解除外力后,能完全消失的变形称为,不能消失而残余的的那部分变形称为。
(8)根据条件,可以认为构件的变形远其原始尺寸。
1-3 选择题(1)材料力学中对构件的受力和变形等问题可用连续函数来描述;通过试件所测得的材料的力学性能,可用于构件内部的任何部位。
这是因为对可变形固体采用了()假设。
(A)连续均匀性;(B)各向同性;(C)小变形;(D)平面。
(2)研究构件或其一部分的平衡问题时,采用构件变形前的原始尺寸进行计算,这是因为采用了()假设。
(A)平面;(B)连续均匀性;(C)小变形;(D)各向同性。
