材料力学复习题(附答案)
材料力学题库题库练习题复习题带答案
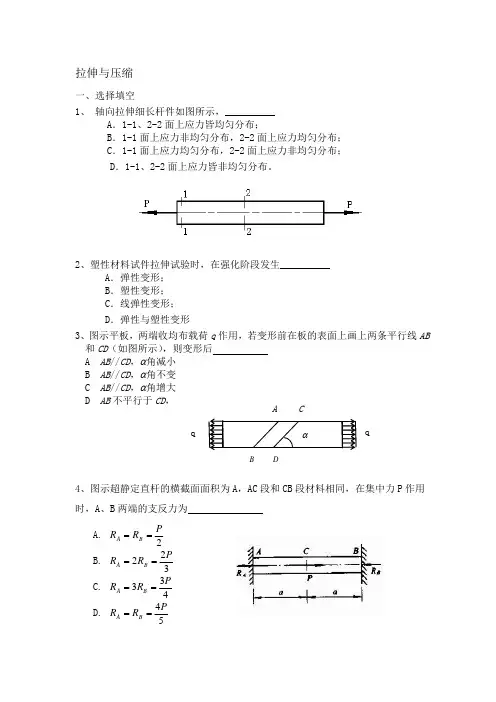
拉伸与压缩一、选择填空1、 轴向拉伸细长杆件如图所示，__________A ．1-1、2-2面上应力皆均匀分布；B ．1-1面上应力非均匀分布，2-2面上应力均匀分布；C ．1-1面上应力均匀分布，2-2面上应力非均匀分布；D ．1-1、2-2面上应力皆非均匀分布。
2、塑性材料试件拉伸试验时，在强化阶段发生__________A ．弹性变形；B ．塑性变形；C ．线弹性变形；D ．弹性与塑性变形3、图示平板，两端收均布载荷q 作用，若变形前在板的表面上画上两条平行线AB 和CD （如图所示），则变形后 A AB //CD ，α角减小 B AB //CD ，α角不变 C AB //CD ，α角增大 D AB 不平行于CD ，4、图示超静定直杆的横截面面积为A ，AC 段和CB 段材料相同，在集中力P 作用时，A 、B 两端的支反力为B DCA qqαA. 2P R R B A == B. 322PR R B A ==C. 433PR R B A ==D. 54PR R B A ==5、设杆件横截面面积为A ，轴力为N;该横截面上某点B 处的微小面积为∆A ，∆A 上的微小内力为∆N ，则下列结论中正确的是 (1).=AN为该横截面上的平均正应力． (2).B σ=AN∆∆为点B 处微小面积上的平均正应力．(3).ANA B ∆∆=→∆0limσ为点B 处的正应力．(4).点B 可选在横截面上的任一点处，故横截面上某点处的正应力可表示为A NA ∆∆=→∆0limσ A 、(1)，(2) 。
B 、（3)，(4)。
C 、(1)，(2)，(3)。
D 、全对。
6、图示桁架，1、2两杆为铝杆，3杆为钢轩今欲使3杆的内力增大，正确的做法是 。
7、阶梯形杆（如图所示），横截面面积分别为A A A A ==212，，长度分别为l 和2/l ，材料的弹性模量均为E 。
杆件受轴向拉力P 作用时，最大的线应变是 。
材料力学复习题(答案)
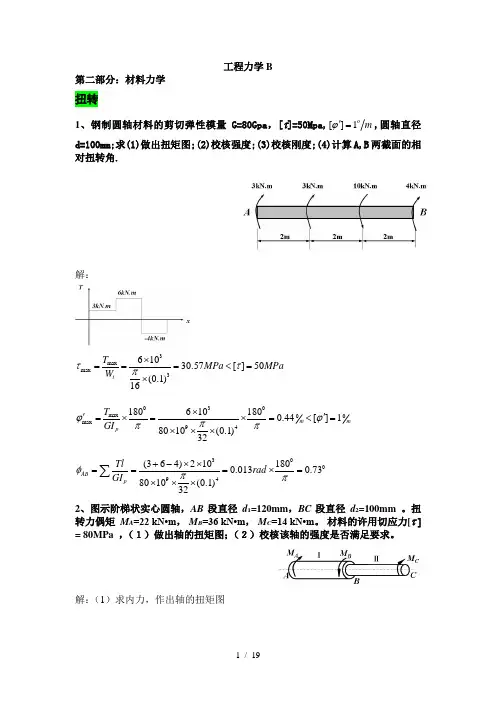
工程力学B 第二部分：材料力学扭转1、钢制圆轴材料的剪切弹性模量G=80Gpa，[τ]=50Mpa,mo1][='ϕ,圆轴直径d=100mm;求(1)做出扭矩图;(2)校核强度;(3)校核刚度;(4)计算A,B两截面的相对扭转角.解：3maxmax361030.57[]50(0.1)16tTMPa MPaWττπ⨯===<=⨯030max00 max941806101800.44[]18010(0.1)32m mpTGIϕϕπππ⨯''=⨯=⨯=<=⨯⨯⨯3094(364)2101800.0130.738010(0.1)32ABpTlradGIφππ+-⨯⨯===⨯=⨯⨯⨯∑2、图示阶梯状实心圆轴，AB段直径d1=120mm，BC段直径d2=100mm 。
扭转力偶矩M A=22 kN•m，M B=36 kN•m，M C=14 kN•m。
材料的许用切应力[τ ] = 80MPa ，（１）做出轴的扭矩图；（２）校核该轴的强度是否满足要求。
解：（1）求内力，作出轴的扭矩图（2）计算轴横截面上的最大切应力并校核强度AB段：11,max1tTWτ=()333221064.8MPaπ1201016-⨯==⨯⨯[]80MPaτ<=BC段：()322,max332141071.3MPaπ1001016tTWτ-⨯===⨯⨯[]80MPaτ<=综上，该轴满足强度条件。
3、传动轴的转速为n=500r/min，主动轮A输入功率P1=400kW，从动轮B，C 分别输出功率P2=160kW，P3=240kW。
已知材料的许用切应力[τ]=70MP a，单位长度的许可扭转角[ϕ， ]=1º/m，剪切弹性模量G=80GP a。
(1)画出扭矩图。
(2)试确定AB段的直径d1和BC段的直径d2；(3)主动轮和从动轮应如何安排才比较合理?为什么？解：（1）mNnPM.7639500400954995491e1=⨯==，mNnPM.3056500160954995492e2=⨯==mNnPM.4583500240954995493e3=⨯==，扭矩图如下（2）AB段，按强度条件：][163maxτπτ≤==dTWTt，3][16τπTd≥，mmd2.821070763916361=⨯⨯⨯≥π按刚度条件：m p d GT GI T 004max1][18032180='≤⨯=⨯='ϕπππϕ，4218032π⨯⨯≥G T d mm d 4.86108018076393242901=⨯⨯⨯⨯≥π综合强度和刚度条件得到：mm d 871= BC 段，按强度条件：mm d 3.691070458316362=⨯⨯⨯≥π； 按刚度条件：mm d 0.76108018045833242902=⨯⨯⨯⨯≥π综合强度和刚度条件得到：mm d 762=（3）将主动轮放置中央B 点，受力合力，此时m N T .4583max =弯曲内力4、(1)做出梁的剪力图和弯矩图；(2)求最大剪力maxsF 和弯矩maxM数值。
材料力学复习题答案
材料力学复习题答案1. 材料力学中，材料的弹性模量（E）表示材料抵抗形变的能力，其单位是帕斯卡（Pa）。
若某材料的弹性模量为200 GPa，试计算该材料在受到10 MPa应力作用下产生的应变。
答案：根据胡克定律，应变（ε）等于应力（σ）除以弹性模量（E），即ε = σ/E。
将给定的数值代入公式，得到ε = 10 MPa / 200 GPa = 0.00005 或5×10^-5。
2. 简述材料在拉伸过程中的四个阶段，并说明各阶段的特点。
答案：材料在拉伸过程中的四个阶段包括弹性阶段、屈服阶段、强化阶段和断裂阶段。
弹性阶段中，材料在外力作用下发生形变，当外力移除后，材料能恢复原状。
屈服阶段开始时，材料的形变不再与应力成正比，即使应力不再增加，形变也会继续增加。
强化阶段中，材料在屈服后继续承受应力，需要更大的应力才能使形变继续增加。
最后，在断裂阶段，材料因无法承受进一步的应力而发生断裂。
3. 计算圆轴在扭转时的剪切应力。
已知圆轴的直径为50 mm，材料的剪切模量为80 GPa，扭矩为500 N·m。
答案：圆轴在扭转时的剪切应力（τ）可以通过公式τ = T·r/J计算，其中T为扭矩，r为圆轴的半径，J为极惯性矩。
对于直径为50 mm的圆轴，半径r = 25 mm = 0.025 m。
极惯性矩J = π·r^4/2 = π·(0.025)^4/2 ≈ 9.82×10^-6 m^4。
代入公式得到τ = 500 N·m × 0.025 m / 9.82×10^-6 m^4 ≈ 127.6 MPa。
4. 描述梁在弯曲时的正应力和剪切应力的分布规律。
答案：梁在弯曲时，正应力沿着梁的横截面高度线性分布，最大正应力出现在横截面的最外层纤维上，且与中性轴的距离成正比。
剪切应力在梁的横截面上分布不均匀，最大剪切应力出现在中性轴处，向两侧逐渐减小至零。
(完整版)材料力学试题及答案
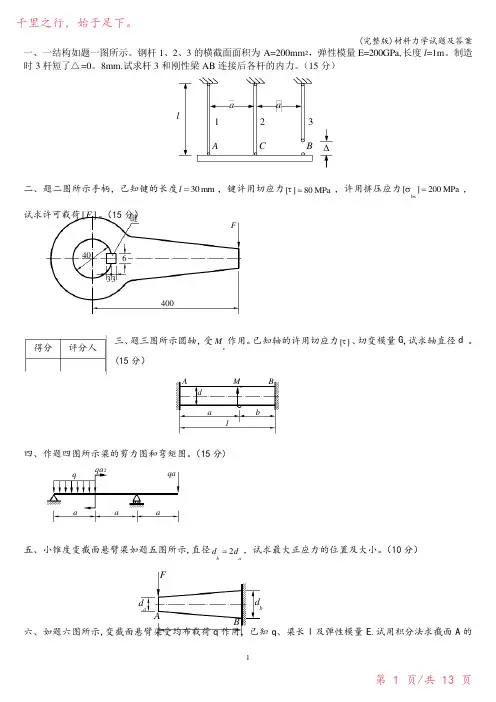
一、一结构如题一图所示。
钢杆1、2、3的横截面面积为A=200mm 2，弹性模量E=200GPa,长度l =1m 。
制造时3杆短了△=0。
8mm.试求杆3和刚性梁AB 连接后各杆的内力。
（15分）aalABC123∆二、题二图所示手柄，已知键的长度30 mm l =，键许用切应力[]80 MPa τ=，许用挤压应力bs[]200 MPa σ=，试求许可载荷][F 。
（15分）三、题三图所示圆轴，受eM 作用。
已知轴的许用切应力[]τ、切变模量G ,试求轴直径d 。
(15分）四、作题四图所示梁的剪力图和弯矩图。
（15分)五、小锥度变截面悬臂梁如题五图所示,直径2bad d =，试求最大正应力的位置及大小。
（10分）六、如题六图所示,变截面悬臂梁受均布载荷q 作用，已知q 、梁长l 及弹性模量E .试用积分法求截面A 的得分评分人F键40633400Aal bM eBd a a aqqaqa 2dbBda AF挠度w A 和截面C 的转角θC .（15分)七、如图所示工字形截面梁AB ,截面的惯性矩672.5610zI -=⨯m 4，求固定端截面翼缘和腹板交界处点a 的主应力和主方向。
（15分）一、（15分)（1）静力分析（如图（a）)1N F2N F3N F图(a)∑=+=231,0N N N yF F F F（a)∑==31,0N N CF F M(b)（2）几何分析（如图（b)）1l∆2l∆3l∆∆图（b）wql /3x lhb 0b (x )b (x )BAC 50kN AB0.75m303030140150zya∆=∆+∆+∆3212l l l(3）物理条件EA l F l N 11=∆，EA l F l N 22=∆，EAl F l N 33=∆ （4）补充方程∆=++EAlF EA l F EA l F N N N 3212 （c） （5）联立（a）、（b）、(c)式解得:kN FkN FF N N N 67.10,33.5231===二、(15分）以手柄和半个键为隔离体，S0, 204000OM F F ∑=⨯-⨯=取半个键为隔离体，bsS20F F F ==由剪切：S []s FA ττ=≤，720 N F = 由挤压:bs bs bs bs[][], 900N FF Aσσ=≤≤取[]720N F =.三、（15分）eABM M M +=0ABϕ=， A B M a M b ⋅=⋅得 e B a M M a b =+, e A b MM a b=+当a b >时 e316π ()[]M ad a b τ≥+；当b a >时 e316π ()[]M bd a b τ≥+。
材料力学试题及答案
材料力学试题及答案一、选择题（每题2分，共20分）1. 材料力学中，下列哪一项不是基本力学性质？A. 弹性B. 塑性C. 硬度D. 韧性2. 材料在拉伸过程中，当应力达到屈服点后，材料将：A. 断裂B. 产生永久变形C. 恢复原状D. 保持不变3. 材料的弹性模量是指：A. 材料的密度B. 材料的硬度C. 材料的抗拉强度D. 材料在弹性范围内应力与应变的比值4. 根据材料力学的胡克定律，下列说法正确的是：A. 应力与应变成正比B. 应力与应变成反比C. 应力与应变无关D. 应力与应变成线性关系5. 材料的疲劳寿命是指：A. 材料的总寿命B. 材料在循环加载下达到破坏的周期数C. 材料的断裂寿命D. 材料的磨损寿命6. 材料的屈服强度是指：A. 材料在弹性范围内的最大应力B. 材料在塑性变形开始时的应力C. 材料的抗拉强度D. 材料的极限强度7. 材料的断裂韧性是指：A. 材料的硬度B. 材料的抗拉强度C. 材料抵抗裂纹扩展的能力D. 材料的屈服强度8. 材料力学中的泊松比是指：A. 材料的弹性模量B. 材料的屈服强度C. 材料在拉伸时横向应变与纵向应变的比值D. 材料的断裂韧性9. 在材料力学中，下列哪一项是衡量材料脆性程度的指标？A. 弹性模量B. 屈服强度C. 断裂韧性D. 泊松比10. 材料在受力过程中，当应力超过其极限强度时，将：A. 发生弹性变形B. 发生塑性变形C. 发生断裂D. 恢复原状答案1. C2. B3. D4. A5. B6. B7. C8. C9. C10. C试题二、简答题（每题10分，共30分）1. 简述材料力学中材料的三种基本力学性质。
2. 解释什么是材料的疲劳现象，并简述其对工程结构的影响。
3. 描述材料在拉伸过程中的四个主要阶段。
答案1. 材料的三种基本力学性质包括弹性、塑性和韧性。
弹性指的是材料在受到外力作用时发生变形，当外力移除后能够恢复原状的性质。
塑性是指材料在达到一定应力水平后，即使外力移除也无法完全恢复原状的性质。
材料力学考试题(卷)集(含答案解析)
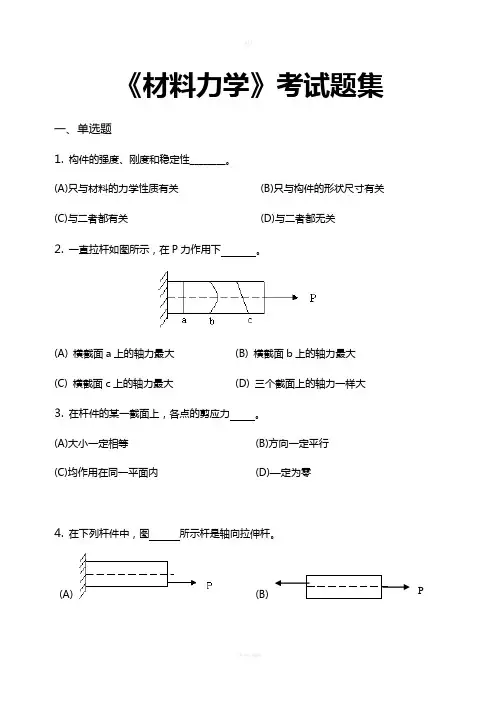
《材料力学》考试题集一、单选题1.构件的强度、刚度和稳定性________。
(A)只与材料的力学性质有关(B)只与构件的形状尺寸有关(C)与二者都有关(D)与二者都无关2.一直拉杆如图所示，在P力作用下。
(A) 横截面a上的轴力最大(B) 横截面b上的轴力最大(C) 横截面c上的轴力最大(D) 三个截面上的轴力一样大3.在杆件的某一截面上，各点的剪应力。
(A)大小一定相等(B)方向一定平行(C)均作用在同一平面内(D)—定为零4.在下列杆件中，图所示杆是轴向拉伸杆。
(A) (B) P(C) (D)5.图示拉杆承受轴向拉力P的作用，斜截面m-m的面积为A，则σ=P/A 为。
(A)横截面上的正应力(B)斜截面上的剪应力(C)斜截面上的正应力(D)斜截面上的应力6.解除外力后，消失的变形和遗留的变形。
(A)分别称为弹性变形、塑性变形(B)通称为塑性变形(C)分别称为塑性变形、弹性变形(D)通称为弹性变形7.一圆截面轴向拉、压杆若其直径增加—倍，则抗拉。
(A)强度和刚度分别是原来的2倍、4倍(B)强度和刚度分别是原来的4倍、2倍(C)强度和刚度均是原来的2倍(D)强度和刚度均是原来的4倍8.图中接头处的挤压面积等于。
P(A)ab (B)cb (C)lb (D)lc9.微单元体的受力状态如下图所示，已知上下两面的剪应力为τ则左右侧面上的剪应力为。
(A)τ/2 (B)τ(C)2τ(D)010.下图是矩形截面，则m—m线以上部分和以下部分对形心轴的两个静矩的。
(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(C)绝对值不等，正负号相同(D)绝对值不等，正负号不同11.平面弯曲变形的特征是。
(A)弯曲时横截面仍保持为平面(B)弯曲载荷均作用在同—平面内；(C)弯曲变形后的轴线是一条平面曲线(D)弯曲变形后的轴线与载荷作用面同在—个平面内12.图示悬臂梁的AC段上，各个截面上的。
(A)剪力相同，弯矩不同(B)剪力不同，弯矩相同(C)剪力和弯矩均相同(D)剪力和弯矩均不同13.当横向力作用于杆件的纵向对称面内时，关于杆件横截面上的内力与应力有以下四个结论。
《材料力学》习题册附答案
F12312练习 1 绪论及基本概念1-1 是非题（1） 材料力学是研究构件承载能力的一门学科。
（ 是 ）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。
（是）（3） 构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。
（ 是 ） （4） 应力是内力分布集度。
（是 ）（5） 材料力学主要研究构件弹性范围内的小变形问题。
（是 ） （6） 若物体产生位移，则必定同时产生变形。
（非 ） （7） 各向同性假设认为，材料沿各个方向具有相同的变形。
（F ） （8） 均匀性假设认为，材料内部各点的力学性质是相同的。
（是）（9） 根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。
（非） （10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。
（非 ）1-2 填空题（1） 根据材料的主要性质对材料作如下三个基本假设：连续性假设、均匀性假设 、各向同性假设 。
（2） 工程中的强度 ，是指构件抵抗破坏的能力； 刚度 ，是指构件抵抗变形的能力。
（3） 保证构件正常或安全工作的基本要求包括 强度 ， 刚度 ，和 稳定性三个方面。
3（4） 图示构件中，杆 1 发生 拉伸 变形，杆 2 发生 压缩 变形，杆 3 发生 弯曲 变形。
（5） 认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为 连续性假设。
根据这一假设构件的应力，应变和位移就可以用坐标的 连续 函数来表示。
（6） 图示结构中，杆 1 发生 弯曲变形，构件 2发生 剪切 变形，杆件 3 发生 弯曲与轴向压缩组合。
变形。
（7） 解除外力后，能完全消失的变形称为 弹性变形，不能消失而残余的的那部分变形称为 塑性变形 。
（8） 根据 小变形 条件，可以认为构件的变形远 小于 其原始尺寸。
1-3选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。
材料力学试题及答案7套
材料力学试卷1一、结构构件应该具有足够的 、 和 。
（本题3分） 二、低碳钢拉伸破坏经历了四个典型阶段： 阶段、 阶段、 阶段和 阶段。
衡量材料强度的指标是 、 。
（本题6分） 三、在其他条件不变的前提下，压杆的柔度越大，则临界应力越 、临界力越 ；材料的临界柔度只与 有关。
（本题3分） 四、两圆截面杆直径关系为：123D D =，则12Z Z I I =；12Z Z W W =；12P P I I =；12P P W W =； （本题8分）五、已知构件上危险点的应力状态，计算第一强度理论相当应力；第二强度理论相当应力；第三强度理论相当应力；第四强度理论相当应力。
泊松比3.0=μ。
（本题15分）六、等截面直杆受力如图，已知杆的横截面积为A=400mm 2， P =20kN 。
试作直杆的轴力图；计算杆内的最大正应力；材料的弹性模量E =200Gpa ，计算杆的轴向总变形。
（本题15分）七、矩形截面梁，截面高宽比h=2b ，l =4米，均布载荷q =30kN /m 许用应力[]MPa 100=σ， 1、画梁的剪力图、弯矩图 2、设计梁的截面 (本题20分)。
八、一圆木柱高l=6米，直径D=200mm ，两端铰支，承受轴向载荷F=50kN，校核柱子的稳定性。
已知木材的许用应力[]MPa10=σ，折减系数与柔度的关系为：23000λϕ=。
(本题15分)九、用能量法计算结构B点的转角和竖向位移，EI已知。
（本题15分）材料力学试卷2一、（5分）图（a ）与图（b ）所示两个矩形微体，虚线表示其变形后的情况，确定该二微体在A 处切应变b aγγ的大小。
二、（10分）计算图形的惯性矩yz I I 。
图中尺寸单位：毫米。
三、（15分）已知构件上危险点的应力状态，计算第三强度理论相当应力；第四强度理论相当应力。
四、（10分）画图示杆的轴力图；计算横截面上最大正应力；计算杆最大轴向应变ε。
已知杆的横截面积A =400 mm 2，E =200GPa 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、填空题1．标距为100mm的标准试件，直径为10mm，拉断后测得伸长后的标距为123mm，缩颈处的最小直径为6.4mm，则该材料的伸长率δ=23%，断面收缩率ψ=59.04%。
2、构件在工作时所允许产生的最大应力叫许用应力σ，极限应力与许用应力的比叫安全系数n。
3、一般来说，脆性材料通常情况下以断裂的形式破坏，宜采用第一二强度理论。
塑性材料在通常情况下以流动的形式破坏，宜采用第三四强度理论。
4、图示销钉的切应力τ=（Pπdh ），挤压应力σbs=（4Pπ(D2-d2)）（4题图）（5题图）5、某点的应力状态如图，则主应力为σ1=30Mpa，σ2=0，σ3=-30Mpa。
6、杆件变形的基本形式有拉伸或压缩、剪切、扭转和弯曲四种。
7、低碳钢在拉伸过程中的变形可分为弹性阶段、屈服阶段、强化阶段和局部变形阶段四个阶段。
8、当切应力不超过材料的剪切比例极限时，切应变γ和切应力τ成正比。
9、工程实际中常见的交变应力的两种类型为对称循环，脉动循环。
10、变形固体的基本假设是：连续性假设；均匀性假设；各向同性假设。
11、低碳钢拉伸时大致分为以下几个阶段：弹性；屈服；强化；缩颈。
12、通常计算组合变形构件应力和变形的过程是：先分别计算每种基本变形各自引起的应力和变形，然后再叠加。
这样做的前提条件是构件必须为线弹性、小变形杆件。
13、剪切胡克定律的表达形式为τ=Gγ。
14、通常以伸长率 <5%作为定义脆性材料的界限。
15、提高梁弯曲刚度的措施主要有提高抗弯刚度EI、减少梁的跨度、改善梁的载荷作用方式。
16、材料的破坏按其物理本质可分为屈服和断裂两类。
二、选择题1、一水平折杆受力如图所示，则AB杆的变形为（D）。
（A）偏心拉伸；（B）纵横弯曲；（C）弯扭组合；（D）拉弯组合。
2、铸铁试件试件受外力矩Me作用，下图所示破坏情况有三种，正确的破坏形式是（A）3、任意图形的面积为A，Z0轴通过形心O，Z1轴与Z0轴平行，并相距a，已知图形对Z1轴的惯性矩I1，则对Z0轴的惯性矩I Z0为：（B）（A ）00Z I =；（B ）20Z Z I I Aa =-；（C ）20Z Z I I Aa =+；（D ）0Z Z I I Aa =+。
4、长方形截面细长压杆，b/h ＝1/2；如果将长方形截面改成边长为h 的正方形，后仍为细长杆，临界力Pcr 是原来的（C ）倍。
（A ）2倍；（B ）4倍；（C ）8倍；（D ）16倍。
5、图示应力状态，用第三强度理论校核时，其相当应力为（D ）。
（A ）1/2τ；（B ）τ；（C ）1/23τ；（D ）2τ。
6、已知材料的比例极限σp=200MPa ，弹性模量E ＝200GPa ，屈服极限σs=235MPa ，强度极限σb=376MPa 。
则下列结论中正确的是（C ）。
（A ）若安全系数n ＝2，则[σ]＝188MPa ； （B ）若ε＝1x10-10，则σ=E ε=220MPa ； （C ）若安全系数n ＝1.1，则[σ]=213.6MPa ；（D ）若加载到使应力超过200MPa ，则若将荷载卸除后，试件的变形必不能完全消失。
7、不同材料的甲、乙两杆，几何尺寸相同，则在受到相同的轴向拉力时，两杆的应力和变形的关系为（C ）。
（A ）应力和变形都相同；（B ）应力不同，变形相同； （C ）应力相同，变形不同；（D ）应力和变形都不同。
8、电梯由四根钢丝绳来吊起，每根钢丝绳的许用应力为100MPa ，横截面为240mm ，电梯自重为0.5吨，则能吊起的最大重量为 （B ）（A ）2吨；（B ）1.1吨；（C ）1吨；（D ）11吨。
9、当梁发生平面弯曲时，其横截面绕（C ）旋转。
（A ）梁的轴线；（B ）截面对称轴；（C ）中性轴；（D ）截面形心 10、直径为d 的实心圆截面，下面公式不正确的是(B) （A ）0xy S S ==；（B ）4/32x y I I d π==；（C ）4/32p I d π=；（D ）4/16p W d π=11、电机轴的直径为20mm ，电机功率为5KW ，转速为1000rpm 。
当电机满负荷工作时，轴上的扭矩是（C ）。
（A ）475.5 N.m ；（B ）4.755 N.m ；（C ）47.75 N.m ；（D ）477 N.m 。
12、下列说法正确的是 （A ）。
（A ）在材料力学中我们把物体抽象化为变形体； （B ）在材料力学中我们把物体抽象化为刚体； （C ）稳定性是指结构或构件保持原有平衡状态；（D ）材料力学是在塑性范围内，大变形情况下研究其承载能力。
13、剪切强度的强度条件为 （B ）。
（A ）/[]N A σσ=≤；（B ）max /[]X P M W ττ=≤；（C ）][/C C C A P σσ≤=；D.][/ττ≤=A Q 。
14、一钢质细长压杆，为提高其稳定性，可供选择的有效措施有 （D ）。
（A ）采用高强度的优质钢； （B ）减小杆件的横截面面积； （C ）使截面两主惯轴方向的柔度相同； （D ）改善约束条件、减小长度系数。
15、用同一材料制成的实心圆轴和空心圆轴，若长度和横截面面积均相同，则抗扭刚度较大的是哪个？（B ）。
（A ）实心圆轴；（B ）空心圆轴；（C ）两者一样；（D ）无法判断。
16、一水平折杆受力如图所示，则AB 杆的变形为（C ）。
（A ）偏心拉伸；（B ）纵横弯曲；（C ）弯扭组合；（D ）拉弯组合。
ABCP17．图示扭转轴1－1截面上的扭矩T 1为（A ）。
112kN.m 2kN.m6kN.m2kN.m（A ）T 1＝－2m kN ⋅（B ）T 1＝5m kN ⋅ （C ）T 1＝1m kN ⋅（D ）T 1＝－4m kN ⋅ 18、下面属于第三强度理论的强度条件是（C ） （A ）][1σσ≤；（B ）][)(321σσσμσ≤+-； （C ）][31σσσ≤-；（D ）()()()[][]σσσσσσσ≤-+-+-21323222121。
19、对图示梁，给有四个答案，正确答案是（C ）。
（A ）静定梁；（B ）一次静不定梁； （C ）二次静不定梁；（D ）三次静不定梁。
20、在工程上，通常将延伸率大于（B ）%的材料称为塑性材料。
（A ）2；（B ）5；（C ）10；（D ）15。
21、图中应力圆a 、b 、c 表示的应力状态分别为（C ）A 二向应力状态、纯剪切应力状态、三向应力状态；B 单向拉应力状态、单向压应力状态、三向应力状态；C 单向压应力状态、纯剪切应力状态、单向拉应力状态；D 单向拉应力状态、单向压应力状态、纯剪切应力状态。
22、下面有关强度理论知识的几个论述，正确的是（D ）。
A 需模拟实际应力状态逐一进行试验，确定极限应力；B 无需进行试验，只需关于材料破坏 原因的假说；C 需要进行某些简单试验，无需关于材料破坏原因的假说；D 假设材料破坏的共同原因。
同时，需要简单试验结果。
23、关于斜弯曲变形的下述说法，正确的是（C ）。
A 是在两个相互垂直平面内平面弯曲的组合变形； B 中性轴过横截面的形心； C 挠曲线在载荷作用面内； D 挠曲线不在载荷作用面内。
24、对莫尔积分⎰=∆l dx EIx M x M )()(的下述讨论，正确的是（C ）。
A 只适用于弯曲变形； B 等式两端具有不相同的量纲； C 对于基本变形、组合变形均适用； D 只适用于直杆。
25、要使试件在交变应力作用下经历无数次循环而不破坏，必须使试件最大工作应力小于（B ）。
A 材料许用应力；B 材料屈服极限；C 材料持久极限；D 构件持久极限。
三、作图题1、一简支梁AB 在C 、D 处受到集中力P 的作用，试画出此梁的剪力图和弯矩图。
2、绘制该梁的剪力、弯矩图m8m2m2四、计算题托架AC 为圆钢杆，直径为d ，许用应力[σ]钢＝160MPa ；BC 为方木，边长为b ，许用应力[σ]木＝4MPa ，F ＝60kN ，试求d 和b 。
解：kN R BC 17.108133013260===kN R AC 90= MPa bA R BC 4][100017.1082=≤⨯=木木木＝σσmm b 4.164≥取b=165mm MPa d A R A 160][41000902C =≤⨯=钢钢钢＝σπσ mm d 8.26≥取d=27mm 五、计算题已知一点为平面应力状态如图所示：（1）求该平面内两个主应力的大小及作用方位，并画在单元体图上。
（2）按照第三强度理论，给出该单元体的当量应力。
解：按应力的正负号原则 MPa x80=σMPa y 30-=∆τMPa MPa 1090{)30()280(280}22max min -=-+±=σσ 4380)30(2tan 0=-⨯-=α，5.180=αMPa MPa 10,0,90321-===σσσ MPa aq 100213=-=σσσ六、计算题已知应力状态如图。
试求主应力及其方向角，并确定最大剪应力值。
解：Mpa Mpa xy y x20;50;100=-==τσσMpa Mpaxy y x y x 62.5262.102{)2(2}22min max 21-=+-±+==τσσσσσσσσMpa Mpa 62.52;0;62.102321-===σσσ 46.7;2667.05010020222tan 00-=-=+⨯-=--=σσσταyx xy1046.7σσσσ确定 -=∴>y x七、计算题图示为一铸铁梁，P 1=9kN ，P 2=4kN ，许用拉应力[t ]=30MPa ，许用压应力[c ]=60MPa ，I y =7.6310-6m 4，试校核此梁的强度。
1m 1m 1mP 1P 280201202052形心Cy (单位:mm)解：（1）由梁的静力学平衡方程可以解得B 、D 处的约束反力为：B F 10.5KN= ，A F 2.5KN=由此绘出梁的剪力图和弯矩图由图可见，B 、C 截面分别有绝对值最大的负、正弯矩。
（2）校核强度：校核B 截面的抗拉和抗压强度以及C 截面的抗拉强度。
B 截面：C 336B c Bcmax 6z M (14y )410(14052)1046.1310I 7.6310σ---⨯⨯-⨯==≈⨯⨯Pa 46.13=MPa c []60σ<=Mpa C 336B c Bt max6z M y 410521027.2610I 7.6310σ--⨯⨯⨯==≈⨯⨯Pa 27.26=MPa t []30σ<=Mpa C 截面：C 336C c Ct max6z M y 2.510(14052)1028.8310I 7.6310σ--⨯⨯-⨯==≈⨯⨯Pa 28.83=MPa t []30σ<=Mpa 所以该梁满足正应力强度条件。