典型相关分析论文
毕业论文中如何正确运用相关性分析和因子分析

毕业论文中如何正确运用相关性分析和因子分析在毕业论文中,正确运用相关性分析和因子分析是非常重要的。
相关性分析是一种用于确定变量之间关系的统计方法,而因子分析则是用于确定潜在因素的方法。
本文将探讨如何正确运用这两种分析方法,并提供几个例子来说明它们在毕业论文中的应用。
第一部分:相关性分析相关性分析是通过计算变量之间的相关系数来确定它们之间关系的一种方法。
相关系数的范围从-1到+1,-1表示完全负相关,+1表示完全正相关,0表示没有相关性。
在毕业论文中,相关性分析可以用于研究两个或多个变量之间的关系。
例如,在教育领域的研究中,一个研究者可能对学生的成绩和参与课外活动之间的关系感兴趣。
通过进行相关性分析,可以确定这两个变量之间的关系强度和方向。
在运用相关性分析时,研究者需要注意以下几点:1. 确定要分析的变量:在进行分析之前,需要明确要研究的变量。
在上述例子中,研究者需要确定他们要分析的是学生的成绩和参与课外活动。
2. 收集数据:研究者需要收集相关的数据,例如学生的成绩和他们的课外活动参与情况。
数据可以通过问卷调查、观察或其他方法获得。
3. 计算相关系数:通过计算相关系数,研究者可以确定变量之间的相关性。
常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。
皮尔逊相关系数适用于连续变量,而斯皮尔曼相关系数适用于有序变量。
举个例子,研究者收集了100名学生的成绩和他们的课外活动参与情况。
通过计算皮尔逊相关系数,研究者发现成绩和课外活动参与之间存在正相关关系,相关系数为0.7,说明两者之间的关系较为密切。
第二部分:因子分析因子分析是一种用于确定潜在因素的方法。
在毕业论文中,因子分析可以用于确定一组变量背后的共同因素。
它可以帮助研究者简化数据集,并找到隐藏的模式和关联。
在运用因子分析时,研究者需要注意以下几点:1. 确定要进行因子分析的变量:在进行因子分析之前,需要明确要进行分析的变量。
例如,在心理学研究中,研究者可能想要确定一组变量(如压力水平、焦虑水平和抑郁水平)背后的共同因素。
管理学案例分析论文六篇

管理学案例分析论文六篇管理学案例分析论文范文1【关键词】网络环境财务管理案例教学教学模式案例教学法是一种启发式、争论式、互动式的教学方法,以典型案例为载体,引导同学阅读、思索、争论案例,在互动争论中关心同学把握和运用理论学问,并培育同学分析、推断、表达以及运用所学学问处理问题的力量。
传统的案例教学采纳在课堂中集中争论的教学形式,由于受课堂教学时间和条件的限制,同学难以在短时间内对案例绽开全面分析。
尤其是财务管理教学中的一些案例,案例内容包括公司背景状况、经营状况说明以及许多报表数据,同学很难在短时间内把其中的财务问题分析清晰,更难以提出有效的对策建议,大大降低了案例教学的效果。
网络科技的进展,多媒体教学平台的广泛应用,为财务管理教学模式的创新和改革供应了有力的技术支持。
网络环境下建设网络案例教学平台,给同学供应自主探究、协作学习的环境,使得教学活动突破时间和空间的限制,同学能够实现更具弹性的自主学习。
利用网络教学平台,可以供应参考资料、案例答疑以及争论区,增加同学与老师间、同学与同学间的教学沟通,可以提高同学的参加度,增加教学效果。
本文结合教学实践,构建了网络环境下财务管理案例教学模式。
一、网络环境下财务管理案例教学的理论依据建构主义理论、情境学习理论是构建网络环境下财务管理案例教学模式的重要理论依据。
建构主义关于教学的基本观点:同学是认知的主体,是意义的主动建构者,老师是意义建构的指导者、促进者,而不是学问的灌输者;情境对意义建构具有重要作用,要尽量创设能够促进同学乐观主动地建构学问的情景;注意协作学习,通过同学与老师之间、同学与同学之间沟通争论建构自己的学问结构;学习环境的设计具有重要意义,要细心设计教学环境,让同学能够利用各种工具和资源来达到学习目标。
建构主义理论的启示是:利用网络平台创建“学习社区”,在老师指导下,同学对案例情景绽开自主探究、协作学习,最终提高同学分析问题、解决问题的力量。
典型相关分析论文

海南省备市县农村住户结构特性经济活动特性与经济活动后果三者相关分析吴学品李均立傅国华冯子华摘要:本文在建立海南省农村住户结构特性、经济活动特性、经济活动后果三者评价指标体系的基础上,依据海南省第一次农业普查资料,利用多元统计中的主成分分析和典型相关分析方法,对上述三者的各指标体系进行分析。
主成分分析方法概述:主成分分析方法是处理多变量(多指标)问题的一种方法,即将研究对象的多个相关变量(指标)化为少数几个不相关的变量,而这较少的不相关变量尽可能地反映原变量提供的大部分信息。
典型相关分析概述:研究多个变量之间的相关性的一种方法。
本文把上述两种方法有机结合起来,先利用主成分的降维思想,分别对各市县农村住户结构特性,经济活动特性,经济活动后果进行主成分分析,然后对上述三者的主成分进行典型相关分析。
1.各市县农住户结构特性的主成分分析1.l评价指标体系及各指标水平见《海南省农村住户结构特性的研究》。
1.2程序:DATA HNO1;INPUT X1-X11;LABEL X1=“民族乡占乡镇百分比”......Xl1=“非农村住户农业生产经营单位从事种植业率”;(依各指标水平顺序) CARDS:(按INPUT格式输入数据);PROC PRINCOMP OUT=PRINHNO1;PREFIX=APRIN;RUN;PROC PRINT;VAR APRIN1-APRIN4;RUN;1.3结果分析1.3.1运行结果显示,X1,X2,X3,X4的标准差较大,它们相对应的指标为民族乡占乡镇百分比,老边区占乡镇百分比,山区占乡镇百分比,乡镇平均土地面积,这说明各省县区的生活居住条件极其不平衡,还有X7、X8、X9、X10、Xl1也较大,它们相对应的指标为文盲半文盲占农村住户从业人员百分比(住户成员个体的素质),及住户成员个体户的经济活动(X8-X11)相对指标的总称也极不平衡,从附表1的(1)~(2)相关表中可看出X9与大多数变量都为负相关(即X9与X1、X2、X3、X4、X6、X10),结合他们本身意义,相当于农村住户从业人员在农村从事非农业率与生活居住条件(Xl-X4),住户类型(X6),从业人员从事种植业率(Xl0)有很大的负相关关系,从附表1的(3)给出的特征值和各成分所占的贡献率可以看出:前4个特征及相应的累计贡献率为85%,因此可从说,前4个主成分几乎已经概括了大部分信息,后7个主成分的贡献率小于5.5%,因此,我们可以取4个主成分作为该问题的主成分。
【毕业论文】相关分析和回归分析
相关分析和回归分析客观事物之间的关系分为函数关系和统计关系,函数关系也就是我们通常所说的一一对应的关系,而统计关系是指两事物之间的一种非一一对应的关系,即当一个变量x取一定值时,另一变量y无法依确定的函数取唯一确定的值。
事物之间的统计关系是普遍存在,且有的关系强,有的关系弱。
相关分析和回归分析都是以不同方式测度事物之间统计关系的有效工具。
实际应用中。
这两种分析方法经常互相结合渗透。
一、相关分析相关分析通过图形和数值两种方式,能够有效的揭示事物之间统计关系的强弱程度。
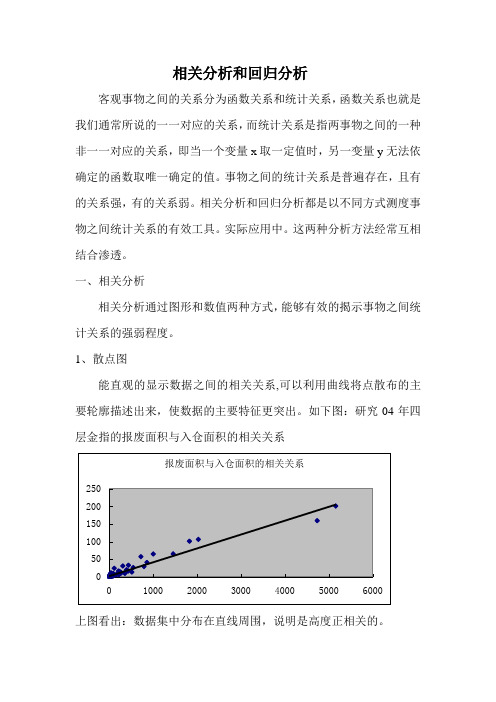
1、散点图能直观的显示数据之间的相关关系,可以利用曲线将点散布的主要轮廓描述出来,使数据的主要特征更突出。
如下图:研究04年四层金指的报废面积与入仓面积的相关关系上图看出:数据集中分布在直线周围,说明是高度正相关的。
2、相关系数散点图能直观的展现变量之间的统计关系,但并不精确。
相关系数以数值的方式精确的反映了两个变量间线形相关的强弱程度。
➢ R=yyxx xy L L L ,其中xx L =∑=--ni ix x12)(,∑=----=ni i i xy y y x x L 1))((,∑=--=ni i yy y y L 12)(.➢ 相关系数R 的取值在-1~+1之间。
➢ R>0表示两变量之间存在正的线性相关关系;R<0表示两变量之间存在负的线性相关关系。
➢ R=1表示两变量存在完全正相关;R=-1表示两变量存在完全负相关;R=0表示两变量不存在线性相关关系。
➢ |R|>0.8表示两变量之间具有较强的线性关系;|R|<0.3表示两变量之间的线性相关关系较弱。
上例中,R=0.974,说明报废面积与入仓面积之间是强正相关的。
二、一元线性回归在实际应用中,我们常常需要考虑某一现象与影响它的最主要因素的关系,回归分析不仅可以揭示变量x 对变量y 的影响大小,还可以由回归方程进行预测和控制。
一元线性回归是最简单的回归模型。
会计案例研究论文六篇

会计案例研究论文六篇会计案例讨论论文范文1一、案例教学应是一种综合性的教学形式笔者认为,目前所进行的案例教学一般来说还是一种综合性的课堂教学形式,它是将课堂讲授(老师预备案例和对同学分析与报告内容的点评等)、争论、试验(同学实际操作)和习题(撰写分析报告)等教学形式相结合的课堂教学形式。
在案例教学中,老师需要在大量收集资料的基础上形成需要进行分析的案例内容,在同学对案例进行分析、报告以及争论后要对分析报告的内容和争论的状况进行点评,这些工作都是与课堂讲授有关的内容。
成本会计学案例分析中有的内容是需要同学进行实际计算与复核(如成本核算案例中的计算与复核),撰写分析报告,所做工作类似于同学做习题和试验。
同学就案例作分析报告和问答是争论教学形式的运用。
而成本会计学案例教学的深化进展应是将课堂教学形式与现场教学形式相结合,在老师的引导下,将同学分为若干组到企业单位实地调查和实习,收集第一手资料,编写企业单位的成本会计案例和分析报告,在肯定程度上还可以依据所学学问解决实际问题。
课堂教学与现场教学相结合的形式在成本会计学课程的特地实习或学年实习条件下采纳比较合适。
二、案例教学应注意所学学问的融会贯穿和综合力量的培育成本会计学案例教学一般是在已经学习了肯定的成本会计学学问的基础上进行的。
因此,进行案例教学首先是检测和巩固所学学问,然后才是在这一基础上进行问题分析和提出解决问题的对策。
在案例教学的学问检测和巩固部分,要求同学能结合所学学问进行推断,通过同学的推断来检查同学对有关学问的把握程度。
通过这种教学方法,可以有效地发觉同学对有关概念和方法理解上的偏差或错误,从而在老师讲解点评时予以准时订正,加速同学对有关学问点、方法和相互关系的熟悉。
在案例教学其次部分的分析与解决问题中,同学通过案例分析和解决问题对策的讨论,提高发觉问题、分析问题和解决问题的力量,团队合作的力量,分析报告的文字表述和口头表述的力量以及课件的制作力量。
(概率论与数理统计专业论文)Copula理论与相关性分析

华中科技大学博士学位论文Copula理论与相关性分析姓名:***申请学位级别:博士专业:概率论与数理统计指导教师:任佳刚;刘次华20091024华中科技大学博士学位论文摘要本文主要研究利用Copula理论分析多维随机变量的相关性及其应用。
Copula是一个“连接”多维联合分布及其边缘分布的函数,其优点主要有两点:第一,它能完整地刻划变量之间的相关性结构;其次,它可以将单个随机变量的边缘分布与变量间的相关结构拆开来处理,然后再加以整合,这样能生成灵活多样的高维概率分布。
论文首先分析了多元Copula函数的特点,然后基于Copula理论研究了随机变量的相关性,探讨了多元Copula参数模型的选择问题,以及利用Copula函数在多元极值理论中获得了一些成果,最后研究了Copula模型在金融和保险等领域的应用。
本文的创新点和主要工作如下:1. 深入分析了Copula理论在研究多变量的相关性中的重要作用,与传统的相关性分析方法相比,Copula函数所具有的优势和特点。
讨论了当边缘分布是连续和非连续的两种情形时Sklar定理的不同结果,并用一种新的方法更简单地证明了此定理。
利用Copula理论研究了Kendall’s τ系数与 Spearman’s ρ系数之间的关系,得到了两者比值ρτ变化的不等式。
针对一类Copula参数族,证明了比值ρτ的极限值是3/2.2. 如何选取合适的Copula函数来描述多维随机变量的相关性结构是目前Copula 理论研究中的一个难题。
论文讨论了一类多元Copula参数模型的选择问题,其Copula 函数能与一个一元函数构成一一对应的关系,从而达到降维的目的。
研究了4种此类常见的Copula模型的性质和图形,并分别在参数已知或未知两种情况下进行了拟合优度检验。
对中国股市的上证指数与深证综指作了实证分析,结果表明两者存在着较强的正相关性,相关性模型选取Gumbel Copula模型最合适。
相关分析构建原理分析论文

相关分析的构建原理分析摘要:联系是自然现象、社会现象普遍具备的特点。
通过各种形态的联系,事物间构成了一个相互影响、相互制约的整体系统。
人们在各类实践活动中,总结和积累了大量的有着明显类别之分的专业知识。
其中大量的知识是关于事物、现象间联系问题的探讨、研究、总结。
从某个角度讲,关于事物、现象之间联系的方式、特点、规律的信息构成人类的全部知识。
关键词:联系相关分析统计中根据联系在数学上的特点的不同,将联系区分为两大类:函数关系、相关关系。
函数关系指如果事物间的联系可以用明确的函数表达式进行描述,那么这种关系称为函数关系。
相关关系与函数关系相对应,指如果事物间存在关联,但关联并不能描述为明确的函数表达式,那么这种关联称为相关关系。
函数关系简洁、直观,如确定了自变量数值大小,就能唯一确定因变量数值大小,为我们掌握事物变化规律提供了一条捷径。
然而,这种理想色彩浓厚的联系形式在揭示客观事物变化,尤其是揭示社会、经济现象变化时,显得过于呆板,常常漏洞百出。
与函数关系相比相关关系对关联特征的描述更具灵活性。
由于事物间的联系以相关关系的形态为表现具有普遍性,并且也是确定事物间函数关系的前提,所以相关关系的研究具有重要意义,引入相关关系来完善联系的类别结构也显得十分必要。
相关关系根据相关的程度可以分为完全相关、不完全相关、不相关;根据相关的方向可以划分为正相关和负相关;根据涉及变量的多少可以分为单相关、复相关、偏相关;根据计量结果是否与实际吻合可分为真实相关和虚假相关;根据的曲线特征的不同,相关关系又可以区分为线性相关和非线性相关两种类型。
线性相关如果现象之间的关系大致呈现为线性的特征,称之为线性相关。
其线性相关的程度可由指标相关系数(r)进行测度。
相关系数的测度公式:x:表示某一指标 y:表示相关联的另一指标这一公式包括分子和分母两个部分,我们对两部分分别进行探讨。
1 分子部分cov(x,y)是两个变量之间的协方差。
典型火灾事故案例分析论文范文

典型火灾事故案例分析论文范文随着城市现代化建设的不断推进,大型商业建筑、高层住宅、办公楼等高耸入云的建筑层出不穷,加之近年来天气异常,气温不断飙升,空气湿度不足等情况,火灾事故也愈加频繁。
为了更好地预防和处理火灾事故,进行典型火灾事故案例分析就显得尤为必要。
本文将从火灾事故的成因以及防范措施、相关的法律法规和典型火灾安全事故案例等方面进行分析。
一、火灾事故的成因以及防范措施1.火源环境火源环境是指火灾发生的物理环境,包括温度、湿度、氧气含量等。
夏季气温高、空气干燥、氧气含量低,这都是火源环境的助长因素。
针对该环境,采取的防范措施包括提高建筑的抗火等级和隔热等级,加强消防设施建设,增加灭火器和消防栓等装备的数量。
2.人为因素人为因素是造成火灾事故最主要的原因。
通常是由于人们的不注意,例如抽烟、使用明火、乱扔火柴等,结果导致火灾。
针对这种情况,应对普及消防知识,增强公众消防意识,并提高消防设施和人员的防范及应急处理能力。
3.电气因素电气因素是造成火灾的常见原因。
这包括电线电缆的老化、接头松动、负载过重、电器故障等因素。
针对这种原因,应对建筑物内部的电线电缆进行定期检查和维护,稳定电网负荷,也可设置电器安全开关等装置,确保电路的安全性。
二、相关的法律法规火灾事故的相应法律法规颇为完善。
如《消防法》和《建筑法》、《安全生产法》等都对防范火灾、保护建筑和人员安全等方面的内容进行了详细规定。
其中重要的一项法规是《消防法》第六十二条规定,规定建筑物、构筑物内应当设置火灾自动报警系统,装配必要的灭火设备;同时也明确规定各级政府、国有企事业单位和其他有管理权限的组织,应当成立消防组织,配备专职消防队伍,指定专人负责组织实施消防安全预防措施。
三、典型火灾安全事故案例1. 沈阳防控三期工地火灾2015年10月4日下午4点许,沈阳某工地发生火灾,当时现场有8名工人正在作业,事故造成2死6伤。
指向该事件的原因是由于建筑工程进展速度较快,钢汁液体未及时清理过滤,致使热量积聚导致发生火源,后来短时间内火源迅速扩散。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海南省备市县农村住户结构特性经济活动特性与经济活动后果三者相关分析吴学品李均立傅国华冯子华摘要:本文在建立海南省农村住户结构特性、经济活动特性、经济活动后果三者评价指标体系的基础上,依据海南省第一次农业普查资料,利用多元统计中的主成分分析和典型相关分析方法,对上述三者的各指标体系进行分析。
主成分分析方法概述:主成分分析方法是处理多变量(多指标)问题的一种方法,即将研究对象的多个相关变量(指标)化为少数几个不相关的变量,而这较少的不相关变量尽可能地反映原变量提供的大部分信息。
典型相关分析概述:研究多个变量之间的相关性的一种方法。
本文把上述两种方法有机结合起来,先利用主成分的降维思想,分别对各市县农村住户结构特性,经济活动特性,经济活动后果进行主成分分析,然后对上述三者的主成分进行典型相关分析。
1.各市县农住户结构特性的主成分分析1.l评价指标体系及各指标水平见《海南省农村住户结构特性的研究》。
1.2程序:DATA HNO1;INPUT X1-X11;LABEL X1=“民族乡占乡镇百分比”......Xl1=“非农村住户农业生产经营单位从事种植业率”;(依各指标水平顺序) CARDS:(按INPUT格式输入数据);PROC PRINCOMP OUT=PRINHNO1;PREFIX=APRIN;RUN;PROC PRINT;VAR APRIN1-APRIN4;RUN;1.3结果分析1.3.1运行结果显示,X1,X2,X3,X4的标准差较大,它们相对应的指标为民族乡占乡镇百分比,老边区占乡镇百分比,山区占乡镇百分比,乡镇平均土地面积,这说明各省县区的生活居住条件极其不平衡,还有X7、X8、X9、X10、Xl1也较大,它们相对应的指标为文盲半文盲占农村住户从业人员百分比(住户成员个体的素质),及住户成员个体户的经济活动(X8-X11)相对指标的总称也极不平衡,从附表1的(1)~(2)相关表中可看出X9与大多数变量都为负相关(即X9与X1、X2、X3、X4、X6、X10),结合他们本身意义,相当于农村住户从业人员在农村从事非农业率与生活居住条件(Xl-X4),住户类型(X6),从业人员从事种植业率(Xl0)有很大的负相关关系,从附表1的(3)给出的特征值和各成分所占的贡献率可以看出:前4个特征及相应的累计贡献率为85%,因此可从说,前4个主成分几乎已经概括了大部分信息,后7个主成分的贡献率小于5.5%,因此,我们可以取4个主成分作为该问题的主成分。
1.3.2对于第一主成分,除X9,X2,Xll的分量绝对值较小外,其余几乎都在0.1~0.4之间,说明影响农村住户结构特性因素有共同的原因,所以可把第一主成分称为指标因子。
从原指标水平及附表一的(8)也可看出,各市县的各项指标值大的,它们的第一主成分值也较高。
从第二主成分可看出X7,X8,X9,X11的系数较高,相应于评价指标体系就是个体的素质(X7),从业人员在本乡从业率(X8),从业人员在农村从事非农业率(X11),所以第二主成分主要反映了从业人员的素质和经济活动因素。
第三主成分的分量中X2的值特别大,这主要反映老边区占乡镇百分比的因素。
从第四主成分的向量分量中注意到X2、X3、X4、Xll的系数都为正且都较大,而其余分量的系数都为负,所以第四主成分主要反应生活居住条件(X2-X4)和非农村住户农业生产经营单位从事种植业率因素与其它农村住户结构特性(X5-Xl0)的对比。
2.各市县农村经济活动特性的主成分分析2.1评价指标体系及各指标水平见《海南省农村住户经济活动特性研究》2.2程序:DATA HN02;TNPUT Y1-Y2;LABEL Y1=“家庭外雇人员三个月以下占全部外雇人员百分比”......Y22=“平均每户鸡鸭鹅存栏数”(依各指标水平顺序)CSRDS;(按INPUT格式输入数据)PROC PRINCOMP OUT=PRINHNO2;PREFIX=BPRIN;PROC PRINT;VAR BPRIN1-BPRIN6;RUN;2.3结果分析2.3.1运行结果显示,Y1、Y2、Y7、Yl0、Y12、Y17、Y16、Y22等指标的方差很大(除Y8、Yl4、Yl8-Y21较小以外),结合它们原指标水平的意义,即各市县的外雇人员情况(Y1-Y2)住户经营类别,农户用地情况,农作物种植情况,农业技术应用部分情况及牲畜与家禽饲养情况极不平衡。
前6个主成分相应的累计贡献率已达到87%,所以可以认为前6个主成分几乎概括了所有的信息,而剩下的16个主成分的贡献率均小4,所以取前6个主成分为该问题的主成分。
2.3.2从第一主成分的分量可看出,所有分量的绝对值相差不大,且有正有负,除分量Y20、Y22的绝对值较小外,其他负的分量都对应于各项指标的百分比,所以第一主成分主要反映各项指标中的非百分比因素。
第二主成分的Y1、Y3、Y5的值较大,Y20、Y21的值也较大,结合它们的意义,所以第二主成分表示外雇人员三个月以下占全部外雇人员百分比(Yl),收入来源于农业占收入主要来源户数的百分比(Y3),农业收入中主要来源于种植业的户数所占百分比(Y5),平均每月存栏数(Y20),平均每月猪存栏数(Y22)等因素。
第三主成分中相应于Y2、Y3、Y10的值较大,相应地主要反映了家庭外雇人员三个月以上占全部外雇人员百分比(Y2),收入来源于农业占收入主要来源户数的百分比(Y3),粮食训种植占农作物种值面积的百分比(Yl0)等因素。
第四主成分到第六主成分的贡献率都小于10%,这里不述。
3.各市县农村经济活动后果的数据分析3.1评价指标体系及各指标水平3.2程序:DATA HN03;INPUT Z1-Z24;LABEL Z1=“户均农业增加值”......Z24=“户均纯收入”(按指标水平顺序);CARDS;(按INPUT的格式输入数据);PROC PRINCOMP OUT= PRINHN03;PREFIX=CPRIN;RUN;PROC PRINT;VAR CPRINl-CPRIN7;RUN;3.3结果分析3.3.1运行结果显示,各市县的经济活动后果的标准差非常大,其中较小的为Z13与Z16,其它的都很大,可见对于海南各市县来说,各种经济活动后果极不均匀。
导致各市县的收入极不平衡,贫富差距非常大。
3.3.2前7个特征值所对应的主成分为该问题的主成分,可看出,前7个主成分的累计贡献率已达83%,基本上已概括了所有的信息。
3.3.3第一主成分中Z22-Z24的值较大,相对应于Z22-Z24的指标是收入,也就是说第一主成分主要反映收入情况,而收入主要是由各项经济活动结果所影响,第二主成分分量值较大的是Z22(林业增加值)、Z11(户均橡胶产量),与其它分量绝对值相差较大,即第二主成分主要反映林业增加值及橡胶的因素。
从第三主成分的分量上看,Z3、Z4、Z7的值较大,所以第三主成分主要反映牧渔业增加值和户均甘蔗产量的因素,而第四主成分Z1、Z5的值较大,主要反映了农业增加值与户均粮食产量的因素,其它主成分的贡献率小于5%,不述。
4.农村住户结构、经济活动特性和经济活动后果三者之间相关分析利用主成分的降维思想,农村住户结构、经济活动特性、经济活动后果三者之间的典型相关,可通过三者主成分之间的典型相关得到。
4.1农村住户结构与经济活动特性的相关4.1.1程序:DATA HN12;INPUT APRIN1-APRIN4 BPRIN1-BPRIN6;CARDS;(按INPUT格式把附表1的(5)APRIN1-APRIN4,把附表2的(5)BPRIN1-BPRIN6依数据输入)PROC CANCORR ALL;VAR APRIN1-APRIN4;WITH BPRIN1-BPRIN6;RUN;4.1.2结果分析(1)第一典型相关系数为0.982381,第二典型相关系数为0.872052,两个相关系数比两组主成分之间任一相关系数都大,检验总体所有典型相关系数假设,概率水平为0.0001及0.0811,故在X=0.10的显著水平下,否定所有典型相关系数均为0的假设。
(2)农村住户结构特性的主成分的第一典型变量为:V1=0.8948APRIN1-0.2568APRIN2-0.2689APRIN3-0.2471APRIN4来自农村住户活动特性的主成分的第一典型变量为:W1=0.7821BPRIN1+0.1560BPRIN2+0.4452BPRIN3+0.1305BPRIN4+0.3849BPRIN5-0.0269BPRIN6相关系数为0.982381从第一对典型变量可看出APRIN1与BPRIN1有较强的相依关系,结合两个主成分的意义,即农村结构特性与农村活动特性有很强的相关关系。
来自农村住户结构特性的主成分和活动,特性的主成分的第二典型变量为:V2=0.2226APRIN1+0.8043APRIN2+0.3577APRIN3-0.4191APRIN4W2=-0.0886BPRIN1+0.9258BPRIN2+0.1086BPRIN3-0.1203BPRIN4+0.0061BPRIN5+0.3299BPRIN6第二对典型相关的相关系数为0.872052,主要反映了APRIN2与BPRIN2有较强的相关关系,结合两个主成分的意义,主要反映了从业人员的素质和经济活动与外雇人员情况及牲畜与家禽饲养有很强的相关关系。
4.2对农村住户结构特性与农村经济活动后果的相关关系4.2.1程序类似于4.1.1程序4.2.2结果分析运行结果得到全部变量的均值、方差和它们之间的相关系数,以及两对显著的典型相关变量:第一对典型相关变量为:V1=-0.8005APRIN1+0.5015APRIN2+0.2916APRIN3+0.1507APRIN4W1=0.5659CRIN1-0.7248CPRIN2+0.2695CPRIN3-0.1800CPRIN4-0.106CPRIN5+0.1351CPRIN6+0.1408CPRIN7它们的典型相关系数为0.938376,由上可以看出,APRIN2与BPRIN1有较强的相依关系,结合它们的意义即为农村住户结构中从业人员的素质和经济活动(APRIN2)与经济活动后果的收入(CPRINl)有很大的相关关系。
第二对典型相关变量为:V2=0.4735APRIN1+0.7105APRIN2+0.2984APRIN3-0.4266APRIN4W2=-0.5847CPRIN1-0.6434CPRIN2-0.3021CPRIN3-0.3368CPRIN4+0.1559CPRIN5+0.1064CPRIN6+0.0621CPRIN7它们的相关系数为0.842080由上可知APRIN2与CPRIN4有很大的相关关系。
