河南省濮阳市2014届高三第二次模拟考试 数学(文)试题(word版)
2024届河南省濮阳市高三二模语文试题(解析版)

濮阳市普通高中2023—2024学年高三第二次模拟考试语文全卷满分150分,考试时间150分钟。
注意事项:1.答卷前,考生务必将自己的姓名、班级、考场号、座位号、考生号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,18分)阅读下面的文字,完成下面小题。
在微粒说与波动说的第一次交锋中,以牛顿为首的微粒说战胜了波动说,取得了在物理学界被普遍公认的地位。
近一个世纪过去了,英国米尔沃顿的一个教徒的家庭里诞生了一个男孩,他被取名为托马斯·杨。
经过学习和探究,他最终形成了光具有波动性质的想法,这个认识源于波动中所谓的“干涉”现象,波的干涉现象是各种波所独有的基本特征。
我们都知道,普通的物质是具有累加性的,一滴水加上一滴水一定是两滴水,而不会一起消失。
但是波动就不同了,一列普通的波,有着波的高峰和波的谷底,如果两列振幅相同的波相遇,当它们正好都处在高峰时,那么叠加起来的这个波就会达到两倍的峰值,如果都处在低谷时,叠加的结果就会是两倍深的谷底。
但是,等等,如果正好一列波在它的高峰,另一列波在它的谷底呢?答案是它们会互相抵消。
如果两列波在这样的情况下相遇——物理上叫作“反相”——那么在它们重叠的地方将会波平如镜,既没有高峰,也没有谷底。
这就像一个人把你往左边拉,另一个人用相同的力气把你往右边拉,结果是你会站在原地不动。
托马斯·杨在研究牛顿环的明暗条纹的时候,被这个关于波动的想法给深深打动了。
为什么会形成一明一暗的条纹呢?一个想法渐渐地在杨的脑海里成形:用波来解释不是很简单吗?明亮的地方,那是因为两道光正好是“同相”的,就好像有两个人同时在左边或者右边拉你,它们的波峰和波谷都得到增强,结果造成了两倍光亮的效果;而黑暗的那些条纹,则一定是两道光处于“反相”,它们的波峰、波谷相对时,就好像两个人同时往两边拉你,正好互相抵消了。
河南省濮阳市2014届高三第二次模拟考试 英语试题(word版)

河南省濮阳市2014届高三第二次模拟考试英语试题(word版)本卷分为第I卷(选择题)和第II卷(非选择题)两部分。
第I卷1至10页,第Ⅱ卷10至12页。
考试结束,将本试卷和答题卡.并交回。
第I卷注意事项:1.开始答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在本试卷上,否则无效。
第一部分听力(共两节,满分30分)略第二部分阅读理解(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
AThe connection shared by grandparents and grandchildren is something very special and despite the changing family situation, it still remains strong across generations. For most of us, our grandparents were our first best friends, the ones with whom we shared our secrets and our pain.In majority of the cases, grandparents would have babysat their grandchildren while parents were busy working and didn't have much time for their children. Even as a kid grows up, the love and affection for grandparents never dies, and for many teens, visiting grandparents or living with them in the same house is a pleasure. Kedar Patwary, a mass communication student, says, "I often end up having long conversations with my grandfather about the evolution of Indian society and I really admire him for the patience with which he answers all my questions. "Many teenagers feel that their parents treat them as grown-ups, while their grandparents give them much freedom.Leela Narayanan, a grandmother. says that she loves to pamper her grandchildren and cook favorite dishes for them. She further adds that her eldest granddaughter, who is now 19, was brought up by her till she was four and the closeness they shared remains the same even now。
河南省濮阳市2014届高三第二次模拟考试 数学(理)试题(扫描版)

2014年高中三年级模拟考试理科数学参考答案及评分标准一. 选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符二.填空题:本大题共4小题,每小题5分。
(13)31-(14) (1,5)4 (15) ①③⑤ (16) nn 23-三.解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分)(1)证明:acos 2C 2+ccos 2A2=a ·1+cos C 2+c ·1+cos A 2=32b ,即a(1+cos C)+c(1+cos A)=3b.-------------------------------------------------2分由正弦定理得:sin A +sin Acos C +sin C +cos Asin C =3sin B , 即sin A +sin C +sin(A +C)=3sin B , ∴sinA+sinC=2sinB.-----------------------------------------------4分由正弦定理得,a +c =2b , 故a,b,c成等差数列. -----------------------------------------------6分(2)由∠B =60°,b =4及余弦定理得: 42=a 2+c 2-2accos 60°, ∴(a+c)2-3ac =16,---------------------------------------------------------------------8分又由(1)知a +c =2b , 代入上式得4b 2-3ac =16, 解得ac=16,-----------------------------------------------------------------------10分∴△ABC 的面积S =12acsin B =12acsin 60°=4 3.-----------------------------12分(18)(本小题满分12分)解:(I ) PD PA =,Q 为AD 的中点,AD PQ ⊥∴,又 底面ABCD 为菱形,︒=∠60BAD ,AD BQ ⊥∴ ,------------------------------------------------2分又Q BQ PQ =∴⊥AD 平面PQB ,又 ⊂AD 平面PAD ,∴平面⊥PQB 平面PAD ;-----------------------------6分(II ) 平面⊥PAD 平面ABCD ,平面 PAD 平面AD ABCD =,AD PQ ⊥⊥∴PQ 平面ABCD .以Q 为坐标原点,分别以QP QB QA ,,为z y x ,,轴建立空间直角坐标系如图.则)0,3,2(),0,3,0(),3,0,0(),0,0,0(-C B P Q ,设−→−−→−=PC PM λ(10<<λ), 所以))1(3,3,2(λλλ--M ,平面CBQ 的一个法向量是)1,0,0(1=n ,设平面MQB 的一个法向量为=2n ),,(z y x ,所以⎪⎩⎪⎨⎧=⋅=⋅−→−−→−22n QB n QM取=2n )3,0,233(λλ-,-----------------------------------------9分由二面角C BQ M --大小为︒60,可得:||||||212121n n n n ⋅=,解得31=λ,此时31=PC PM --------------------------------12分 (19)(本小题满分12分)解:(Ⅰ)设“在本年内随机抽取一天,该天经济损失S 大于200元且不超过600元”为事件A由600200≤<S ,得250150≤<w ,频数为39,……3分.4分 (Ⅱ)根据以上数据得到如下列联表:.8分K 2的观测值()2100638227 4.575 3.84185153070k ⨯⨯-⨯=≈>⨯⨯⨯……………….10分所以有95%的把握认为空气重度污染与供暖有关. ……………………….12分(20)(本小题满分12分)(1)证明:由题意可知A (2,1),B (-2,1).设P (x 0,y 0),则x 204+y 20=1.由OP →=mOA →+nOB →,得⎩⎪⎨⎪⎧x 0=2(m -n ),y 0=m +n ,-------------------------------2分所以4(m -n )24+(m +n )2=1,即m 2+n 2=12.故点Q (m ,n )在定圆x 2+y 2=12上.---------------------------------5分(2)设M (x 1,y 1),N (x 2,y 2),则y 1y 2x 1x 2=-14.平方得x 21x 22=16y 21y 22=(4-x 21)(4-x 22),即x 21+x 22=4. ---------------7分因为直线MN 的方程为(x 2-x 1)x -(y 2-y 1)y +x 1y 2-x 2y 1=0,所以O 到直线MN 的距离为d =|x 1y 2-x 2y 1|(x 2-x 1)2+(y 2-y 1)2,---------9分所以△OMN 的面积S =12MN ·d =12|x 1y 2-x 2y 1|=12 x 21y 22+x 22y 21-2x 1x 2y 1y 2 =12 x 21⎝⎛⎭⎫1-x 224+x 22⎝⎛⎭⎫1-x 214+12x 21x 22=12x 21+x 22=1. 故△OMN 的面积为定值1.--------------------------------12分(21)(本小题满分12分)解:(I )由于函数f (x )=212x ,g (x )=elnx , 因此,F (x )=f (x )-g (x )=212x -elnx ,则'()e F x x x=-=2x e x -(0,)x ∈+∞,当0<x '()F x <0,所以F (x )在(0当x '()F x >0,所以F (x ∞)上是增函数;因此,函数F (x )的单调减区间是(0,+∞)……………4分(II )由(I )可知,当x 时,F (x )取得最小值F 0,则f (x )与g (x )的图象在x 2e)假设f (x )与g (x )存在“分界线”2e)……………………….6分故设其方程为:(2e y k x -=,即2ey kx =+-由f (x )≥2e kx +-对x ∈R 恒成立, 则2220x kx e --+≥对x ∈R 恒成立,所以,22244(2)484(k e k e e k ∆=-=-=-≤0成立,因此k,“分界线“的方程为:2e y =-…………………………………..10分 下面证明g (x2e -对x ∈(0,+∞)恒成立, 设G (x)=ln 2e e x -,则'()e G x x =-=, 所以当0<x'()0G x >,当x时,'()G x <0,当xG (x )取得最大值0,则g (x2e -对x ∈(0,+∞)恒成立,故所求“分界线“的方程为:2e y =-………………………………………..12分 (22)(本小题满分10分)(Ⅰ)连接BD ,则ABD AGD ∠=∠,90︒∠+∠=ABD DAB ,90︒∠+∠=C CAB 所以∠=∠C AGD ,所以180︒∠+∠=C DGE ,所以,,,C E G D 四点共圆.………………………………..5分(Ⅱ)因为2⋅=EG EA EB ,则2=EB ,又F 为EB 三等分,所以23=EF ,43=FB , 又因为2FB FC FE FD FG =⋅=⋅,所以83=FC ,2=CE …………………….10分(23) (本小题满分10分)(I )直线l 的普通方程为:0333=+-y x ;曲线的直角坐标方程为1)2(22=+-y x ---------------------------4分(II )设点)sin ,cos 2(θθ+P )(R ∈θ,则 2|35)6cos(2|2|33sin )cos 2(3|++=+-+=πθθθd 所以d 的取值范围是]2235,2235[+-.--------------------------10分 (24.)(本小题满分10分) (I )不等式的解集是),3[]3,(+∞--∞ ------------------------------5分(II )要证)()(a b f a ab f >,只需证|||1|a b ab ->-,只需证22)()1(a b ab ->-而0)1)(1(1)()1(22222222>--=+--=---b a b a b a a b ab ,从而原不等式成立.----------------------------------------10分。
河南省各地2014届高三数学 最新模拟试题分类汇编14 排列组合与二项式定理.pdf

河南省各地2014届高三最新模拟数学理试题分类汇编:
排列组合与二项式定理
1、(河南省洛阳市2014届高三12月统考)将5名实习教师分配到高一年级的3个班实习,每班至少1名,则不同的分配方案有
A.30种 B.60种 C.90种 D.150种
答案:D
2、(河南省安阳市2014届高三第一次调研)的展开式中的常数项为a,则直线y=ax与曲线y=围成图形的面积为 A. B.9 C. D.
答案:C
3、((河南省淇县一中2014届高三第四次模拟)若将函数f(x)=x5表示为
f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1 +x)5,其中a0,a1,a2,…,a5为实数,则a3=________
答案:10
4、(河南省武陟一中西区2014届高三12月月考)的二项式展开式中项的系数是____(用数字作答)。
答案:280
5、(河南省郑州外国语学校2014届高三11月月考)设,则展开式的常数项为
答案:160
6、(河南省郑州一中2014届高三上学期期中考试)若的
A.1 B. C. D.
答案:C
7、(河南省中原名校2014届高三上学期期中联考)的展开式中常数项为_________________
答案:
8、(河南省开封市2014届高三第一次模拟考试)
答案:70
9、(河南省豫东、豫北十所名校2014届高三第四次联考)
答案:B
10、(河南省郑州市2014届高中毕业年级第一次质量预测)
答案:B。
河南省濮阳市2014高三第二次模拟考试文综历史试卷

河南省濮阳市2014高三第二次模拟考试文综历史试卷本试题卷分第I卷(选择题)和第II卷(必考题和选考题两部分)。
考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试题卷上答题无效。
考试结束后,将本试题卷和答题卡一并交回。
第I卷本卷共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
24.清代学者王国维在《殷周制度论》中说:“欲观周之所以定天下,必自其制度始矣。
周人制度之大异于商者,日立子立嫡之制,由是而生宗法及丧服之制,并由是而有封建子弟之制,君天下臣诸侯之制。
”材料说明西周政治制度的显著特征是A.通过血缘姻亲关系与地缘结合以强化王权B.通过主要分封同姓诸侯以加强对地方的统治C.通过世袭制和嫡长子继承制以巩固奴隶主专政。
.D.通过服饰规范等礼乐制度以维护贵族等级特权25.隋唐君主为加强统治,致力于削弱门阀势力,唐初曾将民间声望最高的崔氏降格为第三等姓氏,武则天提高进士科地位以打击擅长明经科的世族。
到了晚唐时,唐文宗欲把公主下嫁给门阀世族时感慨:“我家二百年天子,顾不及崔、卢耶!”这反映出隋唐时A.宗法制与封建专制互为表里B.科举制对士族产生的影响很小C.社会结构的改变十分缓慢D.九品中正制与科举制并行26.《三国志》载:“景元元年(260年)蜀领户二十八万,口九十四万……魏有户六十六万三千四百二十三,口有四百四十三万二千八十一……吴户五十二万三千,男女口二百三十万。
”材料中的史实对三国魏晋时期历史发展的主要影响是A.有利于南北方人口的均衡发展B.奠定了魏晋统一的经济基础C.促进了成都平原和太湖流域的开发D.形成了三国鼎立的对峙局面27.1824年,法国史学家米涅的《法国革命史》问世,在书的最后他写到:“1814年是延续了25年的大动荡结束的一年。
今后要长期治理法国,就只能首先满足引起法国革命的双重需要,在政府中,要有真正的政治自由,在社会方面,要有物质福利,这是不断提高的文明发展的必然结果。
河南省实验中学2014届高三第二次模拟考试 数学(文) Word版含答案

4545输出河南省实验中学2014届高三二测模拟卷数学(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.集合P={3,4,5},Q={6,7},定义},|),{(*Q b P a b a Q P ∈∈=,则Q P *的子集个数为A .7B .12C .32D .642.已知复数2ii ia b -=+(a ,b ∈R ,i 为虚数单位),则2a b -= A. 1 B. 2 C. 3 D.4 3. “p 或q ”为真命题是“p 且q ”为真命题的A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件 4.一个几何体的三视图如图所示,则该几何体的体积是A .6B .8C .10D .125.已知数阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛333231232221131211aa aa a aa a a 中,每行的3个数依次成等差数列,每列的3个数也依次成等差数列,若822=a ,则这9个数的和为A .16B .32C .36D .72 6.如图所示的程序框图,它的输出结果是A .3B .4C .5D .67.已知三个数2,m ,8构成一个等比数列,则圆锥曲线2212x y m +=的离心率为A .B. C.或 D8.若0≥a ,0≥b ,且当⎪⎩⎪⎨⎧≤+≥≥100y x y x 时,恒有≤+by ax 1,则以b a ,为坐标的点),(b a P 所形成的平面区域的面积是 A .21 B .4π C .1 D .2π 9.在平行四边形ABCD 中,1,60AD BAD =∠=,E 为CD 的中点.若12AD BE ⋅=, 则AB 的长为A.12 B.1 C .32D .2 10.过抛物线)0(22>=p px y 的焦点F ,斜率为34的直线交抛物线于A ,B 两点,若)1(>=λλFB AF ,则λ的值为A .5B .4C .34 D .25 11.已知函数()f x 对定义域R 内的任意x 都有()f x =(4)f x -,且当2x ≠时,其导函数()f x '满足()2()xf x f x ''>,若24a <<,则有A. 2(2)(3)(l o g)af f fa << B. 2(3)(log )(2)a f f a f << C. 2(l o g )(3)(2)af a f f<< D. 2(log )(2)(3)a f a f f << 12.函数[]11,0,2()1(2),(2,)2x x f x f x x ⎧--∈⎪=⎨-∈+∞⎪⎩,则下列说法中正确命题的个数是①函数()ln(1)y f x x =-+有3个零点; ②若0x >时,函数()k f x x ≤恒成立,则实数k 的取值范围是3,2⎡⎫+∞⎪⎢⎣⎭; ③函数()f x 的极大值中一定存在最小值,④)(),2(2)(N k k x f x f k ∈+=,对于一切[)0,x ∈+∞恒成立.A .1B .2C .3D .4二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题纸的相应位置. 13.若非零向量b a ,满足||||b a =,0)2(=⋅+b b a ,则与的夹角为______.14.函数()sin cos f x x x =+,在各项均为正数的数列{}n a 中对任意的*n N ∈都有()()n n f a x f a x +=-成立,则数列{}n a 的通项公式可以为(写一个你认为正确的)______15.将一颗骰子先后投掷两次分别得到点数b a 、,则直线0=+by ax 与圆2)2(22=+-y x 有公共点的概率为_______.16.已知四棱柱1111D C B A ABCD -中,侧棱⊥1AA 底面ABCD ,且21=AA ,底面ABCD 的边长均大于2,且︒=∠45DAB ,点P 在底面ABCD 内运动,且在AB ,AD 上的射影分别为M ,N ,若|PA|=2,则三棱锥MN D P 1-体积的最大值为______.三、解答题:本大题共6个小题,共70分.解答应写文字说明、证明过程或演算步骤17.(本小题满分12分)在ABC ∆中,已知角A 、B 、C 所对的边分别为a 、b 、c ,直线1:10l ax y ++=与直线()222:40l b c bc x ay +-++=互相平行(其中4a ≠).(I )求角A 的值, (II )若22,,sin cos 2232A C B B ππ+⎡⎫∈+⎪⎢⎣⎭求的取值范围.18.(本小题满分12分) 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm 和195cm 之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.(Ⅰ)求第七组的频率; (Ⅱ)估计该校的800名男生的身高的中位数以及身高在180cm 以上(含180cm )的人数;(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为,x y ,事件=E {5x y -≤},事件F ={15->x y },求()P E F .19.(本题满分12分)如图,四边形ABCD 中,AB ⊥AD ,AD ∥BC ,AD =6,BC =4,AB =2,E 、F 分别在BC 、AD 上,EF ∥AB .现将四边形ABEF 沿EF 折起,使得平面ABEF ⊥平面EFDC .(Ⅰ) 当1BE =,是否在折叠后的AD 上存在一点P ,且AP PD λ=,使得CP ∥平面ABEF ?若存在,求出λ的值;若不存在,说明理由;(Ⅱ) 设BE =x ,问当x 为何值时,三棱锥A -CDF 的体积有最大值?并求出这个最大值.20.(本小题满分12分)已知函数xe xf =)(,若函数)(xg 满足)()(x g x f ≥恒成立,则称)(x g 为函数)(x f 的下界函数.(1)若函数kx x g =)(是)(x f 的下界函数,求实数k 的取值范围;A B C D EFE F A B CD(2)证明:对任意的2≤m ,函数x m x h ln )(+=都是)(x f 的下界函数.21.(本小题满分12分)已知2212221x y F F a b +=、是椭圆的左、右焦点,O 为坐标原点,点P ⎛- ⎝⎭在椭圆上,线段PF 2与y 轴的交点M 满足20PM F M +=; (I )求椭圆的标准方程;(II )O 是以12F F 为直径的圆,一直线:l y kx m =+与相切,并与椭圆交于不同的两点A 、B.当23,34OA OB AOB λλ⋅=≤≤∆且满足时,求面积S 的取值范围.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分。
河南省郑州市高三第二次模拟考试 数学文试题 扫描版试题word版答案.pdf

2014年高中毕业年级第二次质量预测 文科数学 参考答案 选择题 DBAC BAAC BADD 二、填空题 13. 14. 15. 16. 三、解答题 17.解(Ⅰ), 因为,所以,---------2分 即, 故或,---------4分 又,所以. ---------6分 (Ⅱ)因为,所以, ① 由余弦定理,---------8分 及得,, ② ---------10分 由①、②解得. ---------12分 18. (2):在中,由E、F分别是AC、BC的中点,所以EF//AB, 又平面DEF,平面DEF, ∴平面DEF. (Ⅱ)由直二面角知平面平面 , 又在正中,为边AB中点, 所以平面 ,---------9分 , , 所以,多面体D-ABFE的体积=.-----12分 19., 由分层抽样知:. (Ⅱ)总体平均数,---------7分 从这6个分数中任取2个的所有可能取法为:、、、、、、、、、、、、、、,共计15种.--------10分 由知,当所取的两个分数都在内时符合题意,即、、、、、符合,共计6种,所以,所求概率. 20.解(Ⅰ)由题知,且,, 则,---2分 整理得,曲线的方程为.-----------5分 (Ⅱ)设与轴交于,则直线的方程为, 记,由对称性知, 由消得:,-----7分 所以,且, 故 ------------9分 由三点共线知,即, 所以, 整理得,-----------10分 所以,即,, 所以直线过定点.--------12分 21.解(Ⅰ)由题知, 当时,,当时,,-----------2分 所以函数的增区间为,减区间为, 其极大值为,无极小值.-----------5分 (Ⅱ)设切点为,则所作切线的斜率, 所以直线的方程为:, 注意到点在上,所以,-----7分 整理得:,故此方程解的个数,即为可以做出的切线条数, 令,则, 当时,,当时,或, 所以,函数在上单调递减,在上单调递增,---9分 注意到, 所以方程的解为,或, 即过点与曲线相切直线时,对应的切线斜率, 当时,对应的切线斜率, 令,则, 所以在上为减函数,即,, 所以.------------12分 22.解(Ⅰ)如图,连结,由为直径可知 , 又 ,所以,因此四点共圆.四点共圆,所以 ,---6分 在中, ,------8分 又由知 ,所以 ,.---10分 23.,即, 故圆的直角坐标方程为:,------2分 直线 ,即, 则直线的直角坐标方程为:.------4分 (Ⅱ)由⑴知圆与直线的直角坐标方程, 将两方程联立得解得------6分 即圆与直线在直角坐标系下的公共点为(0,1),------8分 将(0,1)转化为极坐标为,即为所求.------10分 24.解 (Ⅰ)由化简可得,即或,--2分 解得: 或, 所以,不等式的解集为.------4分 (Ⅱ)不等式等价于, 即化简得------6分 若 ,则原不等式的解集为=, 此时, ;------8分 若 ,则原不等式的解集为=, 此时, .综上所述, 或.------10分。
河南省郑州市2014届高三第二次模拟考试 数学文试题 含答案
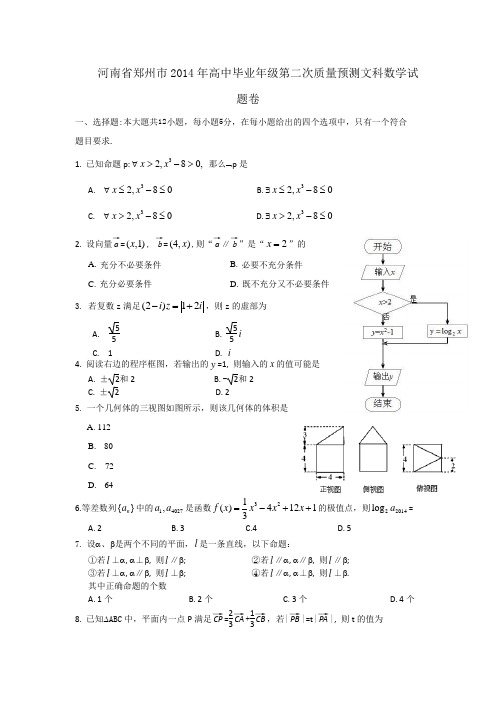
河南省郑州市2014年高中毕业年级第二次质量预测文科数学试题卷一、选择题:本大題共12小題,每小題5分,在每小題给出的四个选项中,只有一个符合 题目要求.1. 已知命题p: ∀32,80,x x >-> 那么⌝p 是A. ∀32,80x x ≤-≤ B. ∃32,80x x ≤-≤ C. ∀32,80x x >-≤ D. ∃32,80x x >-≤2. 设向量→a =(,1)x , →b =(4,)x ,则“→a ∥→b ”是“2x =”的 A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件A. 55B. 55i C. 1 D. i4. 阅读右边的程序框图,若输出的y =1, 则输入的x 的值可能是 A. ±2和2 B. -2和2 C. ± 2 D. 25. 一个几何体的三视图如图所示,则该几何体的体积是 A. 112B. 80C. 72D. 646.等差数列{}n a 中的14027,a a 是函数321()41213f x x x x =-++的极值点,则22014log a = A. 2 B. 3 C.4 D. 5 7. 设α、β是两个不同的平面,l 是一条直线,以下命题:①若l ⊥α, α⊥β, 则l ∥β; ②若l ∥α, α∥β, 则l ∥β; ③若l ⊥α, α∥β, 则l ⊥β; ④若l ∥α, α⊥β, 则l ⊥β. 其中正确命题的个数A. 1个B. 2个C. 3个D. 4个8. 已知∆ABC 中,平面内一点P 满足→CP =23→CA +13→CB ,若|→PB |=t |→PA |, 则t 的值为A. 3B. 13C. 2D. 12 9. 已知直线512x π=和点(,0)6π恰好是函数())f x x ωϕ=+图象的相邻的对称轴和对称中心,则()f x 的表达式可以是A. ())6f x x π=-B. ())3f x x π=-C. ())3f x x π=+D. ())6f x x π=+ 10.已知双曲线)0,0(12222>>=-b a by a x 的两个焦点分别为F 1,F 2 ,以线段F 1F 2 为直径的圆与双曲线渐近线的一个交点位(4,3),则双曲线的方程为11.若曲线2(0)y ax a =>与曲线ln y x =在它们的公共点P (s,t )处具有公共切线,则a =12. 已知正项数列{}n a 的前n 项和为S n , 若21()n n nS a a n N *+∈=, 则S 2014= A. 2014+20142014 B. 2014- 20142014C. 2014D. 2014二、填空题:本大题共4小题,每小题5分,共20分. 14.已知等比数列{}n a 的前n 项和为S n ,若253652,62a a a S ==-,则1a 的值是15.设实数,x y 满足不等式组⎩⎪⎨⎪⎧x +y ≤2y -x ≤2y ≥1, 则22x y +的取值范围是_______.16.已知,x y ∈(-12 ,12 ), m ∈R 且m ≠0, 若222sin 201,2sin cos 041xx m x y y y m y ⎧++=⎪+⎪⎨⎪+-=+⎪⎩ 则y x =_______.三、解答题:解答应写出说明文字,证明过程或演算步骤. 17.(本小题满分12分)已知向量→m =(cosA, -sinA ),→n = (cosB, sinB ), →m ·→n =cos2C,A,B,C 为∆ABC 的内角.(Ⅰ)求角C 的大小;(Ⅱ)若AB=6,且→CA ·→CB =18, 求AC, BC 的长.18.(本小题满分12分)正∆ABC 的边长为2, CD 是AB 边上的高,E 、F 分别是AC 和BC 的中点(如图(1)).现将∆ABC 沿CD 翻成直二面角A -DC -B (如图(2)).在图(2)中:(Ⅰ)求证:AB ∥平面DEF ;(Ⅱ)求多面体D -ABFE 的体积.抽取了45人,求n 的值;(Ⅱ)接受调查的的人同时对这项活动进行打分,其中6人打出的分数如下: 9.2,9.6,8.7,9.3,9.0,8.2.把这6个人打出的分数看作一个总体,从中任取2个数,求这两个数与总体平均数之差的绝对值都不超过0.5的概率.B20. (本小题满分12分)已知平面上的动点(,)R x y 及两定点A(-2,0),B(2,0),直线RA 、RB 的斜率分别为k 1、k 2,且k 1·k 2=- 34, 设动点R 的轨迹为曲线C.(I)求曲线C 的方程;(II)过点S(4,0)的直线与曲线C 交于M 、N 两点,过点M 作MQ ⊥x 轴,交曲线C 于点Q.求证:直线NQ 过定点,并求出定点坐标.21.(本小题满分12分)已知函数()xx f x e =. (I)求函数()f x 的单调区间和极值;(II)过点P(0,4e2 ) 作直线l 与曲线y =()f x 相切,求证: 这样的直线l 至少有两条,且这些直线的斜率之和2322121(,)e e m e e--∈.请考生从22、23、24三个小题中任选一题作答,如果多做,则按所做的第一题计分.并用铅笔在对应方框中涂黑.22. (本小题满分10分)选修4—1:几何证明选讲如图,AB 为圆O 的直径, CD 为垂直于AB 的一条弦,垂直为E ,弦BM 与CD 交于点F. (I )证明: A E F M 、、、四点共圆; (II)若MF=4BF=4,求线段BC 的长.23. (本小题满分10分)选修4一4:坐标系与参数方程在极坐标系下,已知圆O:cos sin ρθθ=+和直线l :sin()42πρθ-=. (I)求圆O 和直线l 的直角坐标方程;(II)求直线l 与圆O 的公共点的极坐标(0,02)ρθπ≥≤< .24. (本小题满分10分) 选修4―5:不等式选讲已知函数()|2|5f x x a x =-+. (Ⅰ)求不等式()51f x x >+的解集;(Ⅱ)若不等式()f x ≤0的解集为{|1}x x ≤-,求a 的值.2014年高中毕业年级第二次质量预测文科数学 参考答案 一、 选择题DBAC BAAC BADD 二、填空题13.1(0,);2 14.2;- 15.[1,4]; 16.1.2- 三、解答题17.解(Ⅰ)cos cos sin sin cos()A B A B A B ⋅=-=+m n ,因为A B C π++=,所以cos()cos cos 2A B C C +=-=,---------2分即22cos cos 10C C +-=,故1cos 2C =或cos 1C =-,---------4分 又0C π<<,所以3C π=. ---------6分(Ⅱ)因为18CA CB ⋅=,所以36CA CB ⋅=, ① 由余弦定理2222cos 60AB AC BC AC BC ︒=+-⋅⋅,---------8分及6AB =得,12AC BC +=, ②---------10分由①、②解得6,6AC BC ==. ---------12分18. 解(Ⅰ)如图(2):在ABC ∆中,由E 、F 分别是AC 、BC 的中点,所以EF //AB ,又⊄AB 平面DEF ,⊂EF 平面DEF , ∴//AB 平面DEF . ---------6分(Ⅱ)由直二面角A DC B --知平面ADC ⊥平面BCD , 又在正ABC ∆中,D 为边AB 中点,AD CD ⊥ 所以AD ⊥平面BCD ,---------9分136BCD A BCD V S AD ∆-=⋅⋅=三棱锥 , 11132224BCD FCD V S AD ∆-=⋅⋅=三棱锥E ,所以,多面体D-ABFE 的体积V =A BCD V --三棱锥FCD V -=三棱锥E -----12分 19.解(Ⅰ)所有参与调查的人数为8001004501502003002000+++++=, 由分层抽样知:452000100900n =⨯=. ---------5分 (Ⅱ)总体平均数9.29.68.79.39.08.29.06x +++++==,---------7分从这6个分数中任取2个的所有可能取法为:(9.2,9.6)、(9.2,8.7)、(9.2,9.3)、(9.2,9.0)、(9.2,8.2)、(9.6,8.7)、(9.6,9.3)、(9.6,9.0)、(9.6,8.2)、(8.7,9.3)、(8.7,9.0)、(8.7,8.2)、(9.3,9.0)、(9.3,8.2)、(9.0,8.2),共计15种.--------10分由|9.0|0.5x -≤知,当所取的两个分数都在[8.5,9.5]内时符合题意,即(9.2,8.7)、(9.2,9.3)、(9.2,9.0)、(8.7,9.3)、(8.7,9.0)、(9.3,9.0)符合,共计6种,所以,所求概率615P =. ---------12分 20.解(Ⅰ)由题知2x ≠±,且12y k x =+,22y k x =-, 则3224y y x x ⋅=-+-,---2分整理得,曲线C 的方程为221(0)43x y y +=≠.-----------5分(Ⅱ)设NQ 与x 轴交于(,0)D t ,则直线NQ 的方程为(0)x m y t m =+≠,记1122(,),(,)N x y Q x y ,由对称性知22(,)M x y -,由223412,x y x my t⎧+=⎨=+⎩消x 得:222(34)63120m y mty t +++-=,-----7分所以2248(34)0m t ∆=+->,且1,2262(34)mt y m -=+,故12221226,34312,34mt y y m t y y m ⎧+=-⎪⎪+⎨-⎪⋅=⎪+⎩------------9分 由M N S 、、三点共线知NS MS k k =,即121244y y x x -=--, 所以1221(4)(4)0y my t y my t +-++-=,整理得12122(4)()0my y t y y +-+=,-----------10分所以222(312)6(4)034m t mt t m ---=+,即24(1)0m t -=,1t =, 所以直线NQ 过定点(1,0)D .--------12分 21.解(Ⅰ)由题知1()()R xxf x x e -'=∈, 当()0f x '>时,1x <,当()0f x '<时,1x >,-----------2分 所以函数()f x 的增区间为(,1)-∞,减区间为(1,)+∞, 其极大值为1(1)f e=,无极小值.-----------5分 (Ⅱ)设切点为00(,())x f x ,则所作切线的斜率001()x x k f x e-'==,所以直线l 的方程为:000001()x x x x y x x e e--=-, 注意到点24(0,)P e在l 上,所以00000214()x x x x x e e e --=-,-----7分整理得:020240x x e e-=,故此方程解的个数,即为可以做出的切线条数,令224()x x g x e e =-,则(2)()xx x g x e -'=-,当()0g x '>时,02x <<,当()0g x '<时,0x <或2x >,所以,函数()g x 在(,0),(2,)-∞+∞上单调递减,在(0,2)上单调递增,---9分注意到2244(0)0,(2)0,(1)0g g g e e e=-<=-=->, 所以方程()0g x =的解为2x =,或(10)x t t =-<<,即过点24(0,)P e恰好可以作两条与曲线()y f x =相切的直线.----10分当2x =时,对应的切线斜率121(2)k f e'==-, 当x t =时,对应的切线斜率21ttk e -=, 令1()(10)t t h t t e -=-<<,则2()0t t h t e-'=<,所以()h t 在(1,0)-上为减函数,即1(0)()(1)2h h t h e =<<-=,212k e <<,所以231222121(,)e e m k k e e--=+∈.------------12分22.解(Ⅰ)如图,连结AM ,由AB 为直径可知90AMB ︒∠= , 又CD AB ⊥ ,所以90AEF AMB ︒∠=∠=,因此A E F M 、、、四点共圆. ------4分(Ⅱ)连结AC ,由A E F M 、、、四点共圆,所以BF BM BE BA ⋅=⋅ ,---6分在RT ABC ∆中,2BC BE BA =⋅ ,------8分又由44MF BF ==知1,5BF BM == ,所以25BC = ,BC =.---10分23.解(Ⅰ)圆:cos sin O ρθθ=+,即2c o s s i n ρρθρθ=+,故圆O 的直角坐标方程为:220x y x y +--=,------2分直线:sin 42l πρθ⎛⎫-= ⎪⎝⎭,即si n cos 1ρθρθ-=, 则直线l 的直角坐标方程为:10x y -+=.------4分 (Ⅱ)由⑴知圆O 与直线l 的直角坐标方程,将两方程联立得220,10x y x y x y ⎧+--=⎨-+=⎩解得0,1,x y =⎧⎨=⎩------6分即圆O 与直线l 在直角坐标系下的公共点为(0,1),------8分将(0,1)转化为极坐标为1,2π⎛⎫⎪⎝⎭,即为所求.------10分24.解 (Ⅰ)由()51f x x >+化简可得|2|1x a ->,即21x a ->或21x a -<-,--2分解得:12a x -<或12a x +>, 所以,不等式()51f x x >+的解集为11{|}22a a x x x -+<>或.------4分 (Ⅱ)不等式|2|50x a x -+≤等价于525x x a x ≤-≤-,即52,25,x x a x a x ≤-⎧⎨-≤-⎩化简得,3,7a x a x ⎧≤-⎪⎪⎨⎪≤⎪⎩------6分 若0a < ,则原不等式的解集为{|}7ax x ≤={|1}x x ≤-, 此时,7a =- ;------8分若0a ≥ ,则原不等式的解集为{|}3a x x ≤-={|1}x x ≤-, 此时,3a = .综上所述,7a =- 或3a =.------10分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省濮阳市2014届高三第二次模拟考试 数学(文)试题(word 版)注意事项:1.本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,第I 卷l 至3页,第Ⅱ卷3至5页。
2.答卷前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成,答在本试卷上无效。
4.考试结束后,将本试题和答题卡一并交回。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{}{}|02,|(1)(1)0A x x B x x x =<<=-+>,则 AB = ( )A.(0,1)B.(1,2) C .( -∞,-l)U(0,+∞) D .(-∞,-l)U(l ,+∞) (2)在复平面内,复数22i+对应的点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限(3)如图,一个封闭的长方体,它的六个表面各标出A 、B 、C 、D 、E 、F 这六个字母,现放成下面三种不同的位置,所看见的表面上的字母已表明,则字母A 、B 、C 对面的字母依次分别为 ()A. E.D.FB. F .D.EC. E.F.DD. D.E.F (4)将函数 sin y x =的图象上所有点向右平行移动10π个单位长度,再把所得的各点的横 坐标伸长到原的2倍(纵坐标不变),所得图象的函数解析式是 ( ) A . sin(2)10y x π=- B .sin(2)5y x π=-C . sin()220x y π=- D.sin()210x y π=- (5)设 n S 是公差不为0的等差数列 {}n a 的前n 项和,且 124,,S S S 成等比数列,则 21a a 等于 ( )A .1B .2C .3D .4(6)在△ABC 中,内角A ,B ,C 的对边分别是a ,b ,c ,若22,sin a b C B -==,则A= ( )A. 30B. 60C. 120D. 150(7)过P(2,0)的直线 l 被圆 22(2)(3)9x y -+-=截得的线段长为2时,直线的斜率为 ( ) A.4±B.2± C. 1±D. 3± (8)已知变量名 ,x y 满足 202300x y x y x -≤⎧⎪-+≥⎨⎪≥⎩,则 4log (24)z x y =++的最大值为 ( )A .23 B .1 C . 32D .2 (9)已知经过曲线 22:1916x y S -=的一个顶点和一个焦点,圆心M 在双曲线S 上,则圆心M 到双曲线S 的中心的距离为 ( )A .13743或 B . 15843或 C . 133 D . 163(10)如左图所示,在正四棱锥S-A BCD 申,E 是BC 的中点,P 点在侧面△SCD 内及其边界上运动,并且总是保持PE ⊥A C .则动点P 的轨迹与△SCD 组成的相关图形最有可能是右图中的(11)若 2,1a b ==,且a 与b 的夹角为60,当 a xb -取得最小值时,实数x 的值为 ( )A .2B .-2C .1D .-1(12)已知函数 ()f x 是定义在R 上的奇函数,若对于任意给定的不等实数 12,x x ,不等式1212()[()()]0x x f x f x --<恒成立,则不等式 (1)0f x -<的解集为 ( ) A. (1,)+∞ B. (0,)+∞ B. (,0)-∞ D. (,1)-∞第Ⅱ卷本卷包含必考题和选考题两部分。
第(13)题~第(21)题为必考题,每个试题考生都必须 做答,第(22)题~第(24)题为选考题,考生根据要求做答:二、填空题:本大题共4小题,每小题5分。
(13)从一堆苹果中任取5个,称得它们的质量如下(单位:克)125,124,121,123,127,则该样本标准差=___________(14)执行如图所示的程序框图,输出的所有值之和为__________.( 15) 若点 (cos ,sin )P a a 在直线 2y x =-上,则tan()4a π+=___________.(16)已知函数 ()ln 2x f x x =+,若 2(4)2f x -<,则实数x 的取值范围___________. 三、解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分l2分)设 {}n a 是等差数列, {}n b 是各项为正项的等比数列,且 11351,21a b a b ==+=,5313a b +=.( I)求 {}{},n n a b 的通项公式;(Ⅱ)求数列 n n a b ⎧⎫⎨⎬⎩⎭的前n 项和 n S .(18)(本小题满分12分).以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a 表示. (I)若甲、乙两个小组的数学平均成绩相同,求a 的值; (Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;(Ⅲ)当a=2时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.(19)(本小题满分12分).如图,在四棱锥S-ABCD 中,底面ABCD 是正方形,SA ⊥底面ABCD .SA =AD=1,点M 是SD 的中点,AN ⊥SC ,交SC 于点N. (I)求证:平面SACV 平面AMN ; (Ⅱ)求三棱锥S-A CM 的体积.(20)(本小题满分12分)设椭圆 22221(0)x y a b a b +=>>的左焦点为F,离心率为 3,过点F 且与x 轴垂直的直线被椭圆截得的线段长为3. (I)求椭圆的标准方程;(Ⅱ)没A ,B 分别为椭圆的左右顶点,过点F 且斜率为 k 的直线与椭圆交于C ,D 两点, 若 8AC DB AD CB ⋅+⋅=,求k 的值. (21)(本小题满分12分) 已知函数 ()(1)1x f x x e =--. (I)求函数 ()f x 的最大值; (Ⅱ)设 ()(),1f x g x x x=>-,且 0x ≠,证明: ()1g x <. 请考生在第(22)、(23)、(24)三题中任选一题做答。
注意:只能做所选定的题目。
如果多做,则按所做的第一个题目计分,做答时请用28铅笔在答题卡上将所选题号后的方框涂黑. (22)(本小题满分10分)选修4-1:几何证明选讲如图.AB 是直径,CB 与相切于B ,E 为线段CB 上一点,连接AC 、AE 分别交于D 、G 两点,连接DG 交CB 于点F(I)求证:C 、D 、G 、E 四点共圆;(Ⅱ)若F 为EB 的三等分点且靠近E ,EG=1,GA =3,求线段CE 的长.(23)(本小题满分10分)选修4-4,坐标系与参数方程 已知在直角坐标系xOy 中,直线 l 的参数方程为3x t y =-⎧⎪⎨=⎪⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为24cos 0ρρθ-=. (I)求直线l 的普通方程和曲线C 的直角坐标方程;(Ⅱ)设点P 是曲线C 上的一个动点,求它到直线l 的距离d 的取值范围.(24)(本小题满发10分)选修4-5:不等式选讲 已知函数 ()1f x x =-.(I)解不等式 (1)(3)6f x f x -++≥;(Ⅱ)若 1,1a b <<,且 0a ≠,求 ()()b f ab a f a<.2014年高中三年级模拟考试文科数学参考答案及评分标准一. 选择题:本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(13) 2 (14) 48 (15) 31-(16) ()2,5--)5,2( 三.解答题:解答应写出文字说明,证明过程或演算步骤。
(17)(本小题满分12分) 解:(1)设{a n }的公差为d,{b n }的公比为q,则依题意有q>0,⎪⎩⎪⎨⎧=++=++1341212124q d q d解得d=2,q=2. ----------------------------------------3分 所以a n =2n-1, b n =2n-1----------------------------------------------------------5分((2)1212--=n n n n b a , S n =1+12212122322523---+-+++n n n n2S n =2+3+2523212232---+-++n n n n ,-----------------------------7分两式相减得:S n =2+2(122212)2121211----++++n n n =2+11123262122112112---+-=----⨯n n n n n -------------------------12分(18)(本小题满分12分)解:(1)依题意,得 11(889292)[9091(90)]33a ++=+++,解得 1a =. ………… 4分(2)设“乙组平均成绩超过甲组平均成绩”为事件A ,依题意 0,1,2,,9a =,共有10种可能.由(1)可知,当1a =时甲、乙两个小组的数学平均成绩相同, 所以当2,3,4,,9a =时,乙组平均成绩超过甲组平均成绩,共有8种可能.所以乙组平均成绩超过甲组平均成绩的概率84()105P A ==. …… 8分 (3)设“这两名同学的数学成绩之差的绝对值不超过2分”为事件B , 当2a =时,分别从甲、乙两组同学中各随机选取一名同学, 所有可能的成绩结果有339⨯=种,它们是:(88,90),(88,91),(88,92),(92,90),(92,91),(92,92),(92,90),(92,91),(92,92),事件B 的结果有7种,它们是:(88,90),(92,90),(92,91),(92,92),(92,90),(92,91),(92,92).因此这两名同学的数学成绩之差的绝对值不超过2分的概率7()9P B =……12分(19)(本小题满分12分)证明:(1)∵SA ⊥底面ABCD ,∴SA CD ⊥又AD CD ⊥∴CD ⊥面SAD∴CD AM ⊥…………①…………………………3分又1SA AD ==,且M 是SD 的中点,∴AM SD ⊥……………………② 由①②得AM ⊥面SDC ∴AM SC ⊥又AN SC ⊥ ∴SC ⊥面AMN∴平面SAC ⊥平面AMN ……………………………………………………6分 (2)∵M 是SD 的中点,∴S ACM D ACM M DAC V V V ---==……………………9分1111113232212S ACM ACD V S SA -∆∴=⋅=⋅⋅= …………12分(20)(本小题满分12分))根据椭圆方程为.过焦点且垂直于长轴的直线被椭圆截得的线段长为∴离心率为,∴=b=a=椭圆的方程为由﹣=,∴+(+(=6+k=(21)(本小题满分12分)解:(Ⅰ)f'(x)=-x e x.当x∈(-∞,0)时,f'(x)>0,f(x)单调递增;当x∈(0,+∞)时,f'(x)<0,f(x)单调递减.所以f(x)的最大值为f(0)=0.…5分(Ⅱ)由(Ⅰ)知,当x>0时,f(x)<0,g(x)<0<1.…7分当-1<x<0时,g(x)<1等价于设f(x)>x.设h(x)=f(x)-x,则h'(x)=-x e x-1.当x∈(-1,-0)时,0<-x<1,0<e x<1,则0<-x e x<1,从而当x∈(-1,0)时,h'(x)<0,h(x)在(-1,0)单调递减.当-1<x<0时,h(x)>h(0)=0,即g(x)<1.综上,总有g(x)<1.…12分(22)(本小题满分10分)(Ⅰ)连接BD ,则ABD AGD ∠=∠,90︒∠+∠=ABD DAB ,90︒∠+∠=C CAB 所以∠=∠C AGD ,所以180︒∠+∠=C DGE ,所以,,,C E G D 四点共圆. ………………………………..5分(Ⅱ)因为2⋅=EG EA EB ,则2=EB ,又F 为EB 三等分,所以23=EF ,43=FB , 又因为2FB FC FE FD FG =⋅=⋅,所以83=FC ,2=CE …………………….10分(23) (本小题满分10分)(I )直线l 的普通方程为:0333=+-y x ;曲线的直角坐标方程为1)2(22=+-y x ---------------------------4分 (II )设点)sin ,cos 2(θθ+P )(R ∈θ,则2|35)6cos(2|2|33sin )cos 2(3|++=+-+=πθθθd 所以d 的取值范围是]2235,2235[+-.--------------------------10分 (24.)(本小题满分10分)(I )不等式的解集是),3[]3,(+∞--∞ ------------------------------5分(II )要证)()(ab f a ab f >,只需证|||1|a b ab ->-,只需证22)()1(a b ab ->-而0)1)(1(1)()1(22222222>--=+--=---b a b a b a a b ab ,从而原不等式成立.----------------------------------------10分。
