2010年高三第二次教学质量检测数学试题(文科)(
广东佛山2010届普通高中高三教学质量检测二数学文

2010年佛山市普通高中高三教学质量检测(二)数学(文科)2010.4本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生要务必填写答题卷上的有关项目.2.选择题每小题选出答案后,用黑色字迹的钢笔或签字笔把答案代号填在答题卷对应的空格内.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动, 先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卷的整洁.考试结束后,将答题卷和答题卡交回.1参考公式:锥体的体积公式:V - Sh.其中S是锥体的底面积,h是锥体的高.3一、选择题:本大题共10小题,每小题5分,共50 分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设U R , 集合A y|y v x 1,x 1 , B2,1,1,2,则下列结论正确的是A. AI B2,1B. (6U A)U B(,0)C. AU B(0,)D. (e u A)I B2, 1uuu2.设复数Z 1 bi( b R)在复平面对应的点为Z ,若OZ 2 ( O为复平面原点),则复数z的虚部为A.廳B C.D. 1分组[100,200](200,300](300, 400](400,500](500,600](600,700]频数1030408020m频率0.050.150.20.4a bA. 10B. 20C. 30D. 40r r r r4.单位向量a与b的夹角为一,则a b3A. ■. 3B. 1C. 12D. 25.已知命题p:幕函数的图像不过第四象限,命题q:指数函数都是增函数.则下列命题中为真命题的是A. ( p) qB. p q C ( p) ( q) D. ( p) ( q)6•我国西南今春大旱.某基金会计划给与援助,6家矿泉水企业参与了竞标.其中A企业来自浙江省,B、C两家企业来自福建省,D、E、F三家企业来自广东省.此项援助计划从两家企业购水,假设每家企业中标的概率相同.则在中标的企业中,至少有一家来自广东省的概率是4 A. 一5 7.已知B.是两个不同的平面,C. D.l, m,n是不同的直线, F列命题不正确的是A .若 l m,l n,m ,n ,则 1B . 若 l //m,l ,m ,则 l // ;C. 若 ,Il, m , m l,则 m D .若 ,m,n,,则 m n&如图给出的是计算2 4 其中菱形判断框内应填入的条件疋 A . i 8? B. i C. i 10? D. —的值的一个框图, 209? 11? A . f(3) f( 2) f (1) B . f(1) C. f( 2) f(1) f(3) D . f(3) x y 110.设x, y 满足约束条件 x y 1,若目标函数 2x y 2 小值为A . 4B . 7 4.3 7C . 9.已知函数f (x ) log a x 在(0,)上单调递增,则 f( 2) f (3) f(1) f( 2) 3 4z ax by(a 0,b 0)的最大值为7,则的最a b24 D . 77、填空题:本大共5小题,考生作答4小题,每小题5分,满分20 分) (一)必做题(11〜13题) 11. 两个志愿者组织共有志愿者 2400人,现用分层抽样的方法,从所有志愿者中抽取一个容量为 160的样本,已知从甲志愿者组织中抽取的人数为 150,那么乙志愿者组织志愿者的人数是 _______________ . 12. 已知椭圆上一点 P 到两个焦点之间距离的和为 4 ,其中一个焦点的坐标为 c ,3, 0),则椭圆的离心率为 13.已知函数 f (x ) a x 1 2a (a 0,且 a (二)选做题(14〜15题,考生只能从中选做一题 14 .(坐标系与参数方程)在极坐标中,已知点 cos sin 1所表示的曲线上一动点, Q 2,—,则PQ 的最小值为315.(几何证明选讲)如图,以AB 4为直径的圆与△ ABC 的两边 '第15题图分别交于E,F 两点, ACB 60°,贝U EF ___________ . 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤 16 .(本题满分12分).1)有两个零点,则a 的取值范围是 ) P 为方程 Ax406425634y01120112(I)求f (x)的解析式;1(n)若在ABC中,AC 2, BC 3, f(A) ,求ABC的面积. 217.(本题满分12分)1已知函数f (x) x3 ax2 bx(a,b R)在x 1时取得极值.3(l)试用含a的代数式表示b ;(n)求f (x)的单调区间.18 .(本题满分14分)如图所示,AD 平面ABC , CE 平面ABC , AC AD AB 1, BC .2 ,凸多面体ABCDE 1的体积为丄,F为BC的中点.2(I)求证:AF//平面BDE ;(n)求证:平面BDE 平面BCE .19 .(本题满分14分)国家助学贷款是由财政贴息的信用贷款,旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2010届毕业生凌霄在本科期间共申请了24000元助学贷款,并承诺在毕业后3年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第13个月开始,每月工资比前一个月增加5%直到4000元.凌霄同学计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一月多x元.(I)若凌霄恰好在第36个月(即毕业后三年)还清贷款,求x的值;(n)当x 50时,凌霄同学将在第几个月还清最后一笔贷款?他当月工资的余额是否能满足每月3000元的基本生活费?(参考数据:1.0518 2.406,1.0519 2.526,1.0520 2.653,1.0521 2.786 )20.(本题满分14分)已知函数f(x) sin( x )( 0,0 )的一系列对应值如下表:222X 如图,抛物线 C 「y 8x 与双曲线C 2: 2 a b-21(ab 0,b 0)有公共焦点F 2,点A 是曲线C 1,C 2在第一象限的交点,且|AF 2 5. (I)求双曲线C 2的方程;(n)以F 1为圆心的圆M 与双曲线的一条渐近线相切, 圆 N : (x 2)2 y 21 •已知点 P(1,「3), 直且分别与圆M 、圆N 相交的直线l 1和|2, 得的弦长为s , 12被圆 N 截得的弦长为t .过点P 作互相垂 设11被圆M 截 S 是否为定值? t 请说明理由. 第加題图21 .(本题满分14分) 设曲线C n : f (X )n 1 * X (n N )在点P 1 1 ,f ()处的切线与y 轴交于点Q n (0, y n ).2 2(I)求数列{y n }的通项公式; (H)设数列{y n }的前n 项和为S n ,猜测S n 的最大值并证明你的结论• 2010年佛山市普通高中高三教学质量检测(二)数学试题(文科)参考答案和评分标准、选择题 本大题共10小题,每小题5分,共50分.题号1 2345678910答案DCBBCAACBD、填空题 本大题共5小题,考生作答 4小题,每小题5分,满分20分.17.(本题满分12分)2解: ( I )依题意,得 f (x) x 2ax b由于x1为函数的一个极值点,贝U f ( 1) 1 2a b 0,得b 2a 111. 15012」213. 014.」215. 2三、解答题 本大题共6小题,共80分•解答应写出文字说明、演算步骤或推证过程. 16 .(本题满分12分)解:(I)由题中表格给出的信息可知,函数f (x)的周期为T所以 注意到sin(2 ( -)) 0,也即42k (k Z),由 02,所以 一2所以函数的解析式为 f (x) si n(2x 2)(或者f(x) (□)•••f(A) cos 2 A1 ,• A —或 A 2233在ABC 中,由正弦定理得,BCACsin A sin BAC sin A2 23…sin B—BC33•/ BC AC ,••• BA • cosB —,3,3二 sin C sin(A B)sin AcosB cos As in B仝2cos2x ) ............................. 5 分............................................... 6分…… 8分恵 1 43 3血爲 3 2 36,........ 9分S ABC1 .AC BC sin C 22同理可求得,当A 时,S ABC3丄 AC BC sinC212分(注:本题中第一问由于取点的不同而导致求周期和方法众多,只要言之有理并能正确求出即给分)............................ 7分10分1 3 23由(D 得 f (x )3x ax(2a 1)x故 f (x) x 2 2ax 2a 1 (x 1)(x 2a 1)令 f (x) 0,则 x 1 2a由于 1(1 2a) 2a2 2(a 1)①当a 1时,1 2ax(,1 2a)(1 2a, 1)(1,)f (x)f(x) Z] Zf (x)的单调增区间为(当x 变化时,f (x)与f (x)的变化情况如下表:由上表 可得, 函数 ②当a 1时,1 间为R 1. ③当a 1时,1 (1,12a) 综上: 当a1时 当a 1时, 函数 当a 1时, 函数 2a 2a,函数 f (x)的单调增区间为R ;f (x)的单调增区间为( 1,此时,f (x)1,同理可得函数 18 .(本题满分14分) ,1 2a)和(1,),单调减区间为(1 2a, 1); 0恒成立,且仅在x 1处f (x)0,故函数f(x)的单调区f (x)的单调增区间为(,1)和(1 2a,),单调减区间为f (x)的单调增区间为 (,1 2a)和(1,),单调减区间为(1 2a, 1)和(1 2a,),单调减区间为(1,1 2a) 11分1);12分证明:(I): AD 平面 ABC ,CE 平面 ABC , •••四边形 ACED 为梯形,且平面 ABC 平面 ACED ,••• BC 2 AC 2 AB 2,• AB AC , •••平面 ABC I 平面 ACED AC• AB 平面ACED ,即卩AB 为四棱锥 B ACED 的高,4分1 1 11 VB ACED3 S ACEDAB3 2(1 CE) 1 12,CE 2,.............. 6 分作BE 的中点G ,连接GF , GD , ••• GF 为三角形BCE 的中位线, 1 • GF//EC//DA , GF CE DA ,................................................ 8 分•四边形GFAD 为平行四边形,• AF //GD ,又 GD 平面 BDE , • AF // 平面 BDE . ........................................ 10 分 (□)••• AB AC ,F 为 BC 的中点, • AF BC ,又 GF AF , • AF 平面 BCE ,.................................. 12 分••• AF //GD , • GD 平面 BCE ,又GD 平面BDE , •平面BDE 平面BCE . ................................... 14分19 .(本题满分14分) 解:(I)依题意,从第13个月开始,每个月的还款额为a n 构成等差数列,其中 务 500 x ,公差为X .................................. 2 分24 (24 1)从而,到第36个月,凌霄共还款12 500 24a 1x .......................... 4分224 (24 1) 令 12 500 (500 X) 24 ........................... x 24000,解之得 x 20(元)................................... 6 分2即要使在三年全部还清,第 13个月起每个月必须比上一个月多还20元.............. 7分(n)设凌霄第n 个月还清,则应有12 500 (50050) (n 12) (n 12) (n 12 1 50 24000.................... 8 分2 23 V3321整理可得n 2 3n 8280,解之得n30 ,取n 31............. 10分2即凌霄工作31个月就可以还清贷款. 这个月凌霄的还款额为(30 12) (30 12 1)24000 [12 500 (500 50) (30 12)50] 450 元 .............. 12 分2第31个月凌霄的工资为 1500 1.05191500 2.5263789元.因此,凌霄的剩余工资为 3789 450 3339,能够满足当月的基本生活需求. ............. 14分20.(本题满分14分)2解:(I ):抛物线 G:y 8x 的焦点为F 2(2,0), •••双曲线C 2的焦点为F i ( 2,0)、F 2(2,0),、厂2设A(x 0, y 0)在抛物线G : y 8x 上,且 AF 2…y 0 8 3 ,• y °2 6 ,又•••点A 在双曲线上,2•双曲线的方程为:x 2—3s(n) ?为定值.下面给出说明t弹逍_k2)亦,故s为定值込.20- 3 k 2) t由抛物线的定义得,x 0 2 5,…x 03,•- | AF 1 | .. (3 2)2(2 6)27 ,由双曲线定义得,2a|7 5|设圆的方程为: (x 2)2双曲线的渐近线方程为:y3x , •••圆 与渐近线y、、3x 相切, •••圆 M 的半径为r 22、3 -.1 (;3)2.3,故圆:(x 2)2 y 2 3,10分设11的方程为y .3 k(x 1),即kx y 、3 k 0,设l 2的方程为yk1),即 x ky ■. 3k 1 匕 3k_1|「厂k 2 '11分12分13分14分0 ,•••点M 至煩线11的距离为d••直线11被圆M 截得的弦长s直线12被圆N 截得的弦长t221.(本题满分14分)解:(I)Q f /(x) (n 1)x n(n),•••点P 处的切线斜率 k n (n 1)•切线方程为 (n 1)n(x 1),y n,故数列{ y n }的通项公式为:y nn------两边同乘 S n①②得: Sn1-------- ②3S n •S n 2 3n y1 ,S2 y1y 20, S 3猜测S n 的最大值为 S 2 0.证明如下:(i)当n 为奇数时, S n 2 3n(ii)当n 为偶数时,S n2 3n 2* 1h(n 2) h(n)8 3n 2 2n 3 :I 3n2* 11!S 4,设h(n)9n c 2* 3,1610分11分! 3n 山 厂,则 h(n2) ••• h(n 2) h(n).13分2 3n故h(n) 的最大值为h(2) 1,即S n的最大值为S2 0.14分。
广东省惠州市2010届高三第二次调研考试数学文(word版)答案

广东省惠州市2010届高三第二次调研考试数学试题(文科)答案一、选择题:本大题共10 小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项符合题目要求.1.解析:2(2)2112()1i i i i i i i i ++-===-+--,故选A. 2.解析:∵{}20,2,A a =,{}1,B a =,{}1A B =∴211a a ⎧=⎨≠⎩∴1a =-,故选C.3.解析: 0AB AC ⋅=uu u r uuu r ,∴AB AC ⊥uu u r uuu r 。
||BC ==uu u r D4.解析: 可得22()()()()y a x x b x a x b =--=--- ,a b 是函数的两个零点当 x a <时, 则()0f x > 当a x b <<时, 则()0,f x < 当x b >时, 则()0,f x < 故选B5.解析:2211()1(1)(1)x x x y x x x +-''===+++,211(21)k ==-+,2221y -==-+,故切点坐标为(2,2)-。
切线方程为40x y -+=,故选B6.解析:几何体为一个圆锥和一个半球的组合体,且1,3r R l ===22325S rl R πππππ=+=+=,故选C7.解析:2837a a a a ⋅=⋅,373713,2n n a a a a a a++=⎧⎪⋅=⎨⎪>⎩解得371,2a a =⎧⎨=⎩,711732a a a a ==,故选D 8.解析:依题意得11sin()sin(2)sin()666y x x x ππππ=-=-+=+,将s i n y x =的图象向左平移116π个单位后得到11sin()6y x π=+的图象,即sin()6y x π=-的图象,故选B 9.解析:平均销售量2()1016161018f t t t y t t t t++===++≥ 当且仅当[]16,4130t t==∈即t ,等号成立,即平均销售量的最小值为18,故选A 10.解析:当0x >,()(1)1f x f x --=,(2010)(2010)(2009)(2009)(2008)(1)(0)(0)f f f f f f f f =-+-++-+2010111(0)f =++++=22010log 1+=2010故选C二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
惠州市2010届高三第二次调研考试文科答案(打印版)

惠州市2010届高三第二次调研考试数学试题(文科)答案一、选择题:本大题共10 小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项符合题目要求.1.解析:2(2)2112()1i i i i i i i i ++-===-+--,故选A. 2.解析:∵{}20,2,A a =,{}1,B a =,{}1A B =∴211a a ⎧=⎨≠⎩∴1a =-,故选C.3.解析:0AB AC ⋅=,∴AB AC ⊥。
22||||||13BC AB AC =+=D4.解析: 可得22()()()()y a x x b x a x b =--=--- ,a b 是函数的两个零点当 x a <时, 则()0f x > 当a x b <<时, 则()0,f x < 当x b >时, 则()0,f x < 故选B5.解析:2211()1(1)(1)x x x y x x x +-''===+++,211(21)k ==-+,2221y -==-+,故切点坐标为(2,2)-。
切线方程为40x y -+=,故选B6.解析:几何体为一个圆锥和一个半球的组合体,且1,3r R l ===22325S rl R πππππ=+=+=,故选C7.解析:2837a a a a ⋅=⋅,373713,2n n a a a a a a++=⎧⎪⋅=⎨⎪>⎩解得371,2a a =⎧⎨=⎩,711732a a a a ==,故选D 8.解析:依题意得11sin()sin(2)sin()666y x x x ππππ=-=-+=+,将sin y x =的图象向左平移116π个单位后得到11sin()6y x π=+的图象,即sin()6y x π=-的图象,故选B 9.解析:平均销售量2()1016161018f t t t y t t t t++===++≥ 当且仅当[]16,4130t t==∈即t ,等号成立,即平均销售量的最小值为18,故选A 10.解析:当0x >,()(1)1f x f x --=,(2010)(2010)(2009)(2009)(2008)(1)(0)(0)f f f f f f f f =-+-++-+2010111(0)f =++++=22010log 1+=2010故选C二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
2010年广州市高三二模数学试题及答案(文科)
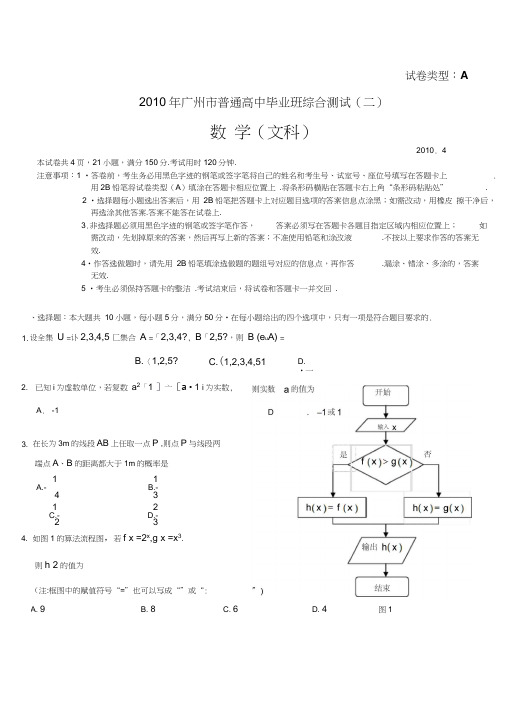
试卷类型:A2010年广州市普通高中毕业班综合测试(二)数学(文科)2010. 4本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1 •答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B铅笔将试卷类型(A)填涂在答题卡相应位置上.将条形码横贴在答题卡右上角“条形码粘贴处”.2 •选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案.答案不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4•作答选做题时,请先用2B铅笔填涂选做题的题组号对应的信息点,再作答.漏涂、错涂、多涂的,答案无效.5 •考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.、选择题:本大题共10小题,每小题5分,满分50分•在每小题给出的四个选项中,只有一项是符合题目要求的.设全集U =讣2,3,4,5 匚集合A =「2,3,4?, B「2,5?,则B (e u A) =2.3.4.B.〈1,2,5?C.(1,2,3,4,51已知i为虚数单位,若复数a2「1 ]亠[a • 1 i为实数,A. -1在长为3m的线段AB上任取一点P ,则点P与线段两端点A、B的距离都大于1m的概率是1A.-41C.-21B.-32D.-3如图1的算法流程图,若f x =2x,g x =x3.则h 2的值为(注:框图中的赋值符号“=”也可以写成“”或“:A. 9B. 8C. 6D.•一图1D. 41.5.命题“若x, y 都是偶数,则x y 也是偶数”的逆否命题是xx若x . 0且a ■ b 1,则下列不等式成立的是仰角相等的点的轨迹为正确的是 A •若x y 是偶数,则x 与y 不都是偶数 B •若x • y 是偶数,则x 与y 都不是偶数 C •若x y 不是偶数,则x 与y 不都是偶数D •若x• y 不是偶数,则x 与y 都不是偶数6.x^2,设变量x, y 满足约束条件* y 兰x, 则目标函数x + y 32.z = 2x y 的最小值为A. 6B. 4C.D. 28. A. 0 ::: b ::: a ::: 1B. 0 ■. a ::: b ::: 1C.函数 f x 二 cos x — !A.最小正周期为2二的偶函数B.C. 最小正周期为2二的奇函数D.9.高8m 和4m 的两根旗杆笔直地竖在水平地面上1 ::: b ■. a 最小正周期为 最小正周期为 D. 1 :: a b二的偶函数 二的奇函数,且相距10m ,则地面上观察两旗杆顶端7. A.圆 B.椭圆 C.双曲线 D.抛物线10.已知函数 f x 二 x -sinx ,若 x 1,x 2—且f 咅 f x 20,则下列不等式中A. xx 2 B.捲:x 2 C. x x 2 0D.为X 2 :: 0二、填空题:本大题共 5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11〜13题)(1)求tan 的值;⑵求tani*亠2 的值.(二)选做题(14~ 15题,考生只能从中选做一题) 14.(坐标系与参数方程选做题)已知直线I 的参数方程为 ^1 t ,(参数L R ),“ =4—2t.'x=2cos0+2,- .圆C 的参数方程为(参数v • 10,2二I ),y =2si n 日.则直线I 被圆C 所截得的弦长为 __________ .15. (几何证明选讲选做题)如图3,半径为5的圆O 的两条弦BC =6,则弦AD 的长度为 ___________三、解答题:本大题共 6小题,满分80分•解答须写出文字说明、证明过程和演算步骤, 16. (本小题满分12分)17. (本小题满分12分)关系?(3)若从这20个人中抽出1人来了解有关情况,求抽到的学生数学成绩与物理成绩至少有一门 不优秀的概率• 参考数据:2某学校课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级 分)如下表所示: 若单科成绩85分以上(含85分),则该科成绩为优秀. 20名学生某次考试成绩(满分 100①假设有两个分类变量为2 2列联表)为:则随机变量K2n ad -bea b cd a c b d,其中n = a b c d 为样本容量;X 和Y ,它们的值域分别为l 为,x 2』和]% , y 2』,其样本频数列联表(称218. (本小题满分14分)在长方体ABCD-ABQ I D,中,AB 二BC =1,AA =2,1点M是BC的中点,点N是AA的中点.⑴求证:MN //平面ACD ;⑵过N,C,D三点的平面把长方体ABCD-ABQ I U截成两部分几何体,求所截成的两部分几何体的体积的比值.19. (本小题满分14分)我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的•某市用水收费标准是:水费二基本费超额费定额损耗费,且有如下三条规定:①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月定额损耗费②若每月用水量超过m立方米时,除了付基本费和定额损耗费外,超过部分每立方米付③每户每月的定额损耗费a不超过5元.(1)求每户每月水费y (元)与月用水量x (立方米)的函数关系;(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.a元;n元的超额20. (本小题满分14分)2 2已知椭圆G :笃•爲=1(a b .0)的右焦点F2与抛物线C2:y2 = 4x的焦点重合,a b5椭圆C l与抛物线C2在第一象限的交点为P , | PF2 | .圆C3的圆心T是抛物线C2上的动点,3圆C3与y轴交于M ,N两点,且|MN |=4.(1)求椭圆G的方程;(2)证明:无论点T运动到何处,圆C3恒经过椭圆C i上一定点.21. (本小题满分14分)f l 1(i)判断数列g '是否为等差数列,并说明理由2n Jn + n⑵证明:1a n bn 1.已知数列和:b n [满足a i,且对任意n • N *都有a n b^1,an 1a nb n1-a ;2010年广州市普通高中毕业班综合测试(二)数学(文科)试题参考答案及评分标准说明:1 •参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2•对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半; 如果后继部分的解答有较严重的错误,就不再给分.3 •解答右端所注分数,表示考生正确做到这一步应得的累加分数.4 •只给整数分数,选择题和填空题不给中间分.、选择题:本大题主要考查基本知识和基本运算•共10小题,每小题5分,满分50分.题号12345678910答案B A B B C C B D A C、填空题:本大题主要考查基本知识和基本运算•本大题共满分20分•其中14〜15题是选做题,考生只能选做一题.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤•16 •(本小题满分12分)(本小题主要考查同角三角函数的基本关系、两角和与差的正切等知识,考查化归与转化的数学思想方法和运算求解能力)(兀)I0,?!,sin a二tan :cos acos:5小题,考生作答4小题,每小题5分, 11 •12. =1 213. 3n —3n 1 15. 2,5(1) 解:T sin -■52 ^551 ⑵解法1:••• tan J ,32 tan -2 13_21—13..., 2 =潮:潮2〔1 - tan a tan 2卩132 4=2.解法2■- tan :■:亠,]-tan 二tan :1 12 3“ 1 11 一-2 3.tan: 2 严1 - tan(a + P )tan P6分,8分10分12分6分8分10分1111-1 -3=2. 12分17 .(本小题满分12分)(本小题主要考查独立性检验的基本思想、方法及其简单应用和概率等知识 以及数据处理能力、运算求解能力和应用意识 )(1)解:2X2列联表为(单位:人):数学成绩优秀数学成绩不优秀 合计 物理成绩优秀 5 2 7 物理成绩不优秀 1 12 13 合计61420,4分(2) 解:提出假设H 。
2010年宝鸡市高三市二检数学文试题

2010年宝鸡市高三教学质量检测(二)数 学 试 题(文)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,其中第II 卷第15考题为三选一,其它题为必考题,考生作答时,将答案写在答题卡上,在本试卷上答题无效,本试卷满分150分,考 试时间120分钟。
注意事项: 1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2.选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚,将答案书写在答题卡规定的位置上。
3.所有题目必须在答题卡上作答,在试卷上答题无效。
第Ⅰ卷一、选择题. 本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U=}51|{≤≤-∈x Z x ,A ={1,2,5},}41|{<<-∈=x N x B ,则B ∩C U A =( )A .{3}B .{0,3}C .{0,4}D .{0,3,4} 2.若复数21i i-的实部与虚部分别为a 、b ,则a b 等于( )A .2 B. 2i C -2 D i 2- 3.已知函数()21l o g 3xfx x ⎛⎫=- ⎪⎝⎭,若实数0x 是方程()0f x =的解,且100x x <<,则()1fx 的值为A .恒为正值B .等于0C .恒为负值D .不大于04.已知()()2,1,1,3-=-=b a ,若()()b k a b a ++-∥2,则实数k 的值是A. -17B. 21-C.1819 D.355.设cb a ,,是空间三条直线,βα,是空间两个平面,则下列命题中,逆命题不成立的是 ( ) A .当α⊥c 时,若β⊥c ,则βα// B .当α⊂b 时,若β⊥b ,则βα⊥C .当α⊂b ,且c 是a 在α内的射影时,若c b ⊥,则b a ⊥D .当α⊂b ,且α⊄c 时,α//c ,则c b //6.已知直线422=+=+y x a y x 与圆交于A ,B 两点,且||||B O A O B O A O -=+(其中O 为坐标原点),则实数a 是( )A .2B .-2C .2或-2D .或6-68.已知变量x y ,满足约束条件⎪⎩⎪⎨⎧≤-+≥≤+-07102y x x y x ,则y x 的取值范围是( )A .⎥⎦⎤⎢⎣⎡6,59B .[)965⎛⎤-∞+∞ ⎥⎝⎦,, C .(][)36-∞+∞ ,, D .[36],9. “21=m ”是“直线03)2()2(013)2(=-++-=+++y m x m my x m 与直线互相垂直”的( ).A .充要条件B .必要而不充分条件C .充分而不必要条件D .既不充分也不必要条件10.函数221ln )(x x x f -=的图象大致是A .B .C .D .第II 卷本卷包括必做题和选做题两部分.其中第15题为选做题,考生根据要求做答;其余题为必做题,每个试题考生都必须做答.二、填空题. 本大题共7小题, 11~14题为必做题,15题为选做题;考生作答5小题,每小题5分,满分25分11. 下图是一个空间几何体的主视图、侧视图、俯视图,如果主视图、侧视图所对应的三角形都是边长为2的正三角形,俯视图对应的四边形为正方形,那么这个几何体的体积为 .12 .设n S 为等差数列{}n a 的前n 项和,若41a =,510S =,则当n S 取得最大值时,n 的值为 .13.对一个作直线运动的质点的运动过程观测了8次,得到如下表所示的数据.在上述统计数据的分析中,一部分计算见如图所示的算法流程图(其中a 是这8个数据的平均数),则输出的S 的值是________.14.如下图,对大于或等于2的自然数m 的n 次幂进行如下方式的“分裂”.仿此,52的“分裂”中最大的数是___________,若m 3的“分裂”中最小的数是211,则m 的值为___________.15.选做题:A .在极坐标系中,圆2cos ρθ=的圆心的极坐标是 ,它与方程(0)4πθρ=>所表示的图形的交点的极坐标是 .B. 如图B, AB 为⊙O 的直径, AC 切⊙O 于点A ,且cm AC 22=,过C 的割线CMN 交AB 的延长线于点D ,CM=MN=ND.AD 的长等于 cm . C .若关于x 的不等式23x x a -+-<的解集为∅,则实数a 的取值范围是 .三、解答题. 本大题共6小题,满分75分,解答须写出文字说明、证明过程或演算步骤.16.(本题满分12分) 已知函数)0)(2sin(sin 3sin )(2>++=ωπωωωx x x x f π的最小正周期为.(1)求);(x f (2)当)(,]2,12[x f x 求函数时ππ-∈的值域.17. (本题满分12分)现有8名数理化成绩优秀者,其中123A A A ,,数学成绩优秀,123B B B ,,物理成绩优秀,12C C ,化学成绩优秀.从中选出数学、物理、化学成绩优秀者各1名,组成一个小组代表学校参加竞赛.(Ⅰ)求1C 被选中的概率;(Ⅱ)求1A 和1B 不全被选中的概率. 18. (本题满分12分)如图,已知三棱锥A —BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 中点,D 为PB 中点,且△PMB 为正三角形. (1)求证:DM ∥平面APC ; (2)求证:平面ABC ⊥平面APC ;19.(本题满分12分)已知函数3()=3(0)f x x ax a ->. (1)当1a =时,求()f x 的单调区间; (2)求函数()y f x =在[]x ∈0,1上的最小值. 20.(本题满分13分)已知椭圆22122:1(0)xyC a b a b+=>>的离心率为33,直线l :2y x =+与以原点为圆心、以椭圆1C 的短半轴长为半径的圆相切.(1)求椭圆1C 的方程;(2)设椭圆1C 的左焦点为1F ,右焦点2F ,直线1l 过点1F 且垂直于椭圆的长轴,动直线2l 垂直1l 于点P ,线段2P F 垂直平分线交2l 于点M ,求点M 的轨迹2C 的方程;(3)设00(,)P x y 是轨迹2C 上一定点,过点P 且倾斜角互补的两条直线与轨迹2C 的另一个交点分别为点A 、B .求证:直线AB 的斜率为定值.21.(本题满分14分)已知数列{}n a 满足121n n a a +=-,且13a =,11n n n n a b a a +-=,数列{}n b 的前n 项和为n S .(1)求证数列{1}n a -是等比数列; (2)求{}n a 的通项公式;(3)求数列{}n b 的前n 项和为n S ;数学(文科)参考答案:一、选择题:11.334 12. 4或5 13.7 14. 52的“分裂”为其中最大的数为9,m 3的分裂数的数构成211为首项,2为公差且项数为m 的等差数列,其m 项的和即为m 3,则3(1)21122m m m m-⨯+⨯=,22100m m --=,(15)(14)0m m -+=,15m =,故填9;15.15.A.(1,0),)4πB.27 C.(,1]-∞ 三、解答题: 16. 解:(1)x x xx f ωωωcos sin 322cos 1)(+-=.21)62sin(212cos 212sin 23+-=+-=πωωωx x x,0,)(>ωπ且的最小正周期为函数x f.1,22==∴ωπωπ解得.21)62sin()(+-=∴πx x f(2)].65,3[62],2,12[πππππ-∈-∴-∈x x 根据正弦函数的图象可得:当3,262πππ==-x x 即时,)62sin()(π-=x x g 取最大值1当12,362πππ-=-=-x x 即时,.23)62sin()(--=取最小值πx x g,2321)62sin(2321≤+-≤-∴πx即].23,231[)(-的值域为x f 17. 解:(1)从8人中选出数学、物理、化学成绩优秀者各1名,其一切可能的结果组成的基本事件空间Ω={111112121()()()A B C A B C A B C ,,,,,,,,,122131()()A B C A B C ,,,,,, 132()A B C ,,,211212221()()()A B C A B C A B C ,,,,,,,,,222()A B C ,,, 231()A B C ,,,232()A B C ,,,311312321()()()A B C A B C A B C ,,,,,,,,, 322331332()()()A B C A B C A B C ,,,,,,,,}由18个基本事件组成.由于每一个基本事件被抽取的机会均等,因此这些基本事件的发生是等可能的.用M 表示“1C 恰被选中”这一事件,则M ={111()A B C ,,,121()A B C ,,,131()A B C ,,,211()A B C ,, ,221()A B C ,,,231()A B C ,,,311()A B C ,,,321()A B C ,,,331()A B C ,,}事件M 由9个基本事件组成,因而91()182P M ==.(2)用N 表示“11,A B 不全被选中”这一事件,则其对立事件N 表示“11,A B 全被选中”这一事件,由于N ={111112()()A B C A B C ,,,,,},事件N 有2个基本事件组成, 所以21()189P N ==,由对立事件的概率公式得18()1()199P N P N =-=-=.18. 【解】(1)∵M 为AB 中点,D 为PB 中点,∴MD//AP , 又∴MD ⊄平面ABC∴DM//平面APC .(2)∵△PMB 为正三角形,且D 为PB 中点. ∴MD ⊥PB .又由(1)∴知MD//AP , ∴AP ⊥PB . 又已知AP ⊥PC ∴AP ⊥平面PBC , ∴AP ⊥BC , 又∵AC ⊥BC . ∴BC ⊥平面APC , ∴平面ABC ⊥平面PAC ,19. 解:(Ⅰ)当1a =时,3()3f x x x =-,所以()()'2()33311f x x x x =-=+-,令'()0f x =得:1x =±.列表:∴()f x 的单调递增区间是(),1-∞-,()1,+∞;单调递减区间是()1,1-.(Ⅱ)由3()3(0)f x x ax a =->得('2()333f x x a x x =-=+-∵[]0,1x ∈∴①当0<a <1时,∴当x =()f x 取得最小值,最小值为2-②当a ≥1时()f x ≤0,()f x 在[]0,1x ∈上是减函数,当1x =时,()f x 取得最小值,最小值为1-3a . 综上可得:m in2(01)()13,(1)a f x a a ⎧-⎪=⎨-⎪⎩<<≥ 20. 解:(1)∵2222222232,31,33b acb a ace e =∴=-==∴=∵直线22202:b y x y x l =+=--与圆相切, ∴2,2,222==∴=b b b ,∴32=a∵椭圆C 1的方程是12322=+yx.(2)∵MP=MF 2,∴动点M 到定直线1:1-=x l 的距离等于它到定点F 1(1,0)的距离, ∴动点M 的轨迹是C 为l 1准线,F 2为焦点的抛物线∴点M 的轨迹C 2的方程为 x y 42=(3)设A 11(,)x y 、B 22(,)x y ,因为A 、B 、P 三点在抛物线x y 42=上,则2114y x = ① , 2224y x = ② , 2004y x = ③,由直线PA 与直线PB 的斜率互补可得:PA PB k k =-,即10201020y y y y x x x x --=--- ,结合①②③可得1020222211y y y y y yy y--=---,从而有1202y y y +=所以2121222121214()42AB y y y y k x x y y y y y --====--+,即直线AB 的斜率为定值21. 解:(1)∵13a =,121n n a a +=-,∴112(1)n n a a +-=-{1}n a ∴-是以112a -=为首项,以2为公比的等比致列(2)由(1)知11222n n n a -∴-=⋅= ,21,n n a ∴=+(3)由(2)知1122(21)(21)nn n nn n n b a a ++∴==++1112121nn -=-++12231111111111()()()321212121212121n nn n S ++∴=++-+++=-+++++++ .。
2010吉林市高三第二次市统考(数学文)

吉林市普通中学2009—2010学年度高中毕业班下学期期中教学质量检测数学(文科)审核:朱攀本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22题~第24题为选考题,其他题为必考题。
考生作答时将答案答在答题卡上,在本试卷上答题无效。
注意事项:1、答题前,考生务必将自己的学校、班级、姓名、准考证号填写在答题卡上,认真核对条形码上的准考证号,并将条形码粘贴在答题卡指定的位置上。
2、选择题答案使用2B 铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整,笔迹清楚。
3、请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4、保持卡面清洁,不折叠、不破损。
参考公式:样本数据n x x x ,21,的标准差])()()[(122221x x x x x x ns n -++-+-=其中x 为样本的平均数 柱体体积公式Sh V =其中S 为底面面积,h 为高锥体体积公式Sh V 31=其中S 为底面面积,h 为高 球的表面积、体积公式24R S π=,334R V π=其中R 表示球的半径第Ⅰ卷一、选择题:本大题共12题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合x x M <-=1{≤1},x N {=0}2<<x ,则=N M A .x {}21<<-x B .x {0x <≤1}C .x x <-1{≤1}D .∅2.已知i 是虚数单位,复数ii-1的虚部是 A .2i -B .12C .12-D .12i 3.已知双曲线的焦点分别为)05(1,-F 、)05(2,F ,若双曲线上存在一点P 满足8=-,则此双曲线的标准方程为A .191622=-yx B .116922=-yx C .1366422=-y xD .13422=-y x 4.阅读右边的程序框图,若输入的a 、b 、c 分别是1、2、3, 则输出的a 、b 、c 分别是 A .3、1、2B .1、2、3C .2、1、3D .3、2、15.化简=-20sin 2135sin 2A .21B .21-C .-1D .16.若a 3.02=,b 2sin =,c 3.0log 2=,则第4题图A .a <b <cB .c <a <bC . b <c <aD .c <b <a7.已知三条不同直线m ,n ,l ,三个不同平面γβα,,,有下列命题: ①若m ∥n ,α⊥m ,则α⊥n ;②若m n m ⊥=⊥,,βαβα ,则β⊥n ;③若α∥β,γβ⊥,则γα⊥; ④若βαβα////n m ,,⊥,则n m ⊥. 其中正确的命题个数是 A .1 B .2C .3D .48.高三某班50名学生,在一模数学考试中, 成绩全部介于70分与130分之间,将成 绩按如下方式分成六组: 第一组,成绩 大于等于70分且小于80分;第二组,成 绩大于等于80分且小于90分;…… 第 六组,成绩大于等于120分且小于等于 130分.右图是按上述分组方法得到的频 率分布直方图.则90分以下(不含90分) 的人数为 A .9 B .10 C .18D .199.已知△ABC 的面积为23,AC =2,60=∠BAC 则=∠ACB A . 30B . 60C . 90D . 15010.已知实数x ,y 满足⎪⎩⎪⎨⎧ ,则y x -3的最大值为A .1B .2C .4D .511. 如右图所示,点P 是函数)sin(2ϕω+=x y (x ∈R ,0>ω)的图像的最高点,M 、N 是图像与x 轴的交点,若0=⋅,则=ωA .8B .8πC .4π D .2π 12.已知定义在R 上的偶函数f (x )在[0,+∞)上是增函数,则使不等式f (2x - 1)≤f (x -2)x ≥1 y ≤2 y x -≤0第11题图第8题图成立的实数x 的取值范围是A .[–1,1]B .(-∞,1]C .[0,1]D .[-1,+∞)第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,第22题~第24题为选考题,考生根据要求作答.二.填空题:本大题共4个小题,每小题5分.13.右图是一个几何体的三视图,根据图中数据,可得该几何体的体积为 . 14.抛物线x y 42=的焦点到准线的距离为 .15.函数xxe x f =)(在1=x 处的切线斜率为 .16.已知单位向量a ,b满足ak -=+ (k >0),则⋅ 的最小值为 .三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知在公比为实数的等比数列}{n a 中,43=a ,且4a ,45+a ,6a 成等差数列. (Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设数列}{n a 的前n 项和为n S ,求10S 。
2010深圳二模数学文科试题与答案

广东省深圳市2010年高三年级第二次调研考试数学试题(文科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,有且只有一项是符合题目要求的. 1.{}1234U =若,,,,{}12M =,,{}23N =,,则 U M N =() ð( )A .{}2B .{}4C .{}1 2 3,,D .{}1,2,42.设i 是虚数单位,则复数2i 1i +-()()在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3.命题:“若21x <,则11x -<<”的逆否命题是 ( ) A .若21x ≥,则1x ≥,或1x ≤- B .若11x -<<,则21x < C .若1x >,或1x <-,则21x > D .若1x ≥,或1x ≤-,则21x ≥ 4.已知等差数列{}n a 中,6104202a a a +==,,则12a 的值是 ( )A .18B .20C .26D .28 5.在ABC ∆中,若sin :sin :sin 4A B C ABC ∆是( )A .锐角三角形B .直角三角形C .钝角三角形D .等边三角形6.若函数y f x =()的图象如左下图所示,则函数1y f x =-+()的图象大致为( )7.若实数x y ,满足100x y x y ≤⎧⎪≥⎨-≥⎪⎩,则x y +的取值范围是 ( )A .20-[,]B .01[,]C .12[,]D .02[,] 8.两个完全相同的长方体的长、宽、高分别为5cm ,4cm ,3cm ,把它们重叠在一起组成一个对角线最长的新长方体,则该最长对角线的长度是 ( )AcmB.C.D.9.如图,在OAB ∆中,P 为线段AB 上的一点,OP xOA yOB =+ , 且2BP PA =,则 ( )A .2133x y ==, B .1233x y ==,C .1344x y ==,D .3144x y ==,A BCDD. C.B.A. (xf y =y f x =()10.若曲线21:20C y px p =>()的焦点F 恰好是曲线22222:100x y C a b a b-=>>(,)的右焦点,且1C 与2C 交点的连线过点F ,则曲线2C 的离心率为 ( )A1 B1 CD二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11~13题)11.上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》,因其诞生于大芬村,因此被命名为《大芬丽莎》.根据下图所示的频率分布直方图,估计这507个画师中年龄在[)30 35,岁的人数约为12133x =+-(二)选做题(14、15题,考生只能从中选做一题,如两题都做,只按第14题计分) 14.(坐标系与参数方程选做题)极坐标方程分别为4cos ρθ=和8sin ρθ=-的两个圆的圆心距为 .15.(几何证明选讲选做题)已知圆的直径10AB =,C 为圆上一点,过C 作CD AB ⊥于D (AD BD <),若4CD =,则AC 的长为 . 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.已知向量m (sin cos )x x =-,,n (cos sin )θθ=-,,其中0πθ<<.函数f x =()m n ⋅在πx =处取最小值. (Ⅰ)求θ的值;(Ⅱ)设A ,B ,C 为ABC ∆的三个内角,若sin 2sin B A =,12f C =(),求A . 17.汽车是碳排放量比较大的行业之一.欧盟规定,从2012年开始,将对2CO 排放量超过130g/km 的M1型新车进行惩罚.某检测单位对甲、乙两类M1型品牌车各抽取5辆进行2CO 排放量检测,记录如下(单位:g/km ). (第11题图)(第12题图)经测算发现,乙品牌车2CO 排放量的平均值为120x =乙g/km .(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,则至少有一辆不符合2CO 排放量的概率是多少? (Ⅱ)若90130x <<,试比较甲、乙两类品牌车2CO 排放量的稳定性.18.(本小题满分14分)一个三棱柱111ABC A B C -直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设E 、F 分别为1AA 和11B C(Ⅰ)求几何体11E B C CB -(Ⅱ)证明:1//A F 平面1EBC ; (Ⅲ)证明:平面EBC ⊥平面1EB19.已知函数29()(3)e 4x f x x x =-+(Ⅰ)求函数f x ()的图象在0x =处的切线方程; (Ⅱ)求函数f x ()在区间[]1 2-,上的最大值与最小值. 20.(本小题满分14分)已知圆22:50C x t y t ++=>()()和椭圆2222:1x y E a b+=0a b >>()的一个公共点为02B (,).F 为椭圆E 的右焦点,直线BF 与圆C 相切于点B . (Ⅰ)求t 值和椭圆E 的方程; (Ⅱ)圆C 上是否存在点M ,使M B F ∆为等腰三角形?若存在,求出点M 的坐标.21.(本小题满分14分)已知数列{}n a 满足:1221,222,2n n n na n a n a n +⎧+⎪⎪=⎨⎪+⎪⎩为正奇数为正偶数. (Ⅰ)问数列{}n a 是否为等差数列或等比数列?说明理由; (Ⅱ)求证:数列22nna ⎧⎫⎨⎬⎩⎭是等差数列,并求数列{}2n a 的通项公式; (Ⅲ)设21n n b a -=,求数列{}n b 的前n 项和n S .参考答案一、选择题:本大题共10小题,每小题5分,共50分.二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题) 11.177; 12.54;(如写45A = 不扣分) 13.223+; (二)选做题(14、15题,考生只能从中选做一题) 14.52; 15.54三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)解:(Ⅰ) ()f x =m n ⋅sin cos cos sin x x θθ=+)sin(θ+=x ……………………………2分又 函数()f x 在πx =处取最小值,1)sin(-=+∴θπ , 即 s i n1θ=- ……………………………3分 又0πθ<<,π2θ∴=…………………………5分 π()sin()cos 2f x x x ∴=+= …………………6 分(Ⅱ)法一:∵21)(=C f ,21cos =∴C0πC << , π3C ∴=. ………………………………8 分πA B C ++= ,∴ 2π3B A =- ………………………………9分 代入A B sin 2sin =中,2πsin()2sin 3A A ∴-=, 2π2πsin cos cos sin 2sin 33A A A ∴-=,33tan =∴A , ……………10分 0πA << ,π6A ∴=. …………………12分(Ⅱ)法二:∵21)(=C f ,21cos =∴C 0πC << ,π3C ∴=. ………………………………8 分 A B sin 2sin = ,由正弦定理有a b 2=. ……………………………9分又由余弦定理得222222π2cos 422cos 33c a b ab C a a a a a =+-=+-⋅⋅=222b c a =+∴, π2B ∴=……………………………11分πA B C ++= ,π6A ∴=. ……………………………12分 17.(本小题满分13分)解:(Ⅰ)从被检测的5辆甲类品牌车中任取2辆,共有10种不同的2CO 排放量结果:110,80;120,80;140,80;150,80;120,110;140,110;150,110;140,120;150,120;150,140 ……3分设“至少有一辆不符合2CO 排放量”为事件A ,则事件A 包含以下7种不同的结果:140,80;150,80;140,110;150,110;140,120;150,120;150,140 ………………5分所以,7.0107)(==A P ………6分 答:至少有一辆不符合2CO 排放量的概率为7.0 …………………7分 (Ⅱ)由题可知,120==乙甲x x ,220=+y x ………………7分()22580120S =-+甲()+-2120110()+-2120120()+-2120140()30001201502=-25S =乙()+-2120100()+-2120120()+-2120x ()+-2120y ()2120160- +=2000()+-2120x ()2120-y ………………8分220,x y +=∴ 25S =乙+2000()+-2120x ()2100-x ,令t x =-120,13090<<x ,1030<<-∴t ,25S ∴=乙+2000+2t ()220+t ,2255S S ∴-=乙甲22406002(30)(10)0t t t t +-=+-< ……………12分 120==乙甲x x ,22<S S 乙甲, ∴乙类品牌车碳排放量的稳定性好。
安微省合肥市2010年高三第二次教学质量检测(数学文)

安徽省合肥市2010年高三第二次教学质量检测数学试题(文科)(考试时间:120分钟,满分:150分)注意事项: 1.答卷前,考生先使用黑色字迹的签字笔将自己的学校、姓名、准考证号填写在指定位置;核对条形码上本人的姓名和准考证号码,无误后,将共粘贴在指定的方框内。
2.非选择题答题书写要工整,字迹清晰。
修改答案时禁止使用涂改液或涂改胶条。
3.请在题号指定的答题区域内作答,在题号指定区域以外答题或超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.考试结,监考人将答题卷收回,试卷不收回。
第Ⅰ卷(满分50分)一、选择题(本大题共10小题,每题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合{|06,},{1,3,6},{1,4,5}U x x x Z A B =≤≤∈==,则()U A C B ⋂= ( )A .{1}B .{3,6}C .{4,5}D .{1,3,4,5,6} 2.复数132ii +=+( )A .5533i +B .1533i -+ C .1i +D .1755i -+ 3.已知sin()2sin(),sin cos 2ππαααα-=-+⋅=则 ( )A .25B .25-C .25或25- D .15-4.某农科院在2×2的4块式验田中选出2块种植某品种水稻进行试验,则每行每列都有一块试验田种植水稻的概率为 ( ) A .23B .12C .16D .135.函数()y f x =的图像如右图所示,则()y f x '=的图像可能是 ( )6.甲乙两名学生,六次数学测验成绩(百分制)如图所示。
①甲同学成绩的中位数大于乙同学成绩的中位数 ②甲同学的平均分比乙同学高 ③甲同学的平均分比乙同学低 ④甲同学珠方差小于乙同学成绩的方差 上面说法正确的是 ( ) A .③④ B .①②④ C .②④ D .①③④ 7.右图是某四棱锥的三视图,则该几何体的表面积等于( )A .34+B .6+C .6+D .17+8.在直角梯形ABCD 中,AB//CD ,,45AD AB B ⊥∠=°,AB=2CD=2,M 为腰BC 的中点,则MA MD ⋅= ( )A .1B .2C .3D .49.已知双曲线22221x y a b-=,F 1是左焦点,O 是坐标原点,若双曲线上存在点P ,使1||||PO PF =,则此双曲线的离心率的取值范围是( )A .(]1,2B .(1,)+∞C .(1,3)D .[)2,+∞10.已右函数21(0)()(1)1(0)x x f x f x x ⎧-≤=⎨-+>⎩,把函数()()g x f x x =-的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为( )A .*(1)()2nn n an N -=∈ B .*(1)()n a n n n N =-∈ C .*1()n a n n N =-∈D .*22()nn a n N =-∈第Ⅱ卷(满分100分)二、填空题(本大题共5题,每小题5分,共25分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽省合肥市2010年高三第二次教学质量检测数学试题(文科)(考试时间:120分钟,满分:150分)注意事项: 1.答卷前,考生先使用黑色字迹的签字笔将自己的学校、姓名、准考证号填写在指定位置;核对条形码上本人的姓名和准考证号码,无误后,将共粘贴在指定的方框内。
2.非选择题答题书写要工整,字迹清晰。
修改答案时禁止使用涂改液或涂改胶条。
3.请在题号指定的答题区域内作答,在题号指定区域以外答题或超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.考试结,监考人将答题卷收回,试卷不收回。
第Ⅰ卷(满分50分)一、选择题(本大题共10小题,每题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合{|06,},{1,3,6},{1,4,5}U x x x Z A B =≤≤∈==,则()U A C B ⋂= ( )A .{1}B .{3,6}C .{4,5}D .{1,3,4,5,6} 2.复数132ii +=+( )A .5533i +B .1533i -+ C .1i +D .1755i -+ 3.已知sin()2sin(),sin cos 2ππαααα-=-+⋅=则 ( )A .25B .25-C .25或25- D .15-4.某农科院在2×2的4块式验田中选出2块种植某品种水稻进行试验,则每行每列都有一块试验田种植水稻的概率为 ( ) A .23B .12C .16D .135.函数()y f x =的图像如右图所示,则()y f x '=的图像可能是 ( )6.甲乙两名学生,六次数学测验成绩(百分制)如图所示。
①甲同学成绩的中位数大于乙同学成绩的中位数 ②甲同学的平均分比乙同学高[来源:学科网ZXXK] ③甲同学的平均分比乙同学低④甲同学珠方差小于乙同学成绩的方差 上面说法正确的是 ( )A .③④B .①②④C .②④D .①③④7.右图是某四棱锥的三视图,则该几何体的表面积等于( )A .3465+B .66543+C .663413+D .1765+8.在直角梯形ABCD 中,AB//CD ,,45AD AB B ⊥∠=°,AB=2CD=2,M 为腰BC 的中点,则MA MD ⋅=( )A .1B .2C .3D .49.已知双曲线22221x y a b-=,F 1是左焦点,O 是坐标原点,若双曲线上存在点P ,使1||||PO PF =,则此双曲线的离心率的取值范围是( )A .(]1,2B .(1,)+∞C .(1,3)D .[)2,+∞10.已右函数21(0)()(1)1(0)x x f x f x x ⎧-≤=⎨-+>⎩,把函数()()g x f x x =-的零点按从小到大的顺序排列成一个数列,则该数列的通项公式为 ( )A .*(1)()2nn n an N -=∈ B .*(1)()n a n n n N =-∈ C .*1()n a n n N =-∈D .*22()n n a n N =-∈第Ⅱ卷(满分100分)二、填空题(本大题共5题,每小题5分,共25分。
) 11.不等式1101x ->-的解集是 。
[来源:学|科|网Z|X|X|K]12.已知,x y 满足不等式组00639x y x y x y ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩,则2x y +的最大值是 。
13.已知下列命题: ①已知,αβ表示两个不同的平面,m 为平面α内的一条直线,则“αβ⊥”是“m β⊥”的充要条件; ②函数()sin(2)6f x x π=+图象对称中心的坐标为(,0),212k k Z ππ-∈; ③同时抛掷两枚质地均匀的硬币“一枚正面向上,一枚反面向上”概率为12; ④在ABC ∆中,若2sin b a B =(其中,a b 分别为,A B ∠∠的对边),则A 等于30°,其中真命题的序号是 (填上所有正确的序号)。
14.直线l 与曲线ln y x =相切,且平行于直线260x y -+=,则l 的方程为 。
15.以正方体八个顶点中的四个顶点为顶点的四面体中,其中对棱互相垂直的四面体的个数是 。
三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.) 16.(本小题满分12分)已知向量(sin ,23sin ),(2cos ,sin )a x x b x x ==,定义() 3.f x a b =⋅(I )求函数(),y f x x R =∈的单调递减区间; (I I )若函数()(0)2y f x πθθ=+<<为偶函数,求θ的值。
某市教育行政部门为了对2010届高毕业生学业水平进行评价,从该市高中毕业生抽取1000名学生学业水平考试数学成绩为样本进行统计,已知该样本中的每个值都是[40,100]中整数,且在[)[)[)[)[)40,50,50,60,60,70,70,80,80,90,[80,100]上的频率分布直方图如右图所示。
记这1000名学生学业水平考试数学平均成绩的最小可能值为a ,最大可能值为b 。
(1)求,a b 的值;(2)从这1000名学生中任取1人,试根据直方图估计其成绩位于[,a b ]中的概率(假设各小组 数据平均分布在相应区间内的所有整数上。
)18.(本小题满分12分)如图,PO ⊥平面ABCD ,点O 在AB 上,EA//PO ,四边形ABCD 为直角梯形,BC ⊥AB ,BC=CD=BO=PO ,1.2EA AO CD ==(1)求证:BC ⊥平面ABPE ;(2)直线PE 上是否存在点M ,使DM//平面PBC ,若存在,求出点M ;若不存在,说明理由。
[来源:学§科§网Z §X §X §K]某电视生产厂家有A 、B 两种型号的电视机参加家电下乡活动。
若厂家投放A 、B 型号电视机的价值分别为,p q 万元,农民购买电视机获得的补贴分别为12,ln 105p q 万元。
已知厂家把总价值为10万元的A 、B 两种型号电视机投放市场,且A 、B 两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到0.1,参考数据:ln 4 1.4=)[来源:学科网] 20.(本小题满分13分)各项均不为零的数列{}n a ,首项11a =,且对于任意*n N ∈均有111620,.n n n n n na a a ab a ++--==(1)求数列{}n b 的通项公式;(2)数列{}n a 的前n 项和为n T ,求证: 2.n T <已知焦点在x 轴上,中心在坐标原点的椭圆C 的离心率为45,且过点102(3(1)求椭圆C 的方程;(2)直线l 分别切椭圆C 与圆222:M x y R +=(其中35R <<)于A 、B 两点,求|AB|的最大值。
参考答案一、选择题(本大题共10小题,每小题5分,共50分.) 1.B 2.C 3.B 4.D 5.C 6.A 7.A 8.B 9.D 10.C 二、填空题11.(,1)(2,)-∞⋃+∞ 12.12 13.②③14.21ln 20x y ---= 15.10三、解答题:16.解:21cos 2()2sin cos 233sin 2223xf x x x x x -=+=+sin 2322sin(2)3x x x π=-=-(1)令3222232k x k πππππ+≤-≤+解得单调递减区间是511[,],.122k k k Z ππππ++∈ (2)()2sin(22)3f x x πθθ+=+-根据三角函数图像性质可知(),(0)02y f x x πθθ=+<<=在处取最值。
sin(2)13πθ-=±52,,32212k k k Z ππππθπθ∴-=+=+∈ 又02πθ<<解得512πθ=12分 17.解:(1)0.050.1500.25600.35700.15800.19067.5a =⨯+⨯+⨯+⨯+⨯+⨯=0.05490.1590.25690.35790.15890.110076.6b =⨯+⨯+⨯+⨯+⨯+⨯= 6分 (2)127(0.2510000.351000)0.2951001010p =⨯⨯⨯+⨯⨯= 12分 18.解:(1)PO ⊥ 平面ABCD ,BC ⊂ 平面ABCD ,BC ⊥PO , 又BC ⊥AB ,AB PO O ⋂=所以BC ⊥平面ABP , 又EA//PO ,AO ⊂平面ABP ,EA ∴⊂平面PAB ,BC ∴⊥平面ABPE 。
6分 (2)点E 即为所求的点,即点M 与点E 重合。
取PB 的中点F ,连结EF ,CF ,DE , 由平面几何知识知EF//AB , 且EF=DE ,[来源:学_科_网] ∴四边形DCFE 为平行四边形, 所以DE//CF , CF 在平面PBC 内,DE 不在平面PBC 内,//DE ∴平面PBC 。
12分 19.解:[来源:] 设B 型号电视机的价值为x 万元(19x ≤≤),农民得到的补贴为y 万元, 则A 型号电视机的价值为(10)x -万元, 由题意得,1221(10)ln ln 1105510y x x x x =-+=-+ 6分 21,510y x '=-由0, 4.y x '==得 当[)1,4x ∈时,0y '>, 当(]4,9x '∈时,y <0所以当4x =时,y 取最大值,max 2ln 40.41 1.2.5y =-+≈即厂家分别投放A 、B 两型号电视机6万元和4万元时,农民得到补贴最我,最多补贴约1.2万元。
13分 20.解:(1)由11620n n n n a a a a ++--=得13112n a a =-+, 则111113(),44n n a a +-=-1113()44n n b b +-=-所以1||4n b -是以3为公比,34为首项的等比数列1133313,4444n n n n b b -+-=⨯== 6分(2)21444431313131n n n T -=++++++++2111114()3333n n -<++++11(1)13342(1) 2.1313n n -=⨯=-<- 13分[来源:学科网][来源:学,科,网Z,X,X,K] 21.解:(1)设椭圆的方程为22221(0)x y a b a b+=>>,则[来源:Z §xx §]44,55c c a a ==,2222925b ac a ∴=-=椭圆过点102(22200191925aa ∴+=,解处2225,9a b ==故椭圆C 的方程为221.259x y += 6分 (2)设1122(,),(,)A x y B x y 分别为直线l 与椭圆和圆的切点, 直线AB 的方程为:y kx m =+因为A 既在椭圆上,又在直线AB 上,从而有221259x y y kx m ⎧+=⎪⎨⎪=+⎩, 消去y 得:222(259)5025(9)0k x kmx m +=+-= 由于直线与椭圆相切,故222(50)4(259)25(9)0km k m ∆=-+⨯-=从而可得:22925m k =+ ①125kx m=-②由222x y R y kx m ⎧+=⎨=+⎩消去y 得:2222(1)0k x kmx m R +++-=由于直线与圆相切,得222(1)m R k =+ ③22kR x m= ④由①③得:222925R k R -=-22222212121||()()(1)()AB x x y y k x x ∴=-+-=+-222222222222(25)9(25)22525925m k R R R R R m R R R ---=⋅=⋅=+---2222534234304R R≤-⨯=-= 即||2AB ≤,当且仅当15R =|AB|的最大值为2。
