吉林省桦甸市第四中学2013届高考数学一轮复习数列部分训练题(二))

合集下载

吉林省桦甸市第四中学2013届高考数学第一轮复习数列部分训练题(5)

吉林省桦甸市第四中学2013届高考数学一轮复习数列部分训练题（五）班级姓名一、选择题1、（浙江理）设S n 是公差为d (d ≠0)的无穷等差数列{a n }的前n 项和，则下列命题错误．．的是 A ．若d ＜0，则数列{S n }有最大项 B ．若数列{S n }有最大项，则d ＜0C ．若数列{S n }是递增数列，则对任意的n N*，均有S n ＞0D ．若对任意的n N*，均有S n ＞0，则数列{S n }是递增数列2、（重庆理）在等差数列}{n a 中，52=a ，则}{n a 的前3项和3S = A.7 B.15 C.20 D.25 二、填空题3、（浙江理）设公比为q (q ＞0)的等比数列{a n }的前n 项和为S n ．若2232S a =+，4432S a =+，则q ＝______________．4、（重庆文）首项为1，公比为2的等比数列的前4项和S 4=___________5、（重庆文）已知{a n }为等差数列，且a 1+a 3=8，a 2+a 4=12.则n a ＝6、（江苏）现有10个数，它们能构成一个以1为首项，3-为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是．三、解答题7、（天津文）已知｛n a ｝是等差数列，其前项和为n S ，｛n b ｝是等比数列，且1a =1b =2,2744=+b a ,44b S - =10（I ）求数列｛n a ｝与｛n b ｝的通项公式；（II ）记*2211,N n b a b a b a T n n n ∈+++= ，证明：)2,(,8*11>∈=-+-n N n b a T n n n 。

8、（浙江文）已知数列{a n }的前n 项和为S n ，且S n =2n 2+n ，n ∈N ﹡，数列{b n }满足a n =4log 2b n ＋3，n ∈N ﹡。

（1）求a n ，b n ；（2）求数列{a n ·b n }的前n 项和T n 。

吉林省桦甸市第四中学2013届高考数学一轮复习程序框图部分训练题Word版含答案

吉林省桦甸市第四中学2013届高考数学一轮复习程序框图部分训练题 Word版含答案吉林省桦甸市第四中学2013届高考数学一轮复习程序框图部分训练题一、选择题1、(吉林文理)如果执行右边的开始程序框图，输入正整数aaa和实数，aaa,,...,NN(2),？N2112n？，，，输入N，输出，则( ) AB,aa11 ，B, k,1，A,为的和 AB，aaa,,...,()A12nx=k,k+1akAB，，1 为的算aaa,,...,()B12n2是 ak x>A 术平均数否 A=x AB和分别是aaa,,...,()C12n是 x<B 中最大的数和最小的数B=x 否 AB和分别是aaa,,...,()D12n中最小的数和最大的数 K?N 否是输出A，B结束2、(安徽文理)如图所示，程序框图(算法流程图)的输出结果是( )34 ()A()B,, ()C()D3、(北京文理)执行如图所示的程序框图，输出的S值为( )A. 2 B .4C.8D. 1614、(福建文理)阅读右图所示的程序框图，运行相应的程序，输出值等于( ) s,3,10A( B( C(0 D( ,25、(广东文)执行如下图所示的程序框图，若输入n的值为6，则输出S的值为( )A.105B.16C.15D.1开始 6、(辽宁文理)执行如图所示的程序框图，则输出的S的值S=4 是i=1 231 (B) (C) (D) 4 (A) ,327、(山东文理)执行下面的程序图，如果输入=4，a否 i<9 那么输出的n的值为输出S 是开始2 S=结束输入 a2,SP,0，Q,1，n,0 i,i+1否 P?Q输出n 是n结束 (A)2(B)3(C)4(D)5 aP=P+Q=2Q+1n,n+1 ，128、(陕西理)右图是用模拟方法估计圆周率,值的程序框图，表示估计结果，则图中空白P框内应填入( )N(A) P,10004N(B) P,1000MP,(C) 10004M(D) P,10009、(陕西文)下图是计算某年级500名学生期开始末考试(满分为100分)及格率q的程序框图，则图中空白框内应填入( ) 输入x,x,？,x12500NA. q= MM=0,N=0,i=1 MB q= NN否 C q= ? x,60iMN，M是开始 D.q= N,N+1 MN，M=M，1 10、(天津理)阅输入x 读右边的程序框i=i+1 图，运行相应的程否 |x|>1? 序，当输入的值x否 ,25为时，输出xi>500 是的值为 x,2x+1 是 ,11(A) (,) x= |x|,139(,) (,) 输出x 输出q结束结束311、(天津文)阅读右边的程序框图，运行相应的程序，则输出S的值为(A)8 (B)18 (C)26 (D)80二、填空题1、(广东理)执行如图所示的程序框图，若输入n开始的值为8，则输出s的值为_______(输入n 2、(湖北文理)阅读如图所示的程序框图，运行相应的程序，输出的结果s=___________.i,2，k,1，s,1否 i<n输出s 是1(s，i)S= 结束 ki=i+2k,k+1，13、(湖南理)如果执行如图所示的程序框图，输入S= . x,,1,n=3,则输出的数4x,4.54、(湖南文)如果执行如图所示的程序框图，输入,则输出的数i = .开始k?1 5、(江苏)右图是一个算法流程图，则输出的N 2k的值是 ( k,5k+4>0 k?k +1Y输出k结束6、(江西文)下图是某算法的程序框图，则程序运行后输入的结果是_________。

2013届高考数学数列的综合问题复习课件和训练题

2013届高考数学数列的综合问题复习课件和训练题2013年高考数学总复习 6-4 数列的综合问题与数列的应用但因为测试新人教B版1.(文)(2011•德州模拟)等比数列{an}的前n项和为Sn，若a1＝1，且4a1、2a2、a3成等差数列，则S4＝( ) A．7 B．8 C．15 D．16 [答案] C [解析] ∵4a1,2a2，a3成等差数列，∴4a2＝4a1＋a3，∵{an}是等比数列，a1＝1，∴4q＝4＋q2，解之得，q＝2，∴S4＝－1－1＝15. (理)(2011•丹东模拟)已知{an}为等差数列，{bn}为等比数列，其公比q≠1，且bi>0(i ＝1,2，…，n)，若a1＝b1，a11＝b11，则( ) A．a6>b6 B．a6＝b6 C．a6<b6 D．a6>b6或a6<b6 [答案] A [解析] 由条件知，a6＝a1＋a112＝b1＋b112>b1b11＝b6. 2．(2011•淄博模拟)已知{an}是递增数列，且对任意n∈N*都有an＝n2＋λn恒成立，则实数λ的取值范围是( ) A．(－72，＋∞) B．(0，＋∞) C．[－2，＋∞) D．(－3，＋∞) [答案] C [解析] an＝n2＋λn＝(n＋λ2)2－λ24，∵对任意n∈N*，an＋1>an，∴－λ2≤1，∴λ≥－2，故选C. 3．(文)(2011•福建质检)在各项均为正数的等比数列{an}中，a3a5＝ 4，则数列{log2an}的前7项和等于( ) A．7 B．8 C．27 D．28 [答案] A [解析] 在各项均为正数的等比数列{an}中，由a3a5＝4，得a24＝4，a4＝2. 设bn＝log2an，则数列{bn}是等差数列，且b4＝log2a4＝1. 所以{bn}的前7项和S7＝＋＝7b4＝7. (理)设函数f(x)＝xm＋ax的导函数f ′(x)＝2x＋1，则数列的前n项和是( ) A.nn＋1 B.n＋2n＋1 C.nn－1 D.n＋1n [答案] A [解析] f ′(x)＝mxm－1＋a＝2x＋1，∴a ＝1，m＝2，∴f(x)＝x(x＋1)，＝＋＝1n－1n＋1，∴Sn＝1－12＋12－13＋…＋1n－1n＋1＝nn＋1. 4．(文)(2011•山西运城教学检测)已知数列{an}的前n项和为Sn，过点P(n，Sn)和Q(n ＋1，Sn＋1)(n∈N*)的直线的斜率为3n－2，则a2＋a4＋a5＋a9的值等于( ) A．52 B．40 C．26 D．20 [答案] B [解析] 由题意得Sn＋1－＋－n＝3n－2，∴Sn＋1－Sn＝3n－2，即an＋1＝3n－2，∴an＝3n－5，因此数列{an}是等差数列，a5＝10，而a2＋a4＋a5＋a9＝2(a3＋a7)＝4a5＝40，故选B. (理)两个正数a、b 的等差中项是72，一个等比中项是23，且a<b，则双曲线x2a2－y2b2＝1的离心率e等于( ) A.34 B.152 C.54 D.53 [答案] D [解析] ∵a＋b＝7，a•b＝12，b>a>0，∴a＝3，b＝4.∴e＝ca＝a2＋b2a＝53. 5．(2011•江西新余四中期末)在△ABC中，sinAcosA＝2cosC ＋cosA2sinC－sinA是角A、B、C成等差数列的( ) A．充分非必要条件 B．充要条件 C．必要非充分条件 D．既不充分也不必要条件 [答案] A[来源:学#科#网] [解析] sinAcosA＝2cosC＋cosA2sinC－sinA⇒2sinAsinC－sin2A＝2cosAcosC＋cos2A⇒2cos(A ＋C)＋1＝0⇒cosB＝12⇒B＝π3⇒A＋C＝2B⇒A、B、C成等差数列．但当A、B、C成等差数列时，sinAcosA＝2cosC＋cosA2sinC－sinA不一定成立，如A＝π2、B＝π3、C＝π6.故是充分非必要条件．故选A. 6．(文)(2011•哈师大附中、东北师大附中、辽宁省实验中学联考)已知{an}是等差数列，Sn为其前n项和，若S21＝S4000，O为坐标原点，点P(1，an)，点Q(2011，a2011)，则OP→•OQ→＝( ) A．2011 B．－2011 C．0 D．1 [答案] A [解析] 由S21＝S4000得到Sn关于n＝21＋40002＝2010.5对称，故Sn的最大(或最小)值＝S2010＝S2011 ，故a2011＝0，OP→•OQ→＝2011＋an•a2011＝2011＋an×0＝2011，故选A. (理)(2011•北京西城期末)已知各项均不为零的数列{an}，定义向量cn＝(an，an＋1)，bn＝(n，n＋1)，n∈N*.则下列命题中为真命题的是( ) A．若对于任意n∈N*总有cn∥bn成立，则数列{an}是等差数列 B．若对于任意n∈N*总有cn∥bn成立，则数列{an}是等比数列 C．若对于任意n∈N*总有cn⊥bn成立，则数列{an}是等差数列 D．若对于任意n∈N*总有cn⊥bn成立，则数列{an}是等比数列 [答案] A [解析] 若对任意n∈N*，有cn∥bn，则ann＝an＋1n＋1＝an＋2n＋2，所以an＋1－an＝an＋2－an＋1，即2an＋1＝an＋an＋2，所以数列{an}为等差数列． 7．(文)(2010•浙江杭州)如图，是一个算法的程序框图，该算法输出的结果是( ) A.12 B.23 C.34 D.45 [答案] C [解析] 循环过程为i＝1<4→i＝2，m＝1，n＝11×2； i＝2<4→i＝3，m＝2，n＝11×2＋12×3； i ＝3<4→i＝4，m＝3，n＝11×2＋12×3＋13×4； i＝4<4不成立，输出n的值．故n＝11×2＋12×3＋13×4＝1－12＋12－13＋13－14＝1－14＝34. (理)(2010•北京延庆县模考)某程序框图如图所示，该程序运行后输出的k的值是( ) A．4 B．5 C．6 D．7 [答案] D [解析] 由程序框图可知，S＝1＋2＋22＋ (2)＝2k＋1－1，由S<100得，2k＋1<101，∵26＝64,27＝128，∴k＋1＝7，∴k＝6，结合语句k＝k＋1在S＝S＋2k后面知，当k＝6时，S ＝127，k的值再增加1后输出k值为7. [点评] 这是最容易出错的地方，解这类题时，既要考虑等比数列求和，在k取何值时，恰满足S≥100，又要顾及S与k的赋值语句的先后顺序． 8．(文)(2011•临沂模拟)数列{an}、{bn}都是等差数列，a1＝5，b1＝7，且a20＋b20＝60，则{an＋bn}的前20项和为( ) A．700 B．710 C．720 D．730 [答案] C [解析] ∵{an}与{bn}均为等差数列，∴{an＋bn}为等差数列，首项a1＋b1＝12，又a20＋b20＝60，∴前20项和为S20＝＋＝720. (理)(2010•湖北质检)若数列{an}满足1an＋1－1an＝d(n∈N*，d为常数)，则称数列{an}为调和数列．已知数列{1xn}为调和数列，且x1＋x2＋…＋x20＝200，则x5＋x16＝________. [答案] 20 [解析] 由题意，若{an}为调和数列，则{1an}为等差数列，∵{1xn}为调和数列，∴数列{xn}为等差数列，由等差数列的性质可知，x5＋x16＝x1＋x20＝x2＋x19＝…＝x10＋x11＝20010＝20.故填20. 9．(文)(2011•潍坊模拟)已知等比数列中，a1＝3，a4＝81，若数列{bn}满足bn＝log3an，则数列{1bnbn＋1}的前n项和Sn＝________. [答案] nn＋1 [解析] ∵a4＝a1q3，∴81＝3q3，∴q＝3，∴an＝3n，∴bn＝log3an＝n，令cn＝1bnbn＋1，则cn＝＋＝1n－1n＋1，∴{cn}的前n项和Sn＝c1＋c2＋…＋cn＝(1－12)＋(12－13)＋…＋(1n－1n＋1)＝nn＋1. (理)(2011•杭州二检)已知{an}是公差不为0的等差数列，{bn}是等比数列，其中a1＝2，b1＝1，a2＝b2,2a4＝b3，且存在常数α、β，使得an＝logαbn＋β对每一个正整数n都成立，则αβ＝________. [答案] 4 [解析] 设{an} 的公差为d，{bn}的公比为q，则2＋d＝＋＝q2，解得q＝2d＝0(舍去)或q＝4d＝2，所以an＝2n，bn＝4n －1.若an＝logαbn＋β对每一个正整数n都成立，则满足2n＝logα4n－1＋β，即2n＝(n－1)logα4＋β，因此只有当α＝2，β＝2时上式恒成立，所以αβ＝4. 10．(文)(2011•江苏镇江市质检)已知1，x1，x2,7成等差数列，1，y1，y2,8成等比数列，点M(x1，y1)，N(x2，y2)，则线段MN的中垂线方程是________． [答案] x ＋y－7＝0 [解析] 由条件得x1＝3，x2＝5，y1＝2，y2＝4，∴MN 的中点(4,3)，kMN＝1，∴MN的中垂线方程为y－3＝－(x－4)，即x ＋y－7＝0. (理)(2010•哈尔滨模拟)已知双曲线an－1y2－anx2＝an －1an(n≥2，n∈N*)的焦点在y轴上，一条渐近线方程是y＝2x，其中数列{an}是以4为首项的正项数列，则数列{an}的通项公式是________． [答案] an＝2n＋1 [解析 ] 双曲线方程为y2an－x2an －1＝1，∵焦点在y轴上，又渐近线方程为y＝2x，∴anan－1＝2，又a1＝4，∴an＝4×2n－1＝2n＋1. 11.在圆x2＋y2＝10x内，过点(5,3)有n条长度成等差数列的弦，最短弦长为数列{an}的首项a1，最长弦长为an，若公差d∈(13，23]，那么n的取值集合为( ) A．{4,5,6} B．{6,7,8,9} C．{3,4,5} D．{3,4,5,6} [答案] A [解析] ∵圆x2＋y2＝10x，∴(x－5)2＋y2＝5，圆心为(5,0)，半径为5.故最长弦长an＝10，最短弦长a1＝8，∴10＝8＋(n－1)d，∴d＝2n－1，∵d∈(13，23]，∴13<2n－1≤23，∴4≤n<7，又∵n∈N*，∴n的取值为4,5,6，故选A. 12．(文)(2011•安徽百校论坛联考)已知a>0，b>0，A为a，b的等差中项，正数G为a，b的等比中项，则ab与AG的大小关系是( ) A．ab＝AG B．ab≥AG C．ab≤AG D．不能确定 [答案] C [解析] 由条件知，a＋b＝2A，ab＝G2，∴A＝a ＋b2≥ab＝G>0，∴AG≥G2，即AG≥ab，故选C. [点评] 在知识交汇点处命题是常见命题方式，不等式与数列交汇的题目要特别注意等差(等比)数列的公式及性质的运用． (理)已知等比数列{an}的各项均为正数，公比q≠1，设P＝12(log0.5a5＋log0.5a7)，Q＝log0.5a3＋a92，P与Q的大小关系是( ) A．P≥Q B．P<Q C．P≤Q D．P>Q [答案] D [解析] P＝log0.5a5a7＝log0.5a3a9，Q＝log0.5a3＋a92，∵q≠1，∴a3≠a9，∴a3＋a92>a3a9 又∵y＝log0.5x在(0，＋∞)上递减，∴log0.5a3＋a92<log0.5a3a9，即Q<P.故选D. 13．(文)(2011•南昌一模)小王每月除去所有日常开支，大约结余a元．小王决定采用零存整取的方式把余钱积蓄起来，每月初存入银行a元，存期1年(存12次)，到期取出本和息．假设一年期零存整取的月利率为r，每期存款按单利计息．那么，小王存款到期利息为_____元． [答案] 78ar [解析] 依题意得，小王存款到期利息为12ar＋11ar＋10ar＋…＋3ar＋2ar＋ar＝＋＝78ar 元． (理)(2011•湖北荆门调研)秋末冬初，流感盛行，荆门市某医院近30天每天入院治疗流感的人数依次构成数列{an}，已知a1＝1，a2＝2，且an＋2－an＝1＋(－1)n (n∈N*)，则该医院30天入院治疗流感的人数共有________人． [答案] 255 [解析] ∵an＋2－an ＝1＋(－1)n (n∈N*)，∴n为奇数时，an＋2＝an，n为偶数时，an ＋2－an＝2，即数列{an}的奇数项为常数列，偶数项构成以2为首项，2为公差的等差数列．故这30天入院治疗流感人数共有15＋(15×2＋15×142×2)＝255人． 14．(文)(2011•江苏，13)设1＝a1≤a2≤…≤a7，其中a1，a3，a5，a7成公比为q的等比数列，a2，a4，a6成公差为1的等差数列，则q的最小值是_____． [答案] 33 [解析] ∵a1，a3，a5，a7成公比为q的等比数列，且a1＝1，∴a3＝q，a5＝q2，a7＝q3，∵a2，a4，a6成公差为1的等差数列，∴a4＝a2＋1，a6＝a2＋2，∵a2≥1，q＝a3≥a2≥1，∴q2＝a5≥a4＝a2＋1≥2，q3＝a7≥a6＝a2＋2≥3，∵q≥1，∴q≥2且q≥33，∴q≥33，∴q的最小值为33. (理)(2011•福州市期末、河北冀州期末)已知实数a、b、c、d成等比数列，且函数y＝ln(x＋2)－x当x ＝b时取到极大值c，则ad等于________． [答案] －1 [分析] 利用导数可求b、c，由a、b、c、d成等比数列可得ad＝bc. [解析] y′＝1x＋2－1，令y′＝0得x＝－1，当－2<x<－1时，y′>0，当x>－1时，y′<0，∴b＝－1，c＝ln(－1＋2)－(－1)＝1，∴ad＝bc ＝－1. 15．(2011•蚌埠质检)已知数列{an}满足，a1＝1，a2＝2，an ＋2＝an＋an＋12，n∈N*. (1)令bn＝an＋1－an，证明：{bn}是等比数列； (2)求{an}的通项公式． [解析] (1)b1＝a2－a1＝1，当n≥2时， bn＝an＋1－an＝an－1＋an2－an＝－12(an－an－1)＝－12bn－1，所以{bn}是以1为首项，－12为公比的等比数列． (2)由(1)知bn＝an＋1－an＝－12n－1，当n≥2时， an＝a1＋(a2－a1)＋(a3－a2)＋…＋(an－an－1) ＝1＋1＋－12＋…＋－12n－2＝1＋1－－12n－11－－12 ＝1＋231－－12n－2＝53－23－12n－1，当n＝1时，53－23－121－1＝1＝a1. 所以an＝53－23－12n－1(n∈N*)． 16．(文)(2011•焦作模拟)已知函数f(x)＝ax的图象过点(1，12)，且点(n－1，ann2)(n∈N＋)在函数f(x)＝ax的图象上． (1)求数列{an}的通项公式； (2)令bn＝an＋1－12an，若数列{bn}的前n项和为Sn，求证：Sn<5. [解析] (1)∵函数f(x)＝ax的图象过点(1，12)，∴a＝12，f(x)＝(12)x. 又点(n－1，ann2)(n∈N＋)在函数f(x)＝ax的图象上，从而ann2＝12n－1，即an＝n22n－1. (2)由bn＝＋－n22n＝2n＋12n得， Sn＝32＋522＋…＋2n＋12n，则12Sn＝322＋523＋…＋2n－12n＋2n＋12n＋1，两式相减得：12Sn＝32＋2(122＋123＋…＋12n)－2n＋12n＋1，∴Sn＝5－2n ＋52n，∴Sn<5. (理)(2011•山东文，20)等比数列{an}中，a1、a2、a3分别是下表第一、二、三行中的某一个数，且a1、a2、a3中的任何两个数不在下表的同一列．第一列第二列第三列第一行 3 2 10 第二行 6 4 14 第三行 9 8 18 (1) 求数列{an}的通项公式； (2)若数列{bn}满足：bn＝an＋(－1)nlnan，求数列{bn}的前2n项和S2n. [解析] (1)依次验证知a1＝2，a2 ＝6，a3＝18时符合题意，∴an＝2•3n－1 (2)∵bn＝an＋(－1)nlnan＝2•3n－1＋(－1)nln(2•3n－1)＝2•3n－1＋(－1)n(ln2－ln3)＋(－1)nnln3 ∴S2n＝b1＋b2＋…＋b2n＝2(1＋3＋…＋32n－1)＋[－1＋1－1＋…＋(－1)2n](ln2－ln3)＋[－1＋2－3＋…＋(－1)2n•2n]ln3 ＝2×1－32n1－3＋nln3＝32n＋nln3－1. 1．(2011•湖南六校联考)已知{an}是等差数列，Sn是其前n项和，a5＝19，S5＝55，则过点P(3，a3)，Q(4，a4)的直线的斜率是( ) A．4 B.14 C．－4 D．－14 [答案] A [解析] a1＋4d＝195a1＋5×42d＝55，∴a1＝3d＝4，∴kPQ＝4. 2．在直角坐标系中，O是坐标原点，P1(x1，y1)，P2(x2，y2)是第一象限的两个点，若1，x1，x2,4依次成等差数列，而1，y1，y2,8依次成等比数列，则△OP1P2的面积是( ) A．1 B．2 C．3 D．4 [答案] A [解析] 由条件知x1＝2，x2＝3，y1＝2，y2＝4，∴S＝12×4×3－12×2×2－12(2＋4)×1＝1. 3．数列{an}是公差d≠0的等差数列，数列{bn}是等比数列，若a1＝b1，a3＝b3，a7＝b5，则b11等于( ) A．a63 B．a36 C．a31 D．a13 [答案] A [解析] 设数列{bn}的首项为b1，公比为q，则 a1＋2d＝a1q2a1＋6d＝a1q4，得d＝a14(q4－q2)．∴a1＋a12(q4－q2)＝a1q2，∵q≠1，∴q2＝2，d＝a12，于是b11＝a1q10＝32a1. 设32a1＝a1＋(n－1)•a12，则n＝63，∴b11＝a63. 4．(2011•黄冈月考)在数列{an}中，a1＝1，anan－1＝an－1＋(－1)n(n≥2，n∈N*)，则a3a5的值是( ) A.1516 B.158 C.34 D.38 [答案] C [解析] ∵a1＝1，anan－1＝an－1＋(－1)n，∴a2a1＝a1＋1，∴a2＝2，；∵a3a2＝a2－1，∴a3＝12；∵a4a3＝a3＋1，∴a4＝3；∵a5a4＝a4－1，∴a5＝23，∴a3a5＝34. 5．等差数列{an}的公差d≠0，且a1、a4、a8成等比数列，则a1＋a4＋a8a2＋a5＋a9＝________. [答案] 3740 [分析] 此类问题一般依据条件和等差(比)数列的通项(或前n项和)公式列方程求解．解方程时，注意等比数列的首项和公比都不能为0. [解析] ∵a1、a4、a8成等比数列，∴a24＝a1•a8，又{an}成等差数列，公差d，∴(a1＋3d)2＝a1(a1＋7d)，∴a1＝9d≠0，∴原式＝9d＋12d＋16d10d＋13d＋17d＝37d40d＝3740. 6．(2011•上饶市四校联考)设等比数列{an}的公比为q，前n项和为Sn，若Sn＋1，Sn，Sn＋2成等差数列，则q的值为________． [答案] －2 [解析] 若q＝1，则由2Sn＝Sn＋1＋Sn＋2⇒2na1＝(n＋1)a1＋(n＋2)a1⇒2n＝2n＋3矛盾，∴q≠1，由2Sn ＝Sn＋1＋Sn＋2可得－－q ＝－qn＋－q＋－qn＋－q⇒qn＋2＋qn＋1－2qn＝0 ⇒q2＋q－2＝0(∵q≠1)，解得q＝－2. 7．(2011•天津市二十区县联考)已知Sn是数列{an}的前n项和，向量a＝(an－1，－2)，b＝(4，Sn)满足a⊥b，则S5S3＝________. [答案] 317 [解析] ∵a＝(an－1，－2)，b ＝(4，Sn)满足a⊥b，∴a•b＝0，∴4an－4－2Sn＝0，即Sn＝2an －2，∴Sn－1＝2an－1－2(n≥2)．两式相减得an＝2an－1，∴anan －1＝2. 由Sn＝2an－2(n∈N*)，得a1＝2. ∴{an}是以2为首项，2为公比的等比数列，∴an＝2n. ∴S5S3＝－－－－2＝317. 8．(2011•苏州检测)正整数按下列方法分组：{1}，{2,3,4}，{5,6,7,8,9}，{10,11,12,13,14,15,16}，…，记第n组中各数之和为An；由自然数的立方构成下列数组：{03,13}，{13,23}，{23,33}，{33,43}，…，记第n组中后一个数与前一个数的差为Bn，则An＋Bn＝________. [答案] 2n3 [解析] 由题意知，前n组共有1＋3＋5＋…＋(2n－1)＝n2个数，所以第n－1组的最后一个数为(n－1)2，第n组的第一个数为(n－1)2＋1，第n组共有2n－1个数，所以根据等差数列的前n项和公式可得 An＝－＋1]＋－＋2n－1]2(2n－1)＝[(n－1)2＋n](2n－1)，而Bn＝n3－(n－1)3，所以An＋Bn＝2n3.。

2013高考数学一轮复习试题 2-3 答案

2013高考数学一轮复习试题 2-3 理答案一、选择题(每小题5分，共25分)1.解析由f (－0)＝－f (0)，即f (0)＝0.则b ＝－1，f (x )＝2x ＋2x －1，f (－1)＝－f (1)＝－3.答案 D2．解析 (构造法)构造函数f (x )＝sin π2x ，则有f (x ＋2)＝sin ⎣⎢⎡⎦⎥⎤π2x ＋2＝－sin π2x ＝－f (x )，所以f (x )＝sin π2x 是一个满足条件的函数，所以f (6)＝sin 3π＝0，故选B.答案 B【点评】根据函数的性质构造出一个符合条件的具体函数，是解答抽象函数选择题的常用方法，充分体现了由抽象到具体的思维方法. 3.解析 (特例法)∵f (x )＝x2x ＋1x －a 是奇函数，∴f (－1)＝－f (1)， ∴－1－2＋1－1－a ＝－12＋11－a ，∴a ＋1＝3(1－a )，解得a ＝12.答案 A【点评】本题采用特例法，可简化运算，当然也可用奇函数的定义进行解题，不过过程较为繁琐，若运算能力较弱容易出错.4.解析由已知条件对x ∈R 都有f (－x ＋1)＝－f (x ＋1)，f (－x －1)＝－f (x －1)因此f (－x ＋3)＝f [－(x －2)＋1]＝－f [(x －2)＋1]＝－f (x －1)＝f (－x －1)＝f (－x －2＋1)＝f (－(x ＋2)＋1)＝－f ((x ＋2)＋1)＝－f (x ＋3)，因此函数f (x ＋3)是奇函数．答案 D5.解析 f (x )＝ln 1|x |满足f (－x )＝f (x )，且当x ∈(0，＋∞)时，f (x )＝－ln x ，显然f (x )在(0，＋∞)上是减函数，故选A.答案 A6解析 (直接法)∵g (x )为偶函数，f (x )为奇函数， ∴g (2)＝g (－2)＝a ，f (－2)＝－f (2)， ∴f (2)＋g (2)＝a 2－a －2＋2，① f (－2)＋g (－2)＝－f (2)＋g (2)＝a －2－a 2＋2，②联立①②解得g (2)＝2＝a ，f (2)＝a 2－a －2＝22－2－2＝154.故选B.答案 B 【点评】本题采用直接法，所谓直接法，就是直接从题设的条件出发，运用有关的概念、定义、性质、定理、法则和公式等知识，通过严密的推理与计算来得出题目的结论，然后再对照题目所给的四个选项来“对号入座”.其基本策略是由因导果，直接求解.7.解析当0≤x ＜2时，令f (x )＝x 3－x ＝0，得x ＝0或x ＝1或x ＝－1(舍去)，又f (x )的最小正周期为2，∴f (0)＝f (2)＝f (4)＝f (6)＝0，f (1)＝f (3)＝f (5)＝0，∴y ＝f (x )的图象在区间[0,6]上与x 轴的交点个数为7. 答案 B二、填空题(每小题4分，共12分)8．解析由f (x )是奇函数，利用赋值法得f (－1)＝－f (1)即12－1－1＋a ＝－121－1－a 整理得：－1＋2a ＝0，即a ＝12.答案 129解析 ∵f (x ＋5)＝f (x )且f (－x )＝－f (x )，∴f (3)＝f (3－5)＝f (－2)＝－f (2)＝－2，f (4)＝f (－1)＝－f (1)＝－1，故f (3)－f (4)＝(－2)－(－1)＝－1. 答案－110．解析由原函数是奇函数，所以y ＝f (x )在[－5,5]上的图象关于坐标原点对称，由y ＝f (x )在[0,5]上的图象，得它在[－5,0]上的图象，如图所示．由图象知，使函数值y ＜0的x 的取值集合为(－2,0)∪(2,5)．答案 (－2,0)∪(2,5)11.解析法一当x ＝1，y ＝0时，f (0)＝12；当x ＝1，y ＝1时，f (2)＝－14；当x ＝2，y ＝1时，f (3)＝－12；当x ＝2，y ＝2时，f (4)＝－14；当x ＝3，y ＝2时，f (5)＝14；当x ＝3，y ＝3时，f (6)＝12；当x ＝4，y ＝3时，f (7)＝14；当x ＝4，y ＝4时，f (8)＝－14；….∴f (x )是以6为周期的函数，∴f (2 013)＝f (3＋335×6)＝f (3)＝－12.法二 ∵f (1)＝14，4f (x )·f (y )＝f (x ＋y )＋f (x －y )，∴构造符合题意的函数f (x )＝12cos π3x ，∴f (2 013)＝12cos ⎝ ⎛⎭⎪⎫π3×2 013＝－12.答案－1212．解析由已知条件：f (x ＋2)＝f (x )，则y ＝f (x )是以2为周期的周期函数，①正确；当－1≤x ≤0时0≤－x ≤1，f (x )＝f (－x )＝⎝ ⎛⎭⎪⎫121＋x ，函数y ＝f (x )的图象如图所示：当3<x <4时，－1<x －4<0，f (x )＝f (x －4)＝⎝ ⎛⎭⎪⎫12x －3，因此②④正确．③不正确．答案 ①②④ 三、解答题(共23分)13.已知f (x )是R 上的奇函数，且当x ∈(－∞，0)时，f (x )＝－x lg(2－x )，求f (x )的解析式．解 ∵f (x )是R 上的奇函数，可得f (0)＝0. 当x ＞0时，－x ＜0，由已知f (－x )＝x lg(2＋x )， ∴－f (x )＝x lg(2＋x )，即f (x )＝－x lg(2＋x )(x ＞0)．∴f (x )＝⎩⎪⎨⎪⎧－x lg 2－x x ＜0，－x lg 2＋x x ≥0.即f (x )＝－x lg(2＋|x |)(x ∈R )．14．设定义在[－2,2]上的偶函数f (x )在区间[－2,0]上单调递减，若f (1－m )<f (m )，求实数m 的取值范围．解由偶函数性质知f (x )在[0,2]上单调递增，且f (1－m )＝f (|1－m |)，f (m )＝f (|m |)，因此f (1－m )<f (m )等价于⎩⎪⎨⎪⎧－2≤1－m ≤2，－2≤m ≤2，|1－m |<|m |.解得：12<m ≤2.因此实数m 的取值范围是⎝ ⎛⎦⎥⎤12，2.15．(2012·扬州模拟)已知函数f (x )对任意x ，y ∈R ，都有f (x ＋y )＝f (x )＋f (y )，且x ＞0时，f (x )＜0，f (1)＝－2. (1)求证f (x )是奇函数；(2)求f (x )在[－3,3]上的最大值和最小值． (1)证明令x ＝y ＝0，知f (0)＝0；再令y ＝－x ，则f (0)＝f (x )＋f (－x )＝0，所以f (x )为奇函数．(2)解任取x 1＜x 2，则x 2－x 1＞0，所以f (x 2－x 1)＝f [x 2＋(－x 1)]＝f (x 2)＋f (－x 1)＝f (x 2)－f (x 1)＜0，所以f (x )为减函数．而f (3)＝f (2＋1)＝f (2)＋f (1)＝3f (1)＝－6，f (－3)＝－f (3)＝6. 所以f (x )max ＝f (－3)＝6，f (x )min ＝f (3)＝－6.16．已知函数f (x )＝x 2＋a x(x ≠0，常数a ∈R ) (1)讨论函数f (x )的奇偶性，并说明理由；(2)若函数f (x )在x ∈[2，＋∞)上为增函数，求实数a 的取值范围．解 (1)函数f (x )的定义域为{x |x ≠0}，当a ＝0时，f (x )＝x 2，(x ≠0)显然为偶函数；当a ≠0时，f (1)＝1＋a ，f (－1)＝1－a ，因此f (1)≠f (－1)，且f (－1)≠－f (1)，所以函数f (x )＝x 2＋a x既不是奇函数，也不是偶函数．(2)f ′(x )＝2x －a x 2＝2x 3－ax2，当a ≤0，f ′(x )＞0，则f (x )在(2，＋∞)上是增函数，当a ＞0时，由f ′(x )＝2x 3－ax 2＞0，解得x ＞ 3a 2，由f (x )在[2，＋∞)上是增函数，可知 3a 2≤2.解得0＜a ≤16综上可知实数a 的取值范围是(－∞，16]．。

高考数学一轮复习数列多选题测试试题及答案

高考数学一轮复习数列多选题测试试题及答案一、数列多选题1．如图，已知点E 是ABCD 的边AB 的中点，()*n F n ∈N为边BC 上的一列点，连接n AF 交BD 于n G ，点()*n G n ∈N 满足()1223n n n n n G D a G A a G E +=⋅-+⋅，其中数列{}n a 是首项为1的正项数列，n S 是数列{}n a 的前n 项和，则下列结论正确的是（）A ．313a =B ．数列{}3n a +是等比数列C ．43n a n =-D ．122n n S n +=--【答案】AB 【分析】化简得到()()12323n n n n n n G D a a G A a G B +=--⋅-+⋅，根据共线得到1230n n a a +--=，即()1323n n a a ++=+，计算123n n a +=-，依次判断每个选项得到答案. 【详解】()()112232n n n n n n G D a G A a G A G B +=⋅-+⋅+，故()()12323n n n n n n G D a a G A a G B +=--⋅-+⋅，,n n G D G B 共线，故1230n n a a +--=，即()1323n n a a ++=+，11a =，故1342n n a -+=⨯，故123n n a +=-.432313a =-=，A 正确；数列{}3n a +是等比数列，B 正确；123n n a +=-，C 错误；2124323412nn n S n n +-=-=---，故D 错误.故选：AB . 【点睛】本题考查了向量运算，数列的通项公式，数列求和，意在考查学生的计算能力，转化能力和综合应用能力.2．设n S 是公差为()d d ≠0的无穷等差数列{}n a 的前n 项和，则下列命题正确的是（） A ．若0d <，则数列{}n S 有最大项 B ．若数列{}n S 有最大项，则0d <C ．若对任意*n N ∈，均有0n S >，则数列{}n S 是递增数列D ．若数列{}n S 是递增数列，则对任意*n N ∈，均有0n S > 【答案】ABC 【分析】由等差数列的求和公式可得()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭，可看作关于n 的二次函数，由二次函数的性质逐个选项验证可得. 【详解】由等差数列的求和公式可得()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭，选项A ，若0d <，由二次函数的性质可得数列{}n S 有最大项，故正确；选项B ，若数列{}n S 有最大项，则对应抛物线开口向下，则有0d <，故正确；选项C ，若对任意*n ∈N ，均有0n S >，对应抛物线开口向上，0d >，可得数列{}n S 是递增数列，故正确；选项D ，若数列{}n S 是递增数列，则对应抛物线开口向上，但不一定有任意*n ∈N ，均有0n S >，故错误. 故选：ABC . 【点睛】本题考查等差数列的求和公式的应用，()2111222n n n d d S na d n a n -⎛⎫=+=+- ⎪⎝⎭可看成是二次函数，然后利用二次函数的性质解决问题，考查分析和转化能力，属于常考题.3．已知数列{}n a ，{}n b 满足，11a =，11n n n a a a +=+，1(1)n n b n a =+，若23100100122223100b b b T b =++++，则（） A ．n a n = B ．1n n b n =+ C ．100100101T =D ．10099100T =【答案】BC 【分析】先证明数列1n a 是等差数列得1n a n =，进而得1(1)1n n n b n a n ==++，进一步得()211111n b n n n n n ==-++，再结合裂项求和得100100101T =. 【详解】解:因为11nn n a a a +=+,两边取倒数得:1111n n a a +=+,即1111n na a ,所以数列1na 是等差数列,公差为1,首项为111a ,故()1111n n n a =+-⨯=,所以1n a n=, 所以1(1)1n n nb n a n ==++，故()211111n b n n n n n ==-++，所以31002100122211112310022334100101b b b T b =++++=++++⨯⨯⨯11111111100122334100101101101⎛⎫⎛⎫⎛⎫=+-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故BC 正确，AD 错误；故选：BC 【点睛】本题考查数列通项公式的求解，裂项求和，考查运算求解能力，是中档题.本题解题的关键在于证明数列1na 是等差数列，进而结合裂项求和求解100T .4．已知数列{}n a ，{}n b 满足：12n n n a a b +=+，()*1312lnn n n n b a b n N n++=++∈，110a b +>，则下列命题为真命题的是（）A ．数列{}n n a b -单调递增B ．数列{}n n a b +单调递增C ．数列{}n a 单调递增D ．数列{}n b 从某项以后单调递增【答案】BCD 【分析】计算221122ln 2a b a b a b -=--<-，知A 错误；依题意两式相加{}ln +-n n a b n 是等比数列，得到()1113ln -+=+⋅+n n n a b a b n ，知B 正确；结合已知条件，计算10n n a a +->，即得C 正确；先计算()11113ln(1)2ln n n n b b a b n n -+-=+⋅++-，再结合指数函数、对数函数增长特征知D 正确. 【详解】由题可知，12n n n a a b +=+①，1312lnn n n n b a b n++=++②，①-②得，1131lnn n n n n a b a b n+++-=--，当1n =时，2211ln 2a b a b -=--，∴2211-<-a b a b ，故A 错误．①+②得，()113ln(1)3ln n n n n a b a b n n +++=+++-，()11ln(1)3ln n n n n a b n a b n +++-+=+-，∴{}ln +-n n a b n 是以11a b +为首项，3为公比的等比数列，∴()111ln 3-+-=+⋅n n n a b n a b ，∴()1113ln -+=+⋅+n n n a b a b n ，③又110a b +>，∴B 正确．将③代入①得，()()11113ln n n n n n n a a a b a a b n -+=++=++⋅+，∴()11113ln 0n n n a a a b n -+-=+⋅+>，故C 正确．将③代入②得，()()11113311ln 3ln ln n n n n n n n n b b a b b a b n n n-+++=+++=++⋅++，∴()11113ln(1)2ln n n n b b a b n n -+-=+⋅++-．由110a b +>，结合指数函数与对数函数的增长速度知，从某个()*n n N∈起，()1113ln 0n a b n -+⋅->，又ln(1)ln 0n n +->，∴10n n b b +->，即{}n b 从某项起单调递增，故D 正确．故选：BCD ．【点睛】判定数列单调性的方法：（1）定义法：对任意n *∈N ，1n n a a +>，则{}n a 是递增数列，1n n a a +<，则{}n a 是递减数列；（2）借助函数单调性：利用()n a f n =，研究函数单调性，得到数列单调性.5．若数列{}n a 的前n 项和是n S ，且22n n S a =-，数列{}n b 满足2log n n b a =，则下列选项正确的为（） A ．数列{}n a 是等差数列B ．2nn a =C ．数列{}2na 的前n 项和为21223n +-D ．数列11n n b b +⎧⎫⎨⎬⋅⎩⎭的前n 项和为n T ，则1n T <【答案】BD 【分析】根据22n n S a =-，利用数列通项与前n 项和的关系得1,1,2n nS n a S n =⎧=⎨≥⎩，求得通项n a ，然后再根据选项求解逐项验证. 【详解】当1n =时，12a =，当2n ≥时，由22n n S a =-，得1122n n S a --=-，两式相减得：12n n a a -=，又212a a =，所以数列{}n a 是以2为首项，以2为公比的等比数列，所以2nn a =，24nn a =，数列{}2na 的前n 项和为()141444143n n nS +--'==-，则22log log 2nn n b a n ===，所以()1111111n n b b n n n n +==-⋅⋅++，所以 1111111 (11123411)n T n n n =-+-++-=-<++，故选：BD 【点睛】方法点睛：求数列的前n 项和的方法 (1)公式法：①等差数列的前n 项和公式，()()11122n n n a a n n S na d +-==+②等比数列的前n 项和公式()11,11,11nn na q S a q q q =⎧⎪=-⎨≠⎪-⎩；(2)分组转化法：把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解．(3)裂项相消法：把数列的通项拆成两项之差求和，正负相消剩下首尾若干项．(4)倒序相加法：把数列分别正着写和倒着写再相加，即等差数列求和公式的推导过程的推广．(5)错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列对应项之积构成的，则这个数列的前n 项和用错位相减法求解.(6)并项求和法：一个数列的前n 项和中，可两两结合求解，则称之为并项求和．形如a n ＝(－1)n f (n )类型，可采用两项合并求解．6．设等差数列{}n a 的前n 项和为n S ，公差为d .已知312a =，120S >，70a <则（）A ．60a >B ．数列1n a ⎧⎫⎨⎬⎩⎭是递增数列 C ．0n S <时，n 的最小值为13 D ．数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项【答案】ACD 【分析】由已知得()()612112712+12+220a a a a S ==>，又70a <，所以6>0a ，可判断A ；由已知得出2437d -<<-，且()12+3n a n d =-，得出[]1,6n ∈时，>0n a ，7n ≥时，0n a <，又()1112+3n a n d =-，可得出1na 在1,6n n N上单调递增，1na 在7n nN ，上单调递增，可判断B ；由()313117713+12203213a a a S a ⨯==<=，可判断C ；判断 n a ，n S 的符号， n a 的单调性可判断D ；【详解】由已知得311+212,122d a a a d ===-，()()612112712+12+220a a a a S ==>，又70a <，所以6>0a ，故A 正确；由7161671+612+40+512+3>0+2+1124+7>0a a d d a a d d a a a d d ==<⎧⎪==⎨⎪==⎩，解得2437d -<<-，又()()3+312+3n a n d n d a =-=-，当[]1,6n ∈时，>0n a ，7n ≥时，0n a <，又()1112+3n a n d =-，所以[]1,6n ∈时，1>0na ，7n ≥时，10n a <，所以1na 在1,6nn N上单调递增，1na 在7nn N，上单调递增，所以数列1n a ⎧⎫⎨⎬⎩⎭不是递增数列，故B 不正确；由于()313117713+12203213a a a S a ⨯==<=，而120S >，所以0n S <时，n 的最小值为13，故C 选项正确；当[]1,6n ∈时，>0n a ，7n ≥时，0n a <，当[]1,12n ∈时，>0n S ，13n ≥时，0n S <，所以当[]7,12n ∈时，0n a <，>0n S ，0nnS a <，[]712n ∈，时，n a 为递增数列，n S 为正数且为递减数列，所以数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项，故D 正确；【点睛】本题考查等差数列的公差，项的符号，数列的单调性，数列的最值项，属于较难题.7．设等差数列{a n }的前n 项和为S n ，公差为d ．已知a 3＝12，S 12＞0，a 7＜0，则（） A ．a 6＞0 B ．2437d -<<- C ．S n ＜0时，n 的最小值为13D ．数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项【答案】ABCD 【分析】S 12＞0，a 7＜0，利用等差数列的求和公式及其性质可得：a 6+a 7＞0，a 6＞0．再利用a 3＝a 1+2d ＝12，可得247-＜d ＜﹣3．a 1＞0．利用S 13＝13a 7＜0．可得S n ＜0时，n 的最小值为13．数列n n S a ⎧⎫⎨⎬⎩⎭中，n ≤6时，n n S a ＞0.7≤n ≤12时，n n S a ＜0．n ≥13时，n n S a ＞0．进而判断出D 是否正确．【详解】 ∵S 12＞0，a 7＜0，∴()67122a a +＞0，a 1+6d ＜0．∴a 6+a 7＞0，a 6＞0．∴2a 1+11d ＞0，a 1+5d ＞0，又∵a 3＝a 1+2d ＝12，∴247-＜d ＜﹣3．a 1＞0． S 13＝()113132a a +＝13a 7＜0．∴S n ＜0时，n 的最小值为13．数列n n S a ⎧⎫⎨⎬⎩⎭中，n ≤6时，n n S a ＞0，7≤n ≤12时，n n S a ＜0，n ≥13时，n n S a ＞0．对于：7≤n ≤12时，nnS a ＜0．S n ＞0，但是随着n 的增大而减小；a n ＜0，但是随着n 的增大而减小，可得：nnS a ＜0，但是随着n 的增大而增大． ∴n ＝7时，nnS a 取得最小值．综上可得：ABCD 都正确．故选：ABCD ．【点评】本题考查了等差数列的通项公式与求和公式及其性质，考查了推理能力与计算能力，属于难题．8．已知等差数列{}n a 的前n 项和为n S ，若981S =，713a =，3S ，1716S S -，k S 成等比数列，则（） A ．2n S n = B ．122310*********a a a a a a ++⋅⋅⋅+= C ．11k = D ．21n a n =-【答案】ACD 【分析】先根据题意求出等差数列的首项和公差，再根据等差数列的通项公式和求和公式求得,n n a S ，再由3S ，1716S S -，k S 成等比数列列出式子求解得出k 的值，再利用裂项相消法求和，得到122310111111021a a a a a a ++⋅⋅⋅+=，从而判断各项的正误. 【详解】依题意，95981S a ==，解得59a =；而713a =，故75275a a d -==-，则1541a a d =-=，则21n a n =-，2n S n =，故D 、A 正确：因为3S ，1716S S -，k S 成等比数列，故()223171617k S S S S a =-=，则22933k =，解得11k =，故C 正确；而122310111111021a a a a a a ++⋅⋅⋅+=，故B 错误．故选：ACD ．【点睛】思路点睛：该题考查的是有关数列的问题，解题方法如下：（1）根据题意，求得通项公式，进而求得前n 项和；（2）根据三项成等比数列的条件，列出等式，求得k 的值；（3）利用裂项相消法，对12231011111a a a a a a ++⋅⋅⋅+求和；（4）对选项逐个判断正误，得到结果.二、平面向量多选题9．定义空间两个向量的一种运算sin ,a b a b a b ⊗=⋅，则关于空间向量上述运算的以下结论中恒成立的有（） A ．()()a b a b λλ⊗=⊗ B ．a b b a ⊗=⊗C ．()()()a b c a c b c +⊗=⊗+⊗D ．若()11,a x y =，()22,b x y =，则122a b x y x y ⊗=- 【答案】BD 【分析】对于A,B,只需根据定义列出左边和右边的式子即可,对于C,当λab 时,()()1sin ,a b c b c b c λ+⊗=+⋅,()()()sin ,sin,1sin ,a c b c b c b c b c b c b c b c λλ⊗+⊗=⋅+⋅=+⋅,显然不会恒成立. 对于D,根据数量积求出cos ,a b ,再由平方关系求出sin ,a b 的值,代入定义进行化简验证即可. 【详解】解：对于A ：()()sin ,a b a b a b λλ⊗=⋅，()sin ,a b a b a bλλλ⊗=⋅，故()()a b a b λλ⊗=⊗不会恒成立；对于B ，sin ,a b a b a b ⊗=⋅，=sin ,b a b a b a ⊗⋅，故a b b a ⊗=⊗恒成立；对于C ，若λab ，且0λ>，()()1sin ,a b c b c b c λ+⊗=+⋅，()()()sin,sin ,1sin ,a c b c b c b c b c b c b c b c λλ⊗+⊗=⋅+⋅=+⋅，显然()()()a b c a c b c +⊗=⊗+⊗不会恒成立；对于D ，1212cos ,x x y y a b a b+=⋅，212sin ,1a b a b ⎛ ⎪=- ⎪⋅⎭，即有222121212121x x y y x x y y a b a b a b a a b ⎛⎫⎛⎫++ ⎪⊗=⋅⋅-=⋅- ⎪ ⎪ ⎪⋅⎝⎭⎭21y =⎪+⎭==1221x y x y =-.则1221a b x y x y ⊗=-恒成立. 故选：BD. 【点睛】本题考查向量的新定义，理解运算法则正确计算是解题的关键，属于较难题.10．在三棱锥P ABC -中，三条侧棱,,PA PB PC 两两垂直，且3PA PB PC ===，G 是PAB △的重心，E ，F 分别为,BC PB 上的点，且::1:2BE EC PF FB ==，则下列说法正确的是（） A ．EG PG ⊥ B ．EG BC ⊥C ．//FG BCD ．FG EF ⊥【答案】ABD 【分析】取,,PA a PB b PC c ===，以{},,a b c 为基底表示EG ，FG ，EF ，结合向量数量积运算性质、向量共线定理即可选出正确答案. 【详解】如图，设,,PA a PB b PC c ===，则{},,a b c 是空间的一个正交基底，则0a b a c b c ⋅=⋅=⋅=，取AB 的中点H ，则22111()33233PG PH a b a b ==⨯+=+， 1121111,3333333EG PG PE a b b c a b c BC c b =-=+--=--=-，11113333FG PG PF a b b a =-=+-=，1121133333EF PF PE b c b c b ⎛⎫=-=-+=-- ⎪⎝⎭，∴0EG PG ⋅=，A 正确；0EG BC ⋅=，B 正确；()FG BC R λλ≠∈，C 不正确；0FG EF ⋅=，D 正确.故选:ABD.【点睛】本题考查了平面向量共线定理，考查了由数量积求两向量的位置关系，考查了平面向量基本定理的应用，属于中档题.。

高考数学一轮复习数列多选题测试含答案

高考数学一轮复习数列多选题测试含答案一、数列多选题1．设{}n a 是无穷数列，若存在正整数()2k k ≥，使得对任意n *∈N ，均有n k n a a +>，则称{}n a 是“间隔递增数列”，k 是{}n a 的“间隔数”，下列说法正确的是（） A ．公比大于1的等比数列一定是“间隔递增数列” B ．若()21nn a n =+-，则{}n a 是“间隔递增数列”C ．若(),2n ra n r r n*=+∈≥N ，则{}n a 是“间隔递增数列”且“间隔数”的最小值为r D ．已知22021n a n tn =++，若{}n a 是“间隔递增数列”且“间隔数”的最小值为3，则54t -<≤-【答案】BCD 【分析】利用新定义，逐项验证是否存在正整数()2k k ≥，使得0n k n a a +->，即可判断正误. 【详解】选项A 中，设等比数列{}n a 的公比是()1q q >，则()1111111n k n n n k k n a a a a q q q a q +---+=-=--，其中1k q >，即()110n k q q -->，若10a <，则0n k n a a +-<，即n k n a a +<，不符合定义，故A 错误；选项B 中，()()()()()21212111n kn n k n k n a a n k n k ++⎡⎤⎡⎤⎡⎤++--+-=+---⎣⎦-=⎣⎦⎣⎦，当n 是奇数时，()211kn k n a a k +=---+，则存在1k时，0n k n a a +->成立，即对任意n *∈N ，均有n k n a a +>，符合定义；当n 是偶数时，()211kn k n a a k +-=+--，则存在2k ≥时，0n k n a a +->成立，即对任意n *∈N ，均有n k n a a +>，符合定义.综上，存在2k ≥时，对任意n *∈N ，均有n k n a a +>，符合定义，故B 正确；选项C 中，()()1n k n r r kr r a a n k n k k n k n n k n n k n +⎡⎤-⎛⎫⎛⎫++-+=+=-⎢⎥ ⎪ ⎪+++⎝⎭⎝⎭⎢⎣-⎦=⎥()2n kn r k n k n +-=⋅+，令2()f n n kn r =+-，开口向上，对称轴02k -<，故2()f n n kn r =+-在n *∈N 时单调递增，令最小值(1)10f k r =+->，得1k r >-，又k *∈N ，2k ≥，,2r r *∈≥N ，故存在k r ≥时，0n k n a a +->成立，即对任意n *∈N ，均有n k n a a +>，符合定义，“间隔数”的最小值为r ，故C 正确；选项D 中，因为22021n a n tn =++，是“间隔递增数列”，则()()()2222021202012n k n a a n k t n k kn k t n n k t +⎡⎤-=-=++>⎣++++⎦++，即20k n t ++>，对任意n *∈N 成立，设()2g n k n t =++，显然在n *∈N 上()g n 递增，故要使()20g n k n t =++>，只需(1)20g k t =++>成立，即2t k --<. 又“间隔数”的最小值为3，故存在3k ≥，使2t k --<成立，且存在k 2≤，使2t k --≥成立，故23t --<且22t --≥，故54t -<≤-，故D 正确. 故选：BCD. 【点睛】本题的解题关键在于读懂题中“间隔递增数列”的定义，判断是否存在正整数()2k k ≥，使0n k n a a +->对于任意的n *∈N 恒成立，逐项突破难点即可.2．已知数列{}n a 满足11a =，()111n n na n a +-+=，*n N ∈，其前n 项和为n S ，则下列选项中正确的是（）A ．数列{}n a 是公差为2的等差数列B ．满足100n S <的n 的最大值是9C ．n S 除以4的余数只能为0或1D ．2n n S na = 【答案】ABC 【分析】根据题意对()111n n na n a +-+=变形得()1111111n n a a n n n n n n +=-+-=++，进而根据累加法求得()*21n a n n N =-∈，再依次讨论各选项即可得答案.【详解】解：因为()111n n na n a +-+=，故等式两边同除以()1n n +得：()1111111n n a a n n n n n n +=-+-=++，所以()1111111n n a a n n n n n n -=-----=，()()12111221211n n a a n n n n n n --=------=--，，2111121122a a =-⨯-= 故根据累加法得：()11121n a a n nn =-≥-，由于11a =，故()212n a n n =-≥，检验11a =满足，故()*21n a n n N=-∈所以数列{}n a 是公差为2的等差数列，故A 选项正确；由等差数列前n 项和公式得：()21212n n n S n +-==，故2100n n S =<，解得：10n <，故满足100n S <的n 的最大值是9，故B 选项正确；对于C 选项，当*21,n k k N =-∈时，22441n n k S k ==-+，此时n S 除以4的余数只能为1；当*2,n k k N =∈时，224n n k S ==，此时n S 除以4的余数只能0，故C 选项正确；对于D 选项，222n S n =，()2212n n n n n n a =-=-，显然2n n S na ≠，故D 选项错误.故选：ABC 【点睛】本题考查累加法求通项公式，裂项求和法，等差数列的相关公式应用，考查运算求解能力，是中档题.本题解题的关键在于整理变形已知表达式得()1111111n n a a n n n n n n +=-+-=++，进而根据累加法求得通项公式.3．下列说法中正确的是（）A ．数列{}n a 成等差数列的充要条件是对于任意的正整数n ，都有122n n n a a a ++=+B ．数列{}n a 成等比数列的充要条件是对于任意的正整数n ，都有212n n n a a a ++=C ．若数列{}n a 是等差数列，则n S 、2n n S S -、32n n S S -也是等差数列D ．若数列{}n a 是等比数列，则n S 、2n n S S -、32n n S S -也是等比数列【答案】AC 【分析】利用等差中项法可判断A 选项的正误；取0n a =可判断B 选项的正误；利用等差数列求和公式以及等差中项法可判断C 选项的正误；取1q =-，n 为偶数可判断D 选项的正误. 【详解】对于A 选项，充分性：若数列{}n a 成等差数列，则对任意的正整数n ，n a 、1n a +、2n a +成等差数列，则121n n n n a a a a +++-=-，即122n n n a a a ++=+，充分性成立；必要性：对任意的正整数n ，都有122n n n a a a ++=+，则121n n n n a a a a +++-=-，可得出2132431n n a a a a a a a a +-=-=-==-=，所以，数列{}n a 成等差数列，必要性成立.所以，数列{}n a 成等差数列的充要条件是对于任意的正整数n ，都有122n n n a a a ++=+，A 选项正确；对于B 选项，当数列{}n a 满足0n a =时，有212n n n a a a ++=，但数列{}n a 不是等比数列，B选项错误；对于C 选项，设等差数列{}n a 的公差为d ，则()112n n n dS na -=+，()2122122n n n d S na -=+，()3133132n n n dS na -=+，所以，()()()22111322112222n n n n d n n d n n d S S na na na ---⎡⎤⎡⎤-=+-+=+⎢⎥⎢⎥⎣⎦⎣⎦， ()()()232111533122132222n n n n d n n d n n d S S na na na ---⎡⎤⎡⎤-=+-+=+⎢⎥⎢⎥⎣⎦⎣⎦，所以，()()()()22232111532222n n n n n d n n d n n d S S S na na na ⎡⎤⎡⎤⎡⎤---⎢⎥⎢⎥⎢⎥-+=+++=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦()22n n S S =-，所以，n S 、2n n S S -、32n n S S -是等差数列，C 选项正确；对于D 选项，当公比1q =-，且n 是偶数时，n S 、2n n S S -、32n n S S -都为0，故n S 、2n n S S -、32n n S S -不是等比数列，所以D 选项错误. 故选：AC. 【点睛】方法点睛；1.判断等差数列有如下方法：（1）定义法：1n n a a d +-=（d 为常数，n *∈N ）；（2）等差中项法：()122n n n a a a n N*++=+∈；（3）通项法：n a p n q =⋅+（p 、q 常数）；（4）前n 项和法：2n S p n q n =⋅+⋅（p 、q 常数）.2.判断等比数列有如下方法：（1）定义法：1n na q a +=（q 为非零常数，n *∈N ）；（2）等比中项法：212n n n a a a ++=⋅，n *∈N ，0n a ≠；（3）通项公式法：nn a p q =⋅（p 、q 为非零常数）；（4）前n 项和法：nn S p q p =⋅-，p 、q 为非零常数且1q ≠.4．已知数列{}n a ，{}n b 满足：12n n n a a b +=+，()*1312lnn n n n b a b n N n++=++∈，110a b +>，则下列命题为真命题的是（）A ．数列{}n n a b -单调递增B ．数列{}n n a b +单调递增C ．数列{}n a 单调递增D ．数列{}n b 从某项以后单调递增【答案】BCD 【分析】计算221122ln 2a b a b a b -=--<-，知A 错误；依题意两式相加{}ln +-n n a b n 是等比数列，得到()1113ln -+=+⋅+n n n a b a b n ，知B 正确；结合已知条件，计算10n n a a +->，即得C 正确；先计算()11113ln(1)2ln n n n b b a b n n -+-=+⋅++-，再结合指数函数、对数函数增长特征知D 正确. 【详解】由题可知，12n n n a a b +=+①，1312lnn n n n b a b n ++=++②，①-②得，1131lnn n n n n a b a b n+++-=--，当1n =时，2211ln 2a b a b -=--，∴2211-<-a b a b ，故A 错误．①+②得，()113ln(1)3ln n n n n a b a b n n +++=+++-，()11ln(1)3ln n n n n a b n a b n +++-+=+-，∴{}ln +-n n a b n 是以11a b +为首项，3为公比的等比数列，∴()111ln 3-+-=+⋅n n n a b n a b ，∴()1113ln -+=+⋅+n n n a b a b n ，③又110a b +>，∴B 正确．将③代入①得，()()11113ln n n n n n n a a a b a a b n -+=++=++⋅+，∴()11113ln 0n n n a a a b n -+-=+⋅+>，故C 正确．将③代入②得，()()11113311ln 3ln ln n n n n n n n n b b a b b a b n n n -+++=+++=++⋅++，∴()11113ln(1)2ln n n n b b a b n n -+-=+⋅++-．由110a b +>，结合指数函数与对数函数的增长速度知，从某个()*n n N∈起，()1113ln 0n a b n -+⋅->，又ln(1)ln 0n n +->，∴10n n b b +->，即{}n b 从某项起单调递增，故D 正确．故选：BCD ．【点睛】判定数列单调性的方法：（1）定义法：对任意n *∈N ，1n n a a +>，则{}n a 是递增数列，1n n a a +<，则{}n a 是递减数列；（2）借助函数单调性：利用()n a f n =，研究函数单调性，得到数列单调性.5．（多选）设数列{}n a 是等差数列，公差为d ，n S 是其前n 项和，10a >且69S S =，则（） A ．0d >B ．80a =C ．7S 或8S 为n S 的最大值D ．56S S >【答案】BC 【分析】根据69S S =得到80a =，再根据10a >得到0d <，可得数列{}n a 是单调递减的等差数列，所以7S 或8S 为n S 的最大值，根据6560S S a -=>得65S S >，故BC 正确. 【详解】由69S S =得，960S S -=，即7890a a a ++=，又7982a a a +=，830a ∴=，80a ∴=，∴B 正确；由8170a a d =+=，得17a d =-，又10a >，0d ∴<， ∴数列{}n a 是单调递减的等差数列，()()0,70,9n n a n N n a n N n **⎧>∈≤⎪∴⎨<∈≥⎪⎩， 7S ∴或8S 为n S 的最大值，∴A 错误，C 正确； 6560S S a -=>，65S S ∴>，所以D 错误.故选：BC ．【点睛】关键点点睛：根据等差中项推出80a =，进而推出0d <是解题关键.6．若数列{}n a 的前n 项和是n S ，且22n n S a =-，数列{}n b 满足2log n n b a =，则下列选项正确的为（） A ．数列{}n a 是等差数列B ．2nn a =C ．数列{}2na 的前n 项和为21223n +-D ．数列11n n b b +⎧⎫⎨⎬⋅⎩⎭的前n 项和为n T ，则1n T <【答案】BD 【分析】根据22n nS a =-，利用数列通项与前n 项和的关系得1,1,2n n S n a S n =⎧=⎨≥⎩，求得通项n a ，然后再根据选项求解逐项验证. 【详解】当1n =时，12a =，当2n ≥时，由22n n S a =-，得1122n n S a --=-，两式相减得：12n n a a -=，又212a a =，所以数列{}n a 是以2为首项，以2为公比的等比数列，所以2nn a =，24nn a =，数列{}2na 的前n 项和为()141444143n n nS +--'==-，则22log log 2nn n b a n ===，所以()1111111n n b b n n n n +==-⋅⋅++，所以 1111111 (11123411)n T n n n =-+-++-=-<++，故选：BD 【点睛】方法点睛：求数列的前n 项和的方法 (1)公式法：①等差数列的前n 项和公式，()()11122n n n a a n n S na d +-==+②等比数列的前n 项和公式()11,11,11nn na q S a q q q=⎧⎪=-⎨≠⎪-⎩；(2)分组转化法：把数列的每一项分成两项或几项，使其转化为几个等差、等比数列，再求解．(3)裂项相消法：把数列的通项拆成两项之差求和，正负相消剩下首尾若干项．(4)倒序相加法：把数列分别正着写和倒着写再相加，即等差数列求和公式的推导过程的推广．(5)错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列对应项之积构成的，则这个数列的前n 项和用错位相减法求解.(6)并项求和法：一个数列的前n 项和中，可两两结合求解，则称之为并项求和．形如a n ＝(－1)n f (n )类型，可采用两项合并求解．7．在n n n A B C （1,2,3,n =）中，内角,,n n n A B C 的对边分别为,,n n n a b c ，n n n A B C 的面积为n S ，若5n a =，14b =，13c =，且222124n n n a c b ++=，222124n n n a b c ++=，则（） A ．n n n A B C 一定是直角三角形 B ．{}n S 为递增数列 C ．{}n S 有最大值 D ．{}n S 有最小值【答案】ABD 【分析】先结合已知条件得到()222211125=252n n n n b c b c +++-+-，进而得到22225=n n n b c a +=，得A 正确，再利用面积公式得到递推关系1221875=644n n S S ++，通过作差法判定数列单调性和最值即可. 【详解】由222124n n n a c b ++=，222124n n n a b c ++=得，222222112244n n n n n n a c a b bc+++++=+()2221122n n n a b c =++()2225122n n b c =++，故()222211125=252n n n n b c b c +++-+-，又221125=0b c +-，22250n n b c ∴+-=，22225=n n n b c a ∴+=，故n n n A B C 一定是直角三角形，A 正确；n n n A B C 的面积为12n n n S b c =，而()4222222222221124224416n n n n n n n n n n n n a b c a b c a c a b bc+++++++=⨯=，故()42222222222111241875161875==1616641n n n n n n n n n n n a b c a b bS S c c S +++++++==+，故22212218751875==6446434n n n n n S S SS S +-+--，又22125=244n n n n n b c b c S +=≤（当且仅当==2n n b c 时等号成立） 22121875=06344n n n S SS +∴--≥，又由14b =，13c =知n n b c ≠不是恒成立，即212n n S S +>，故1n n S S +>，故{}n S 为递增数列，{}n S 有最小值16=S ，无最大值，故BD 正确，C 错误. 故选：ABD. 【点睛】本题解题关键是利用递推关系得到()222211125=252n n n n b c b c +++-+-，进而得到22225=n n n b c a +=，再逐步突破.数列单调性常用作差法判定，也可以借助于函数单调性判断.8．下面是关于公差0d >的等差数列{}n a 的几个命题，其中正确的有（） A ．数列{}n a 递增B ．n S 为{}n a 的前n 项和,则数列n S n ⎧⎫⎨⎬⎩⎭是递增的等差数列 C ．若n a n =，n S 为{}n a 的前n 项和，且n S n c ⎧⎫⎨⎬+⎩⎭为等差数列，则0cD ．若70a =，n S 为{}n a 的前n 项和，则方程0n S =有唯一的根13n = 【答案】ABD 【分析】选项A. 由题意10n n a a d +-=>可判断；选项B.先求出112n S n a d n -=+⨯，根据1012n n S S dn n +-=>+可判断；选项C. 若n a n =,则()12n n n S +=，则0c 或1c =时n S n c ⎧⎫⎨⎬+⎩⎭为等差数列可判断；选项D.由1602n n S dn -⎛⎫=--= ⎪⎝⎭可判断. 【详解】选项A. 由题意10n n a a d +-=>，则1n n a a +>，所以数列{}n a 递增，故A 正确. 选项B. ()112n n n S na d -=+⨯,则112n S n a d n -=+⨯ 所以1012n n S S d n n +-=>+，则11n n S S n n +>+，所以数列n S n ⎧⎫⎨⎬⎩⎭是递增的等差数列. 故B 正确. 选项C. 若n a n =,则()12n n n S +=，则()()12n n n S n c n c =+++当0c时，12+n S n c n =+为等差数列. 当1c =时，2n S n c n=+为等差数列.所以选项C 不正确.选项D. 70a =,即7160a a d =+=，则16a d =-又()()1111660222n n n n n n S na d dn d dn ---⎛⎫=+⨯=-+⨯=--= ⎪⎝⎭由0,0d n >>，所以1602n --=，得13n =，故选项D 正确. 故选：ABD【点睛】关键点睛：本题考查等差数列的判定和单调性的单调，解答本题的关键是利用等差数列的定义和前n 项和公式进行判断，求出162n n S dn -⎛⎫=-+ ⎪⎝⎭，从而判断，属于中档题.二、平面向量多选题9．已知向量(4,3)a k =，(4,3)b k =，则（） A ．若a b ⊥，则0k = B ．若//a b ，则1k =C ．若a b >，则1k <D ．若a b a b +=-，则a b ⊥【答案】AD 【分析】先根据a b ⊥建立方程44330k k ⨯+⨯=解得0k =，判断选项A 正确；再根据//a b ，建立方程(4,3)(4,3)k k λ=解得1k =±，判断选项B 错误；接着根据a b >建立不等式4(3)(4)3k k +>+解得11k -<<，判断选项C 错误；最后根据a b a b +=-，化简整理得到a b ⊥，判断选项D 正确.【详解】解：因为(4,3)a k =，(4,3)b k =，a b ⊥，则44330k k ⨯+⨯=，解得0k =，故选项A 正确；因为(4,3)a k =，(4,3)b k =，//a b ，则λa b ，即(4,3)(4,3)k k λ=，解得1k =±，故选项B 错误；因为(4,3)a k =，(4,3)b k =，a b >，则>，解得11k -<<，故选项C 错误；因为(4,3)a k =，(4,3)b k =，a b a b +=-，则0a b ⋅=，0a ≠，0b ≠，所以a b ⊥，故选项D 正确.故答案为：AD. 【点睛】本题考查利用向量垂直求参数、利用向量共线求参数、根据向量的模的大小关系求参数的范围、利用向量的运算判断向量垂直，是中档题.10．已知向量()1,3OA =-，()2,1OB =-，()3,8OC t t =+-，若点A ，B ，C 能构成三角形，则实数t 可以为（） A ．-2B ．12C ．1D ．-1【答案】ABD【分析】若点A ，B ，C 能构成三角形，故A ，B ，C 三点不共线，即向量,AB BC 不共线，计算两个向量的坐标，由向量共线的坐标表示，即得解【详解】若点A ，B ，C 能构成三角形，故A ，B ，C 三点不共线，则向量,AB BC 不共线，由于向量()1,3OA =-，()2,1OB =-，()3,8OC t t =+-，故(3,4)AB OB OA =-=-，(5,9)BC OC OB t t =-=+-若A ，B ，C 三点不共线，则 3(9)4(5)01t t t ---+≠∴≠故选：ABD【点睛】本题考查了向量共线的坐标表示，考查了学生转化划归，概念理解，数学运算能力，属于中档题.。

吉林省桦甸市第四中学2013届高考数学一轮复习立体几何部分训练题(二) 新人教A版

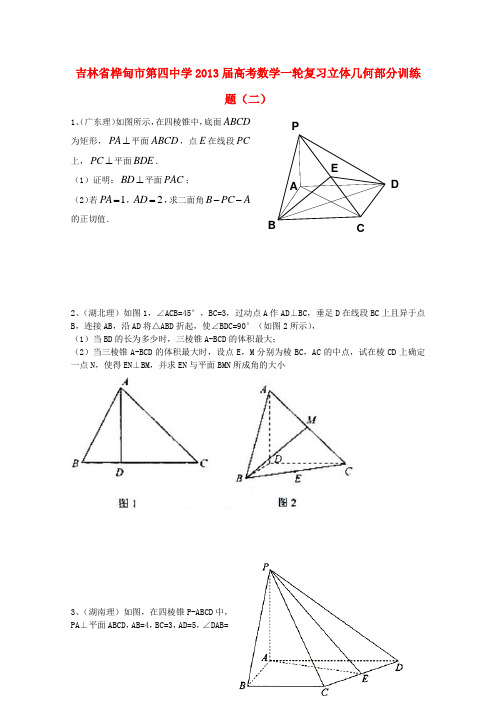
吉林省桦甸市第四中学2013届高考数学一轮复习立体几何部分训练题（二）1、（广东理）如图所示，在四棱锥中，底面ABCD 为矩形，PA ⊥平面ABCD ，点E 在线段PC 上，PC ⊥平面BDE ．（1）证明：BD ⊥平面PAC ；（2）若1PA =，2AD =，求二面角B PC A --的正切值．2、（湖北理）如图1，∠ACB=45°，BC=3，过动点A 作AD ⊥BC ，垂足D 在线段BC 上且异于点B ，连接AB ，沿AD 将△ABD 折起，使∠BDC=90°（如图2所示），（1）当BD 的长为多少时，三棱锥A-BCD 的体积最大；（2）当三棱锥A-BCD 的体积最大时，设点E ，M 分别为棱BC ，AC 的中点，试在棱CD 上确定一点N ，使得EN ⊥BM ，并求EN 与平面BMN 所成角的大小3、（湖南理）如图，在四棱锥P-ABCD 中，PA ⊥平面ABCD ，AB=4，BC=3，AD=5，∠DAB=EDCBA P∠ABC=90°，E 是CD 的中点. （Ⅰ）证明：CD ⊥平面PAE ；（Ⅱ）若直线PB 与平面PAE 所成的角和PB 与平面ABCD 所成的角相等，求四棱锥P-ABCD 的体积.4、（辽宁理）如图，直三棱柱///ABC A B C -，90BAC ∠=，/,AB AC AA λ==点M ，N 分别为/A B 和//B C 的中点。

(Ⅰ)证明：MN ∥平面//A ACC ;(Ⅱ)若二面角/A MN C --为直二面角，求λ的值。

5、（全国文理）如图，四棱锥P ABCD -中，底面ABCD 为菱形，PA ⊥底面ABCD，AC =2PA =，E 是PC 上的一点，2PE EC =。

（Ⅰ）证明：PC ⊥平面BED ；（Ⅱ）设二面角A PB C --为90，求PD 与平面PBC所成/CD角的大小。

6、（山东理）在如图所示的几何体中，四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB=60°，FC ⊥平面ABCD ，AE ⊥BD ，CB=CD=CF 。

高三一轮复习数列测试题及答案(K12教育文档)

高三一轮复习数列测试题及答案(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高三一轮复习数列测试题及答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高三一轮复习数列测试题及答案(word版可编辑修改)的全部内容。

数列一．选择题：1．等差数列｛b n }中，b 1＝1, b 1＋b 2＋b 3＋……＋b 10＝145, 则数列{b n ｝的通项公式b n 是（）。

（A ）3n －2 (B ）4－3n （C )16n －15 (D )37310-n 2．在公比为q 且各项均为正数的等比数列｛a n }中，若a n －3 ·a n ＋1＝a k 2(n ， k 均为自然数），则a k 为（）。

（A ）a 1q n －1 （B ）a 1q n －2 （C ）a 1q n －3 （D ）以上答案都不正确3．在等差数列{a n ｝中,a 3＋a 7－a 10＝8, a 11－a 4＝4，记S n ＝a 1＋a 2＋a 3＋……＋a n ，则S 13等于（）。

（A )168 （B ）156 （C ）78 （D ）1524．数列｛a n }的前n 项和是S n ，如果S n ＝3＋2a n (n ∈N ），则这个数列一定是（）. （A ）等比数列（B )等差数列（C ）除去第一项后是等比数列 (D ）除去第一项后是等差数列5．等差数列{a n ｝的前n 项和是S n ,a 3＋a 8>0, S 9<0, 则S 1， S 2， S 3, ……，S n 中最小的是（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

吉林省桦甸市第四中学2013届高考数学一轮复习数列部分训练题（二）
班级姓名
一、选择题
1、（湖北文理）定义在（-∞，0）∪（0，+∞）上的函数f （x ），如果对于任意给定的等比数列{n a }，{f （n a ）}仍是等比数列，则称f （x ）为“保等比数列函数”。

现有定义在（-∞，0）∪（0，+∞）上的如下函数：①f （x ）=x ²；②f （x ）=2x ；③||)(x x f =；④f （x ）=ln|x |。

则其中是“保等比数列函数”的f （x ）的序号为
A.①②
B.③④
C.①③
D.②④
二、填空题
2、（湖北文）传说古希腊毕达哥拉斯学派的数学家经常在沙滩上面画点或用小石子表示数。

他们研究过如图所示的三
角形数：
将三角形数1,3， 6,10，…记
为数列{a n }，将可被5整除的
三角形数按从小到大的顺序
组成一个新数列{b n }，可以推
测：
（Ⅰ）b 2012是数列{n a }中的第______项；
（Ⅱ）b 2k-1=______。

（用k 表示）
三、解答题
3、（湖北文理）已知等差数列{n a }前三项的和为-3，前三项的积为8.
（1）求等差数列{n a }的通项公式；
（2）若a 2,a 3,a 1成等比数列，求数列{}
n a 的前n 项的和。

4、（湖南文）某公司一下属企业从事某种高科技产品的生产.该企业第一年年初有资金2000万元，将其投入生产，到当年年底资金增长了50％.预计以后每年资金年增长率与第一年的相同.公司要求企业从第一年开始，每年年底上缴资金d 万元，并将剩余资金全部投入下一年生产.设第n 年年底企业上缴资金后的剩余资金为n a 万元.
（Ⅰ）用d 表示a 1，a 2，并写出1n a +与n a 的关系式；
（Ⅱ）若公司希望经过m （m ≥3）年使企业的剩余资金为4000万元，试确定企业每年上缴资金d 的值（用m 表示）.
5、（湖南理）已知数列{a n }的各项均为正数，记A （n ）=a 1+a 2+……+a n ，B （n ）=a 2+a 3+……+a n+1，C （n ）=a 3+a 4+……+a n+2，n=1,2，……
（1）若a 1=1，a 2=5，且对任意n ∈N ﹡，三个数A （n ），B （n ），C （n ）组成等差数列，
求数列{ n a }的通项公式.
（2）证明：数列{ n a }是公比为q 的等比数列的充分必要条件是：对任意N n *∈，
三个数A （n ），B （n ），C （n ）组成公比为q 的等比数列.
6、（江苏）已知各项均为正数的两个数列{}n a 和{}n b
满足：1n a n *+∈N ．
（1）设11n n n b b n a *+=+∈N ，，求证：数列2n n b a ⎧⎫⎛⎫⎪⎪⎨⎬ ⎪⎝⎭⎪⎪⎩⎭
是等差数列；（2
）设1n n n
b b n a *+=∈N ，，且{}n a 是等比数列，求1a 和1b 的值．
答案：
一、选择题
1、C
二、填空题
2、（Ⅰ）5030；（Ⅱ）
()5512k k -【解析】由以上规律可知三角形数1,3,6,10,…,的一个通项公式为(1)2
n n n a +=，写出其若干项有：1,3,6,10,15,21,28,36,45,55,66,78,91,105,110,发现其中能被5整除的为10,15,45,55,105,110,故142539*********,,,,,b a b a b a b a b a b a ======. 从而由上述规律可猜想：255(51)2
k k k k b a +==
（k 为正整数）， 2151(51)(511)5(51)22
k k k k k k b a ----+-===，故201221006510065030b a a a ⨯⨯===,即2012b 是数列{}n a 中的第5030项. 三、解答题
3、
4、【解析】（Ⅰ）由题意得12000(150%)3000a d d =+-=-，
2113(150%)2
a a d a d =+-=
-， 13(150%)2
n n n a a d a d +=+-=-. （Ⅱ）由（Ⅰ）得132
n n a a d -=- 2233()22
n a d d -=-- 233()22n a d d -=-- =
12213333()1()()2222n n a d --⎡⎤=-++++⎢⎥⎣⎦
. 整理得 1133()(3000)2()122n n n a d d --⎡⎤=---⎢⎥⎣⎦
13()(30003)22
n d d -=-+. 由题意，134000,()(30003)24000,2
n n a d d -=∴-+= 解得13()210001000(32)232()12
n n n n n n d +⎡⎤-⨯⎢⎥-⎣⎦==--. 故该企业每年上缴资金d 的值为缴11000(32)32n n n n +--时，经过(3)m m ≥年企业的剩余资金为４０００元.
5、【解析】
解（１）对任意N n *
∈,三个数(),(),()A n B n C n 是等差数列，所以
()()()(),B n A n C n B n -=-
即112,n n a a a ++-=－2a 亦即2121 4.n n a a a a +--=-=
故数列{}n a 是首项为１，公差为４的等差数列.于是1(1)44 3.n a n n =+-⨯=- （Ⅱ）（１）必要性：若数列{}n a 是公比为ｑ的等比数列，则对任意N n *∈，有 n n a qa =-1由0n a >知，(),(),()A n B n C n 均大于０，于是
12)2311212(......(),()......n n n n
q a a a a a a B n q A n a a a a a a +++++++===++++++
231)342231231
(......(),()......n n n n q a a a a a a C n q B n a a a a a a ++++++++++===++++++ 即()()B n A n ＝()()
C n B n ＝q ，所以三个数(),(),()A n B n C n 组成公比为q 的等比数列. （２）充分性：若对于任意N n *∈，三个数(),(),()A n B n C n 组成公比为q 的等比数列，
则
()(),()B n q A n C n q B n
==，于是[]()()()(),C n B n q B n A n -=-得2211(),n n a a q a a ++-=-即
212.n n a qa a a ++-=-1qa
由1n =有(1)(1),B qA =即21a qa =，从而210n n a qa ++-=.
因为0n a >，所以2211
n n a a q a a ++==，故数列{}n a 是首项为1a ，公比为q 的等比数列，综上所述，数列{}n a 是公比为q 的等比数列的充分必要条件是：对任意n ∈N ﹡，三个数(),(),()A n B n C n 组成公比为q 的等比数列.
6、。