北师大版八年级数学下：2.3《不等式的解集》同步练习(含答案)

合集下载

2021-2022学年北师大版八年级数学下册《2-3不等式的解集》同步练习题(附答案)

2021-2022学年北师大版八年级数学下册《2-3不等式的解集》同步练习题（附答案）1．如图，数轴上表示的解集是（）A．﹣3＜x≤2B．﹣3≤x＜2C．x＞﹣3D．x≤22．在数轴上表示﹣2≤x＜1正确的是（）A．B．C．D．3．在数轴上表示不等式x＞﹣1的解集正确的是（）A．B．C．D．4．在数轴上表示不等式﹣1＜x⩽2，其中正确的是（）A．B．C．D．5．交通法规人人遵守，文明城市处处安全．在通过桥洞时，我们往往会看到如图所示的标志，这是限制车高的标志．则通过该桥洞的车高x（m）的范围在数轴上可表示为（）A．B．C．D．6．定义新运算“⨂”，规定：a⨂b＝a﹣2b．若关于x的不等式x⨂m＞3的解集为x＞﹣1，则m的值是（）A．﹣1B．﹣2C．1D．27．下列解集中，不包括﹣4的是（）A．x≤﹣3B．x≥﹣4C．x≤﹣5D．x≥﹣68．已知关于x的不等式组有解，则a的取值不可能是（）A．0B．1C．2D．39．如果不等式组无解，则下列数轴示意图正确的是（）A．B．C．D．10．若不等式组无解，则a的取值范围是．11．若关于x的不等式组有解，则m的取值范围为．12．已知关于x的不等式组有实数解，则m的取值范围是．13．如图，此不等式的解集为．14．若关于x的一元一次不等式组有解，则m的取值范围为．15．若关于x的不等式组的解集是x＜4，则P（m+1，2﹣m）在第象限．16．若不等式（a+1）x＞a+1的解集是x＜1，则a的取值范围是．17．若关于x的不等式（a+1）x＞a+1的解集为x＞1，则a的取值范围是．18．在数轴上表示下列不等式：（1）x＞﹣2；（2）﹣1≤x＜3．19．分别用含x的不等式表示如图数轴中所表示的不等式的解集：①；②．20．如图，在数轴上，点A、B分别表示数1和﹣2x+3．（1）求x的取值范围；（2）将x的取值范围在数轴上表示出来．21．解不等式组．请结合题意，完成本题的解答．（1）解不等式①，得．（2）解不等式③，得．（3）把不等式①、②和③的解集在数轴上表示出来．（4）从图中可以找出三个不等式解集的公共部分，得不等式组的解集．参考答案1．解：由图可得，x＞﹣3且x≤2∴在数轴上表示的解集是﹣3＜x≤2，故选：A．2．解：﹣2是实心点，方向向右，1是空心点，方向向左，如图所示：故选：D．3．解：在数轴上表示不等式x＞﹣1的解集如下：故选：A．4．解：“＞”空心圆圈向右画折线，“≤”实心圆点向左画折线．故在数轴上表示不等式﹣1＜x⩽2如下：故选：A．5．解：由题意可得：通过该桥洞的车高x（m）的取值范围是：0＜x≤4.5．在数轴上表示如图：故选：D．6．解∵a⊗b＝a﹣2b，∴x⨂m＝x﹣2m．∵x⨂m＞3，∴x﹣2m＞3，∴x＞2m+3．∵关于x的不等式x⨂m＞3的解集为x＞﹣1，∴2m+3＝﹣1，∴m＝﹣2．故选：B．7．解：A选项，﹣3以及比﹣3小包括﹣4，不合题意；B选项，可以等于﹣4，不合题意；C选项，﹣5以及比﹣5小的数不包括﹣4，符合题意；D选项，﹣6以及比﹣6大的数包括﹣4，不合题意；故选：C．8．解：∵关于x的不等式组有解，∴a＜3，∴a的取值可能是0、1或2，不可能是3．故选：D．9．解：若不等式组无解，则数轴示意图正确的是：故选：D．10．解：因为不等式组无解，所以a≤﹣3，故答案为：a≤﹣311．解：不等式组有解，则m≤x＜2，解得m＜2．故答案为：m＜2．12．解：已知关于x的不等式组有实数解，则两个不等式一定有公共部分，则m的取值范围是m＞3．故答案为：m＞3．13．解：根据数轴可知：此不等式的解集为﹣2＜x≤3．故答案为：﹣2＜x≤3．14．解：解不等式2x＞﹣m得：x＞﹣，∵不等式组有解，∴﹣＜2，∴﹣m＜4，∴m＞﹣4，故答案为：m＞﹣4．15．解：∵关于x的不等式组的解集是x＜4，∴m≥4．∴m+1＞0，2﹣m＜0，∴P（m+1，2﹣m）在第四象限．故答案为：四．16．解：不等式（a+1）x＞a+1两边都除以a+1，得其解集为x＜1，∴a+1＜0，解得：a＜﹣1，故答案为：a＜﹣1．17．解：∵关于x的不等式（a+1）x＞a+1的解集为x＞1，∴a+1＞0，解得a＞﹣1，故答案为：a＞﹣1．18．解：（1）将x＞﹣2表示在数轴上如下：（2）将不等式组﹣1≤x＜3表示在数轴上如下：．19．解：①数轴表示不等式解集为x＞0，②数轴表示不等式解集为x≤3，故答案为：x＞0；x≤3．20．解：（1）由数轴可知：﹣2x+3＞1，解得：x＜1，即x的取值范围是x＜1；（2）在数轴上表示为：．21．解：（1）解不等式①，得x≥﹣3，依据是：不等式的基本性质．（2）解不等式③，得x＜1．（3）把不等式①，②和③的解集在数轴上表示出来．（4）从图中可以找出三个不等式解集的公共部分，得不等式组的解集为：﹣2＜x＜1，故答案为：（1）x≥﹣3；（2）x＜1；（4）﹣2＜x＜1．。

北师大版初中数学八年级下册《2.3 不等式的解集》同步练习卷(含答案解析

北师大新版八年级下学期《2.3 不等式的解集》同步练习卷一．选择题（共26小题）1．不等式组的解集在数轴上表示正确的是（）A．B．C．D．2．如图，数轴上表示的是某不等式组的解集，那么这个不等式组可能是（）A．B．C．D．3．如果不等式组无解，则k的取值范围是（）A．k＞2B．k＜2C．k≥2D．k＜24．若不等式组的解为x＜m，则m的取值范围为（）A．m≤1B．m=1C．m≥1D．m＜15．若元一次不等式组（a≠b）的解集是x＞a，则a，b的关系是（）A．a＜b B．a≤b C．a＞b D．a≥b6．已知实数a＞2，且a是关于x的不等式x+b≥3的一个解，则b不可能是（）A．0B．1C．2D．37．若关于x的不等式mx+1＞0的解集是x＜，则关于x的不等式（m﹣1）x＞﹣1﹣m的解集是（）A．x B．x C．x D．x8．不等式组的解集在数轴上表示为（）A．B．C．D．9．如图是甲、乙丙三人玩跷跷板的示意图（支点在跷跷板中点处），图中已知了乙、丙的体重，则甲的体重的取值范围在数轴上表示正确的是（）A．B．C．D．10．如图，不等式组的解集在同一数轴上表示正确的是（）A．B．C．D．11．如图，在数轴上表示关于x的不等式组的解集是（）A．x≥﹣1B．﹣1≤x≤2C．﹣1≤x＜2D．x＜212．若关于x的不等式组的解集是x≤a，则a的取值范围是（）A．a＜3B．a≤3C．a＞3D．a≥313．已知关于x的不等式组的解集是x≥1，则a的取值范围是（）A．a＞1B．a≥1C．a＜1D．a≤114．如果不等式组的解集为x＞a，则a的取值范围是（）A．a=2B．a＞2C．a≥2D．a≤215．若关于x的不等式（a﹣b）x＞a﹣b的解集是x＜1，那么下列结论正确的是（）A．a＞b B．a＜bC．a=b D．无法判断a、b的大小16．下列各数中，能使不等式x﹣3＞0成立的是（）A．﹣3B．5C．3D．217．已知不等式组无解，则a的取值范围是（）A．a≤1B．a≥1C．a＜1D．＞118．下列四个不等式组中，解集在数轴上表示如图所示的是（）A．B．C．D．19．如图是两个关于x的一元一次不等式的解集在同一数轴上的表示，由它们组成的不等式组的解集是（）A．x＞﹣1B．x＞2C．x≥2D．﹣1＜x≤2 20．不等式x≤﹣1的解集在数轴上表示正确的是（）A．B．C．D．21．函数y=中，自变量x的取值范围在数轴上表示正确的是（）A．B．C．D．22．若关于x的不等式组有解，且关于x的方程kx=2（x﹣2）﹣（3x+2）有非负整数解，则符合条件的所有整数k的和为（）A．﹣5B．﹣9C．﹣12D．﹣1623．已知关于x的不等式（2﹣a）x＞1的解集是x＜；则a的取值范围是（）A．a＞0B．a＜0C．a＜2D．a＞224．已知关于x的不等式＞1的解都是不等式＞0的解，则a的范围是（）A．a=5B．a≥5C．a≤5D．a＜525．如果不等式组有解，那么m的取值范围是（）A．m＞5B．m≥5C．m＜5D．m≤826．若关于x的不等式组无解，则a的取值范围是（）A．a＞2B．a≥2C．1＜a≤2D．1≤a＜2二．填空题（共15小题）27．不等式组的解集是3＜x＜a+2，若a是整数，则a等于．28．若不等式组没有解，则m的取值范围是．29．x=﹣1不等式≤+1的其中一个解．（填“是”或“不是”）30．已知x=3﹣2a是不等式2（x﹣3）＜x﹣1的一个解，那么a的取值范围是．31．如图，小雨把不等式3x+1＞2（x﹣1）的解集表示在数轴上，则阴影部分盖住的数字是．32．已知如图是关于x的不等式2x﹣a＞﹣3的解集，则a的值为．33．若不等式2x＜4的解都能使不等式x﹣a＜5成立，则a的取值范围是．34．若关于x的不等式﹣2x+a≥2的解集是x≤﹣1，则a的值是．35．若不等式组的解集是空集，则a、b的大小关系是．36．如果不等式组无解，那么m的取值范围是．37．关于x的不等式组的解集是x＞﹣2，则m=．38．在实数范围内规定新运算“△”，其规则是：a△b=2a﹣b．已知不等式x△k ≥1的解集在数轴上如图表示，则k的取值范围是．39．若x=5是关于x的不等式2x+5＞a的一个解，但x=4不是它的解，则a的取值范围是．40．如果不等式组有解，则的解集为．41．已知不等式2x+★＞2的解集是x＞﹣4，则“★”表示的数是．三．解答题（共9小题）42．在数轴上表示下列不等式（1）x＜﹣1（2）﹣2＜x≤3．43．已知关于x的不等式≤的解是x≥，求m的值．44．已知关于x、y的方程组的解满足不等式3﹣x＜2y，求实数a的取值范围．45．如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．（1）在方程①3x﹣1=0，②x+1=0，③x﹣（3x+1）=﹣5中，不等式组的关联方程是；（填序号）（2）若不等式组的一个关联方程的根是整数，则这个关联方程可以是；（写出一个即可）（3）若方程3﹣x=2x，3+x=2（x+）都是关于x的不等式组的关联方程，直接写出m的取值范围．46．请阅读求绝对值不等式|x|＜3和|x|＞3的解集的过程：因为|x|＜3，从如图1所示的数轴上看：大于﹣3而小于3的数的绝对值是小于3的，所以|x|＜3的解集是﹣3＜x＜3；因为|x|＞3，从如图2所示的数轴上看：小大于﹣3的数和大于3的数的绝对值是大于3的，所以|x|＞3的解集是x＜﹣3或x＞3．解答下面的问题：（1）不等式|x|＜a（a＞0）的解集为；不等式|x|＞a（a＞0）的解集为．（2）解不等式|x﹣5|＜3；（3）解不等式|x﹣3|＞5．47．如果t＞0，试证必在a与b之间．48．对于任意实数m，n定义一种新运算m※n=mn﹣m+3，等式的右边是通常的加减法和乘法运算，例如：3※5=3×5﹣3+3=15．请根据上述定义解决问题：若a＜2※x＜7，且解集中恰有两个整数解，求a的取值范围．49．已知x=1满足不等式组，求a的取值范围．50．已知不等式组（1）当k=﹣2时，不等式组的解集是：；当k=3时，不等式组的解集是：（2）由（1）可知，不等式组的解集随k的值变化而变化，若不等式组有解，求k的取值范围并求出解集？北师大新版八年级下学期《2.3 不等式的解集》同步练习卷参考答案与试题解析一．选择题（共26小题）1．不等式组的解集在数轴上表示正确的是（）A．B．C．D．【分析】把不等式的解集表示在数轴上即可．【解答】解：由得不等式组的解集是2＜x≤4，在数轴上表示为：故选：C．【点评】把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．2．如图，数轴上表示的是某不等式组的解集，那么这个不等式组可能是（）A．B．C．D．【分析】根据不等式组解集的确定方法：大小小大中间找，可得答案．【解答】解：由数轴上表示的不等式组的解集，得﹣2＜x≤3．故选：B．【点评】本题考查了在数轴上表示不等式的解集，不等式的解集，不等式组解集的确定方法：同大取大，同小取小，大小小大中间找，大大小小无处找．3．如果不等式组无解，则k的取值范围是（）A．k＞2B．k＜2C．k≥2D．k＜2【分析】根据不等式组无解得出答案即可．【解答】解：∵不等式组无解，∴k≥2，故选：C．【点评】本题考查了不等式的解集和不等式组的解集，根据找不等式组解集的规律得出答案是解此题的关键．4．若不等式组的解为x＜m，则m的取值范围为（）A．m≤1B．m=1C．m≥1D．m＜1【分析】先解不等式，然后根据解集为x＜m，可得结论．【解答】解：，∵不等式组的解集为x＜m，∴m≤1．故选：A．【点评】本题考查了解一元一次不等式组，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．5．若元一次不等式组（a≠b）的解集是x＞a，则a，b的关系是（）A．a＜b B．a≤b C．a＞b D．a≥b【分析】根据不等式组解集的“同大取较大”的原则，a≥b，由已知得a＞b．【解答】解：∵组（a≠b）的解集是x＞a，∴a＞b．故选：C．【点评】本题考查了不等式组解集的四种情况：①同大取较大，②同小取较小，③小大大小中间找，④大大小小解不了．6．已知实数a＞2，且a是关于x的不等式x+b≥3的一个解，则b不可能是（）A．0B．1C．2D．3【分析】求出b=0、1、2、3时不等式的解集，判断是否包括实数a即可得．【解答】解：A、当b=0时，不等式x+b≥3的解集为x≥3，此时不一定包括实数a的解，此选项符合题意；B、当b=1时，不等式x+b≥3的解集为x≥2，此时不等式的解集一定包括实数a，此选项不符合题意；C、当b=2时，不等式x+b≥3的解集为x≥1，此时不等式的解集一定包括实数a，此选项不符合题意；D、当b=3时，不等式x+b≥3的解集为x≥0，此时不等式的解集一定包括实数a，此选项不符合题意；故选：A．【点评】本题主要考查不等式的解集，解题的关键是掌握解不等式和不等式的解集．7．若关于x的不等式mx+1＞0的解集是x＜，则关于x的不等式（m﹣1）x ＞﹣1﹣m的解集是（）A．x B．x C．x D．x【分析】根据不等式mx+1＞0的解集，得出m的值，再代入不等式（m﹣1）x ＞﹣1﹣m中，求解即可．【解答】解：∵关于x的不等式mx+1＞0的解集是x＜，∴m=﹣5，把m=﹣5代入（m﹣1）x＞﹣1﹣m得4x＞﹣6，解得x＜﹣，故选：A．【点评】本题考查了不等式的解集，掌握不等式的解法是解题的关键．8．不等式组的解集在数轴上表示为（）A．B．C．D．【分析】同大取大；同小取小；大小小大中间找；大大小小找不到；依此可求不等式组的解集，再在数轴上表示出来即可求解．【解答】解：不等式组的解集在数轴上表示为．故选：D．【点评】考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．9．如图是甲、乙丙三人玩跷跷板的示意图（支点在跷跷板中点处），图中已知了乙、丙的体重，则甲的体重的取值范围在数轴上表示正确的是（）A．B．C．D．【分析】根据示意图就可以得到两个不等关系，从而求出甲的体重的范围．然后就可以在数轴上表示出来．【解答】解：由第1个跷跷板知甲的体重＞45kg，由第2个跷跷板知甲的体重＜55kg，即45kg＜甲的体重＜55kg，表示在数轴上如下：故选：C．【点评】本题考查在数轴上表示不等式的解集，需要注意当包括原数时，在数轴上表示时应用实心圆点来表示，当不包括原数时，应用空心圆圈来表示．10．如图，不等式组的解集在同一数轴上表示正确的是（）A．B．C．D．【分析】根据不等式组确定出解集，表示在数轴上即可．【解答】解：不等式组的解集为﹣1＜x≤2，表示在同一数轴为，故选：B．【点评】此题考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．11．如图，在数轴上表示关于x的不等式组的解集是（）A．x≥﹣1B．﹣1≤x≤2C．﹣1≤x＜2D．x＜2【分析】数轴的某一段上面，表示解集的线的条数，与不等式的个数一样，那么这段就是不等式组的解集．实心圆点包括该点，空心圆圈不包括该点，＞向右＜向左．两个不等式的公共部分就是不等式组的解集．【解答】解：由图示可看出，从﹣1出发向右画出的折线且表示﹣1的点是实心圆，表示x≥﹣1；从3出发向左画出的折线且表示2的点是空心圆，表示x＜2，不等式组的解集是指它们的公共部分．所以这个不等式组的解集是：﹣1≤x＜2．故选：C．【点评】此题主要考查不等式组的解法及在数轴上表示不等式组的解集．不等式组的解集在数轴上表示的方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．12．若关于x的不等式组的解集是x≤a，则a的取值范围是（）A．a＜3B．a≤3C．a＞3D．a≥3【分析】先根据第一个不等式为x＜3，由于不等式组的解集为x≤a，则利用同小取小可得到a的范围．【解答】解：∵关于x的不等式组的解集是x≤a，∴a＜3．故选：A．【点评】本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．13．已知关于x的不等式组的解集是x≥1，则a的取值范围是（）A．a＞1B．a≥1C．a＜1D．a≤1【分析】利用不等式取解集的方法判断即可确定出a的范围．【解答】解：∵关于x的不等式组的解集是x≥1，∴a＜1，故选：C．【点评】此题考查了不等式的解集，熟练掌握不等式取解集的方法是解本题的关键．14．如果不等式组的解集为x＞a，则a的取值范围是（）A．a=2B．a＞2C．a≥2D．a≤2【分析】根据方程组的解集的表示方法，可得答案．【解答】解：由不等式组的解集为x＞a，得a≥2，故选：C．【点评】本题考查了不等式组的解集，利用同大取大是解题关键．15．若关于x的不等式（a﹣b）x＞a﹣b的解集是x＜1，那么下列结论正确的是（）A．a＞b B．a＜bC．a=b D．无法判断a、b的大小【分析】由已知不等式的解集确定出a与b的大小即可．【解答】解：∵关于x的不等式（a﹣b）x＞a﹣b的解集是x＜1，∴a﹣b＜0，即a＜b，故选：B．【点评】此题考查了不等式的解集，熟练掌握不等式的基本性质是解本题的关键．16．下列各数中，能使不等式x﹣3＞0成立的是（）A．﹣3B．5C．3D．2【分析】根据不等式的解集的概念即可求出答案．【解答】解：不等式x﹣3＞0的解集为：x＞3．故选：B．【点评】本题考查不等式的解集，解题的关键是正确理解不等式的解的概念，本题属于基础题型．17．已知不等式组无解，则a的取值范围是（）A．a≤1B．a≥1C．a＜1D．＞1【分析】根据不等式的解集的定义即可求出答案．【解答】解：由不等式组无解可知，两不等式在数轴上没有公共部分，即a≤1故选：A．【点评】本题考查不等式的解集，解题的关键是熟练运用不等式的解集的定义，本题属于基础题型．18．下列四个不等式组中，解集在数轴上表示如图所示的是（）A．B．C．D．【分析】根据不等式组的表示方法，可得答案．【解答】解：由解集在数轴上的表示可知，该不等式组为，故选：D．【点评】本题考查了在数轴上表示不等式的解集，利用不等式组的解集的表示方法：大小小大中间找是解题关键．19．如图是两个关于x的一元一次不等式的解集在同一数轴上的表示，由它们组成的不等式组的解集是（）A．x＞﹣1B．x＞2C．x≥2D．﹣1＜x≤2【分析】找出两个不等式解集的方法部分确定出不等式组的解集即可．【解答】解：根据数轴得：不等式组的解集为x≥2，故选：C．【点评】此题考查了在数轴表示不等式的解集，弄清不等式组取解集的方法是解本题的关键．20．不等式x≤﹣1的解集在数轴上表示正确的是（）A．B．C．D．【分析】将已知解集表示在数轴上即可．【解答】解：不等式x≤﹣1的解集在数轴上表示正确的是，故选：B．【点评】此题考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．21．函数y=中，自变量x的取值范围在数轴上表示正确的是（）A．B．C．D．【分析】根据被开方数大于等于0列式计算即可得解，然后在数轴上表示即可．【解答】解：由题意得，1﹣x≥0，解得x≤1．在数轴上表示如下：故选：B．【点评】本题考查了函数自变量的范围及在数轴上表示不等式的解集，解题的关键是从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．22．若关于x的不等式组有解，且关于x的方程kx=2（x﹣2）﹣（3x+2）有非负整数解，则符合条件的所有整数k的和为（）A．﹣5B．﹣9C．﹣12D．﹣16【分析】先根据不等式组有解得k的取值，利用方程有非负整数解，将k的取值代入，找出符合条件的k值，并相加．【解答】解：，解①得：x≥1+4k，解②得：x≤6+5k，∴不等式组的解集为：1+4k≤x≤6+5k，1+4k≤6+5k，k≥﹣5，解关于x的方程kx=2（x﹣2）﹣（3x+2）得，x=﹣，因为关于x的方程kx=2（x﹣2）﹣（3x+2）有非负整数解，当k=﹣4时，x=2，当k=﹣3时，x=3，当k=﹣2时，x=6，∴﹣4﹣3﹣2=﹣9；故选：B．【点评】本题考查了解一元一次不等式组、方程的解，有难度，熟练掌握不等式组的解法是解题的关键．23．已知关于x的不等式（2﹣a）x＞1的解集是x＜；则a的取值范围是（）A．a＞0B．a＜0C．a＜2D．a＞2【分析】根据已知不等式的解集，结合x的系数确定出2﹣a为负数，求出a的范围即可．【解答】解：∵关于x的不等式（2﹣a）x＞1的解集是x＜，∴2﹣a＜0，解得：a＞2．故选：D．【点评】此题考查了不等式的解集，熟练掌握不等式的基本性质是解本题的关键．24．已知关于x的不等式＞1的解都是不等式＞0的解，则a的范围是（）A．a=5B．a≥5C．a≤5D．a＜5【分析】先把a看作常数求出两个不等式的解集，再根据同大取大列出不等式求解即可．【解答】解：由＞1得，x＞，由＞0得，x＞﹣，∵关于x的不等式＞1的解都是不等式＞0的解，∴≥﹣，解得a≤5．即a的取值范围是：a≤5．故选：C．【点评】本题考查了不等式的解集，解一元一次不等式，分别求出两个不等式的解集，再根据同大取大列出关于a的不等式是解题的关键．25．如果不等式组有解，那么m的取值范围是（）A．m＞5B．m≥5C．m＜5D．m≤8【分析】依据小大大小中间找，可确定出m的取值范围．【解答】解：∵不等式组有解，∴m＜5．故选：C．【点评】本题主要考查的是不等式的解集，依据口诀列出不等式是解题的关键．26．若关于x的不等式组无解，则a的取值范围是（）A．a＞2B．a≥2C．1＜a≤2D．1≤a＜2【分析】分别表示出不等式组中两不等式的解集，由不等式组无解，确定出a 的范围即可．【解答】解：不等式组整理得：，由不等式组无解，得到a≥2，故选：B．【点评】此题考查了不等式的解集，熟练掌握不等式组取解集的方法是解本题的关键．二．填空题（共15小题）27．不等式组的解集是3＜x＜a+2，若a是整数，则a等于2或3．【分析】根据已知不等式组和不等式组的解集得出关于a的不等式组，求出不等式组的解集即可．【解答】解：∵不等式组的解集是3＜x＜a+2，∴，解得：1＜a≤3，∵a为整数，∴a=2或3，故答案为：2或3．【点评】本题考查了解一元一次不等式组和不等式组的解集，能根据题意得出关于a的不等式组是解此题的关键．28．若不等式组没有解，则m的取值范围是m≥2．【分析】利用不等式组取解集的方法判断即可求出m的范围．【解答】解：∵不等式组没有解，∴m﹣1≥1，解得m≥2．故答案为：m≥2．【点评】此题考查了不等式的解集，熟练掌握不等式取解集的方法是解本题的关键．29．x=﹣1是不等式≤+1的其中一个解．（填“是”或“不是”）【分析】求出不等式的解集，判断即可．【解答】解：不等式去分母得：2+2x≤3+6x+6，移项合并得：4x≥﹣7，解得：x≥﹣，则x=﹣1是不等式一个解，故答案为：是【点评】此题考查了不等式的解集，求出不等式的解集是解本题的关键．30．已知x=3﹣2a是不等式2（x﹣3）＜x﹣1的一个解，那么a的取值范围是a ＞﹣1．【分析】根据题意得到关于a的一元一次不等式，解不等式即可．【解答】解：由题意得，2（3﹣2a﹣3）＜3﹣2a﹣1，﹣4a＜2﹣2a，﹣2a＜2，a＞﹣1，故答案为：a＞﹣1．【点评】本题考查的是一元一次不等式的解法，掌握解一元一次不等式的一般步骤是解题的关键．31．如图，小雨把不等式3x+1＞2（x﹣1）的解集表示在数轴上，则阴影部分盖住的数字是﹣3．【分析】根据去括号、移项、合并同类项，可得不等式的解集，根据不等式解集的表示方法，可得答案．【解答】解：去括号，得3x+1＞2x﹣2，移项、合并同类项，得x＞﹣3，故答案为：﹣3．【点评】本题考查了在数轴上表示不等式的解集，不等式的解集在数轴上表示出来＞或≥，向右画；＜或≤，向左画，注意在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．32．已知如图是关于x的不等式2x﹣a＞﹣3的解集，则a的值为1．【分析】解出不等式2x﹣a＞﹣3的解集是x＞，由数轴上的解集得出x＞﹣1，从而得到一个一元一次方程=﹣1，解得a的值即可．【解答】解：解不等式2x﹣a＞﹣3，解得x＞，由数轴上的解集，可得x＞﹣1，∴=﹣1，解得a=1．【点评】当题中有两个未知字母时，应把关于某个字母的不等式中的字母当成未知数，求得解集，再根据解集进行判断，求得另一个字母的值．本题需注意，在不等式两边都除以一个负数时，应只改变不等号的方向，余下运算不受影响，该怎么算还怎么算．33．若不等式2x＜4的解都能使不等式x﹣a＜5成立，则a的取值范围是a≥﹣3．【分析】根据题意得出x＜2，再解关于a的不等式即可得出答案．【解答】解：∵不等式2x＜4的解为x＜2，∴a+5≥2，∴a≥﹣3，故答案为a≥﹣3．【点评】本题考查了不等式的解集，掌握不等式的解法是解题的关键．34．若关于x的不等式﹣2x+a≥2的解集是x≤﹣1，则a的值是0．【分析】根据不等式的性质，可得答案．【解答】解：由题意，得2﹣a=2，解得a=0，故答案为：0．【点评】本题考查了不等式的解集，利用不等式的性质是解题关键．35．若不等式组的解集是空集，则a、b的大小关系是b≥a．【分析】根据大大小小无解进行解答即可．【解答】解：∵不等式组的解集是无解，∴b≥a，故答案为：b≥a．【点评】此题主要考查了不等式的解集，关键是正确理解“大大小小无解”的含义．36．如果不等式组无解，那么m的取值范围是m≤3．【分析】由不等式组无解，利用不等式组取解集的方法确定出m的范围即可．【解答】解：∵不等式组无解，∴m≤3，故答案为：m≤3【点评】此题考查了不等式的解集，熟练掌握不等式组取解集的方法是解本题的关键．37．关于x的不等式组的解集是x＞﹣2，则m=﹣4．【分析】根据同大取大，可得答案．【解答】解：由的解集是x＞﹣2，得∵m+2＞m﹣1，∴m+2=﹣2，解得m=﹣4，故答案为：﹣4．【点评】本题考查了不等式组的解集，利用同大取大是解题关键，要分类讨论，以防遗漏．38．在实数范围内规定新运算“△”，其规则是：a△b=2a﹣b．已知不等式x△k ≥1的解集在数轴上如图表示，则k的取值范围是k=﹣3．【分析】根据新运算法则得到不等式2x﹣k≥1，通过解不等式即可求k的取值范围，结合图象可以求得k的值．【解答】解：根据图示知，已知不等式的解集是x≥﹣1．则2x﹣1≥﹣3∵x△k=2x﹣k≥1，∴2x﹣1≥k且2x﹣1≥﹣3，∴k=﹣3．故答案是：k=﹣3．【点评】本题考查了在数轴上表示不等式的解集、解一元一次不等式．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．39．若x=5是关于x的不等式2x+5＞a的一个解，但x=4不是它的解，则a的取值范围是13≤a＜15．【分析】表示出不等式的解集，由x=5是一个解，x=4不是它的解，确定出a的范围即可．【解答】解：不等式2x+5＞a，解得：x＞，由x=5是不等式的一个解，但x=4不是它的解，得到4≤＜5，解得：13≤a＜15，则a的取值范围是13≤a＜15，故答案为：13≤a＜15【点评】此题考查了不等式的解集，熟练掌握不等式解集的定义是解本题的关键．40．如果不等式组有解，则的解集为x＜1﹣b．【分析】根据不等式组有解，得出a＜b，进一步得出1﹣a＞1﹣b，即可得出的解集．【解答】解：∵不等式组有解，∴a＜b，∴﹣a＞﹣b，∴1﹣a＞1﹣b，∴不等式组的解集为：x＜1﹣b．故答案为：x＜1﹣b．【点评】此题主要考查了不等式的解集求法，根据已知得出a＜b是解决问题的关键．41．已知不等式2x+★＞2的解集是x＞﹣4，则“★”表示的数是10．【分析】设“★”表示的数a，则不等式是2x+a＞2，解不等式利用a表示出不等式的解集，则可以得到一个关于a的方程，求得a的值．【解答】解：设“★”表示的数a，则不等式是2x+a＞2，移项，得2x＞2﹣a，则x＞．根据题意得：=﹣4，解得：a=10．故答案是：10．【点评】主要考查了一元一次不等式组解集的求法，解答此题的关键是掌握不等式的性质，在不等式两边同加或同减一个数或式子，不等号的方向不变，在不等式两边同乘或同除一个正数或式子，不等号的方向不变在不等式两边同乘或同除一个负数或式子，不等号的方向改变．三．解答题（共9小题）42．在数轴上表示下列不等式（1）x＜﹣1（2）﹣2＜x≤3．【分析】（1）根据不等式的解集在数轴上表示方法可画出图示．（2）根据不等式的解集在数轴上表示方法可画出图示．【解答】解：（1）将x＜﹣1表示在数轴上如下：（2）将不等式组﹣2＜x≤3表示在数轴上如下：【点评】本题主要考查在数轴上表示不等式的解集，不等式的解集在数轴上表示出来的方法：“＞”空心圆点向右画折线，“≥”实心圆点向右画折线，“＜”空心圆点向左画折线，“≤”实心圆点向左画折线．43．已知关于x的不等式≤的解是x≥，求m的值．【分析】不等式组整理后表示出解集，根据已知解集确定出m的值即可．【解答】解：原不等式可化为：4m+2x≤12mx﹣3，即（12m﹣2）x≥4m+3，又因原不等式的解为x≥，则12m﹣2＞0，m＞，比较得：=，即24m+18=12m﹣2，解得：m=﹣（舍去）．故m无值．【点评】此题考查了不等式的解集，熟练掌握运算法则是解本题的关键．44．已知关于x、y的方程组的解满足不等式3﹣x＜2y，求实数a的取值范围．【分析】先求出二元一次方程组的解，再带入不等式，即可解答．【解答】解：方程组的解为：∵3﹣x＜2y，∴3﹣解得：a＞1．【点评】本题考查了二元一次方程组的解，解决本题的关键是解二元一次方程组．45．如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．（1）在方程①3x﹣1=0，②x+1=0，③x﹣（3x+1）=﹣5中，不等式组的关联方程是③；（填序号）（2）若不等式组的一个关联方程的根是整数，则这个关联方程可以是x﹣1=0（答案不唯一）；（写出一个即可）（3）若方程3﹣x=2x，3+x=2（x+）都是关于x的不等式组的关联方程，直接写出m的取值范围．【分析】（1）先求出方程的解和不等式组的解集，再判断即可；（2）先求出不等式组的解集，求出不等式组的整数解，再写出方程即可；（3）先求出方程的解和不等式组的解集，即可得出答案．。

2020-2021学年八年级数学下册北师大版第二章第3节《不等式的解集》同步练习(有答案)

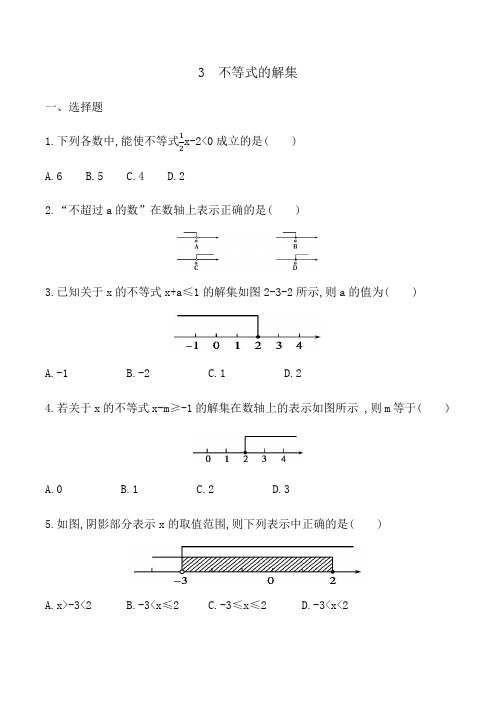
3 不等式的解集一、选择题x-2<0成立的是( )1.下列各数中,能使不等式12A.6B.5C.4D.22.“不超过a的数”在数轴上表示正确的是( )3.已知关于x的不等式x+a≤1的解集如图2-3-2所示,则a的值为( )A.-1B.-2C.1D.24.若关于x的不等式x-m≥-1的解集在数轴上的表示如图所示 ,则m等于( )A.0B.1C.2D.35.如图,阴影部分表示x的取值范围,则下列表示中正确的是( )A.x>-3<2B.-3<x≤2C.-3≤x≤2D.-3<x<26.不等式3x-3≥0的解的情况是( )A.有无数个解B.有两个解C.只有一个解D.无解7.函数y=63+x 中自变量x 的取值范围在数轴上表示正确的是( )8.若实数3是关于x 的不等式2x-a-2<0的一个解,则a 可取的最小正整数为 ( )A.2B.3C.4D.5二、填空题9.在-1,23,2.5,4,5中,是不等式x+5<9的解的有个,不等式x+5<9的解集为 .10.若关于x 的不等式x ≥m-1的解集如图所示,则m 等于 .11.方程51x=-2的解有个,不等式51x>-2的解有个,其中负整数解有个.12.在数4,5,6,-1中,是不等式x-2<3的解的为 .13.若关于x 的不等式(1-a)x>2可化为x<a 12-,则a 的取值范围是 .三、解答题14.已知关于x的不等式(x-5)(ax-3a+4)≤0.(1)若x=2是该不等式的解,求a的取值范围;(2)在(1)的条件下,且x=1不是该不等式的解,求符合题意的一个无理数a.15.定义新运算“⊕”:对于任意实数a,b,都有a⊕b=ab+1,等式右边是通常的加法、减法及乘法运算.比如2⊕5=2×5+1=11.若3⊕x的值小于13,求x的取值范围,并写出满足条件的非负整数解.16.用A、B两种型号的钢丝各两根焊接成周长不小于2.4 m的长方形框架,已知每根A型钢丝的长度比每根B型钢丝长度的2倍少3 cm.(1)设每根B型钢丝长为x cm,按题意列出不等式并求出它的解集;(2)如果每根B型钢丝长度有以下四种选择:30 cm,40 cm,41 cm,45 cm,那么其中哪些钢丝合适?答案1.D2.B3.A4.D5.B6.A7.A8.D9. 3;x<410. 311. 1;无数;912. 4和-113. a>114.(1)把x=2代入(x-5)(ax-3a+4)≤0,得(2-5)(2a-3a+4)≤0,解得a≤4,所以a的取值范围是a≤4.(2)由(1)得,a≤4,取a=π,此时原不等式变为(x-5)(πx-3π+4)≤0,当x=1时,不等式的左边=(1-5)(π-3π+4)=-4(4-2π),∵4-2π<0,∴不等式的左边大于0,∴x=1不是该不等式的解,∴符合题意的无理数a可以是π.15.由已知得3⊕x=3x+1<13,解得x<4,∴所求的非负整数解为0,1,2,3.16.(1)∵每根B型钢丝的长度为x cm,∴每根A型钢丝的长度为(2x-3)cm,∴2x+2(2x-3)≥240,解得x≥41.(2)∵x≥41,∴只有长度为41 cm和45 cm的钢丝满足要求.。

北师版八年级下数学2.3不等式的解习题精选(含答案)

数学2.3习题精选（含答案）一．选择题（共20小题）1．（2013•淮安）不等式组的解集是（）2．（2012•庆阳）关于x的不等式﹣2x+a≥2的解集如图所示，a的值是（）不等式组不等式组不等式组不等式组5．（2004•泉州）不等式组的解集情况为（）8．不等式组的解集是（）9．已知关于x 的不等式组无解，则a的取值范围是（）12．若关于x的一元一次不等式组无解，则a的取值范围是（）13．如果不等式组无解，那么m 的取值范围是（）14．不等式（m﹣2）x＞1的解集是，则a的取值范围是（）15．如果不等式组的解集是x＞2，则a的取值范围是（）．C D．17．（2013•红河州）不等式组的解集在数轴上表示为（）．C D．18．（2011•仙桃）某不等式组的解集在数轴上表示如图，则这个不等式组可能是（）．C D．19．（2011•六盘水）把不等式组的解集表示在数轴上，正确的是（）．．．．．B．．．二．填空题（共10小题）21．（2006•衢州）写一个解集是x＞2的不等式：_________．22．（2006•南充）若不等式﹣3x+n＞0的解集是x＜2，则不等式﹣3x+n＜0的解集是_________．23．对于一次函数y=x﹣，若﹣2≤x≤2，则y的取值范围是_________．24．（2013•合肥模拟）如图，数轴上所表示的不等式组的解集是：_________．25．（2011•路南区一模）写出如图所表示的某不等式组的解集_________．26．如果关于x的一元一次不等式组的解集在数轴上的表示如图所示，那么该不等式组的解集为_________．27．若关于x的不等式x﹣a≤﹣3的解集如下图所示，则a的值是_________．28．关于x的某个不等式组的解集在数轴上表示如图所示，则该不等式组的解集为_________．29．如图，用不等式表示公共部分x的范围_________．30．关于x的不等式3x﹣2a＜﹣2的解集如图所示，则a=_________．数学2.3习题精选（含答案）参考答案与试题解析一．选择题（共20小题）1．（2013•淮安）不等式组的解集是（）的解集是2．（2012•庆阳）关于x的不等式﹣2x+a≥2的解集如图所示，a的值是（）＜不等式组不等式组不等式组不等式组的解集是无解，故选项错误；的解集是无解，故选项错误；5．（2004•泉州）不等式组的解集情况为（）＜＞8．不等式组的解集是（）的解集是无解，故选9．已知关于x的不等式组无解，则a的取值范围是（）无解，12．若关于x的一元一次不等式组无解，则a的取值范围是（），13．如果不等式组无解，那么m的取值范围是（）无解，14．不等式（m﹣2）x＞1的解集是，则a的取值范围是（）的解集是，据此即可得到的解集是，15．如果不等式组的解集是x＞2，则a的取值范围是（）解：因为不等式组16．（2013•益阳）已知一次函数y=x﹣2，当函数值y＞0时，自变量x的取值范围在数轴上表示正确的是（）．C D．17．（2013•红河州）不等式组的解集在数轴上表示为（）．C D．的解集在数轴上表示18．（2011•仙桃）某不等式组的解集在数轴上表示如图，则这个不等式组可能是（）．C D．19．（2011•六盘水）把不等式组的解集表示在数轴上，正确的是（）．．．．的解集在数轴上表示为：．B．．．二．填空题（共10小题）21．（2006•衢州）写一个解集是x＞2的不等式：2x＞4或x﹣2＞0或2x+1＞x+3．22．（2006•南充）若不等式﹣3x+n＞0的解集是x＜2，则不等式﹣3x+n＜0的解集是x＞2．可求得，23．对于一次函数y=x﹣，若﹣2≤x≤2，则y的取值范围是﹣≤y≤0．；k=＞的取值范围是﹣≤24．（2013•合肥模拟）如图，数轴上所表示的不等式组的解集是：﹣2＜x≤1．25．（2011•路南区一模）写出如图所表示的某不等式组的解集x＞2．26．如果关于x的一元一次不等式组的解集在数轴上的表示如图所示，那么该不等式组的解集为﹣1＜x≤2．27．若关于x的不等式x﹣a≤﹣3的解集如下图所示，则a的值是2．28．关于x的某个不等式组的解集在数轴上表示如图所示，则该不等式组的解集为x≥1．解：根据数轴得：29．如图，用不等式表示公共部分x的范围﹣3≤x＜2．30．关于x的不等式3x﹣2a＜﹣2的解集如图所示，则a=﹣2．＜=，=。

最新【北师大版】八年级下册数学：2.3《不等式的解集》同步练习(含答案)

最新北师大版数学精品教学资料《不等式的解集》习题一、选择题1．下列数值中不是不等式5x≥2x+9的解的是（）A．5 B．4 C．3 D．22．如果关于x的不等式（m+1）x＞m+1的解集为x＜1，则m的取值范围是（）A．m＜0 B．m＜﹣1 C．m＞1 D．m＞﹣13．下列说法错误的是（）A．2x＜﹣8的解集是x＜﹣4 B．x＜5的正整数解有无穷个C．﹣15是2x＜﹣8的解D．x＞﹣3的非负整数解有无穷个4．如图，数轴上所表示关于x的不等式组的解集是（）A．x≥2B．x＞2 C．x＞﹣1 D．﹣1＜x≤25．不等式3x﹣1＞x+1的解集在数轴上表示为（）A．B．C．D．6．在数轴上表示不等式x﹣1＜0的解集，正确的是（）A．B．C．D．7．关于x的不等式x+m＞2的解集为x＞1，则m的值为（）A．0 B．1 C．2 D．3二、填空题8．不等式x2≥0的解集是．9．一个关于x的不等式的解集为一切实数，这个不等式可以是．10．关于x的不等式﹣2x+a≤2的解集如图所示，则a的值是．11．某不等式的解集如图，则这个解集用不等式表示为．三、解答题12．下列各数中，是不等式x+1＜4解的数有哪些？哪些不是不等式的解？8、7、5.5、4、2、1、0、2.5、﹣6．13．解不等式：﹣x＞1，并把解集在数轴上表示出来．14．解不等式，并把它的解集表示在数轴上：5x﹣2＞3（x+1）15．请用不等式表示如图的解集．参考答案一、选择题1．答案：D解析：【解答】移项得，5x﹣2x≥9合并同类项得，3x≥9系数化为1得，x≥3所以，不是不等式的解集的是x=2．故选：D．【分析】根据一元一次不等式的解法，移项、合并，系数化为1求出不等式的解集，再确定答案．2．答案：B解析：【解答】∵不等式（m+1）x＞m+1的解集为x＜1∴m+1＜0∴m＜﹣1故选：B．【分析】本题是关于x的不等式，应先只把x看成未知数，求得x的解集，再根据数轴上的解集，来求得a的取值范围．3．答案：B解析：【解答】A、两边同时除以2，即可得到，故原说法正确；B、x＜5的正整数解有1，2，3，4共有4个，故原说法错误；C、解2x＜﹣8得：x＜﹣4，﹣15是不等式的解，故原说法正确；D、原说法正确．故选B．【分析】利用等式的性质，以及不等式的解集．4．答案：A解析：【解答】由数轴可得：关于x的不等式组的解集是：x≥2．故选：A．【分析】根据在数轴上表示不等式组解集的方法进行解答．5．答案：C解析：【解答】由3x﹣1＞x+1，可得2x＞2，解得x＞1，所以一元一次不等式3x﹣1＞x+1的解在数轴上表示为：故选：C．【分析】首先根据解一元一次不等式的方法，求出不等式3x﹣1＞x+1的解集，然后根据在数轴上表示不等式的解集的方法，把不等式3x﹣1＞x+1的解集在数轴上表示出来即可．6．答案：C解析：【解答】x﹣1＜0解得：x＜1，故选：C．【分析】解不等式x﹣1＜0得：x＜1，即可解答．7．答案：B解析：【解答】解不等式x+m＞2得：x＞2﹣m，根据题意得：2﹣m=1，解得：m=1．故选B．【分析】首先解关于x的不等式，然后根据不等式的解集是x＞1，即可得到一个关于m的方程，从而求解．二、填空题8．答案：一切实数．解析：【解答】x2≥0，x是任意实数.【分析】根据解不等式的方法，可得答案．9．x2+1＞0．解析：【解答】∵一个关于x的不等式的解集为一切实数，∴这个不等式可以是x2+1＞0．【分析】根据不等式的解集的定义，任意写出一个不等式符合提出的条件即可．10．答案：0．解析：【解答】∵﹣2x+a≤2∴22ax-≥∵x≥﹣1∴22a-=﹣1解得：a=0．【分析】先用a表示出x的取值范围，再根据数轴上x的取值范围求出a的值即可．11．答案：x≤3解析：【解答】根据图示知，该不等式的解集是：x≤3；【分析】把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．三、解答题12．答案：8、7、5.5、4不是不等式的解．解析：【解答】∵x+1＜4，∴x＜3．∴2、1、0、2.5、﹣6是不等式的解．8、7、5.5、4不是不等式的解．【分析】利用不等式的基本性质，将不等式左边的常数项1改变符号以后移到右边，再合并同类项，解出x的解集，即可求解．13．答案：x＜﹣1．解析：【解答】不等式﹣x＞1，解得：x＜﹣1，【分析】不等式x系数化为1，求出解集，表示在数轴上．14．答案：见解答过程．解析：【解答】5x﹣2＞3x+3，2x＞5，∴52x＞．【分析】先求此不等式的解集，再根据不等式的解集在数轴上表示方法画出图示即可求得．15．答案：见解答过程．解析：【解答】（1）由数轴表示的不等式的解集，得x＜﹣1；（2）由数轴表示的不等式的解集，得x≥1；（3）由数轴表示的不等式的解集，得x≤﹣1；（4）由数轴表示的不等式的解集，得x＞3．【分析】根据不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示，可得答案．。

北师大八年级数学下《2.3不等式的解集》课时练习含答案

八年级下册2.3不等式的解集课时练习一、选择题1．已知x=2是不等式（x－5）（ax－3a+2）≤0的解，且x=1不是这个不等式的解，则实数a的取值范围是（）A．a＞1 B．a≤2C．1＜a≤2D．1≤a≤2答案：C解析：解答：∵x=2是不等式（x－5）（ax－3a+2）≤0的解，∴（2－5）（2a－3a+2）≤0，解得：a≤2，∵x=1不是这个不等式的解，∴（1－5）（a－3a+2）＞0，解得：a＞1，∴1＜a≤2，故选：C．分析：根据x=2是不等式（x－5）（ax－3a+2）≤0的解，且x=1不是这个不等式的解，列出不等式，求出解集，即可解答．2. 下列数值中不是不等式5x≥2x+9的解的是（）A.5B. 4C.3D. 2答案：D解析：解答：移项得，5x－2x≥9，合并同类项得，3x≥9，系数化为1得，x≥3，所以，不是不等式的解集的是x=2．故选：D．分析：根据一元一次不等式的解法，移项、合并，系数化为1求出不等式的解集，再根据各选项确定答案．3．一元一次不等式2（x+1）≥4的解在数轴上表示为（）A. B. C. D.答案：A解析：解答：由2（x+1）≥4，可得x+1≥2，解得x≥1，所以一元一次不等式2（x+1）≥4的解在数轴上表示为：故选：A．分析：首先根据解一元一次不等式的方法，求出不等式2（x+1）≥4的解集，然后根据在数轴上表示不等式的解集的方法，把不等式2（x+1）≥4的解集在数轴上表示出来即可．4．如果（m+3）x＞2m+6的解集为x＜2，则m的取值范围是（）A．m＜0 B．m＜-3 C．m＞-3 D．m是任意实数答案：B解析：解答：由不等式（m+3）x＞2m+6，得（m+3）x＞2（m+3），∵（m+3）x＞2m+6的解集为x＜2，∴m+3＜0，解得，m＜-3；故选B．分析：由原不等式变形为（m+3）x＞2（m+3），解该不等式的下一步是两边都除以x的系数（m+3），题中给出的解集是x＜2，改变了不等号的方向，所以x的系数是小于0的，据此可以求得m的取值范围．5．不等式（a-）x＞a-的解集是x＜1．则a应满足的条件是（）A．a= B．a＜C．a＞D．无法确定答案：B解析：解：∵不等式（a-）x＞a-的解集是x＜1，∴a-＜0，∴a＜，即a应满足的条件是：a＜．故选：B．分析：首先根据不等式（a-）x＞a-的解集是x＜1，应用不等式的性质，可得a-＜0；然后解一元一次不等式，求出a应满足的条件即可．6．关于x的不等式（a-1）x＞a-1的解集为x＜1，则下列判断正确的是（）A．a＜0 B．a＞1 C．a＜1 D．a为任意数答案：C解答：∵（a-1）x＞a-1的解集为x＜1，∴a-1＜0，∴a＜1，故选：C．分析：根据不等式的基本性质解出a的取值，即可得出答案．7有意义，那么x的取值范围在数轴上表示出来，正确的是（）A. B. C. D.答案：C解析：解：由题意得，2x+6≥0，解得，x≥－3，故选：C．∴（2-5）（2a-3a+2）≤0，解得：a≤2，∵x=1不是这个不等式的解，∴（1-5）（a-3a+2）＞0，解得：a＞1，∴1＜a≤2，故选：C．分析：根据x=2是不等式（x-5）（ax-3a+2）≤0的解，且x=1不是这个不等式的解，列出不等式，求出解集，即可解答．9. 下列说法正确的是（）A．x=4是不等式2x＞－8的一个解B．x=－4是不等式2x＞－8的解集C．不等式2x＞－8的解集是x＞4 D．2x＞－8的解集是x＜－4解析：解：因为2x＞－8的解为x＞－4，所以A. x=4是不等式2x＞－8的一个解，正确；B. x=－4是不等式2x＞－8的解集，错误；C. 不等式2x＞－8的解集是x＞4，错误；D. 2x＞－8的解集是x＜－4，错误．故选A．分析：据题意只要解出不等式2x＞－8的解，再用排除法解题即可．10．下列说法正确的是（）A．x=1是不等式-2x＜1的解B．x=3是不等式-x＜1的解集C．x＞-2是不等式-2x＜1的解集D．不等式-x＜1的解集是x＜-1答案：A答案：C解析：解答：由于不等式（a－1）x＞a－1的解集为x＜1，可知不等号的方向发生了改变：1.1axa-<-可判断出a－1＜0，所以a＜1．故选C．分析：首先对不等式组进行化简，根据不等式的解集的确定方法，就可以得出a的范围．12. x=-1不是下列哪一个不等式的解（）A．2x+1≤-3 B．2x-1≥-3 C．-2x+1≥3D．-2x-1≤3答案：A解析：解答：因为：A,2x+1≤-3中，x≤-2．B,2x-1≥-3中，x≥-1．C,-2x+1≥3中，x≤-1．D,-2x-1≤3中，x≥-2．故选A．分析：解出各个不等式，然后检验-1是否在解集内，就可以进行判断．13. 设a，b，c，d都是整数，且a＜2b，b＜3c，c＜4d，d＜20，则a的最大值是（）A．480 B．479 C．448 D．447答案：D解析：解答：∵a，b，c，d都是整数，且a＜2b，b＜3c，c＜4d，d＜20，∴d=19，c＜4×19=76，∴c=75，b＜3×75=225，∴b=224，a＜2×224=448，∴a=447，故选D．分析：根据d＜20，d都整数，就可以求出d的值，进而就可以得到a，b，c的值．14. 下列各数中，不是不等式2-3x＞5的解的是（）A．-2 B．-3 C．-1 D．1.35答案：C解析：解答：不等式2-3x＞5的解集为x＜-1．四个选项中只有-1不小于-1．故选C．分析：先解出不等式的解集，根据不等式解的定义，就能得到使不等式成立的未知数的值，即可作出判断．15. 下列说法正确的有（）①4是x－3＞1的解；②不等式x－2＜0的解有无数个；③x＞5是不等式x+2＞3的解集；④x=3是不等式x+2＞1的解；⑤不等式x+2＜5有无数个正整数解．A．1个B．2个C．3个D．4个答案：B解析：解：①x－3＞1，解得：x＞4，则4不是不等式的解，本选项错误；②不等式x－2＜0，解得：x＜2，则不等式的解有无数个，本选项正确；③不等式x+2＞3，解得x＞1，本选项错误；④不等式x+2＞1，解得：x＞－1，故x=3是不等式的解，本选项正确；⑤不等式x+2＜5，解得：x＜3，正整数解为1，2，本选项错误，则其中正确的个数为2个．故选B．分析：①求出x－3＞1的解集，即可做出判断；②求出不等式x－2＜0的解集即可做出判断；③求出不等式x+2＞3的解集即可做出判断；④求出不等式x+2＞1的解集，即可做出判断；⑤求出不等式x+2＜5的解集即可做出判断．二、填空题16．写出一个解集为x＞1的一元一次不等式：_________．答案：3x-3＞0 |解析：解答：移项，得3x＞3（答案不唯一）．故答案为x＞1．分析：根据一元一次不等式的求解逆用，把1进行移项就可以得到一个；也可以对原不等式进行其它变形，所以答案不唯一．17. 当a ________ 时，不等式（a－1）x＞1的解集是x11a-＞答案：＞1 解析：解答：∵不等式（a－1）x＞1的解集是x11a-＞，∴a－1＞0，∴a＞1，故答案为：＞1．分析：根据不等式的解集得a－1＞0，从而得出a的取值范围．18．某中学初中生在做练习册作业上解一个一元一次不等式时，发现不等式右边的一个数被墨迹污染看不清了，所看到的不等式是1－3x＜▇，他查看练习本后的答案知道，这个不等式的解集是x＞5，那么被污染的数是__________ ．答案：－14解析：解答：设被污染的数为a，不等式为1－3x＜a．解得：1.3a x-＞19. 如果m是实数，且不等式（m+1）x＞m+1的解是x＜1，那么实数m的值为__________. 答案：m＜－1解析：解答：因为（m+1）x＞m+1的解集是x＜1，不等号的方向改变了，所以m+1＜0，解得m＜－1．故答案为m＜－1．分析：根据两边同时除以m+1，不等号的方向改变，可得m+1＜0，解得m＜－1．20.定义一种新的运算：a※b=2a+b，已知关于x不等式x※k≥-1的解集在数轴上表示如图，则k= __________答案：3解析：解答：∵a※b=2a+b，∴x※k=2x+k，∵x※k≥-1∴2x+k≥-1解得x1,2k-≥∵解集为x≥－1，1 2k-=－1.∴k=3，故答案为：3．分析：先运用新的运算：a※b=2a+b，求出x※k≥-1的不等式，再解这个不等式，从图上看出解集为x≥－1，列出一元一次方程求解．三、解答题21. 若不等式ax-2＞0的解集为x＜-2，求关于y的方程ay+2=0的解答案：2解析：解答：∵不等式ax-2＞0，即ax＞2的解集为x＜-2，∴a=-1，代入方程得：-y+2=0，解得：y=2．分析：根据已知不等式解集确定出a的值，代入方程计算即可求出y的值22．已知不等式5x+a＜3的解集与－2x+5＞1的解集相同，试求a的值．答案：a=－7解析：解答：解不等式5x+a＜3得到：35a x-＜.方程，求出a的值即可．23．若不等式ax－2＞0的解集为x＜－2，求关于y的方程ay+2=0的解.答案：y=2解析：解答：∵不等式ax－2＞0，即ax＞2的解集为x＜－2，∴a=－1，代入方程得：－y+2=0，解得：y=2．分析：根据已知不等式解集确定出a的值，代入方程计算即可求出y的值．24．已知x=3是关于x的不等式3x2223ax x+-＞的解，求a的取值范围.答案：a＜4 解析：解答：∵x=3是关于x的不等式3x2223ax x+-＞的解,∴3×3322323a+⨯-＞.整理得3a＜12，解得a＜4．故a的取值范围是a＜4．分析：先根据不等式的解的定义，将x=3代入不等式3x2223ax x+-＞，得到．9322323a+⨯-＞，解此不等式，即可求出a的取值范围．25．如果关于x的不等式|x-2|+|x+3|≥a对于x取任意数都成立，则a的取值范围是多少？并说明理由．答案：a≤5解析：解答：∵|x-2|+|x+3|≥5，∴关于x的不等式|x-2|+|x+3|≥a对于x取任意数都成立，a≤5．分析：根据线段上的点到线两端点的距离的和最小，可得答案．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2．3 不等式的解集
一、选择题
1．－3x ≤6的解集是（）
A B C D
2．用不等式表示图中的解集，其中正确的是
A ． x ≥－2
B ． x ＞－2
C ． x ＜－
2 D ． x ≤－2 3．下列说法中，错误的是( )
A ．不等式x ＜5的整数解有无数多个
B ．不等式x ＞－5的负数解有无限个
C ．不等式－2x ＜8的解集是x ＜－4
D ．－40是不等式2x ＜－8的一个解 4．下列说法正确的是( )
A ．x ＝1是不等式－2x ＜1的解集
B ．x ＝3是不等式－x ＜1的解集
C ．x ＞－2是不等式－2x ＜1的解集
D ．不等式－x ＜1的解集是x ＞－1 5．不等式x －3＞1的解集是( )
A ．x ＞2
B ． x ＞4
C ．x －2＞
D ． x ＞－4 6．不等式2x ＜6的非负整数解为( )
A ．0，1，2
B ．1，2
C ．0，－1，－2
D ．无数个 7．下列四种说法：① x＝
45是不等式4x －5＞0的解；② x＝2
5
是不等式4x －5＞0的一个解；③ x ＞
4
5
是不等式4x －5＞0的解集；④ x＞2中任何一个数都可以使不等式4x －5＞0成立，所以x ＞2也是它的解集，其中正确的有（）
A ．1个
B ．2个
C ．3个
D ．4个 8．若(1)1a x a -<-的解集为x ＞1，那么a 的取值范围是（ A ．a ＞0 B ．a ＜0 C ．a ＜1 D ．a ＞1
二、填空题
9．不等式的解集在数轴上表示如图所示，则该不等式可能是_____________．
10．当x_______时，代数式2x －5的值为0；当x_______时，代数式2x －5的值不大于0． 11．不等式－5x ≥－13的解集中，最大的整数解是__________． 12．不等式x+3≤6的正整数解为___________________． 13．不等式－2x ＜8的负整数解的和是______．
－1
2题
－1
9题
14．直接写出不等式的解集：
（1） x ＋3＞6的解集；（2）2x ＜12的解集；（3） x －5＞0的解集；（4）0.5x ＞5的解集．
15．一个不等式的解集如图所示，则这个不等式的正整数解是．
16．恩格尔系数n 是指家庭日常饮食开支占家庭收入的比例，它反映了居民家庭的实际生活水平，各
种类型家庭的n 值如下所示：
贫困如用含n 的不等式表示，则贫困家庭为；小康家庭为；最富裕国家为；当某一家庭n ＝0.6时，表明该家庭的实际生活水平是．
三、能力提升
17．在数轴上表示下列不等式的解集：
（1）x ≥－3.5 （2）x ＜－1.5 （3）x ≥2 （4）－1≤x ＜2 18．试写出一个不等式，使它的解集满足下列条件：
（1）不等式的正整数解只有1，2，3；（2）不等式的整数解只有－2，－1，0，1．
19．某种饮料重约300g ，罐上注有“蛋白质含量≥0.5%”，其中蛋白质的含量为多少克？
20．求不等式1＋x ＞x －1成立的x 取值范围．
21．求不等式4
1
x ＋1＞0
的解集和它的非负整数解，并把解集在数轴上表示出来．
22．x 取什么值时，代数式2x －5大于代数式2
1
(2－x)的值？
23．|2a －24|＋（3a －b －k ）2
＝0，那么k 取什么值时，b 为负数．
24．要使不等式－3x －a ≤0的解集为x ≥1，那么a 应满足什么条件？四、聚沙成塔
一堆有红、白两种颜色的球若干个，已知白球的个数比红球少，但白球的2倍比红球多．若把每一个白球都记作“2”，每一个红球都记作“3”，则总数为“60”，那么这两种球各有多少个？
1
4
15题
1．3 不等式的解集
1．A ；2．B ；3．C ；4．D ；5．B ；6．A ；7．B ；8．C ；9．答案不唯一，如x －1≤0，2x≤2等． 10．＝52
，≤
5
2
．11．x ＝2． 12．x ＝1，2，3 13．－6． 14．（1）x ＞3；（2）x ＜6；（3）x ＞5；（4）x ＞10． 15．x ＝1，2 16．n ＞75% 40%≤n ≤49% n ＜20％温饱．
17．图略．18．答案不惟一：（1）x ＜4；（2）－3<x ≤1． 19．不少于1.5克． 20．x 可取一切实数． 21．非负整数为0，1，2，3． 22． x ＞
5
12
． 23． k 大于36时b 为负数． 24． a=－3 聚沙成塔
解：设白球有x 个，红球有y 个，由题意，得⎩
⎨⎧=+60322y x x
y x
由第一个不等式得：3x ＜3y ＜6x ，由第二个不等式得，3y=60－2x ，则有3x ＜60－2x ＜6x ∴7.5＜x ＜12，∴x 可取8，9，10，11．又∵2x=60－3y=3（20－y ） ∴2x 应是3的倍数 ∴x 只能取9，y =
3
9
260⨯-= 14 答：白球有9个，红球有14个．。