图与网络作业
箭条图-网络表-甘特图
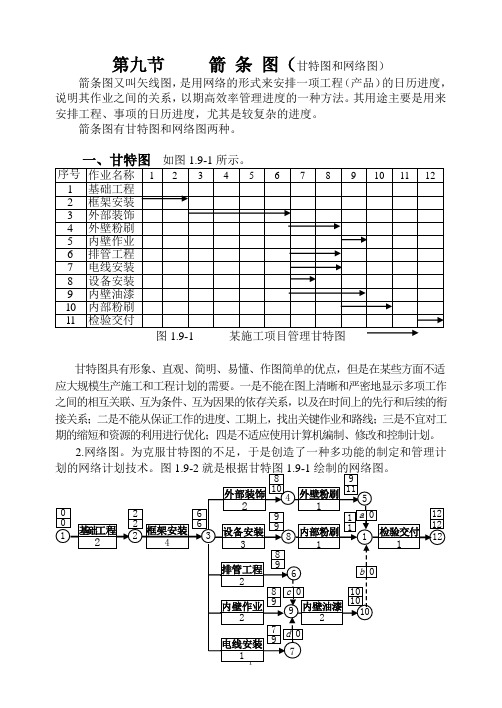
第九节箭条图(甘特图和网络图)箭条图又叫矢线图,是用网络的形式来安排一项工程(产品)的日历进度,说明其作业之间的关系,以期高效率管理进度的一种方法。
其用途主要是用来安排工程、事项的日历进度,尤其是较复杂的进度。
箭条图有甘特图和网络图两种。
甘特图具有形象、直观、简明、易懂、作图简单的优点,但是在某些方面不适应大规模生产施工和工程计划的需要。
一是不能在图上清晰和严密地显示多项工作之间的相互关联、互为条件、互为因果的依存关系,以及在时间上的先行和后续的衔接关系;二是不能从保证工作的进度、工期上,找出关键作业和路线;三是不宜对工期的缩短和资源的利用进行优化;四是不适应使用计算机编制、修改和控制计划。
2.网络图。
为克服甘特图的不足,于是创造了一种多功能的制定和管理计2图1.9-2 根据图1.9-1绘制的网络图二、网络图及其用途网络图又称网络计划技术,它是安排和编制最佳日程计划,有效实施进度管理的一种科学管理方法。
其用途主要有:1.制定详细的实施计划;2.可以在计划阶段对方案进行仔细推敲,从而保证计划的严密性;3.进入计划实施阶段后,对于情况的变化和计划的变更都可以作适当的调整;4.能够具体而迅速地了解某项工作延误对总体工作的影响,从而及早采取措施,计划规模越大,越能反映出该方法的作用。
三、网络图的绘制规则1.符号及含义。
方向、时序和编号是网络图的三要素,网络图的结构和表示方法如下:⑴作业名称或代号,一般标注在箭条的上面或左边。
⑵节点和编号。
节点表示作业的开始和/编号表示工序的顺序,且只能由小指向大; ⑶矢线。
表示具体的作业、工作任务。
箭尾的节点表示本作业的开始,箭头的节点表示本作业的结束和/或下一作业的开始;实矢线表示确实存在的作业,而虚矢线表示虚拟工序(实际不存在的),只表示作业间的相互关系。
⑷作业时间。
表示作业需要的时间,一般标在矢线下面或右边。
⑸粗实线。
表示工时无法压缩工序的路线,是整个工程的关键作业路线。
横道图与网络图

(3)网络图严禁出现双向箭头或无向 3
4
箭头的连线。(图2)
3
5
3
5
图1
5
图2
(4)网络图严禁出现没有箭头或箭尾节点的箭线。(图3)
i
j
k
i
j
k
图3
2、网络图的绘制规则
(5)双代号网络图中,一项工作只能有唯一的一条箭线和相应 的一对节点编号。(图4)
2A
2
A
3
B
3
错误画法
图4
正确画法
B
4
(6)在绘制网络图时,应尽可能地避免箭线交叉,如不可能避 免时,应采用过桥法或指向法。(图5)
施工
段
1
2
3
4
项目
绑柱墙筋 2
3
2
3
支模板
3
4
4
3
绑梁板筋 2
1
2
2
浇注混凝土 1
2
1
2
案例解
• 2、组织无节奏流水施工 • (1)确定流水步距:(运用口诀)
绑柱墙筋(Ⅰ)与支模板( Ⅱ )之间:2,5,7,10 -)3,7,11,14 2,2,0, -1,-14
支模板( Ⅱ )与绑梁板筋(Ⅲ)之间: 3,7,11,14 -) 2,3, 5,7 3,5, 8, 9,-7
过程最大限度地相互搭接起来,以提高效率,最大限度地节约
时间。
•
流水施工参数:
•
施工过程数(n):(工艺参数)指施工时划分的最小
对象。一幢建筑物等的建造过程,通常是由许多施工过程
(如挖土、混凝土垫层、支模、扎筋、混凝土等)所组成。
•
施工段数(m):(空间参数)指整体建筑物(群)或
SAP ps模块概念

SAP-PS,项目、WBS与网络作业概念项目定义项目定义是项目的唯一标识。
通过项目定义,决定了包含于其中的所有WBS元素的组织结构、计划方法、预算方式以及结算方法等信息。
而项目定义中的数据,则主要来源于“项目参数文件”,所以创建项目定义时必须选择好适当的“项目参数文件”。
WBS是项目管理中的T作分解结构,其WBS元素即为T作分解结构单元,是项目细分的结果。
WBS元素之间具有层次关系,通过层次建立起它们的时间关系和成本关系。
另外,根据WBS元素的属性,可以定义该WBS元素是否作为成本对象或是统计对象、是否有项目库存或是无项目库存。
在项目比较复杂的情况下,可以在WBS元素上创建相应的“重大事件”作为工程进度的转折点。
同时,工程中有许多的工程图纸和项目资料,也可以通过PS文本或文档的形式挂接在对应的WBS元素上,供有关人员查询。
项目定义和WBS元素等的关系如图9-2所示。
图9-2项目定义和WBS元素组织结构网络和网络活动网络在SAP系统中是一个独立存在的实体。
通过选择的“网络参数文件”,决定了该网络的网络类型、组织架构、计划、实际成本核算变式以及时间上排产的方法等。
网络包含了网络活动的所有属性,但网络可以有网络活动,也可以无网络活动。
如果有网络活动,则为一个工程进度施工的完整网络;如果没有网络活动,则此网络只是一个网络头结构,从项目管理的角度来说没有实际的意义。
网络活动也叫做网络作业,就是通常人们所理解的施工丁序。
通过对工序作业的排列,施工过程就按照排列好的网络活动完成一个项目。
网络活动可以分为以下4种类型。
●内部作业:指通过公司内部人员完成的活动。
一般南选定的工作中心,根据其作业的性质来完成该活动的成本估价。
●外部采购作业:指由外包施工单位承包该公司的业务来完成的活动。
可以通过建立采购订单的形式,向外部“购买”。
●服务作业:指外包施工单位承包的作业。
它比外部采购作业更明细,其采购的金额可以具体到每个条款发生的金额。
计算机网络(作业)附参考答案

作业1-1什么是计算机网络?1-2局域网、城域网与广域网的主要特征是什么?1-3计算机网络的功能主要有哪些?1-4由n个结点构成的星状拓扑结构的网络中,共有多少个直接连接?对于n个结点的环状网络呢?对于n个结点的全连接网络呢?答:采用星状、环状、全连接拓扑结构的网络如图所示。
星状、环状、全连接拓扑结构网络如上图,在n个结点的星状网络中,直接连接数为n-1;在n个结点的环状网络中,直接连接数为n;在n个结点的全连接网络中,直接连接数为n(n-1)/2。
1-5.假设一个系统具有n层协议,其中应用进程生成长度为m字节的数据。
在每层都加上长度为h字节的报头。
计算为传输报头所占用的网络带宽百分比。
解答:在同一结点内,当应用进程产生数据从最高层传至最低层时,所添加的报头的总长度为nh字节,数据部分仍为m字节。
因此,为传输报头所占用的网络带宽百分比为:nh/(nh+m)×100%1-6.什么是体系结构?在设计计算机网络体系结构时,引入了分层思想带来了哪些好处?在网络体系结构中,有两个比较重要的概念———协议和服务,试谈谈对它们的理解。
2-1 物理层主要解决哪些问题?物理层的主要特点是什么?2-2 对于带宽为4000Hz通信信道,如果采用16种不同的物理状态来表示数据,信道的信噪比S/N为30dB,按照奈奎斯特定理,信道的最大传输速率是多少?按照香农定理,信道的最大传输速率是多少?2-3.假设需要在相隔1000km的两地间传送3kb的数据。
有两种方式:通过地面电缆以4.8kb/s的数据传输速率传送或通过卫星通信以50kb/s的数据传输速率传送。
则从发送方开始发送数据直至接收方全部收到数据,哪种方式的传送时间较短?已知电磁波在电缆中的传播速率为光速的2/3,卫星通信的端到端单向传播延迟的典型值为270ms。
解答:从发送方开始发送数据直至接收方收到全部数据的时间T=数据发送时延+信号传播时延。
对于通过地面电缆的传送方式,电磁波在电缆中的传播速率=3×105×2/3=2×105(km/s),则T=3/4.8+1000/200000=0.63(s)。
网络教育工程制图作业《工程制图Ⅲ》作业答案

1.图纸幅面的代号有哪几种?2.图纸格式分为哪两种?按标题栏的方位又可将图纸格式分为哪两种?3.一个完整的尺寸,一般应包括哪四个组成部分,它们分别有哪些规定?4.标注平面图形的尺寸应达到哪三个要求?这三个要求主要体现哪些内容?5.什么是平面图形的尺寸基准、定形尺寸和定位尺寸?通常按哪几个步骤标注平面图形的尺寸?6.圆弧连接指什么?在图样上的圆弧连接处,为何必须比较准确作出连接圆弧的圆心和切点?在平面图形圆弧连接处的线段可分为哪三类?它们是根据什么区分的?在作图时应按什么顺序画这三类线段?7.机械图样中的线宽分为哪两种?设粗实线的线宽为d,虚线、点画线、细实线、波浪线的线宽是多少?参考答案: 1.A0/A1/A2/A3/A42.图纸格式分为需要装订和不需要装订两种。
按标题栏的长边置于水平方向并与图纸的长边平行时,构成X型图纸;若标题栏的长边与图纸的长边垂直时,则构成Y型图纸。
3.包括尺寸线、尺寸界线、尺寸数字和尺寸终端(箭头)。
尺寸数字注写在尺寸线上方;尺寸线用细实线绘制;尺寸界线用细实线绘制,一般应与尺寸线垂直,并超出尺寸线2mm;尺寸终端采用实心箭头。
4.正确、完整、清晰。
正确是指尺寸数字不能写错;完整是指尺寸要注写完全,不遗漏各组成部分的定形尺寸和定位尺寸。
清晰是指尺寸的位置要安排在图形的明显处,标注清楚,布局整齐。
5、尺寸基准是指尺寸的起点。
定形尺寸指确定各部分形状大小的尺寸;定位尺寸指确定各部分之间相对位置大小的尺寸。
先分析形状,确定尺寸基准;注出各部分定形尺寸;注出各部分所需的定位尺寸。
6.圆弧连接指直线与圆弧相切,圆弧与圆弧相切。
为了得到光滑相切的图形,必须准确作出连接圆弧的圆心和切点。
圆弧连接处的线段可分为已知线段、中间线段和连接线段。
有足够的定形尺寸和定位尺寸,称为已知线段;缺少一个定位尺寸,必须依靠一端与另一线段相切而画出的线段,称为中间线段;缺少两个定位尺寸,因而要依靠两端与另两线段相切,才能画出的线段,称为连接线段。
箭条图-网络表-甘特图

第九节箭条图(甘特图和网络图)箭条图又叫矢线图,是用网络的形式来安排一项工程(产品)的日历进度,说明其作业之间的关系,以期高效率管理进度的一种方法。
其用途主要是用来安排工程、事项的日历进度,尤其是较复杂的进度。
箭条图有甘特图和网络图两种。
甘特图具有形象、直观、简明、易懂、作图简单的优点,但是在某些方面不适应大规模生产施工和工程计划的需要。
一是不能在图上清晰和严密地显示多项工作之间的相互关联、互为条件、互为因果的依存关系,以及在时间上的先行和后续的衔接关系;二是不能从保证工作的进度、工期上,找出关键作业和路线;三是不宜对工期的缩短和资源的利用进行优化;四是不适应使用计算机编制、修改和控制计划。
2.网络图。
为克服甘特图的不足,于是创造了一种多功能的制定和管理计划的网络计划技图1.9-2 根据图1.9-1绘制的网络图二、网络图及其用途网络图又称网络计划技术,它是安排和编制最佳日程计划,有效实施进度管理的一种科学管理方法。
其用途主要有:121.制定详细的实施计划;2.可以在计划阶段对方案进行仔细推敲,从而保证计划的严密性;3.进入计划实施阶段后,对于情况的变化和计划的变更都可以作适当的调整;4.能够具体而迅速地了解某项工作延误对总体工作的影响,从而及早采取措施,计划规模越大,越能反映出该方法的作用。
三、网络图的绘制规则1.符号及含义。
方向、时序和编号是网络图的三要素,网络图的结构和表示方法如下:⑴作业名称或代号,一般标注在箭条的上面或左边。
⑵节点和编号。
节点表示作业的开始和/编号表示工序的顺序,且只能由小指向大; ⑶矢线。
表示具体的作业、工作任务。
箭尾的节点表示本作业的开始,箭头的节点表示本作业的结束和/或下一作业的开始;实矢线表示确实存在的作业,而虚矢线表示虚拟工序(实际不存在的),只表示作业间的相互关系。
⑷作业时间。
表示作业需要的时间,一般标在矢线下面或右边。
⑸粗实线。
表示工时无法压缩工序的路线,是整个工程的关键作业路线。
如何绘制网络计划图

如何绘制网络计划图:绘制计划网络网络图怎么绘制双代号网络图绘制视频绘制网络图的基本要求篇一:如何绘制网络图如何绘制网络图一、网络图的组成网络图是一种表示一项工程或任务中的各环节或各作业先后顺序、衔接关系和所需作业时间的图解模型,网络图有两种基本类型:箭线式网络图和节点式网络图。
以下内容仅介绍箭线式网络图。
1、作业。
在网络计划技术中,作业是一个广义的概念。
在工程项目中,一项作业是指一个相对独立的具体活动过程,往往需要消耗一定的资源和时间来完成。
在网络图中,为了准确清楚地表示作业间的逻辑关系,需引入“虚作业”的概念。
虚作业指既不消耗时间,又不需消耗资源工序或活动。
它表示以虚箭头为始点的作业必须在以虚箭尾为终点的作业完成后才能进行。
2、节点。
在网络计划技术中,节点指连接各项作业、表示作业的开始或结束的瞬间。
3、路线。
在网络计划技术中,是指从网络图的起始节点出发,沿箭线方向,经过一系列节点和箭线,至网络图终止节点所经过的通道。
二、绘制网络图的规则1、网络图中只能有一个起始节点和一个终止节点。
2、网络图中不允许出现循环路线。
3、箭线的首尾都必须有节点。
4、相邻网络节点间只能有一条箭线。
5、节点编号的正确标注。
6、正确反映作业间的逻辑关系。
7、正确表示平行、交叉作业。
8、避免出现“桥路”。
“桥路”是指网络图中出现的箭线与箭线的交叉。
三、网络图的绘制1、工程项目的分解与分析。
对工程项目进行分解,是把一项工程分解为若干作业。
项目分析则指研究作业间的相互关系和先后顺序。
(1)工程项目的分解。
根据工程项目的复杂程度,使用网络图的管理层次和计划的项目数确定分解的详略程度。
(2)确定作业间的相互关系:①紧后作业,即处于某项作业结束后才能开始的作业;②紧前作业,即某项作业开始前必须先行结束的作业;③平行作业,即同时进行的作业;④中途作业,指当某项作业进行到一定程度才能进行的作业。
作业间相互关系可在图5—2中表现出来。
其中A是C的紧前作业,E是C的紧后作业。
一级建造师项目管理网络图计算讲解图文并茂有习题

3.工作最迟时间的计算 1)工作最迟完成时间的计算 2)工作最迟开始时间的计算
1.2按工作法计算时间参数
四、工作总时差的计算 五、工作自由时差的计算 六、关键工作和关键路线 关键工作——总时差最小(=Tp-Tc)的工作 或,持续时间最长的路线
[例题]
1.3按节点法计算时间参数
5.自由时差* 6.最迟时间计算
3.2单代号网络计划时间参数的计算
计算顺序: (1)ESi EFi Tc Tp LAGi,j TFi FFi LFi LSi (2)ESi EFi Tc Tp LFi LSi LAGi,j TFi FFi
[例题]
在单代号网络计划中,设H工作的紧后工作有I和J,其总时差分别是3天和4天,工作H、I之间的工作间隔为8天,工作H、J之间的间隔时间为6天,则工作H的总时差为______.
说明 标注 定义
1.3按节点法计算时间参数
1.节点最早时间的计算 2.网络计划工期的计算 3.节点最迟时间的计算
1.3按节点法计算时间参数
4.节点法和工作法时间参数的对应关系 可以推知 及
[例题]
2 双代号时标网络计划
2.1双代号时标网络计划的概念 2.2双代号时标网络计划的时间参数计算
解: 对I工作:3+8=11 对J工作:4+6=10
4 单代号搭接网络计划
4.1单代号搭接网络计划概述 4.2单代号搭接网络计划的计算
4.1单代号搭接网络计划概述
1.搭接关系的种类和表达方式 两种关系,四种时距
4.2单代号搭接网络计划的计算
1.结束到开始时距FTS(Finish to Start)
22
12
1.1双代号网络计划概述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%两个仆人过河引起的状态变化
((i+1)>=j+1)&((3-(i+1))>=3-(j+1))|…
%一个商人与一个仆人过河引起的状态变化
((i+1)>=j)&(3-(i+1)>=3-j)|…
%一个商人过河引起的状态变化
(i>=j+1)&(3-i>=3-(j+1))
问题一:将匈牙利算法修改为求二分图的最大对集
二分图最大对集算法:
( )从 中任意取定一个初始对集 。
( )若 把 中的顶点皆许配,停止, 即完美对集(最大对集的极限);否则取 中未被 许配的一顶点 ,记 , 。
( )若 ,停止,边集合M为最大对集;否则取 。
( )若 是被 许配的,设 , , ,转( );否则,取可增广轨 ,令 ,转( )。
fprintf('此时过河方案为\n ');
for k=1:temp
fprintf('(%d,%d)\n',zhuangtai(R(k),:));
if k<temp
fprintf('------>\r\n');
end
end
过河最少步数为5
此时过河方案为
(3,3)
------>
(3,1)
------>
function [D,path]=floyd(a)
n=size(a,1);
D=a;
path=zeros(n,n);
for i=1:n
for j=1:n
if D(i,j)~=inf
path(i,j)=j;
end
end
end
for k=1:n
for i=1:n
for j=1:n
if D(i,k)+D(k,j)<D(i,j)
由题意知:18分钟后又山洪,四人17分钟完成过桥,所以四人可及时过桥。
用图论解释:
可以以4个人在桥对岸状态来作为节点来构造一个有向图,起始状态桥对岸是空集合。第一次的可能情况有6种:{(甲,乙),(甲,丙)(甲,丁)(乙,丙)(乙,丁)(丙,丁)}对应的权值为{w(甲,乙)=10,w(甲,丙)=10,w(甲,丁)=10,w(乙,丙)=5,w(乙,丁)=5,w(丙,丁)=2};第二次的可能可能情况有4种:{甲,乙,丙,丁},对应的权值集合为:{w(甲)=10,w(乙)==5,w(丙)=2,w(丁)=1};第三次的可能情况有4种:{(甲,乙,丙),(甲,乙,丁),(甲,丙,丁),(乙,丙,丁)},对应权值为:{w(乙,丙)=5,w(甲,丙)=10,w(丙,丁)=2,w(乙,丁)=5,w(甲,丁)=10,w(甲,丙)=10,};第四次的可能情况有6种:{(甲,乙),(甲,丙)(甲,丁)(乙,丙)(乙,丁)(丙,丁)},对应的权值为:{w()=10,w()=10,w()=10,w()=5,w()=5,w()=2};第五次的可能情况有1种:{甲,乙,丙,丁},对应的权值为:{w(丙,丁)=2,w(乙,丁)=5,w(乙,丙)=5,w(甲,丁)=10,w(甲,丙)=10,w(甲,乙)=10}。
D(i,j)=D(i,k)+D(k,j);
path(i,j)=path(i,k);
end
end
end
end
%配合floyd算法的后续程序,s为源点,t为宿点
%L为长度,R为路由
function [L,R]=router(D,path,s,t)
L=zeros(0,0);
R=s;
while 1
if s==t
(3,2)
------>
(3,0)
------>
(1,1)
------>
(0,0)
键入不同的商人人数和船的承载人数,它的结果也是不同的!
问题三:四人过桥问题
有一天晚上,有四个人需要通过架在山谷间的危桥,任意时刻最多只能有两个人在桥上,过桥需要一盏闪光灯,这些人只有一盏闪光灯。如果单独过桥他们分别需要10、5、2、1分钟,如果两人同时过桥则所需时间是较慢者所需的时间。18分钟后,沿山谷滚滚而下的山洪将把这座桥冲毁。这四个人能及时过桥吗?用图论知识,证明你的结论;并说明如何用图论知识获得答案。
2)假设此岸的状态集合为X;
3)假设彼岸的状态集合为Y;
4)假设状态转移的边集合为M;
4.模型建立
由题可知:该问题可以使用二分图求完美对集的模型。
5.模型求解
由匈牙利算法,
利用Matlab数学软件进行计算,编程如下:
%floyd算法通用程序,输入a为赋权邻接矩阵
%输出为距离矩阵D,和最短路径矩阵path
作图如下:【黑线条表示最短路径】
由图可知:T=2+1+10+2+2=17min
问题二:安全过河问题
1.问题重述
三名商人各带一名随从乘船渡河,一只小船只能容纳二人,由他们自己划行。随从们密约,在河的任一岸,一旦随从的人数比商人多,就杀人抢货.但是乘船渡河的方案由商人决定,那么商人们怎样才能安全过河?如果可以安全渡河,请找出所有可行方案.如果是n名商人,小船只能容纳m人,情况又将如何?
2.问题分析
问题条件是:三个商人与仆人要过河,船的承载量一次为两人,目的是:商人们均安全过河;约束条件是:只要两岸任意一岸的仆人个数超过商人个数,仆人就会杀人越货,即:商人无法安全过河。求:1)能使商人安全过河的所有可行性方案;2)如果是n名商人,小船只能容纳m人,方案情况。
3.模型假设
1)假设河两岸商人与仆人的人数状态构成一个二分图G;
W(x)x表示有向图弧的权值,x ;
模型求解
a)用时较少的两人丙,丁先过桥,用时T(丙丁)=2;
b)用时小的丁返回,T(丁)=1;
c)用时比较接近的两人甲,乙过桥,用时T(甲乙)=10;
d)用时少的丙返回,T(丙)=2;
e)最后两组丙,丁过桥,T(丙丁)=2.
所以总时间为:T=2+1+10+2+2=17
zhuantai(3,3)=zhuantai(4,4)=1;
[n,m]=size(zhuangtai);d=zeros(2*n);
%根据状态变化规律作出一个赋权二分图
for i=0:n-1
for j=0:n-1
if (((i+2)>=j)&(3-(i+2))>=(3-j)|...
%两个商人过河引起的状态变化
问题分析
过桥条件是:要有闪光灯;两人过桥,过桥按时间长的算。要是过桥时间最短:要花费时间最短的人带灯返回,那么容易知道时间长度接近的一同前往可以减少时间,时间越短的人回来速度快,可以减少时间。
符号说明
甲表示用时10min的人;
乙表示用时5min的人;
丙表示用时2min的人;
丁表示用时1min的人;
T(x)x表示过桥所需时间,x ;
%一个仆人过河引起的状态变化
)
d(i,j)=1;
d(j,i)=1;
endendຫໍສະໝຸດ endd(find(d==0))=inf;
for i=1:n
d(i,i)=0;
end
[D,path]=floyd(d);
%求图中各点的最短路,即得过河最优方案
[L,R]=router(D,path,1,n);
temp=length(L);fprintf('过河最少步数为%d\n',L(temp));
L=fliplr(L);
L=[0,L];
return
end
L=[L,D(s,t)];
R=[R,path(s,t)];
s=path(s,t);
end
clear;clc;
%商人安全过河问题
zhuangtai=zeros(4,4);
%允许状态,矩阵每行表示一个状态
zhuangtai(1,:)=ones(1,4);
