一次函数K与b的意义
一次函数k和b的意义

k 结论:y 几2个x 一次函数的 值相-等3 时-2 , -1 0 1 2 3 x
y 它2们x 的1图象是一组平行线.
-1
y 2x 2
-2
-3
二、问题探究
k 探究2:对于一次函数 y 2x 4 (k 0)
求它的图象与 y 轴的交点坐标. (0, 4)
一、编题小能手
对于一次函数 y 2x 4
一次函数k、b的意义
二、问题探究
b 探究1:对于一次函数 y 2x 4
求它的图象与 y 轴的交点坐标. (0, b)
当 b 的值分别为2,1,0,-1,-2时,y
画出它的图象.
3
观察图象,你发现了什么? 2
y 2x 2
1
1B
若直线 y 2x b
-3
-2
-1
0
1
与正方形 ABCD有公共点,
-1
求: b 的取值范围.
-2
D
C
2
3x
-3 -4
三、知识巩固
2、如图,在平面直角坐标系中,
正方形 ABCD的边长为1,B(1,1),且BC∥ x 轴,
若直线 y kx(k 0) 与正方形 ABCD 有公共点,
求:k 的取值范围.
y
变式一:y kx 2?
3
A
D
2
1B
C
-3
-2
-1
0
1
2
3x
-1
-2
-3
四、能力提升
在平面直角坐标系中,线段 AB 的端点坐标为 A(2, 4), B(4, 2) ,直线 y kx 2 与线段 AB有
一次函数与几何综合(一)(K,b的几何意义)(北师版)(含答案)

学生做题前请先回答以下问题问题1:若一次函数表达式为y=kx+b(k,b为常数,k≠0),k是______,表示___________,可以用几何中的坡度来解释.坡面的____________与____________的比叫坡度或坡比.问题2:b表示____________________________.问题3:一次函数与几何综合解题思路中,求直线表达式的思路有哪些?一次函数与几何综合(一)(K,b的几何意义)(北师版)一、单选题(共8道,每道12分)1.如图,点B,C分别在直线y=3x和直线y=kx上,A,D是x轴上两点,若四边形ABCD是长方形,且,则k的值是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:k的几何意义2.如图,已知点A的坐标为(5,0),直线y=x+b(b>0)与x轴、y轴分别交于点B,C,连接AC,,则点B的坐标为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:k的几何意义3.如图,直线AP的解析式为,且点P的坐标为(4,2),PA=PB,则点B的坐标是( )A.(5,0)B.(6,0)C.(7,0)D.(8,0)答案:C解题思路:试题难度:三颗星知识点:k的几何意义4.如图,已知一条直线经过A(0,2),B(1,0)两点,将这条直线向左平移,与x轴、y 轴分别交于点C,点D.若DB=DC,则直线CD的函数解析式为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转5.已知点,B(0,0),,AE平分∠BAC,交BC于点E,则直线AE的函数表达式是( )A. B.y=x-2C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转6.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,点C 是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,则直线CD的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转7.如图,已知长方形纸片OABC,D是OA上的一点,且OD:AD=5:3,CD=,把△OCD 沿折痕CD向上翻折,若点O恰好与AB边上的点E重合,则CD所在直线的表达式为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:一次函数、坐标、几何三角通道互转8.如图,在平面直角坐标系中放入一张长方形纸片ABCO,OC=9,将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知,则折痕B′E所在直线的解析式为( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:一次函数与几何综合学生做题后建议通过以下问题总结反思问题1:做完本套试题,在求解一次函数表达式的时候你有什么感触?简单列举一下!。
理解一次函数中k与b的实际意义

o
一
嚣
( 2 ) 求甲车维修所用时间.
( 3 ) 求 两车 在途 中第 二 次相遇 时t 的值. ( 4 ) 当两车 相距4 0 千米时, £ 的取 值范 围是
时 的速 度 为4 0 千 米, 时, l  ̄ p a = 4 0 千米/ 时.
.
分析 : 从 函数 图象 可 知 甲车 前3 个小 时行驶 1 2 0 千米, 因此 , 这 三 个 小
. .
8 0 一 5 ) + 1 2 O + 2 × 4 0 — 4 ) = 2 4 O .
解得t = 5 . 2 5 .
・
.
.
两车在 途 中第二 次相遇 时, f 的值 为5 . 2 5 .
上 面的三 种解 法各 有特 点 ,全 面掌 握这 些方 法对 于认 识 一 次函数 的 意义 很有 帮助 . 在 这 里s = 8 0 t 一 2 0 0 中 的8 0 正 是 甲车 从 修 好后 驶 向 地 的速 度 ,那 么 6 = 一 2 0 0 是 什么 意思 呢 ?式 子 中8 0 t 表 示如 果在t d , 时 内都 是 以8 0 千 米/ 时 的 速度 行 驶所 驶过 的距 离 ,而 事 实上前 3 个 小 时速度 为4 0 千 米/ 时, 3 小 时 中
根 据题 意 , s - % 之 间 的函数 图象经 过 ( 4 , 1 2 0 ) , ( 5 . 5 , 2 4 0 ) 两点,
f 4 1 + 6 】 = 1 2 0 ,
・
.
.
{ 【 5‘
.
5 后 1 + 6 1 = - 2 4 0 .
解得{
f k l = 8 0 ,
x+
—
一次函数图象-k,b对图象的影响

一次函数的定义一、引入共同特征:函数的关系式都是用含自变量的一次整式 二、归纳1、一次函数的定义:函数的关系式都是用含自变量的一次整式表示的函数。
式子表示:y =kx +b (k,b 为常数,k ≠0)条件:○1含自变量 ○2自变量的次数为1 ○3整式 特别地,当b=0,一次函数y=kx(k ≠0)叫正比例函数 注:(1)对于y =kx +b当k ≠0,b 为任意数时是一次函数 当k ≠0,且b=0时是正比例函数 (2)正比例函数是特殊的一次函数 一次函数不一定是正比例函数(3)若y 是x 的一次函数关系,则函数关系一定可表示为y =kx +b (k ≠0)形式,反过来,能化为y =kx +b (k ≠0)形式的函数一定是一次函数若y 是x 的正比例函数关系,则函数关系一定可表示为y =kx (k ≠0)形式,反过来,能化为y =kx (k ≠0)形式的函数一定是正比例函数 三、典例1、函数:○1y=2x ○2y=4x=3 ○3y=12○4y=3x +1 ○5y=3x+1 ○6y=ax ○7xy=3 ○82x+3y-1=0 ○9y=12x 2+1 ○10y=x2 ○11 y=x(x-4)-x 2 ○12 y=-5x 2_ 一次函数是__________ ___ 正比例函数是___________2、 关于x 的函数y=(5m-3)x 2-m+(m+n) (1) 当m 、n 为何值时,它是一次函数 (2) 当m 、n 为何值时,它是正比例函数。
3、 关于x 的函数3)3(3+--=-n xm y m(1) 当m 、n 为何值时,它是一次函数(2) 当m 、n 为何值时,它是正比例函数。
4、 已知y 与x-3成正比例,当x=4时,y=3(1) 写出y 与x 的函数关系式 (2) Y 与x 之间是什么函数关系。
(3) 当x=2.5时,求y 的值。
小结:1. y 与x 成正比例,则函数关系可设为y=kx(k ≠0)2. 成正比例不一定是正比例函数,但正比例函数一定成正比例。
一次函数概念及求解K,B的值
又∵当x=-1时,y=1 ; 代入即有 1 =-k+b
k b 5① ①+ ②得出 2b =6, ∴b=3 k b 1 ②
②
b 3 将b=3代入①式,解得 k=2 ∴ k 2
例2.画出函数y =-6x与 y =-6x +5的图象。
解:函数y =-6x与 y =-6x +5中,自变量x 可以是 任意的实数, 列表表示几组对应值:
(2)C=7t-35; (4)y=0.1x+22
观察上面的几个式子,在形式上它们有什 么样的共同特征? 这些函数的形式都是自变量的k(常数) 倍与一个常数的和。
一次函数的定义: 一般地,形如y=kx+b(k,b是常数,k≠0) 的函数,叫做一次函数(注意y、x都是1次) 当b=0时,y=kx+b就变成了 y = kx ,从中 你有什么发现?
X y =-6x y =-6x +5 -2 -1 0 1 2
3.下列说法正确的是 (填序号) ①正比例函数一定是一次函数; ②一次函数一定是正比例函数; ③若y-1与x成正比例,则y是x的一次函数; ④若y=kx+b,则y是x的一次函数。
(2)当 m 2; n 2 时,此函数是正比例函数. ① ③
2a b 3 a b 6
如果是你画正比例函数的图像,你会选 择哪两个点呢
y=kx经过(0,0)点,另外在x=1时,y=k
∴画正比例函数选择(0,0)点
和 ( 1, k)
某登山队大本营所在地的 气温为0 c 1km 5º º c,海拔每升高 , 气温下降6º c. 设:登山队员由大 本营向上登高xkm时, 他们所在的位置的气 温是yº c,试用解析式 表示y与x的关系.
一次函数(三)一次函数的k b

一次函数—— k 、b 与图像的关系【知识要点】1.一次函数解析式)0(≠+=k b kx y 中两个特征量的几何意义(1)b 是直线b kx y +=与y 轴交点的纵坐标,反映直线与y 轴交点的位置; 当0>b 时,直线与y 轴的正方向相交; 当0=b 时,直线过原点;当0<b 时,直线与y 轴的负方向相交.(2)k 反映直线b kx y +=从左到右的升降趋势以及直线的倾斜程度; 当0>k 时,直线从左到右上升;当0<k 时,直线从左到右下降.||k 越大,直线与x 轴相交所成的锐角越大. 2、一次函数y=kx+b 的图像与k 、b 的符号关系如下表:【典型例题】例1(1)已知一次函数3)2(-+-=m x m y 的图像经过第一、三、四象限,求m 的取值范围.(2)已知一次函数y=(6+3m )x+(n -4)。
求:○1m 为何值时,y 随x 的增大而减小;○2m 、n 分别为何值时,函数图像经过原点;○3m 、n 满足什么条件时,函数图像不经过第二象限。
例2(1)直线y kx b =+,经过一、二、四象限,到直线y bx k =-的图象只能是( )(2)设b >a ,将一次函数y=bx+a 与y=ax+b 的图象画在平面直角坐标系内,则有一组a 、b 的取值,使得下列四个图中的一个为正确的是( )(A ) (B ) (C ) (D )(3)当ab >0,ac <0,直线0ax by c ++=不通过的象限是( ) (A )第一象限 (B )第二象限(C )第三象限 (D )第四象限例3、已知abc ≠0,且p acb bc a c b a =+=+=+,那么直线y=px+p 一定经过( )。
A .第一、二象限 B .第二、三象限C .第三、四象限D .第一、四象限ABC D例4(1)已知一次函数的图象经过不同的点A (a ,b )和点B (b ,a ),问这个 函数图象可能经过哪几个象限?(2)如果一条直线l 经过不同的三点A (a ,b ),B (b ,a ), C (a -b ,b -a ),那么,直线l 经过( )。
深刻理解一次函数中k与b的含义
深刻理解一次函数中k 与b 的含义我们知道,一次函数y=kx+b (其中k,b 为常数,且k ≠0)的图象是过两点(0,k)和(kb ,0)的一条直线.当k>0时,直线经过第一、三象限;当k<0时,直线经过第二、四象限.当b>0时,直线与纵轴的正半轴相交;当b<0时,直线与纵轴的负半轴相交;当b=0时,直线经过原点.并且,当k>0时,y 随x 的增大而增大;当k<0时,y 随x 的增大而减小.这些都是数学书上明确写出来的.在实际应用中,k 与b 的含义并非仅此而已.一、k 、b 的符号与直线的位置 对于正比例函数y=kxk 的符号 k>0 k<0 直线位置 第一、三象限第二、四象限对于一次函数y=kx+b k,b 符号k>0, b>0k>0, b<0k<0, b>0k<0, b<0直线位置第一、二、三象限第一、三、四象限第一、二、四象限第二、三、四象限例1.直线y= -2x+3不经过第几象限?解析:由k<0,b>0可知,此直线经过第一、二、四象限.故此直线不经过第三象限.例2.已知一次函数y=kx+b 的图象不经过第三象限.试判断k,b 的符号.解析:根据题意可知,直线y=kx+b 在平面直角坐标系中的位置可以分为以下两种情况:⑴如图1,直线y=kx+b 经过第一、二、四象限,此时,k<0,b>0; ⑵如图2,直线y=kx+b 经过第二、四象限,此时,k<0,b=0. 综上所述,可知,k,b 的符号为:k<0,b ≥0.二、k 的大小与函数值的增减速度一次函数y=kx+b 中,k 越大,直线越陡峭,函数值增减速度越快;k 越小,直线越平缓,函数值增减速度越慢;k=0时,直线与横轴平行,函数值保持不变,此时,函数值没有增减变化. 例3.如图,请举出一个实际情境来进行描述它.解析:结合本题图象,可以考虑利用距离、时间、速度来对此进行描述.解:王爷爷早晨外出散步.他从家里出发以慢速匀速行走,到了报亭前,他看了一会儿报纸,然后以快速匀速回到家里.则王爷爷离家的距离s(m)与行走时间t(min)的函数关系 可以用来描述此图象.三、k 的值与实际应用问题在利用一次函数解决实际问题中,如果函数值逐渐增大,那么k>0;如果函数值逐渐减少,那么k<0;如果函数值保持不变,那么例3图t / mins / m ox y o xy o 图⑴ 图⑵例2图k=0;如果两个一次函数y 1=k 1x+b 1与y 2=k 2x+b 2的增减速度相同,那么21k k =.例4.一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为(h)x ,两车之间的距离.......为(km)y ,图中的折线表示y 与x 之间的函数关系. 根据图象进行以下探究: 信息读取(1)甲、乙两地之间的距离为 km ; (2)请解释图中点B 的实际意义; 图象理解(3)求慢车和快车的速度;(4)求线段BC 所表示的y 与x 之间的函数关系式,并写出自变量x 的取值范围; 问题解决(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时? 解:(1)900;(2)图中点B 的实际意义是:当慢车行驶4h 时,慢车和快车相遇. (3)由图象可知,慢车12h 行驶的路程为900km , 所以慢车的速度为90075(km /h)12=; 当慢车行驶4h 时,慢车和快车相遇,两车行驶的路程之和为900km ,(第28题)ABC DOy /km 90012 x /h4所以慢车和快车行驶的速度之和为900225(km /h)4=,所以快车的速度为150km/h .(4)根据题意,快车行驶900km 到达乙地,所以快车行驶9006(h)150=到达乙地,此时两车之间的距离为675450(km)⨯=,所以点C 的坐标为(6450),.设线段BC 所表示的y 与x 之间的函数关系式为y kx b =+,把(40),,(6450),代入得044506.k b k b =+⎧⎨=+⎩,解得225900.k b =⎧⎨=-⎩, 所以,线段BC 所表示的y 与x 之间的函数关系式为225900y x =-. 自变量x 的取值范围是46x ≤≤.(5)慢车与第一列快车相遇30分钟后与第二列快车相遇,此时,慢车的行驶时间是4.5h .把 4.5x =代入225900y x =-,得112.5y =.此时,慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km ,所以两列快车出发的间隔时间是112.51500.75(h)÷=,即第二列快车比第一列快车晚出发0.75h .。
一次函数中K`b的作用
y=2x y=2x+1 y=2x-1
•从图象中可以清楚地看 出它们是一组平行的直线, 它们的图象是方向相同且 两两互相平行的直线。这 是为什么呢?请同学们自 己猜想:是否与K值有关 呢?b值又确定直线的什 么呢?
3
y .
y=2x+1 y=2x
.
2
y=2x-1
.
1
..
0. 1 2 x
活动2:请同学们在同一坐标系中作
(八年级教材)
一次函数中“K”、“b”的作
y
用
x
杜蒙胡吉吐莫镇蒙古族中学
教学创意:
1、在课堂教学中,灵活运用个人学习、小组学习、全班学习的形式, 使之有机结合、相互渗透,是提高学习效率的一种新颖形式。
2、通过学生自己动手操作,培养学生独立探究能力,同时加强学生 的思维训练,培养学生的思维能力。
3、本节课的教学重点是使学生掌握一次函数y=kx+b(k、b为常数 k≠0 )的图象特点。
出下列函数图象:
y=-x+2 y=x+2
y y=4x+2
y=x+2y=-4x+2
•从图象中可以看到,它们 都是经过(0、2)的一束 直线。请同学们猜想:一次 函数表达式中的b都相等时, 它们的图象是一束经过一 个什么特殊点的直线?
.. .. 0.
x
.
y=-x+2
y=-4x+2
归纳总结1:
从两个图中我们发现: 一次函数表达式中的K的作用有三: 其一,K的正负决定着对应直线所在的象限(K>0时 一、三象限;K<0时二、四象限)K相等b不等时, 图象都是平行的直线。 其二,K的正负决定着这个函数的增减性。 其三,K的大小决定着对应直线与Y轴的位置关系, 即 K 越大,直线离y轴越近;
一次函数与二次函数的认识知识点总结
一次函数与二次函数的认识知识点总结一、一次函数的定义和特点:一次函数亦称为线性函数,在数学中表示为y = kx + b的形式,其中k和b为常数。
1. 定义:一次函数是一种变量之间的线性关系,其中x为自变量,y为因变量,k为斜率,b为截距。
2. 斜率:斜率k代表函数曲线的倾斜程度,其定义为曲线上任意两点之间的纵向变化量与横向变化量的比值。
斜率越大,曲线越陡峭,斜率为正表示曲线上升,斜率为负表示曲线下降。
3. 截距:截距b表示函数曲线与y轴的交点,即当x=0时,对应的y值。
4. 图像特点:一次函数的图像是一条直线,特点是直线上的所有点都满足y = kx + b的方程。
二、二次函数的定义和特点:二次函数是一类非线性函数,其中数学表示为y = ax^2 + bx + c,其中a、b、c为常数,且a ≠ 0。
1. 定义:二次函数是变量之间的二次关系,其中x为自变量,y为因变量,a、b、c为常数。
2. 平移:二次函数可以通过将一般形式y = ax^2 + bx + c表示为标准形式y = a(x - h)^2 + k,其中(h, k)为顶点坐标。
此变换称为平移,它可以使得二次函数图像在坐标平面上上下左右移动。
3. 对称轴:二次函数的对称轴是通过顶点和开口方向确定的,对称轴与平移后顶点的横坐标相等。
4. 开口方向:二次函数的开口方向由二次项系数a的正负决定,a > 0时,开口向上;a < 0时,开口向下。
5. 最值点:当二次函数开口向上时,二次函数的最小值为顶点坐标;开口向下时,二次函数的最大值为顶点坐标。
三、一次函数与二次函数的比较:1. 变化速率:一次函数的斜率是恒定的,代表了以恒定速率变化;而二次函数的斜率是不断变化的,代表了以不同速率变化。
2. 图像形状:一次函数的图像是一条直线,而二次函数的图像是一个抛物线。
3. 极值点:一次函数没有极值点,而二次函数有极值点(最大值或最小值)。
4. 开口方向:一次函数没有开口方向的区别,而二次函数的开口方向由二次项系数a的正负决定。
一次函数--平行与k、b性质
.
【变式题组】
01. (广西南宁)从 2,3,4,5 这四个数中,任取两个数 p 和 q(p≠q),构成函数 y=px-2 和 y=x+q,并使这两个
函数图象的交点在直线 x=2 的右侧,则这样的有序数对(p,q)共有( )
A.12 对
B.6 对
C.5 对
D.3 对
02. (浙江竞赛试题)直线 l:y=px(p 是不等于 0 的整数)与直线 y=x+10 的交点恰好是整点(横坐标和纵坐标都是
x2 kx k
得
x
y
k2 1 k k2 1 k
2
,
∵两直线交点为整数,∴x、y 均为整数。 又当 x 为整数时,y 为整数,
∴
k2 1 k
为整数即可,
k2 1 k
k k
2 1
k
1 k 1
3
1
k
3 1
,
4
5
∵k-1 是整数,∴k-1=±1,±3 时,x、y 为整数,∴k=-2,0,2,4.所以选
1
3. 直线 y= x 向右平移 2 个单位得到直线
2
当
时,两直线相交。
当
时,两直线交于 y 轴上同一点。
☆特殊直线方程:
X 轴 : 直线
Y 轴 : 直线
与 X 轴平行的直线
与 Y 轴平行的直线
一、三象限角平分线
二、四象限角平分线
4. 直线 y= 3 x 2 向左平移 2 个单位得到直线 2
3、某校部分住校生,放学后到学校锅炉房打水,每人接水 2 升,他们先同时打开两个放水龙头,后来因故障关闭一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
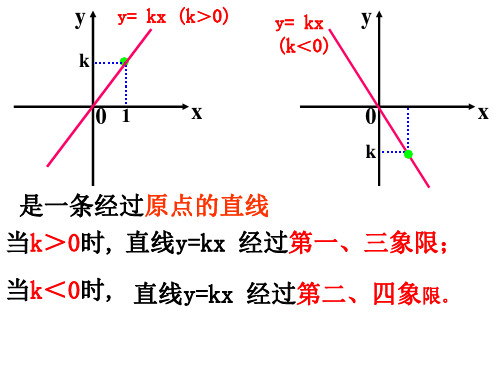
一次函数K与b的意义
尹敏华
一次函数y=kx+b的图象是经过(0,b)和(-b/k,0)的一条直线.
一次函数y=kx+b(k≠0)的图象上的点满足函数关系式,满足函数关系式
的点都在直线上.
在一次函数y=kx+b(k≠0)中,
当k>0,b>0时,则图象过一,二,三象限.
当k>0,b<0时,则图象过一,三,四象限.
当k<0,b>0时,则图象过一,二,四象限.
当k<0,b<0时,则图象过二,三,四象限.
当k>0时,y随x的增大而增大.图像经过一、三象限.
当k<0时,y随x的增大而减小.图像经过二、四象限.
当b>0时,图象与y轴的交点在x轴的上方.
当b<0时,图象与y轴的交点在x轴的下方.
在x轴上的点,y=0,则kx+b=0,则x=-b/k.点的坐标为(-b/k,0).
在y轴上的点,x=0,则b=y.点的坐标为(0,b).
例:教室里放有一台饮水机,饮水机上有两个放水管。
课间同学们依次到饮水机前用茶杯接水,假设接水过程中水不发生泼洒,每个同学所接水量都是相等的,两个放水管同时打开时,它们的流量相同,放水时先打开一个水管,过一会儿,
再打开第二个水管,放水过程中阀门一直开着,饮水机的存水量与放水时间
的函数关系如图所示:
(1)求出饮水机的存水量y(L)与放水时间x(min)的函数关系式。
(2)如果打开第一个水管后2min时,恰好有4个同学接完水,则前22个同学接完水共需要几分钟?
(3)按(2)的放法,求出在课间10min内班级最多有多少个同学能及时接完水?
分析:先审清题意,用待定系数法求出两段解析式。
再利用斜率k的几何意义,验证所求结果。
解:(1)设线段AB为:,把A(0,18),B(2,17)分别代入可得:
即
所以线段AB为:。
设线段BC为:,把B(2,17),C(12,8)分别代入可得:
即
所以线段BC为:。
注:在求线段AB时,由b的几何意义可知:b=18,验证所得结果。
(2)误解:一个水管2分钟可接满4个同学,则一个水管1分钟可接满2个同学;二个水管1分钟可接满4个同学,所以22个同学中,前4个同学用时2分
钟,后18个同学用时分钟,所以共需要分钟。
误解原因:根据第(1)问中所求结果可知,
则,
就是说,在单位时间内打开一个水管和打开两个水管时的出水量不是1:2,所以解答错误。
正解一:前4个同学共接水:
水,
则每人需水量为:,
所以22个同学共需要水量为:,
所以22个同学接完水后的存水量为:
,
则对于线段BC:,可令,则有:
,
即分钟。
正解二:利用斜率k的几何意义来求解,斜率k<0表示存水量在下降,其绝对值0.9表示存水量每分钟减少0.9L。
所以22个同学中,前4个同学用时2分钟,
后18个同学用时0.25分钟,所以共用时分钟。
(3)令x=10,则存水量
,
则放水量为:,
所以人数为:人。
本题中:斜率k<0表示存水量在下降,其绝对值表示存水量每分钟减少了多少。
练习:如图所示,向放在水槽底部的烧杯注水(流量一定,水注满烧杯后,继续注水,直到注满水槽),水槽中水面上升高度h与注水时间t之间的函数关系大致是()
分析:先审清题意,本题中的时间可分为三个段。
第一段从注水开始到水注满烧杯结束,在这段时间内水槽的水面高度为零;第二段时间从水槽内有水开始到高度上升到烧杯的高度为止,在这段时间内水槽内水的高度迅速增加;第三段时间从水到烧杯高度开始到水槽内的水注满结束,在这段时间内水槽内的水的高度缓慢增加。
所以在图象上表示为第一段时间内高度为零,可先排除C答案和D答案。
再看A答案和B答案,由于第三段时间内水高上升的速度要比第二段时间内上升的缓慢,在图象上表示为第三部分要比第二部分平缓,所以应选择B答案。
另外:若水先注入水槽中,水的高度h与时间t的关系如何?或在上述两种情况下,烧杯中水的高度h与时间t的关系大致如何?。
小结:从上面两个习题可以看出真正理解斜率k与b的几何意义是非常重要的,它有助于我们抓住问题的本质,在解决有关问题时能够快速的达到目的。
