上海市中考物理汇编-压强计算 (2)
上海--初三--中考--物理--压强压轴题计算基础题---专题复习.doc

上海中考物理压强计算专题复习1. -个底面积为2x10 2米彳的薄壁圆柱形容器放在水平桌面中央,容器高为0.12米,内盛有0」米深的水,如图10 (a) 所示,另有质量为2千克,体积为1x10—3米'的实心止方体A, 如图10 (b)所示,求:(1)图10 (a)中水对容器底部的压强。
(2)图10 (b)实心正方体A的密度。
(3)将实心正方体A放入图10 (a)的水中后,水而上升的髙度。
2、重为10牛、底面积为2X1CT米彳的薄壁容器放在水平地面上,内盛0.18米深的水。
若在此容器内再放入一密度为0.5X10’千克/米',质量为0.5千克的觀料块,使水面上升0.02米(水未溢出)。
求:(1) 須料块受到的重力;(2) 放入澈料块后静止时,水对容器底部的压强;(3) 现在小张和小李两位同学想计算犁料块静止在水面上时,容器对地面压强的増加量A P。
他们的计算过程如下农所示:计算过程小张容器对地而增加的压力AF就是容器内上升的水的重力4G水,即AF=AG *=△ mg= pAvg=1.0X103千克/米3X2X 10'2米‘X0.02 米X9. 8 牛/千克二3.92 牛则容器对地而压强的增加量△ p=AF/s=AG水/s=3.92牛/2xi(y2米帕。
小李容器对地面增加的压力4F就是塑料块的重力G,叩AF-G旷mg-0.5千克X9.8牛/千克=4.9牛则容器对地而压强的增加:tAp=AF/s= G垫/s=4.9牛/2X10'2米2=2.45X1()2帕。
请判断:小张的计算过程是____________ ,小李的计算过程是(均选填“止确”或“错误”)3.(2007年上海中考第17题)如图11所示,边长分别为0.2米和0.1米的实心止方休A、B放置在水平地面上,“A为0.IX103千克冰3, “B为O.8XIO3千克/米\求:(1)物体A的质量加A。
姓名(2)物体B对地面的压力F B O图1 [(3) 小明和小华两位同学设想在止方体A、B上部沿水平方向分别截去一定的厚度后,通过计算比较A、B剩余部分对地而压强的大小关系。
(完整版)上海中考物理压强计算专题一附答案.doc
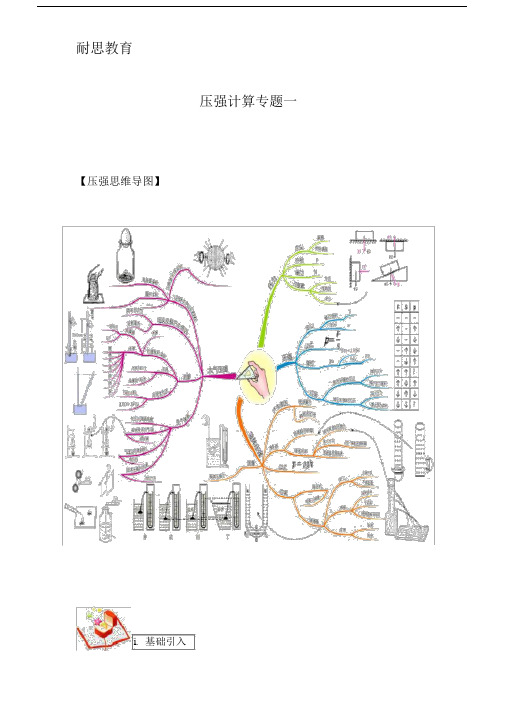
耐思教育压强计算专题一【压强思维导图】i.基础引入:压强变化类计算题和电学压轴题对于大部分考生来说,是两座大山,压的孩子们踹不过气来,接下来,我们一起来剖析一下这块难啃的骨头到底长什么样?我们先来看看压强变化类计算问题主要考到过哪几种题型?注意:思维导图中红色字体标出的是2012 年上海一模出现的新题型。
(4)压强变化范围(1)压强变化量(2)液体压强:抽倒加物( h、 m)(3)固体压强:压强变化类计算(5)v、 n取值范围(6)判断计算过程正误切割叠放( h、v、m)七大题型(7)判断解题思路正误:很多学生在这类题目上存在的主要问题是没有思路,不知道该选用哪个公式?所以我们先来看看两个公式的根本区别到底在哪里?压强的估值人站立时、物理课本对桌面、“二指禅”:接下来我们再来看看主要用到哪些知识点?开放性试题压强可能是多少?三个实心正方体水平切割固体压强叠放竖直切割F切去相同质量ps切割切去相同高度p gh压强变化分析切去相同厚度p gh施压竖直向上p' p原p竖直向下p' p原p液体压强杯中球杯中木块抽出相同质量p F s相同深度倒入p gh相同体积ii. 例题讲解1、如图12 所示,实心均匀正方体A、 B 放置在水平地面上,它们的重均为980 牛, A 的边长为 0.25 米, B 的边长为0.4 米。
①求正方体 A 的密度ρA。
②求正方体 B 对水平地面的压强p B。
③若在正方体 A、B 上沿水平方向分别截去相同的体积V 后,A、B剩余部分对水平地面的压强p A ′和 B′,请通过计算比较它们的大小关系及其对应的V的取值范围。
p⑴ρA= m A = G A = 980牛 3 千克 / 米 3 ( 3 分)V 3 = 6.4 × 10A V A g 9.8牛 / 千克(0.25米)( ρB= mB = G B =1.5625 ×103千克 / 米3) B V B V B g A⑵ p B=FB=GB=980牛/(0.4米)2 = 6.125 × 103帕。
上海市中考物理汇编-压强压轴计算

压强压轴计算青浦21.柱形轻质薄壁容器的底面积为1×102 米2,如图8 所示,内盛2 千克的水后置于水平地面上。
①求容器对水平地面的压强p。
②现将一块体积为1×10-3 米3 的物体完全浸没在容器的水中后,测得容器底部受到水的压强为2450 帕。
通过计算判断将物体放入容器时是否有水溢出,若有水溢出请求出溢出水的质量m 溢水,若无水溢出请说明理由。
图8静安21.如图9所示,薄壁圆柱形容器置于水平地面上,容器内盛有质量为6千克、深为0.3 米的水。
①求容器中水的体积V水。
图9②求水对容器底部的压强p水。
③若容器对地面的压强为3920 帕,求容器对地面的压力F容。
松江21.如图10所示,置于水平桌面上的A、B是两个完全相同的薄壁柱形容器,质量为0.5千克,底面积为0.01米2,分别装有体积为2.5×10﹣3米3的水和深度为0.3米的酒精,(ρ酒精=0.8×103千克/米3)。
求:①水的质量m水。
② A容器对水平桌面的压强p A。
③若在两个容器中抽出相同深度的液体△h后,两容器中液体对底部的压强相等,请计算出△h的大小。
长宁21.如图11所示,轻质薄壁柱形溢水杯甲和柱形容器乙放在水平桌面上,溢水杯甲和容器乙的底面积分别为2×10-2米2和1×10-2米2。
在溢水杯甲中注入水直到溢水口,此时水的深度为0.2米。
求:①溢水杯甲底部受到水的压强p水。
②溢水杯甲对水平地面的压力F甲。
③若将一个金属球浸没在溢水杯甲中,水通过溢水口流入柱形容器乙中,发现此时溢水杯甲对水平地面的压强增加量等于容器乙对水平地面的压强(乙容器中水未溢出),求放入金属球的密度ρ。
21 (8分)①p水=ρgh=1000千克/米3×9.8牛/千克×0.2米=1960帕2分②F甲=G甲=m甲g=ρVg2分=1000千克/米3×2×10-2米2×0.2米×9.8牛/千克=39.2牛1分③Δp甲=p乙1分1分ρ=3000千克/米3 1分杨浦25. 如图14 所示,轻质薄壁圆柱形容器甲和圆柱体乙置于水平地面上。
上海市中考物理二模专题整理 压强计算(无答案)

压强计算题类型一、固体压强奉贤22.如图15所示,边长为0.1米、密度为2×103千克/米3的实心正方体静止在水平面上,求:(1)正方体的质量;(2)正方体对水平面的压强;(3)若正方体的边长为a,密度为ρ,现设想把该正方体截取一半,并将截取部分叠放在剩余部分上方的中央,使截取部分对剩余部分的压强与叠放后水平面受到的压强相等。
小华和小明两位同学分别用下表的方法进行截取,判断能截取方法能否满足上述要求小华沿竖直方向截取一半小明沿水平方向截取一半小强同学把该正方体截取一半并将截取部分放在水平面上,使其对水平面的压强最小,求出最小压强(用字母表示)。
闸北21. 如图11所示,实心正方体A、B放置在水平地面上,受到的的重力均为64牛,A的边长为0.2米,B的边长为0.3米。
①正方体A对水平地面的压强p A。
②正方体A、B的密度之比。
③若在正方体A和B上沿水平方向分别截去相同的体积V后,A、B剩余部分对水平地面的压强为p´A、p´B,请通过计算比较它们的大小关系及其对应的V的取值范围。
图11长宁22.如图13所示,实心正方体甲和轻质柱形容器乙放在水平地面上。
正方体甲的边长为0.1米,密度为2×103千克/米3;容器乙的底面积为1⨯10-2米2,内盛有0.15米深的水,且容器乙足够高。
求:①实心正方体甲的质量; ②水对容器乙底部的压强;③现从正方体甲中挖出一个高度为0.1米,底面积为S 的柱体,并将该柱体放入容器乙中,请通过计算比较正方体甲剩余部分对地面的压强p 甲'和放入柱状物体后水对容器乙底部的压强p 乙'的大小关系及其对应S 的取值范围。
类型二、液体压强 松江22.如图13所示,边长为4h 的正方体A 和轻质薄壁圆柱形容器B 置于水平桌面上,容器B 中盛有高为5h 、体积为5×10-3米3的某液体乙(ρ乙=0.8×103千克/米3)。
① 求液体乙的质量m 乙。
2024年上海中考物理专题复习精练 专题05 压强计算(判断柱体浸没)含详解

专题05压强计算—判断柱体浸没一、常见题目类型1.把柱状实心物体B 全部或切去一部分放入柱状容器中的液体中(图1)。
图2图12.把柱状实心物体先放入柱状容器中,然后向里面加液体(图2)。
二、常用到的分析方法1.柱状实心物体先放入柱状容器中,如果物体未被浸没(水未溢出),如图2所示,则水为柱形,底面积为(S A -S B ),高度为h 水=V 水/(S A -S B );图12.柱状实心物体先放入柱状容器中,如果物体被浸没(水未溢出),如图3所示,则物体排开水的体积等于物体的体积V 物,水升高的高度为∆h 水=V物/S 容器。
S 容器图3三、例题分析【例题1】(2023浦东新区二模)如图所示,足够高的薄壁圆柱形容器甲和实心均匀圆柱体乙置于水平地面上。
容器甲的底面积为3×10-2米2;内盛有0.2米深的水;圆柱体乙的底面积为1×10-2米2、高0.5米,密度为3×103千克/米3。
(1)求容器中水的质量m 水;(2)求水对容器甲底部的压强p 水;(3)现从乙的上方沿水平方向切去一定的厚度Δh ,竖直放入甲内水中,当水对容器甲底部的压强最大时,求乙切去厚度Δh 的范围。
甲乙【例题2】(2021杨浦一模)如图(a )所示,轻质薄壁圆柱形容器甲置于水平地面,底面积为2S ,容器高0.2米,内盛0.15米深的水。
(1)若容器的底面积为4×10-2米2,求容器中水的质量m ;(2)求0.1米深处水的压强p ;(3)现有密度为6ρ水的圆柱体乙,如图(b )所示,将乙竖放入容器甲中,若要使水对容器底部的压强p 水最大,求乙的底面积的最小值S 乙小。
【例题3】(2022徐汇区二模)如图13所示,圆柱形容器甲放在水平地面上(容器足够高),底面积为S ,甲内盛有深为h 的水。
有一质量为m 、底面积为S 1、高为h 1的实心金属块乙竖直放置在容器甲底部。
①若乙的质量m 为8千克、S 1为2×10-2米2、h 1为0.2米,求乙的密度ρ乙。
上海市2020年中考物理备考复习资料汇编专题10固体与液体的压强计算(含参考答案)
中考物理备考复习资料汇编:专题10 固体与液体的压强计算一、柱体切割、液体抽取(倒入)一、常见题目类型1.在柱形物体沿水平方向切切割:切去某一厚度(体积或质量)(图1)。
(体积或质量)(图3)。
二、例题【例题1】如图1所示,实心均匀正方体甲、乙放置在水平地面上,它们的重力G均为90牛,甲的边长a 为0.3米,乙的边长b为0.2米。
求:①正方体甲对地面的压强p甲②若沿水平方向将甲、乙截去相同的厚度Δh后,它们剩余部分对地面的压强p甲′和p乙′相等,请计算截去的厚度Δh。
【答案】①1000帕;②0.16米。
【解析】① p甲=F甲/s甲=G /a2==90牛/9×10-2米2=1000帕②先比较原来两个立方体压强的大小关系:它们的重力G均为90牛,对地面的压力均为90牛,因为甲的底面积大于乙的底面积,根据p=F/S=G/S所以原来两个立方体的压强p甲´<p乙´。
可以先求出甲乙两立方体密度的大小关系:它们的重力G均为90牛,所以m甲=m乙ρ甲V甲=ρ乙V乙ρ甲(0.3米)3= ρ乙(0.2米)3图2B图3图1图1甲乙两立方体密度的大小关系ρ甲︰ρ乙=8︰:27设截去的厚度Δh时,它们剩余部分对地面的压强相等,即p甲´=p乙´ρ甲g(a−Δh)=ρ乙g(b−Δh)8 ×(0.3米−Δh)=27 ×(0.2米−Δh)Δh=0.16米【例题2】(2019上海中考题)如图7所示,足够高的薄壁圆柱形容器甲、乙置于水平桌面上,容器甲、乙底部所受液体的压强相等。
容器甲中盛有水,水的深度为0.08米,容器乙中盛有另一种液体。
①若水的质量为2千克,求容器甲中水的体积V水。
②求容器甲中水对容器底部的压强P水。
③现往容器甲中加水,直至与乙容器中的液面等高,此时水对容器底部的压强增大了196帕,求液体乙的密度ρ液。
【答案】①2×10-3米3;②【解析】甲图7 乙①V水=m水/ρ水=2千克/1.0×103千克/米3= 2×10-3米3②p水=ρ水gh=1.0×103千克/米3×9.8牛/千克×0.08米=784帕③由甲水对容器底部的压强增大了196帕可求增加的水的深度△h水:△P水=ρg△h△h水=△p水/(ρ水g)=196帕/(1000千克/米3×9.8牛/千克)=0.02米容器乙中盛液体的深度:h乙= h水'=h水+△h水=0.08米+0.02米 = 0.1米根据容器甲、乙底部所受液体的压强相等可求液体的密度:p水=p乙ρ水gh水=ρ乙gh乙1000千克/米3×0.08米=ρ乙0.1米ρ乙=800千克/米3【例题3】相同的薄壁圆柱形容器甲、乙置于水平桌面上。
上海市2020年中考物理二模试卷按考点分类汇编 压强计算 (2)(含答案)

压强计算宝山:21.如图9所示,高为1米、底面积为0.5米2的轻质薄壁圆柱形容器置于水平地面上,且容器内盛满水。
⑴求水对容器底部的压强p 。
⑵若将一个体积为0.05米3的实心小球慢慢地放入该容器中,当小球静止不动时,发现容器对水平地面的压强没有发生变化。
求小球质量的最大值m 球最大。
答案:奉贤:21.如图11所示,两个均匀的实心正方体甲和乙放置在水平地面上,甲的质量为6千克,边长为0.1米。
求:(1)甲的密度 (2)甲对地面的压强P 甲(3)a.若甲乙对水平地面的压强相等,且密度之比为3:2,现分别在两物体上沿竖直方向切去质量相等的部分并分别放在对方剩余部分上,则甲乙切去部分和地面的接触面积之比 ΔS 甲:ΔS 乙=b.若叠放后甲乙对地面的压强的增加量分别为ΔP 甲、ΔP 乙,且当ΔP 甲:ΔP 乙=5:1时,甲物体沿竖直方向切去的质量是 千克。
(第三小题无需写出计算过程) 答案:图9h =1米甲 乙图14虹口:22. 如图10所示,轻质薄壁圆柱形容器置于水平地面,容器盛有质量为4千克的水. ①求水的体积V 水;②求0.1米深处水的压强P 水;③现有质量为4千克的物体,其底面积是容器的一半。
若通过两种方法增大地面受到的压强,并测出压强的变化量,如下表所示.根据表中的信息,通过计算判断将物体放入容器时是否有水溢出,若有水溢出请求出溢出水的重力G 溢水,若无水溢出请说明理由. 答案:金山:23.如图14所示,底面积为102米2、高为0.4米长方体甲(ρ甲=2×103千克/米3)和底面积为2102米2的薄壁柱形容器乙放在水平地面上。
乙容器足够高,内盛有0.1米深的水。
(1)求甲的质量m 甲。
(2)求水对乙容器底部的压强p 水。
(3)现沿水平方向将长方体甲截取一定的厚度,并将截取部分竖直放入乙容器中,使得水对容器底部的压强最大,且长方体甲对地面的压强减少量最小,请求出甲对地面的压强减少量。
2024年上海中考物理专题复习精练 专题03 压强计算(在柱体或液体中加物体)含详解

专题03压强计算—在柱体或液体中加物体一、常见题目类型1.将物体甲全部或切去一部分体积浸没在容器乙的液体中(见图1)。
2.将乙容器放在甲的上方(见图1)。
3.将另一物体A分别放在柱体甲表面的上方或浸没在容器乙的液体中(见图2)。
4.将一实心物体A分别浸没于甲、乙液体中(见图3)。
图3二、常用到的基础知识与分析方法1.压强:p=ρgh,p=F/S2.变化(增大或减小)的压强:△p=△F/S△p=ρg△h3.把物体放入柱形液体中浸没时,液体对容器底部产生的压力:F=pS=ρghS+ρg△h S=G液+G排(F浮)即等于原来液体的重力与物体受到的浮力之和。
F浮=ρ液gV排增大的压力△F=G排=就是物体排开的液体所受到的重力(即浮力)。
4.区别液体的压强与固体的压强(容器对地面的压强)在液体不溢出时,则液体对容器底部的压强p液=ρ液gh液=F液/S容器容器对地面的压强p地=F地/S容器=G物体+G容器/S容器5.区别液体的压强与固体的压强(容器对地面的压强)在液体不溢出时,则液体对容器底部压强的增加量Δp液=ρ液gΔh液=ρ液gV物体/S容器容器对地面压强的增加量Δp地=ΔF地/S甲==G物体/S甲=ρ物体gV物体/S容器6.理解“轻质薄壁”容器即容器的重力为0,内部液体的受力面积与水平面的受力面积相等。
三、例题分析【例题1】(2023闵行二模)将足够高的薄壁柱形容器甲、乙放置在水平地面上,如图9所示,甲、乙两容器中分别盛有深度为0.1米的酒精和质量为1千克的水。
已知容器乙的底面积为1×10-2米2,酒精的密度为0.8×103千克/米3。
甲乙图9。
①求水的体积V水②现将密度为2×103千克/米3的小球放入某个容器内,小球浸没于液体中,此时两液体对容器底部的压强恰好。
相等,求该容器对地面压强的增加量Δp地【例题2】(2023普陀二模)如图所示,实心正方体甲和盛有水的轻质柱形容器乙放在水平桌面上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压强计算
宝山:21.如图所示,高为1.3米,底面积分别为0.15米2和0.05米2的甲、乙两个轻质薄壁圆柱形容器在下部用轻质细管连通后放在水平地面上,且容器内盛有1米深的水.
(1)求水对甲容器底部的压强p甲.
(2)若将一体积为0.04米3的实心小球慢慢地放到甲容器中的水里(已知ρ球=1×103千克/米3),求:直到小球在水中不动为止,水对乙容器底部压力的增加量△F乙.
嘉定:22.如图14所示,甲、乙两圆柱形容器(容器足够高)放在水平桌面上,甲的底面积为9S,乙的底面积为10S,分别盛有1.8×10-3米3体积的水和0.25米高的酒精。
(ρ酒=0.8×103千克/米3)求:(1)水的质量m水。
(2)若甲容器的质量为0.2千克,底面积为1×10-2米2,求甲容器对水平桌面的压强p甲。
(3)若水和酒精对甲、乙容器底部的压强相等,为了使甲、乙容器底部受到的水和酒精的压力相等,以下方法可行的是(选填“A”、“B”或“C”)。
并计算出抽出(或加入)的ΔV或Δh。
图14
A 抽出ΔV体积的水和酒精
B 加入Δh高的水和酒精
C 抽出Δh高的水和酒精
闵行:25.质量为 0.2 千克、底面积为 0.01 米2 、容积为2×10-3 米 3 的薄壁容器内装入 0.15 米深的某液体后,容器对桌面的压力与液体对容器底部的压力恰好为 11.76 牛。
(1)求该液体对容器底的压强。
(2)求该液体的密度、体积。
(3)若在容器内再放入一质量为 1.5 千克、体积为1.5×10-1 米3 的实心物块,且物块浸没。
求物块静止
后容器对桌面压强的增加量。
黄浦:21.如图11所示,薄壁圆柱形容器甲和均匀圆柱体乙置于水平地面上。
①若甲中盛有质量为3千克的水,求水的体积V1及水对甲底部的压力F1。
②若容器甲足够高、底面积为2S,其内装有深为H、密度为ρ的液体;圆柱体乙的底面积为S高h。
现将乙沿水平方向在上部切去一半,并将切去部分浸没在甲的液体中,此时液体对甲底部压强P恰等于乙剩余部分对水平地面压强P1。
求乙的密度ρ1。
青浦:25.薄壁圆柱形容器甲的质量为0.4千克,底面积为1×10﹣2米2,容积为3×10﹣3米3,置于水平桌面上,内盛0.2米深的水.
①求甲底部受到的水的压强p水.
②现将质量为3.6千克的物体乙轻放入甲内,且乙浸没在水中.
(a)求甲对桌面达到的最大压强p甲.
(b)当甲对桌面达到最大压强时,求乙的最小密度ρ乙.
静安:21.如图所示,圆柱体甲和薄壁圆柱形容器乙置于水平地面.甲的重力为10牛,底面积为5×10﹣3米2.
①求甲对地面的压强p甲.
②求乙容器内水面下0.1米深处的压强p水.
③将甲浸没在乙容器的水中后(无水溢出),若乙容器对地面压强的增加量是水对乙容器底部压强增加量的
2.7倍,则求甲的密度ρ甲.
浦东:22.如图所示,薄壁轻质圆柱形容器甲内盛有水,水深为容器高度的,金属圆柱体乙与甲内水面等高.甲、乙均置于水平地面上.
(1)若甲内水深0.2米,求水对容器甲底部的压强.
(2)若乙的质量5千克,底面积10﹣2米2,求乙对地面的压强.
(3)将乙浸没在甲容器内的水中后,水不溢出,甲对地面的压强恰为原压强的2.5倍,求乙密度的最小值.
虹口:21.如图(a)所示,轻质薄壁圆柱形容器甲置于水平地面,容器高0.2米,内盛0.15米深的水,水对容器底部压力为29.4牛.
①求水对容器底部的压强p水.
②求容器的底面积S容.
③现有底面积为0.5S容、高为h、密度为5×103千克/米3圆柱体乙,如图(b)所示,将乙竖直放入容器甲中,若要使水对容器底部的压强p水′最大,求h的最小值.
崇明:22.如图所示,柱形容器A和均匀柱体B置于水平地面上,A中盛有质量为5千克的水,B受到的重力为200牛,B的底面积为5×10﹣2米2.
(1)求A中水的体积V水;
(2)求B对水平地面的压强p B;
(3)现沿水平方向在圆柱体B上截去一定的厚度,B剩余部分的高度与容器A中水的深度之比hB′:h水为2:5,且B剩余部分对水平地面的压强大于水对容器A底部的压强,求B的密度ρB的范围.
解:(1)V水===5×10﹣3m3,
(2)p B===4000Pa;
(3)p B′===ρB gh B′,p水=ρ水gh水,h B′:h水=2:5,
因为B剩余部分对水平地面的压强大于水对容器A底部的压强,
所以ρB gh B′>ρ水gh水,ρB>ρ水=ρ水=×1×103kg/m3=2.5×103kg/m3.
所以ρB>1.5×103kg/m3.
松江:21.如图所示,均匀长方体甲和薄壁圆柱形容器乙置于水平地面上.长方体甲的底面积为3S.容器乙足够高、底面积为2S,盛有体积为5×10﹣3米3的水.
①若甲的重力为20牛,底面积为5×10﹣4米2,求甲对地面的压强p甲.
②求乙容器中水的质量m水.
③若将甲沿水平方向切去厚度为h的部分,并将切去部分浸没在乙容器的水中时,甲对水平地面压强的变化量△p甲恰为水对乙容器底部压强增加量△p水的2倍.求甲的密度ρ甲.
徐汇:23.一个底面积为2×10﹣2米2的轻质薄壁圆柱形容器放在水平桌面中央,内盛有0.1米深的水,求:
①水对容器底部的压强;
②水的质量m1;
③继续加入一定量的水,容器对桌面的压强为P1,再将一个物块放入水中(无水溢出),当物块自然静止时,水对容器底的压强变为P2,容器对桌面的压强变为P3.
i)若该物块自然静止时未浸没在水中,则该物块的密度的取值范围是ρ物<千克/米3.(写出具体数值)ii)若该物块自然静止时浸没在水中,请用字母表示该物块的密度ρ物.
普陀:22. 如图所示,底面积为S1的均匀圆柱体A和底面积为S2的圆柱形容器B置于水平地面上。
已知知A的密度为2×103千克/米3,B中盛有重为200牛的液体,
①若A的体积为4×10-3米3,求A的质量m A;
②若B的底面积为5×10-2米2,求液体对B容器底部的压强P B;
③现将质量为m,密度为ρ的甲物体分別放在A上面和浸没在B容器的液体中(液体求溢出),当圆柱体体A 对桌面压强的变化量与液体对B容器底压强的变化量相等时,求B容器中液体的密度ρ液
甲
乙
图17
B
A
杨浦:26. 如图17所示,均匀实心正方体甲、乙放在水平地面上,甲的底面积为4×10-2
米2
,质量为16千克,乙的体积为1×10-3
米3。
求: ①甲对地面的压强p ;
②若将乙叠放在甲的上方中央,乙对甲的压强为p 1,若将甲叠放在乙的上方中央,甲对乙的压强为p 2,已知p 2=4p 1。
求乙的密度。
③当甲、乙分别平放在水平地面上时,若分别沿水平方向切去相同的体积V ,则求甲、乙对地面压强变化量△
p 甲与△p 乙的比值。
奉贤:21.如图13所示,一足够高的薄壁圆柱形容器静止在水平地面上。
求: (1)当容器内盛有1×10-3
米3
的酒精时,酒精的质量m 酒;(ρ酒=0.8×103
千克/米3
) (2)当容器内盛有0.1米深的水时,水对容器底部的压强p 水;
(3)当容器中盛有质量、体积分别为m 、2V ,的液体时,把一质量、体积分别为2m 、
V 的金属圆柱体浸没在此液体中,设容器对水平地面的压强变化量为Δp 容,液体对容器底部的压强变化量为
Δp 液,试计算Δp 容:Δp 液的值。
图13。
