原子惯性器件的基本工作原理及主要特点共24页
惯性导航难懂?看懂只需这一篇!全面解读惯性导航系统与技术

惯性导航难懂?看懂只需这一篇!全面解读惯性导航系统与技术惯性导航系统(INS,Inertial Navigation System)是一种利用惯性敏感器件、基准方向及最初的位置信息来确定运载体在惯性空间中的位置、方向和速度的自主式导航系统,也简称为惯导。
惯性导航技术的发展历程第一代惯性导航技术指1930 年以前的惯性技术,奠定了整个惯性导航发展的基础。
牛顿三大定律成为惯性导航的理论。
第二代惯性技术开始于上世纪 40 年代火箭发展的初期,其研究内容从惯性仪表技术发展扩大到惯性导航系统的应用。
70 年代初期,第三代惯性技术发展阶段出现了一些新型陀螺、加速度计和相应的惯性导航系统,其研究目标是进一步提高INS 的性能,并通过多种技术途径来推广和应用惯性技术。
当前,惯性技术正处于第四代发展阶段,其目标是实现高精度、高可靠性、低成本、小型化、数字化、应用领域更加广泛的导航系统。
比如随着量子传感技术的迅速发展,在惯性导航技术中,利用原子磁共振特性构造的微小型核磁共振陀螺惯性测量装置具有高精度、小体积、纯固态、对加速度不敏感等优势,成为新一代陀螺仪的研究热点方向之一。
惯性导航的组成惯性导航包括惯性测量单元(Inertial Measurement Unit,简称IMU)和计算单元两大部分。
通过IMU感知物体方向、姿态等变化信息,再经过各种转换、补偿计算得到更准确的信息。
比如检测物体的初始位置、初始朝向、初始姿态以及接下来每一刻朝向、角度的改变,然后把这些信息加一起不停地推,推算出物体现在的朝向和位置。
IMU主要由加速度计和陀螺仪组成,可实时检测物体的重心方向、俯仰角、偏航角等信息,如果还加上电子罗盘和气压计等传感器,那IMU的测量信息量与精度也相应地能得到一定的提高。
而计算单元则主要由姿态解算单元,积分单元和误差补偿单元这三部分组成。
惯性导航的工作原理惯性导航的目的是实现自主式导航,即不依赖外界信息,包括卫星信号、北极指引等。
惯性元件ppt(1)

形状对称的刚体,只要以其中心点为坐标系原点,选 取使刚体对称的轴为坐标轴,则刚体的三个惯性积必 然为0。这是因为在刚体内任意一点(xi,yi,zi),必然存 在另外7个对称点:(xi,yi,-zi)、(xi,-yi,-zi)、(xi,yi,zi)、(-xi,yi,zi)、(-xi,yi,-zi)、(-xi,yi,-zi)、-xi,yi,zi),这8个点的惯性积之和为0,因此整个刚体的三 个惯性积必为0:
对于小型陀螺而言,常用单位是克· 厘米2/秒。
例 设转子的转动惯量J=398g· cm2,转子的转速为 n=24000r/min,求转子的角动量。 解 转子的自转角速度为 n 2 24000 2 2513 .27 rad / s
角动量的大小为
60 60
H J 398 2513 .27 10 g cm / s
第六讲 第三章 惯性元件——陀螺仪与加速度计 1,陀螺仪能测得载体的转角或角速度, 2,加速度计能测得比力或加速度, 3,惯性元件;陀螺仪与加速度计依据的都是惯性力 或惯性矩.而且测量结果都是相对惯性空间的,所以 把陀螺仪和加速度计称作惯性元件。 陀螺仪和加速度计是惯性导航系统中使用的核心元件, 它们的类型和品质直接影响惯性导航系统的构成和工 作特性。
mi ( y z )
2 i 2 i
J y mi ( xi2 zi2 )
2 i 2 i
J z mi ( y x ) J xy mi xi yi J yz mi yi zi J zx mi xi zi
得
用陀螺动量矩H在惯性空间的转动角速度来表示 H的矢端速度vH则有
vH H
H M
式中,ω是H相对惯性空间的进动角速度,该式表示 了进动角速度ω与动量矩H及外力矩M之间的关系。 图3-4(a)、(b)分别给出了沿内环轴方向施加力矩 和沿外环轴方向施加力矩时陀螺转子的进动情况。 进动时,动量矩的方向总是沿捷径方向向外力矩方 向靠拢
惯性器件.ppt

光纤陀螺仪工作示意图
光纤陀螺仪
与机电陀螺或激光陀螺相比,光纤陀螺具有如下 特点:
(1)零部件少,具有较强的抗冲击和抗加速运动的能力; (2)灵敏度和分辨率比激光陀螺仪提高了好几个数量级 ; (3)较长的使用寿命; (4)易于采用集成光路技术,信号稳定,且可直接用数字输 出,并与计算机接口联接; (5)通过改变光纤的长度或光在线圈中的循环传播次数,可 以实现不同的精度,并具有较宽的动态范围; (6)相干光束的传播时间短,因而原理上可瞬间启动,无需 预热; (7)结构简单、价格低,体积小、重量轻.
摩擦及对策、漂移率
漂移、漂移率
漂移:受干扰影响,陀螺转子轴相对惯性空间的转动 漂移率:陀螺转子轴漂移的角速率(度/小时) 惯性级精度:0.01度/小时 陀螺的发展历史: 消除各种有害力矩、降低漂移率的历史
傅科陀螺仪
傅科:法国地球物理学家(1819-1868) 验证地球自转 傅科陀螺仪 (1852)
傅科摆
(1851)
L=67m M=28kg A=6m
精度较低,无法验证地球自转
之后轴承工艺得到改进
陀螺罗经——航海方面的最早应用
人类早期航海采用磁罗盘(指南针) 19世纪后期,钢质轮船逐渐取代 木质轮船,磁罗盘无法再保证精度 在极地附近磁罗盘也会失灵
寻找能够替代磁罗盘的方位指使仪
如果借助陀螺仪,需要解决实 时、自主寻北的问题
激光陀螺 60年代初开始研制,70年代进 入实用
1983-1994美国各类陀螺比例
振动陀螺、微机械陀螺 音叉振动陀螺、压电振动陀螺、 半球谐振陀螺
光纤陀螺 70年代开始研制,80年代初进 入实用
导航原理_惯性器件

单自由度陀螺 仪(只有一个框 架,使转子自 转轴具有一个 转动自由度)。
转子陀螺的力学原理 陀螺绕主轴转动的角动量以H表 示,H=JΩ,式中J为陀螺转子的转 动惯量。H是矢量,方向与角速度 的方向一致。 转子陀螺的力学原理就是动量矩定 理。
动量矩定理
dH dt
i
M
式中,H为定点转动质点系对该定点的角动量 总和,M为作用在该质点系上对该定点的合外 dH 力矩, dt 表示在惯性坐标系内观察到的时间 i 变化率。 2.3.1.1双自由度陀螺仪的基本特性
由动量矩定理,当没有外力矩作用在陀螺 dH 0 仪上时, ,表明 H 相对惯性空间保持恒 dt 定不变,H=JΩ(H的方向和Ω的方向相同)即 转子自转轴相对惯性空间的指向不变。这就是 陀螺仪的定轴性。
i
定轴性是双自由度陀螺仪的 一个基本特性。无论基座绕 陀螺仪自转轴转动,还是绕 内框架轴或外框架轴方向转 动,都不会直接带动陀螺转 子一起转动(指转子自转之外 的转动)。由内、外框架所组 成的框架装置,将基座的转 动与陀螺转子隔离开来。这 样,如果陀螺仪自转轴稳定 在惯性空间的某个方位上, 当基座转动时,它仍然稳定 在原来的方位上。
eG
Hie sin V ie O E H sin
方向自O 指向 O ,即 ωeG ω ie
当自由陀螺的角动量与地 球自转角速度间的夹角时, 0 地球上的观察者所看到的 陀螺自转轴以为角速度 ω ie 作旋转,旋转所形成的曲 面为一圆锥面,对称轴平 行于地轴,半锥角为 , 陀螺的这种运动称为表观 运动。
第2章 惯性器件
2.1
概述
2.2 陀螺仪 2.2.1 机械转子陀螺仪 2.2.2 光学陀螺仪 2.2.3 微机械陀螺仪 2.3 加速度计
原子物理学的基础知识

原子物理学的基础知识原子物理学是研究原子的结构、特性及其相互作用的一门基础科学。
它不仅是物理学的一个重要分支,而且在化学、材料科学和生物医学等多个领域中扮演着至关重要的角色。
随着科技的飞速发展,原子物理学中的许多理论和应用正逐步被深入研究和拓展。
本文将从原子的基本构成、原子的特性、实验方法以及原子物理学的重要应用等多个方面,为您详细阐述原子物理学的基础知识。
原子的基本构成最基本的原子构成可以分为三个主要部分:质子、中子和电子。
质子和中子共同组成了原子的核心——原子核,而电子则围绕着原子核旋转。
质子质子是带正电的粒子,其电荷量为+1e(1.602×10^-19库仑),是决定元素种类的核心粒子。
换句话说,质子的数量决定了一个元素的原子序数,例如氢元素有一个质子,而氧元素有八个质子。
中子中子是没有电荷的粒子,质量略大于质子。
当质子的数量不变时,中子的数量可以变化,从而形成同位素。
例如,氢的同位素包含氘(一个中子)和氚(两个中子),同位素在化学特性上相似,但在某些物理性质上却有所不同。
电子电子是带负电的微小粒子,其电荷量为-1e,质量极小,几乎可以忽略不计。
电子根据一定的能量层级排列在原子的不同电子壳层上,这种排列形成了电子云。
原子核与电子云结构在标准模型中,原子的结构是类似于太阳系的模型,其中原子核如同太阳,而电子如同行星在其周围运转。
虽然这种描述形象生动,但实际上,并不能完全准确地反映它们之间的关系。
量子力学为我们提供了更精确的描述,即通过波动函数来表示电子的位置和能量分布。
因此,原子的真实结构是一种概率分布形式。
原子的性质及其量化离散能级与量子跃迁根据量子力学,电子围绕核旋转不是任意分布的,而是在某些特定的能级上。
每个能级都对应着特定的能量值,电子之间可以通过跳跃到高能级或低能级而释放或吸收光子的形式来实现这种量化。
这使得我们能够理解光谱现象,例如氢原子的发射光谱和吸收光谱。
这些光谱线对应于不同能级之间的跃迁,是分析元素成分的重要工具。
原子力显微镜AtomicForceMicroscope

σ:原子的直径 r : 原子之间的距离
AFM工作过程
原子力显微镜的基本原理是:将一个对 微弱力极敏感的微悬臂一端固定,另一 端有一微小的针尖,针尖与样品表面轻 轻接触,由于针尖尖端原子与样品表面 原子间存在极微弱的排斥力,通过在扫 描时控制这种力的恒定,带有针尖的微 悬臂将对应于针尖与样品表面原子间作 用力的等位面而在垂直于样品的表面方 向起伏运动。利用光学检测法或隧道电 流检测法,可测得微悬臂对应于扫描各 点的位置变化,从而可以获得样品表面 的形貌。
量子力学则认为,即使粒子能量小于阈值能量,很多粒子冲向势垒,一部分 粒子反弹,还会有一些粒子能过去,好像有一个隧道,故名隧道效应。就像 在山坡上开一隧道,自行车从中穿过一样。可见,宏观上的确定性在微观上 往往就具有不确定性。虽然在通常的情况下,隧道效应并不影响经典的宏观 效应,因为隧穿几率极小,但在某些特丁的条件下宏观的隧道效应也会出现。
假设两个原子中,一个是在悬臂的探针尖端, 另一个是在样本的表面,它们之间的作用力 会随距离的改变而变化,其作用力与距离的 关系如右图所示,当原子与原子很接近时, 彼此电子云斥力的作用大于原子核与电子云 之间的吸引力作用,所以整个合力表现为斥 力的作用,反之若两原子分开有一定距离时, 其电子云斥力的作用小于彼此原子核与电子 云之间的吸引力作用,故整个合力表现为引 力的作用。若以能量的角度来看,这种原子 与原子之间的距离与彼此之间能量的大小也 可从Lennard –Jones的公式中到另一种印证。
假设两个原子中一个是在悬臂的探针尖端假设两个原子中一个是在悬臂的探针尖端另一个是在样本的表面它们之间的作用力另一个是在样本的表面它们之间的作用力会随距离的改变而变化其作用力与距离的会随距离的改变而变化其作用力与距离的关系如右图所示当原子与原子很接近时关系如右图所示当原子与原子很接近时彼此电子云斥力的作用大于原子核与电子云彼此电子云斥力的作用大于原子核与电子云之间的吸引力作用所以整个合力表现为斥之间的吸引力作用所以整个合力表现为斥力的作用反之若两原子分开有一定距离时力的作用反之若两原子分开有一定距离时其电子云斥力的作用小于彼此原子核与电子其电子云斥力的作用小于彼此原子核与电子云之间的吸引力作用故整个合力表现为引云之间的吸引力作用故整个合力表现为引力的作用
第一章《原子结构与性质》知识点归纳

第一章《原子结构与性质》知识点归纳课标要求.了解原子核外电子的能级分布,能用电子排布式表示常见元素的(1~36号)原子核外电子的排布。
了解原子核外电子的运动状态。
2.了解元素电离能的含义,并能用以说明元素的某种性质3.了解原子核外电子在一定条件下会发生跃迁,了解其简单应用。
4.了解电负性的概念,知道元素的性质与电负性的关系。
要点精讲一.原子结构1.能级与能层2.原子轨道3.原子核外电子排布规律(1)构造原理:随着核电荷数递增,大多数元素的电中性基态原子的电子按右图顺序填入核外电子运动轨道(能级),叫做构造原理。
能级交错:由构造原理可知,电子先进入4s轨道,后进入3d轨道,这种现象叫能级交错。
说明:构造原理并不是说4s能级比3d能级能量低(实际上4s能级比3d能级能量高),而是指这样顺序填充电子可以使整个原子的能量最低。
也就是说,整个原子的能量不能机械地看做是各电子所处轨道的能量之和。
(2)能量最低原理现代物质结构理论证实,原子的电子排布遵循构造原理能使整个原子的能量处于最低状态,简称能量最低原理。
构造原理和能量最低原理是从整体角度考虑原子的能量高低,而不局限于某个能级。
(3)泡利(不相容)原理:基态多电子原子中,不可能同时存在4个量子数完全相同的电子。
换言之,一个轨道里最多只能容纳两个电子,且电旋方向相反(用“↑↓”表示),这个原理称为泡利(Pauli)原理。
(4)洪特规则:当电子排布在同一能级的不同轨道(能量相同)时,总是优先单独占据一个轨道,而且自旋方向相同,这个规则叫洪特(Hund)规则。
洪特规则特例:当p、d、f轨道填充的电子数为全空、半充满或全充满时,原子处于较稳定的状态。
即p0、d0、f0、p3、d5、f7、p6、d10、f14时,是较稳定状态。
4.基态原子核外电子排布的表示方法(1)电子排布式①用数字在能级符号的右上角表明该能级上排布的电子数,这就是电子排布式。
②为了避免电子排布式书写过于繁琐,把内层电子达到稀有气体元素原子结构的部分以相应稀有气体的元素符号外加方括号表示,例如k:[Ar]4s1。
惯性器件原理-第六章光学陀螺基础
第六章
光学陀螺基本理论
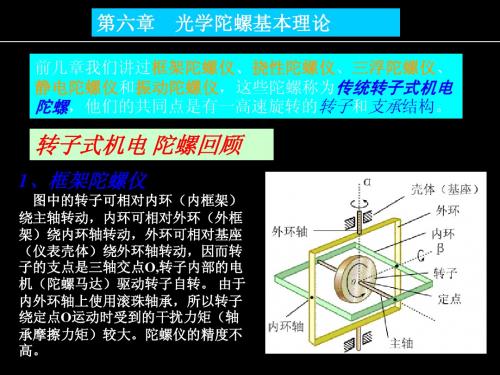
转子式机电 陀螺回顾
4、静电陀螺仪
转子是球形的,支承则是不动 的球腔;通电时依靠球腔内壁三对 电极时转子的静电吸力来支承后者, 球形转子的中心即为支承点。转子 中空,内壁有一赤道带以区分转子 的主轴与赤道轴。转子表面刻有图 谱,当转子旋转时可由光电传感器 识别转子主轴的方向。 静电陀螺 的精度极高,但要工作在高真空状 态,以防止高压静电击穿。
6.2 Sagnac效应
第六章
光学陀螺基本理论
6.2 Sagnac效应 迈克尔逊实验:
矩形面积 A = 600×300 m2 光源波长λ= 0.7μm 计算得: ΔL=0.175μm,即 λ/ 4 干涉条纹只移动了 1/ 4 条纹 间距 如果用来测量 0.015 0/h 的 角速度,则干涉条纹将只移 动 1/ 400 条纹间距 测量精度无法保证
E h
第六章
光学陀螺基本理论
6.4 谐振腔和谐振条件
光谐振腔 :
放电管中充有氦一氖混合气 通过给电极加电压产生放电电流进行激励 在放电管轴线的两端,装有一对高面反射率的球面反射 镜,对放电管中发生的先进行反射
E h
第六章
光学陀螺基本理论
6.4 谐振腔和谐振条件
激光陀螺谐振腔 :
第六章
光学陀螺基本理论
陀螺仪表发展方向
高精度:光学陀螺 中低精度:MEMS、MOEMS
第六章
光学陀螺基本理论
光学陀螺仪发展
1897年法国人Oliver Ladge采用白炽灯作光源,在一个1mx6m的矩形光路中, 试图测量转动引起的光的干涉条纹的变化。采用白炽灯作光源,在一个1mx6m 的矩形光路中,试图测量转动引起的光的干涉条纹的变化。(失败) 1911年,Harress第一个从实验上观察到环形光路中,转动引起干涉条纹变化。 1913年,法国科学家Sagnac重新进行了环形光路中外界转动引起的干涉条纹变 化的实验并从理论上对此现象进行了解释,提出了著名的Sagnac效应。建立了 激光陀螺和光纤陀螺的基本理论。 随后近半个世纪的时间中,光学Sagnac效应的研究基本没有任何进展—空白! 1960年发明的激光 ,光学陀螺曙光再现! 1961年,美国人迈塞克就提出了用环形激光器测量转速的理论,即激光陀螺的 理论,这为光学陀螺的发展奠定了理论基础。 1961年美国科学家C. V. Heer在美物理学会的年会上首次发表关于激光陀螺文 章,标志着第一代光学陀螺―激光陀螺诞生!随后激光陀螺开始蓬勃发展 1963年美国科学家Macek和Davis报道了环形激光谐振腔Sagnac效应验证实验。 1976年美国Uath大学的V.Vali和R.W.Shorthill首次提出了干涉式光纤陀螺的概 念,它标志着第二代光学陀螺―干涉式光纤陀螺的诞生。 随后光纤陀螺开始蓬 勃发展
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
56、极端的法规,就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要,人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益, 而是为 了公共 的利益 ;一部 分靠有 害的强 制,一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ,那么 法律作 为一件 无用之 物自己 就会消 灭。— —洛克
25、学习是劳动,是充满思想的人民的幸福是至高无个的法。— —西塞 罗
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
