2018年中考数学特训方案(42份) 人教版39(免费推荐下载)
2018年中考数学特训方案(42份) 人教版6(免费推荐下载)

第讲二次函数.将抛物线=平移得到抛物线=(-)+,下列平移正确的是().先向左平移个单位长度,再向上平移个单位长度.先向左平移个单位长度,再向下平移个单位长度.先向右平移个单位长度,再向下平移个单位长度.先向右平移个单位长度,再向上平移个单位长度.(黔东南中考)如图,抛物线=++(≠)的对称轴为直线=-,给出下列结论:①=;②>;③>;④-+>,其中正确的个数有().个.个.个.个.(徐州中考)若函数=-+的图象与坐标轴有三个交点,则的取值范围是().<且≠.>.<<.<.(陕西中考)已知抛物线=--(>)的顶点关于坐标原点的对称点为′,若点′在这条抛物线上,则点的坐标为().(,-) .(,-) .(,-) .(,-).(威海中考)已知二次函数=++(≠)的图象如图所示,则正比例函数=(+)与反比例函数=在同一坐标系中的大致图象是().(乐山中考)已知二次函数=-(为常数),当-≤≤时,函数值的最小值为-,则的值是()或.-或.(临沂中考)足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度(单位:)与足球被踢出后经过的时间(单位:)之间的关系如下表:下列结论:①足球距离地面的最大高度为;②足球飞行路线的对称轴是直线=;③足球被踢出时落地;④足球被踢出时,距离地面的高度是.其中正确结论的个数是().....(河南中考)如图①,点从△的顶点出发,沿→→匀速运动到点,图②是点运动时,线段的长度随时间变化的关系图象,其中为曲线部分的最低点,则△的面积是..若抛物线=-+与轴没有交点,则的取值范围是>..(上海中考)已知一个二次函数的图象开口向上,顶点坐标为(,-),那么这个二次函数的解析式可以是=-.(只需写一个).(陕西中考模拟)如图,抛物线=++过(,),(,)两点.()求抛物线的函数解析式;()求抛物线与轴的交点的坐标及其对称轴.解:()∵抛物线=++过(,),(,)两点,∴解得∴抛物线的函数解析式为=-+;()在=-+中,令=可得=,∴点坐标为(,),又=-+=(-)-,∴抛物线对称轴为直线=..(呼和浩特中考节选)在平面直角坐标系中,抛物线=++与轴交于点,其顶点记为,自变量=-和=对应的函数值相等.若点在直线:=-+上,点(,-)在抛物线上.求该抛物线的解析式.解:∵自变量=-和=对应的函数值相等,∴抛物线的对称轴为=.∵点在直线:=-+上,∴=-.设抛物线的解析式为=(-)-.将(,-)代入得:-=-,解得:=.∴抛物线的解析式为=(-)-,整理得:=-+..(连云港中考节选)如图,已知二次函数=++(≠)的图象经过点(,),(,),且与轴交于点,连接,,.()求此二次函数的关系式;()判断△的形状;若△的外接圆记为⊙,请直接写出圆心的坐标.解:()把点(,),(,)代入=++中,得解得∴所求函数关系式为:=-+;()△是直角三角形,过点作⊥轴于点,在=-+中,令=可得=,∴点的坐标为(,),∴=,∴∠=°.又∵点的坐标为(,),∴=,∴∠=°,∴∠=°-°-°=°,∴△是直角三角形,圆心的坐标为(,)..(德州中考)随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为处达到最高,水柱落地处离池中心.()请你建立适当的直角坐标系,并求出水柱抛物线的函数解析式;()求出水柱的最大高度.解:()如图,以水管与地面交点为原点,原点与水柱落地点所在直线为轴,水管所在直线为轴,建立平面直角坐标系.由题意可设抛物线的函数解析式为=(-)+(≤≤).抛物线过点(,)和(,),代入抛物线解析式得:解得∴抛物线的解析式为=-(-)+(≤≤),化为一般形式为:=-++(≤≤);()由()知抛物线的解析式为=-(-)+(≤≤);当=时,=,∴抛物线水柱的最大高度为.。
[初中数学]2018年中考数学特训方案(42份) 人教版39
![[初中数学]2018年中考数学特训方案(42份) 人教版39](https://img.taocdn.com/s3/m/eb9ffb6cc850ad02de804160.png)
题型7一次函数与反比例函数的图象与性质1.(2017佳木斯中考)如图,是反比例函数y1=kx和一次函数y2=mx+n的图象,若y1<y2,则相应的x的取值范围是(A)A.1<x<6 B.x<1 C.x<6 D.x>12.(2017连云港中考)设函数y=3x与y=-2x-6的图象的交点坐标为(a,b),则1a+2b的值是__-2__.3.(2017天水中考)如图所示,一次函数y=kx+b与反比例函数y=mx的图象交于A(2,4),B(-4,n)两点.(1)分别求出一次函数与反比例函数的解析式;(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.解:(1)将点A(2,4)代入y =mx ,得:m =8,∴反比例函数解析式为y =8x ,当x =-4时,y =-2,即n =-2;∴点B(-4,-2),将点A(2,4),B(-4,-2)代入y =kx +b ,得⎩⎨⎧2k +b =4,-4k +b =-2,解得⎩⎨⎧k =1,b =2,∴一次函数解析式为y =x +2; (2)由题意知BC =2, ∴S △ACB =12×2×6=6.4.(2017辽宁中考)如图,在平面直角坐标系xOy 中,双曲线y =kx 经过▱ABCD 的顶点B ,D.点D 的坐标为(2,1),点A 在y 轴上,且AD ∥x 轴,S ▱ABCD =5.(1)填空:点A 的坐标为________; (2)求双曲线和AB 所在直线的解析式.解:(1)(0,1); (2)∵双曲线y =kx 经过点D(2,1), ∴k =2×1=2,∴双曲线的解析式为y =2x .∵D(2,1),AD ∥x 轴, ∴AD =2.∵S ▱ABCD =5, ∴AE =52,∴OE =32,∴B 点纵坐标为-32.把y =-32代入y =2x 得,-32=2x ,解得x =-43,∴B ⎝⎛⎭⎫-43,-32, 设直线AB 的解析式为y =ax +b ,代入A(0,1),B ⎝⎛⎭⎫-43,-32得⎩⎪⎨⎪⎧b =1,-43a +b =-32, 解得⎩⎪⎨⎪⎧k =158,b =1.∴AB 所在直线的解析式为y =158x +1. 5.(2017河南中考)如图,一次函数y =-x +b 与反比例函数y =kx (x >0)的图象交于点A(m ,3)和B(3,1).(1)填空:一次函数的解析式为________,反比例函数的解析式为________; (2)点P 是线段AB 上一点,过点P 作PD ⊥x 轴于点D ,连接OP ,若△POD 的面积为S ,求S 的取值范围.解:(1)y =-x +4;y =3x;(2)由(1)得3m =3,∴m =1,则A(1,3). 设P(a ,-a +4)(1≤a ≤3),则S =12OD·PD =12a(-a +4)=-12(a -2)2+2.∵-12<0,∴当a =2时,S 有最大值2, 当a =1或3时,S 有最小值32,∴32≤S ≤2.。
[初中数学]2018年中考数学特训方案(42份) 人教版40
![[初中数学]2018年中考数学特训方案(42份) 人教版40](https://img.taocdn.com/s3/m/3ce6027cbe23482fb4da4c60.png)
题型8圆的证明与计算类型①与圆的基本性质有关的计算与证明1.(2017海南中考)如图,点A,B,C在⊙O上,AC∥OB,∠BAO=25°,则∠BOC 的度数为(B)A.25°B.50°C.60°D.80°2.(2017西宁中考)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC =30°.则CD的长为(C)A.15 B.2 5 C.215 D.83.(2017荆州中考)如图,A,B,C是⊙O上的三点,且四边形OABC是菱形.若点D 是圆上异于A,B,C的另一点,则∠ADC的度数是__60°或120°__.4.如图,已知四边形ABCD 内接于⊙O ,A 是BDC ︵的中点,AE ⊥AC 于点A ,与⊙O 及CB 的延长线交于点F ,E ,且BF ︵=AD ︵.(1)求证:△ADC ∽△EBA ;(2)如果AB =8,CD =5,求tan ∠CAD 的值.解:(1)∵四边形ABCD 内接于⊙O , ∴∠CDA =∠ABE.∵BF ︵=AD ︵, ∴∠DCA =∠BAE.∴△ADC ∽△EBA ; (2)∵A 是BDC ︵的中点, ∴AB ︵=AC ︵,∴AB =AC =8, ∵△ADC ∽△EBA ,∴∠CAD =∠AEB ,DC AB =ACAE ,即58=8AE ,∴AE =645, ∴tan ∠CAD =tan ∠AEC =AC AE =8645=58.5.(2017温州中考)如图,在△ABC 中,AC =BC ,∠ACB =90°,⊙O(圆心O 在△ABC 内部)经过B ,C 两点,交AB 于点E ,过点E 作⊙O 的切线交AC 于点F.延长CO 交AB 于点G ,作ED ∥AC 交CG 于点D.(1)求证:四边形CDEF 是平行四边形; (2)若BC =3,tan ∠DEF =2,求BG 的值.解:(1)连接CE,∵在△ABC中,AC=BC.∠ACB=90°,∴∠B=45°,∴∠COE=90°,又EO=EC,∴∠OEC=∠OCE=45°.∵EF是⊙O的切线,∠FEO=90°,∴∠FEC=∠OCE=45°,∴EF∥CD.又∵DE∥CF,∴四边形CDEF是平行四边形;(2)过G作GM∥AC于M.∴△GMB是等腰三角形,∴MB=GM.∵四边形CDEF是平行四边形,∴∠FCD=∠FED.∵∠ACD+∠GCB=∠GCB+∠CGM=90°,∴∠CGM=∠ACD=∠FED.∵tan∠DEF=2,∴tan∠CGM=CMGM=2,∴CM=2GM,∴CM+BM=2GM+GM=BC=3,∴GM=1,∴BG=2GM=2,6.(2017贵州中考)如图,C ,D 是半圆O 上的三等分点,直径AB =4,连接AD ,AC ,DE ⊥AB ,垂足为E ,DE 交AC 于点F.(1)求∠AFE 的度数;(2)求阴影部分的面积.(结果保留π和根号)解:(1)连接OD ,OC ,∵C ,D 是半圆O 上的三等分点,∴AD ︵=CD ︵=BC ︵, ∴∠AOD =∠DOC =∠COB =60°, ∴∠CAB =30°.∵DE ⊥AB ,∴∠AEF =90°,∴∠AFE =90°-30°=60°;(2)由(1)知,∠AOD =60°,∵OA =OD ,AB =4, ∴△AOD 是等边三角形,OA =2. ∵DE ⊥AO ,∴DE =3,∴S 阴影=S 扇形AOD -S △AOD =60π·22360-12×2×3=23π- 3.类型②与圆的切线有关的证明1.(2017张家界中考)在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.(1)求证:DF是⊙O的切线;(2)分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.解:(1)连接OD,∵AC=BC,OB=OD,∴∠ABC=∠A,∠ABC=∠ODB,∴∠A=∠ODB,∴OD∥AC,∵DF⊥AC,∴DF⊥OD.∵OD是⊙O的半径,∴DF是⊙O的切线;(2)∵AC=BC,∠A=60°,∴△ABC是等边三角形,∴∠ABC=60°.∵OD=OB,∴△OBD是等边三角形,∴∠BOD=60°.∵DF⊥OD,∴∠ODG=90°,∴∠G=30°,∴OG=2OD=2×6=12,∴DG=3OD=63,∴S阴影=S△ODG-S扇形OBD =12×6×63-60π×62360=183-6π.2.(2017咸宁中考)如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.(1)求证:DF 是⊙O 的切线; (2)若AE =4,cos A =25,求DF 的长.解:(1)连接OD ,作OG ⊥AC 于点G. ∵OB =OD , ∴∠ODB =∠B. 又∵AB =AC , ∴∠C =∠B , ∴∠ODB =∠C , ∴OD ∥AC. ∵DF ⊥AC , ∴DF ⊥OD.∵OD 是⊙O 的半径, ∴DF 是⊙O 的切线; (2)AG =12AE =2,∵cos A =AG OA =25,∴OA =AG cos A =225=5,∴OG =OA 2-AG 2=21, ∵∠ODF =∠DFG =∠OGF =90°, ∴四边形OGFD 为矩形,∴DF =OG =21.3.如图,AB 是以BC 为直径的半圆O 的切线,D 为半圆上一点,AD =AB ,AD ,BC 的延长线相交于点E.(1)求证:AD 是半圆O 的切线; (2)连接CD ,求证:∠A =2∠CDE ;(3)若∠CDE =27°,OB =2,求BD ︵的长.解:(1)连接OD ,BD , ∵AB 是半圆O 的切线,∴AB ⊥BC ,即∠ABO =90°. ∵AB =AD ,∴∠ABD =∠ADB , ∵OB =OD ,∴∠DBO =∠BDO ,∴∠ABD +∠DBO =∠ADB +∠BDO , ∴∠ADO =∠ABO =90°,∵OD 是半圆O 的半径,∴AD 是半圆O 的切线;(2)由(1)知,∠ADO =∠ABO =90°,∴∠A =360°-∠ADO -∠ABO -∠BOD =180°-∠BOD. ∵∠DOC =180°-∠BOD , ∴∠A =∠DOC.∵AD 是半圆O 的切线, ∴∠ODE =90°,∴∠ODC +∠CDE =90°. ∵BC 是半圆O 的直径, ∴∠ODC +∠BDO =90°, ∴∠BDO =∠CDE , ∵∠BDO =∠OBD , ∴∠DOC =2∠BDO , ∴∠DOC =2∠CDE ,∴∠A =2∠CDE ; (3)∵∠CDE =27°,∴∠DOC =2∠CDE =54°,∴∠BOD =180°-54°=126°, ∵OB =2,∴lBD ︵=126×π×2180=75π.4.(2017遵义中考)如图,PA ,PB 是⊙O 的切线,A ,B 为切点,∠APB =60°,连接PO 并延长与⊙O 交于C 点,连接AC ,BC.(1)求证:四边形ACBP 是菱形;(2)若⊙O 半径为1,求菱形ACBP 的面积.解:(1)连接AO ,BO.∵PA ,PB 是⊙O 的切线, ∴∠OAP =∠OBP =90°, PA =PB ,∠APO =∠BPO =12∠APB =30°,∴∠AOP =60°.∴∠ACP =12∠AOP =30°,∴∠ACP =∠APC ,∴AC =AP. 同理BC =PB ,∴AC =BC =BP =AP ,∴四边形ACBP 是菱形; (2)连接AB 交PC 于D.∴AD ⊥PC.∵OA =1,∠AOP =60°, ∴AD =OA·sin 60°=32, ∴PD =AD tan 30°=32,∴PC =2×32=3,AB =2×32=3,∴菱形ACBP 的面积=12AB·PC =3 32.5.(2017永州中考)如图,已知AB 是⊙O 的直径,过O 点作OP ⊥AB ,交弦AC 于点D ,交⊙O 于点E ,且使∠PCA =∠ABC.(1)求证:PC 是⊙O 的切线;(2)若∠P =60°,PC =2,求PE 的长.解:(1)连接OC.∵OB =OC ,∴∠ABC =∠OCB. 又∵∠PCA =∠ABC , ∴∠PCA =∠OCB.∵AB 为⊙O 直径,∴∠ACB =90°.∴∠ACO +∠OCB =90°,∴∠ACO +∠PCA =90°, 即∠OCP =90°,∴PC 是⊙O 的切线; (2)在Rt △PCO 中,tan P =OCPC ,∴OC =PC tan P =2tan 60°=23, sin P =OC OP,∴OP =OC sin P =2332=4,∴PE =OP -OE =OP -OC =4-2 3.6.(2017荆门中考)已知:如图,在△ABC 中,∠C =90°,∠CAB 的平分线AD 交BC 于点D ,过点D 作DE ⊥AD 交AB 于点E ,以AE 为直径作⊙O.(1)求证:BC 是⊙O 的切线;(2)若AC =3,BC =4,求BE 的长.解:(1)连接OD ,在Rt △ADE 中,点O 为AE 的中心, ∴DO =AO =EO =12AE ,∴点D 在⊙O 上,且∠DAO =∠ADO.又∵AD 平分∠CAB ,∴∠CAD =∠DAO , ∴∠ADO =∠CAD ,∴AC ∥DO.∵∠C =90°,∴∠ODB =90°,即OD ⊥BC. 又∵OD 为半径,∴BC 是⊙O 的切线;(2)∵在Rt △ACB 中,AC =3,BC =4,∴AB =5. 设OD =r ,则BO =5-r.∵OD ∥AC ,∴△BDO ∽△BCA , ∴DO AC =BO BA ,即r 3=5-r 5,解得:r =158, ∴BE =AB -AE =5-154=54.错题重做 原因:________________________________________________________________________________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 更正:________________________________________________________________________________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________类型③ 与弧长、半径、阴影面积有关的计算1.(2017东营中考)若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( C )A .60°B .90°C .120°D .180°2.(2017遵义中考)已知圆锥的底面积为9π cm 2,母线长为6 cm ,则圆锥的侧面积是( A )A .18π cm 2B .27π cm 2C .18 cm 2D .27 cm 23.(2017绥化中考)一个扇形的半径为3 cm ,弧长为2π cm ,则此扇形的面积为__3π__cm 2.(用含π的式子表示)4.(2017哈尔滨中考)已知扇形的弧长为4π,半径为8,则此扇形的圆心角为__90°__. 5.如图,⊙O 的半径为2,点A ,C 在⊙O 上,线段BD 经过圆心O ,∠ABD =∠CDB =90°,AB =1,CD =3,则图中阴影部分的面积为__53π__.6.如图,半圆O 的直径AB =2,弦CD ∥AB ,∠COD =90°,则图中阴影部分的面积为__π4__.7.(2017黔东南中考)如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.(1)求证:PT2=PA·PB;(2)若PT=TB=3,求图中阴影部分的面积.解:(1)连接OT.∵PT是⊙O的切线,∴PT⊥OT,∴∠PTO=90°,∴∠PTA+∠OTA=90°.∵AB是直径,∴∠ATB=90°,∴∠TAB+∠B=90°.∵OT=OA,∴∠OAT=∠OTA,∴∠PTA=∠B,∵∠P=∠P,∴△PTA∽△PBT,∴PTPB=PAPT,∴PT2=PA·PB.(2)∵TP=TB=3,∴∠P=∠B=∠PTA.∵∠TAB=∠P+∠PTA,∴∠TAB=2∠B,∵∠TAB+∠B=90°,∴∠TAB=60°,∠B=30°,∴tan B =AT TB =33,∴AT =1.∵OA =OT ,∠TAO =60°, ∴△AOT 是等边三角形, ∴S 阴=S 扇形OAT -S △AOT =60π×12360-34·12=π6-34.8.(2017孝感中考)如图,⊙O 的直径AB =10,弦AC =6,∠ACB 的平分线交⊙O 于点D ,过点D 作DE ∥AB 交CA 延长线于点E ,连接AD ,BD.(1)由AB ,BD ,AD ︵围成的曲边三角形的面积是________; (2)求证:DE 是⊙O 的切线; (3)求线段DE 的长. 解:(1)252+25π4;(2)连接OD ,∵AB 是⊙O 的直径,∴∠ACB =90°.∵CD 平分∠ACB , ∴∠BCD =∠ACD =12∠ACB =45°,∴∠AOD =90°,∴OD ⊥AB.∵DE∥AB,∴OD⊥DE,∴DE是⊙O的切线;(3)∵AB=10,AC=6,∴BC=AB2-AC2=8.过点A作AF⊥DE于点F.∵OD⊥DE,OD⊥AO,∴四边形AODF为矩形,又∵OA=OD,∴矩形AODF为正方形.∴AF=OD=FD=5,∴∠EAF=90°-∠CAB=∠ABC,∴tan∠EAF=tan∠CBA,∴EFAF=ACBC,即EF5=68,∴EF=154,∴DE=DF+EF=5+154=354.。
2018年中考数学特训方案(42份) 人教版(免费推荐下载)

题型解答题压轴之函数与几何综合类型①线段“最值”问题探究.如图,已知点是抛物线=上的一个点,点,的坐标分别为(,),(,),连接,,求+的最小值.解:作点关于轴的对称点′,则过点′平行于轴的直线为=-,过点作⊥于点,交抛物线于点,此时=,则点,,三点共线,∴+的最小值即为的长,∵(,),⊥轴,∴(,-).∴+=+==,∴+的最小值为..(温州中考)如图,过抛物线=-上一点作轴的平行线,交抛物线于另一点,交轴于点,已知点的横坐标为-.()求抛物线的对称轴和点的坐标;()在上任取一点,连接,作点关于直线的对称点;①连接,求的最小值;②当点落在抛物线的对称轴上,且在轴上方时,求直线的函数解析式.解:()∵的横坐标为-,代入抛物线解析式得=,∴(-,),对称轴=-=,∵点,关于对称轴对称,∴(,);()①如答图①,由题意点在以为圆心,为半径的圆上,∴当,,共线时,的最小值=-=-=-;②如答图②,当点在对称轴上时,在△中,==,=,∴===,∴点的坐标为(,).设==,在△中,=(-)+,∴=,∴.设直线的解析式为=+(≠),代入(,),得:解得∴直线的解析式为=-+..如图,已知一次函数=+的图象与二次函数=-++的图象′都经过点(,)和点,且图象′过点(-,).()求二次函数的最大值;()设使>成立的取值的所有整数和为,若是关于的方程+=的根,求的值;()若点,在图象′上,长度为的线段在线段上移动,与始终平行于轴,当四边形的面积最大时,在轴上求点,使+最小,求出点的坐标.解:()∵二次函数=-++经过点(,)与(-,),∴解得∴:=+;′:=-++=-(-)+.∴=;()联立与得:+=-++,解得=或=,当=时,=×+=,∴.∴使>成立的的取值范围为<<,∴=++=.代入方程得×+=,解得=,经检验,=是方程的解;()∵点,在直线:=+上,∴设,,其中>>.如答图①,过点作⊥于点,则=-,=(-).在△中,由勾股定理得:+=,即(-)+=(),解得-=,即=+.∴=,.当=时,=-++,∴(,-++),∴=(-++)-=-+;当=+时,=-(+)+(+)+=-+,∴(+,-+),∴=(-+)-=--+.四边形=(+)·=×=-++=-+,∴当=时,四边形的面积取得最大值,∴,.如答图②所示,过点关于轴的对称点′,则′;连接′,交轴于点.+=′+=′,由两点之间线段最短可知,此时+最小.设直线′的解析式为:=+(≠),把,代入解析式,得:解得∴直线′的解析式为=-.令=,得=,∴..如图①,在平面直角坐标系中,一块等腰直角三角板的直角顶点在轴上,坐标为(,-),另一顶点坐标为(-,),已知二次函数=++的图象经过,两点.现将一把直尺放置在直角坐标系中,使直尺的边′′∥轴且经过点,直尺沿轴正方向平移,当′′与轴重合时运动停止.()求点的坐标及二次函数的解析式;()若运动过程中直尺的边′′交边于点,交抛物线于点,求线段长度的最大值;()如图②,设点为直尺的边′′上的任一点,连接,,,为的中点,试探究:在直尺平移的过程中,当=时,线段,,之间的数量关系.请直接写出结论,并指出相应的点与抛物线的位置关系.(说明:点与抛物线的位置关系可分为三类,例如,图②中,点在抛物线内,点在抛物线上,点′在抛物线外.)解:()如图①,过点作⊥轴于点.由题意得:=,∠=∠=∠=°,∴∠+∠=∠+∠=°,∴∠=∠,∴△≌△,∴==,==,∴=+=,∴(-,-).将(-,),(-,-)代入抛物线解析式可得:解得∴抛物线的解析式为=+-;()设:=+,∵把(-,),(-,-)代入可得:解得∴:=--,∴设(,--),+()-)).∵=(记为),≥,∴线段长度=---=-+(-≤≤-),∴当=-时,线段长度的最大值为;()当点在抛物线外时,+≥;当点在抛物线上时,+=;当点在抛物线内时,+≥..(怀化中考)如图①,在平面直角坐标系中,已知抛物线=+-(≠)与轴交于(-,),(,)两点,与轴交于点.()求抛物线的函数解析式;()若点是轴上的一点,且以,,为顶点的三角形与△相似,求点的坐标;()如图②,∥轴与抛物线相交于点,点是直线下方抛物线上的动点,过点且与轴平行的直线与,分别交于点,,试探究当点运动到何处时,四边形的面积最大,求点的坐标及最大面积;()若点为抛物线的顶点,点(,)是该抛物线上的一点,在轴,轴上分别找点,,使四边形的周长最小,求出点,的坐标.解:()∵点(-,),(,)在抛物线=+-上,∴∴∴抛物线的解析式为=--;()令=,则=-,∴(,-),∴=,∴∠=∠=°,∴=,=,如图①,要使以,,为顶点的三角形与△相似,则有=或=,①当=时,==,∴(,);②当=时,∴=,∴=,∴.综上所述,的坐标为(,)或;()设(,--),∵∥轴,∴点的纵坐标为-,∵在抛物线上,∴--=-,∴=(舍)或=,∴(,-),∴=,设直线的解析式为=+(≠),∵(,),(,-),∴直线的解析式为=-,∴(,-),∴=--(--)=-+,∵∥轴,∥轴,∴⊥,∴四边形=·=-+,当=时,四边形的面积最大为.∴此时的坐标为;()如图,∵为抛物线的顶点,∴(,-),∴关于轴的对称点′(-,-),∵(,)在抛物线上,∴(,-),∴点关于轴的对称点′(,),连接′′,交轴于点,轴于点,则′′的长即为四边形周长的最小值.设直线′′的解析式为=+(≠),∴直线′′的解析式为=-,∴,.类型②图形面积存在性问题探究.(深圳中考)如图,抛物线=++(≠)经过点(-,),(,),交轴于点.()求抛物线的解析式;(用一般式表示)()点为轴右侧抛物线上一点,是否存在点使△=△?若存在请直接给出点坐标;若不存在请说明理由;()将直线绕点顺时针旋转°,与抛物线交于另一点,求的长.解:()∵抛物线=++经过点(-,),(,),∴解得∴抛物线的解析式为=-++;()存在满足条件的点,其坐标为(,)或(,)或(,-);()∵点为抛物线上一点,且在轴上,∴令=,则=.∴(,).∵=,=,=,=,∴==,==,∴+=,∴△为直角三角形,即⊥.如图,设直线与直线交于点,过点作⊥轴于点,由题意可知∠=°,∴∠=°,∴==,∴=+=.∵⊥,⊥,∴∥.∴=,即=,解得=,=,即=,解得=,∴(,),且(,),设直线解析式为=+(≠),则可得解得∴直线解析式为=-+,联立直线和抛物线解析式可得解得或∴(,-),∴==..如图,抛物线=+-(≠)经过点(,-),与轴的负半轴交于点,与轴交于点,且=,抛物线的顶点为点.()求这条抛物线的解析式;()连接,,,,求四边形的面积;()如果点在轴的正半轴上,且∠=∠,求点的坐标.解:()抛物线=+-与轴交于点.∴(,-),∴=.∵=,∴=.又点在轴的负半轴上,∴(-,).∴抛物线经过点(,-)和点(-,).∴解得∴抛物线的解析式为=--;()由=--,得顶点的坐标是(,-).连接.∵(,-),(,-),∴=,=,∴△=××=,△=××=,∴四边形=△+△=,()过点作⊥,垂足为点.∵(,-),(,-),∴==.又∵△=××=,∴=.在△中,∠=°,==,==,∴∠==.在△中,∠=°,∠=,∵∠=∠,∴∠=∠=,∴=,∴=,∴点的坐标为..如图①,在平面直角坐标系中,点(,-),点(,).△中,∠=°,=,=.直角边在轴上,且点与点重合.△沿轴正方向平行移动.当点运动到点时停止运动.解答下列问题:()如图②,当△运动到点与点重合时,设交于点,求∠的度数;()如图③,在△的运动过程中,当经过点时,求的长;()在△的运动过程中,设=,△与△重叠部分的面积为,请写出与之间的函数关系式,并求出面积的最大值.解:()∵(,-),(,),∴=,∴∠=∠=°.在△中,∠===,∴∠=°.∵∠+∠=∠,∴∠=°;()由题意可知∥,∴∠=∠=°,在△中,∠=°==,∴=,∴=;()当≤≤时,如图④,作⊥轴于点,作⊥于点,∵=,=,=,=,∴=-,==+-,∴△∽△,∴=,∴=,∴=-,∴=△-△=××-(--)×(-)=-++,最大=-;当<≤-时,=△-△=××-(+)=-+,最大=-;当-<≤时,如图③,=△=×(-)×(-)=(-),∴最大=-.类型③等腰三角形存在性问题探究.(昆明中考模拟)如图①,对称轴为直线=的抛物线经过(,),(,)两点,抛物线与轴的另一交点为.()求抛物线的解析式;()若点为第一象限内抛物线上的一点,设四边形的面积为,求的最大值;()如图②,若是线段上一动点,在轴上是否存在这样的点,使△为等腰三角形且△为直角三角形?若存在,求出点的坐标;若不存在,请说明理由.解:()由对称性得(-,),设抛物线的解析式为=(+)(-)(≠),把(,)代入抛物线解析式,得=-,=-,∴=-(+)(-),∴抛物线的解析式为:=-++;()如答图①,设点(,-++),过点作⊥轴,垂足为点,连接.∴=梯形+△=(-+++)+(-++)(-),=-++=-(-)+,∵-<,∴有最大值,且的最大值为;()存在点,使△为等腰三角形且△为直角三角形.分以下两种情况:①当∠=°时,如答图②所示,∵∠>°,∴只能=.设直线的解析式为=+(≠),把(,),(,)代入直线的解析式,得解得∴直线的解析式为=-+.设点坐标为(,-+),则=-+,=,=-.在△中,===.∵∥,∴△∽△,∴=,即=,∴=(-)=-.∴=-=-(-)=.∵=,∴=-+,∴==-,∴(-,).②当∠=°时,如答图③所示,∵∠=°,∴只能=.设点坐标为(,-+).在△和△中,∵∠=∠====,由①知=-,==,∴∠===,∴=-,∴=,∴,此时,=-=,=,∴===,∴=-=-=,∴.综上所述,满足条件的点的坐标为(-,)或..如图,抛物线=++(,,为常数,≠)经过点(-,),(,-),(,).()求抛物线的解析式;()如图,在直线下方的抛物线上是否存在点使四边形的面积最大?若存在,请求出点的坐标;若不存在,请说明理由;()若点为抛物线的对称轴上的一个动点,试指出△为等腰三角形的点一共有几个?并求出其中某一个点的坐标.解:()设抛物线的解析式为=(+)(-)(≠),把(,-)代入解析式得:(+)(-)=-,解得=,∴抛物线的解析式为=(+)(-)=--;()存在.如答图①,分别过点,向轴作垂线和,垂足分别为点,,设(,--),四边形的面积为,则=-++,=+,=-,=-=,=,∴=△+梯形+△=(-++)(+)+(-++)(-)+××=-++=-(-)+,∵-<,∴有最大值,当=时,有最大值为,这时--=-×-=-,∴(,-);()这样的点一共有个,如答图②,连接、,过点作⊥对称轴于点,抛物线对称轴交轴于点.=--=-;∵在对称轴上,∴设(<).∵△是等腰三角形,且=,∴由勾股定理得:=+,=+,即+(-)=(+)+,∴=-,∴..(南宁中考)如图,已知抛物线=--(≠)与坐标轴交于,,三点,其中(,),∠的平分线交轴于点,交于点,过点的直线与射线,分别交于点,.()直接写出的值、点的坐标及抛物线的对称轴;()点为抛物线的对称轴上一动点,若△为等腰三角形,求出点的坐标.解:()=-,(-,),抛物线的对称轴为直线=;()∵=,=,∴∠==,∴∠=°.∵为∠的平分线,∴∠=°.∴=°·==.∴点的坐标为(,).设点的坐标为(,).依据两点间的距离公式可知:=,=+,=+(-).当=时,=+,方程无解.当=时,=+(-),解得=或=,∴点的坐标为(,)或(,).当=时,+=+(-),解得=-.∴点的坐标为(,-).综上所述,点的坐标为(,)或(,)或(,-).类型④直角三角形存在性问题探究(枣庄中考)如图,直线=+与抛物线=++(≠)相交于和(,),点是线段上异于,的动点,过点作⊥轴于点,交抛物线于点.()求抛物线的解析式;()是否存在这样的点,使线段的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;()求△为直角三角形时点的坐标.解:()∵(,)在直线=+上,∴=+=,∴(,),∵和(,)在抛物线=++上,∴解得∴抛物线的解析式为=-+;()存在.设动点的坐标为(,+),则点的坐标为(,-+),∴=(+)-(-+)=-+-=-+,∵>,-<,∴当=时,线段有最大值为;()∵△为直角三角形,①若点为直角顶点,则∠=°.由题意易知,∥轴,∠=°,因此这种情形不存在;②若点为直角顶点,则∠=°,即⊥.∵直线的解析式为=+,∴设直线的解析式为=-+,把代入,得-+=,解得=,∴直线的解析式为:=-+.又抛物线的解析式为:=-+,联立直线和抛物线解析式,得-+=-+,解得:=或=(与点重合,舍去).∴(,),即点,点重合.当=时,=+=,∴(,);③若点为直角顶点,则∠=°,∵,∴点的纵坐标为=,代入抛物线解析式,得-+=,解得=(舍去)或=,当=时,=+=.∴.∴综上所述,点的坐标为(,)或.类型⑤相似三角形存在性问题探究.(渭滨一模)如图所示,抛物线=++经过,两点,,两点的坐标分别为(-,),(,-).()求抛物线的函数解析式;()点为抛物线的顶点,点为抛物线与轴的另一交点,点为轴上一点,且=,求出点的坐标;()在第()问的条件下,在直线上存在点,使得以点,,为顶点的三角形与△相似,请你直接写出所有满足条件的点的坐标.解:()∵抛物线=++经过(-,),(,-),∴解得∴抛物线的函数解析式为=--;()令--=,解得=-,=,则点的坐标为(,).∵=--=(-)-,∴点坐标为(,-).设点的坐标为(,),作⊥轴于点,∵=+=+,=+=(+)+,且=,∴+=+++,解得=-,∴点的坐标为(,-);()满足条件的点共有个,其坐标分别为,,(-,),(,-)..(鄂州中考)如图,在平面直角坐标系中,直线=+与轴交于点,与轴交于点.抛物线=++(≠)的对称轴是直线=-且经过,两点,与轴的另一交点为点.()①直接写出点的坐标;②求抛物线解析式;()若点为直线上方的抛物线上的一点,连接,.求△的面积的最大值,并求出此时点的坐标;()抛物线上是否存在点,过点作垂直轴于点,使得以点,,为顶点的三角形与△相似?若存在,求出点的坐标;若不存在,请说明理由.解:()①(,);②抛物线的解析式为=--+;()设.如图,过点作⊥轴交于点,∴(,+),∴=--+-=--.∵△=××==--=-(+)+,∴当=-时,△的面积有最大值是,此时(-,);()存在.∵点,在直线=+上,且点在轴上,点在轴上,∴当=时,=,当=时,=-,∴(,),(-,),又∵(,),∴=-+,∴×=×(-)=-,∴⊥,⊥轴.若以点,,为顶点的三角形与△相似,则=,=,设(,--+),∴(,),①=,∴=,∴=或=,∴(,)或(,-);②=,∴=,∴=或=-,∴(,-)或(-,).综上所述,点的坐标为(,)或(,-)或(,-)或(-,).类型⑥全等三角形存在性问题探究如图,在平面直角坐标系中,抛物线=++(≠)与轴的一个交点为(-,),与轴的交点为,对称轴是直线=,对称轴与轴交于点.()求抛物线的函数解析式;()经过,的直线平移后与抛物线交于点,与轴一个交点为,当以,,,为顶点的四边形是平行四边形时,求出点的坐标;()若点在轴上,在抛物线上是否存在点,使得△≌△?若存在,直接写出点的坐标;若不存在,请说明理由.解:()∵抛物线=++与轴的一个交点为(-,),对称轴是直线=,∴解得∴抛物线的函数解析式为=-++;()以,,,为顶点的四边形是平行四边形,应分∥,∥两种情况.如图.①当∥时.∵点和点(,)关于对称轴直线=对称,∴点的坐标为(,);②当∥时.∵点的纵坐标是-,点在抛物线上,∴-++=-,解得=+或-,∴点的坐标为(+,-)或(-,-),综上所述,点的坐标为(,)或(+,-)或(-,-);()存在,点的坐标为或或(-+,-+)或(--,--).类型⑦平行四边形及矩形、菱形、正方形存在性问题探究.如图,在平面直角坐标系中,已知抛物线=-++与轴交于,两点,点在这条抛物线上,点在轴上,如果以点,,,为顶点的四边形是平行四边形,求点的坐标.解:∵抛物线=-++与轴交于,两点,∴令=则-++=,解得=-或=,∴(-,),(,).①如答图①,当是对角线时,==,∵与互相平分,∴点与点关于的中点(,)对称,∴点的横坐标为,在=-++中令=,则=,∴(,);如答图②,答图③,当为边时,∥,==,∴点的横坐标为或-,∴(,-)或(-,-),综上所述,点的坐标为(,)或(,-)或(-,-)..(岳阳中考)如图,抛物线=++经过点(,),(,-),直线:=--交轴于点,且与抛物线交于,两点.为抛物线上一动点(不与,重合).()求抛物线的解析式;()当点在直线下方时,过点作∥轴交于点,∥轴交于点.求+的最大值;()设为直线上的点,以,,,为顶点的四边形能否构成平行四边形?若能,求出点的坐标;若不能,请说明理由.解:()把(,),(,-)代入=++得,解得∴抛物线的解析式为:=--;()设(,--),∵∥轴,∥轴,点,在直线上,∴,,∴+=-++----++=-++=-+.∵-<,∴当=时,+的最大值是;()能.理由:∵=--交轴于点,∴,∴=,设,①以为边,∴∥,=,∴,∴---++=,∴=,=(舍去),∴;②如图以为对角线,连接交于,∴=,=,∴.设,则,∴×=-,∵Δ<,∴此方程无实数根.综上所述,点的坐标为。
2018年中考数学特训方案(42份) 人教版10(免费推荐下载)
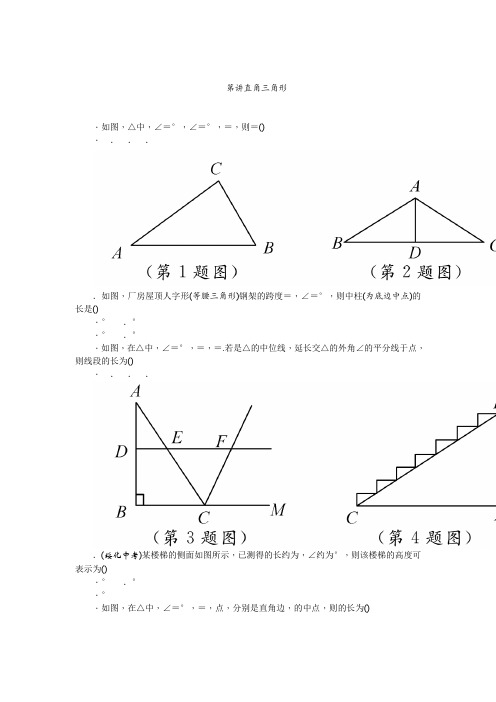
第讲直角三角形.如图,△中,∠=°,∠=°,=,则=().....如图,厂房屋顶人字形(等腰三角形)钢架的跨度=,∠=°,则中柱(为底边中点)的长是().°.°.°.°.如图,在△中,∠=°,=,=.若是△的中位线,延长交△的外角∠的平分线于点,则线段的长为().....(绥化中考)某楼梯的侧面如图所示,已测得的长约为,∠约为°,则该楼梯的高度可表示为().°.°.°.如图,在△中,∠=°,=,点,分别是直角边,的中点,则的长为()...+.(年中考试题)如图,四边形中,∥,∠+∠=°,且=.以,,为边向外作正方形,其面积分别为,,.若=,=,则的值为().....如图①,这个图案是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”.此图案的示意图如图②,其中四边形和四边形都是正方形,△,△,△,△是四个全等的直角三角形,若=,=,则的长为..(宿迁中考)如图,在△中,∠=°,点,,分别是,,的中点.若=,则线段的长是..如图,在△中,∠=°,,分别是,的中点,延长至点,使=,连接,,.若=,则=..(绥化中考)如图,顺次连接腰长为的等腰直角三角形各边中点得到第个小三角形,再顺次连接所得的小三角形各边中点得到第个小三角形,如此操作下去,则第个小三角形的面积为..如图,点是△内一点,连接,,并将,,,的中点,,,依次连接,得到四边形.()求证:四边形是平行四边形;()若为的中点,=,∠和∠互余,求的长度.解:()∵,分别是,的中点,∴∥,=,∵,分别是,的中点,∴∥,=.∴=,∥,∴四边形是平行四边形;()∵∠和∠互余,∴∠+∠=°,∴∠=°.∵为的中点,=,∴==.由()有四边形是平行四边形,∴==..(眉山中考)在如图的正方形网格中,每一个小正方形的边长为.格点三角形(顶点是网格线交点的三角形)的顶点,的坐标分别是(-,),(-,).()请在图中的网格平面内建立平面直角坐标系;()请画出△关于轴对称的△;()请在轴上求作一点,使△的周长最小,并写出点的坐标.解:()如图所示;()如图,即为所求;()作点关于轴的对称点′,连接′交轴于点,则点即为所求.设直线′的解析式为=+(≠),∵(-,-),′(,),∴解得∴直线′的解析式为=+,∴当=时,=,∴(,)..(徐州中考)如图,已知⊥,垂足为,=,=,将线段绕点按逆时针方向旋转°,得到线段,连接,.()线段=;()求线段的长度.解:();()作⊥于点.∵△是等边三角形,∴∠=°,又∵⊥,∴∠=∠-∠=°-°=°,∴△中,==,=·°=×=,∴=-=-=.∴△中,===..如图,在等腰△中,∠是直角,=,把一个°角的顶点放在处,两边分别与交于,两点.()将所得△以为中心,按逆时针方向旋转到△,试求证:△≌△;()若=,∶=∶,求的长.解:()由旋转知:△≌△.∴=,∠=∠.∵∠+∠=°,∴∠+∠=°,即∠=∠=°,而为公共边,∴△≌△();()连接.由△≌△知:∠=∠=°,∴∠=∠+∠=°,由△≌△知:=.设==,=,则在△中,=,∴==,∴=++=,∴=,∴==.。
[初中数学]2018年中考数学特训方案(42份) 人教版33
![[初中数学]2018年中考数学特训方案(42份) 人教版33](https://img.taocdn.com/s3/m/be19319b960590c69ec3765e.png)
专项三压轴题题型1选择题、填空题类型①函数综合问题1.(2017威海中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=a-b+cx在同一坐标系中的大致图象是(C)2.(2017荆州中考)规定:如果关于x 的一元二次方程ax 2+bx +c =0(a ≠0)有两个实数根,且其中一个根是另一个根的2倍,则称这样的方程为“倍根方程”.现有下列结论:①方程x 2+2x -8=0是倍根方程;②若关于x 的方程x 2+ax +2=0是倍根方程,则a =±3;③若关于x 的方程ax 2-6ax +c =0(a ≠0)是倍根方程,则抛物线y =ax 2-6ax +c 与x 轴的公共点的坐标是(2,0)和(4,0);④若点(m ,n)在反比例函数y =4x 的图象上,则关于x的方程mx 2+5x +n =0是倍根方程.上述结论中正确的有( C )A .①②B .③④C .②③D .②④3.(2017威海中考)如图,正方形ABCD 的边长为5,点A 的坐标为(-4.0),点B 在y 轴上,若反比例函数y =kx(k ≠0)的图象过点C ,则该反比例函数的解析式为( A )A .y =3xB .y =4xC .y =5xD .y =6x4.在一条笔直的公路上有A ,B ,C 三地,C 地位于A ,B 两地之间,甲、乙两车分别从A ,B 两地出发,沿这条公路匀速行驶至C 地停止.从甲车出发至甲车到达C 地的过程,甲、乙两车各自与C 地的距离y(km )与甲车行驶时间t(h )之间的函数关系如图表示,当甲车出发__32__h 时,两车相距350 km . 5.(2017南京中考)函数y 1=x 与y 2=4x 的图象如图所示,下列关于函数y =y 1+y 2的结论:①函数的图象关于原点中心对称;②当x <2时,y 随x 的增大而减小;③当x >0时,函数的图象最低点的坐标是(2,4),其中所有正确结论的序号是__①③__.6.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为__16__cm2.类型② 动点问题1.(2017咸宁中考)在平面直角坐标系xOy 中,将一块含有45°角的直角三角板如图放置,直角顶点C 的坐标为(1,0),顶点A 的坐标为(0,2),顶点B 恰好落在第一象限的双曲线上,现将直角三角板沿x 轴正方向平移,当顶点A 恰好落在该双曲线上时停止运动,则此点C 的对应点C′的坐标为( C )A .⎝⎛⎭⎫32,0B .(2,0)C .⎝⎛⎭⎫52,0 D .(3,0) 2.(2017济宁中考)如图甲,A ,B 是半径为1的⊙O 上两点,且OA ⊥OB ,点P 从点A出发,在⊙O 上以每秒一个单位长度的速度匀速运动,回到点A 运动结束,设运动时间为x(单位:s ),弦BP 的长为y ,那么图乙中可能表示y 与x 函数关系的是( D )A .①B .③C .②或④D .①或③3.(2017兰州中考)如图①,在矩形ABCD 中,动点E 从A 出发,沿AB →BC 方向运动,当点E 到达点C 时停止运动,过点E 做FE ⊥AE ,交CD 于F 点,设点E 运动路程为x ,FC =y ,如图②所表示的是y 与x 的函数关系的大致图象,当点E 在BC 上运动时,FC 的最大长度是25,则矩形ABCD 的面积是( B )A .235B .5C .6D .2544.(2017贵港中考)如图,在Rt △ABC 中,∠ACB =90°,将△ABC 绕点C 逆时针旋转得到△A′B′C ,M 是BC 的中点,P 是A′B′的中点,连接PM ,若BC =2,∠BAC =30°,则线段PM 的最大值是( B )A .4B .3C .2D .15.(2017岳阳中考)观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,…,根据这个规律,则21+22+23+24+…+22 017的末位数字是( B )A .0B .2C .4D .66.(2017内江中考)如图,过点A 0(2,0)作直线l :y =33x 的垂线,垂足为点A 1,过点A 1作A 1A 2⊥x 轴,垂足为点A 2,过点A 2作A 2A 3⊥l ,垂足为点A 3,…,这样依次下去,得到一组线段:A 0A 1,A 1A 2,A 2A 3,…,则线段A 2 016A 2 107的长为( B )A .⎝⎛⎭⎫32 2 015B .⎝⎛⎭⎫32 2 016C .⎝⎛⎭⎫32 2 017D .⎝⎛⎭⎫32 2 0187.(2017连云港中考)如图所示,一动点从半径为2的⊙O上的A0点出发,沿着射线A0O 方向运动到⊙O上的点A1处,再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处;接着又从A2点出发,沿着射线A2O方向运动到⊙O上的点A3处,再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处;……按此规律运动到点A2 017处,则点A2 017与点A0间的距离是(A)A.4 B.2 3 C.2 D.08.(2017海南中考)如图,AB 是⊙O 的弦,AB =5,点C 是⊙O 上的一个动点,且∠ACB=45°,若点M ,N 分别是AB ,AC 的中点,则MN 长的最大值是2.类型③ 规律探究1.(2017重庆中考)下列图象都是由相同大小的按一定规律组成的,其中第①个图形中一共有4颗,第②个图形中一共有11颗,第③个图形中一共有21颗,……,按此规律排列下去,第⑨个图形中的颗数为( B )A .116B .144C .145D .1502.(2017郴州中考)已知a 1=-32,a 2=55,a 3=-710,a 4=917,a 5=-1126,…,则a 8=__1765__.3.一列数a 1,a 2,a 3,…满足条件:a 1=12,a n =11-a n -1(n ≥2,且n 为整数),则a 2 016=__-1__.4.观察下列等式:第1个等式:a 1=11+2=2-1, 第2个等式:a 2=12+3=3-2, 第3个等式:a 3=13+2=2-3, 第4个等式:a 4=12+5=5-2, 按上述规律,回答以下问题: (1)请写出第n 个等式:a n =1n +n +1=n +1-n ;(2)a 1+a 2+a 3+…+a n =. 5.观察下列砌钢管的横截面图:则第n 个图的钢管数是__32n 2+32n __.(用含n 的式子表示)6.(2017齐齐哈尔中考)如图,在平面直角坐标系中,等腰直角三角形OA 1A 2的直角边OA 1在y 轴的正半轴上,且OA 1=A 1A 2=1,以OA 2为直角边作第二个等腰直角三角形OA 2A 3,以OA 3为直角边作第三个等腰直角三角形OA 2 017A 2 018,则点A 2 017的坐标为__(0,21__008)__.错题重做原因:________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________更正:________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________。
[初中数学]2018年中考数学特训方案(42份) 人教版
![[初中数学]2018年中考数学特训方案(42份) 人教版](https://img.taocdn.com/s3/m/dc65bbfa5022aaea998f0ffe.png)
题型2解答题压轴之函数与几何综合类型①线段“最值”问题探究1.如图,已知点P是抛物线y=14x2上的一个点,点D,E的坐标分别为(0,1),(1,2),连接PD,PE,求PD+PE的最小值.解:作点D关于x轴的对称点D′,则过点D′平行于x轴的直线l为y=-1,过点E作EH⊥l于点H,交抛物线于点P,此时PD=PH,则点P,E,H三点共线,∴PD+PE的最小值即为PH的长,∵E(1,2),EH⊥x轴,∴H(1,-1).∴PD+PE=PE+PH=EH=3,∴PD+PE的最小值为3.2.(2017温州中考)如图,过抛物线y=14x2-2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为-2.(1)求抛物线的对称轴和点B的坐标;(2)在AB上任取一点P,连接OP,作点C关于直线OP的对称点D;①连接BD,求BD的最小值;②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数解析式.解:(1)∵A 的横坐标为-2,代入抛物线解析式得y =5,∴A(-2,5),对称轴x =--22×14=4,∵点A ,B 关于对称轴对称, ∴B(10,5); (2)①如答图①,由题意点D在以O为圆心,OC为半径的圆上,∴当O,D,B共线时,BD的最小值=OB-OD=52+102-5=55-5;②如答图②,当点D在对称轴上时,在Rt△ODE中,OD=OC=5,OE=4,∴DE=OD2-OE2=52-42=3,∴点D 的坐标为(4,3).设PC =PD =x ,在Rt △PDK 中,x 2=(4-x)2+22, ∴x =52,∴P ⎝⎛⎭⎫52,5. 设直线PD 的解析式为y =kx +b(k ≠0),代入D(4,3),P ⎝⎛⎭⎫52,5得:⎩⎪⎨⎪⎧4k +b =3,52k +b =5,解得⎩⎨⎧k =-43,b =253.∴直线PD 的解析式为y =-43x +253.3.如图,已知一次函数y 1=12x +b 的图象l 与二次函数y 2=-x 2+mx +b 的图象C′都经过点B(0,1)和点C ,且图象C′过点A(2-5,0).(1)求二次函数的最大值;(2)设使y 2>y 1成立的x 取值的所有整数和为s ,若s 是关于x 的方程⎝⎛⎭⎫1+1a -1x +3x -3=0的根,求a 的值;(3)若点F ,G 在图象C′上,长度为5的线段DE 在线段BC 上移动,EF 与DG 始终平行于y 轴,当四边形DEFG 的面积最大时,在x 轴上求点P ,使PD +PE 最小,求出点P 的坐标.解:(1)∵二次函数y 2=-x 2+mx +b 经过点B(0,1)与A(2-5,0),∴⎩⎨⎧b =1,-(2-5)2+(2-5)m +b =0, 解得⎩⎪⎨⎪⎧m =4,b =1.∴l :y 1=12x +1;C ′:y 2=-x 2+4x +1=-(x -2)2+5. ∴y max =5;(2)联立y 1与y 2得:12x +1=-x 2+4x +1,解得x =0或x =72,当x =72时,y 1=12×72+1=114,∴C ⎝⎛⎫74,114.∴使y 2>y 1成立的x 的取值范围为0<x <72,∴s =1+2+3=6.代入方程得⎝⎛⎭⎫1+1a -1×6+36-3=0,解得a =17,经检验,a =17是方程的解;(3)∵点D ,E 在直线l :y 1=12x +1上,∴设D ⎝⎛⎭⎫p ,12p +1,E ⎝⎛⎭⎫q ,12q +1,其中q >p >0. 如答图①,过点E 作EH ⊥DG 于点H , 则EH =q -p ,DH =12(q -p).在Rt △DEH 中,由勾股定理得:EH 2+DH 2=DE 2,即(q -p)2+⎣⎡⎦⎤12(q -p )2=(5)2,解得q -p =2,即q =p +2. ∴EH =2,E ⎝⎛⎭⎫p +2,12p +2. 当x =p 时,y 2=-p 2+4p +1,∴G(p ,-p 2+4p +1),∴DG =(-p 2+4p +1)-⎝⎛⎭⎫12p +1=-p 2+72p ; 当x =p +2时,y 2=-(p +2)2+4(p +2)+1=-p 2+5, ∴F(p +2,-p 2+5),∴EF =(-p 2+5)-⎝⎛⎭⎫12p +2=-p 2-12p +3. S四边形DEFG=12(DG +EF)·EH =12⎣⎡⎦⎤⎝⎛⎭⎫-p 2+72p +(-p 2-12p +3)×2=-2p 2+3p +3=-2⎝⎛⎭⎫p -342+338,∴当p =34时,四边形DEFG 的面积取得最大值,∴D ⎝⎛⎭⎫34,118,E ⎝⎛⎭⎫114,198.如答图②所示,过点D 关于x 轴的对称点D′,则 D ′⎝⎛⎭⎫34,-118; 连接D′E ,交x 轴于点P. PD +PE =PD′+PE =D′E ,由两点之间线段最短可知,此时PD +PE 最小.设直线D′E 的解析式为:y =kx +b(k ≠0),把D ⎝⎛⎭⎫34,118,E ⎝⎛⎭⎫114,198代入解析式,得:⎩⎨⎧34k +b =-118,114k +b =198,解得⎩⎨⎧k =158,b =-8932, ∴直线D′E 的解析式为y =158x -8932. 令y =0,得x =8960,∴P ⎝⎛⎭⎫8960,0. 4.如图①,在平面直角坐标系中,一块等腰直角三角板ABC 的直角顶点A 在y 轴上,坐标为(0,-1),另一顶点B 坐标为(-2,0),已知二次函数y =32x 2+bx +c 的图象经过B ,C 两点.现将一把直尺放置在直角坐标系中,使直尺的边A′D′∥y 轴且经过点B ,直尺沿x 轴正方向平移,当A′D′与y 轴重合时运动停止.(1)求点C 的坐标及二次函数的解析式;(2)若运动过程中直尺的边A′D′交边BC 于点M ,交抛物线于点N ,求线段MN 长度的最大值;(3)如图②,设点P 为直尺的边A′D′上的任一点,连接PA ,PB ,PC ,Q 为BC 的中点,试探究:在直尺平移的过程中,当PQ =102时,线段PA ,PB ,PC 之间的数量关系.请直接写出结论,并指出相应的点P 与抛物线的位置关系.(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A 在抛物线内,点C 在抛物线上,点D′在抛物线外.)解:(1)如图①,过点C 作CD ⊥y 轴于点D.由题意得:BA =AC ,∠BAC =∠BOA =∠ADC =90°,∴∠ABO +∠BAO =∠BAO +∠CAD =90°,∴∠ABO =∠CAD ,∴△CDA ≌△AOB , ∴AD =BO =2,CD =AO =1, ∴OD =OA +AD =3, ∴C(-1,-3).将B(-2,0),C(-1,-3)代入抛物线解析式可得:⎩⎪⎨⎪⎧6-2b +c =0,32-b +c =-3,解得⎩⎪⎨⎪⎧b =32,c =-3,∴抛物线的解析式为y =32x 2+32x -3;(2)设l BC :y =kx +b ,∵把B(-2,0),C(-1,-3)代入可得:⎩⎨⎧0=-2k +b ,-3=-k +b , 解得⎩⎨⎧k =-3,b =-6,∴l BC :y =-3x -6,∴设M(x M ,-3x M -6),N ⎝⎛⎭⎫x N ,32x 2N +32x N -3. ∵x M =x N (记为x),y M ≥y N ,∴线段MN 长度=-3x -6-⎝⎛⎭⎫32x 2+32x -3=-32⎝⎛⎭⎫x +322+38(-2≤x ≤-1), ∴当x =-32时,线段MN 长度的最大值为38;(3)当点P 在抛物线外时,BP 2+CP 2≥PA 2;当点P 在抛物线上时,BP +CP =2AP ;当点P 在抛物线内时,BP 2+CP 2≥PA 2.5.(2017怀化中考)如图①,在平面直角坐标系中,已知抛物线y =ax 2+bx -5(a ≠0)与x 轴交于A(-1,0),B(5,0)两点,与y 轴交于点C.(1)求抛物线的函数解析式;(2)若点D 是y 轴上的一点,且以B ,C ,D 为顶点的三角形与△ABC 相似,求点D 的坐标;(3)如图②,CE ∥x 轴与抛物线相交于点E ,点H 是直线CE 下方抛物线上的动点,过点H 且与y 轴平行的直线与BC ,CE 分别交于点F ,G ,试探究当点H 运动到何处时,四边形CHEF 的面积最大,求点H 的坐标及最大面积;(4)若点K 为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x 轴,y 轴上分别找点P ,Q ,使四边形PQKM 的周长最小,求出点P ,Q 的坐标.解:(1)∵点A(-1,0),B(5,0)在抛物线y =ax 2+bx -5上,∴⎩⎨⎧a -b -5=0,25a +5b -5=0,∴⎩⎨⎧a =1,b =-4,∴抛物线的解析式为y =x 2-4x -5; (2)令x =0,则y =-5, ∴C(0,-5), ∴OC =OB ,∴∠OBC =∠OCB =45°, ∴AB =6,BC =52,如图①,要使以B ,C ,D 为顶点的三角形与△ABC 相似,则有AB CD =BC BC 或AB BC =BCCD ,①当AB CD =BCBC 时,CD =AB =6,∴D(0,1); ②当AB BC =BCCD 时,∴652=52CD ,∴CD =253,∴D ⎝⎛⎭⎫0,103.综上所述,D 的坐标为(0,1)或⎝⎛⎭⎫0,103; (3)设H(t ,t 2-4t -5),∵CE ∥x 轴,∴点E 的纵坐标为-5, ∵E 在抛物线上,∴x 2-4x -5=-5,∴x =0(舍)或x =4, ∴E(4,-5),∴CE =4,设直线BC 的解析式为y =kx +b(k ≠0), ∵B(5,0),C(0,-5),∴直线BC 的解析式为y =x -5, ∴F(t ,t -5),∴HF =t -5-(t 2-4t -5)=-⎝⎛⎭⎫t -522+254, ∵CE ∥x 轴,HF ∥y 轴,∴CE ⊥HF ,∴S 四边形CHEF =12CE·HF =-2⎝⎛⎭⎫t -522+252,当t =52时,四边形CHEF 的面积最大为252.∴此时H 的坐标为⎝⎛⎭⎫52,-354; (4)如图,∵K 为抛物线的顶点,∴K(2,-9),∴K关于y轴的对称点K′(-2,-9),∵M(4,m)在抛物线上,∴M(4,-5),∴点M关于x轴的对称点M′(4,5),连接K′M′,交x 轴于点P ,y 轴于点Q ,则K′M′的长即为四边形PQKM 周长的最小值. 设直线K′M′的解析式为y =kx +b(k ≠0), ∴直线K′M′的解析式为y =73x -133,∴P ⎝⎛⎭⎫137,0,Q ⎝⎛⎭⎫0,-133.类型② 图形面积存在性问题探究1.(2017深圳中考)如图,抛物线y =ax 2+bx +2(a ≠0)经过点A(-1,0),B(4,0),交y 轴于点C.(1)求抛物线的解析式;(用一般式表示)(2)点D 为y 轴右侧抛物线上一点,是否存在点D 使S △ABC =23S △ABD ?若存在请直接给出点D 坐标;若不存在请说明理由;(3)将直线BC 绕点B 顺时针旋转45°,与抛物线交于另一点E ,求BE 的长.解:(1)∵抛物线y =ax 2+bx +2经过点 A(-1,0),B(4,0),∴⎩⎨⎧a -b +2=0,16a +4b +2=0,解得⎩⎨⎧a =-12,b =32,∴抛物线的解析式为y =-12x 2+32x +2;(2)存在满足条件的点D ,其坐标为(1,3)或(2,3)或(5,-3);(3)∵点C 为抛物线上一点,且在y 轴上, ∴令x =0,则y =2.∴C(0,2).∵AO =1,OC =2,OB =4,AB =5,∴AC=12+22=5,BC=22+42=25,∴AC2+BC2=AB2,∴△ABC为直角三角形,即BC⊥AC.如图,设直线AC与直线BE交于点F,过点F作FM⊥x轴于点M,由题意可知∠FBC=45°,∴∠CFB=45°,∴CF=BC=25,∴AF=AC+CF=3 5.∵FM⊥AB,OC⊥AB,∴FM∥OC.∴AOOM=ACCF,即1OM=525,解得OM=2,OCFM=ACAF,即2FM=535,解得FM=6,∴F(2,6),且B(4,0),设直线BE 解析式为y =kx +m(k ≠0),则可得⎩⎨⎧2k +m =6,4k +m =0,解得⎩⎨⎧k =-3,m =12,∴直线BE 解析式为y =-3x +12,联立直线BE 和抛物线解析式可得⎩⎪⎨⎪⎧y =-3x +12,y =-12x 2+32x +2,解得⎩⎪⎨⎪⎧x =4,y =0或⎩⎨⎧x =5,y =-3, ∴E(5,-3),∴BE =(5-4)2+(-3)2=10.2.如图,抛物线y =ax 2+bx -5(a ≠0)经过点A(4,-5),与x 轴的负半轴交于点B ,与y 轴交于点C ,且OC =5OB ,抛物线的顶点为点D.(1)求这条抛物线的解析式;(2)连接AB ,BC ,CD ,DA ,求四边形ABCD 的面积;(3)如果点E 在y 轴的正半轴上,且∠BEO =∠ABC ,求点E 的坐标.解:(1)抛物线y =ax 2+bx -5与y 轴交于点C.∴C(0,-5), ∴OC =5.∵OC =5OB ,∴OB =1.又点B 在x 轴的负半轴上,∴B(-1,0). ∴抛物线经过点A(4,-5)和点 B(-1,0).∴⎩⎨⎧16a +4b -5=-5,a -b -5=0,解得⎩⎪⎨⎪⎧a =1,b =-4.∴抛物线的解析式为y =x 2-4x -5;(2)由y =x 2-4x -5,得顶点D 的坐标是(2,-9). 连接AC.∵A(4,-5),C(0,-5), ∴AC =4,OC =5,∴S △ABC =12×4×5=10,S △ACD =12×4×4=8,∴S 四边形ABCD =S △ABC +S △ACD =18,(3)过点C 作CH ⊥AB ,垂足为点H. ∵A(4,-5),C(0,-5), ∴AB =(4+1)2+52=5 2.又∵S △ABC =12×AB ×CH =10,∴CH =2 2.在Rt △BCH 中,∠BHC =90°,BC =OB 2+OC 2=26,BH =BC 2-CH 2=32, ∴tan ∠CBH =CH BH =23.在Rt △BOE 中,∠BOE =90°,tan ∠BEO =BOEO,∵∠BEO =∠ABC ,∴tan ∠BEO =tan ∠ABC =23,∴BO EO =23,∴EO =32,∴点E 的坐标为⎝⎛⎭⎫0,32. 3.如图①,在平面直角坐标系中,点A(0,-6),点B(6,0).Rt △CDE 中,∠CDE =90°,CD =4,DE =43.直角边CD 在y 轴上,且点C 与点A 重合.Rt △CDE 沿y 轴正方向平行移动.当点C 运动到点O 时停止运动.解答下列问题:(1)如图②,当Rt △CDE 运动到点D 与点O 重合时,设CE 交AB 于点M ,求∠BME 的度数;(2)如图③,在Rt △CDE 的运动过程中,当CE 经过点B 时,求BC 的长;(3)在Rt △CDE 的运动过程中,设AC =h ,△OAB 与△CDE 重叠部分的面积为S ,请写出S 与h 之间的函数关系式,并求出面积S 的最大值.解:(1)∵A(0,-6),B(6,0),∴OA=OB,∴∠OBA=∠OAB=45°.在Rt△CDE中,tan∠DEC=DCDE=443=33,∴∠DEC=30°.∵∠DEC+∠BME=∠OBA,∴∠BME=15°;(2)由题意可知DE∥OB,∴∠OBC=∠DEC=30°,在Rt △OBC 中,cos ∠OBC =cos 30°=OB BC =32,∴32=6BC,∴BC =43;(3)当0≤h ≤2时,如图④,作MN ⊥y 轴于点N ,作MF ⊥DE 于点F , ∵CD =4,DE =43,AC =h ,AN =NM , ∴CN =4-FM ,AN =MN =4+h -FM , ∴△CMN ∽△CED , ∴CN CD =MN DE, ∴4-FM 4=4+h -FM43, ∴FM =4-3+12h ,∴S =S △EDC -S △EFM=12×4×43-12(43-4-h)×(4-3+12h) =-1+34h 2+4h +8,S 最大=15-3;当2<h ≤6-23时, S =S △AOB -S △EFM=12×6×6-12h(h +3-12h) =-3+34h 2+18,S 最大=15-3;当6-23<h ≤6时,如图③, S =S △OBC =12×(6-h)×3(6-h)=32(6-h)2, ∴S 最大=143-36.类型③ 等腰三角形存在性问题探究1.(2016昆明中考模拟)如图①,对称轴为直线x =12的抛物线经过B(2,0),C(0,4)两点,抛物线与x 轴的另一交点为A.(1)求抛物线的解析式;(2)若点P 为第一象限内抛物线上的一点,设四边形COBP 的面积为S ,求S 的最大值; (3)如图②,若M 是线段BC 上一动点,在x 轴上是否存在这样的点Q ,使△MQC 为等腰三角形且△MQB 为直角三角形?若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)由对称性得A(-1,0),设抛物线的解析式为y=a(x+1)(x-2)(a≠0),把C(0,4)代入抛物线解析式,得4=-2a,a=-2,∴y=-2(x+1)(x-2),∴抛物线的解析式为:y=-2x2+2x+4;(2)如答图①,设点P(m,-2m2+2m+4),过点P作PD⊥x轴,垂足为点D,连接PB.∴S=S梯形CODP+S△PDB=12m(-2m2+2m+4+4)+12(-2m2+2m+4)(2-m),S=-2m2+4m+4=-2(m-1)2+6,∵-2<0,∴S有最大值,且S的最大值为6;(3)存在点Q,使△MQC为等腰三角形且△MQB为直角三角形.分以下两种情况:①当∠BQM=90°时,如答图②所示,∵∠CMQ >90°,∴只能CM =MQ. 设直线BC 的解析式为y =kx +b(k ≠0),把B(2,0),C(0,4)代入直线BC 的解析式,得⎩⎨⎧2k +b =0,b =4,解得⎩⎨⎧k =-2,b =4,∴直线BC 的解析式为y =-2x +4.设M 点坐标为(t ,-2t +4),则MQ =-2t +4,OQ =t ,BQ =2-t. 在Rt △OBC 中,BC=OB2+OC2=22+42=2 5.∵MQ∥OC,∴△BMQ∽△BCO,∴BMBC=BQBO,即BM25=2-t2,∴BM=5(2-t)=25-5t.∴CM=BC-BM=25-(25-5t)=5t.∵CM=MQ,∴5t=-2t+4,∴t=45+2=45-8,∴Q(45-8,0).②当∠QMB=90°时,如答图③所示,∵∠CMQ =90°,∴只能CM =MQ. 设M 点坐标为(t ,-2t +4). 在Rt △COB 和Rt △QMB 中, ∵tan ∠CBO =tan ∠MBQ =OC OB =MQ BM =42=2, 由①知BM =25-5t ,MQ =CM =5t , ∴tan ∠MBQ =MQ BM =5t25-5t =2,∴5t =45-25t ,∴t =43,∴M ⎝⎛⎭⎫43,43,此时,BM =25-5t =235,MQ =435,∴BQ =BM 2+MQ 2=1009=103, ∴OQ =BQ -OB =103-2=43,∴Q ⎝⎛⎭⎫-43,0. 综上所述,满足条件的点Q 的坐标为(45-8,0)或⎝⎛⎭⎫-43,0. 2.如图,抛物线y =ax 2+bx +c(a ,b ,c 为常数,a ≠0)经过点A(-1,0),B(5,-6),C(6,0).(1)求抛物线的解析式;(2)如图,在直线AB 下方的抛物线上是否存在点P 使四边形PACB 的面积最大?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)若点Q 为抛物线的对称轴上的一个动点,试指出△QAB 为等腰三角形的点Q 一共有几个?并求出其中某一个点Q 的坐标.解:(1)设抛物线的解析式为y =a(x +1)(x -6)(a ≠0), 把B(5,-6)代入解析式得:a(5+1)(5-6)=-6, 解得a =1,∴抛物线的解析式为y =(x +1)(x -6)=x 2-5x -6; (2)存在.如答图①,分别过点P,B向x轴作垂线PM和BN,垂足分别为点M,N,设P(m,m2-5m-6),四边形PACB的面积为S,则PM=-m2+5m+6,AM=m+1,MN=5-m,CN=6-5=1,BN=6,∴S=S△AMP+S梯形PMNB+S△BNC=12(-m 2+5m +6)(m +1)+12(6-m 2+5m +6)(5-m)+12×1×6 =-3m 2+12m +36 =-3(m -2)2+48,∵-3<0,∴S 有最大值,当m =2时,S 有最大值为48,这时m 2-5m -6=22-5×2-6=-12, ∴P(2,-12);(3)这样的Q 点一共有5个,如答图②,连接Q 3A 、Q 3B ,过点B 作BH ⊥对称轴于点H ,抛物线对称轴交x 轴于点E.y =x 2-5x -6=⎝⎛⎭⎫x -522-494; ∵Q 3在对称轴上,∴设Q 3⎝⎛⎭⎫52,y (y <0). ∵△Q 3AB 是等腰三角形,且Q 3A =Q 3B ,∴由勾股定理得:Q 3A 2=EA 2+Q 3E 2,Q 3B 2=Q 3H 2+BH 2,即⎝⎛⎭⎫722+(-y)2=(6+y)2+⎝⎛⎭⎫522,∴y =-52,∴Q 3⎝⎛⎭⎫52,-52.3.(2017南宁中考)如图,已知抛物线y=ax2-23ax-9a(a≠0)与坐标轴交于A,B,C三点,其中C(0,3),∠BAC的平分线AE交y轴于点D,交BC于点E,过点D的直线l 与射线AC,AB分别交于点M,N.(1)直接写出a 的值、点A 的坐标及抛物线的对称轴;(2)点P 为抛物线的对称轴上一动点,若△PAD 为等腰三角形,求出点P 的坐标. 解:(1)a =-13,A(-3,0),抛物线的对称轴为直线x =3;(2)∵OA =3,OC =3, ∴tan ∠CAO =OCOA =3,∴∠CAO =60°.∵AE 为∠BAC 的平分线, ∴∠DAO =30°. ∴DO =tan 30°·AO =33AO =1. ∴点D 的坐标为(0,1).设点P 的坐标为(3,t).依据两点间的距离公式可知:AD 2=4,AP 2=12+t 2,DP 2=3+(t -1)2. 当AD =PA 时,4=12+t 2,方程无解.当AD =DP 时,4=3+(t -1)2,解得t =2或t =0,∴点P 的坐标为(3,2)或(3,0).当AP =DP 时,12+t 2=3+(t -1)2,解得t =-4.∴点P 的坐标为(3,-4).综上所述,点P 的坐标为(3,2)或(3,0)或(3,-4).类型④ 直角三角形存在性问题探究(枣庄中考)如图,直线y =x +2与抛物线y =ax 2+bx +6(a ≠0)相交于A ⎝⎛⎭⎫12,52和B(4,m),点P 是线段AB 上异于A ,B 的动点,过点P 作PC ⊥x 轴于点D ,交抛物线于点C. (1)求抛物线的解析式;(2)是否存在这样的P 点,使线段PC 的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC 为直角三角形时点P 的坐标.解:(1)∵B(4,m)在直线y =x +2上, ∴m =4+2=6, ∴B(4,6),∵A ⎝⎛⎭⎫12,52和B(4,6)在抛物线y =ax 2+bx +6上, ∴⎩⎪⎨⎪⎧52=⎝⎛⎭⎫122a +12b +66=16a +4b +6解得⎩⎨⎧a =2,b =-8,∴抛物线的解析式为y =2x 2-8x +6;(2)存在.设动点P 的坐标为(n ,n +2),则C 点的坐标为(n ,2n 2-8n +6), ∴PC =(n +2)-(2n 2-8n +6) =-2n 2+9n -4 =-2⎝⎛⎭⎫n -942+498, ∵PC >0,-2<0,∴当n =94时,线段PC 有最大值为498;(3)∵△PAC 为直角三角形,①若点P 为直角顶点,则∠APC =90°.由题意易知,PC ∥y 轴,∠APC =45°,因此这种情形不存在; ②若点A 为直角顶点,则∠PAC =90°,即AC ⊥AB. ∵直线AB 的解析式为y =x +2, ∴设直线AC 的解析式为y =-x +b , 把A ⎝⎛⎭⎫12,52代入,得-12+b =52,解得b =3, ∴直线AC 的解析式为:y =-x +3. 又抛物线的解析式为:y =2x 2-8x +6,联立直线和抛物线解析式,得-x +3=2x 2-8x +6,解得:x =3或x =12(与点A 重合,舍去).∴C(3,0),即点C ,M 点重合. 当x =3时,y =x +2=5, ∴P 1(3,5);③若点C 为直角顶点,则∠ACP =90°,∵A ⎝⎛⎭⎫12,52,∴点C 的纵坐标为y =52,代入抛物线解析式,得2x 2-8x +6=52,解得x =12(舍去)或x=72, 当x =72时,y =x +2=112.∴P 2⎝⎛⎭⎫72,112.∴综上所述,点P 的坐标为(3,5)或⎝⎛⎭⎫72,112.类型⑤ 相似三角形存在性问题探究1.(2017渭滨一模)如图所示,抛物线y =x 2+bx +c 经过A ,B 两点,A ,B 两点的坐标分别为(-1,0),(0,-3).(1)求抛物线的函数解析式;(2)点E 为抛物线的顶点,点C 为抛物线与x 轴的另一交点,点D 为y 轴上一点,且DC =DE ,求出点D 的坐标;(3)在第(2)问的条件下,在直线DE 上存在点P ,使得以点C ,D ,P 为顶点的三角形与△DOC 相似,请你直接写出所有满足条件的点P 的坐标.解:(1)∵抛物线y =x 2+bx +c 经过A(-1,0), B(0,-3),∴⎩⎨⎧1-b +c =0,c =-3,解得⎩⎨⎧b =-2,c =-3,∴抛物线的函数解析式为y =x 2-2x -3; (2)令x 2-2x -3=0, 解得x 1=-1,x 2=3, 则点C 的坐标为(3,0).∵y =x 2-2x -3=(x -1)2-4,∴点E 坐标为(1,-4).设点D 的坐标为(0,m),作EF ⊥y 轴于点F , ∵DC 2=OD 2+OC 2=m 2+32, DE 2=DF 2+EF 2=(m +4)2+12, 且DC =DE ,∴m 2+9=m 2+8m +16+1, 解得m =-1,∴点D 的坐标为(0,-1);(3)满足条件的点P 共有4个,其坐标分别为⎝⎛⎭⎫-13,0,⎝⎛⎭⎫13,-2,(-3,8),(3,-10). 2.(鄂州中考)如图,在平面直角坐标系xOy 中,直线y =12x +2与x 轴交于点A ,与y轴交于点C.抛物线y =ax 2+bx +c(a ≠0)的对称轴是直线x =-32且经过A ,C 两点,与x 轴的另一交点为点B.(1)①直接写出点B 的坐标;②求抛物线解析式;(2)若点P 为直线AC 上方的抛物线上的一点,连接PA ,PC.求△PAC 的面积的最大值,并求出此时点P 的坐标;(3)抛物线上是否存在点M ,过点M 作MN 垂直x 轴于点N ,使得以点A ,M ,N 为顶点的三角形与△ABC 相似?若存在,求出点M 的坐标;若不存在,请说明理由.解:(1)①B(1,0);②抛物线的解析式为y =-12x 2-32x +2;(2)设P ⎝⎛⎭⎫m ,-12m 2-32m +2. 如图,过点P 作PQ ⊥x 轴交AC 于点Q ,∴Q(m ,12m +2),∴PQ =-12m 2-32m +2-⎝⎛⎭⎫12m +2 =-12m 2-2m.∵S △PAC =12×PQ ×4=2PQ =-m 2-4m=-(m +2)2+4,∴当m =-2时,△PAC 的面积有最大值是4, 此时P(-2,3); (3)存在.∵点A ,C 在直线y =12x +2上,且点A 在x 轴上,点C 在y 轴上,∴当x =0时,y =2,当y =0时,x =-4, ∴C(0,2),A(-4,0),又∵B(1,0),∴y BC =-2x +2, ∴k AC ×k BC =12×(-2)=-1,∴AC ⊥BC ,MN ⊥x 轴.若以点A ,M ,N 为顶点的三角形与△ABC 相似, 则MN NA =AC BC ,MN NA =BCAC, 设M(2t ,-2t 2-3t +2), ∴N(2t ,0), ①|2t 2+3t -22t +4|=525,∴|2t -12|=12,∴t =0或t =1,∴M(0,2)或(2,-3); ②|2t 2+3t -22t +4|=255,∴|2t -12|=2,∴t =52或t =-32,∴M(5,-18)或(-3,2).综上所述,点M 的坐标为(0,2)或(2,-3)或(5,-18)或(-3,2).类型⑥ 全等三角形存在性问题探究如图,在平面直角坐标系中,抛物线y =ax 2+bx +4(a ≠0)与x 轴的一个交点为A(-2,0),与y 轴的交点为C ,对称轴是直线x =3,对称轴与x 轴交于点B.(1)求抛物线的函数解析式;(2)经过B ,C 的直线l 平移后与抛物线交于点M ,与x 轴一个交点为N ,当以B ,C ,M ,N 为顶点的四边形是平行四边形时,求出点M 的坐标;(3)若点D 在x 轴上,在抛物线上是否存在点P ,使得△PBD ≌△PBC ?若存在,直接写出点P 的坐标;若不存在,请说明理由.解:(1)∵抛物线y =ax 2+bx +4与x 轴的一个交点为A(-2,0),对称轴是直线x =3, ∴⎩⎪⎨⎪⎧4a -2b +4=0,-b 2a =3,解得⎩⎨⎧a =-14,b =32,∴抛物线的函数解析式为y =-14x 2+32x +4;(2)以B ,C ,M ,N 为顶点的四边形是平行四边形,应分CM ∥BN ,CN ∥BM 两种情况.如图.①当CM ∥BN 时.∵点M 和点C(0,4)关于对称轴直线x =3对称, ∴点M 的坐标为(6,4);②当CN ∥BM 时.∵点M 的纵坐标是-4,点M 在抛物线上,∴-14x 2+32x +4=-4, 解得x =3+41或3-41,∴点M 的坐标为(3+41,-4)或(3-41,-4),综上所述,点M 的坐标为(6,4)或(3+41,-4)或(3-41,-4);(3)存在,点P 的坐标为⎝⎛⎭⎪⎫4+26,-1+262或⎝ ⎛⎭⎪⎫4-26,26-12或(-1+41,-8+241)或(-1-41,-8-241).类型⑦ 平行四边形及矩形、菱形、正方形存在性问题探究1.如图,在平面直角坐标系中,已知抛物线y =-x 2+2x +3与x 轴交于A ,B 两点,点M 在这条抛物线上,点P 在y 轴上,如果以点P ,M ,A ,B 为顶点的四边形是平行四边形,求点M 的坐标.解:∵抛物线y=-x2+2x+3与x轴交于A,B两点,∴令y=0则-x2+2x+3=0,解得x=-1或x=3,∴A(-1,0),B(3,0).①如答图①,当PM是对角线时,PM=AB=4,∵PM与AB互相平分,∴点M与点P关于AB的中点(1,0)对称,∴点M的横坐标为2,在y=-x2+2x+3中令x=2,则y=3,∴M(2,3);如答图②,答图③,当PM为边时,PM∥AB,PM=AB=4,∴点M的横坐标为4或-4,∴M(4,-5)或(-4,-21),综上所述,点M的坐标为(2,3)或(4,-5)或(-4,-21).2.(2017岳阳中考)如图,抛物线y=23x2+bx+c经过点B(3,0),C(0,-2),直线l:y=-23x-23交y轴于点E,且与抛物线交于A,D两点.P为抛物线上一动点(不与A,D重合).(1)求抛物线的解析式;(2)当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N.求PM +PN的最大值;(3)设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.解:(1)把B(3,0),C(0,-2)代入y =23x 2+bx +c 得,⎩⎪⎨⎪⎧23×32+3b +c =0,c =-2,解得⎩⎪⎨⎪⎧b =-43,c =-2,∴抛物线的解析式为:y =23x 2-43x -2; (2)设P(m ,23m 2-43m -2), ∵PM ∥x 轴,PN ∥y 轴,点M ,N 在直线AD 上,∴N ⎝⎛⎭⎫m ,-23m -23, M ⎝⎛⎭⎫-m 2+2m +2,23m 2-43m -2, ∴PM +PN =-m 2+2m +2-m -23m -23-23m 2+43m +2=-53m 2+53m +103=-53⎝⎛⎭⎫m -122+154. ∵-53<0, ∴当m =12时,PM +PN 的最大值是154;(3)能.理由:∵y =-23x -23交y 轴于点E , ∴E ⎝⎛⎭⎫0,-23, ∴CE =43, 设P ⎝⎛⎭⎫m ,23m 2-43m -2, ①以CE 为边,∴CE ∥PF ,CE =PF ,∴F ⎝⎛⎭⎫m ,-23m -23, ∴-23m -23-23m 2+43m +2=43, ∴m =1,m =0(舍去),∴F ⎝⎛⎭⎫1,-43; ②如图以CE 为对角线,连接PF 交CE 于G , ∴CG =GE ,PG =FG ,∴G ⎝⎛⎭⎫0,-43.设P ⎝⎛⎭⎫m ,23m 2-43m -2,则F ⎝⎛⎭⎫-m ,23m -23, ∴12×⎝⎛⎭⎫23m 2-43m -2+23m -23=-43, ∵Δ<0,∴此方程无实数根.综上所述,点F 的坐标为。
[初中数学]2018年中考数学特训方案(42份) 人教版38
![[初中数学]2018年中考数学特训方案(42份) 人教版38](https://img.taocdn.com/s3/m/6bc4d164a8956bec0975e361.png)
题型6平行四边形、矩形、菱形、正方形的判定与性质1.(2017怀化中考)如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周长为(C)A.20 B.18 C.16 D.152.(2017荆州中考)如图,将边长为8 cm的正方形ABCD折叠,使点D落在BC边的中点E 处,点A落在F处,折痕为MN,则线段CN的长是(A)A.3 cm B.4 cm C.5 cm D.6 cm3.(2017哈尔滨中考)如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为__125__°.4.(2017北京中考)如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.(1)求证:四边形BCDE为菱形;(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.解:(1)∵∠ABD =90°,E 为AD 中点,∴在Rt △ABD 中,AD =2BE.又∵AD =2BC ,∴BC =ED.∵AD ∥BC ,∴ED ∥BC ,∴四边形BCDE 是菱形;(2)∵AD ∥BC ,AC 平分∠BAD ,∴∠BAC =∠DAC =∠BCA ,∴BA =BC =1.∵AD =2BC =2,∴sin ∠ADB =12,∴∠ADB =30°, ∴∠DAC =30°,∠ADC =60°.∴∠ACD =180°-30°-60°=90°.在Rt △ACD 中,∵AD =2,CD =1,∴AC = 3.5.如图,抛物线y =x 2+bx +c 与直线y =12x -3交于A ,B 两点,其中点A 在y 轴上,点B 坐标为(-4,-5),点P 为y 轴左侧的抛物线上一动点,过点P 作PC ⊥x 轴于点C ,交AB 于点D.(1)求抛物线的解析式;(2)以O ,A ,P ,D 为顶点的平行四边形是否存在?如存在,求点P 的坐标;若不存在,说明理由.解:(1)∵直线y =12x -3与抛物线交于A ,B 两点,其中点A 在y 轴上, ∴A(0,-3).∵B(-4,-5),把A(0,-3),B(-4,-5)代入y =x 2+bx +c ,得⎩⎨⎧c =-3,16-4b +c =-5,解得⎩⎪⎨⎪⎧b =92,c =-3,∴抛物线解析式为y =x 2+92x -3; (2)存在,设P ⎝⎛⎭⎫m ,m 2+92m -3(m <0), ∴D ⎝⎛⎭⎫m ,12m -3,∴PD =|m 2+4m|∵PD ∥AO ,∴当PD =OA =3时,就存在以O ,A ,P ,D 为顶点的平行四边形,∴|m 2+4m|=3,①当m 2+4m =3时,∴m 1=-2-7,m 2=-2+7(舍),∴m 2+92m -3=-1-72, ∴P ⎝⎛⎭⎫-2-7,-1-72, ②当m 2+4m =-3时,∴m 1=-1,m 2=-3,ⅰ.m 1=-1,∴m 2+92m -3=-132, ∴P ⎝⎛⎭⎫-1,-132; ⅱ.m 2=-3,∴m 2+92m -3=-152, ∴P ⎝⎛⎭⎫-3,-152. ∴综上所述,点P 的坐标为⎝⎛⎭⎫-2-7,-1-72或⎝⎛⎭⎫-1,-132或⎝⎛⎭⎫-3,-152. 错题重做原因:________________________________________________________________________________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ 更正:________________________________________________________________________________________________________________________________________________ ________________________________________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题型一次函数与反比例函数的图象与性质
.(佳木斯中考)如图,是反比例函数=和一次函数=+的图象,若<,则相应的的取值范围是()
.<<.<.<.>
.(连云港中考)设函数=与=--的图象的交点坐标为(,),则+的值是-.
.(天水中考)如图所示,一次函数=+与反比例函数=的图象交于(,),(-,)两点.()分别求出一次函数与反比例函数的解析式;
()过点作⊥轴,垂足为点,连接,求△的面积.
解:()将点(,)代入=,得:=,
∴反比例函数解析式为=,
当=-时,=-,
即=-;
∴点(-,-),
将点(,),(-,-)代入=+,
得解得
∴一次函数解析式为=+;
()由题意知=,
∴△=××=.
.(辽宁中考)如图,在平面直角坐标系中,双曲线=经过▱的顶点,.点的坐标为(,),=.
点在轴上,且∥轴,
▱
()填空:点的坐标为;
()求双曲线和所在直线的解析式.
解:()(,);
()∵双曲线=经过点
(,),
∴=×=,
∴双曲线的解析式为=.
∵(,),∥轴,
∴=.
=,
∵
▱
∴=,
∴=,
∴点纵坐标为-.
把=-代入=得,-=,解得=-,
∴,
设直线的解析式为=+,
代入(,),得
解得
∴所在直线的解析式为=+.
.(河南中考)如图,一次函数=-+与反比例函数=(>)的图象交于点(,)和(,).
()填空:一次函数的解析式为,反比例函数的解析式为;
()点是线段上一点,过点作⊥轴于点,连接,若△的面积为,求的取值范围.解:()=-+;=;
()由()得=,∴=,则(,).
设(,-+)(≤≤),则
=·=(-+)=-(-)+.
∵-<,
∴当=时,有最大值,
当=或时,有最小值,
∴≤≤.。
