【浙教版】八年级数学上1.5 三角形全等的判定(4)同步练习(含答案)
浙教版初中数学八年级上册 1.5 三角形全等的判定同步练习题测试卷题

重点知识精选
掌握知识点,多做练习题,基础知识很重要! 浙教版初中数学 和你一起共同进步学业有成!
1.5 三角形全等的判定
一、选择题:
1、下 列各组条件中能判定△ABC≌△DEF 的是( )
A、AB=DE,BC=EF,∠A=∠D
B、∠A=∠D,∠C=∠ F,AC=EF
C、AB=DE,BC=EF,ΔABC 的周长等于 ΔDEF 的周长 D、∠ A=∠D,∠B=∠ E, ∠C=∠F
)个.
A. 4 B. 3 C. 2
D. 1
C
E 1 A 2
B
D
5、如图,已知 ∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其
中能使 ΔABC≌ΔAED 的条件有(
)个.
A.4
B.3
C.2
D.1
C
E
1 A
2 B
D
6、在△ABC 和△ A‘B’C‘ 中,①AB= A‘B’,②BC= B’C‘③AC= A‘C‘ ④∠A=∠ A‘ ⑤∠B=∠ B’
C、∠A=∠A / ,AB= A / B / ,BC= B / C / D、AB= A / B / , AC=A / C / ,BC= B / C /
4、如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其
中能使 ΔABC≌ΔAED 的条件有(
已知: EG∥AF 求证:
相信自己,就能走向成功的第一步 教师不光要传授知识,还要告诉学生学会生活。数学思维
可以让他们更理性地看待人生
6、如图,Rt ABC 中,直角边 、 ,斜边
7、如图,AB BE 于 B,DE BE 于 E,
全等三角形 浙教版八年级数学上册同步练习卷(含解析)

1.4 全等三角形同步练习卷一.选择题1.如果△ABC与△DEF是全等形,则有()(1)它们的周长相等;(2)它们的面积相等;(3)它们的每个对应角都相等;(4)它们的每条对应边都相等.A.(1)(2)(3)(4)B.(1)(2)(3)C.(1)(2)D.(1)2.如图,已知CB=DB,△ABC≌△ABD,则∠C的对应角为()A.∠DAB B.∠D C.∠ABD D.∠CAD3.如图是两个全等三角形,则∠1的度数为()A.48°B.60°C.62°D.72°4.如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为()A.15°B.20°C.25°D.30°5.如图,若△ABC≌△DEF,BC=6,EC=4,则CF的长为()A.1B.2C.2.5D.36.已知,△ABC≌△DEF,且△ABC的周长为20,AB=8,BC=3,则DF等于()A.3B.5C.9D.117.如图,已知△OAB≌△OCD,若OA=4,∠AOB=35°,∠OCA=62°,则下列结论不一定正确的是()A.∠BDO=62°B.∠BOC=21°C.OC=4D.CD∥OA8.如图,锐角△ABC中,F、G分别是AB、AC边上的点,△ACF≌△ADF,△ABG≌△AEG,且DF∥BC∥GE,BG、CF交于点H,若∠BAC=40°,则∠BHC的大小是()A.95°B.100°C.105°D.110°二.填空题9.如图中有6个条形方格图,图上由实线围成的图形与(1)是全等形的有.10.如图,△ABC≌△AED,AE=2cm,∠D=30°,∠B=60°,则∠C=;∠DAE =;BC=.11.如图是由6个边长相等的正方形组合成的图形,∠1+∠2+∠3=.12.如图,△ABD和△ACE全等,点B和点C对应.AB=8,BD=7,AE=3,则CD=.13.如图,△ABC≌△ADE,且∠EAB=112°,则∠EFC=度.14.三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于.三.解答题15.如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.16.如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.17.如图,△ABC≌△ADE,∠B=10°,∠AED=20°,AB=4cm,点C为AD中点.(1)求∠BAE的度数和AE的长.(2)延长BC交ED于点F,则∠DFC的大小为度.18.如图所示,已知△ABD≌△CFD,AD⊥BC于D.(1)求证:CE⊥AB;(2)已知BC=7,AD=5,求AF的长.参考答案一.选择题1.解:根据全等形的概念可以判定:(1)(2)(3)(4)都成立.故选:A.2.解:∵CB=DB,△ABC≌△ABD,∴∠C=∠D,故选:B.3.解:∵∠B=48°,∠C=60°,∴∠A=180°﹣48°﹣60°=72°,∵两个三角形全等,∴∠1=∠A=72°,故选:D.4.解:∵△ADB≌△EDB≌△EDC∴∠A=∠BED=∠CED,∠ABD=∠EBD=∠C∵∠BED+∠CED=180°∴∠A=∠BED=∠CED=90°在△ABC中,∠C+2∠C+90°=180°∴∠C=30°故选:D.5.解:∵△ABC≌△DEF,∴BC=EF,∵BC=6,EC=4,∴EF=6,∴CF=EF﹣EC=6﹣4=2,故选:B.6.解:∵△ABC的周长为20,AB=8,BC=3,∴AC=20﹣3﹣8=9,∵△ABC≌△DEF,∴DF=AC=9,故选:C.7.解:A、∵△OAB≌△OCD,∴OA=OC,OB=OD,∠COD=∠AOB,∴∠OAC=∠OCA=62°,∠OBD=∠ODB,∠BOD=∠AOC,∴∠AOC=180°﹣∠OAC﹣∠OCA=56°,∴∠BOD=∠AOC=56°,∴∠BDO=×(180°﹣56°)=62°,故本选项说法正确,不符合题意;B、∵∠AOC=56°,∠AOB=35°,∴∠BOC=56°﹣35°=21°,故本选项说法正确,不符合题意;C、∵△OAB≌△OCD,OA=4,∴OC=OA=4,故本选项说法正确,不符合题意;D、∵∠AOC=56°,∠OCD不一定是56°,∴CD与OA不一定平行,故本选项说法错误,符合题意;故选:D.8.解:延长EG交AB于Q,交AD于P,∵△ACF≌△ADF,△ABG≌△AEG,∠BAC=40°,∴∠DAF=∠BAC=40°,∠EAG=∠BAC=40°,∠D=∠ACF,∠E=∠ABG,∴∠P AE=120°,∴∠APE+∠E=60°,∵DF∥EP,∴∠APE=∠D,∴∠APE=∠ACF,∴∠ABG+∠ACF=60°,∵∠BFH=∠BAC+∠ACF,∴∠BHC=∠ABG+∠BFH=∠ABG+∠BAC+∠ACF=60°+40°=100°,故选:B.二.填空题9.解:由图可知,图上由实线围成的图形与(1)是全等形的有(2),(3),(6),故答案为:(2),(3),(6),10.解:∵△ABC≌△AED,∴∠C=∠D=30°,∠DAE=∠BAC,AB=AE=2cm,∵∠B=60°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣30°=90°,∴∠DAE=90°,在Rt△ABC中,BC=AB=2×2=4cm.故答案为:30°;90°;4cm.11.解:如图,根据题意得DE=BC,EC=AB,GF=GC,∠DEC=∠ABC=∠FGC=90°,∴△CGF为等腰直角三角形,∴∠2=45°,在△ABC和△CED中,,∴△ABC≌△CED(SAS),∴∠1=∠DCE,∵∠DCE+∠3=90°,∴∠1+∠3=90°,∴∠1+∠2+∠3=90°+45°=135°.故答案为135°.12.解:∵△ABD≌△ACE,点B和点C对应,∴AB=AC,AD=AE,∴AB﹣AE=AC﹣AD,即CD=BE,已知AB=8,AE=3,∴CD=BE=AB﹣AE=8﹣3=5.故答案填:5.13.解:∵△ABC≌△ADE,∠EAB=112°,∴∠EAD=DAB=56°,∠D=∠B,∴∠ACB+∠B=180°﹣56°=124°,∵∠ACB=∠FCD,∴∠FCD+∠D=124°,∵∠EFC是△FCD的一个外角,∴∠EFC=∠FCD+∠D=124°,故答案为:124.14.解:如图所示:由图形可得:∠1+∠4+∠5+∠8+∠6+∠2+∠3+∠9+∠7=540°,∵三个三角形全等,∴∠4+∠9+∠6=180°,又∵∠5+∠7+∠8=180°,∴∠1+∠2+∠3+180°+180°=540°,∴∠1+∠2+∠3的度数是180°.故答案为:180°.三.解答题15.解:∵△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,∴对应边:AN与AM,BN与CM;对应角:∠BAN=∠CAM,∠ANB=∠AMC.16.证明:∵△ABC≌△DEC,∴∠B=∠DEC,BC=EC,∴∠B=∠BEC,∴∠BEC=∠DEC,∴CE平分∠BED.17.解:(1)∵△ABC≌△ADE,∠B=10°,AB=4cm,∴∠ADE=∠B=10°,∠EAD=∠CAB,AD=AB=4cm,∵∠AED=20°,∴∠EAD=180°﹣∠EAD﹣∠AED=180°﹣10°﹣20°=150°,∴∠CAB=150°,∴∠EAB=360°﹣150°﹣150°=60°,∵点C为AD中点,∴AC=AD=×4=2(cm),∴AE=2cm;(2)∵∠B=10°,∠CAB=150°,∴∠ACB=180°﹣150°﹣10°=20°,∴∠FCD=20°,∴∠DFC=180°﹣20°﹣10°=150°,故答案为:150.18.(1)证明:∵△ABD≌△CFD,∴∠BAD=∠DCF,又∵∠AFE=∠CFD,∴∠AEF=∠CDF=90°,∴CE⊥AB;(2)解:∵△ABD≌△CFD,∴BD=DF,∵BC=7,AD=DC=5,∴BD=BC﹣CD=2,∴AF=AD﹣DF=5﹣2=3.。
八年级数学上册1.4全等三角形同步练习(新版)浙教版【含解析】

1.4 全等三角形一、选择题(共15小题;共75分)1. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )A. ①,②B. ①,④C. ③,④D. ②,③2. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是 ( )A. SASB. ASAC. AASD. SSS3. 如图,已知△ABC≌△CDA,AB与CD是对应边,AB=4,BC=5,AC=6,则AD的长为( )A. 4B. 5C. 6D. 不确定4. 下列说法中正确的是( )A. 面积相等的两个三角形是全等三角形B. 周长相等的两个三角形是全等三角形C. 三个角对应相等的两个三角形是全等三角形D. 能够完全重合的两个三角形是全等三角形5. 边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4.若△DEF的周长为偶数,则DF的取值为( )A. 3B. 4C. 5D. 3或4或56. 如图,已知△ABE≌△ACD,下列等式不正确的是( )A. AB=ACB. ∠BAE=∠CADC. BE=DCD. AD=DE7. 以右图方格纸中的3个格点为顶点,有多少个不全等的三角形 ( )A. 6B. 7C. 8D. 98. 下列语句:①面积相等的两个三角形全等;②两个等边三角形一定是全等图形;③如果两个三角形全等,它们的形状和大小一定都相同;④边数相同的图形一定能互相重合.其中错误的说法有 ( )A. 4个B. 3个C. 2个D. 1个9. 如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8 cm,AD=10 cm,OD=OC=2 cm,那么OB的长是 ( )A. 8 cmB. 10 cmC. 2 cmD. 无法确定10. 已知△A1B1C1,△A2B2C2的周长相等,现有两个判断:①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,对于上述的两个判断,下列说法正确的是 ( )A. ①正确,②错误B. ①错误,②正确C. ①,②都错误D. ①,②都正确11. 如图所示,在△ABC,△ADE中,∠BAC=∠DAE=90∘,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,BE.下列结论正确的有( )① BD=CE② BD⊥CE③ ∠ACE+∠DBC=45∘④ BE2=2(AD2+AB2)A. 1个B. 2个C. 3个D. 4个12. 如图,在△ABC中,AB=AC,∠BAC=90∘,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:① AE=CF;② △PEF是等腰直角三角形;③ EF=AP;④ S四边形AEPF =12S△ABC .当∠EPF在△ABC内部绕顶点P旋转时(点E不与点A,B重合),上述结论中始终正确的是( )A. ①②③B. ①②④C. ②③④D. ①③④13. 如图,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上,下列正确的有( )① ∠1=∠2=∠3;② AB=BE=EC;③ ∠4=∠5=∠6=60∘;④ AD=DE.A. 1个B. 2个C. 3个D. 4个14. 如图,E是BC边上一点,AB⊥BC于点B,DC⊥BC于点C,AB=BC,∠A=∠CBD,AE与BD交于点O,有下列结论:① AE=BD;② AE⊥BD;③ BE=CD;④ △AOB的面积等于四边形CDOE的面积.其中正确的结论有( )A. 1个B. 2个C. 3个D. 4个15. 如图,BE⊥AC于点D,且AD=CD,BD=ED .若∠ABC=72∘,则∠E等于( )A. 18∘B. 36∘C. 54∘D. 72∘二、填空题(共15小题;共75分)16. 如图,△ABC≌△DEF,则EF=.17. 如图,点C在线段AB的延长线上,AD=AE,BD=BE,CD=CE,则图中共有对全等三角形,它们分别是 .18. 一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=.19. 如图,△ABC≌△ADE,∠BAE=130∘,∠BAD=42∘,则∠BAC=.20. 一个三角形的三边长分别为2,5,x,另一个三角形的三边长分别为y,2,6.若这两个三角形全等,则x+y=.21. 如图,△ABC≌△AʹBʹCʹ,其中∠A=36∘,∠Cʹ=24∘,则∠B=∘.22. 如图,△ABC≌△ADE,BC的延长线交DE于点G,若∠B=24∘,∠CAB=54∘,∠DAC=16∘,则∠DGB=.23. 如图,△AEB≌△DFC,AE⊥CB,DF⊥BC,AE=DF,∠C=28∘,则∠A=.24. 如图,在△ABC中,AB=AC,AE=CF,BE=AF,则∠E=∠,∠CAF=∠ .25. 如图,已知A,B,C三点在同一条直线上,∠A=∠C=90∘,AB=CD,请添加一个适当的条件:,使得△EAB≌△BCD .26. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x=.27. 在如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7= .28. 如图,在△ABC中,∠B=∠C=50∘,BD=CF,BE=CD,则∠EDF的度数是.29. 如图,点B在AE上,∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是:(写一个即可).30. 如图,点C在线段AB上,DA⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=51∘,则∠DFE=.三、解答题(共5小题;共65分)31. 如图,已知△ABC≌△EFC,∠A与∠E,∠B与∠EFC分别是对应角,且FC=5 cm,∠EFC=65∘.求∠B的度数和BC的长.32. 用三种方法将一个等边三角形分成三个全等的图形.33. 如图,正方形ABCD中,点E,F分别在AB,BC上,AF=DE,AF和DE相交于点G,Ⅰ观察图形,写出图中所有与∠AED相等的角;Ⅱ选择图中与∠AED相等的任意一个角,并加以证明.34. 如图,△ABC≌△ADE,∠DAC=60∘,∠BAE=100∘,BC,DE相交于点F,求∠DFB的度数.35. 如图,在△ABC中,∠ACB=90∘,AC=6,BC=8.点P从点A出发沿路径A→C→B向终点B运动;点Q从点B出发沿路径B→C→A向终点A运动.点P和点Q分别以1个单位/秒和3个单位/秒的速度同时开始运动,两点都要到相应的终点时才能停止运动,在某一时刻,过点P作PE⊥l于点E,过点Q作QF⊥l于点F.问:点P运动多少时间时,△PEC与△CFQ 全等?请说明理由.答案第一部分1. D2. D3. B4. D5. B6. D7. C8. B9. A 10. D11. C 12. B 13. D 14. D 15. B第二部分16. 517. 3;△ADB≌△AEB,△DBC≌△EBC,△ADC≌△AEC18. 1119. 88∘20. 1121. 12022. 70∘23. 62∘24. F;ABE25. AE=CB或(∠EBD=90∘或∠E=∠DBC等)26. 2027. 315∘28. 50∘29. 答案不唯一如:∠CBA=∠DBA;∠C=∠D;AC=AD;∠CBE=∠DBE.30. 39∘第三部分31. ∵△ABC≌△EFC,∠A与∠E,∠B与∠EFC分别是对应角,∴BC=FC=5 cm,∠B=∠EFC=65∘(全等三角形的对应边,对应角相等)32. 如解图所示(答案不唯一).33. (1)如图,与∠AED相等的角是∠DAG,∠AFB,∠CDE.(2)如图,选择∠1=∠2,正方形ABCD中,∠DAB=∠B=90∘,AD=AB,∵AF=DE,∴△ADE≌△ABF,∴∠1=∠2.34. ∵△ABC≌△ADE,∴∠B=∠D,∠BAC=∠DAE .又∠BAD=∠BAC−∠CAD,∠CAE=∠DAE−∠CAD,∴∠BAD=∠CAE .∵∠DAC=60∘,∠BAE=100∘,∴∠BAD=12(∠BAE−∠DAC)=12(100∘−60∘)=20∘ .在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,∴∠DFB=∠BAD=20∘.35. 设运动时间为t(s)时,△PEC≌△CFQ.∵△PEC≌△CFQ,∴斜边CP=QC.当0<t<6时,点P在AC上;当6≤t≤14时,点P在BC上.当0<t<83时,点Q在BC上;当83≤t≤143时,点Q在AC上.有三种情况:①当点P在AC上,点Q在BC上时,如解图①,此时0<t<83.易得CP=6−t,QC=8−3t,∴6−t=8−3t,解得t=1.②当点P,Q都在AC上时(83≤t≤143),此时点P,Q重合,如解图②.易得CP=6−t=3t−8,解得t=3.5.③当点Q与点A重合,点P在BC上时(6<t≤14),如解图③.易得CP=t−6,QC=6,∴t−6=6,解得t=12.综上所述,当点P运动1 s或3.5 s或12 s时,△PEC与△CFQ全等.。
浙教版八年级上1.5《三角形全等的判定》同步练习题含答案

浙教版八年级数学上册第一章三角形初步认识1.5《三角形全等的判定》同步练习题一选择题1.如图,已知∠A=∠D,∠1=∠2,要利用“ASA”得到△ABC≌△DEF,还应给出的条件是(D) A.∠E=∠B B.ED=BCC.AB=EF D.AF=CD(第1题)(第2题)2.如图,一块玻璃碎成三片,现要去玻璃店配一块一模一样的玻璃,最省力的办法是带哪块去(C) A. ① B. ②C. ③D. ①②③3.在△ABC与△A1B1C1中,下列不能判定△ABC≌A1B1C1的是(B)A.AB=A1B1,BC=B1C1,∠B=∠B1B.AB=A1B1,AC=A1C1,∠C=∠C1C.∠B=∠B1,∠C=∠C1,BC=B1C1D.AB=A1B1,BC=B1C1,AC=A1C14.如图,已知△ABC的六个元素,则下面甲、乙、丙三个三角形中和△ABC全等的图形是(B)(第4题)A.甲和乙B.乙和丙C.只有乙D.只有丙5.如图,已知BD⊥AC于点D,CE⊥A B于点E,BD=EC,则△ABD≌△ACE,其三角形全等的判定方法是(C)A. ASAB. SASC. AASD. 以上都不对(第5题)(第6题)6.如图,已知AC=FC,CE是∠ACF的平分线,则图中全等三角形有(D)A. 1对B. 2对C. 3对D. 4对7.如果两个三角形的两条边和其中一条边上的中线分别对应相等,那么这两个三角形第三边所对的角的关系是(A)A. 相等B. 互余C. 互补D. 以上答案都不正确(第8题)8.如图,点E在BC上,AB⊥BC于点B,DC⊥BC于点C,AB=BC,∠A=∠CBD,AE交BD 于点O,下列结论:①AE=BD;②△AOB的面积=四边形CDOE的面积;③AE⊥BD;④BE=CD.其中正确的结论有(D)A.1个B.2个C.3个D.4个二填空题9.如图,AD平分∠BAC,AB=AC,BF与CE交于点D,则图中有4对全等的三角形.(第9题)(第10题)10.如图,AD是△ABC的高线,∠BAD=∠ABD,DE=DC,∠ABE=15°,则∠C=60°.11.如图,已知AE=CE,∠B=∠D=∠AEC=90°,AB=3 cm,C D=2 cm,则△CDE和△A BE 的面积之和是6cm2.(第11题)12. 在△ABC和△DEF中,已知AB=4,∠A=35°,∠B=70°,DE=4,∠D=__35°__,∠E=70°,可以根据__ASA__判定△ABC≌△DEF.(第12题)13.如图,在△ABC中,AB=AC=10cm,DE是AB的中垂线,△BDC的周长为16 cm,则BC 的长为6 cm.14.如图,点B在AE上,且∠CAB=∠DAB,要使△ABC≌△ABD,可补充的一个条件是(写一个即可):AC=AD或∠C=∠D等.15.如图,在△ABC 中,∠C =90°,AD 是△ABC 的角平分线,BC =10,CD ∶BD =2∶3,则点D 到AB 的距离为4.三、解答题16.如图,在△ABC 中,∠B =∠C ,D ,E 分别在BC ,AC 边上,且∠1=∠B ,AD =DE ,求证:△ADB ≌△DEC.(第16题)【解】 ∵∠B +∠BAD =∠1+∠CDE , ∠B =∠1, ∴∠BAD =∠CDE. 在△ADB 和△DEC 中, ∵⎩⎪⎨⎪⎧∠BAD =∠CDE ,∠B =∠C ,AD =DE , ∴△ADB ≌△DEC(AAS).17.如图,在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于点D ,BE ⊥MN 于点E .(1)当直线MN 绕点C 旋转到图①的位置时,求证:DE =AD +BE ; (2)当直线MN 绕点C 旋转到图②的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图③的位置时,试问:DE ,AD ,BE 具有怎样的等量关系?请直接写出这个等量关系.(第17题)【解】 (1)∵∠ACB =90°,∴∠ACD +∠ECB =90°. ∵AD ⊥MN ,BE ⊥MN ,∴∠AD C =∠BEC =90°. ∴∠DAC +∠ACD =90°,∴∠DAC =∠ECB . 在△ADC 和△CEB 中, ∵⎩⎪⎨⎪⎧∠DAC =∠ECB ,∠ADC =∠CEB ,AC =CB ,∴△ADC ≌△CEB (AAS ). ∴AD =CE ,DC =EB .∴DE =AD +B E .(2)同(1)证明,∠DAC =∠ECB . ∴△ADC ≌△CEB (AAS ). ∴AD =CE ,CD =BE .∵DE =CE -CD ,∴DE =AD -BE .(3)DE =BE -AD .(第18题)18.如图,BE ,CF 是△ABC 的两条高线,延长BE 到点P ,使BP =CA ,CF 与BE 交于点Q ,连结AQ ,且QC =AB.(1)猜想AQ 与AP 的大小关系,并说明理由; (2)按三角形内角判断△APQ 的类型,并说明理由. 【解】 (1)AQ =AP.理由如下: ∵BE ,CF 是△ABC 的两条高线, ∴BE ⊥AC ,CF ⊥AB , ∴∠ABP +∠BAC =90°, ∠QCA +∠BAC =90°, ∴∠ABP =∠QCA . 在△ABP 和△QCA 中, ∵⎩⎪⎨⎪⎧BP =CA ,∠ABP =∠QCA ,AB =QC , ∴△ABP ≌△QCA (SAS ), ∴AP =QA ,即AQ =AP . (2)△APQ 是等腰直角三角形.理由:∵△ABP ≌△QCA , ∴∠P =∠QAC .∵BP⊥AC,∴∠P+∠P AE=90°,∴∠QAC+∠P AE=90°.∴∠QAP=90°.又∵AQ=AP,∴△APQ是等腰直角三角形.。
2019秋浙教版八年级上册数学同步测试题:1.5三角形全等的判定【含答案】

1.5三角形全等的判定第1课时“边边边”知识点1.三角形全等的判定(SSS)1.如图1所示,如果AB=A′B′,BC=B′C′,AC=A′C′,则下列结论正确的是(A)图1A.△ABC≌△A′B′C′B.△ABC≌△C′A′B′C.△ABC≌△B′C′A′D.这两个三角形不全等2.下列三角形中,与图2中△ABC全等的是__③__.3.如图3所示,AD=BC,AC=BD,用三角形全等的判定“SSS”可证明__△ADC__≌__△BCD__或__△ABD__≌__△BAC__.图3知识点2.三角形的稳定性4.[2018春·泉港区期末]如图4,人字梯中间一般会设计一“拉杆”,这样做的道理是(C)图4A.两点之间,线段最短B.垂线段最短C.三角形具有稳定性D.两直线平行,内错角相等知识点3.三角形全等的判定与性质的综合5.在△ABC和△A1B1C1中,AB=A1B1,BC=B1C1,AC=A1C1,且∠A=110°,∠B=40°,则∠C1=(C)A.110°B.40°C.30°D.20°6.如图5所示,在△ABC和△DBC中,已知AB=DB,AC=DC,则下列结论中错误的是(D)图5A.△ABC≌△DBCB.∠A=∠DC.BC是∠ACD的平分线D.∠A=∠BCD7.如图6,在四边形ABCD中,AB=CD,AD=CB,连结AC,求证:∠ACD =∠CAB.图6证明:在△ADC 与△CBA 中,⎩⎨⎧CD =AB ,AD =CB ,AC =CA ,∴△ADC ≌△CBA (SSS ),∴∠ACD =∠CAB .8.雨伞的截面如图7所示,伞骨AB =AC ,支撑杆OE =OF ,AE =13AB ,AF =13AC ,当O 沿AD 滑动时,雨伞开闭,问雨伞开闭的过程中,∠BAD 与∠CAD 有何关系?请说明理由.图7解:∠BAD =∠CAD .理由:∵AB =AC ,AE =13AB ,AF =13AC ,∴AE =AF .在△AOE 和AOF 中,⎩⎨⎧AO =AO ,AE =AF ,OE =OF ,∴△AOE ≌△AOF (SSS ),∴∠EAO =∠F AO ,即∠BAD =∠CAD . 知识点4.尺规作角平分线9.[2018春·历城区期末]如图8,作∠AOB 的角平分线的作图过程如下,作法:图8(1)在OA和OB上,分别截取OD,OE,使OD=OE;(2)分别以D,E为圆心,大于DE的长为半径作弧,在∠AOB内,两弧交于点C;(3)作射线OC,OC就是∠AOB的平分线.用三角形全等判定法则解释其作图原理,最为恰当的是__SSS__.【易错点】证明两个三角形全等时,对于有公共部分的角或线段,错把不是对应的边或角当成三角形的对应边或对应角.10.如图9,AB=AC,AD=AE,BE=CD,∠2=110°,∠BAE=60°,下列结论错误的是(C)图9A.△ABE≌△ACDB.△ABD≌△ACEC.∠ACE=30°D.∠1=70°第2课时“边角边”与线段的垂直平分线的性质知识点1.三角形全等的判定(SAS)1.如图1中全等的三角形是(D)①②③④图1A.①和②B.②和③C.②和④D.①和③2.如图2所示,在△ABD和△ACE中,AB=AC,AD=AE,要证△ABD≌△ACE,需补充的条件是(C)A.∠B=∠C B.∠D=∠EC.∠DAE=∠BAC D.∠CAD=∠DAC图2 图33.如图3,在四边形ABCD中,AB=AD,CB=CD,若连结AC,BD相交于点O,则图中全等三角形共有(C)A.1对B.2对C.3对D.4对4.已知:如图4,OA=OB,OC平分∠AOB,求证:△AOC≌△BOC.图4证明:∵OC 平分∠AOB , ∴∠AOC =∠BOC . 在△AOC 和△BOC 中,⎩⎨⎧OA =OB ,∠AOC =∠BOC ,OC =OC ,∴△AOC ≌△BOC (SAS ).知识点2.利用“SAS ”判定三角形全等证明线段或角相等5.如图5,在△ABC 和△ABD 中,AC 与BD 相交于点E ,AD =BC ,∠DAB =∠CBA ,求证:AC =BD .图5证明:在△ADB 和△BCA 中,⎩⎨⎧AD =BC ,∠DAB =∠CBA ,AB =BA ,∴△ADB ≌△BCA (SAS ),∴AC =BD .6.如图6,在△ABC 中,已知AB =AC ,AD 平分∠BAC ,点M ,N 分别在AB ,AC 边上,AM =2MB ,AN =2NC .求证:DM =DN .图6证明:∵AM =2MB ,∴AM =23AB ,同理,AN =23AC , 又∵AB =AC ,∴AM =AN . ∵AD 平分∠BAC , ∴∠MAD =∠NAD .在△AMD 和△AND 中,⎩⎨⎧AM =AN ,∠MAD =∠NAD ,AD =AD ,∴△AMD ≌△AND ,∴DM =DN .知识点3.利用“SAS ”判定三角形全等来解决实际问题7.如图7所示,有一块三角形镜子,小明不小心将它打破成Ⅰ,Ⅱ两块,现需配成同样大小的一块.为了方便起见,需带上__Ⅰ__块,其理由是__两边及其夹角分别相等的两个三角形全等__.图7知识点4.线段的垂直平分线的性质8.[2017秋·浉河区期末]如图8,DE 是△ABC 中AC 边的垂直平分线,若BC =8,AB =10,则△EBC 的周长是( C ) A .13B .16C .18D .20【解析】 ∵DE 是△ABC 中AC 边的垂直平分线,∴EA =EC ,∴△EBC 的周长=BC +BE +EC =BC +BE +EA =BC +BA =18.图8 图99.如图9,在△ABC中,AB=AC=20 cm,DE垂直平分AB,垂足为E,交AC 于D,若△DBC的周长为35 cm,则BC的长为(C)A.5 cm B.10 cmC.15 cm D.17.5 cm【解析】∵△DBC的周长=BC+BD+CD=35 cm,又∵DE垂直平分AB,∴AD=BD,∴BC+AD+CD=35 cm,∵AC=AD+DC=20 cm,∴BC=35-20=15 cm.【易错点】“SSA”不能判定两个三角形全等.10.下列条件能够判断△ABC与△A′B′C全等的是(D)A.∠A=∠A′B.AB=A′B′,∠B=∠B′,AC=A′C′C.AB=A′B′,AC=A′C′D.AB=A′B′,∠A=∠A′,AC=A′C′【解析】A.已知条件为一组对应角相等,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;B.已知条件为边边角,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;C.已知条件为两条边对应相等,不符合全等三角形的判定定理,无法证明两个三角形全等,故此选项错误;D.由边角边定理可证两个三角形全等,故此选项正确.第3课时“角边角”知识点三角形全等的判定(ASA)1.如图1,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是(B)图1A.甲B.乙C.甲和乙都是D.都不是2.如图2所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是__ASA__.图23.如图3,∠1=∠2,∠3=∠4,求证:AC=AD.图3证明:∵∠3=∠4,∴∠ABC=∠ABD.在△ABC和△ABD中,⎩⎨⎧∠1=∠2,AB =AB ,∠ABC =∠ABD ,∴△ABC ≌△ABD (ASA ),∴AC =AD .4.[2018秋·延庆区期中]如图4,AB =AC ,点D ,E 分别在AB ,AC 上,CD ,BE 交于点F ,且∠B =∠C .求证:△ABE ≌△ACD .图4证明:在△ABE 与△ACD 中,⎩⎨⎧∠A =∠A ,AB =AC ,∠B =∠C ,∴△ABE ≌△ACD (ASA ).5.[2018秋·金坛区期中]如图5,在△ABC 和△ADE 中,AB =AD ,∠B =∠D ,∠1=∠2.求证:△ABC ≌△ADE .图5证明:∵∠1=∠2,∴∠DAC +∠1=∠2+∠DAC , ∴∠BAC =∠DAE ,在△ABC 和△ADE 中,⎩⎨⎧∠B =∠D ,AB =AD ,∠BAC =∠DAE ,∴△ABC ≌△ADE (ASA ).【易错点】错用判定三角形全等的判定方法.6.已知:如图6,∠AOD =∠BOC ,∠A =∠C ,O 是AC 的中点.求证:△AOB ≌△COD .图6证明:∵∠AOD =∠BOC ,∴∠AOD +∠DOB =∠BOC +∠BOD , 即∠AOB =∠COD ,∵O 是AC 的中点,∴AO =CO ,在△AOB 与△COD 中,⎩⎨⎧∠A =∠C ,AO =CO ,∠AOB =∠COD ,∴△AOB ≌△COD .第4课时 “角角边”与角平分线的性质知识点1.三角形全等的判定(AAS )1.如图1,AB =AE ,∠1=∠2,∠C =∠D .求证:△ABC ≌△AED .图1证明:∵∠1=∠2,∴∠1+∠EAC =∠2+∠EAC ,即∠BAC =∠EAD . 又∵∠C =∠D ,AB =AE ,∴△ABC ≌△AED (AAS ).2.如图2,已知:在△AFD 和△CEB 中,点A ,E ,F ,C 在同一直线上,AE =CF ,∠B =∠D ,AD ∥BC .求证:AD =BC .图2证明:∵AE =CF ,∴AF =CE . ∵AD ∥BC ,∴∠A =∠C . 在△AFD 和△CEB 中,⎩⎨⎧∠A =∠C ,∠B =∠D ,AF =CE ,∴△AFD ≌△CEB (AAS ),∴AD =BC . 知识点2.三角形全等判定方法的选用3.如图3,已知∠ABC =∠BAD ,添加下列条件还不能判定△ABC ≌△BAD 的是( A )A .AC =BDB .∠CAB =∠DBAC .∠C =∠DD .BC =AD图3图44.如图4所示,在△ABC 中,∠B =∠C ,D 为BC 边的中点,过点D 分别向AB ,AC 作垂线段,则能够说明△BDE ≌△CDF 的理由是( D ) A .SSSB .SASC .ASAD .AAS知识点3.角平分线的性质5.如图5,OC 是∠AOB 的平分线,P 是OC 上一点,PD ⊥OA 于点D ,PD =6,则点P 到边OB 的距离为( A )图5A .6B .5C .4D .36.[2019·辽阳模拟]如图6,BD 平分∠ABC ,DE ⊥BC 于点E ,AB =7,DE =4,则S △ABD =( C ) A .28 B .21 C .14D .7图6第6题答图【解析】 如答图,作DH ⊥BA 于H .∵BD 平分∠ABC ,DE ⊥BC ,DH ⊥AB , ∴DH =DE =4,∴S △ABD =12×7×4=14,故选C.7.如图7,已知BD 为∠ABC 的平分线,AB =BC ,点P 在BD 上,PM ⊥AD 于M ,PN ⊥CD 于N ,求证:PM =PN .图7证明:∵BD 为∠ABC 的平分线, ∴∠ABD =∠CBD , 在△ABD 和△CBD 中,⎩⎨⎧AB =CB ,∠ABD =∠CBD ,BD =BD ,∴△ABD ≌△CBD (SAS ),∴∠ADB =∠CDB , ∵点P 在BD 上,且PM ⊥AD ,PN ⊥CD ,∴PM =PN .【易错点】对于全等三角形开放性问题,常常不能正确选用判定方法. 8. 如图8,在△ABC 和△DEF 中,∠B =∠DEF ,AB =DE ,添加下列一个条件后,仍然不能证明△ABC ≌△DEF ,这个条件是( D )图8A .∠A =∠DB .BC =EF C .∠ACB =∠FD .AC =DF【解析】 ∵∠B =∠DEF ,AB =DE ,∴添加∠A =∠D ,利用ASA 可得△ABC ≌△DEF ;∴添加BC=EF,利用SAS可得△ABC≌△DEF;∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;添加AC=DF不能证明△ABC≌△DEF,故选D.。
2022-2023年浙教版八年级数学上册《1-5三角形全等的判定》解答题专题训练(附答案)
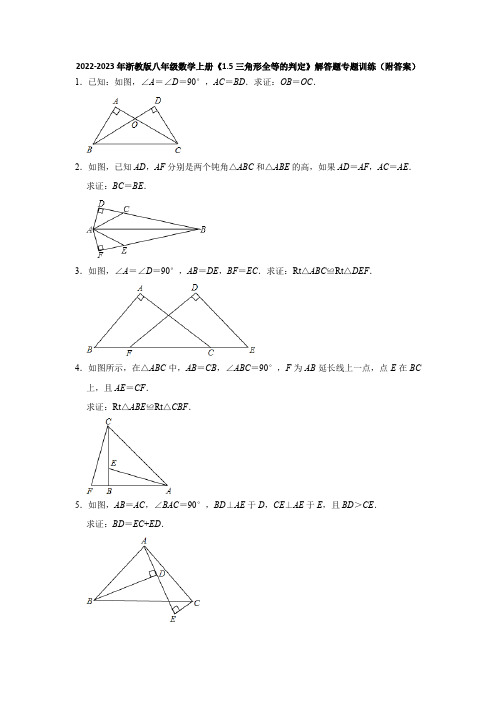
2022-2023年浙教版八年级数学上册《1.5三角形全等的判定》解答题专题训练(附答案)1.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.2.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE.3.如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.4.如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC 上,且AE=CF.求证:Rt△ABE≌Rt△CBF.5.如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.求证:BD=EC+ED.6.如图,CD⊥AB于D点,BE⊥AC于E点,BE,CD交于O点,且AO平分∠BAC.求证:OB=OC.7.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.求证:△ABE≌△CDF.8.如图,在Rt△ABC中,∠B=90°,CD∥AB,DE⊥AC于点E,且CE=AB.求证:△CED≌△ABC.9.已知:点A,D,C,B在同一条直线上,DF∥CE,DF=CE,AD=BC.求证:(1)CF=DE;(2)AF∥EB.10.如图,在等腰△ABC中,BA=BC,点F在AB边上,延长CF交AD于点E,BD=BE,∠ABC=∠DBE.(1)求证:AD=CE;(2)若∠ABC=30°,∠AFC=45°,求∠EAC的度数.11.如图,在四边形ABCD中,AB∥CD,连接BD,点E在BD上,连接CE,若∠1=∠2,AB=ED,求证:DB=CD.12.如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠F AG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.13.已知:如图,在△ABC中,AB=CB,∠ABC=45°,高AD与高BE相交于点F,G为BF的中点.求证:(1)DG=DE;(2)∠DEG=∠DEC.14.已知:如图,在△ABC中,AD⊥BC于点D,E为AC上一点,且BF=AC,DF=DC.(1)求证:△BDF≌△ADC.(2)已知AC=5,DF=3,求AF的长.15.如图,在△ABC中,∠A=∠ACB,CD平分∠ACB,点E为CD延长线上一点,过点E 作EF∥AC交AB于点F,连接CF.(1)若CD=DE,求证:AD=DF;(2)若∠ABC=∠ECF=24°,求∠CFE的度数.16.如图,AB=AC,AD=AE,∠BAC=∠DAE.(1)求证:△ABD≌△ACE;(2)若∠1=25°,∠2=30°,求∠3的度数.17.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.(1)求证:AB=FE;(2)若ED⊥AC,AB∥CE,求∠A的度数.18.如图,AB=AC,直线l经过点A,BM⊥l,CN⊥l,垂足分别为M、N,BM=AN.(1)求证:MN=BM+CN;(2)求证:∠BAC=90°.19.如图,在△ABC中,点D为AB边上一点,DE∥BC交AC于点E,点F为BC延长线上一点,BF=AD,∠ACF=∠ADF.(1)求证:AE=FD;(2)若∠FDB=80°,∠B=70°,求∠1的度数.20.已知:如图,BD、CE是△ABC的高,BD、CE交于点F,BD=CD,CE平分∠ACB.(1)如图1,试说明BE=CF.(2)如图2,若点M在边BC上(不与点B重合),MN⊥AB于点N,交BD于点G,请直接写出BN与MG的数量关系,并画出能够说明该结论成立的辅助线,不必书写过程.21.已知:如图,AD、BF相交于O点,OA=OD,AB∥DF,点E、C在BF上,BE=CF.(1)求证:△ABO≌△DFO;(2)判断线段AC、DE的关系,并说明理由.22.如图,在△ABC中,D是边AB上一点,E是边AC的中点,作CF∥AB交DE的延长线于点F.(1)证明:△ADE≌△CFE;(2)若AB=AC,CE=5,CF=7,求DB的长.参考答案1.证明:∵∠A=∠D=90°,AC=BD,BC=BC,∴Rt△BAC≌Rt△CDB(HL)∴∠ACB=∠DBC.∴∠OCB=∠OBC.∴OB=OC(等角对等边).2.证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,∴Rt△ADC≌Rt△AFE(HL).∴CD=EF.∵AD=AF,AB=AB,∴Rt△ABD≌Rt△ABF(HL).∴BD=BF.∴BD﹣CD=BF﹣EF.即BC=BE.3.证明:∵BF=EC,∴BF+FC=FC+EC,即BC=EF,∵∠A=∠D=90°,∴△ABC和△DEF都是直角三角形,在Rt△ABC和Rt△DEF中,∴Rt△ABC≌Rt△DEF(HL).4.证明:在Rt△ABE和Rt△CBF中,∵,∴Rt△ABE≌Rt△CBF(HL).5.证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.∴∠ABD=∠DAC.∵在△ABD和△CAE中,∴△ABD≌△CAE(AAS).∴BD=AE,EC=AD.∵AE=AD+DE,∴BD=EC+ED.6.证明:∵BE⊥AC,CD⊥AB,∴∠ADC=∠BDC=∠AEB=∠CEB=90°.∵AO平分∠BAC,∴∠1=∠2.在△AOD和△AOE中,,∴△AOD≌△AOE(AAS).∴OD=OE.在△BOD和△COE中,,∴△BOD≌△COE(ASA).∴OB=OC.7.证明:∵AB∥CD,∴∠A=∠DCF,∵AF=CE,∴AF﹣EF=CE﹣EF,即AE=CF,在△ABE和△CDF中,,∴△ABE≌△CDF(SAS).8.证明:∵DE⊥AC,∠B=90°,∴∠DEC=∠B=90°,∵CD∥AB,∴∠A=∠DCE,在△CED和△ABC中,,∴△CED≌△ABC(ASA).9.证明:(1)∵DF∥CE,∴∠FDC=∠ECD,在△FDC和△ECD中,,∴△FDC≌△ECD(SAS),∴CF=DE;(2)∵△FDC≌△ECD,∴∠FCD=∠EDC,∵AD=BC,∴AD+DC=BC+DC,∴AC=BD,在△F AC和△EBD中,,∴△F AC≌△EBD(SAS),∴∠A=∠B,∴AF∥EB.10.(1)证明:∵∠ABC=∠DBE,∴∠ABC+∠ABE=∠DBE+∠ABE,∴∠ABD=∠CBE.在△ADB和△CEB中,,∴△ADB≌△CEB(SAS),∴AD=CE;(2)解:∵BA=BC,∠ABC=30°,∴∠BAC=∠BCA=(180°﹣30°)=75°,∵∠AFC=45°,∴∠BCE=∠AFC﹣∠ABC=45°﹣30°=15°,∵△ADB≌△CEB,∴∠BAD=∠BCE=15°,∴∠EAC=∠BAD+∠BAC=15°+75°=90°.11.证明:∵AB∥CD,∴∠ABD=∠EDC,在△ABD和△EDC中,,∴△ABD≌△EDC(AAS),∴DB=CD.12.(1)证明:∵∠BAC=∠F AG,∴∠BAC﹣∠CAD=∠F AG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,,∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAG,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,,∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.13.证明:(1)AD⊥BD,∠BAD=45°,∴AD=BD,∵∠BFD=∠AFE,∠AFE+∠CAD=90°,∠CAD+∠ACD=90°,∴∠BFD=∠ACD,在△BDF和△ACD中,,∴△BDF≌△ACD(AAS),∴BF=AC,∵G为BF的中点.∴DG=BF,∵AB=CB,BE⊥AC,∴E为AC的中点.∴DE=AC,∴DG=DE;(2)由(1)知:∠DBG=∠DAE,BG=BF,AE=AC,BF=AC,∴BG=AE,在△BDG和△ADE中,,∴△BDG≌△ADE(SAS),∴∠BDG=∠ADE,∴∠DGB=∠DBG+∠BDG,∵∠DEC=∠DAE+∠ADE,∴∠DGB=∠DEC,∵DG=DE,∴∠DGE=∠DEG,∴∠DEG=∠DEC.14.(1)证明:∵AD⊥BC,∴∠ADB=∠ADC=90°,在Rt△BDF和Rt△ADC中,,∴Rt△BDF≌Rt△ADC(HL).(2)解:∵Rt△BDF≌Rt△ADC,∴DC=DF.在Rt△ADC中,(AF+3)2+32=52,∴AF=1或AF=7(舍)∴AF=1.15.(1)证明:∵EF∥AC,∴∠A=∠EFD,∠ACD=∠E,在△ADC和△FDE中,,∴△ADC≌△FDE(AAS),∴AD=DF;(2)解:∵∠A=∠ACB,∠ABC=∠ECF=24°,∴∠A=∠ACB==78°,∴∠ACE=∠BCE=39°,∵EF∥AC,∴∠A=∠EFD=78°,∠ACD=∠E=39°,∵∠ECF=24°,∴∠CFE=180°﹣∠ECF﹣∠E=180°﹣24°﹣39°=117°.16.(1)证明:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵△ABD≌△ACE,∴∠ABD=∠2=30°,∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°.17.证明:(1)∵CB为∠ACE的角平分线,∴∠ACB=∠FCE,在△ABC与△FEC中,,∴△ABC≌△FEC(AAS),∴AB=FE;(2)∵AB∥CE,∴∠B=∠FCE,∴∠E=∠B=∠FCE=∠ACB,∵ED⊥AC,即∠CDE=90°,∴∠E+∠FCE+∠ACB=90°,即3∠ACB=90°,∴∠B=30°,∴∠A=180°﹣∠B﹣∠ACB=180°﹣30°﹣30°=120°.18.证明:(1)∵BM⊥直线l,CN⊥直线l,∴∠AMB=∠CNA=90°,在Rt△AMB和Rt△CNA中,,∴Rt△AMB≌Rt△CNA(HL),∴BM=AN,CN=AM,∴MN=AM+AN=BM+CN;(2)由(1)得:Rt△AMB≌Rt△CNA,∴∠BAM=∠ACN,∵∠CAN+∠ACN=90°,∴∠CAN+∠BAM=90°,∴∠BAC=180°﹣90°=90°.19.(1)证明:∵∠ACF=∠ADF,∴∠B+∠A=∠B+∠F,∴∠A=∠F,∵DE∥BC,∴∠ADE=∠B,在△ADE和△FBD中,,∴△ADE≌△FBD(ASA),∴AE=FD;(2)解:∵∠FDB=80°,∠B=70°,∴∠F=30°,∴∠ACF=∠ADF=∠B+∠F=100°,∴∠1=∠F+∠ACF=130°.20.解:(1)∵BD⊥AC,CE⊥AB,∴∠ADB=∠BDC=∠AEC=90°,∴∠A+∠ABD=90°,∠A+∠ACE=90°,∴∠ABD=∠ACE,在△ABD和△FCD中,,∴△ABD≌△FCD(ASA),∴AB=CF,∵CE平分∠ACB,∴∠ACE=∠BCE=22.5°,在△ACE和△BCE中,,∴△ACE≌△BCE(ASA),∴AE=BE,∴BE=AB=CF;(2)BN=MG,理由如下:如图,过点M作MH∥AC,交AB于H,交BD于P,∵BD=CD,BD⊥CD,∴∠DBC=∠DCB=45°,∵MH∥AC,∴∠PMB=∠DCB=∠PBM=45°,∠BPM=∠BDC=90°,∴BP=PM,∵∠BHP+∠HBP=90°,∠BHP+∠HMN=90°,∴∠HBP=∠HMN,在△BHP和△MGP中,,∴△BPH≌△MPG(ASA),∴GM=BH,∵MN⊥AB,CE⊥AB,∴MN∥CE,∴∠BMN=∠BCE=∠ACB=22.5°,∴∠BMN=∠HMN=22.5°,在△BMN和△HMN中,,∴△BMN≌△HMN(ASA)∴BN=NH,∴BN=BH=MG.21.(1)证明:∵AB∥DF,∴∠B=∠F,∠BAO=∠FDO,在△ABO和△DFO中,,∴△ABO≌△DFO(AAS);(2)解:AC=DE,AC∥DE,理由如下:∵△ABO≌△DFO,∴BO=FO,∵BE=CF,∴EO=CO,在△AOC和△DOE中,,∴△AOC≌△DOE(SAS),∴AC=DE,∠DAC=∠ADE,∴AC∥DE.22.(1)证明:∵E是边AC的中点,∴AE=CE.又∵CF∥AB,∴∠A=∠ACF,∠ADF=∠F,在△ADE与△CFE中,,∴△ADE≌△CFE(AAS).(2)解:∵△ADE≌△CFE,CF=7,∴CF=AD=7,∵AB=AC,E是边AC的中点,CE=5,∴AC=2CE=10.∴AB=10,∴DB=AB﹣AD=10﹣7=3.。
新浙教版八年级上1.5三角形全等的判定(4)

∴∠PAB=∠PAC(角平分线的定义) B ∵PB⊥AB,PC⊥AC(已知) ∴∠ABP=∠ACP=Rt∠
在△APB与△APC中, A (已证) PAB PAC ABP ACP (已证) AP AP (公共边) ∴△ APB ≌△APC(AAS) ∴PB=PC(全等三角形对应边相等)
这个例子告诉我们,在判定两个三角形全等时, 不能笼统地看它们之间有多少个角、多少条边分 A 8 12 别相等,而要看它们是否满足“ SSS、SAS、 ASA、AAS”中对应相等的条件,特别是领会 C B 18 “对应相等”中的“对应”两字的含义。
知识回顾
1.已知,AB=DE,BC=EF,请添加一个条件,使得 △ABC≌△DEF。 2.已知, AB=DE , C F
A
B
D
E
练一练
如图,已知AB=DE ,∠A=∠D,,∠C=∠F,则 △ABC 和△DEF全等吗?用学过的知识说明。 C F
2:如图,BD是△ABC的一条角平分线, AB=10,BC=8,且S△ABD=25, 求△BCD的面积.
B
A
∟
E
E
D
F
C
巩固提高
1.如图,CD⊥AB,BE⊥AC,垂足分别是D﹑E, BE﹑CD相交于点O,若∠1=∠2,求证 : (1)OD=OE (2)OB=OC
A
12
D O
E
B
C
如果有两个三角形,它们的三个角对应相等, 并且其中一个三角形的两边与另一个三角形的 两边分别相等,这样的两个三角形一定全等吗?
A
B
D
E
结论: 有两个角和其中一个角的对边对应相等的两 个三角形全等(简写成“角角边”或 “AAS”) C F
1.5 三角形全等的判定八年级上册数学浙教版

如果可以用“角边角”判定两个三角形全等,那么也可以转化为用“角角边”判定两个三角形全等,反之亦然
3.三角形全等的条件的灵活选用
已知条件
作出图形
是否全等
形成结论
三条边
是
两边一角
两边夹角
是
两边对角
运用角平分线的性质定理求线段长的步骤
本节知识归纳
中考常考考点
难度
常考题型
考点1:判定两个三角形全等,主要考查根据题中所给的条件选择适当的方法证明两个三角形全等.
选择题、填空题、解答题
考点2:线段垂直平分线性质定理的应用,主要考查在三角形中求线段长(或周长),或解决实际问题.
2.线段的垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等.
垂直平分线上的任意一点几何语言:如图所示, , ,点 是直线 上任意一点, .
典例5 如图,在 中, , 的垂直平分线分别交 , 于点 , , 的周长为 ,求线段 的长.
解: 为 的垂直平分线, , . , .
典例6 [2022·义乌期末] 如图,在 和 中,点 , , , 在同一直线上,已知 ,且 ,若利用“ ”证明 ,则需添加的条件是( )
A. B. C. D.
C
[解析] 需添加的条件是 .理由: , .在 和 中,∵ .
例题点拨
知识点7 两个三角形全等的判定定理:角角边( ) 重点
选择题、填空题
考点3:角平分线性质定理的应用,主要考查在图形中求图形的面积.
选择题、填空题
考点1 判定两个三角形全等
典例9 [2021·杭州中考改编] 在① ,② ,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.问题:如图,在 中, ,点 在 边上(不与点 ,点 重合),点 在 边上(不与点 ,点 重合),连结 , , 与 相交于点 .若____________,求证: .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.5 三角形全等的判定(四)
1.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是(A)
A. AC=BD
B. ∠CAB=∠DBA
C. ∠C=∠D
D. BC=AD
(第1题) (第2题)
2.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有(C)
A. 1个
B. 2个
C. 3个
D. 4个
3.如图,P是∠AOB的平分线OC上的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,延长DP交OB于点F,延长EP交OA于点G,则图中有__4__对全等三角形,它们分别是△FPE≌△GPD,△OEP≌△ODP,△OPF≌△OPG,△ODF≌△OEG.
(第3题) (第4题) (第5题)
4.如图,∠B =∠D ,请添加一个条件(不得添加辅助线),使得△ABC ≌△ADC ,你所添加的条件是∠BAC =∠DAC (答案不唯一)(只添一个即可).
5.如图,在△ABC 中,∠ACB =90°,AC =BC ,AD ⊥CE ,BE ⊥CE ,D ,E 为垂足.求证:DE +BE =CE .
【解】 ∵AD ⊥CE ,BE ⊥CE , ∴∠ADC =∠CEB =90°. 又∵∠ACB =90°,
∴∠ACD +∠BCE =∠BCE +∠CBE =90°, ∴∠ACD =∠CBE .
在△ADC 和△CEB 中,∵⎩⎪⎨⎪
⎧∠ADC =∠CEB ,∠ACD =∠CBE ,AC =CB ,
∴△ADC ≌△CEB (AAS ).∴CD =BE . ∴DE +BE =DE +CD =CE .
6.如图,已知点B ,E ,F ,C 在同一条直线上,∠A =∠D ,BE =CF ,且AB ∥C D.求证:AF ∥E D.
(第6题)
【解】 ∵BE =CF ,∴BE +EF =CF +EF ,∴BF =CE . ∵AB ∥CD ,∴∠B =∠C.
在△ABF 和△DCE 中,∵⎩⎪⎨⎪
⎧∠A =∠D ,∠B =∠C ,BF =CE ,
∴△ABF ≌△DCE (AAS ). ∴∠AFB =∠DE C.∴AF ∥E D.
7.如图,在正方形ABCD 中,G 是BC 上任意一点,连结AG ,DE ⊥AG 于点E ,BF ∥DE
交AG 于点F ,探究线段DE ,BF ,EF 三者之间的数量关系,并说明理由.
(第7题)
【解】 DE =BF +EF .理由如下: ∵四边形ABCD 是正方形, ∴AB =DA ,∠DAB =∠ABC =90°.
∵DE ⊥AG 于点E ,BF ∥DE 交AG 于点F , ∴∠DEA =∠DEF =∠AFB =90°, ∴∠ADE +∠DAE =90°. ∵∠DAE +∠BAF =90°, ∴∠ADE =∠BAF . 在△ABF 和△DAE 中, ∵⎩⎪⎨⎪
⎧∠BAF =∠ADE ,∠AFB =∠DEA ,AB =DA , ∴△ABF ≌△DAE (AAS ). ∴BF =AE ,AF =DE .
∵AF =AE +EF ,∴DE =BF +EF .
8.如图,已知AE ⊥AB 且AE =AB ,BC ⊥CD 且BC =CD ,按照图中所标注的数据,则图中阴影部分图形的面积S 等于(A )
(第8题)
A. 50
B. 62
C. 65
D. 68
【解】 ∵EF ⊥AC ,BG ⊥AC ,
∴∠EF A =∠AGB =90°,∠FEA +∠EAF =90°. ∵EA ⊥AB , ∴∠EAB =90°. ∴∠EAF +∠GAB =90°. ∴∠FEA =∠GA B. 又∵AE =BA , ∴△EF A ≌△AGB (AAS ). ∴AF =BG ,EF =AG . 同理,△BGC ≌△CHD , ∴GC =HD ,BG =CH .
∴FH =F A +AG +GC +CH =3+6+4+3=16. ∴S =12×(6+4)×16-12×3×4×2-12
×6×3×2=50.
9.如图,在四边形ABCD 中,AB =BC ,∠ABC =∠CDA =90°,BE ⊥AD 于点E ,且四边形ABCD 的面积为9,则BE =(B )
(第9题) (第9题解)
A. 2
B. 3
C. 4
D. 5 【解】 如解图,过点B 作BF ⊥DC ,交DC 的延长线于点F . ∵∠CDA =90°,BE ⊥AD ,BF ⊥CD , ∴∠EBF =90°. 又∵∠ABC =90°,
∴∠ABE +∠EBC =∠CBF +∠EBC , ∴∠ABE =∠CBF . ∵BE ⊥AD ,BF ⊥DF , ∴∠AEB =∠CFB =90°.
又∵AB =CB , ∴△ABE ≌△CBF (AAS ). ∴BE =BF .
易知四边形BEDF 为正方形,
∴四边形ABCD 的面积等于正方形BEDF 的面积,即等于9, ∴BE 2=9,即BE =3.
10.如图,在△ABC 中,∠ABC =90°,AB =BC ,三角形的顶点在相互平行的三条直线l 1,l 2,l 3上,且l 1,l 2之间的距离为1,l 2,l 3之间的距离为2,过点A 作AE ⊥l 3于点E ,求BE 的长.
(第10题)
【解】 过点C 作CF ⊥l 3于点F .
∵l 1,l 2之间的距离为1,l 2,l 3之间的距离为2,AE ⊥l 3,CF ⊥l 3, ∴CF =3,∠AEB =∠BFC =90°. ∴∠EAB +∠ABE =90°. ∵∠ABC =90°, ∴∠ABE +∠FBC =90°. ∴∠EAB =∠FB C.
在△AEB 和△BFC 中,∵⎩⎪⎨⎪
⎧∠EAB =∠FBC ,∠AEB =∠BFC ,AB =BC ,
∴△AEB ≌△BFC (AAS ). ∴BE =CF =3.
11.如图,在四边形ABCD 中,AB ∥DC ,BE ,CE 分别平分∠ABC ,∠BCD ,且点E 在AD 上.求证:BC =AB +C D.
(第11题)
【解】在BC上截取BF=AB,连结EF.
∵BE平分∠ABC,CE平分∠BCD,
∴∠ABE=∠FBE,∠DCE=∠FCE.
又∵BE=BE,AB=FB,
∴△ABE≌△FBE(SAS).
∴∠A=∠BFE.
∵AB∥DC,∴∠A+∠D=180°.
∵∠BFE+∠CFE=180°,
∴∠D=∠CFE.
又∵∠DCE=∠FCE,CE=CE,
∴△DCE≌△FCE(AAS).∴CD=CF.
∴BC=BF+CF=AB+C D.
12.如图,在直角三角形ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分线,AD 与CE相交于点F,FM⊥AB,FN⊥BC,垂足分别为M,N.求证:FE=F D.
(第12题)
【解】连结BF.
∵F是∠BAC与∠ACB的平分线的交点,
∴BF是∠ABC的平分线.
又∵FM⊥AB,FN⊥BC,
∴FM =FN ,∠EMF =∠DNF =90°. ∵∠ACB =90°,∠ABC =60°, ∴∠BAC =30°,
∴∠DAC =1
2∠BAC =15°,
∴∠CDA =75°. 易得∠ACE =45°,
∴∠CEB =∠BAC +∠ACF =75°, 即∠NDF =∠MEF =75°.
在△DNF 和△EMF 中,∵⎩⎪⎨⎪
⎧∠DNF =∠EMF ,∠NDF =∠MEF ,NF =MF ,
∴△DNF ≌△EMF (AAS ). ∴FE =F D.。
