典型环节传递函数
合集下载
典型环节传递函数

θ 1 θ 2
u(t ) K1[1 (t ) 2 (t )] K1 (t )
K1 2 K11 图2-9 电位器
U(t)
K1是单个电位器的传递函数, (t ) 1 (t ) 2 (t ) 是两个电位器电刷角位移之差,称误差角。
U (s) K1 ( s )
5 振荡环节
n 1 G( s) 2 2 2 2 T S 2TS 1 S 2 n S n
2
T
1
式中 ξ-阻尼比 , (0 1) n -自然振荡角频率(无阻尼振荡角频率)
n
振荡环节的单位阶跃响应曲线
特点:环节中有两个独立的储能元件,并可进行能量交换,其
电位器的负载效应一般要求rl17测速发电机测量角速度并将它转换成电压量的装置直流测速发电机交流测速发电机dt图210测速发电机转子角速度radsktktsk18电枢控制直流伺服电动机例29中求得电枢控制直流电动机简化后的微分方程为tmk2tmk1tmk1stm图212两相伺服电动机两相定子线圈和一个高电阻值的转子组成
(b)
(t ) 转子角速度(rad/s)
Kt
Ω (s)
H (s)
Kt SKt 图2-11
U(s)
输出斜率(v/rad/s)
U ( s) Kt S ( s)
U(s)
G( s)
G( s)
U ( s) Kt ( )
18
电枢控制直流伺服电动机 例2-9中求得电枢控制直流电动机简化后的微分方程为
G (s) C (s) R( s)
如果将
S
d dt
置换 传递函数 微分方程
8
性质7
传递函数G(s)的拉氏反变换是脉冲响应g(t) 脉冲响应(脉冲过渡函数)g(t)是系统在单位脉冲输 入时的输出响应。
u(t ) K1[1 (t ) 2 (t )] K1 (t )
K1 2 K11 图2-9 电位器
U(t)
K1是单个电位器的传递函数, (t ) 1 (t ) 2 (t ) 是两个电位器电刷角位移之差,称误差角。
U (s) K1 ( s )
5 振荡环节
n 1 G( s) 2 2 2 2 T S 2TS 1 S 2 n S n
2
T
1
式中 ξ-阻尼比 , (0 1) n -自然振荡角频率(无阻尼振荡角频率)
n
振荡环节的单位阶跃响应曲线
特点:环节中有两个独立的储能元件,并可进行能量交换,其
电位器的负载效应一般要求rl17测速发电机测量角速度并将它转换成电压量的装置直流测速发电机交流测速发电机dt图210测速发电机转子角速度radsktktsk18电枢控制直流伺服电动机例29中求得电枢控制直流电动机简化后的微分方程为tmk2tmk1tmk1stm图212两相伺服电动机两相定子线圈和一个高电阻值的转子组成
(b)
(t ) 转子角速度(rad/s)
Kt
Ω (s)
H (s)
Kt SKt 图2-11
U(s)
输出斜率(v/rad/s)
U ( s) Kt S ( s)
U(s)
G( s)
G( s)
U ( s) Kt ( )
18
电枢控制直流伺服电动机 例2-9中求得电枢控制直流电动机简化后的微分方程为
G (s) C (s) R( s)
如果将
S
d dt
置换 传递函数 微分方程
8
性质7
传递函数G(s)的拉氏反变换是脉冲响应g(t) 脉冲响应(脉冲过渡函数)g(t)是系统在单位脉冲输 入时的输出响应。
大学自动控制原理2.4典型环节传递函数

02
传递函数的零点和极点决定了系统的动态特性和稳定性。
03
传递函数的分子和分母多项式决定了系统的频率响应特性。
典型环节的分类
比例环节
输出信号与输入信号成正比,传递函 数为 G(s) = K,其中 K 为常数。
02
积分环节
输出信号与输入信号的时间积分成正 比,传递函数为 G(s) = 1 / (sT),其 中 T 为时间常数。
将介绍控制系统的稳定性 分析方法。
掌握频率响应法在控制系 统设计中的应用。
学习如何利用根轨迹法进 行系统性能分析。
了解现代控制系统的基本 概念和分类。
THANKS FOR WATCHING
感谢您的观看
高阶环节的传递函数具有多个极点和零点,这些极点和零点 决定了环节的动态特性,如响应速度、超调和调节时间等。
实例分析
以一个三阶惯性环节为例,其传递函数为 $G(s) = frac{1}{s^3 + 2s^2 + 3s + 1}$,该环节具有三个极点 $s = -1, -1, -1$ 和一个 零点 $s = 0$。
拉普拉斯变换中的频率。
该传递函数是一个有理分式,分 母为线性多项式,分子为常数。
当输入信号 (s) 变化时,输出信 号 (G(s)) 会根据增益 (K) 和时间
常数 (T) 进行相应的变化。
实例分析
实例1
一阶惯性环节在电机控制系统中的应用,用于描述电机的动态响应特性。
实例2
在温度控制系统中的一阶惯性环节,用于描述加热元件的热量传递和散热过程。
04 一阶惯环节
定义与特点
定义
一阶惯性环节的传递函数为 (G(s) = frac{K}{T s + 1}),其中 (K) 是增益,(T) 是时间常 数。
传递函数的零点和极点决定了系统的动态特性和稳定性。
03
传递函数的分子和分母多项式决定了系统的频率响应特性。
典型环节的分类
比例环节
输出信号与输入信号成正比,传递函 数为 G(s) = K,其中 K 为常数。
02
积分环节
输出信号与输入信号的时间积分成正 比,传递函数为 G(s) = 1 / (sT),其 中 T 为时间常数。
将介绍控制系统的稳定性 分析方法。
掌握频率响应法在控制系 统设计中的应用。
学习如何利用根轨迹法进 行系统性能分析。
了解现代控制系统的基本 概念和分类。
THANKS FOR WATCHING
感谢您的观看
高阶环节的传递函数具有多个极点和零点,这些极点和零点 决定了环节的动态特性,如响应速度、超调和调节时间等。
实例分析
以一个三阶惯性环节为例,其传递函数为 $G(s) = frac{1}{s^3 + 2s^2 + 3s + 1}$,该环节具有三个极点 $s = -1, -1, -1$ 和一个 零点 $s = 0$。
拉普拉斯变换中的频率。
该传递函数是一个有理分式,分 母为线性多项式,分子为常数。
当输入信号 (s) 变化时,输出信 号 (G(s)) 会根据增益 (K) 和时间
常数 (T) 进行相应的变化。
实例分析
实例1
一阶惯性环节在电机控制系统中的应用,用于描述电机的动态响应特性。
实例2
在温度控制系统中的一阶惯性环节,用于描述加热元件的热量传递和散热过程。
04 一阶惯环节
定义与特点
定义
一阶惯性环节的传递函数为 (G(s) = frac{K}{T s + 1}),其中 (K) 是增益,(T) 是时间常 数。
自动控制理论_哈尔滨工业大学_2 第2章线性系统的数学模型_(2.4.1) 典型环节的传递函数PPT

0
t
积分环节在单位阶跃输入下的响应
例:积分器
i2
C
ui R
_
i1
uo
+i1 i2Fra bibliotek1 Rui
(t)
C
d dt
u0
(t )
uo
(t)
1 RC
ui (t)dt
G(s) Uo (s) 1 1 Ui (s) RC s
二、几种典型环节的数学模型
4.微分环节
c(t) d r(t)
斜率1/T
0τ
t
例: • 汽车加速、火箭升空; ——作用力和输出速度
• 加热系统; ——加热量和温度变化
• 励磁回路; ——输入电压和励磁电流
惯性大小用τ来量度。 ——τ越大,接近目标值越慢 ,惯性越大;τ越小,接近 目标值越快,惯性越小。
几乎任何物理系统都包含 大大小小的惯性。
二、几种典型环节的数学模型
滞后环节
二、几种典型环节的数学模型
1.比例环节
y(t) Ku(t)
G(s) Y(s) K U (s)
K——称为比例系数或放大系数,也称为环节的增益,有量纲。
输出量无失真、无滞后、成比例地复现输入。
• 无弹性变形的杠杆;
——作用力和输出力
• 忽略非线性和时间迟后的运算放大器;
——比例放大器的输入电压和输出电压
τ=RC—时间常数
当 r(t) 1(t) 时, R(s) 1
s
Y(s) s 1 1 s 1 s s 1
t
y(t) e
t=0时,输出幅值为1;
t→∞时,指数衰减至0。
二、几种典型环节的数学模型
第2章_控制系统的动态数学模型_2.4传递函数以及典型环节的传递函数

《控制工程基础》 控制工程基础》
第2章 控制系统的动态数学模型 2.4 传递函数以及典型环节的传递函数
2.4.1 传递函数的基本概念 (1)传递函数的定义 )
线性定常系统在零初始条件下,输出量的 拉氏变换与输入量的拉氏变换之比,称为该系统 的传递函数。
X o (s ) G (s ) = X i (s )
m n bm * K = =K ∏(-Zi ) / ∏(− pj ) an i=1 j =1
∏(s − zj ) j=1
m
∏(s − pi ) i=1
n
为传递函数的增益
b0 K = a0
*
为根轨迹增益
T和τi 为时间常数 i
零、极点分布图:
b0(s − z1)(s − z2 )… (s − zm) M(s) … G(s) = = a0 (s − p1)(s − p2)… (s − pn ) D(s) …
描述该线性定常系统的传递函数为
…+bm−1s + bm Xo (s) b0sm + bsm−1 +… 1 G(s) = = Xi (s) a0sn + a1sn−1 +… …+ an−1s + an M(s) = D(s)
式 : (s) = b0sm + bsm−1 +… 中 M …+ bm−1s + bm 1 D(s) = a0sn + a1sn−1 +… …+ an−1s + an
LCs U c ( s ) + RCsU c ( s ) + U c ( s ) = U r ( s )
2
按照定义,系统的传递函数为:
U c (s) 1 = G (s) = U i ( s ) LCs 2 + RCs + 1
第2章 控制系统的动态数学模型 2.4 传递函数以及典型环节的传递函数
2.4.1 传递函数的基本概念 (1)传递函数的定义 )
线性定常系统在零初始条件下,输出量的 拉氏变换与输入量的拉氏变换之比,称为该系统 的传递函数。
X o (s ) G (s ) = X i (s )
m n bm * K = =K ∏(-Zi ) / ∏(− pj ) an i=1 j =1
∏(s − zj ) j=1
m
∏(s − pi ) i=1
n
为传递函数的增益
b0 K = a0
*
为根轨迹增益
T和τi 为时间常数 i
零、极点分布图:
b0(s − z1)(s − z2 )… (s − zm) M(s) … G(s) = = a0 (s − p1)(s − p2)… (s − pn ) D(s) …
描述该线性定常系统的传递函数为
…+bm−1s + bm Xo (s) b0sm + bsm−1 +… 1 G(s) = = Xi (s) a0sn + a1sn−1 +… …+ an−1s + an M(s) = D(s)
式 : (s) = b0sm + bsm−1 +… 中 M …+ bm−1s + bm 1 D(s) = a0sn + a1sn−1 +… …+ an−1s + an
LCs U c ( s ) + RCsU c ( s ) + U c ( s ) = U r ( s )
2
按照定义,系统的传递函数为:
U c (s) 1 = G (s) = U i ( s ) LCs 2 + RCs + 1
2-4 典型环节及其传递函数

1
气阻的数学表达式为 ∆p = R∆q ∆p 式中, 是气体压力降 ; ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ; R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) (3)喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 1,背压室 2,喷嘴 3,和挡板 4 组成,如图 2-18 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时,可把喷嘴 1 2 4 一挡板机构看作一个比例环节,即 3 D ∆p D = k 1 ∆h 式中, 是喷嘴背压的变化; ∆p D ∆h 是挡板开度变化量; 是比例系数。 k1 d (4)放大器 h 在自动控制系统中用得最多的是运算放大 器,它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成,其符号如图 2- 3 − 喷嘴 4 − 挡板 19 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端,输出电压为 u 0 (t ) 它有两个输入端,一个是同相输入端 b 用 “十”表示,一个是反相输入端 a 用“一”表示。当 放大器工作在放大区而不是饱和区时,输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中, 为开环放大倍数,这个数值很高,可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点: ①由于开环输入电阻很高,运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高,所以 b 端和 C 端电位接近相等,即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节,但可用它来组成其他各种基本环节。
气阻的数学表达式为 ∆p = R∆q ∆p 式中, 是气体压力降 ; ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ; R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) (3)喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 1,背压室 2,喷嘴 3,和挡板 4 组成,如图 2-18 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时,可把喷嘴 1 2 4 一挡板机构看作一个比例环节,即 3 D ∆p D = k 1 ∆h 式中, 是喷嘴背压的变化; ∆p D ∆h 是挡板开度变化量; 是比例系数。 k1 d (4)放大器 h 在自动控制系统中用得最多的是运算放大 器,它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成,其符号如图 2- 3 − 喷嘴 4 − 挡板 19 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端,输出电压为 u 0 (t ) 它有两个输入端,一个是同相输入端 b 用 “十”表示,一个是反相输入端 a 用“一”表示。当 放大器工作在放大区而不是饱和区时,输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中, 为开环放大倍数,这个数值很高,可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点: ①由于开环输入电阻很高,运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高,所以 b 端和 C 端电位接近相等,即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节,但可用它来组成其他各种基本环节。
5-典型环节传递函数-振荡环节
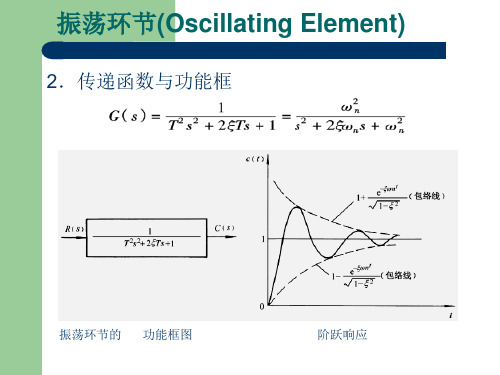
振荡环节(Oscillating Element)
2.传递函数与功能框
振荡环节的 功能框图阶跃响应振荡环节(Oscillating Element)
3.动态
当ξ=0时,c(t)为等幅自由振荡(又称为无阻尼振荡)。 其振荡频率为ωn,ωn称为无阻尼自然振荡 频率。
当0<ξ<1时,c(t)为减幅振荡(又称为阻尼振荡)。其振 荡频率为ωd, ωd称为阻尼自然振荡频率。
振荡环节(Oscillating Element)
4.举例
【实例1】 图为一RLC串联电路。若以 电源电压作为输入电压 ,以电容器两 端电压作为输出电压,此电路的传递 函数。并分析此为振荡电路的条件。 【解】 由基尔霍夫定律有
而流过电容的电流
其传递函数
2.传递函数与功能框
振荡环节的 功能框图阶跃响应振荡环节(Oscillating Element)
3.动态
当ξ=0时,c(t)为等幅自由振荡(又称为无阻尼振荡)。 其振荡频率为ωn,ωn称为无阻尼自然振荡 频率。
当0<ξ<1时,c(t)为减幅振荡(又称为阻尼振荡)。其振 荡频率为ωd, ωd称为阻尼自然振荡频率。
振荡环节(Oscillating Element)
4.举例
【实例1】 图为一RLC串联电路。若以 电源电压作为输入电压 ,以电容器两 端电压作为输出电压,此电路的传递 函数。并分析此为振荡电路的条件。 【解】 由基尔霍夫定律有
而流过电容的电流
其传递函数
2-4 典型环节及其传递函数

∫
G ( s ) = R / Ts ,这也是一个积分环节。从物理意义上说,由于液箱的液容 C 太大,或液阻 R
太大,液箱流出水量不足以影响液位,如果流入水量不变,液位将随时间不断增高(积分作 用)。 另外对直流伺服电动机,由于电气时间常数和机电时间常数大小,忽略不计时,该电动 机以转速为输出量,电枢电压为输入量时的动态特性成为比例环节,其传递函数为 N (s) G( s ) = =k U a (s) 如以电动机输出轴转角为输出量,相应的传递函数是 a ( s) k G( s ) = = U a (s) s 这是一个积分环节。可见,对于同一部件,不同输入或不同输出时,其传递函数是不同的。 最后,考虑气动仪表中常用的气容,它是一个气体容室能储存或放出气体,对气体量的 变化起惯性作用,类似于电路中的电容,见图 2-20。 通常采用“气容”这个概念来定量地表示气室储存气体的能力,其定义为 ∆m C= ∆p 式中, 是空气储存量的增量; ∆m ∆p 是气室压力的增量。 气体的质量流量(kg/s)为 ∆q (t ) = d (∆m ) / dt
5
R2 R1
Ui Ri
图 2-23 运算放大器 组成的一阶惯性环节
−
+
C
U0
式中,时间常数 T=RC。 实际上这是纯微分环节与一阶惯性环节相串联后构成的环节;当时间常数 T<<1 时,一阶 惯性环节相当于 1:1 的比例环节,因而总的传递函数相当于微分环节的传递函数。 当然也可以用运算放大器来组成微分环节,如 R 图 2-24 所示。 该运放电路的传递函数为 if C U 0 (s) Ui G( s ) = = − RCs U i (s) U0 这就相当于一个纯微分环节。 + i
−
2
典型环节的传递函数

典型环节的传递函数
1、比例环节 凡输出量与输入量成正比,输出不失真也不延迟 而按比例地反映输入的环节,称为比例环节又叫 放大环节、无惯性环节、零阶环节
•动力学方程为:
xotKxit
•传递函数为:
Gs
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比,称为积分环节, 又称为理想积分环节
•动力学方程为:
Tdxdottxotxit
•传递函数为:
GsXXoi ss
1 Ts1
典型环节的传递函数
5、导前环节(一阶微分环节) 又称为一阶微分环节,是一个相位超前环节。
•传递函数为:
GsXXoi ssTs1
典型环节的传递函数
6、振荡环节(二பைடு நூலகம்积分环节) 振荡环节是二阶环节,又称二阶振荡环节
•传递函数为:
•动力学方程为:
xotT1xi tdt
•传递函数为:
Gs
Xo s Xi s
1 Ts
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比,称为微分环节, 又称为理想微分环节
•动力学方程为:
xo
t
T
dxi t
dt
•传递函数为:
Gs
Xo s Xi s
Ts
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节,是一个相位滞后环节。
G sX Xo isss22 n 2 nsn 2
GsX Xo issT2s22 1Ts1
典型环节的传递函数
7、二阶微分环节
•传递函数为:
G sX Xo isss22 n 2 nsn 2 GsX Xo issT2s22Ts1
1、比例环节 凡输出量与输入量成正比,输出不失真也不延迟 而按比例地反映输入的环节,称为比例环节又叫 放大环节、无惯性环节、零阶环节
•动力学方程为:
xotKxit
•传递函数为:
Gs
Xo s Xi s
K
典型环节的传递函数
2、积分环节(纯积分环节) 凡输出量与输入量的积分成正比,称为积分环节, 又称为理想积分环节
•动力学方程为:
Tdxdottxotxit
•传递函数为:
GsXXoi ss
1 Ts1
典型环节的传递函数
5、导前环节(一阶微分环节) 又称为一阶微分环节,是一个相位超前环节。
•传递函数为:
GsXXoi ssTs1
典型环节的传递函数
6、振荡环节(二பைடு நூலகம்积分环节) 振荡环节是二阶环节,又称二阶振荡环节
•传递函数为:
•动力学方程为:
xotT1xi tdt
•传递函数为:
Gs
Xo s Xi s
1 Ts
典型环节的传递函数
3、微分环节(纯微分环节) 凡输出量与输入量的微分成正比,称为微分环节, 又称为理想微分环节
•动力学方程为:
xo
t
T
dxi t
dt
•传递函数为:
Gs
Xo s Xi s
Ts
典型环节的传递函数
4、惯性环节(一阶积分环节) 又称一阶惯性环节,是一个相位滞后环节。
G sX Xo isss22 n 2 nsn 2
GsX Xo issT2s22 1Ts1
典型环节的传递函数
7、二阶微分环节
•传递函数为:
G sX Xo isss22 n 2 nsn 2 GsX Xo issT2s22Ts1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电位器的负载效应,一般要求
Rl 10R p
17
测速发电机-测量角速度并将它转换成电压量的装置
直流测速发电机 交流测速发电机
ω
U(t)
TG
ω
激磁绕组 ~ TG
~
永磁铁 (a)
输出绕组、相互垂直 U(t)
d (t ) U (t ) K t (t ) K t dt
图2-10 测速发电机
(Tm S 1) m (s) K1U a (s)
m ( s) K1 U a ( s) Tm S 1
由传递函数定义 B 令 U a (t ) 0
G( s)
Tm Sm (s) m (s) K 2 M c (s)
Gm( s) m ( s) K2 M c ( s) Tm S 1
B( s ) ( s p1 )(s p 2 )]s p1 A( s)
[a1 s a 2 ] s p1 [
c.F(s)含有多重极点时,可展开为
F ( s) an br br 1 b1 ar 1 (s p1 ) r ( s p1 ) r 1 ( s p1 ) ( s pr 1 ) (s pn )
(b)
(t ) 转子角速度(rad/s)
Kt
Ω (s)
H (s)
Kt SKt 图2-11
U(s)
输出斜率(v/rad/s)
U ( s) Kt S ( s)
U(s)
G( s)
G( s)
U ( s) Kt ( s)
18
电枢控制直流伺服电动机 例2-9中求得电枢控制直流电动机简化后的微分方程为
传递函数及其性质
典型元部件的传递函数
1
数学工具-拉普拉斯变换与反变换
⑴ 拉氏变换定义 设函数f(t)满足 ①t<0时 f(t)=0
f (t )e st dt 0 则f(t)的拉氏变换存在,其表达式记作
② t>0时,f(t)分段连续
⑵拉氏变换基本定理
线性定理 位移定理 延迟定理 终值定理
B( s) br [ ( s p1 ) r ] s p1 A( s)
br j 1 d j B( s ) { j[ ( s p1 ) r ]}s p1 j! ds A( s)
br 1 {
d B( s ) [ ( s p1 ) r ]}s p1 ds A( s)
m
2
m
U (s) K1(s)
U ( s) G( s) K1 ( s)
H(s) K1 (c)
U(s)
12
2.3.5典型环节及其传递函数 任何一个复杂系统都是由有限个典型环节组合而成的。
典型环节通常分为以下六种: 1 比例环节
G( s) K
式中 K-增益 特点:输入输出量成比例,无失 真和时间延迟。 实例:电子放大器,齿轮,电阻 (电位器),感应式变送器等。
lim f (t ) lim sF ( s )
s 0
2
数学工具-拉普拉斯变换与反变换续
初值定理
微分定理 积分定理
t 0
lim f (t ) lim sF ( s )
s
df (t ) L[ ] sF ( s ) f (0) dt
F ( s) f 1 (0) L[ f (t )dt] s s
G (s) C (s) R( s)
如果将
S
d dt
置换 传递函数 微分方程
8
性质7
传递函数G(s)的拉氏反变换是脉冲响应g(t) 脉冲响应(脉冲过渡函数)g(t)是系统在单位脉冲输 入时的输出响应。
R( s) L[ (t )] 1
c(t ) L1[C (s)] L1[C (s) R(s)] r (t ) g (t )d r (t ) g ( )d
10
2.3.4典型元部件的传递函数 电位器-将线位移或角位移变换为电压量的装置。 单个电位器用作为信号变换装置。
E -电位器电源(v)
max -电位器最大工作角(rad)
11
图2-8 电位器
E
U (t )
U(t)
θ
-∏
∏
(t )
(b)
(a)
U (t ) K1 (t )
E E K1 2
F (s) L[ f (t )] f (t )e st dt
0
L[a1 f1 (t ) a2 f 2 (t )] a1 F1 (s) a2 F2 (s)
L[e at f (t )] F (s a)
L[ f (t )] e s F (s)
t
d 2 f (t ) L[ ] s 2 F ( s) sf (0) f ' (0) 2 dt
L[
F ( s) f 1 (0) f 2 (0) f (t )dt] 2 s s2 s
⑶ 拉氏反变换
F(s)化成下列因式分解形式:
B(s) k ( s z1 )(s z 2 ) (s z m ) F ( s) A(s) ( s p1 )(s p2 ) (s pn )
5 振荡环节
n 1 G( s) 2 2 2 2 T S 2TS 1 S 2 n S n
2
T
1
式中 ξ-阻尼比 , (0 1) n -自然振荡角频率(无阻尼振荡角频率)
n
振荡环节的单位阶跃响应曲线
特点:环节中有两个独立的储能元件,并可进行能量交换,其
a.F(s)中具有不同的极点时,可展开为
F ( s) an a1 a2 s p1 s p2 s pn
ak [
B( s) ( s p k )]s pk A( s)
3
b.F(s)含有共扼复数极点时,可展开为
F ( s) a3 an a1 s a2 (s p1 )(s p2 ) s p3 s pn
于是,由定义得系统传递函数为:
6
C (s) b0 s m b1 s m1 bm1 s bm M (s) G( s ) n n 1 R(s) a0 s a1 s an1 s an N ( s)
M (s) b0 s m b1s m1 bm1s bm N (s) a0 s n a1s n1 an1 s an
式中c(t)是系统输出量,r(t)是系统输入量,和
是与系统结构和参数有关的常系数。 设r(t)和c(t)及其各阶系数在t=0是的值均为零, 即零初始条件,则对上式中各项分别求拉氏变换, 并令R(s)=L[c(t)],R(s)=L[r(t)],可得s的代 数方程为:
[a0 s n a1s n1 an1s an ]C(s) [b0 s m b1s m1 bm1s am ]R(s)
θ 1 θ 2
u(t ) K1[1 (t ) 2 (t )] K1 (t )
K1 2 K11 图2-9 电位器
U(t)
K1是单个电位器的传递函数, (t ) 1 (t ) 2 (t ) 是两个电位器电刷角位移之差,称误差角。
U (s) K1 ( s )
性质4
如果G(s)已知,那么可以研究系统在各种输入信号作用 下的输出响应。 性质5 如果系统的G(s)未知,可以给系统加上已知的输入,研 究其输出,从而得出传递函数,一旦建立G(s)可以给出 该系统动态特性的完整描述,与其它物理描述不同。 传递函数数学模型 是(表示)输出变量和输入变量 微分方程的运算模型(operational mode) 性质6 传递函数与微分方程之间有关系。
输出信号的拉氏变换 C ( s) 传递函数 输入信号的拉氏变换零初始条件 R(s)
5
设线性定常系统由下述n阶线性常微分方程描述:
dn d n 1 d a0 n c(t ) a1 n 1 c(t ) a n 1 c(t ) a n c(t ) dt dt dt dm d m1 d b0 m r (t ) b1 m1 r (t ) bm1 r (t ) bm r (t ) dt dt dt
1 d r 1 B( s) b1 { r 1 [ ( s p1 ) r ]}s p1 (r 1)! ds A( s)
4
其余各极点的留数确定方法与上同。
2.3 控制系统的复域数学模型 2.3.1 传递函数
是在用拉氏变换求解线性常微分方程的过程中引申出来的
概念。 微分方程是在时域中描述系统动态性能的数学模型,在给 定外作用和初始条件下,解微分方程可以得到系统的输出 响应。系统结构和参数变化时分析较麻烦。 用拉氏变化法求解微分方程时,可以得到控制系统在复数 域的数学模型-传递函数。 定义:线性定常系统的传递函数,定义为零初使条件下, 系统输出量的拉氏变换与输入量的拉氏变换之比。
特点: 输出量正比输入量变化的速度,能预示输入
信号的变化趋势。 实例: 测速发电机输出电压与输入角度间的传递函数 14 即为微分环节。
4 积分环节
1 G (s) TS
特点: 输出量与输入量的积分成正比
例,当输入消失,输出具有记忆功能。 实例: 电动机角速度与角度间的传递 函数,模拟计算机中的积分器等。
Tm d m (t ) m (t ) K1U a (t ) K 2 M c (t ) dt
M c (t ) 可视为负载扰动转矩。根据线性系统的叠加原理,分别求
U a (t )
到
m (t )
