高等数学教学课件-09空间解析几何
大学高数空间解析几何
学习空间解析几何有助于培养人的逻辑思维和抽象 思维能力，提高解决问题的能力。
空间解析几何的历史与发展
早期发展
空间解析几何起源于17世纪，随着笛卡尔坐标系的建立和 解析几何方法的完善，开始形成独立的数学分支。
近代发展
随着计算机科学和数学的不断发展，空间解析几何在理论 和应用方面都取得了重要进展，如微分几何、线性代数和 微分方程等与空间解析几何的交叉融合。
详细描述
如果两个平面的法向量 $mathbf{a}$ 和 $mathbf{b}$ 是共线的，即存在一个非零实数 $lambda$ 使得 $mathbf{a} = lambda mathbf{b}$，那么这两个平面就是平行的。如果两个平面的法向量不共线，那么 这两个平面就是相交的。
04
空间几何的应用
空间几何在计算机图形学中的应用
01
02
03
三维建模
空间几何用于创建三维模 型，包括曲面建模、实体 建模和参数化建模等。
光照计算
空间几何用于计算物体表 面的光照效果，以实现逼 真的渲染效果。
动画制作
空间几何用于动画制作中 的骨骼绑定、运动轨迹规 划和角色动画等，以创建 动态的视觉效果。
05
空间几何的习题与解答
平面与平面的交线
总结词求平面与平面Fra bibliotek交线，需要消元法或参数方程法。
详细描述
平面与平面的交线可以通过消元法或参数方程法来求解。消元法是通过联立两个平面的方程组，然后消元得到一 个一元一次方程，这个一元一次方程就是两平面的交线。参数方程法则是设定一个参数，将两个平面的方程都表 示成参数的函数，然后令参数相等，解出交线的参数方程。
未来展望
随着科技的不断进步和应用领域的拓展，空间解析几何将 继续发挥重要作用，并有望在人工智能、机器学习等领域 取得新的突破和应用。
空间解析几何.pdf
第一章 高等数学 第一节 空间解析几何一、向量代数（一）向量及其线性运算既有大小又有方向的量，如位移、速度、力等这类量，称为向量，向量 a 的大小称为向量 a 的模，记作| a |。
模等于1的向量叫做单位向量，向量的加减法、向量与数的乘法统称为向量的线性运算。
向量a 与向量 b 的和 a + b 是一个向量 c ，利用平行四边形法则或三角形法则可得向量c ，如图 1-1-1 ，图 1-1-2 所示。
向量的加法符合下列运算规律： ① 交换律 a + b = b + a② 结合律(a + b)+c＝ a +(b+c）向量 b 与向量 a 的差 b - a 定义为向量 b 与 a 的负向量-a 的和，即b - a = b + (-a)由向量加法的三角形法则可知：() |a| = |-a|向量 a 与实数λ的积记作λa ，它是一个向量，它的模它的方向当λ＞ 0 时，与向量 a 相同；当λ＜ 0 时，与向量 a 相反。
向量与数的乘积符合下列运算规律：由向量与数的乘积的定义，可得以下定理：定理 设向量 a≠0 ，那么，向量 b 与向量 a 平行的充分必要条件是：存在惟一的实数λ，使 b =λa 。
（二）向量的坐标设有空间直角坐标系 O - xyz ， i、 j、 k 分别表示沿 x 、 y 、 z 轴正向的单位向量， 12a M M是以1111(,,)M x y z 为起点，2222(,,)M x y z 为终点的向量，则向量a 可表示为其中212121x x y y z z ---、、称为向量 a 的坐标。
利用向量的坐标，可得向量的加法、减法以及向量与数的乘法运算如下：非零向量 a 与三条坐标轴正向的夹角αβγ、、称为它的方向角。
向量的模、方向角与坐标之间关系：其中cos cos cos αβγ、、称为向量 a 的方向余弦。
利用向量的坐标可得向量的模与方向余弦如下：（三）数量积 向量积设向量a 和向量 b 的夹角为θθπ≤≤（0）,向量 a 和向量 b 的数量积为一个数量，记作a b ⋅ ，其大小为||||cos a b θ，即a ⊥b 的充分必要条件是 a .b =0向量 a 在轴u 上的投影（记作 Prj u a ）等于向量 a 的模乘以轴与向量a 的夹角φ的余弦，即利用向量在轴上的投影，可将数量积表为向量 a 和向量 b 的向量积为一个向量 c ，记作 a × b ，即c ＝ a × b ，c 的模c 的方向垂直于 a 与 b 所决定的平面， c 的指向按右手法则确定。
《高等数学(下册)》 第9章
（1）结合律： (a) (a) ()a ； （2）分配律： ( )a a a ，(a b) a b ． 这里 a ，b 为向量， ， 为实数．
向量的加法运算以及向量的数乘运算统称为向量的线性运算．
9.1.2 向量的线性运算
设 a 0 ，与 a 同方向的单位向量记为 ea ，由数与向量乘积的定义有 a | a | ea ，
9.2.2 向量的坐标表示
3 4 2
解法一 按对角线法则，有
D 1 2 (2) 2 1 (3) (4) (2) 4 11 4 2 (2) (2) (4) 2 (3) 4 6 32 4 8 24 14．
解法二 按第一行展开，有
2 D 1
1 2 2
1
2
(4)
2 1 (4 4) 2 (4 3) (4) (8 6) 14 ．
x 为数轴上点 P 的坐标．
9.1.3 二阶与三阶行列式
1．二阶行列式 由 4 个数排成 2 行 2 列（横排称行、竖排称列）的数表
a11 a12 a21 a22 ， 表达式 a11a22 a12a21 称为该数表所确定的二阶行列式，并记作
a11 a12 ． a21 a22
数 aij (i 1，2 ；j 1，2) 称为二阶行列式的元素，元素 aij 中的第一个下标 i 和第二个下 标 j 分别表示该元素所在的行数和列数．例如，元素 a21 在行列式中位于第二行、第一列．
9.1.3 二阶与三阶行列式
例1 计算二阶行列式 2 1 ． 1 3
解 2 1 2 (3) 11 7 ． 1 3
9.1.3 二阶与三阶行列式
2．三阶行列式 由 9 个数排成 3 行 3 列的数表
a11 a12 a13 a21 a22 a23 a31 a32 a33 ，
《高数空间解析几何》PPT课件
8
椭圆柱面：
z
x2 a2
y2 b2
1
xoy 坐标面上的椭圆为准线、
3
P26例 5
xoz 坐标面上的双曲线
x2 a2
z2 c2
1分别绕 x、z 轴旋
转一周，求所得旋转曲面方程
x2 y2y2 z2
绕 x 轴转所得曲面称为旋转双叶双曲面,
z
曲面方程为
x2 y2 z2 a2 c2 c2 1
o
x
绕 z 轴转所得曲面称为旋转单叶双曲面,
z
曲面方程为
x2 y2 z2 a2 a2 c2 1
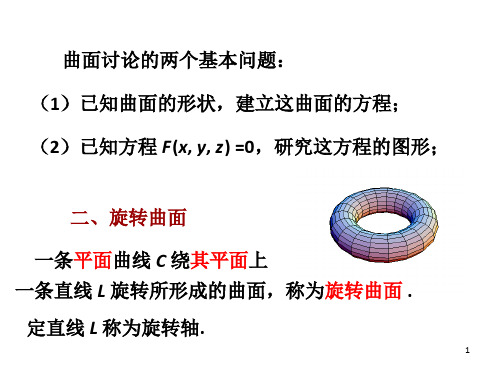
曲面讨论的两个基本问题： （1）已知曲面的形状，建立这曲面的方程； （2）已知方程 F(x, y, z) =0，研究这方程的图形；
二、旋转曲面 一条平面曲线 C 绕其平面上 一条直线 L 旋转所形成的曲面，称为旋转曲面 . 定直线 L 称为旋转轴.
1
建立 y oz 面上曲线 C : f ( y , z ) = 0绕 z 轴旋转所成
例
求曲线
:
x2
x
2
y2 y2
z2 8y
64
,
在 xoy, y0z 坐标面上的投影曲线的方程.
解 关于xo y 坐标面的投影
柱面方程 x 2 y 2 8 y
因而曲线 在 xo y 坐标
面上的投影曲线是圆.
1
y 0
y2 z2
b2
c2
高数课件PPT
插值法的概念与应用
概念
插值法是一种数学方法，通过已知的 离散数据点，构造一个多项式函数， 使得该函数在已知数据点上的取值与 实际值相等。
应用
插值法在数学、物理、工程等领域有 广泛应用，如数据拟合、数值积分、 微分、求解方程等。
拉格朗日插值法与牛顿插值法
拉格朗日插值法
拉格朗日插值法是一种基于拉格朗日多项式的插值方 法，通过构造一个拉格朗日多项式来逼近已知数据点 。该方法具有较好的数值稳定性和收敛性。
两个向量的点积等于它 们的模的乘积和它们夹 角的余弦值的乘积。
两个向量的叉积是一个 向量，其方向垂直于作 为叉积运算输入的两个 向量，大小等于这两个 向量构成的平行四边形 的面积。
三个向量的混合积等于 它们构成的平行六面体 的体积。
两个向量的数量积等于 它们的模的乘积和它们 夹角的余弦值。
空间直角坐标系与向量的表示
详细描述
极限的运算规则包括极限的四则运算法则、复合函数的极限运算法则等。这些规则能够帮助我们简化 极限的计算过程，提高计算的准确性和效率。在进行极限运算时，需要注意一些常见的错误，例如无 穷大与无穷小的混淆、未定式的误解等。
03
导数与微分
导数的定义与性质
导数的定义
01
导数描述了函数在某一点的斜率，即函数值随自变量变化的速
率。
单侧导数
02
在函数定义域的某一点，可以定义左侧或右侧的导数，表示函
数在该点的切线斜率。
导数的几何意义
03
导数在几何上表示函数图像在该点的切线斜率。
导数的运算规则
链式法则
对于复合函数的导数，链式法则是重要的运算规则，表示对复合 函数的内部函数求导后再乘以外部函数的导数。
向量代数与空间解析几何—空间解析几何(高等数学课件)
2 + 2 + 2 + 2 = 0 .
方程组（1）我们称之为直线的一般式方程。
(1)
2.空间直线的点向式方程
1.二元极限定义
与直线平行（共线）的非零向量称为直线的方向向量．
设已知直线 L 过点 M 0 ( x0 , y0 , z0 )，其方向向
（1）过点 A(1, 2,3) ， B(1,1, 1) 的直线方程；
x 1 y 1 z 2
（2）过点 M (0, 2,3) ，且与直线 L1 :
平行的直线方程；
3
2
1
（3）过点 P(2,1,3) ，且与平面 π : 3x 2 y z 1 0 垂直的直线方程．
例题
一点.因为向量 ⊥平面，0 ⊂平面，所以 ⊥ 0 .
由向量垂直的充要条件可知 ⋅ 0 = 0，
而0 = − 0 , − 0 , − 0 ，根据向量数量积的坐标表达式有：
− 0 + − 0 + − 0 = 0
此方程是由平面上一个点的坐标和平面的法向量确定的，因此，我们称之为平面的
出了平面平行或垂
直的判定方法。
空间上点到平面
的距离公式。
思考题
求满足下列条件的平面方程：
(1)过原点且法向量 = 1,2,3 ；
一元函数，但在自然科学和工程两
(2)在, , 轴上的截距分别是2, −3,4
空间直线及其方程
知识点讲解
1.空间直线的一般式方
程
2.空间直线的点向式方程
3.空间直线的参数方程
1.空间直线的一般方程式
大学数学专业空间解析几何向量代数PPT课件
它 们 的 和 是 零 矢 量.
C
证 必 要 性 设 三 矢 量a，b，c可 以
构 成 三 角 形ABC， 即 有AB a, BC A
B
b,CA c， 那 么AB＋BC＋CA＝AA 0,即a b c 0
充 分 性 设a b c 0， 作AB a, BC b, 那 么AC
a b, 所 以AC c 0, 从 而c是 AC的反矢 量，因此c＝
叫 做 矢 量a1 , a2 ,, an的 线 性 组 合.
定理1.4.4 在n 2时，矢量a1, a2 ,, an线性相关的 充 要 条 件 是 其 中 有 一 个矢 量 是 其 余 矢 量 的 线 性组 合.
第34页/共137页
定理1.4.6 两矢量共线的充要条件是它们线性相关.
定 义1.4.2 对 于n(n 1)个 矢 量a1, a2 ,, an， 如 果 存
r xe1 ye2 ze3 ,
(1.4 3)
并 且 其 中 系 数x, y, z被e1 , e2 , e3 , r唯 一 确 定.
这时e1, e2 , e3叫做空间矢量的基底.
第38页/共137页
定 理1.4.3 如 果 矢 量e1 , e2 , e3不 共 面 ， 那 么 空 间
任 意 矢 量r可 以 由 矢 量e1 , e2 , e3线 性 表 示 ， 或 说 空 间 任 意 矢 量r可 以 分 解 成 矢 量e1 , e2 , e3的 线 性 组 合 ， 即
A
Q M
B
P
CB
由条件可知: BC = 2BP, AC = 2AQ.
S
Q
T
P
C
设AS = AP, B2T = BQ,
2
3
吉林大学高职高专《高等数学》第09章
这就是平面的方程, 称为点法式方程.
过点M0(x0, y0, z0)且法线向量为n(A, B, C)的平面的方程
为 A(xx0)B(yy0)C(zz0)0.
41
二、平面的一般方程
由于平面的点法式方程是x, y, z的一次方程, 而任一平面 都可以用它上面的一点及它的法线向量来确定, 所以任一平 面都可以用三元一次方程来表示 .
以轴与向量的夹角的余弦：Pr jl AB | AB | cos
证
B
A
B
A
B
Pr jl AB Pr jl' AB
l'
l
| AB | cos
17
性质1的说明：
(1) 0 , 投影为正；
2
(2) , 投影为负；
2
(3) ,
2
投影为零；
γ
24
利用向量的坐标，可得向量的加法、减法及 向量与数的乘法的运算如下：
设α=x1i+y1j+z1k=(x1 , y1 ,z1), 则有：β=x2i+y2j+z2k= (x2,y2,z2).
α+β =（x1+x2 ）i +（y1+y2）j +（z1+z2) k
=(x1+x2 , y1+y2 , z1+z2 ). α-β=（x1-x2) i+ (y1-y2 ) j+ (z1-z2)k
C( x,o, z)
• M(x, y, z)
o
y
Q(0, y,0)
x P( x,0,0)
A( x, y,0)
6
二、空间两点间的距离公式
《高等数学》向量代数和空间解析几何
a∥ b
运算律
(1) ab ba (2) 分配律 (ab)cacbc
(3) 结合律 (a)ba(b)(ab)
向量积的坐标表达式
ab ( a y b z a z b y ) i ( a z b x a x b z ) j ( a x b y a y b x ) k
i j k a b ax ay az
例5. 求通过 x 轴和点( 4, – 3, – 1) 的平面方程.
解: 因平面通过 x 轴 , 故 AD0 设所求平面方程为 ByCz0
代入已知点 (4,3,1)得 C3B
化简,得所求平面方程 y3z0
空间直线
一般式 A A 21xx B B 2 1y y C C 1 2zz D D 12 00
从柱面方程看柱面的特征：
只含 x, y而缺z的方程F(x, y) 0，在 空间直角坐标系中表示母线平行于 z 轴的柱 面，其准线为 xoy面上曲线C .
(3) 二次曲面
椭球面
a x2 2b y2 2cz2 21 (a,b,c为正 ) 数 z
x
y
抛物面
z
椭圆抛物面
x2 y2 z ( p , q 同号) 2p 2q
n (0 ,B ,C ) i,平面平行于 x 轴; • A x+C z+D = 0 表示 平行于 y 轴的平面; • A x+B y+D = 0 表示 平行于 z 轴的平面; • C z + D = 0 表示平行于 xoy 面 的平面; • A x + D =0 表示平行于 yoz 面 的平面； • B y + D =0 表示平行于 zox 面 的平面.
o
y
3、空间曲线 （1） 空间曲线的一般方程
《空间解析几何》课件
THANKS
感谢观看
通过参数方程表示曲面的形式，如x = x(u, v)，y = y(u, v)，z = z(u, v)。
曲面方程
表示三维空间中曲面的方程形式，如z = f(x, y)。
空间曲线的方程
1 2
参数曲线
通过参数方程表示曲线的形式，如x = x(t)，y = y(t)，z = z(t)。
空间曲线
表示三维空间中曲线的方程形式，如F(x, y, z) = 0。
空间解析几何的应用领域
总结词
空间解析几何在许多领域都有广泛的应用。
详细描述
在物理学中，空间解析几何用于描述物理现象的空间关系，如力学、电磁学和光学等领 域。在计算机图形学中，空间解析几何用于建模和渲染三维场景。在工程学中，空间解 析几何用于设计和分析机械、建筑和航空航天等领域中的物体和结构。此外，空间解析
03
空间平面与直线
空间平面的方程
平面方程的基本形式
Ax + By + Cz + D = 0
特殊平面
平行于坐标轴的平面、过原点的平面、与坐标轴垂直的平面
参数方程
当平面过某一定点时，可以用参数方程表示平面的方程
空间直线的方程
直线方程的基本形式
Ax + By + Cz = 0
特殊直线
与坐标轴平行的直线、过原点的直线、与坐标轴垂直的直线
利用代数方法，如向量运算、线性代数等， 求解空间几何问题。
几何意义
将代数解转化为几何意义，解释其实际意义 。
如何理解空间几何中的概念？
向量的概念
理解向量的表示、向量的加法、数乘以及向量的模 等基本概念。
《空间解析几何基础》PPT课件
24
(5)二次锥面
x2 a2
y2 b2
z2 c2
0
(6)椭圆抛物面
x2 a2
y2 b2
2z
0
(a,b,c 0) (a,b 0)
(7.10) (7.11)
25
(7)双曲抛物面(马鞍面) x2 y2 2z 0 (a,b 0) a2 b2
(7.12)
26
思考题
指出下列方程在平面解析几何中和空 间解析几何中分别表示什么图形？
(1) x 2;
(2) x2 y2 4;
(3) y x 1.
27
思考题解答
方程
平面解析几何中 空间解析几何中
x2
平行于y 轴的直线 平行于 yoz 面的平面
圆心在(0,0) ，
x2 y2 4
半径为2 的圆
以z 轴为中心轴的圆柱面
y x 1 斜率为1的直线 平行于z 轴的平面
பைடு நூலகம்
28
三、平面区域的概念及其解析表示 设P0(x0,y0)是xOy平面上的一定点,δ>0为一实
4
空间两点间的距离
设M1 ( x1 , y1 , z1 )、M 2 ( x2 , y2 , z2 )为空间两点
zR
M1•
P o
d M1M2 ?
• M2
Q N
在直角M1 NM 2 及 直 角 M1 PN
中，使用勾股定
y 理知
x
d 2 M1P 2 PN 2 NM 2 2 ,
5
M1P x2 x1 , PN y2 y1 , NM 2 z2 z1 ,
(7.4)
其 中 a,b,c,d 为 常 数 , 且 a,b,c 不 全 为 零 . 例 如 , 当
高等数学《空间解析几何(第1章)》课件
构成__半__径__为__1_的__球_； 面
|
a
|
|
a
|
a
0
a 0
a与a 反向，
|
a
||
|
|
a
|
a
2a
1
a
2
数与向量的乘积符合下列运算规律：
（1）结合律：
(
a)
(
a)
(
)a
（2）分配律： ( )a a a
(a
b)
a
b
思考
1.向量 a ，b 平行(共线)条件是什么？
2.与向量 a 0共线的单位向量________.
e3 O e2
e1
一个空间标架,决定一个空间坐标系
z
e3
O
e2
e1 x
当{O; e1, e2 , e3 }确定后, e1, e2 , e3依次确定以O为原点 的三数轴:x轴(横轴),y轴(纵轴), y z轴(竖轴),统称坐标轴. 它们构成空间坐标系o xyz.
也用{O; e1, e2 , e3 }表示. 把e1, e2 , e3称为坐标向量.
e3
F
的中点为P1 , 其余各组对边
中点分别为P2 , P3 .
A
P1
e2
C
只需证明P1, P2 , P3三点
重合即可.
E
e1 B
取 AB e1, AC e2 , AD e3 , 先求 AP1用e1, e2 ,e3表示的关系式.
高等数学空间解析几何
（（ （123）））当当a＝0时0时a，，aa与0a（ 同零向向；量当）
0时，a
与
a
反向。
向量与数的的性质
（1）交换律： a a
（2）结合律： (a ) () a (a ) ；（其中为常数）；
（3）分配律：( )a a b ，(a b )a b
M 1 M 2 { x 2 x 1 ,y 2 y 1 ,z2 z 1 }
三、向量的坐标表示
3．向量的模与方向余弦的坐标表示式
方向角：非零向量a与三个坐标轴正向的夹角
记为 ,, 0,, 方向余弦：co,sco,scos
aM
对a {ax,ay,az}
a OM ax 2ay 2az 2
cos
ax
ax2 ay2 az2
cos
ay
ax2 ay2 az2
cos
co 2 s co 2 s co 2 s 1eaa a {co,cso,sco}s
az ax2 ay2 az2
知道其中两个 就可求出第三个 单位向量的方向余弦就是它的坐标
力 位移 速度 加速度
表示方法：1
黑体字母
a,b,c或
a,b,c
2 有向线段表示 MN 表示起点在 M，终点在 N 的向量
向量的模 向量的大小（有向线段的长）
a
b
c
a
b
c
单位向量 模1为的向量，记为 e a 零向量
M N
模为的0向量 ，记为 0
自由向量 与起点无关的向量 （向量可自由平移具有自由性）
四、两向量的数量积
2. 数量积的坐标表示式
设 a ax i a y j a z k {ax,ay,az}
空间解析几何精ppt课件
两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k
个向量共面 .
.
机动 目录 上页 下页 返回 结束
二、向量的线性运算
1. 向量的加法 平行四边形法则:
b ab
(ab)c
c
bc
a(bc)
a 三角形法则: ab
b
过空间一定点 o ,由三条互相垂直的数轴按右手规则
组成一个空间直角坐标系.
• 坐标原点
Ⅲ
zz 轴(竖轴)
Ⅱ
• 坐标轴
Ⅳ
• 坐标面
• 卦限(八个) Ⅶ x
x轴(横轴)
Ⅷ
yoz面 oxoy面
Ⅴ
Ⅰ
y
y轴(纵轴)
Ⅵ
.
机动 目录 上页 下页 返回 结束
在直角坐标系下
点 M 1 1有序数组 (x, y, z) 1 1向径 r
M2
零向量: 模为 0 的向量, 记 0 ， 或 作 0 . M 1
.
机动 目录 上页 下页 返回 结束
若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等,
记作 a＝b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行,记作
a∥b ; 规定: 零向量与任何向量平行 ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量,
ab b a
a
运算规律 : 交换律 a b b a
结合律 (ab)ca(bc)a.
.
机动 目录 上页 下页 返回 结束
s a 1 a 2 a 3 a 4 a 5
a4
a5
a3 s
高等数学 第九章 空间解析几何
第九章 空间解析几何一、本章提要1．基本概念空间直角坐标系，向量，向量的模，单位向量，自由向量，向径，向量的坐标与分解，向量的方向余弦，向量的点积与叉积，平面的点法式与一般式方程，直线的点向式及一般式方程，球面，柱面，旋转面，二次曲面，空间曲线在坐标面上的投影，失函数的导数，失函数的积分．2．基本公式两点间的距离公式，向量模与方向余弦公式，点积与叉积坐标公式，点到平面的距离公 式，平面与直线间的夹角公式．3．方程直线的点向式方程，直线的参数方程，直线的一般式方程，平面的点法式方程，平面的一般式方程．二、要点解析问题1 自由向量的基本特征为何?如何描述其基本特征?解析 向量含有两个基本特征，一个是大小，另一个是方向．所谓自由向量是只考虑大小和方向，而不考虑它的始点和终点位置，即一个向量可以在空间自由地平行移动．不论位置如何，只要其大小相等、方向相同即认为是相等或同一向量．本书讨论的向量均为自由向量．向量特征的描述，从几何上是用有向线段的方向代表向量的方向，有向线段的长度代表向量的大小．从坐标表示上，以),,(1111z y x M 为始点，),,(2222z y x M 为终点的向量为},,{12121221z z y y x x M M ---=，其大小(模)212212212)()()(z z y y x x -+-+-=，其方向由其与坐标轴正向的夹角γβα,,的余弦确定，即2112cos x x M M α-=，cos =β，cos z z -=γ 问题 2 向量的点积与叉积有何物理意义？如何计算？如何利用它们判别向量的位置关系？解析 设向量a 与b 的夹角为θ，则θcos b a b a =⋅， n b a b a ⋅=⨯θsin ，其中n 为与a ，b 同时垂直，方向由右手螺旋法则确定的单位向量．点积为数量，叉积为向量．点积在物理上可以表示功，若物体在力F 的作用下作直线运动，其位移向量为s ，则其功W 为s F s F ⋅=θ=cos W ．叉积在物理上可以表示力矩、磁力等．当单位电荷以速度v 在磁场B 中运动时，它所受的磁力F 为B v F ⨯=，其大小为θsin B v ，方向由右手螺旋法则确定．若{=a },,z y x a a a ，b },,{z y x b b b =，则b a ⋅z z y y x x b a b a b a ++=， y z y zxxa a ab b b ⨯=i j k a b ． 向量之间的位置关系：(1)b a b a ⋅⇔⊥0=++=z z y y x x b a b a b a ； (2)a ∥b 0=⨯⇔b a 或zzy y x x b a b a b a ==； (3)a 与b 的夹角θ由ba ba ⋅=θcos 222222zy x zyxz z y y x x bb b aa ab a b a b a ++++++=确定．例1 设}2,0,1{-=a ，}1,1,3{-=b ，求b a ⋅和b a ⨯． 解 51)2(10)3(1-=⨯-+⨯+-⨯=⋅b a ．}1,5,2{52113201=++=--=⨯k j i kj ib a ． 问题3 说明确定平面的条件及典型的平面方程． 解析 满足下列条件之一者可确定一个平面： (1) 过空间中不共线的三个点； (2) 过直线和直线外一点； (3) 过两条平行或相交的直线．我们用向量的方法可将条件归结为：过一已知点且与一已知向量垂直便可确定一个平面．由此条件建立的平面方程就是平面的点法式方程．平面的主要方程形式：(1) 点法式：过点),,(000z y x ，法向量为}{C B,A,=n 的平面方程为-+-y B x x A ()(00)()00=-+z z C y ；(2) 一般式：0=+++D Cz By Ax ，其中},,{C B A =n ； (3) 截距式：1=++czb y a x ，其中平面与坐标轴交点为),0,0(),0,,0(),0,0,(c b a ；(4) 三点式：0020202010101000=---------z z y y x x z z y y x x z z y y x x ，其中),,(000z y x ，),,(111z y x ，),,(222z y x 为平面上不在一条直线上的三点．例2 求通过点)4,1,2(0-M 和z 轴的平面方程．解 因为z 轴的单位向量}1,0,0{=k 和1,4}{2,0-=OM 均在所求平面内，故可取该平面的一个法向量为}0,2,1{0=⨯=OM k n ，于是所求方程为0)4(0)1(2)2(1=-⨯+++-⨯z y x ，即 02=+y x ．问题4 说明确定直线的基本条件及典型的直线方程．解析 确定一条直线的条件有：过不重合的两点，或者二平面的交线等．我们用向量的方法可将这些条件归结为：过一已知点且与一已知向量平行可以确定一条直线，由此条件建立起来的直线方程为直线的点向式方程． 直线的主要方程形式： (1) 点向式：pz z n y y m x x 000-=-=-，其中),,(000z y x 为直线上定点，},,{p n m =s 为直线的方向向量；(2) 参数式：⎪⎩⎪⎨⎧+=+=+=；pt z z nt y y mt x x 000,,(3) 两点式：121121121z z z z y y y y x x x x --=--=--，其中),,(111z y x ，),,(222z y x 为直线上不重合的两点； (4)一般式：⎩⎨⎧=+++=+++,0,022221111D z C y B x A D z C y B x A 其中此二平面不平行．例3 求过点)0,1,0(0M 且垂直于平面023=+-y x 的直线方程．解 因所求直线的方向向量s 与已知平面的法向量同向，所以可取}0,1,3{-=s ，故所求方程为113z y x =--=． 注意：上式右端一项分母为零是一种记法，它只表示该直线与z 轴垂直． 问题5 列举常见的曲面方程，指明曲面及其方程特征．三、例题精解例4 已知向量21P P 的始点为)5,2,2(1-P ，终点为)7,4,1(2-P ，试求：(1)向量21P P 的坐标表示； (2)向量21P P 的模； (3)向量21P P 的方向余弦；(4)与向量21P P 方向一致的单位向量．解 (1) }2,6,3{}57),2(4,21{21-=-----=P P ； 74926)3(222==++-=；(3) 21P P 在z y x ,,三个坐标轴上的方向余弦分别为362cos ,cos ,cos 777αβγ=-==；(4)k j i k j i 7276737263)(21++-=++-==P P．例5 求与}3,2,1{-=a 共线，且28=⋅b a 的向量b ． 解 由于b 与a 共线，所以可设}3,2,{λλλλ-==a b ，由28=⋅b a ，得28}3,2,{}3,2,1{=-⋅-λλλ，即2894=++λλλ，所以2=λ，从而}6,4,2{-=b ．例6 已知}0,1,1{},2,0,1{=-=b a ，求c ，使b c a c ⊥⊥,且6=c ．解一 待定系数法．设},,{z y x =c ，则由题设知0,0=⋅=⋅b c a c 及6=c ，所以有①20②③6x z ⎧-=⎪= 由①得2xz =， ④ 由②得x y -=， ⑤将④和⑤代入③得62)(222=⎪⎭⎫⎝⎛+-+x x x ，解得 2,4,4±==±=z y x ， 于是 }2,4,4{-=c 或}2,4,4{--=c ．解二 利用向量的垂直平行条件，因为b c a c ⊥⊥,，所以c ∥b a ⨯． 设λ是不为零的常数，则k j i k j i b a c λλλλλ+-=-=⨯=22011201)(，因为6=c ，所以6]1)2(2[2222=+-+λ，解得2±=λ，所以 }2,4,4{-=c 或}2,4,4{-=c ．解三 先求出与向量b a ⨯方向一致的单位向量，然后乘以6±．k j i k j i b a +-=-=⨯22011201，31)2(2222=+-+=⨯b a ，故与b a ⨯方向一致的单位向量为}1,2,2{31-．于是}1,2,2{36-±=c ，即 }2,4,4{-=c 或}2,4,4{--=c ．例7 求满足下列条件的平面方程：(1)过三点)2,1,0(1P ，)1,2,1(2P 和)4,0,3(3P ； (2)过x 轴且与平面025=++z y x 的夹角为π3． 解 (1)解一 用三点式．所求平面的方程为0241003211201210=---------z y x ， 即 01345=+--z y x ．解二 }1,1,1{-=}2,1,3{-=，由题设知，所求平面的法向量为k j i kj in 452131113121--=--=⨯=P P P P ， 又因为平面过点)2,1,0(1P ，所以所求平面方程为0)2(4)1(5)0(=-----z y x ，即 01345=+--z y x ．用下面的方法求出所求平面的法向量},,{C B A =n ，再根据点法式公式写出平面方程也可．因为 3121,P P P P ⊥⊥n n ，所以 {0,320,A B C A B C +-=-+=解得 A C A B 4,5-=-=，于是所求平面方程为0)2(4)1(5)0(=-----z A y A x A ，即 01345=+--z y x ．（2）因所求平面过x 轴，故该平面的法向量},,{C B A =n 垂直于x 轴，n 在x 轴上的投影0=A ，又平面过原点，所以可设它的方程为0=+Cz By ，由题设可知0≠B （因为0=B 时，所求平面方程为0=Cz 又0≠C ，即0=z ．这样它与已知平面025=++z y x 所夹锐角的余弦为π1cos32=≠=，所以0≠B），令CBC'=，则有0='+zCy，由题设得22222212)5(112153cos++'++⨯'+⨯+⨯=πCC，解得3='C或13C'=-，于是所求平面方程为03=+zy或03=-zy．例8已知平面在x轴上的截距为2，且过点)0,1,0(-和)3,1,2(，求此平面方程．解析此题容易想到用三点式求平面方程，其实不然，因为用三点式需要解三阶行列式，比较麻烦．注意到所求平面与三条坐标轴都相交，它在x轴上的截距已知是2，易知它在y 轴上的截距是-1，在z轴上的截距也容易求得．故用截距式求该平面方程方便些．解设所求平面方程为1=++czbyax，由题设知1,2-==ba，平面过点)3,1,2(，所以131122=+-+c，得3=c．于是，所求平面方程为1312=+-+zyx，即06263=-+-zyx．例9求过点)1,1,2(，平行于直线122132--=+=-zyx且垂直于平面0532=+-+zyx的平面方程．解一用点法式．所给直线的方向向量}1,2,3{-=s，所给平面的法向量}3,2,1{1-=n．1321484123⨯=-=-++-i j ks n i j k，由题设知，所求平面的法向量sn⊥且1⊥n n，取11()24=-⨯=--n s n i j k，于是所求平面方程为)1()1(2)2(=-----zyx，即012=+--zyx．解二所求平面方程为0=+++D Cz By Ax ，由平面过点)1,1,2(得02=+++D C B A ， ① 有所求平面垂直于平面0532=+-+z y x ，知 }3,2,1{},,{-⊥C B A ，所以 032=-+C B A ， ② 又由所求平面平行于直线122132--=+=-z y x ，知 }1,2,3{},,{-⊥C B A ，所以 023=-+C B A ， ③解①，②，③联立方程组得D C D B D A -=-==,2,， 所求平面方程为 012=+--z y x ．例10 求过点)1,0,3(-A 且平行于平面1π：3450x y z --+=，又与直线1:2xL = 1111y z -+=-相交的直线L 的方程． 解一 用点向式方程。
高等数学：空间解析几何
a和向量b的数量积(内 积),这种运算也称为点乘,记作a·
b,即
由数量积的定义7-2以及向量夹角的定义7-1可以得到:
(1)a·
a=|a|2;
(2)向量a 和向量b 互相垂直的充分必要条件是a·
b=0.
空间解析几何
两个向量的数量积满足下列运算规律:
当向量a和b至少有一个是零向量时,规定其夹角<a,b>可
以在0到π之间任意取值.
空间解析几何
在物理中,我们已经知道,若力F 作用在物体上,使其产生
位移s,则该力所作的功为
即F 所作的功W 是向量F 和s的模相乘再乘以它们夹角的余
弦.这种运算在其他问题中也 会遇到,因此我们引入向量的结
构性运算.
空间解析几何
例7-13 设一平面与x 轴、y 轴和z 轴的交点分别为
P(a,0,0)、Q(0,b,0)和 R(0,0,c),求这个平面的方程,其中a ≠0,b
≠0,c ≠0.
解 设所求平面的一般方程为
空间解析几何
由 题意可知P(a,0,0)、Q(0,b,0)和R(0,0,c)三点都在该平
面上,所以这三点的 坐标都满足一般方程,即有
空间解析几何
．
例7-16 求点(1,-2,-1)到平面2x +y-2z+4=0的距离.
解 由式(7-13)可得
空间解析几何
7.4 空间直线方程
一、 直线方程
如图7-10所示,在空间直角坐标系中给定一条直线L,任一
个与这条直线平行的非零向量s={a,b,c}称为该直线的方向向
量.在直线L 上取一个定点M0(x0,y0,z0),设M(x,y,z)是直线L上任
空间解析几何28965-PPT文档资料25页
一、平面的点法式方程
法线向量、 平面的点法式方程
二、平面的一般方程
平面的一般方程、特殊的平面、截距式方程
三、两平面的夹角
两平面的夹角、两平面夹角的余弦 两平面平行与垂直的条件 点到平面的距离公式
一、平面的点法式方程
法线向量： 如果一非零向量垂直于一平面，
这向量就叫做该平面的法线向量．
或
C3B．
将其代入所设方程并除以B(B 0)，便得所求的平面方程为 y3z0．
例4 设一平面与x、y、z轴的交点依次为P(a, 0, 0)、Q(0, b, 0)、 R(0, 0, c)三点， 求这平面的方程(其中a 0，b 0，c 0)．
z R (0, 0, c)
n
Q (0, b, 0)
| n 1 | { A x 0 B y 0 C z 0 ( A x 1 B y 1 C z 1 ) } ，
又因Ax1By1Cz1D0，| n | A 2 B 2 C 2 ， 所以 P r j n P 1 P 0 A 0 A 2 B 0 B 2 C x C 0 2 D y ． z
O
y
P (a, 0, 0) x
例4 设一平面与x、y、z轴的交点依次为P(a, 0, 0)、Q(0, b, 0)、 R(0, 0, c)三点， 求这平面的方程(其中a 0，b 0，c 0)．
解 设所求平面的方程为
A x B yC zD0．
因P(a, 0, 0)、Q(0, b, 0)、R(0, 0, c)三点都在这平面上，所以点P、
解 先求出这平面的法线向量 n ．
M 1M 2{3， 4， 6}， n
M 1M3{2， 31}， 可取
空间解析几何平面ppt课件
返回
微积分
第五章 向量代数与空间解析几何
P ( a , 0 , 0 ) x ,y ,z 例 4设 平 面 与 三 轴 分 别 交 于 、
Q ( 0 , b , 0 ) R ( 0 , 0 , c ) a 0 b 0 c 0 、 （ 其 中 ， ， ） ，
求 此 平 面 方 程 .
解
设平面为 Ax By Cz D 0 ,
例 1 求 过 点 A ( 1 , 1 , 1 ) 且 垂 直 于 点 A 的 向 径 O A 的 平 面 方 程 。
例 2 求 过 点 M ( 1 , 1 , 1 ) , M ( 2 , 2 , 2 ) , M ( 1 , 1 , 2 ) 1 2 3 的 平 面 方 程 。
abc返回第五章向量代数与空间解析几何微积分返回第五章向量代数与空间解析几何微积分ax将三点坐标代入得返回第五章向量代数与空间解析几何微积分平面的截距式方程x轴上截距轴上截距z轴上截距返回第五章向量代数与空间解析几何微积分定义通常取锐角三两平面的夹角返回第五章向量代数与空间解析几何微积分两平面夹角余弦公式两平面位置特征
M ( 1 , 1 , 0 ) ( 1 , 1 , 0 ) 1M 2
两平面平行但不重合．
2 1 1 (3) , 4 2 2 两平面平行 M ( 1 , 1 , 0 ) M ( 1 , 1 , 0 ) 1 2
两平面重合.
返回
微积分
类似地可讨论 A 情形. C 0 , B C 0
返回
微积分
第五章 向量代数与空间解析几何
例 3 求 过 z 轴 和 点 A ( 1 , 1 , 1 ) 的 平 面 方 程 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a b a ( b )
a bb c
a
b
abab
b
abab
a(b) B
a1a2… an (a1a2… an1)an A
a
b
ab
C
向量的数乘
设 a 为 向 量 , 为 实 数 , a 为 新 向 ; 0 时 ,与 a反 向 .称 之 为 数 与 向 量 a 的 乘 积 .
对 角 线 作 长 方 体 ,与 坐 标 轴 重 合 的 棱 为 O P, O Q ,
O R ,则
r O P O Q O R
zz
R
又 O P x i , O Q y j , O R z k
M
r
所 以 r x i y j z k
O
y
Qy
x
M r ( x ,y ,z )
xP
称 ( x ,y ,z ) 为 空 间 点 M 或 矢 径 r o M ( 或 向 量 r ) 的 坐 标 ,记 作 :M ( x ,y ,z ) 或 r ( x ,y ,z )
量 (记 i,j,k), 就 构 成 三 个 相 互 垂 直 交 于 O ( 称 为 原 点 ) 的 数 轴 ( 分 别 称 x 轴 ,y 轴 , z 轴 ) 称 之 为 直 角 坐 标 系 . 记 为 ： Oxyz.
按x,y,z轴顺序,坐标系符合
右手定则,称为右手系.
z
任意两坐标轴确定一个平
面称坐标面. x,y 轴确定坐标 面称xOy面(或xy面); x,z 轴
向 量 垂 直 a b 0 . b c
向 量 平 行 a b 0 .
三 向 量 共 面 a(bc)0a
abc,(b0,c0)
c
b
c
c a
设i,j,k为相 b 互垂 b 直且依顺序
k
构成右手系的三单位向量,则 i
j
ijk,jki,ki j.
二、空间直角坐标系
在 空 间 取 定 一 点 O 和 三 个 相 互 垂 直 的 单 位 向
空间点坐标的位置特征
1 . Ⅰ 卦 限 点 x 0 , y 0 , z 0 ; Ⅱ 卦 限 点 x 0 , y 0 , z 0 ; Ⅲ 卦 限 点 x 0 , y 0 , z 0 ; Ⅳ 卦 限 点 x 0 , y 0 , z 0 ; Ⅴ 卦 限 点 x 0 , y 0 , z 0 ; Ⅵ 卦 限 点 x 0 , y 0 , z 0 ; Ⅶ 卦 限 点 x 0 , y 0 , z 0 ; Ⅷ 卦 限 点 x 0 , y 0 , z 0 ;
向量数乘性质 0a 0, 1a a, (1)a a,
(a) (a) ()a
( )a a a
(a b) a b.
定理：(向量平行条件)
向 量 a 与 b 平 行 存 在 唯 一 实 数 ,使 b a .
其 中 a 0 .
证 充 分 性 由 向 量 数 乘 定 义 可 得 ； ( 必 要 性 ) a 0 , 则 a 0 . 当 b 0 时 , 有 b 0 a ; 当 b 0 时 , 因 a 与 b 平 行 , 所 以 a 、 b 或 者 同 向 , 或 者 反 向 ;
k
i
Oj
y
确定坐标面称xOz面; y,z 轴
x
确定坐标面称yOz面.
三个坐标面把空间 分为八个部分，每 个部分叫一个卦限. 如图:
在xy坐标平面的上 部, 依次称为Ⅰ、Ⅱ、 Ⅲ、Ⅳ卦限.
在xy面下部与第一 卦限相对应的称为 第Ⅴ卦限;以后依次 称为第Ⅵ、Ⅶ、Ⅷ 卦限.
任 给 向 量 r , 空 间 对 应 有 点 M , 使 O M r . 以 O M 为
高等数学
微积分
西南财经大学经济数学系 孙疆明
精
空间解析几何与向量代数
向量及其线性运算
数量积、向量积、混合积
曲面及其方程
平面
空间曲线及其方程
一、向量及其线性运算
向量概念 有大小、有方向的量称为向量. 用 符 号 a 、 b 、 v 、 F 、 … 等 标 记 . 如 果 强 调 起 点 A 、 终 点 B ,也 记 A B . 向 量 的 大 小 叫 做 向 量 的 模 .记 为A B、 a… 等 . 模 为 1的 向 量 叫 做 单 位 向 量 . 模 为 0的 向 量 叫 零 向 量 .记 为 0.
b
b
又 a=b,故当a、b同向有= ,使ba;
a
a
b
当a、b反向时,有= ,使ba.
a
证完
注意:a0时,aa a,ba(a)a,且a 1,
a
aa
故选长度1的向量(记ea),就可用数表示各平行向量
向量的乘法(积) 向量的夹角 两 非 零 向 量 a ,b 把 起 点 放 在 一 起 , 构 成 的 不
两向量大小相等、方向相同叫做两向量相等； 两向量方向相同或相反,叫做两向量平行(共线);
起点放在一起，向量在一个平面内，叫做共面;
向量的线性运算(加减、数乘) 记 为 设 a A B ,b B C ,连 接 A 、 C 得 向 量 A C c
叫 做 向 量 a 、 b 的 和 a b ; 记 为 设aAB,bAC,连 接 B、 C得 向 量 CBc
性 质: 1. abba;
(a ,b )
b
a
2. a(bc)abab;
3. a(b)(a)b(ab).4.
aaa2.
2.向量的向量积(叉积)
a,b为 两 向 量 .以 数absin(a,b)为 模 ,以 从 a到 b
右 手 定 则 为 方 向 的 向 量 叫 作 向 量 a与 b的 向 量 积 .
记 为 : ab.
ab
性质: 1. abba;
b
b
2. a(bc)abab;
a
3. a(b)(a)kb(ab).
4. ab a,b为邻边面积. b a
b
b sin(a,b)
3.向量的混合积
a
a ( b c ) 叫 作 a , b , c 的 混 合 积 .
混 合 积 性 质 ：
a (b c) 以 a ,b ,c 为 棱 的 平 行 六 面 体 体 积 .
超 过 的 角 叫 向 量 a ,b 的 夹 角 .记 为 :( a ,b ) , ( a ,b ) .
1.向量的数量积(点积)——投影向量长度乘积
a ,b 为 两 向 量 ,称 数 ab c o s (a ,b ) 为 向 量 a ,b 的
数 量 积 .记 为 :a b .
即 ababco s(a,b)
记 为
叫 做 向 量 a与 b的 差 ab;BCc叫 做 向 量 b与 a的
差 ba;
A
B
a
b
ab C
B a
ab Ab
C
原向与量一的向负量向量a .大记小为相：等、a 方. 向a 相反B 的b 向量叫做
向量加法性质
a b b a
A
ab C
( a b ) c a ( b c )
abc c