浅议灰色关联度分析方法及其应用

合集下载

从零开始的数学建模：（三）灰色关联分析

从零开始的数学建模：（三）灰⾊关联分析灰⾊关联分析适⽤于⼩样本数据，⼤样本数据推荐使⽤标准化回归分析；基本原理是根据曲线的⼏何形状的相似程度来判断联系是否紧密，也就是说，如果y的曲线和某个x的曲线长得很像，那么这个x或许就是最能影响y的因素；灰⾊关联分析可⽤于系统分析与综合评价⼀、系统分析上的运⽤（1）确定分析序列以⾃变量作为⼦序列，因变量作为母序列，对应本题即第⼀、⼆、三产业作为⼦序列，国内⽣产总值为母序列；（2）对变量进⾏预处理计算每⼀列的均值，并将每⼀列的数除以该均值（注意这⾥使⽤的⽅法和Topsis不⼀样），可得到以下结果：（3）计算极差与关联系数分别计算|x1−x0|、|x2−x0|、|x3−x0|，可求出最⼩值a与最⼤值b，本题计算结果如下：对上述结果执⾏:y=a+ρ|x i−x0|+ρ∗b即可得到关联系数：对以上三列分别求均值，可得到三个数值：0.5084、0.6243、0.7573，因此最终得出结论，第三产业对GDP总量影响最⼤；⼆、综合评价上的运⽤综合评价类问题只有⼀列⼜⼀列数据，需要根据这些数据计算得分；在利⽤灰⾊关联分析之前，仍需要进⾏指标正向化；（1）确定⼦序列与母序列⼦序列即各个因素，取出⼦序列构成的矩阵的每⼀⾏中的最⼤值，组成母序列；（2）对变量进⾏预处理步骤同上，得到z ij；（3）计算极差与关联系数步骤同上，得到r i；（4）计算权重与得分计算各个指标的权重与得分：w i=r ir1+r2+⋯+r ms k=∑w i∗z ij 最后对得分进⾏归⼀化处理即可得到每个样本的评分：S k=s k∑s1+s2+⋯+s n本⽂算法思想参考源于，特此注明Processing math: 100%。

灰色关联度分析模型的特征与应用

2019年第24期(总第643期)科学咨询/科技管理去体会的。

第三，让较为优秀的正在创业的在校学生担任创业导师。

这些学生自己正在创业，并且还是在校学生，与其他学生之间的距离更近，更容易沟通，也更清楚他们可能会遇到的困难，效果也就会更好。

(三)建立和完善相应的扶持政策第一，政府要完善相应的法律法规，保障大学生创业的合法权益。

[3]首先，政府可在启动资金方面予以扶持，如提供免息贷款或者低利率贷款，同时减免部分税收，这样可以解决学生创业启动资金方面的困难。

其次，政府要简化相关的审批程序，为学生开通绿色窗口，简化流程，降低门槛。

最后，政府各部门要联动，出台一系列扶持学生创业的政策。

第二，学校要出台相应的配套政策。

一方面，学校要为创业学生提供场地、货架等硬件方面的支持，还可以让快递公司进校园，为创业学生提供方便。

另一方面，学校可实行课程替代制度。

学生创业达到一定程度后，经学校相关部门认定，只要达到学校要求的水平即可申请免修相关的课程。

剩下的部分课程，上课的方式也可以做适当调整，如可以采取集中授课或者网络授课的方式，这样才能解决学生的后顾之忧。

参考文献：[1] 张晓芬，史宪睿.“内外协同”高校创新创业人才培养体系构建[J].现代教育管理，2018(3).[2] 王建武，王增辉.“双创”背景下的大学生创业意识培养研究[J].齐齐哈尔师范高等专科学校学报，2017(6).[3] 刘扬.政府助推大学生创业创新研究[D].中央民族大学，2016.摘要：本文针对灰色关联模型进行分析，通过分析得出灰色关联模型具有处理数据灵活的特点；并且灰色关联模型能应用于样本数量较少且关系为线性关系的系统分析。

关键词：灰色关联模型；线性关系；系统分析引言在实际的工程设计与模型分析过程中，往往存在比较多的变量，而这些变量之间是否存在关系在很大程度上具有不确定性。

但是如果能够明确这些变量之间的关系，它们就会对工程设计以及系统分析起到理论的指导作用。

灰色关联分析详解+结果解读

灰色关联分析1、作用对于两个系统之间的因素，其随时间或不同对象而变化的关联性大小的量度，称为关联度。

在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低。

因此，灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法，其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密，它反映了曲线间的关联程度。

2、输入输出描述输入:特征序列为至少两项或以上的定量变量，母序列（关联对象）为 1 项定量变量。

输出:反应考核指标与母序列的关联程度。

3、案例示例案例:分析 09-18 年内，影院数量，观影人数，票价、电影上线数量这些因素对全年电影票房的影响。

其中电影票房是母序列，影院数量，观影人数，票价、电影上线数量是特征序列。

4、案例数据灰色关联分析案例数据5、案例操作Step1：新建分析；Step2：上传数据；Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；step4：选择【灰色关联分析】；step5：查看对应的数据数据格式，【灰色关联分析】要求特征序列为定量变量，且至少有一项；要求母序列为定量变量，且只有一项。

step6：设置量纲处理方式（包括初值化、均值化、无处理）、分辨系数（ρ越小，分辨力越大，一般ρ的取值区间为 ( 0 ，1 )，具体取值可视情况而定。

当ρ≤ 0.5463 时，分辨力最好，通常取ρ = 0.5 ）step7：点击【开始分析】，完成全部操作。

6、输出结果分析输出结果 1：灰色关联系数图表说明:关联系数代表着该子序列与母序列对应维度上的关联程度值（数字越大，代表关联性越强）。

输出结果 2：关联系数图分析：输出结果 1 和输出结果 2 是一样的，输出结果 1 用了表格形式来呈现关联系数，输出结果 2 用了图表形式来呈现关联系数。

图表很直观地展现了，大多数年份的银幕数量和电影上线数量对票房影响更大。

灰色关联度方法介绍

灰色关联度方法介绍一、灰色关联度方法的概念灰色关联度方法是一种常用的分析方法，它是将各个因素之间的关系转化为数学模型进行计算，从而得出它们之间的相关程度。

灰色关联度方法主要应用于多因素分析和决策评价等领域。

二、灰色关联度方法的原理灰色关联度方法是基于灰色系统理论的，它通过对数据进行处理，将数据转化为一组序列，然后通过对这些序列进行比较，得出各个因素之间的相关程度。

具体来说，它主要包括以下步骤：1. 数据预处理：将原始数据进行标准化处理，使得各个因素之间具有可比性。

2. 灰色关联度计算：通过对标准化后的数据进行加权平均值计算，并与参考序列进行比较，得出各个因素与参考序列之间的相关程度。

3. 灰色预测模型建立：根据各个因素与参考序列之间的相关程度建立预测模型，并对未来趋势进行预测。

三、灰色关联度方法的应用1. 多因素分析：在复杂多变的环境下，往往需要考虑多种因素的影响，灰色关联度方法可以通过对各个因素之间的关系进行分析，得出它们之间的相关程度，从而帮助决策者进行有效的决策。

2. 决策评价：在决策过程中，需要对各种方案进行评价，灰色关联度方法可以通过对各种方案之间的比较，得出它们之间的相关程度，从而帮助决策者选择最优方案。

3. 经济预测：在经济预测中，需要考虑多种因素的影响，灰色关联度方法可以通过对各个因素之间的关系进行分析，得出它们之间的相关程度，并建立预测模型进行未来趋势预测。

四、灰色关联度方法的优缺点1. 优点：（1）能够充分考虑多个因素之间的相互作用和影响。

（2）具有较高的精确性和可靠性。

（3）能够处理样本数据量较小、数据质量较差等问题。

2. 缺点：（1）需要对数据进行标准化处理，增加了计算复杂度。

（2）依赖于参考序列的选择和权重设置，在实际应用中可能存在一定误差。

（3）不适用于非线性系统和高维数据分析。

五、灰色关联度方法的发展趋势随着计算机技术的不断发展和数据处理能力的提高，灰色关联度方法在多因素分析、决策评价和经济预测等领域得到了广泛应用。

灰色关联分析模型及其应用的研究

1
灰色关联分析模型及其应用的研究
工作者不断地对灰色关联分析模型进行改进和完善。本文针对其中的几个量化模型做进一步的改进工作，使其尽量地克服自身存在的不足，以期扩大灰色关联理论与方法的适用范围，使之更加适合于现实问题的分析。
1.2 国内外的研究现状
灰色关联分析作为一种技术方法，是分析系统中各因素关联程度的方法。作为一种数学理论，这种方法实质上是将无限收敛问题转化为近似收敛问题来研究；将无限空间的问题转化为有限数列的问题来解决；将连续的概念用离散的数据而取代的一种分析方法[6]。自从灰色系统理论诞生以来，灰色关联分析理论作为其中最重要的一部分就受到学术界的广泛关注并且展开了相应的理论模型和实际应用方面的研究。因其应用领域的广泛性，这也给人一个错觉，即任何一个系统所进行的系统分析都可利用灰色关联分析法。其实，要利用该方法，这个系统必须是灰色系统。灰色系统中灰的主要含义是信息不完全性(部分性)和非唯一性，其中的“非唯一性”是灰色系统的重要特征，非唯一性原理在决策上的体现是灰靶思想，即体现的是决策多目标、方法多途径，处理态度灵活机动；在分析上体现的是关联序：关联度的大小并不重要，重要的是关联序；在求解过程中体现的是定性与定量相结合，面对许可能的解，需要通过信息补充，定性分析，以确定一个或几个满意解[2]。因此灰关联分析模型不是函数模型，是序关系模型，其技术内涵为：获取序列间的差异信息，建立差异信息空间；建立和计算差异信息比较测度；建立因子间的序关系
i
灰色关联分析模型及其应用的研究
ABSTRACT
This dissertation studies and summarizes the grey incidence analysis theory and its application and discusses the pitfalls of the existing grey incidence analysis models. Especially, the absolute degree of grey incidence model, the properties of positive and negative of grey incidence model and the grey slope incidence model have been improved and studied in order that the grey incidence models are well applied in the practical problem analysis. In conclusion, the work of the dissertation mainly has the following several aspects: Firstly, this dissertation summarizes the development and actuality, content, application of the grey incidence analysis and the main content of the dissertation. Besides, the grey incidence analysis models and its pitfalls are expounded and the data transform and sensibility of the analyzing result have been studied. Secondly, three models are improved and studied from the pitfalls of the models themselves theoretically and the restriction in application. The improved absolute degree of grey incidence is to find out each intersection point of two sequence curves first and then calculate the positive and negative area by time-interval. When sequence of date representing a system characteristics and sequence of relevant factors may possibly appear different trend in every time-interval, we establish a new model which can embody the positive and negative relation of two sequences. Besides, we also improve the slope incidence model because the distinguishing rate of the incidence coefficient of sequences is small. Finally, the improved model of grey slope incidence was applied to analyze the relation of science and technology investment and the economy increase in the period of the tenth five-year in Jiangsu Province. Key Words: Grey system, Grey incidence analysis, Grey incidence order, Models, Science and technology input, Economic growth.

(整理)灰色关联度分析法

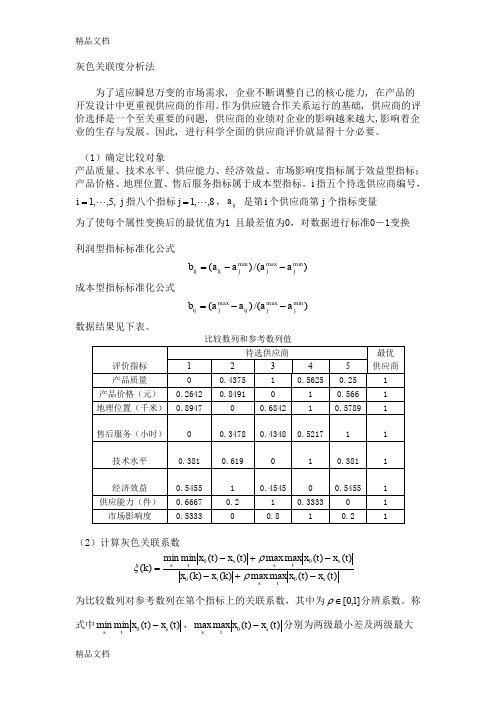
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。

作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。

因此, 进行科学全面的供应商评价就显得十分必要。

（1）确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标；产品价格、地理位置、售后服务指标属于成本型指标。

i 指五个待选供应商编号，,5,,1 =i j 指八个指标8,,1j =，ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0，对数据进行标准0－1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。

（2）计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数，其中为]1,0[∈ρ分辨系数。

称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。

一般来讲，分辨系数ρ越大，分辨率越大；ρ越小，分辨率越小。

在这里ρ取0.5。

（3）计算灰色加权关联度灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。

关联系数和关联度值（4）评价分析根据灰色加权关联度的大小，对各评价对象进行排序，可建立评价对象的关联序，关联度越大其评价结果越好。

灰色关联法确定权重

灰色关联法确定权重1. 引言灰色关联法是一种基于数学模型的分析方法，通过对多个指标进行比较和关联，确定它们之间的相关程度和影响因素的重要性。

在决策分析、综合评价和预测预警等领域中广泛应用。

本文将详细介绍灰色关联法的原理、步骤以及如何利用该方法确定权重。

2. 灰色关联法原理灰色关联法是由中国科学家陈胜武于1981年提出的，其基本原理是通过建立灰色关联度模型，从而判断各个因素对目标因素的影响程度。

该方法主要包括以下几个步骤：2.1 数据标准化首先需要将各个指标的数据进行标准化处理，将其转化为无量纲纯数值。

常用的标准化方法有极差法、标准差法和正态化等。

2.2 确定参考数列参考数列是一个代表目标因素发展趋势的序列，可以是已知数据或者专家经验给出的预测值。

2.3 计算关联系数通过计算各个指标与参考数列之间的关联系数，来评价各个因素对目标因素的影响程度。

关联系数的计算可以采用相关系数、欧氏距离等方法。

2.4 确定权重根据关联系数的大小，确定各个因素的权重。

关联系数越大，说明该指标对目标因素的影响越大，其权重也就越高。

3. 灰色关联法确定权重步骤下面将详细介绍如何利用灰色关联法确定指标的权重：3.1 数据准备首先需要收集所需数据，并进行预处理。

确保数据的准确性和完整性，同时对数据进行标准化处理，使其具有可比性。

3.2 确定参考数列根据研究目的和实际情况，选择一个代表目标因素发展趋势的参考数列。

可以是已知数据或者专家经验给出的预测值。

3.3 计算关联系数通过计算各个指标与参考数列之间的关联系数，来评价各个因素对目标因素的影响程度。

常用的计算方法有相关系数法和欧氏距离法。

相关系数法相关系数是衡量两个变量之间相关程度的指标，常用的相关系数有皮尔逊相关系数和斯皮尔曼相关系数。

可以通过计算各个指标与参考数列的相关系数，得到关联系数。

欧氏距离法欧氏距离是衡量两个向量之间差异程度的指标，可以通过计算各个指标与参考数列之间的欧氏距离，来得到关联系数。

灰色关联法的应用原理

灰色关联法的应用原理1. 灰色系统理论简介灰色系统理论是由我国科学家陈纳德于1982年提出的一种新的系统理论方法。

它是一种用于处理信息不完全、不确定性的数学方法，广泛应用于工程、管理和经济等领域。

灰色关联法是灰色系统理论的重要应用之一，通过建立灰色关联模型，可以分析和预测变量之间的关联程度。

2. 灰色关联法的基本思想灰色关联法是基于系统理论的思想，通过建立灰色关联模型来研究变量之间的关联程度。

其基本思想是利用灰色关联度来度量不同变量之间的相关程度，从而揭示变量之间隐藏的关联关系。

3. 灰色关联度的计算方法灰色关联度是衡量变量之间关联程度的指标，其计算方法有多种。

常见的计算方法包括绝对关联度、相对关联度等。

3.1 绝对关联度的计算方法绝对关联度是将每个变量与参考序列进行比较，计算其相对于参考序列的关联度。

3.2 相对关联度的计算方法相对关联度是将每个变量与样本序列（即变量在不同时刻的取值）进行比较，计算其相对于样本序列的关联度。

计算公式为：相对关联度 = （Xk(i) - Xk(1)) / (Xk(p) - Xk(1))其中，Xk(i)表示变量X在第i个时刻的值，Xk(1)表示变量X在第1个时刻的值，Xk(p)表示变量X在第p个时刻的值。

4. 灰色关联度的应用案例灰色关联法可以应用于各种领域的数据分析和预测中。

以下是几个灰色关联度的应用案例：4.1 城市人口预测利用灰色关联法可以建立城市人口与相关因素之间的关联模型，从而进行人口预测。

通过分析城市人口与经济发展、环境变化等因素的关联度，可以预测未来人口的增长趋势，并为城市规划和政策制定提供参考。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

i 个被评价对象可描述为
xi={xi1，xi2，… ，xip} ， 3.1 确定参考序列
i＝1 ，2 ，… ，n
根据各评价指标的经济含义，在 n 个被评价对象中选出各项指标
的最优值组成参考序列 x0 x0={x01，x02，… ，x0p} 实际上，参考序列 x0 构成了一个相对理想化的最优样本，是综合
x11 x12 … x1n
{x1(t) ，x2(t) ，… ，xp(t)}＝
x21 …
x22 …
… …
x2n …
xp1 xp2 … xpn
上式中，n 为数列的数据长度，即数据的个数。
从几何角度看，关联程度实质上是参考数列与比较数列曲线形状
的相似程度。凡比较数列与参考数列的曲线形状接近，则两者间的关
处理。其方法包括初值化、均值化等。
2.1.1 初值化。即用同一数列的第一个数据去除后面的所有数据，得
到一个各个数据相对于第一个数据的倍数数列，即初值化数列。一般
地，初值化方法适用于较稳定的社会经济现象的无量纲化，因为这样
的数列多数呈稳定增长趋势，通过初值化处理，可使增长趋势更加明
显。比如，社会经济统计中常见的定基发展指数就属于初值化数列。
再分别计算其余 4 年的各绝对差。全部结果如表 3 所示。从中找
出最大值和最小值为：
Δmax＝0.1161
Δmin＝0.002
表 3 绝对差计算表
年份
Δ01(t)
Δ02(t)
Δ03(t
0.0632
2004
0.0061
0.0096
0.0102
2005
0.0781
0.0493
为此，要先计算各被评价对象序列与最优参考序列间的绝对差序
列。计算公式：
Δij= xij-1
i＝1 ，2 ，… ，n；j＝1 ，2 ，… ，p
在此基础上，依公式
Δ(max)= max 1≤i≤0
2 关联度的计算
灰色关联度分析的核心是计算关联度。一般说来，关联度的计算
首先要对原始数据进行处理，然后计算关联系数，由此就可计算出关
联度。
2.1 原始数据的处理
由于各因素各有不同的计量单位，因而原始数据存在量纲和数量
级上的差异，不同的量纲和数量级不便于比较，或者比较时难以得出
正确结论。因此，在计算关联度之前，通常要对原始数据进行无量纲化
显然，当参考数列的长度为 n 时，由 p 个比较数列共可计算出 n×
p 个关联系数。
2.3 求关联度
由于每个比较数列与参考数列的关联程度是通过 n 个关联系数
来反映的，关联信息分散，不便于从整体上进行比较。因此，有必要对
关联信息作集中处理。而求平均值便是一种信息集中的方式。即用比
较数列与参考数列各个时期的关联系数之平均值来定量反映这两个
2007
0.1810
0.2956
0.8382
第四步，计算关联度。利用表 4，分别求各个数列每个时期的关联
系数的平均值即得关联度：
r01=
1 5
(0.4414+0.8596+0.2489+0.9994+0.1810)=0.5460
r02=
1 5
(0.6008+0.7673+0.3478+0.5588+0.2956)=0.5141
= 0.02522 Δ0i(t)+0.02322
当 t＝2003 时
ζ01(2003)=
0.02522 0.0339+0.02322
=0.4414
ζ02(2003)=
0.02522 0.0188+0.02322
=0.6008
ζ03(2003)=
0.02522 0.0632+0.02322
=0.2919
Δok(min)和 Δok(max)。对 p 个比较数列，又记 p 个 Δok(min)中的最小者为
Δ(min)，p 个 Δok(max)中的最大者为 Δ(max)。这样 Δ(min)和 Δ(max)分别
是所有 p 个比较数列在各期的绝对差值中的最小者和最大者。于是，
第 k 个比较数列与参考数列在 t 时期的关联程度(常称为关联系数)可
影响一个经济变量的因素很多。但由于客观事物很复杂，人们对事物
的认识有信息不完全性和不确定性，各个因素对经济总量的影响作用
不是一下子就能够看清楚的，需要进行深入的研究，这就是经济变量
的因素分析。运用灰色关联度进行因素分析是非常有效的，而且特别
适用于各个影响因素和总量之间不存在严格数学关系的情况。
例 1：利用关联度分析方法研究某公路施工企业工资序列（表 1）。
联度较大；反之，如果曲线形状相差较大，则两者间的关联度较小。因
此，可用曲线间的差值大小作为关联度的衡量标准。
将第 k 个比较数列(k＝1，2，…，p)各期的数值与参考数列对应期的
差值的绝对值记为：
Δok(t)= x0(t)-xk(t)
t＝1 ，2 ，… ，n
对于第 k 个比较数列，分别记 n 个 Δok(t)中的最小数和最大数为
工资总额的影响属于同一水平。
3 用灰色关联度分析方法进行综合评价的方法步骤
灰色关联度分析法的应用之二，就是用来进行综合评价。基本思
路是，从样本中确定一个理想化的最优样本，以此为参考数列，通过计
算各样本序列与该参考序列的关联度，对被评价对象做出综合比较和
排序。
设有 n 个被评价对象，每个被评价对象有 p 个评价指标。这样，第
5797.5
2007
24020.3
5744.0
11575.2
6701.0
x軃i
18372.3
4821.7
8450.0
5098.6
根据表 1 中数据，以工资总额为参考数列 x0(t)，以计时工资 x1(t)、档案工资 x2(t)和承包工资 x3(t)为比较数列，计算三种工资对于工资总额的关联度。
通过下式计算：
ζok(t)=
Δ(min)+ρΔ(max) Δok(t)+ρΔ(max)
式中 ρ 为分辩系数，用来削弱 Δ(max)过大而使关联系数失真的影
响。人为引入这个系数是为了提高关联系数之间的差异显著性。 0＜ρ＜
1。
可见，关联系数反映了两个数列在某一时期的紧密程度。例如，在
使 Δok(t)＝Δ(min)的时期，ζok(t)＝1，关联系数最大；而在使 Δok(t)＝Δ(max)的时期，关联系数最小。由此可知，关联系数变化范围为 0＜ζok(t)≤1。
用同样方法分别计算其余 4 年的各个关联系数，计算结果见表
4。
表 4 关联系数计算表
年份
ζ01(t)
ζ02(t)
ζ03(t)
2003
0.4414
0.6008
0.2919
2004
0.8596
0.7673
0.7546
2005
0.2489
0.3478
0.8115
2006
0.9994
0.5588
0.4104
数列的关联程度，其计算公式为：
n
Σ rok=
1 n
ζok(t)
i=1
式中，rok 为第 k 个比较数列与参考数列的关联度。不难看出，关联度与比较数列、参考数列及其长度有关。而且，原
始数据的无量纲化方法和分辩系数的选取不同，关联度也会有变化。
2.4 排关联度
由上述分析可见，关联度只是因素间关联性比较的量度，只能衡
1.1913
1.3695
1.3143
第二步，计算各比较数列同参考数列在同一时期的绝对差。
当 t＝2003 时，
Δ01(2003)＝|0.7606-0.7945|＝0.0339
Δ02(2003)＝|0.7606-0.7794|＝0.0188
Δ03(2003)＝|0.7606-0.6974|＝0.0632
【关键词】灰色关联度；分析方法；综合评价；应用
1 关联度的概念
关联度是事物之间、因素之间关联性大小的量度。它定量地描述了事物或因素之间相互变化的情况，即变化的大小、方向与速度等的相对性。如果事物或因素变化的态势基本一致，则可以认为它们之间的关联度较大，反之，关联度较小。对事物或因素之间的这种关联关系，虽然用回归、相关等统计分析方法也可以做出一定程度的回答，但往往要求数据量较大、数据的分布特征也要求比较明显。而且对于多因素非典型分布特征的现象，回归相关分析的难度常常很大。相对来说，灰色关联度分析所需数据较少，对数据的要求较低，原理简单，易于理解和掌握，对上述不足有所克服和弥补。
表 1 某公路施工企业工资序列表单位：千元
年份
工资总额
计时工资
档案工资
承包工资
2003
13974.2
3831.0
6587.2
3556.0
2004
15997.6
4228.0
7278.0
4491.6
2005
17681.3
5017.0
7717.4
4946.9
2006
20188.3
5288.6
9102.2
r03=
1 5
(0.2919+0.7546+0.8115+0.4104+0.8382)=0.6213
第五步，排关联序
由关联度数值可看出，r03＞r01＞r02。这表明，三种工资对工资总额的关联程度的排列顺序为：承包工资、计时工资、档案工资。即该公路施