大学理论力学 平面图形上各点的加速度分析
理论力学(大学)课件17.1 求平面图形各点加速度的基点法

主要内容
1、基点法求平面图形各点加速度
2、基点法求加速度的应用
1、基点法求平面图形各点加速度
基点法求平面图形内各点加速度
平面图形内任一点的加速度等于基点的加速度与该点随图形绕基点转动的切向加速度和法向加速度的矢量和。
基点 :A 平移坐标系: ''Ax y t BA a AB
a BA ⋅=αt 大小 方向垂直于 ,指向同 AB α
大小 方向由 指向
n BA a n 2BA a AB
ω=⋅B A n r t r e a a a a B ++=n
t BA
BA A B a a a a ++=为什么没有科氏加速度
基点法求平面图形各点加速度
A a t BA a n
BA
a 动点:B 动系: ''Ax y 绝对运动:待求 牵连运动:随同A 点平移 相对运动:B 绕A 的转动。
理论力学06_4刚体平面运动_加速度

§6.3* 平面运动刚体上点的加速度由于平面运动可以看成是随同基点的牵连平移与绕基点的相对转动的合成运动,于是图形上任一点的加速度可以由加速度合成定理求出。
设已知某瞬时图形内A 点的加速度a A ,图形的角速度为ω,角加速度为α,如图6-13所示。
以A 点为基点,分析图形上任意一点B 的加速度a B 。
因为牵连运动为动坐标系随同基点的平移,故牵连加速度a e =a A 。
相对运动是点B 绕基点A 的转动,故相对加速度a r =a BA ,其中a BA 是点B 绕基点A 的转动加速度。
由式 (5.3.7)可得图6-13 加速度分析的基点法 α (6.3.1) BA A B αα+=由于B 点绕基点A 转动的加速度包括切向加速度和法向加速度a ,故式(6.3.1)可写为t BA a n BAa (6.3.2) n t BA BA A B a a a ++=即平面图形上任意一点的加速度,等于基点的加速度与该点绕基点转动的切向加速度和法向加速度的矢量和。
当基点A 和所求点B 均作曲线运动时,它们的加速度也应分解为切向加速度和法向加速度的矢量和,因此,式(6.3.2)可表示为(6.3.3)n t n t n t BA BA A A B B a a a a a a +++=+在式(6.3.3)中,相对切向加速度与点A 和B 连线方向垂直,相对法向加速度沿点A 和B连线方向从B 指向A ;仅当点A 和B 的运动轨迹已知时,才可以确定点A 和B 的切向加速度a 和及法向加速度和a 。
t BA a n BA a t A t B a n A a n B 在应用式(6.3.2)或(6.3.3)计算平面图形上各点的加速度时,只能求解矢量表达式中的两个要素。
因此在解题时,要注意分析所求问题是否可解。
当问题可解时,将式(6.3.2)或(6.3.3)在平面直角坐标系上投影,即可由两个代数方程联立求得所需的未知量。
例6.3-2:半径为R 的车轮沿直线滚动,某瞬时轮心O 点的速度为v O ,加速度为a O ,如图a 所示。
理论力学答案第5章点的复合运动分析
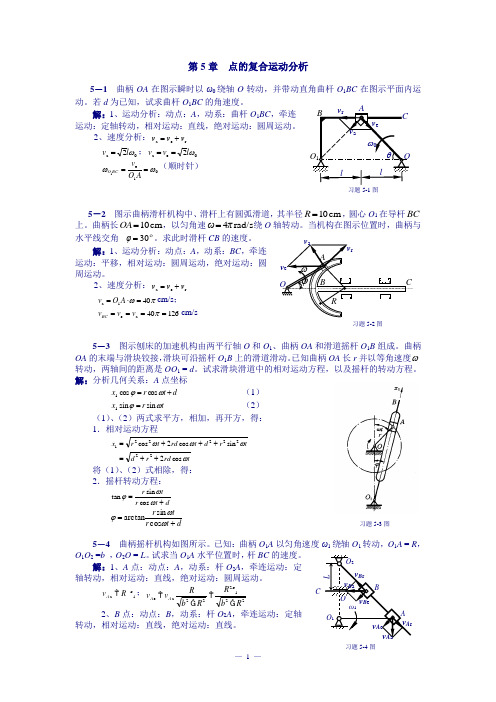
第5章 点的复合运动分析5-1 曲柄OA 在图示瞬时以ω0绕轴O 转动,并带动直角曲杆O 1BC 在图示平面内运动。
若d 为已知,试求曲杆O 1BC 的角速度。
解:1、运动分析:动点:A ,动系:曲杆O 1BC ,牵连运动:定轴转动,相对运动:直线,绝对运动:圆周运动。
2、速度分析:r e a v v v += 0a 2ωl v =;0e a 2ωl v v == 01e 1ωω==AO v BC O (顺时针)5-2 图示曲柄滑杆机构中、滑杆上有圆弧滑道,其半径cm 10=R ,圆心O 1在导杆BC 上。
曲柄长cm 10=OA ,以匀角速rad/s 4πω=绕O 轴转动。
当机构在图示位置时,曲柄与水平线交角 30=φ。
求此时滑杆CB 的速度。
解:1、运动分析:动点:A ,动系:BC ,牵连运动:平移,相对运动:圆周运动,绝对运动:圆周运动。
2、速度分析:r e a v v v +=πω401a =⋅=A O v cm/s ; 12640a e ====πv v v BC cm/s5-3 图示刨床的加速机构由两平行轴O 和O 1、曲柄OA 和滑道摇杆O 1B 组成。
曲柄OA 的末端与滑块铰接,滑块可沿摇杆O 1B 上的滑道滑动。
已知曲柄OA 长r 并以等角速度ω转动,两轴间的距离是OO 1 = d 。
试求滑块滑道中的相对运动方程,以及摇杆的转动方程。
解:分析几何关系:A 点坐标 d t r x +=ωϕcos cos 1 (1) t r x ωϕsin sin 1= (2) (1)、(2)两式求平方,相加,再开方,得: 1.相对运动方程trd r d t r d t rd t r x ωωωωcos 2sin cos 2cos 22222221++=+++=将(1)、(2)式相除,得: 2.摇杆转动方程: dt r tr +=ωωϕcos sin tandt r t r +=ωωϕcos sin arctan5-4 曲柄摇杆机构如图所示。
理论力学10刚体的平面运动

vB = v A + vBA
a a ? a
VB VBA
大小 ? 方向 a
B VA
v B = v A ctg φ且 v BA
vA = sin φ
v BA = AB ⋅ ω AB v BA vA ∴ω = = l l sin φ
φ VA
ω A x
14
[例2] 图示机构 端以速度 A沿X轴负向运动,AB=l; 例 图示机构A端以速度 端以速度V 轴负向运动, 轴负向运动 求B端的速度? 端的速度? 端的速度 解:1)分析AB;2)分析A,B两点的速度 在AB直线上的投影相等,可以得到: y B
行移动 刚体简单运动 平行移动 定轴转动 定轴转动 刚体复杂运动 刚体的平面运动
平动 合成? 合成? 转动
刚体平面运动的分解 本章分析 平面运动刚体的角速度 平面运动刚体各点的速度 平面运动刚体各点的速度
1
第十章 刚体的平面运动
§10–1 刚体平面运动的概述 §10–2 平面运动分解为平动和转动 · 刚体的平面运动方程 §10–3 平面图形内各点的速度· 速度投影定理 速度瞬心 §10–4 平面图形内各点的加速度 · 加速度瞬心的概念
20
5.几种确定速度瞬心位置的方法 ①已知图形上一点的速度v A 和图形角速度ω, 可以确定速度瞬心的位置.(P点)
AP = vA , AP⊥v A ,且P在v A 顺ω转向绕A点 ω
转90º的方向一侧. ②已知一平面图形在固定面上作无滑动的滚 动, 则图形与固定面的接触点P为速度瞬 心.
21
③已知某瞬间平面图形上A,B两点速度 v A ,v B 的方向,且 v A 不平行 v B 。 过A , B两点分别作速度 v A ,v B的垂线,交点 P即为该瞬间的速度瞬心。 ④ 已知某瞬时图形上A ,B两点速度 v A , v B 大小,且 v A ⊥AB, vB ⊥AB v A − vB (a) v A 与vB 同向, ω = AB v A + vB (b) v A 与vB 反向, ω = AB 注意:交点可能在刚体的外部) (注意:交点转动· 刚体的平面运动方程
理论力学——运动学

v2
n
加速度a的大小:
a
aτ + a n
2
2
dv 2 v 2 2 ( ) ( ) dt
加速度和主法线所夹的锐角的正切:
tan
aτ an
4、直角坐标于自然坐标之间的关系:
ds 2 dx 2 dy 2 dz 2 v ( ) ( ) ( ) ( ) dt dt dt dt
2
2
九、刚体的基本运动
1、刚体的平动
(1)刚体平动的定义 刚体运动时,若其上任一直线始终保持与它的初始
位置平行,则称刚体作平行移动,简称为平动或移动 。 (2) 平动刚体的运动特点
刚体平动时,其上各点的轨迹形状相同;同一瞬时,
各点的速度相同,加速度也相同。
刚体平动判别:P169题三图,P176题五图,题七图
点加的速度
i + y j + z k vx
a vx i + v y j + vz k xi + yj + zk
ax v x x ay v y y az v z z
3、自然法
用自然法描述的运动方程:
s பைடு நூலகம் f (t )
a 2 a x a y a z a an
1
2
2
2
2
2
a 2 a v2
2
5、匀速、匀变速公式
(1)
aτ=常数,
v v0 aτ t
( 2)v=常数,
1 2 s s0 v0t aτ t 2 2 v 2 v0 2a ( s s0 )
平面运动。
理论力学重难点及相应题解

运动学部分:一、点的运动学重点难点分析1.重点:点的运动的基本概念(速度与加速度,切向加速度和法向加速度的物理意义等);选择坐标系,建立运动方程,求速度、加速度。
求点的运动轨迹。
2.难点:运动方程的建立。
解题指导:1.第一类问题(求导):建立运动方程然后求导。
若已知点的运动轨迹,且方程易于写出时,一般用自然法,否则用直角坐标法。
根据点的运动性质选取相应的坐标系,对于自然法要确定坐标原点和正向。
不管用哪种方法,注意将点置于一般位置,而不能置于特殊位置。
根据运动条件和几何关系把点的坐标表示为与时间有关的几何参数的函数,即可得点的运动方程。
2.第二类问题(积分):由加速度和初始条件求运动方程,即积分并确定积分常数。
二、刚体的简单运动重点难点分析:1.重点:刚体平移、定轴转动基本概念;刚体运动方程,刚体上任一点的速度和加速度。
2.难点:曲线平移。
解题指导:首先正确判断刚体运动的性质。
其后的分析与点的运动分析一样分两类问题进行。
建立刚体运动方程时,应将刚体置于一般位置。
三、点的合成运动(重要)重点难点分析:1.重点:动点和动系的选择;三种运动的分析。
速度合成与加速度合成定理的运用。
2.难点:动点和动系的选择。
解题指导:1.动点的选择、动系的确定和三种运动的分析常常是同时进行的,不可能按顺序完全分开。
2.常见的运动学问题中动点和动系的选择大致可分以下五类:(1)两个(或多个)不坟大小的物体独立运动,(如飞机、海上的船舶等)对该类问题,可根据情况任选一个物体为动点,而将动系建立在另一个物体上。
由于不考虑物体的大小,因此动系(刚体)与物体(点)只在一个点上连接,可视为铰接,建立的是平移动坐标系。
(2)一个小物体(点)相对一个大物体(刚体)运动,此时选小物体为动点,动系建立在大物体上。
(3)两个物体通过接触而产生运动关系。
其中一个物体的接触只发生在一个点上,而另一个物体的接触只发生在一条线上。
选动点为前一物体的接触点,动系则建立在后一物体上。
瞬心法求平面图形内各点加速度的研究

瞬心法求平面图形内各点加速度的研究田长军(陇南市武都八一中学, 甘肃陇南 746000)摘要:本文说明了加速度瞬心难以确定的依据,给出了在三种特殊情况下确定刚体平面运动加速度瞬心的方法,以实例说明加速度瞬心在运动学以及动力学中的应用,可使一些问题求解大为简化。
并给出用瞬心法求平面图形内各点加速度的步骤。
关键词:加速度;瞬心法;基点法The research of counting all the spot s’ acceleration in plane graph bymethods of instantaneous centerTIAN Chang-jun ,LUO Yue-e(College of Physics and Electronic Engineering, Long-Dong University, QingYang 745000, Gansu)Abstract: The reason why acceleration instantaneous center was difficult to determine has been illustrated. And the methods of determining acceleration instantaneous center of rigid body planar motion have been given for the three special conditions.There are some examples found to note application of the acceleration instantaneous center in the kinematics and dynamics.We also show the steps of sloving acceleration for various points within the plane graphics .Key words: acceleration; methods of instantaneous center; methods of basis points0 引言大多数理论力学教科书[1,2]和参考书中都有用基点法和瞬心法求平面图形内各点的速度以及基点法求平面图形内各点的加速度的例子,却没有用瞬心法求平面图形内各点的加速度的例子,而且都没有阐述平面运动刚体的加速度瞬心。
08-理论力学-第二部分运动学第八章刚体的平面运动

形S在该瞬时的位置也就确定了。
88
运动学/刚体的平面运动
四、平面运动的分解 ——平移和转动
当图形S上A点不动时,则
刚体作定轴转动 。
当图形S上 角不变时,
则刚体作平移。
故刚体平面运动可以看成是 平移和转动的合成运动。
例如:车轮的平面运动可以看成: 车轮随同车厢的平移 和相对车厢的转动的合成。
99
2121
如图示平面图形,某瞬时速度瞬心为P点, 该瞬时平面图形内任一点B速度大小
vB vP vBP vBP
B
大小:vB BP
方向:BP,指向与 转向相一致。
vB
S
vA
C
vC
同理:vA=ω·AP, vC=ω·CP
由此可见,只要已知图形在某一瞬时的速度瞬心 位置和角速度 ,就可求出该瞬时图形上各点的速度。
的平面Ⅱ内的运动。
66
运动学/刚体的平面运动
二、平面运动的简化 刚体的平面运动可以简化为
平面图形S在其自身平面内的运动。 即在研究平面运动时,不需考虑 刚体的形状和尺寸,只需研究平 面图形的运动,确定平面图形上 各点的速度和加速度。
三、平面运动方程 为了确定代表平面运动刚体的
平面图形的位置,我们只需确定平 面图形内任意一条线段的位置。
vBA
s
B
vB vA
A
vA
方向: AB, 指向与 转向一致。
即:平面图形上任一点的速度等于基点的速度与该点随
平面图形绕基点转动的速度的矢量和。 ——基点法
基点法是求解平面图形内一点速度的基本方法。 1414
运动学/刚体的平面运动
二、速度投影法
由于A, B点是任意的,因此
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
aB
a
n BE
cos45
A ar 由于滑块可沿杆OA滑动,因此 vr 应利用点的合成运动方法求杆OA的 vB aB a e 角速度及角加速度。 ve B ac n 以滑块B为动点。 动系与OA杆固结。 ae 45 va ve vr l
vr 0 ve va vB v
2 2
a 2 a 1 2 1 cot
2
即 a 1 a 2 并由此看出 , AB 作瞬时平动时
aA aB
[例3] 曲柄滚轮机构,滚子半径R=OA=15cm, n=60 rpm,作纯滚 动。 求:当 =60º (OAAB),滚轮的B,aB. 时
分析: 要想求出滚轮的B, aB 先要求出vB, aB
解:轮O作平面运动,P为速度瞬心,
v O / R
(
)
由于
n 以O为基点, P a O a PO a PO a
v O / R 在任何瞬时都成立,且O点作直线运动,故而 d 1 d vO aO a ( ) dt R dt R
2
n a PO R 2 R (
而 1 v A / O1 A ,
(b)
2 vB / O2 B ;
n n aA aB
式中
O1 A O 2 B
τ τ aA aB
1 2
aA aB
a 2 aB / O2 B ;
a 1 a A / O1 A ,
a1 a 2
(b) AB杆作平面运动, 图示瞬时AB杆作瞬时平动, 即 v A vB AB 0
解:OA杆作定轴转动,AB杆和轮B作平面运动
研究AB杆:
n / 30 60 / 30 2 rad/s
v A OA 15 2 30 cm/s
P1
AB
P1为其速度瞬心
AB
vA
2 v A / AP 1 30 / 3 15 rad/s 3
ae aA ;
n a r a BA a BA a BA
aa aB ;
于是,由牵连平动时加速度合成定理 a a a e a r 可得如下公式:
n aB aA aBA aBA
a BA
n aB a A aBA aBA
aBA
aB
a
n BA
其中: a BA
a B aB / BP2 131 . 5 / 15 8 . 77 rad/s
2
[例4] 曲柄-滑块机构,OA=r,AB=l,曲柄以等角速度 0绕 O轴旋转。求:图示瞬时,滑块B的加速度aB和连杆AB的角 加速度a AB
A
90o
0
O
30o
B
vA
A
90o
解: 1、确定连杆的角速度:
0
vB
3 cm/s
v B BP1 AB 2 3 15
2 3
20
取A为基点,
a A OA 2 15 ( 2 ) 2 60 2 cm/s
n a B a A a BA a BA
2
a
n BA
AB AB
2
3 15 (
O
AB
vA
30o
以A为基点,
vB
B
vBA
v A r 0 ,
v AB v A tan30 r0 tan30
v AB l r l
AB
0 tan30
0
3
A
90o
0
aA AB O
a
an
30o
BA
3 2、加速度分析
AB
0
BA
aB aA
根据加速度合成定理
时图形上任意两点的加速度在这两点连线上的投影相等.
(3)由于加速度瞬心的位置不象速度瞬心那样容易确定,故
常采用基点法求图形上各点的加速度或图形的角加速度. [例1] 半径为R的车轮沿直线作纯滚动, 已知轮心O点的速度 v O 及加速度 a O ,求车轮与轨道接触点P的加速度.
n a P a O a PO a PO 分析: √ Ra R 2 大小:? √ √ √ 方向: ?
杆OA的角加速度为: a OA a e 2 v 2
OB l
(1)一般情况下,加速度瞬心与速度瞬心不是同一个点. (2)一般情况下,对于加速度没有类似于速度投影定理的关
系式. 即一般情况下,图形上任意两点A, B的加速度
( a A ) AB ( a B ) AB
若某瞬时图形 =0, 即瞬时平动, 则有 ( a A ) AB ( a B ) AB 即:若平面图形在运动过程中某瞬时的角速度等于零,则该瞬
AB
a ,方向AB,指向与a 一致;
aA
n a BA AB 2,方向沿AB,指向A点。
即平面图形内任一点的加速度等于基点的加速度与该点随图形绕
基点转动的切向加速度和法向加速度的矢量和。这种求解加速度
的方法称为基点法,也称为合成法。是求解平面图形内一点加速 度的基本方法。 上述公式是一平面矢量方程。需知其中六个要素,方能求
n n ( a B ) AB ( a B ) AB ( a A ) AB ( a A ) AB 即 ( a A ) AB ( a B ) AB
O 2 B 2 cos O 2 B a 2 sin O1 A 1 cos O1 A a 1 s in
OA
ve OB v l
D
aOA
O l
所以,OA杆的角速度为:
OA
v E
加速度分析 a a a en a e a r a c 式中: a a a B a c 2 OA v r 0 将上式投影到BD轴上
aa ae
2
ae aB
2v 2 l
7.3 平面图形上各点的加速度分析
一. 基点法 (合成法) 已知:图形S 内一点A 的加速度a A 和图形 aBA 的 , a(某一瞬时)。 aB aBA 求: 该瞬时图形上任一点B的加速度。 aA 取A为基点,将平动坐标系固结于A点 n aBA 取B动点,则B点的运动分解为相对运动 为圆周运动和牵连运动为平动.
τ n 出其余两个。由于 a BA , a BA 方位总是已知,所以在使用该公式
中,只要再知道四个要素,即可解出问题的待求量。
二.加速度瞬心. τ n 由于 a BA , a BA 的大小和方向随B点的不同而不同,所以总可以 在图形内找到一点Q,在此瞬时,相对加速度 a QA 大小恰与基点 A的加速度 a A等值反向,其绝对加速度 a Q 0 Q点就称为图形在该瞬时的加速度瞬心.等于零,即它不是加速度
瞬心.当车轮沿固定的直线轨道作纯滚动时,其速度瞬心P的加
速度指向轮心.
[例2] 已知O1A=O2B, 图示瞬时 O1A/O2B 试问(a),(b)两种情况下1和 2,a1和a2是否相等?
n aA
vA aA
n aB
a vB
B
(a) 解:(a) AB杆作平动, v A v B ,
2
n aA
vA
a A
n aB
1 v A / O1 A v B / O 2 B
a BA a B
对AB杆,以A为基点求B点的加速度
n n n a B a B a A a A a BA a BA
vB (b)
n aA
a A
n 式中 a BA 0 将上式投影到AB轴上,有:
45
a BE
aB
n aBE
D
v B BE l v
以E为基点,求滑块B的加速度aB
n a B a E a BE a BE
l
BE
v E l
aE 0
n 2 a BE BE BE
2v 2 l
OA
2v l
2
将上式投影到BE轴上:
a B cos45 a
B
A点的加速度
a A r 0
2
以A为基点,求B点的加速度:
aB a A aBA aBA + + n
2
a BA a AB l
a BA AB AB
n
2 l 0
l 0 9
2
将加速度合成定理中各项向AB方向投影
a B cos 30 = a
n AB
,
9
aB
2 3 27
2 a r0 BA
3 27
2 0
2 l0 (r
3 27
2 l )0
a AB
(
3 3
-
3 27
)
8 3 27
0
2
[例5]图示平面机构,滑块B可沿杆AB滑动,杆BE与BD分别与滑 块B铰接,BD杆可沿水平导轨运动。滑块E以匀速v沿铅直导轨 向上运动,杆BE长为 2 l ;图示瞬时杆OA铅直,且与杆BE夹角 为 45 。求该瞬时杆OA的角速度与角加速度。 解: BE杆作平面运动, 先求滑块B的速度和加速度。 BE杆的速度瞬心为O点 BE v l A vB B
vO R
)2
vO R
y
a
a O P
n aP O
a PO R a a O ,
aO
2 vo
x
n 将 a P a O a PO a PO 分别投影到x、y轴上,有:
